僇儗儞僟乕丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂 丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽傛偍偡偗乿偝傫偐傜偺弌戣偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮椷榓俆擭俁寧俁侽擔晅偗乯
丂師偼丄俀侽俀俁擭俁寧偺僇儗儞僟乕偱偁傞丅
丂丂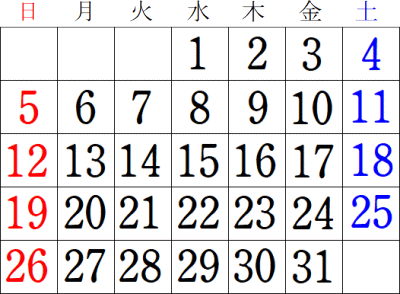
丂丂#擔晅傪僋儕僢僋偡傞偲栤戣傪尒傞偙偲偑弌棃傑偡丅乮仼倣倎倫懏惈傪愝掕乯
丂擔晅偑摎偊偵側傞傛偆偵嶌栤偣傛丅乮仺丂嶲峫丗乽悢妛僇儗儞僟乕乿乯
乮摎乯丂埲壓偼丄嶌栤偺堦椺偱偡丅
侾丒丒丒仜侾/俀亄侾/俁亄侾/俇偺抣
丂丂幚嵺偵丄侾/俀亄侾/俁亄侾/俇亖乮俁亄俀亄侾乯/俇亖侾
丂丂丂 仜40俠20 傪 41 偱妱偭偨梋傝
丂丂幚嵺偵丄40俠20亖係侽丒俁俋丒丒丒丒丒俀俀丒俀侾/乮俀侽丒侾俋丒丒丒丒丒俁丒俀丒侾乯丂偵偍偄偰丄
丂丂乮暘巕乯佭俀侽丒侾俋丒丒丒丒丒俁丒俀丒侾丂乮倣倧倓丂係侾乯丂側偺偱丄40俠20佭侾丂乮倣倧倓丂係侾乯
丂丂丂 仜 侽両 偺抣
丂丂幚嵺偵丄値俹倰亖値両/乮値亅倰乯両偵偍偄偰丄値亖倰 偲偡傞偲丄値両亖値両/侽両 傛傝丄侽両亖侾
丂丂丂 仜倸3亖侾 偺偲偒偺 侾/乮侾亅倸乯亄侾/乮侾亅倸2乯 偺抣
丂丂幚嵺偵丄梌幃亖侾/乮侾亅倸乯亄倸/乮倸亅侾乯亖 乮侾亅倸乯/乮侾亅倸乯亖侾
丂丂丂 仜侾曈偺挿偝偑俀偺惓曽宍偑俀偮偁傝丄壓恾偺傛偆偵丄侾偮偺惓曽宍偺捀揰偑懠偺惓
丂丂丂丂曽宍偺拞怱偵廳側偭偰抲偐傟偰偄傞丅偙偺偲偒偺廳側偭偰偄傞晹暘偺柺愊
丂丂丂丂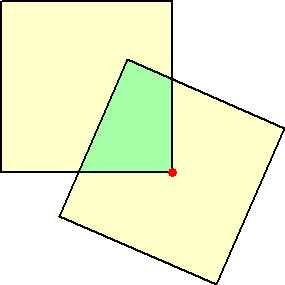
| 丂丂幚嵺偵丄 |
| 丂 |
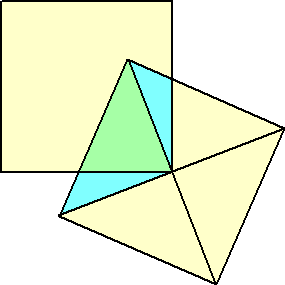 |
丂丂嵍恾偺傛偆偵峫偊傞偲丄悈怓偺晹暘偺柺
丂愊偑摍偟偄偺偱丄媮傔傞柺愊偼丄惓曽宍
丂偺柺愊偺巐暘偺堦偵摍偟偄丅
丂丂傛偭偰丄媮傔傞柺愊偼丄
丂丂俀亊俀亐係亖侾 |
丂丂丂 仜惣楋俀侽俀俁擭乮椷榓俆擭乯偵場傫偩栤戣丅侾偐傜俀侽俀俁傑偱偺惍悢偱嵟傕懡偔巊傢傟
丂丂丂丂偰偄傞悢帤
丂丂幚嵺偵丄侽乣俋偺昿搙傪寁嶼偡傞偲丄
| 丂 |
| 侽 |
侾 |
俀 |
俁 |
係 |
俆 |
俇 |
俈 |
俉 |
俋 |
| 俆俀俇 |
侾俇侾俁 |
俇俁侾 |
俇侽俁 |
俇侽俀 |
俇侽俀 |
俇侽俀 |
俇侽俀 |
俇侽俀 |
俇侽俀 |
|
丂丂忋昞偐傜丄嵟傕懡偔巊傢傟偰偄傞悢帤偼丄侾
丂丂丂 仜嬌尷抣丂limx仺0 {sin(tanx)}/(ex-1)
丂丂幚嵺偵丄sin(tanx)/(ex-1)={sin(tanx)/tanx}亊{(tanx)/x}亊{x/(ex-1)}丂偲曄宍偟丄
丂丂丂limx仺0 {sin(tanx)}/tanx=1丄limx仺0 (tanx)/x=1丄limx仺0 x/(ex-1)=1 傛傝丄乮梌幃乯=1
丂丂乮暿夝乯丂儘僺僞儖偺掕棟傪梡偄偰丄(梌幃)=limx仺0 cos(tanx)丒{1/cos2x}/ex=1
俀丒丒丒仜嬼悢偺慺悢
丂丂幚嵺偵丄慺悢 俀丄俁丄俆丄丒丒丒丂偺拞偱丄嬼悢偼俀偺傒偱偁傞丅
丂丂丂 仜楢庫宍 乮倶2亄倷2乯2亖俀乮倶2亅倷2乯偺埻傓柺愊
丂丂幚嵺偵丄寁嶼偡傞偲丄俀偲側傞丅
丂丂丂 仜愒媴俀屄丄惵媴俀屄傪墌宍偵暲傋傞応崌偺悢
丂丂幚嵺偵丄愒媴俀屄傪墌宍偵暲傋傞曽朄偺悢偼丄侾捠傝丅偦偺寗娫偵惵媴俀屄傪擖傟傞曽
丂丂朄偺悢偼丄俀捠傝丅傛偭偰丄媮傔傞応崌偺悢偼丄侾亊俀亖俀乮捠傝乯
丂丂丂 仜佺0兾倱倝値 倶 倓倶 偺抣
丂丂幚嵺偵丄梌幃亖[亅們倧倱 倶 ]0兾亖亅乮亅侾乯亅乮亅侾乯亖俀
丂丂丂 仜倸5亖侾 偺偲偒偺 侾/乮侾亅倸乯亄侾/乮侾亅倸2乯亄侾/乮侾亅倸3乯亄侾/乮侾亅倸4乯 偺抣
丂丂幚嵺偵丄
丂丂丂梌幃亖侾/乮侾亅倸乯亄侾/乮侾亅倸2乯亄倸2/乮倸2亅侾乯亄倸/乮倸亅侾乯
丂丂丂丂亖侾/乮侾亅倸乯亄倸/乮倸亅侾乯亄侾/乮侾亅倸2乯亄倸2/乮倸2亅侾乯
丂丂丂丂亖乮侾亅倸乯/乮侾亅倸乯亄乮侾亅倸2乯/乮侾亅倸2乯亖俀
丂丂丂 仜俁偮偺嶮俙丄俛丄俠偺偦傟偧傟偵愇偑俀屄丄俁屄丄係屄偺寁俋屄偑偺偭偰偄傞丅
丂丂丂丂
丂丂丂丂峛丄壋偺俀恖偑岎屳偵嶮偺忋偺愇傪庢傞丅偨偩偟丄侾夞枅偵偳傟偐侾偮偺嶮偐傜侾屄
丂丂丂丂埲忋偺愇傪庢傞傕偺偲偡傞丅嵟屻偵愇傪庢偭偨幰偑晧偗偲偡傞丅
丂丂丂丂崱丄峛偑俙偺嶮偐傜愇傪侾屄庢偭偨丅師偵丄壋偑愇傪庢傞偲偒丄昁偢彑偮偨傔偵偼丄偳
丂丂丂丂偺嶮偐傜壗屄偲傟偽傛偄偐丅
丂丂幚嵺偵丄壋偑俠偺嶮偐傜俀屄庢傟偽丄巆傝偼丄丂俙丗侾屄丂丄俛丗俁屄丂丄俠丗俀屄
丂丂師偵丄峛偑俙偐傜侾屄庢傟偽丄壋偼丄俛偐傜侾屄偲傟偽丄壋偑昁彑
丂丂乮峛偑丄俀屄丄俀屄偐傜丄俀屄偲傟偽丄壋偼侾屄庢傞丅峛偑丄俀屄丄俀屄偐傜丄侾屄偲傟偽丄壋
丂丂偼俀屄庢傞丅乯
丂丂丂峛偑丂俛偐傜侾屄庢傟偽丄壋偼丄俙偐傜侾屄偲傟偽丄壋偑昁彑
丂丂丂峛偑丂俛偐傜俀屄庢傟偽丄壋偼丄俠偐傜侾屄偲傟偽丄壋偑昁彑
丂丂丂峛偑丂俛偐傜俁屄庢傟偽丄壋偼丄俠偐傜俀屄偲傟偽丄壋偑昁彑
丂丂丂峛偑丂俠偐傜侾屄庢傟偽丄壋偼丄俛偐傜俀屄偲傟偽丄壋偑昁彑
丂丂丂峛偑丂俠偐傜俀屄庢傟偽丄壋偼丄俛偐傜俁屄偲傟偽丄壋偑昁彑
丂丂埲忋偐傜丄壋偑俠偺嶮偐傜俀屄庢傟偽昁偢彑偰傞丅
丂丂丂 仜師偺捈妏嶰妏宍偺柺愊
丂丂丂
丂丂幚嵺偵丄壓恾偵偍偄偰丄丂乮係亊俀亐俀乯亐俀亖俀
丂丂丂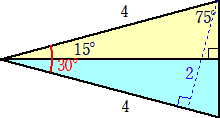
丂丂丂乮暿夝乯丂柺愊亖乮侾/俀乯乮係cos侾俆亱乯乮係倱倝値侾俆亱乯亖係倱倝値俁侽亱亖俀
丂丂丂 仜抝係恖偱俀擔偐偐傝丄彈俇恖偩偲係擔偐偐傞巇帠偑偁傞丅偙偺巇帠傪抝俀恖丄彈俁恖偩
丂丂丂丂偲壗擔偐偐傞偐丠
丂丂幚嵺偵丄抝侾恖偺侾擔偺巇帠検偼丄侾/俉丄彈侾恖偺侾擔偺巇帠検偼丄侾/俀係
丂丂抝俁恖丄彈俁恖偺侾擔偺巇帠検偼丄俁/俉亄俁/俀係亖侾/俀偲側傞丅傛偭偰丄俀擔偐偐傞丅
丂丂丂 仜偁傞巇帠傪惉偟悑偘傞偺偵丄俙偼俇擔丄俛偼俋擔丄俠偼侾俀擔偐偐傞偲偄偆丅偦偺巇帠傪丄
丂丂丂丂俙偲俛偑椡傪崌傢偣偰俁擔娫傗傝丄巆傝傪俠偵擟偣偨丅俠偼壗擔偱廔傢傞偐丅
丂丂幚嵺偵丄俙丄俛偺堦擔摉偨傝偺巇帠検偼丄侾/俇丄侾/俋側偺偱丄俀恖偺堦擔摉偨傝偺巇帠検
丂丂偼丄侾/俇亄侾/俋亖俆/侾俉丂偱丄俁擔娫偱丄俆/侾俉亊俁亖俆/俇丂偑廔傢偭偰偄傞丅
丂丂俠偺堦擔摉偨傝偺巇帠検偼丄侾/侾俀偱丄巆傝侾/俇傪廔偊傞偺偵丄侾/俇亐侾/侾俀亖俀乮擔乯偐
丂丂偐傞丅
丂丂丂 仜懱愊偑俁俀兾/俁偱偁傞偲偒偺媴偺敿宎
丂丂幚嵺偵丄係兾倰3/俁亖俁俀兾/俁丂傛傝丄倰3亖俉丂側偺偱丄倰亖俀
俁丒丒丒仜婏悢偺慺悢偺嵟彫抣
丂丂幚嵺偵丄慺悢 俀丄俁丄俆丄丒丒丒丂偺拞偱丄婏悢偺嵟彫抣偼俁偱偁傞丅
丂丂丂 仜捈曽懱俷俙俛俠-俢俤俥俧 偺俁曈偺挿偝偑俷俙亖 丄俷俠亖
丄俷俠亖 丄俷俢亖
丄俷俢亖 偺偲偒偺
偺偲偒偺
丂丂丂丂仮俙俠俢偺柺愊
丂丂幚嵺偵丄捈曽懱偺懱愊偼丅 丒
丒 丒
丒 亖俇丂側偺偱丄
亖俇丂側偺偱丄
丂丂巐柺懱俷-俙俠俢亖俇丒乮侾/俀乯丒乮侾/俁乯亖侾丂偲側傞丅俁揰俙丄俠丄俢傪捠傞暯柺偺曽掱幃偼丄
丂丂倶/ 亄倷/
亄倷/ 亄倸/
亄倸/ 亖侾丂偲彂偗傞偺偱丄朄慄儀僋僩儖偼丄乮侾/
亖侾丂偲彂偗傞偺偱丄朄慄儀僋僩儖偼丄乮侾/ 丆侾/
丆侾/ 丆侾/
丆侾/ 乯
乯
丂丂倲乮侾/ 丆侾/
丆侾/ 丆侾/
丆侾/ 乯偑暯柺忋偵偁傞偲偒丄乮侾/俇亄侾/俁亄侾/俀乯倲亖侾丂傛傝丄倲亖侾
乯偑暯柺忋偵偁傞偲偒丄乮侾/俇亄侾/俁亄侾/俀乯倲亖侾丂傛傝丄倲亖侾
丂丂傛偭偰丄巐柺懱俷-俙俠俢偺崅偝偼丄併乮侾/俇亄侾/俁亄侾/俀乯亖侾丂偲側傞丅
丂丂偟偨偑偭偰丄丂仮俙俠俢亊侾亊乮侾/俁乯亖侾丂傛傝丄丂仮俙俠俢亖俁
丂丂乮曗懌乯丂捈曽懱俷俙俛俠-俢俤俥俧 偺俁曈偺挿偝偑俷俙亖倎丄俷俠亖倐丄俷俢亖們 偺偲偒丄
丂丂丂丂仮俙俠俢偺柺愊亖乮侾/俀乯併乮倎2倐2亄倐2們2亄們2倎2乯
丂丂丂偲偄偆岞幃偑抦傜傟偰偄傞丅乮嬥戲戝妛乮侾俋俇俇乯偱弌戣偝傟偨偙偲偑偁傞丅乯
丂丂丂 仜壓恾偺墿怓偄晹暘偺柺愊
丂丂丂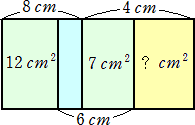
丂丂幚嵺偵丄挿曽宍偺廲偺挿偝傪 倶 們倣 偲偍偔偲丄丂俉倶亖侾俀亄俽丂丄俇倶亖俈亄俽丂側偺偱丄
丂丂丂俀倶亖俆丂偐傜丄倶亖俆/俀丂傛偭偰丄媮傔傞柺愊偼丄丂係亊乮俆/俀乯-俈亖俁乮們倣2乯
丂丂丂 仜倸3亖侾 丄倸亗侾 偺偲偒偺 乮侾亅倸乯乮侾亅倸2乯 偺抣
丂丂幚嵺偵丄倸2亄倸亄侾亖侽丂側偺偱丄
丂丂丂梌幃亖乮侾亅倸乯乮侾亅倸2乯亖侾亅倸亅倸2亄倸3亖俀-乮倸亄倸2乯亖俁
丂丂丂 仜仮ABC偺捀揰A丄B丄C傛傝懳曈偵壓傠偟偨悅慄偺懌傪偦傟偧傟D丄E丄F偲偡傞丅
丂丂丂丂傑偨丄仮ABC偺撪愙墌偺敿宎傪 倰 偲偡傞丅俀/AD亖侾/BE亄侾/CF 偺偲偒丄AD/倰 偺抣
丂丂幚嵺偵丄俛俠亖倎丄俠俙亖倐丄俙俛亖們丄乮倎亄倐亄們乯/俀亖倫丂偲偍偔偲丄
丂丂丂仮俙俛俠亖倫倰亖倎丒俙俢/俀亖倐丒俛俤/俀亖們丒俠俥/俀丂傛傝丄
丂丂丂俙俢亖俀倫倰/倎丂丄俛俤亖俀倫倰/倐丂丄俠俥亖俀倫倰/們
丂丂丂偙傟傜傪丄俀/AD亖侾/BE亄侾/CF丂偵戙擖偟偰丄倎/乮倫倰乯亖倐/乮俀倫倰乯亄們/乮俀倫倰乯丂傛傝丄
丂丂丂俀倎亖倐亄們丂丂偙偺偲偒丄倫亖乮俁/俀乯倎丂側偺偱丄丂俙俢/倰亖俀倫/倎亖俁
丂丂丂 仜侾両亄俀両亄俁両亄係両亄俆両亄俇両亄俈両亄俉両亄俋両丂偺堦偺埵
丂丂幚嵺偵丄丂俆両丄俇両丄俈両丄俉両丄俋両偼丄慺場悢俀偲俆傪昁偢帩偮偺偱丄堦偺埵偼侽偱偁傞丅
丂丂傛偭偰丄侾両亄俀両亄俁両亄係両偩偗傪挷傋傟偽傛偄丅侾両亄俀両亄俁両亄係両亖俁俁丂側偺
丂丂偱丄媮傔傞悢偼丄俁
丂丂丂 仜併乮侾俉侽亄値2乯偑惍悢偲側傞帺慠悢値偺屄悢
丂丂幚嵺偵丄併乮侾俉侽亄値2乯亖倠丂乮倠偼惍悢乯丂偲偍偔偲丄丂倠2亅値2亖侾俉侽
丂丂傛偭偰丄乮倠亄値乯乮倠亅値乯亖侾俉侽丂偱丄乮倠亄値乯亄乮倠亅値乯亖俀倠偼乮嬼悢乯傛傝丄
丂丂乮倠亄値乯丄乮倠亅値乯偼偲傕偵嬼悢偱側偗傟偽側傜側偄丅乮倠亄値乯亜乮倠亅値乯偵拲堄偟偰丄
丂丂乮倠亄値丆倠亅値乯亖乮俋侽丆俀乯丄乮俁侽丆俇乯丄乮侾俉丆侾侽乯丂偺俁捠傝
丂丂傛偭偰丄値亖係丄侾俀丄係係丂偺俁捠傝
係丒丒丒仜懭墌 倶2/係亄倷2亖侾 偺拞怱偱捈岎偡傞俀捈慄偲懭墌偲偺岎揰偱嶌傜傟傞暯峴巐曈
丂丂丂丂宍偺柺愊偺嵟彫抣
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜曽掱幃 倶4亅俁俀倶2亄俀俆俇亖侽偺帺慠悢夝
丂丂幚嵺偵丄丂乮倶亄係乯2乮倶亅係乯2亖侽丂傛傝丄倶亖係
丂丂丂 仜柍尷摍斾媺悢 儼値=1亣 俀2-n 偺榓
丂丂幚嵺偵丄榓偼丄俀/乮侾亅侾/俀乯亖係
丂丂丂 仜俇屄偺摨偠傕偺傪丄婏悢屄偢偮偺偄偔偮偐偺摨偠戃偵暘偗傞曽朄偺悢
丂丂幚嵺偵丄乮侾丆俆乯丄乮侾丆侾丆侾丆俁乯丄乮侾丆侾丆侾丆侾丆侾丆侾乯丄乮俁丆俁乯丂偺係捠傝
丂丂丂 仜峴偒偼侾帪娫枅偵侾侽暘偢偮媥宔偟丄栚揑抧偵拝偔偺偵俀帪娫係侽暘偐偐偭偨丅婣傝
丂丂丂丂偼旀傟偨偺偱曕偔懍偝傪峴偒偺俈侽亾偲偟丄係侽暘枅偵侾侽暘偢偮媥宔偟偨丅偙偺偲偒丄
丂丂丂丂婣傝偵梫偟偨帪娫
丂丂幚嵺偵丄峴偒偼俀夞媥宔偟丄幚嵺偵曕偄偨帪娫偼俀帪娫俀侽暘亖侾係侽暘側偺偱丄婣傝偺
丂丂曕偄偨帪娫偼丄侾係侽亊侾侽/俈亖俀侽侽暘偱偁傞丅偨偩偟丄俀侽侽亐係侽亖俆 傛傝媥宔偼係夞
丂丂埲忋偐傜丄婣傝偵偐偐偭偨帪娫偼丄係亊侾侽亄俀侽侽亖俀係侽暘偱丄係帪娫偐偐偭偨丅
丂丂丂 仜x=a^3+3b丄y=b^3+3a丄ab=1 乮a亜b亜0乯 偺偲偒丄(x+y)^(2/3)-(x-y)^(2/3) 偺抣
丂丂幚嵺偵丄x+y=a^3+3a+3b+b^3=a^3+3a^2b+3ab^2+b^3=(a+b)^3
丂丂x-y=a^3-3a+3b-b^3=a^3-3a^2b+3ab^2-b^3=(a-b)^3丂側偺偱丄
丂丂(x+y)^(2/3)-(x-y)^(2/3)=(a+b)^2-(a-b)^2=4ab=4
丂丂丂 仜暯柺忋偵堎側傞俇杮偺慄暘傪堷偔偲偒丄偙傟傜偺慄暘偺抂揰偲偟偰摼傜傟傞揰偺拞偱丄
丂丂丂丂堎側傞揰偺嵟彫尷屄悢
丂丂幚嵺偵丄暯柺忋偵丄値屄偺揰偑偁傞偲丄慄暘偼丄値俠2亖値(値亅侾)/俀 乮杮乯傑偱堷偗傞偺偱
丂丂丂慄暘俇杮側傜丄揰偼嵟彮係屄偲側傞丅椺偊偽丄
丂丂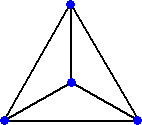 丂
丂
丂丂丂 仜偁傞巇帠傪廔偊傞偺偵丄俙偼俇擔丄俛偼侾俀擔偐偐傞丅俀恖偱傗傞偲壗擔偐偐傞偐丅
丂丂幚嵺偵丄俙丄俛偺堦擔摉偨傝偺巇帠検偼丄侾/俇丄侾/侾俀側偺偱丄俀恖偑堦弿偵摥偄偨巇帠
丂丂検偼丄侾/俇亄侾/侾俀亖侾/係偱偁傞丅傛偭偰丄巇帠傪廔偊傞偺偵丄侾亐侾/係亖係乮擔乯偐偐傞丅
丂丂丂 仜戝拞彫偺僶働僣偱悈憛偵悈傪擖傟傞丅戝偩偲侾俇攖丄拞偩偲俀係攖丄彫偩偲俁俀攖偱
丂丂丂丂枮攖偵側傞丅戝侾屄偲拞俁屄偲彫俀屄偩偲丄壗夞悈傪擖傟傟偽傛偄偐丅
丂丂幚嵺偵丄戝侾屄偲拞俁屄偲彫俀屄偩偲丄侾夞摉偨傝偺悈偺検偼丄
丂丂侾/侾俇亄俁/俀係亄俀/俁俀亖侾/係丂傛傝丄侾亐侾/係亖係乮夞乯丂悈傪擖傟傟偽傛偄丅
丂丂丂 仜乽侾係俈係侾乿偺傛偆偵塃偐傜撉傫偱傕嵍偐傜撉傫偱傕摨偠偵側傞悢偺偙偲傪乽夞暥悢乿偲
丂丂丂丂尵偆丅俀俇仩偺俀忔偑夞暥悢偵側傞偲偒偺仩偵擖傞悢帤
丂丂幚嵺偵丄俀俇係2亖俇俋俇俋俇丂偐傜丄仩亖係
丂丂丂 仜壓恾偺傛偆偵丄俙俛亖俙俠偺俀摍曈嶰妏宍俙俛俠偑墌偵撪愙偟偰偄傞丅墌廃忋偵揰俢傪
丂丂丂丂偲傝丄捈慄俙俢偲曈俛俠偺岎揰傪俤偲偡傞丅
丂丂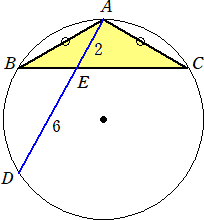
丂丂丂丂俙俤亖俀丄俤俢亖俇丂偺偲偒偺曈俙俛偺挿偝
丂丂幚嵺偵丄
丂丂
丂丂丂忋恾偵偍偄偰丄丂仮俙俛俤佷仮俙俢俛丂傛傝丄丂俙俛 丗 俙俤亖俙俢 丗 俙俛丂側偺偱丄
丂丂丂俙俛 丗 俀亖俉 丗 俙俛丂偡側傢偪丄丂俙俛2亖侾俇丂偐傜丄丂俙俛亖係
俆丒丒丒仜們倧倲2乮兾/俈乯亄們倧倲2乮俀兾/俈乯亄們倧倲2乮俁兾/俈乯偺抣
丂丂幚嵺偵丄寁嶼偡傞偲丄俆偵側傞丅
丂丂丂 仜惓懡柺懱偺庬椶偺悢
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜暯柺偵偍偄偰丄俆杮偺捈慄偱弌棃傞嶰妏宍偺嵟戝悢
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜幚悢 倶 偵懳偟偰丄併乮俆倶2亅侾俇倶亄俀侽乯亄併乮俆倶2亅俀俇倶亄俁俈乯丂偺嵟彫抣
丂丂丂丂乮仺丂嶲峫丗乽嵟彫栤戣乿乯
丂丂幚嵺偵丄梌幃亖併乮乮倶亅係乯2亄乮俀倶亅俀乯2乯亄併乮乮倶亅侾乯2亄乮俀倶亅俇乯2乯丂偲彂偗傞丅
丂丂丂偙傟偼丄俀掕揰俙乮係丆俀乯丄俛乮侾丆俇乯偐傜捈慄 倷亖俀倶 忋偺揰俹乮倶丆俀倶乯偲偺嫍棧偺榓
丂丂丂俙俹亄俛俹傪堄枴偡傞丅捈慄 倷亖俀倶 偵娭偟偰丄俀揰俙丄俛偼斀懳懁偵偁傞偺偱丄俙俹亄俛俹
丂丂丂偑嵟彫偲側傞揰俹偼丄捈慄 倷亖俀倶 偲捈慄俙俛偺岎揰偵側傞偲偒偱偁傞丅
丂丂丂偟偨偑偭偰丄俙俹亄俛俹偺嵟彫抣偼丄俙俛亖併乮俁2亄係2乯亖俆丂偲側傞丅
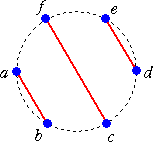
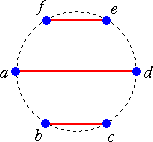
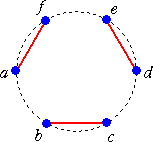
丂丂丂 仜墌廃忋偺俇屄偺揰傪屳偄偵岎嵎偟側偄尫偱寢傇曽朄偺悢
丂丂幚嵺偵丄師偺俆捠傝丂乮仺丂嶲峫丗乽僇僞儔儞悢乿乯
丂丂丂 仜俠亖俋侽亱偺捈妏俀摍曈嶰妏宍俙俛俠偺俁捀揰俙丄俛丄俠偑壓恾偺傛偆偵丄屳偄偺嫍棧
丂丂丂丂偑俇偲俀偺俁杮偺暯峴慄忋偵偁傞丅俠傪捠傞暯峴慄偲幬曈俙俛偺岎揰傪俢偲偍偔丅
丂丂丂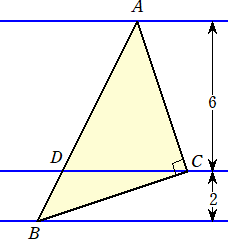
丂丂丂偙偺偲偒偺慄暘俠俢偺挿偝
丂丂幚嵺偵丄壓恾偺傛偆偵丄捈妏嶰妏宍俙俛俠偵奜愙偡傞挿曽宍俧俛俥俤傪峫偊傞丅
丂丂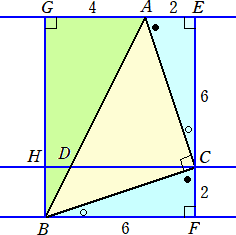
丂丂丂仮俛俥俠佭仮俠俤俙丂側偺偱丄丂俙俧亖係丂偱偁傞丅傛偭偰丄丂俫俢丗係亖俀丗俉丂傛傝丄
丂丂丂俫俢亖侾丂側偺偱丄丂俠俢亖俇亅侾亖俆
丂丂丂 仜(俆p亅侾)/(倫5亅侾)丂偑惍悢偲側傞慺悢倫偺抣
丂丂幚嵺偵丄p=2丄3 偺偲偒偼幚嵺偵帋偡偲妱傝愗傟側偄偑丄p=5 偺偲偒偼幚嵺偵帋偡偲妱傝
丂丂愗傟傞偺偱丄p=5 偼夝偺1偮偱偁傞丅
丂丂p亞7 偵忦審傪枮偨偡慺悢偑懚嵼偟側偄偙偲傪攚棟朄傪梡偄偰帵偡丅
丂丂7埲忋偺偁傞慺悢 p 偑忦審傪枮偨偟偨偲壖掕偡傞丅偙偺偲偒丄 p-1 偼嬼悢偱丄傑偨丄
丂丂52 佭 1 (mod 8) 偱偁傞偙偲偐傜丄5p-1 佭 1 (mod8)丂側偺偱丄 5p-1 佭 4 (mod 8)
丂丂偮傑傝丄5p-1 偼 8 偺攞悢偱偼側偄丅乗乗[A]
丂丂堦曽偱丄p-1 亞 6 亜 1 側偺偱丄p-1 傪妱傝愗傞偁傞慺悢 q 偑懚嵼偡傞丅
丂丂p5-1 偼 p-1 偱妱傝愗傟傞偺偱丄q 偼 p5-1 傕妱傝愗傞丅偝傜偵丄5p-1 偑 p5-1 偱妱傝愗
丂丂傟傞偲偄偆偙偲偼丄q 偼 5p-1 傕妱傝愗傞丅傛偭偰丄5p 佭 1 (mod q) 偱偁傞丅
丂丂傑偨丄5p 佭 0 (mod 5) 偱偁傞偙偲偐傜 q亗5 偲偟偰傛偔丄僼僃儖儅乕偺彫掕棟傛傝丄
丂丂5q-1 佭 1 (mod q) 偱偁傞丅偙偙偱丄0亙q-1亙q亙p-1亙p 傛傝丄q-1 偼 p 偲屳偄偵慺偱偁傞
丂丂偺偱丄奼挘儐乕僋儕僢僪偺屳彍朄傛傝丄a(q-1) - bp = 1 偲側傞帺慠悢 a丄b 偑懚嵼偡傞丅
丂丂偙傟傜傪梡偄傞偲丄q 傪朄偲偟偰丄
丂丂1 佭 1a 佭 {5q-1}a 佭 5a(q-1) 佭 5bp+1 佭 (5p)b亊5 佭 1b亊5 佭 5
丂丂傛偭偰丄4佭0 (mod q) 偱偁傞偺偱丄q=2丂偮傑傝丄p-1 偼慺場悢偲偟偰 2 偟偐帩偨側偄悢偱
丂丂偁傝丄p-1 亞 6 偱偁傞偙偲偐傜偦偺巜悢偼3埲忋偱偁傞丅
丂丂偡側傢偪丄p-1 偼 8 偺攞悢偱偁傝丄偦偺攞悢偱偁傞 p5-1 傗丄偝傜偵偦偺攞悢偱偁傞 5p-1
丂丂傕 8 偺攞悢偱偁傞丅
丂丂偟偐偟丄偙傟偼 [A] 偵柕弬偡傞丅偟偨偑偭偰 p亞7 偵忦審傪枮偨偡 p 偼懚嵼偟側偄丅
丂丂埲忋傛傝丄忦審傪枮偨偡慺悢偼 p=5 偺傒偱偁傞丅乮仺丂嶲峫丗乽悢妛僐儞僥僗僩乿乯
丂丂丂 仜倶/乮倶亄倷乯亄倷/乮倶亅倷乯亖俆/俁丄倶倷亖亅俀 乮倶丄倷 偼幚悢乯偺偲偒丄倶2亄倷2 偺抣
丂丂幚嵺偵丄戞侾幃偺椉曈偵1傪壛偊偰丄 x/(x亄y)亄x/(x亅y)亖俉/俁丂偺嵍曈偺暘巕暘曣偵
丂丂倷傪偐偗偰丄亅俀/(亅俀亄倷2)亅俀/(亅俀亅y2)亖俉/俁丂偙偺椉曈傪俀偱妱偭偰丄
丂 侾/(俀亅倷2)亄侾/(俀亄y2)亖係/俁丂嵍曈傪捠暘偟偰懌偡偲丄丂係/(係亅y4)亖係/俁
丂丂傛偭偰丄y4亖侾 偐傜丄y亖亇侾 側偺偱丄(倶丆倷)亖亇(亅俀丆侾)丂偟偨偑偭偰丄倶2亄倷2亖俆
丂丂丂 仜懢榊偑侾俆擔偐偐傞巇帠傪師榊偼俋擔偱偱偒傞丅懢榊偑堦恖偱壗擔偐摥偄偨屻丄師
丂丂丂丂丂榊偑屻傪堷偒宲偄偱摥偄偨傜侾侾擔偐偐偭偨丅懢榊偑摥偄偨擔悢
丂丂幚嵺偵丄巇帠慡懱偺検傪侾俆偲俋偺嵟彫岞攞悢偺係俆偲峫偊傞偲丄懢榊偼侾擔偱俁偺検丄師
丂丂榊偼侾擔偱俆偺検傪偡傞丅師榊偑屻傪堷偒宲偄偱摥偄偨傜侾侾擔偐偐偭偨偺偱丄偦偺巇帠
丂丂検偼丄俆亊侾侾亖俆俆偱丄巇帠検偺俆俆亅係俆亖侾侽偼丄師榊偺摥偒側偺偱丄幚嵺偵懢榊偑摥
丂丂偄偨偺偼丄侾侽亐乮俆亅俁乯亖俆乮擔娫乯丂摥偄偨偙偲偵側傞丅
丂丂乮暿夝乯丂柺愊恾傪梡偄傟偽丄
丂丂
丂丂乮暿夝乯丂曽掱幃傪梡偄傟偽丄倶丒乮侾/侾俆乯亄乮侾侾亅倶乯丒乮侾/俋乯亖侾丂傛傝丄倶亖俆
俇丒丒丒仜惎鋳宍 倶丱乮2/3乯亄倷丱乮2/3乯亖侾 偺廃偺挿偝
丂丂幚嵺偵丄寁嶼偡傞偲丄俇偵側傞丅
丂丂丂 仜懭墌 倶2/係亄倷2/俀亖侾 偺拞怱偱捈岎偡傞俀捈慄偲懭墌偲偺岎揰偱嶌傜傟傞暯峴巐
丂丂丂丂曈宍偺柺愊偺嵟戝抣
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜係^乮俀/俁乯亐俀係^乮侾/俁乯亊侾俉^乮俀/俁乯偺抣
丂丂幚嵺偵丄梌幃亖俀^乮係/俁乯亐乮俀亊俁^乮侾/俁乯亊俀^乮俀/俁乯亊俁^乮係/俁乯亖俀亊俁亖俇
丂丂丂 仜倖乮倶乯亖倶2亅俀 偺偲偒丄倖乮倖乮倖乮倶乯乯乯亖倶 偺幚悢夝偱丄倖乮倶乯亖倶 偺夝偱偼側偄傕偺偺屄悢
丂丂幚嵺偵丄倷亖倖乮倖乮倖乮倶乯乯乯偺僌儔僼傪彂偗偽丄媮傔傞屄悢偼俇屄偱偁傞丅
丂丂乮仺丂嶲峫丗乽宖帵斅偺榖戣乿乯
丂丂
丂丂丂 仜敿宎俁們倣偺媴偺拞怱傪俷偲偟丄俷傪捀揰偲偡傞捈墌悕偑岎傢偭偰偄傞丅偙偺偲偒偺
丂丂丂丂岎傢偭偰偄傞晹暘偺懱愊
丂丂丂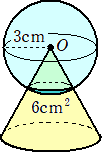
丂丂幚嵺偵丄媴偺昞柺愊偼丄係兾丒俁2亖俁俇兾 偱丄媴偺懱愊偼丄係兾丒俁3/俁亖俁俇兾側偺偱丄
丂丂媮傔傞懱愊偼丄俁俇兾亊乮俇/俁俇兾乯亖俇乮們倣3乯
丂丂乮暿夝乯丂乮掙柺愊乯亊乮崅偝乯亐俁亖俇亊俁/俁亖俇乮們倣3乯
丂丂丂 仜偁傞巇帠傪廔偊傞偺偵丄俙偼俇擔丄俛偼侾俀擔偐偐傞丅嵟弶俀恖偱俁擔娫偟偨屻丄俛偑
丂丂丂丂巆傝傪堦恖偱偡傞偲偒丄巇帠偼慡晹偱壗擔偐偐傞偐丅
丂丂幚嵺偵丄俙丄俛偺堦擔摉偨傝偺巇帠検偼丄侾/俇丄侾/侾俀側偺偱丄俀恖偱傗偭偨巇帠検偼丄
丂丂乮侾/俇亄侾/侾俀乯亊俁亖俁/係丂側偺偱丄巆傝 侾亅俁/係亖侾/係 傪俛偑傗傞応崌丄
丂丂侾/係亐侾/侾俀亖俁丂傛傝丄巇帠傪廔偊傞偺偵丄丂俁亄俁亖俇乮擔乯偐偐傞丅
丂丂丂 仜嵗昗暯柺忋傪塣摦偡傞揰P偺丄弌敪偟偰偐傜 倲 昩屻偺懍搙儀僋僩儖 倴 偑
丂丂丂丂倴 = ( -兾cos2(兾t/3)亊sin(兾t/3) 丆兾sin2(兾t/3)亊cos(兾t/3) )丂偺偲偒丄P偼丄偁傞
丂丂丂丂嬋慄忋傪塣摦偡傞丅弌敪偟偰偐傜6昩娫偵P偑捠夁偡傞摴偺傝
丂丂幚嵺偵丄俹乮倶丆倷乯偵偮偄偰丄倓倶/倓倲亖-兾cos2(兾t/3)亊sin(兾t/3)傛傝丄倶亖cos3(兾t/3)亄俠
丂丂摨條偵偟偰丄倓倷/倓倲亖兾sin2(兾t/3)亊cos(兾t/3)丂傛傝丄倷亖sin3(兾t/3)亄俢
丂丂乮俠丄俢偼擟堄掕悢乯 倲=0丂偺偲偒丄揰俹偑揰乮1丆0乯偵偁傞偲偟偰丄倶亖cos3(兾t/3)丄
丂丂倷亖sin3(兾t/3)丂傛偭偰丄揰俹偼丄傾僗僥儘僀僪丂倶2/3亄倷2/3亖侾忋傪摦偔丅弌敪偟偰偐傜
丂丂6昩娫偵P偑捠夁偡傞摴偺傝偼丄乽惎鋳宍乿偺岞幃偵傛傝丄俇 偲側傞丅
俈丒丒丒仜暯柺偵偍偄偰丄俇杮偺捈慄偱弌棃傞嶰妏宍偺嵟戝悢
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜俁杮偺捈慄偱暘妱偝傟傞暯柺偺嵟戝悢
丂丂幚嵺偵丄
丂丂丂丂丂丂丂丂
丂丂丂 仜倶倷倸嬻娫偺偁傞暯柺俴忋偵懡妏宍俲偑偁傞丅偙偺俲傪倶倷暯柺偵惓幩塭偡傞偲柺愊偼
丂丂丂丂俀丄倷倸暯柺偵惓幩塭偡傞偲柺愊偼俁丄倸倶暯柺偵惓幩塭偡傞偲柺愊偼俇偵側傞偲偄偆丅
丂丂丂丂偙偺偲偒偺俲偺柺愊
丂丂幚嵺偵丄俲偺柺愊傪俽偲偟丄俴偺戝偒偝侾偺朄慄儀僋僩儖傪乮倎丆倐丆們乯偲偡傞偲丄俴偲倶倷暯柺
丂丂丂偺側偡妏兤偼丄乮倎丆倐丆們乯偲乮侽丆侽丆侾乯偺側偡妏偵摍偟偄偺偱丄丂們倧倱兤亖們
丂丂丂傛偭偰丄俽們倧倱兤亖俀丂懄偪丄丂俽們亖俀丂偲側傞丅摨條偵偟偰丄俽倎亖俁丄俽倐亖俇丂偱偁傞丅
丂丂丂偟偨偑偭偰丄俽2乮倎2亄倐2亄們2乯亖俋亄俁俇亄係亖係俋偱丄倎2亄倐2亄們2亖侾丂傛傝丄俽亖俈
丂丂丂 仜惓敧柺懱偺俉柺偺撪丄係柺傪愒丄懠偺係柺傪惵偱揾傝暘偗傞曽朄偺悢
丂丂幚嵺偵丄揾傝暘偗傞曽朄偺悢偼慡晹偱丄俈捠傝偁傞丅乮仺丂嶲峫丗乽揾傝暘偗偺曽朄乿乯
丂丂乮恾帵偵傛傞妋擣乯
丂丂丂 仜嬋慄丂y=(2x/3)3/2丂乮0亝x亝9/2乯丂偺挿偝
丂丂幚嵺偵丄倷乫亖(2x/3)1/2丂傛傝丄侾亄倷乫2亖侾亄俀x/俁丂側偺偱丄媮傔傞嬋慄偺挿偝偼丄
丂丂丂佺09/2 併乮侾亄俀x/俁乯倓倶亖乮俁/俀乯佺03 併乮侾亄倲乯倓倲亖乵乮侾亄倲乯3/2乶03亖係3/2亅侾亖俈
俉丒丒丒仜懭墌 倶2/俇亄倷2/俀亖侾 偺拞怱偱捈岎偡傞俀捈慄偲懭墌偲偺岎揰偱嶌傜傟傞暯峴巐
丂丂丂丂曈宍偺柺愊偺嵟戝抣
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜敿宎侾偺墌偑捈慄忋傪妸傜偢偵侾夞揮偡傞偲偒丄墌廃忋偺揰偑昤偔屖偺挿偝
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜値傪帺慠悢偲偡傞丅暋慺悢 z 偑扨埵墌 |z|亖1 傪堦廃偡傞偲偒丄
丂丂丂丂f(z)亖z亅(1/(n+1))z^(n+1) 偑昤偔嬋慄偺挿偝
丂丂幚嵺偵丄俀佺02兾 |倱倝値(値兤/俀)|倓兤丂偱丄
丂丂倱倝値(n兤/俀) 偼丄[侽丆俀兾/値] 偱偺攇宍傪 [侽丆俀兾] 偱忋壓偵値夞孞傝曉偡偐傜丄
丂丂俀値丒佺02兾/n 倱倝値(値倶/俀)倓兤亖俀値丒(俀/値)[亅們倧倱(値兤/俀)]02兾/n亖俉
丂丂乮暿夝乯丂|z|亖1 傛傝丄倸亖們倧倱兤亄倝丒倱倝値兤丂乮侽亝兤亝俀兾乯丂偲偍偗傞丅偙偺偲偒丄
丂丂丂倖(倸)亖倶亄倝丒倷丂偲偍偔偲丄倶亖們倧倱兤亅乮侾/乮値亄侾乯乯們倧倱乮値亄侾乯兤丄
丂丂丂倷亖倱倝値兤亅乮侾/乮値亄侾乯乯倱倝値乮値亄侾乯兤丂側偺偱丄
丂 丂 倶兤亖亅倱倝値兤亄倱倝値乮値亄侾乯兤亖俀們倧倱乮乮値亄俀乯/俀乯兤倱倝値乮値/俀乯兤
丂丂丂倷兤亖們倧倱兤亅們倧倱乮値亄侾乯兤亖俀倱倝値乮乮値亄俀乯/俀乯兤倱倝値乮値/俀乯兤
丂丂丂傛偭偰丄嬋慄偺挿偝俴偼丄
丂丂丂俴亖佺02兾 併乮倶兤2亄倷兤2乯倓兤亖俀 佺02兾乥倱倝値乮値/俀乯兤乥倓兤
丂丂丂偙偙偱丄乮値/俀乯兤亖倲丂偲偍偔偲丄倓兤亖乮俀/値乯倓倲丂偱丄
丂丂丂俴亖乮係/値乯佺0値兾 乥倱倝値 倲乥倓倲亖乮係/値乯丒値佺0兾 倱倝値 倲 倓倲亖係[亅們倧倱 倲 ]0兾亖俉
丂丂丂 仜僞僐偲僀僇偑偁傢偣偰侾侽旵偄傞丅懌偺悢傪悢偊傞偲慡晹偱俉係杮偱偁偭偨丅偙偺偲偒偺
丂丂丂丂僞僐偺悢
丂丂丂丂乮拲)僞僐偺懌偼8杮丄僀僇偺懌偼10杮
丂丂幚嵺偵丄僀僇偺懌偺偆偪2杮傪乽庤乿偲屇傇偙偲偵偡傞偲丄懌偼8杮偱丄僞僐偲摨偠偵側傝丄崌
丂丂丂傢偣偰10旵側偺偱丄懌偼慡晹偱丄8亊10=80杮丅傛偭偰丄84杮偺偆偪乽庤乿偑84-80=4杮側
丂丂丂偺偱丄僀僇偼丄4亐2=2旵丄僞僐偼丄10-2=8旵丅
丂丂丂乮暿夝乯僀僇偽丄倶 旵丄僞僐偼丄倷 旵偲偡傞偲丄倶亄倷亖侾侽丄侾侽倶亄俉倷亖俉係丂傛傝丄俀倶亖係
丂丂丂丂側偺偱丄倶亖俀 偐傜丄僀僇偼俀旵丄僞僐偼俉旵丅
丂丂丂 仜悢楍丂侾侽 丆俀侾 丆仩 丆侾俋 丆俇 丆侾俈 丆係丂偵偍偄偰丄嬻強仩偵擖傞悢
丂丂幚嵺偵丄悢楍偺奺崁偼帪寁乮俀係帪娫乯偱丄侾侾帪娫屻偺帪崗偵側偭偰偄傞偺偱丄仩亖俉
丂丂丂乮暿夝乯丂婏悢斣偺崁傪敳偒弌偡偲丄侾侽 丆仩 丆俇 丆係丂側偺偱丄岎嵎亅俀偺摍嵎悢楍偐
丂丂丂丂傜丄仩亖俉
丂丂丂 仜偁傞巇帠傪姰惉偝偣傞偺偵丄峛堦恖偩偲侾俀擔丄壋堦恖偩偲俇擔偐偐傞丅嵟弶丄偙偺
丂丂丂丂巇帠傪峛偲壋偺俀恖偱巒傔偨偑丄搑拞偱壋偑夦変傪偟偰壗擔娫偐巇帠傪媥傫偩丅偦
丂丂丂丂偺娫丄巇帠偼峛堦恖偱峴偭偨偑丄壋偺夦変偑捈傝丄傑偨峛壋嫟偵巇帠偵偲傝偐偐偭偨
丂丂丂丂偲偙傠丄侾侽擔偱廔傢偭偨丅偙偺偲偒丄壋偑巇帠傪媥傫偩擔悢
丂丂幚嵺偵丄峛偺侾擔摉偨傝偺巇帠検偼丄侾/侾俀丂偱丄壋偺侾擔摉偨傝偺巇帠検偼丄侾/俇
丂丂丂峛偑侾侽擔丄壋偑 倷 擔巇帠傪偟偨偲偡傞偲丄乮侾/侾俀乯亊侾侽亄乮侾/俇乯倷亖侾
丂丂丂傛偭偰丄俆亄倷亖俇丂傛傝丄倷亖侾丂側偺偱丄壋偑巇帠傪媥傫偩偺偼丄俋擔娫
丂丂丂偟偐傞偵丄栤戣暥偐傜壋偼嵟弶偲嵟屻偼巇帠傪偟偰偄傞偙偲偵側偭偰偄傑偡偺偱丄弶擔
丂丂丂偺嶌嬈拞偵夦変傪偟偰嵟廔擔偺搑拞偱暅婣偟丄崌寁1擔暘偺嶌嬈傪偟偨偲峫偊傜傟傞丅
丂丂丂廬偭偰丄弶擔偼憗戅丄嵟廔擔偼抶崗偱偄偢傟傕乽媥傒乿偱偼側偄偺偱丄媥傫偩偺偼丄8擔
丂丂丂娫丅
丂丂乮暿夝乯峛壋偺侾擔摉偨傝偺巇帠検偼丄偦傟偧傟侾/侾俀偲侾/俇偱丄偁傞巇帠傪姰惉偝偣傞
丂丂丂偺偵梫偟偨擔悢偼侾侽擔丅峛偑侾侽擔摥偔偲丄慡懱偺侾侽/侾俀亖俆/俇丂偑廔椆偟偰偄傞偺
丂丂丂偱丄巆傝偺侾/俇偼壋偺巇帠偲側傞丅偦偺擔悢偼丄侾/俇亐侾/俇亖侾乮擔乯丂側偺偱丄壋偼
丂丂丄侾侽亅侾亖俋乮擔乯巇帠傪媥傫偩偙偲偵側傞丅
丂丂丂偟偐傞偵丄栤戣暥偐傜壋偼嵟弶偲嵟屻偼巇帠傪偟偰偄傞偙偲偵側偭偰偄傑偡偺偱丄弶擔
丂丂丂偺嶌嬈拞偵夦変傪偟偰嵟廔擔偺搑拞偱暅婣偟丄崌寁1擔暘偺嶌嬈傪偟偨偲峫偊傜傟傞丅
丂丂丂廬偭偰丄弶擔偼憗戅丄嵟廔擔偼抶崗偱偄偢傟傕乽媥傒乿偱偼側偄偺偱丄媥傫偩偺偼丄8擔
丂丂丂娫丅
丂丂乮暿夝乯12偲6偺嵟彫岞攞悢偑12乧偙傟傪巇帠偺憤検偲偟傑偡丅峛偼1擔偵1偺巇帠傪偙側
丂丂丂偟傑偡乮慡晹廔偊傞偵偼12擔乯丅壋偼1擔偵2偺巇帠傪偙側偟傑偡乮慡晹廔偊傞偵偼6擔乯丅
丂丂丂峛偑嶌嬈傪偟偰偄傞偲偙傠偵壋偑1擔壛惃偡傞偲丄巇帠検2偩偗偼偐偳傝傑偡偐傜丄廔偊
丂丂丂傞傑偱偺擔偑2擔抁弅偝傟傑偡丅
丂丂丂偝偰丄栤戣暥偐傜丄峛偩偗偩偲12擔偐偐傞偺偑丄壋偑壛傢偭偨傜10擔偵側偭偨偲偄偆偙偲
丂丂丂偼丄2擔暘抁弅偝傟偨偙偲偵側傝傑偡偐傜丄壋偑壛惃偟偨偺偼1擔偩偗偲偄偆偙偲偱偡丅
丂丂丂偮傑傝丄9擔娫偼壋偑嶲壛偟偰偄側偄丄偲丅
丂丂丂偟偐傞偵丄栤戣暥偐傜壋偼嵟弶偲嵟屻偼巇帠傪偟偰偄傞偙偲偵側偭偰偄傑偡偺偱丄弶擔
丂丂丂偺嶌嬈拞偵夦変傪偟偰嵟廔擔偺搑拞偱暅婣偟丄崌寁1擔暘偺嶌嬈傪偟偨偲峫偊傜傟傞丅
丂丂丂廬偭偰丄弶擔偼憗戅丄嵟廔擔偼抶崗偱偄偢傟傕乽媥傒乿偱偼側偄偺偱丄媥傫偩偺偼丄8擔
丂丂丂娫丅
丂丂丂 仜巐妏宍ABC俢偵偍偄偰丄俙俛亖俇丄俠俢亖俀 偱丄俙俢亖俛俠 偲偡傞丅傑偨丄佢俙亖俆侽亱丄
丂丂丂丂佢俛亖係侽亱偺偲偒偺巐妏宍ABC俢偺柺愊
丂丂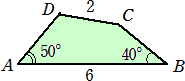
丂丂幚嵺偵丄壓恾偐傜柧傜偐偵丄巐妏宍ABC俢偺柺愊亖乮俁俇亅係乯亐係亖俉
丂丂丂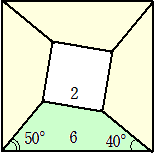
丂丂丂 仜惓偺惍悢偑彂偐傟偨僇乕僪偑壗枃偐偁傝丄慡偰偺僇乕僪偺榓偼侾侾偱偁傞偲偡傞丅侾埲
丂丂丂丂忋侾侾埲壓偺擟堄偺惍悢k偵懳偟丄彂偐傟偨悢偺榓偑k偵側傞傛偆偵壗枃偐傪慖傃弌偡
丂丂丂丂偙偲偑偱偒傞偲偄偆丅傑偨丄偦偺慖傃曽偼丄摨偠悢偺彂偐傟偨僇乕僪傪嬫暿偟側偄傕偺偲
丂丂丂丂偡傞偲偨偩侾捠傝偱偁傞丅偙偺傛偆側僇乕僪偺慻崌偣偺悢
丂丂幚嵺偵丄(6,3,1,1)丄(6,2,2,1)丄(6,1,1,1,1,1)丄(4,4,1,1,1)丄(3,3,3,1,1)丄(2,2,2,2,2,1)丄(1偑11屄)丄
丂丂丂(4,4,2,1) 偱丄慡晹偱俉捠傝
丂丂丂 仜堦枃偱丄壴暡偺70%傪彍嫀偱偒傞僼傿儖僞乕偑偁傞丅偙偺壴暡傪99丏99%彍嫀偡傞偺
丂丂丂丂偵昁梫側僼傿儖僞乕偺枃悢丅偨偩偟丄倢倧倗10俁=0丏4771偲偡傞丅
丂丂幚嵺偵丄僼傿儖僞乕傪 倶 枃梡堄偟偰壴暡偑99丏99%彍嫀偱偒傞偲偒丄乮侽丏俁乯倶亝(侽丏侾)4
丂丂椉曈偺侾侽傪掙偲偡傞懳悢傪偲傞偲丄倶丒倢倧倗10侽丏俁亝亅係丂傛傝丄倶亞係/侽丏俆俀俀俋亖俈丏俇丒丒丒
丂丂偟偨偑偭偰丄僼傿儖僞乕傪嵟掅俉枃梡堄偡傟偽丄壴暡傪99丏99%彍嫀偱偒傞丅
丂丂丂 仜併乮侾俉値乯偲併乮俇値亄侾乯偑偲傕偵惍悢偲側傞傛偆側帺慠悢値偺嵟彫抣
丂丂幚嵺偵丄併乮侾俉値乯亖俁併乮俀値乯丂偵偍偄偰丄値亖俀倠2丂乮倠偼帺慠悢乯偲偍偗傞丅偙偺偲偒丄
丂丂併乮俇値亄侾乯亖併乮侾俀倠2亄侾乯丂倠亖侾丄俀丄丒丒丒丂傪戙擖偟偰弶傔偰惍悢偵側傞偺偼丄倠亖俀
丂丂偺偲偒丅傛偭偰丄値亖俉
俋丒丒丒仜榋妏宍偺懳妏慄偺杮悢
丂丂幚嵺偵丄丂俇亊俁亐俀亖俋
丂丂丂 仜曈偺挿偝偲柺愊偑帺慠悢偱偁傞戜宍偺柺愊偺嵟彫抣
丂丂丂丂乮擇慻偺曈偑暯峴偱偁傞恾宍偼娷傑側偄乯
丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 仜乮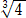 亅
亅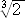 亄侾乯3/乮
亄侾乯3/乮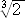 亅侾乯偺抣
亅侾乯偺抣
丂丂幚嵺偵丄乮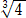 亅
亅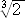 亄侾乯3亖乮
亄侾乯3亖乮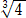 亅
亅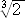 亄侾乯2乮
亄侾乯2乮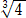 亅
亅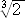 亄侾乯
亄侾乯
丂丂丂丂丂丂丂亖俁乮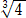 亅侾乯乮
亅侾乯乮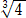 亅
亅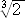 亄侾乯
亄侾乯
丂丂丂丂丂丂丂亖俁乮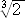 亅侾乯乮
亅侾乯乮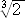 亄侾乯乮
亄侾乯乮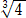 亅
亅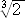 亄侾乯
亄侾乯
丂丂丂丂丂丂丂亖俋乮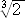 亅侾乯丂丂傛傝丄梌幃亖俋
亅侾乯丂丂傛傝丄梌幃亖俋
丂丂丂 仜佺-33 倶2/(侾亄ex) 倓倶 偺抣
丂丂幚嵺偵丄佺-33 倶2/(侾亄ex) 倓倶 亄佺-33 倶2ex/(侾亄ex) 倓倶亖佺-33 倶2 倓倶 亖侾俉
丂丂丂偙偙偱丄倶亖亅倲 偲偍偄偰丄佺-33 倶2ex/(侾亄ex) 倓倶亖佺-33 倶2/(侾亄ex) 倓倶丂偑帵偝
丂丂丂傟傞偺偱丄丂佺-33 倶2/(侾亄ex) 倓倶亖俋丂偑暘偐傞丅
丂丂丂#丂倶2/(侾亄ex) 偺晄掕愊暘偼懡廳懳悢娭悢傪梡偄偰昞偝傟傞偑丄掕愊暘偺寁嶼偼
丂丂丂丂梕堈偱偁傞偲偙傠偑柺敀偄丅
丂丂丂 仜棨忋婰榐夛偱丄俙偝傫丄俛偝傫丄俠偝傫偺俁恖偑丄俆侽侽侽倣偺搆嫞憱傪偟偨丅
丂丂丂丂侾廃係侽侽倣偺僩儔僢僋偱丄俙偝傫偼枅昩俉倣丄俛偝傫偼枅昩俇倣丄俠偝傫偼枅昩係倣偱
丂丂丂丂憱偭偨丅俙偝傫偑僑乕儖偡傞傑偱偵丄俙偝傫偑丄俛偝傫偲俠偝傫傪捛偄敳偔夞悢
丂丂幚嵺偵丄俙偝傫偑僑乕儖偡傞傑偱偵梫偡傞帪娫偼丄俆侽侽侽/俉亖俇俀俆乮昩乯
丂丂俙偝傫偼俛偝傫傪丄係侽侽/乮俉亅俇乯亖俀侽侽乮昩乯枅偵捛偄敳偔偺偱丄俇俀俆昩娫偵俙偝傫偼俛
丂丂偝傫傪俁夞捛偄敳偔丅摨條偵偟偰丄俙偝傫偼俠偝傫傪丄係侽侽/乮俉亅係乯亖侾侽侽乮昩乯枅偵捛偄
丂丂敳偔偺偱丄俇俀俆昩娫偵俙偝傫偼俠偝傫傪俇夞捛偄敳偔丅傛偭偰丄俙偝傫偼丄俛偝傫偲俠偝傫傪崌
丂丂寁俋夞捛偄敳偔丅
丂丂丂 仜偡傋偰偺曈偑帺慠悢偱柺愊傕帺慠悢偱偁傞嵟彫偺戜宍偺柺愊丅偨偩偟丄擇慻偺曈
丂丂丂丂偑暯峴偱偁傞恾宍偼娷傑側偄丅
丂丂幚嵺偵丄壓恾偺戜宍偺柺愊偼丄俋
丂丂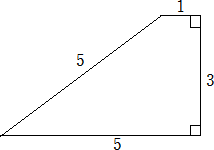
丂丂乮柺愊偑嵟彫偱偁傞偙偲偺徹柧乯
丂丂(忋掙+壓掙)亊崅偝亐2 偑惍悢偵側傞偺偱丄崅偝偼桳棟悢偱偡丅傛偭偰丄戜宍傪暯峴巐曈
丂丂宍偲嶰妏宍偵暘妱偡傞偲丄偦傟偧傟曈偼慡偰惍悢偱柺愊偼桳棟悢偵側傞丅
丂丂嶰妏宍懁偺柺愊偑桳棟悢偲偄偆偙偲偼丄僿儘儞偺岞幃傛傝丄廃挿偑嬼悢側傜丄偦傟偼惍
丂丂悢丄廃挿偑婏悢側傜丄乽婏悢/係乿偺偼偢偩偑丄屻幰偑偁傝偊側偄偙偲偼娙扨偵帵偝傟傞丅
丂丂(4S)2=(a2+b2+c2)2-2(a4+b4+c4) 偵偍偄偰丄a丄b丄c 偺偆偪1偮傑偨偼3偮偑婏悢偩偲丄4
丂丂偱妱偭偨帪偺梋傝偑嵍曈偼1偱塃曈偼3偵側傞偨傔丅
丂丂偮傑傝丄嶰妏宍懁偼柺愊偑惍悢丄偮傑傝丄偙傟偼僿儘儞嶰妏宍偱丄偙偺帪揰偱丄柺愊偑 9
丂丂埲壓偺傕偺偼丄(3丆4丆5) 偺傕偺偟偐側偄丅
丂丂偙傟偵丄柺愊偑惍悢偺暯峴巐曈宍傪偔偭偮偗傞丅5傪掙曈偵梡偄傞偲崅偝偑12/5側偣偄偱丄
丂丂暆5丄柺愊12偺暯峴巐曈宍傪偔偭偮偗傞偼傔偵側傞丅
丂丂偲偄偆偙偲偱丄師揰偺4傪掙曈偵梡偄偰丄暆1丄柺愊 3 偺暯峴巐曈宍傪偔偭偮偗偨柺愊 9 偺
丂丂傕偺偑嵟彫偲側傞丅乮仺丂嶲峫丗乽戜宍偺柺愊乿乯
丂丂丂 仜偁傞巇帠傪惉偟悑偘傞偺偵丄俙偼俇擔丄俛偼俋擔丄俠偼侾俀擔偐偐傞偲偄偆丅偦偺巇帠
丂丂丂丂傪丄俙丄俛丄俠偺弴偱丄偦傟偧傟壗擔娫偐偢偮堦恖偱扴摉偟惉偟悑偘偨丅偨偩偟丄巇帠
丂丂丂丂傪偟偨擔悢偺斾偼丄俙丗俛丗俠亖侾丗俁丗俀 偱偁傞偲偄偆丅壥偨偟偰丄巇帠偼壗擔娫偱廔傢
丂丂丂丂傞偺偐丠
丂丂幚嵺偵丄俙偑侾擔丄俛偑俁擔丄俠偑俀擔巇帠傪偡傞偲丄
丂丂丂侾/俇亊侾亄侾/俋亊俁亄侾/侾俀亊俀亖俀/俁
丂丂偡側傢偪丄俇擔娫偱俀/俁巇帠偑廔傢傞偺偱丄巇帠偑廔傢傞偺偵丄俋擔娫偐偐傞丅
侾侽丒丒丒仜俁丄係丄俈丄俉 偲亄丄亅丄亊丄亐丄乮丂丄乯丂傪梡偄偰丄侾侽傪嶌傞
丂丂丂幚嵺偵丄乮俁亅俈亐係乯亊俉亖侾侽
丂丂丂丂 仜侾丄侾丄俆丄俉 偲亄丄亅丄亊丄亐丄乮丂丄乯丂傪梡偄偰丄侾侽傪嶌傞
丂丂丂幚嵺偵丄俉亐乮侾亅侾亐俆乯亖侾侽
丂丂丂丂 仜俀丄俁丄俁丄俇 偲亄丄亅丄亊丄亐丄乮丂丄乯丂傪梡偄偰丄侾侽傪嶌傞
丂丂丂幚嵺偵丄俇亐俁亊乮俁亄俀乯亖侾侽
丂丂丂丂 仜侾丄俁丄俁丄俈 偲亄丄亅丄亊丄亐丄乮丂丄乯丂傪梡偄偰丄侾侽傪昞偣丅
丂丂丂幚嵺偵丄俁亊乮侾亄俈亐俁乯亖侾侽
丂丂丂丂 仜侾丄侾丄俋丄俋 偲亄丄亅丄亊丄亐丄乮丂丄乯丂傪梡偄偰丄侾侽傪嶌傞
丂丂丂幚嵺偵丄俋亊乮侾亄侾亐俋乯亖侾侽
丂丂丂丂仜棫曽懱傪俀怓偱揾傝暘偗傞曽朄偺悢
丂丂丂幚嵺偵丄揾傝暘偗傞曽朄偺悢偼慡晹偱丄侾侽捠傝偁傞丅乮仺丂嶲峫丗乽揾傝暘偗偺曽朄乿乯
丂丂乮恾帵偵傛傞妋擣乯丂俀怓傪丄愒偲惵偲偡傞丅
丂丂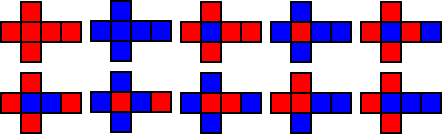
丂丂丂丂仜掙柺愊偑堎側傞俀偮偺悈憛俙丄俛偑偁傞丅俙偵偼怺偝侾俆cm傑偱丄俛偵偼怺偝俋cm傑
丂丂丂丂丂偱悈偑擖偭偰偄傞丅崱丄悈憛俙偺悈傪偡傋偰俛偵擖傟偨傜怺偝偑俁cm憹偊丄侾俀cm偲
丂丂丂丂丂側偭偨丅偦偺屻丄崱搙偼俛偺悈傪A偵備偭偔傝拲偓丄俙偲俛偺怺偝偑摨偠偵側傞傛偆偵偟
丂丂丂丂丂偨丅偙偺偲偒偺怺偝
丂丂丂幚嵺偵丄A丄俛偺掙柺愊偺斾偼丄俁丗侾俆亖侾丗俆丂偱偁傞丅偙偺偲偒丄俛偺悈傪怺偝侾乮cm乯
丂丂丂丂暘傪俙偵堏偡偲俙偺怺偝偼偦偺俆攞偺俆乮cm乯暘憹偊傞丅傛偭偰丄俛偺怺偝侾俀乮cm乯偐傜
丂丂丂丂俀乮們倣乯尭傜偟偰俙偵悈傪堏偣偽丄俙偺怺偝偼侾侽乮們倣乯偲側傝俙偲俛偺怺偝偼摨偠偵側傞丅
丂丂丂乮暿夝乯丂A丄俛偺掙柺愊偺斾偼丄俁丗侾俆亖侾丗俆丂偱偁傞丅傑偨丄俙偲俛偵擖偭偰偄偨悈偺憤
丂丂丂丂検偼丄俛偺掙柺愊偺侾俀攞側偺偱丄媮傔傞怺偝偼丄
丂丂丂丂丂乷乮俛偺掙柺愊乯亊侾俀乸亐乷乮俛偺掙柺愊乯亊乮侾亄侾/俆乯乸亖侾侽乮cm乯
丂丂丂丂仜侾侽侽侽墌嶥丄俀侽侽侽墌嶥丄俆侽侽侽墌嶥偺俁庬椶偺巻暭傪巊偭偰崌寁嬥妟傪侾侽侽侽侽墌
丂丂丂丂偵偡傞曽朄偺悢丅偨偩偟丄巊傢側偄庬椶偺巻暭偑偁偭偰傕椙偄傕偺偲偡傞丅
丂丂丂幚嵺偵丄俆侽侽侽墌嶥傪俀枃巊偆応崌偼侾捠傝丅俆侽侽侽墌嶥傪侾枃巊偆応崌偼丄俀侽侽侽墌嶥
丂丂丂傪俀枃丄侾枃丄侽枃巊偆応崌偑偁傞偺偱俁捠傝丅俆侽侽侽墌嶥傪巊傢側偄応崌丄俀侽侽侽墌嶥
丂丂丂傪俆枃丄係枃丄俁枃丄俀枃丄侾枃丄侽枃巊偆応崌偺俆捠傝丅傛偭偰丄慡晹偱丄侾侽捠傝丅
丂丂丂丂仜堦曈偑侾侽cm偺惓幍妏宍偺俀偮偺懳妏慄偺挿偝傪偦傟偧傟 x cm丄y cm 偲偡傞偲
丂丂丂丂丂偒偺 倶倷/乮倶亄倷乯 偺抣
丂丂丂幚嵺偵丄乽惓幍妏宍偺偁傞惈幙乿傛傝丄侾/倎亖侾/倶亄侾/倷亖乮倶亄倷乯/倶倷丂側偺偱丄
丂丂丂丂倶倷/乮倶亄倷乯亖倎亖侾侽
丂丂丂丂仜悢楍 俇侽丆俁侽丆俀侽丆侾俆丆侾俀丆乮丂丂乯 偵偍偄偰丄嬻強乮丂丂乯偵揔偡傞悢
丂丂丂幚嵺偵丄俇侽/俇侽丆俇侽/俁侽丆俇侽/俀侽丆俇侽/侾俆丆俇侽/侾俀丆俇侽/乮丂丂乯 偲峫偊傟偽丄
丂丂丂丂俇侽/乮丂丂乯亖俇丂側偺偱丄乮丂丂乯亖侾侽
丂丂丂乮暿夝乯弴偵慜偺悢偺丂侾/俀攞丄俀/俁攞丄俁/係攞丄係/俆攞偲暲傫偱偄傞偺偱丄
丂丂丂丂嵟屻偺崁偼丄侾俀亊俆/俇亖侾侽
丂丂丂丂仜俀侽侾俆^80 傪侾俆偱妱偭偨梋傝
丂丂丂幚嵺偵丄俀侽侾俆佭侽丂(mod 俆)丂偩偐傜丄俀侽侾俆80傪俆偱妱偭偨梋傝偼丄侽
丂丂丂俀侽侾俆佭俀丂(mod 俁)丂偩偐傜丄俀侽侾俆80傪俁偱妱偭偨梋傝偼丄乮俀2乯40佭侾丂(mod 俁)
丂丂丂傛偭偰丄俀侽侾俆80傪侾俆偱妱偭偨梋傝傪 倰 偲偡傞偲丄倰佭侽丂(mod 俆)丂偐傜丄倰亖侽丄俆丄侾侽
丂丂丂偙偺偆偪丄倰佭侾丂(mod 俁)丂傪枮偨偡傕偺偼丄侾侽偱丄偙傟偑摎偊偵側傞丅
丂丂丂乮暿夝乯俀侽侾俆佭俆丂(mod 侾俆)丂丄俆3佭俆丂(mod 侾俆)丂丄俆5佭俆丂(mod 侾俆)丂側偺偱丄
丂丂丂丂俀侽侾俆80佭俆80佭乮俆5乯16佭俆16佭乮俆3乯5丒俆佭俆5丒俆佭俆丒俆佭俀俆佭侾侽丂(mod 侾俆)
丂丂丂丂仜偁傞巇帠傪偡傞偺偵丄俙偑堦恖偱偡傞偲俁侽擔偐偐傝丄俛偑堦恖偱偡傞偲丄俀侽擔偐偐
丂丂丂丂傞丅俙丄俛丄俠偺俁恖偱偡傞偲丄俇擔偐偐傝丄俙丄俛丄俢偺俁恖偱偡傞偲丄侾侽擔偐偐傞丅
丂丂丂丂偙偺巇帠傪丄俠丄俢偺俀恖偑偡傞偲壗擔偐偐傞偐丠
丂丂丂幚嵺偵丄慡懱偺巇帠検傪侾偲偟丄偦傟偧傟偺侾擔偺巇帠検偼丄
丂丂丂俙丗侾/俁侽丂丄俛丗侾/俀侽丂丄俙亄俛亄俠丗侾/俇丂傛傝丄俠丗侾/俇亅侾/俁侽亅侾/俀侽亖俆/俇侽
丂丂丂傑偨丄俙亄俛亄俢丗侾/侾侽丂傛傝丄丂俢丗侾/侾侽亅侾/俁侽亅侾/俀侽亖侾/俇侽
丂丂丂傛偭偰丄俠亄俢偺侾擔偺巇帠検偼丄俆/俇侽亄侾/俇侽亖侾/侾侽丂傛傝丄侾侽擔偐偐傞丅
丂丂丂丂仜偁傞巇帠傪侾帪娫偱廔偊傞偺偵丄戝恖偩偗偩偲係恖丄巕嫙偩偗偩偲俉恖昁梫偱偁傞丅
丂丂丂丂戝恖俁恖偲巕嫙壗恖偐偱傗傞偲偒丄俁侽暘偱巇帠傪廔偊傞偵偼巕嫙偼壗恖昁梫偐丠
丂丂丂幚嵺偵丄戝恖侾恖偺侾帪娫摉偨傝偺巇帠検偼丄侾/係側偺偱丄俁侽暘摉偨傝偺巇帠検偼侾/俉
丂丂丂摨條偵丄巕嫙侾恖偺侾帪娫摉偨傝偺巇帠検偼丄侾/俉側偺偱丄俁侽暘摉偨傝偺巇帠検偼侾/侾俇
丂丂丂戝恖俁恖偩偲俁/俉偩偗廔偊傞偺偱丄巆傝俆/俉傪巕嫙偩偗偱峴偆丅
丂丂丂傛偭偰丄丂俆/俉亐侾/侾俇亖侾侽丂傛傝丄巕嫙偼侾侽恖昁梫丅
丂丂丂丂仜壓恾偺恾宍偵娷傑傟傞嶰妏宍偺屄悢
丂丂丂丂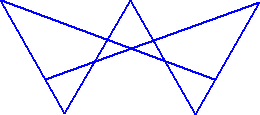
丂丂丂幚嵺偵丄悢偊偰傒傞偲丄侾侽屄偁傞丅
侾侾丒丒丒仜尨揰偲揰乮俀丆俇丆俋乯偲偺嫍棧
丂丂丂幚嵺偵丄併乮俀2亄俇2亄俋2乯亖併乮侾俀侾乯亖侾侾
丂丂丂丂 仜暯柺偵偍偄偰丄俈杮偺捈慄偱弌棃傞嶰妏宍偺嵟戝悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂 仜俙乣俬丂偼丄侾乣俋丂偺悢偱慡偰堎側傞丅俙亄俛亖俠丄俛亄俢亖俤丄俤亊俥亖俠丄俢亊俢亖俧
丂丂丂 丂丂偺偲偒偺 俫亄俬 偺抣
丂丂丂幚嵺偵丄俢亊俢亖俧丂偐傜丄乮俢丆俧乯亖乮俀丆係乯丄乮俁丆俋乯丂偱偁傞偑丄乮俢丆俧乯亖乮俀丆係乯丂偲
丂丂丂偡傞偲丄俤亊俥亖俠丂傪枮偨偡俠丄俤丄俥偼懚嵼偟側偄偺偱丄乮俢丆俧乯亖乮俁丆俋乯丂偙偺偲偒丄
丂丂丂俤亊俥亖俠丂偐傜丄乮俤丆俥丆俠乯亖乮係丆俀丆俉乯丂偱丄俛亖侾丄俙亖俈丂偲掕傑傞丅
丂丂丂傛偭偰丄俫亄俬 亖俆亄俇亖侾侾
侾俀丒丒丒仜俇亊俇偺奿巕揰偵偍偄偰丄偳偺俁揰傕侾捈慄忋偵側偄傛偆偵侾俀揰傪偲傞丅
丂丂丂幚嵺偵丄堦偮偺椺偲偟偰丄
丂丂丂丂
丂丂丂丂 仜惓巐妏悕傪俀怓偱揾傝暘偗傞曽朄偺悢
丂丂丂幚嵺偵丄揾傝暘偗傞曽朄偺悢偼慡晹偱丄侾俀捠傝偁傞丅乮仺丂嶲峫丗乽揾傝暘偗偺曽朄乿乯
丂丂乮恾帵偵傛傞妋擣乯丂俀怓傪丄愒偲惵偲偡傞丅
丂
丂丂丂丂 仜俀侽侾係26 偲 俀俇2014 偺奺壓堦寘偺榓
丂丂丂幚嵺偵丄堦偺埵偑俇偺悢傪壗夞妡偗偰傕堦偺埵偼俇偲側傞丅乮仺嶲峫丗乽嫄戝悢傪嶌傞乿乯
丂丂丂傛偭偰丄俀侽侾係26亖乮4056196乯13 偺堦偺埵偼丄俇丅俀俇2014 偺堦偺埵傕丄俇側偺偱丄
丂丂丂榓偼丄侾俀丂偲側傞丅
丂丂丂丂 仜偁傞巇帠傪偡傞偺偵 倎 偑堦恖偱傗傞偲俀係擔偐偐傝丄倐 偑堦恖偱傗傞偲係侽擔偐偐
丂丂丂丂丂傞丅偙偺巇帠傪 倎丄倐 偑堦弿偵傗傝巒傔偨偑搑拞偱 倎 偑俉擔娫媥傫偩丅偦偺娫偼 倐
丂丂丂丂丂偑堦恖偱傗偭偨丅偙偺偲偒丄倎丄倐 偑堦弿偵摥偄偨擔悢
丂丂丂幚嵺偵丄侾擔偁偨傝偺 a 偺巇帠検偼丄侾/俀係偱丄倐 偺巇帠検偼丄侾/係侽丂側偺偱丄倎丄倐 偑
丂丂丂堦弿偺侾擔偁偨傝偺巇帠検偼丄侾/俀係亄侾/係侽亖侾/侾俆偱偁傞丅倎 偑媥傫偩俉擔娫偺 倐 偺
丂丂丂巇帠検偼丄俉亊侾/係侽亖侾/俆丂側偺偱丄倎丄倐 偑堦弿偵摥偄偨巇帠検偼丄侾亅侾/俆亖係/俆
丂丂丂傛偭偰丄倎丄倐偑堦弿偵摥偄偨擔悢偼丄係/俆亐乮侾/侾俆乯亖侾俀乮擔娫乯
丂丂丂丂 仜俇恖偱俁侽擔偐偐傞巇帠偑偁傞丅偙偺巇帠傪嵟弶偼俋恖偱傗傝丄偦偺屻丄巆傝傪侾俀
丂丂丂丂丂恖偱俇擔娫摥偄偨傜廔傢偭偨丅嵟弶偺俋恖偱摥偄偨擔悢傪媮傔傛丅
丂丂丂幚嵺偵丄巇帠検偼慡晹偱丄俇亊俁侽亖侾俉侽丂偙偺偆偪丄俋恖偱 倶 擔娫巇帠傪偟偨偲偡傞偲丄
丂丂丂戣堄傛傝丄丂侾俉侽亅俋倶亖侾俀亊俇丂側偺偱丄丂俋倶亖侾俉侽亅俈俀亖侾侽俉丂傛傝丄丂倶亖侾俀
丂丂丂傛偭偰丄嵟弶偺俋恖偱摥偄偨擔悢偼丄侾俀擔
丂丂丂丂 仜偁傞巇帠傪廔偊傞偺偵丄俙偩偗偩偲侾俀擔丄俛偩偗偩偲俉擔丄俙丄俛丄俠偺俁恖偩偲係擔丄
丂丂丂丂丂俙丄俛丄俢偺俁恖偩偲係擔偐偐傞偲偄偆丅俠丄俢偱傗傞偲壗擔偐偐傞偐丅
丂丂丂幚嵺偵丄俙偺侾擔摉偨傝偺巇帠検偼丄侾/侾俀丄俛偺侾擔摉偨傝偺巇帠検偼丄侾/俉丂側偺
丂丂丂偱丄俠丄俢偺侾擔摉偨傝偺巇帠検傪偦傟偧傟丄們丄倓丂偲偍偔偲丄戣堄傛傝丄
丂丂丂侾/侾俀亄侾/俉亄們亖侾/係丂偐傜丄們亖侾/俀係丂丄侾/侾俀亄侾/俉亄倓亖侾/係丂偐傜丄倓亖侾/俀係
丂丂丂傛偭偰丄俠丄俢偺侾擔摉偨傝偺巇帠検偼丄侾/俀係亄侾/俀係亖侾/侾俀丂偲側傞偺偱丄
丂丂丂侾亐侾/侾俀亖侾俀丂傛傝丄侾俀擔偱廔傢傞丅
侾俁丒丒丒仜俀70亄俁70偼侾俁偺攞悢
丂丂丂幚嵺偵丄俀6佭亅侾丂乮倣倧倓丂侾俁乯丂傛傝丄俀70亖乮俀6乯11丒俀4佭亅俁丂乮倣倧倓丂侾俁乯
丂丂丂丂俁3佭侾丂乮倣倧倓丂侾俁乯丂傛傝丄俁70亖乮俁3乯23丒俁佭俁丂乮倣倧倓丂侾俁乯
丂丂丂傛偭偰丄丂俀70亄俁70佭侽丂乮倣倧倓丂侾俁乯丂傛傝丄俀70亄俁70偼侾俁偺攞悢偱偁傞丅
丂丂丂丂丂仜堦曈偑侾俀偺惓曽宍ABCD偺曈BC忋偵揰P傪偲傝丄佢PAD偺俀摍暘慄偑曈CD偲岎
丂丂丂丂丂丂傢傞揰傪E偲偡傞丅CE亖係 偱偁傞偲偒偺慄暘AP偺挿偝
丂丂丂
丂丂丂幚嵺偵丄佢俢俙俤=兤偲偡傞偲丄tan兤= 2/3丂傛傝丄tan(2兤) = 2(2/3)/(1-(2/3)^2) = 12/5
丂丂丂丂俛俹 = 倫丂偲偟偰丄12/p = tan(2兤) = 12/ 5 傛傝丄p = 5 側偺偱丄AP2 = 122+52 = 132
丂丂丂丂傛偭偰丄AP = 13
丂丂丂丂丂仜惓偺惍悢偑彂偐傟偨僇乕僪偑壗枃偐偁傝丄慡偰偺僇乕僪偺榓偼丄2014偱偁傞偲偡
丂丂丂丂丂丂傞丅侾埲忋2014埲壓偺擟堄偺惍悢k偵懳偟丄彂偐傟偨悢偺榓偑k偵側傞傛偆偵壗枃
丂丂丂丂丂丂偐傪慖傃弌偡偙偲偑偱偒傞偲偄偆丅傑偨丄偦偺慖傃曽偼丄摨偠悢偺彂偐傟偨僇乕僪
丂丂丂丂丂丂傪嬫暿偟側偄傕偺偲偡傞偲偨偩侾捠傝偱偁傞丅偙偺傛偆側僇乕僪偺慻崌偣偺悢
丂丂丂幚嵺偵丄(403偑4屄丄31偑12屄丄1偑30屄)丄(403偑4屄丄13偑30屄丄1偑12屄)丄
丂丂丂(403偑4屄丄1偑402屄)丄(155偑12屄丄31偑4屄丄1偑30屄)丄(155偑12屄丄5偑30屄丄1偑4屄)丄
丂丂丂(155偑12屄丄1偑154屄)丄(65偑30屄丄13偑4屄丄1偑12屄)丄(65偑30屄丄5偑12屄丄1偑4屄)丄
丂丂丂(65偑30屄丄1偑64屄)丄(31偑64屄丄1偑30屄)丄(13偑154屄丄1偑12屄)丄(5偑402屄丄1偑4屄)丄
丂丂丂(1偑2014屄)丂偺侾俁捠傝
丂丂丂丂丂仜壓恾偺巐妏宍俙俛俠俢偵偍偄偰丄慄暘俙俛偺挿偝
丂丂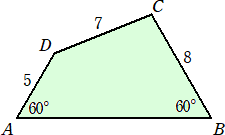
丂丂丂幚嵺偵丄壓恾偺傛偆偵曗彆慄傪堷偄偰丄惓嶰妏宍俙俛俤傪嶌傞丅
丂丂丂乮仺丂嶲峫丗乽曈偲妏偺旤偟偄娭學嘦乿乯
丂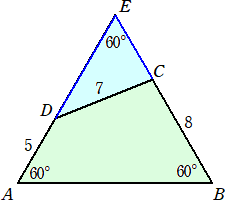
丂丂丂偙偺偲偒丄俙俛亖倶丂偲偍偗偽丄丂俤俢亖倶亅俆丂丄俤俠亖倶亅俉丂側偺偱丄梋尫掕棟傛傝丄
丂丂丂俈2亖乮倶亅俆乯2亄乮倶亅俉乯2亅俀丒乮倶亅俆乯乮倶亅俉乯們倧倱俇侽亱側偺偱丄倶亖侾俁
丂丂丂乮暿夝乯(5^2+8^2-7^2)/(2*5*8)=1/2 偲偄偆寁嶼偐傜丄3曈偑 5丄7丄8 偺嶰妏宍偺 5 偲 8
丂丂丂偺曈偱嫴傑傟傞妏偺妏搙偼60亱偲傢偐傞丅(婛抦偲偡傟偽寁嶼晄梫)
丂丂丂恾偺宍偼丄俁曈偑 5丄7丄8 偺嶰妏宍偺 5 偺曈偲 8 偺曈偺奜懁偵丄偦傟偧傟惓嶰妏宍
丂丂丂傪偔偭偮偗偨宍側偺偱丄AB=5+8=13丅
侾係丒丒丒仜俈暘梡偲俁暘梡偺嵒帪寁傪梡偄偰丄偪傚偆偳侾係暘傪偼偐傞偙偲偑弌棃傞丅
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂丂仜幍妏宍偺懳妏慄偺杮悢
丂丂丂幚嵺偵丄丂俈亊係亐俀亖侾係
丂丂丂丂丂仜壓恾偺幬慄晹暘偺柺愊
丂丂丂丂丂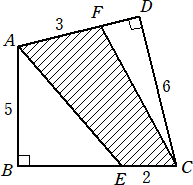
丂丂丂幚嵺偵丄懳妏慄俙俠傪堷偄偰俀偮偵暘妱偟丄俀亊俆亐俀亄俁亊俇亐俀亖侾係
丂丂丂丂丂仜 倶亅侾/倶亖俀 偱偁傞偲偒偺 倶3亅侾/倶3 偺抣
丂丂丂幚嵺偵丄倶3亅侾/倶3亖乮倶亅侾/倶乯3亄俁乮倶亅侾/倶乯亖俉亄俇亖侾係
丂丂丂丂丂仜係偮偺帺慠悢 倶丄倷丄倸丄倵 乮倶亞倷亞倸乯偑偁傝丄愊 倶倷倸 偼丄俈俀偱丄榓 倶亄倷亄倸 偼丄
丂丂丂丂丂丂倵 偱偁傞丅偙偺俀偮偺娭學幃偐傜丄倶丄倷丄倸丄倵 偺抣傪媮傔傞応崌丄倵偺偁傞抣偵偮
丂丂丂丂丂丂偄偰丄倶丄倷丄倸偺抣偺慻崌偣偑俀捠傝弌棃傞応崌偑偁傞丅偦偺偲偒偺倵偺抣
丂丂丂幚嵺偵丄俈俀亖俀3亊俁2丂側偺偱丄峫偊傜傟傞応崌偼師偺俇捠傝丅
丂丂丂俀亊俁亄俀亊俁亄俀亖侾係丄俀亊俁2亄俀亄俀亖俀俀丄俀2亊俁亄俀亄俁亖侾俈丄
丂丂丂俀2亄俀亊俁亄俁亖侾俁丄俀2亄俀亄俁2亖侾俆丄俀3亄俁亄俁亖侾係
丂丂丂傛偭偰丄戣堄傛傝丄媮傔傞悢偼丄倵亖侾係
丂丂丂丂丂仜俇恖偱俀俉擔偐偐傞巇帠偑偁傞丅偙偺巇帠傪嵟弶偼俉恖偱侾侽擔娫傗傝丄巆傝傪
丂丂丂丂丂丂係擔娫偱廔偊傞偵偼丄恖悢傪壗恖憹傗偣偽傛偄偐丅
丂丂丂幚嵺偵丄巇帠検偼慡晹偱丄俇亊俀俉亖侾俇俉丂偙偺偆偪丄侾侽擔娫偱丄俉亊侾侽亖俉侽丂偑廔
丂丂丂傢偭偰偄傞偺偱丄巆傝侾俇俉亅俉侽亖俉俉丂偱偁傞丅偙傟傪係擔娫偱廔傢傜偣傞偵偼丄
丂丂丂俉俉亐係亖俀俀(恖乯昁梫偱偁傞丅傛偭偰丄恖悢傪丄俀俀亅俉亖侾係乮恖乯丂憹傗偣偽傛偄丅
侾俆丒丒丒仜暯柺偵偍偄偰丄俉杮偺捈慄偱弌棃傞嶰妏宍偺嵟戝悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂丂仜壓恾偺傛偆偵丄抧柺偵拰偑俀杮棫偭偰偄偰丄偦偺偆偪偺嵍懁偺拰偵偼丄侾偐傜俆傑
丂丂丂丂丂丂偱偺斣崋偺偮偗傜傟偨墌斅偑丄忋偐傜斣崋弴偵愊傑傟偰偄傞丅
| 丂 |
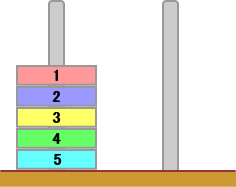 |
丂偄傑丄侾夞偺憖嶌偱丄忋偐傜丄侾枃傑偨偼俀枃偺
墌斅傪丄懠偺拰傊堏摦偝偣傞丅偨偩偟丄俀枃偺偲
偒偼丄忋壓偺弴斣偼丄偦偺傑傑偲偡傞丅
丂壗夞偐憖嶌傪偟偰丄塃懁偺拰偵丄墌斅偑丄忋偐
傜弴斣偵侾偐傜俆傑偱暲傇傛偆偵偟偨偄丅
丂偙偺偲偒偺憖嶌夞悢偺嵟彫抣 |
丂丂丂幚嵺偵丄弶婜忬懺(12345,丂)丄姰惉宍(丂,12345)丂偲偟偰
丂丂丂(12345,丂)仺(345,12)仺(5,3412)仺( ,53412)仺(53,412)仺(4153,2)仺(24153, )仺(153,24)
丂丂丂仺(3,1524)仺( ,31524)仺(31,524)仺(5231,4)仺(45231, )仺(231,45)仺(1,2345)仺(
,12345)
丂丂丂乮仺丂嶲峫丗乽墌斅偺堏摦乿乯
丂丂丂丂丂仜惗搆悢偑俶恖偺妛峑偱偼丄惗搆偑俆偮偺僌儖乕僾俙丄俛丄俠丄俢丄俤偵暘偐傟丄廳暋
丂丂丂丂丂偡傞傕偺偼偄側偄偟僌儖乕僾偺恖悢傕偡傋偰堎側傞偲偄偆丅奺僌儖乕僾偵偮偄偰師偺
丂丂丂丂丂偙偲偑敾柧偟偨丅
丂丂丂丂丂丂俙偺恖悢偼丄慡懱偺俆暘偺侾傛傝俁恖彮側偄丅
丂丂丂丂丂丂俛偺恖悢偼丄俙偺恖悢偺敿暘傛傝係恖懡偄丅
丂丂丂丂丂丂俠偺恖悢偼丄俙偺恖悢傛傝懡偄丅
丂丂丂丂丂丂俢偺恖悢偼丄俠偺恖悢偺俀攞偱偁傞丅
丂丂丂丂丂丂俤偺恖悢偼丄俛偲俠偺恖悢偺暯嬒偱偁傞丅
丂丂丂丂丂偙傟傜偺忣曬傪惍棟偡傞偲偒丄僌儖乕僾俛偺恖悢
丂丂丂丂丂乮嶲峫丗拀攇戝妛晬懏嬵応崅峑悢妛壢妛尋媶夛曇丂乽俠倎倖倕丂俛倧倢倢倵倕們倠丂俶倧丏嘮乿乯
丂丂丂幚嵺偵丄忦審傛傝丄俙亖俶/俆亅俁丄俛亖俙/俀亄係丄俠亜俙丄俢亖俀俠丄俤亖乮俛亄俠乯/俀
丂丂丂俶偼俆偺攞悢側偺偱丄俶亖俆俶乫偲偍偗傞丅偙偺偲偒丄
丂丂丂俙亖俶乫亅俁丄俛亖俶乫/俀亄俆/俀丄俠亜俙丄俢亖俀俠丄俤亖俶乫/係亄俠/俀亄俆/係
丂丂丂俶亖俙亄俛亄俠亄俢亄俤丂側偺偱丄
丂丂丂俆俶乫亖乮俶乫亅俁乯亄乮俶乫/俀亄俆/俀乯亄俠亄俀俠亄乮俶乫/係亄俠/俀亄俆/係乯
丂丂丂傛偭偰丄侾俁俶乫/係亖俈俠/俀亄俁/係丂傛傝丄侾俁俶乫亖侾係俠亄俁
丂丂丂偙偙偱丄侾俁亊乮亅俁乯亖侾係亊乮亅俁乯亄俁丂側偺偱丄侾俁乮俶乫亄俁乯亖侾係乮俠亄俁乯
丂丂丂侾俁偲侾係偼屳偄偵慺側偺偱丄俶乫亄俁亖侾係俿丂乮俿偼帺慠悢乯丂偲偍偗傞丅
丂丂丂偙偺偲偒丄俠亄俁亖侾俁俿丂偲側傞偺偱丄俶乫亖侾係俿亅俁丂偱丄
丂丂丂俙亖侾係俿亅俇丂丄俛亖俈俿亄侾丂丄俠亖侾俁俿亅俁丂丄俢亖俀俇俿亅俇丂丄俤亖侾侽俿亅侾
丂丂丂俠亜俙丂傛傝丄侾俁俿亅俁亜侾係俿亅俇丂側偺偱丄侾亝俿亙俁丂俿偼帺慠悢側偺偱丄俿亖侾丄俀
丂丂丂俿亖侾丂偺偲偒丄俙亖俛亖俉丂偲側傝丄忦審偵斀偡傞丅
丂丂丂俿亖俀丂偺偲偒丄忦審偵揔偟丄俛亖侾俆丂偲側傞丅
侾俇丒丒丒仜俈倶佭俀 乮倣倧倓 俀俀乯傪枮偨偡嵟彫偺帺慠悢夝
丂丂丂幚嵺偵丄丂俀俀倶佭侽 乮倣倧倓 俀俀乯丂丄俀侾倶佭俇 乮倣倧倓 俀俀乯丂傛傝丄丂倶佭亅俇 乮倣倧倓 俀俀乯
丂丂丂傛偭偰丄倶佭侾俇 乮倣倧倓 俀俀乯丂偐傜丄嵟彫偺帺慠悢夝偼丄侾俇
丂丂丂丂 仜俀師曽掱幃 倶2亅係倶亄倠亖侽 偺嫊悢夝偺俁忔偑幚悢偲側傞傛偆側幚悢 倠 偺抣
丂丂丂幚嵺偵丄敾暿幃 俢/係亖係亅倠亙侽丂傛傝丄丂倠亜係
丂丂丂嫊悢夝傪 倶 偲偡傞偲丄倶3亖倶乮係倶亅倠乯亖係乮係倶亅倠乯亅倠倶亖乮侾俇亅倠乯倶亅係倠丂偲側傝丄
丂丂丂偙傟偑幚悢偱偁傞偨傔偵偼丄丂侾俇亅倠亖侽丂傛傝丄丂倠亖侾俇
丂丂丂丂 仜廃埻偺挿偝偑侾俇偱偁傞傛偆側挿曽宍偺柺愊偺嵟戝抣
丂丂丂幚嵺偵丄廲 倶丄墶 倷 偲偡傞偲丄丂俀倶亄俀倷亖侾俇丂偐傜丄倶亄倷亖俉
丂丂丂丂偙偺偲偒丄挿曽宍偺柺愊亖倶倷亖倶乮8亅倶乯亖亅乮倶亅係乯2亄侾俇
丂丂丂丂侽亙倶亙俉 偵偍偄偰丄倶亖係 偺偲偒嵟戝偱丄嵟戝抣 侾俇
丂丂丂丂 仜乮侾亄倝乯8 偺抣
丂丂丂幚嵺偵丄乮侾亄倝乯2亖俀倝丂傛傝丄乮侾亄倝乯8亖乮俀倝乯4亖侾俇
丂丂丂丂 仜俀係俀柤偺惗搆偑偡傋偰係恖埲壓偺拠椙偟僌儖乕僾偵暘偐傟偰偄傞傕偺偲偡傞丅
丂丂丂丂丂偙傟傜偺僌儖乕僾傪曵偝偢偵丄侾俈恖傑偱廂梕偱偒傞晹壆偺偄偔偮偐偵妱傝怳傝偨偄丅
丂丂丂丂丂僌儖乕僾摨巑偺娭學偼峫偊側偄傕偺偲偡傞偲偒丄梡堄偡傋偒晹壆悢偺嵟彫抣
丂丂丂幚嵺偵丄僌儖乕僾偑偡傋偰扨撈偺侾恖偩偲丄俀係俀亐侾俈亖侾係丒丒丒係丂偐傜丄侾俆晹壆昁梫丅
丂丂丂幚偼丄乽奺晹壆偵偼昁偢侾俆恖埲忋廂梕偱偒傞乿偲偄偆偙偲偑師偺傛偆偵偟偰帵偝傟傞丅
丂丂丂偁傞晹壆偱侾係恖埲壓偲壖掕偡傞丅僌儖乕僾偺恖悢偑俀恖埲忋偵偮偄偰丄侾係恖偺峔
丂丂丂惉傪峫偊傞偲丄係係係俀丂丂係係俁俁丂丂俁俁俁俁俀丂丂俁俁俀俀俀俀丂丂俀俀俀俀俀俀俀丂偲偄傠偄傠側
丂丂丂僷僞乕儞偑偁傞丅
丂丂丂奺僌儖乕僾偺恖悢偑懡偄弴偵晹壆偵廂梕偟偰偄偔傕偺偲偡傞丅偁傞晹壆偱丄侾係恖傑偱
丂丂丂偟偐廂梕偱偒側偄偲偡傞偲丄巆傝榞俁恖側偺偱丄師偵擖傞傋偒僌儖乕僾偺恖悢偼丄係恖偺
丂丂丂偼偢丅偲偙傠偑丄偙傟偼丄忋婰偺侾係恖偺僷僞乕儞偱丄恖悢偺懡偄弴偵晹壆偵擖傟偰偄
丂丂丂傞偙偲偵柕弬偡傞丅傛偭偰丄奺晹壆偵偼昁偢侾俆恖埲忋廂梕偱偒傞偙偲偑暘偐傞丅
丂丂丂偟偨偑偭偰丄侾俆偺晹壆偵侾俆恖埲忋擖傟傟偽丄侾俆亊侾俆亖俀俀俆偱丄俀係俀亅俀俀俆亖侾俈
丂丂丂傛傝丄侾俈恖埲壓偺巆偭偨惗搆傪傕偆堦偮偺晹壆偵擖傟傟偽傛偄丅
丂丂丂埲忋偐傜丄昁梫偲偝傟傞晹壆悢偺嵟彫抣偼丄侾俇 偱偁傞丅
丂丂丂丂乮仺丂嶲峫丗乽晹壆妱傝偺栤戣乿乯
丂丂丂丂 仜侾丄俀丄丒丒丒丄侾俇 偲斣崋偑彂偄偰偁傞僇乕僪偑忋偐傜斣崋偺彫偝偄弴偵廳偹偰偁傞丅
丂丂丂丂丂堦斣忋偺僇乕僪傪幪偰丄偦偺師偵堦斣忋偵側偭偨僇乕僪傪巆傝偺僇乕僪偺堦斣壓偵擖
丂丂丂丂丂傟傞丅偙偺憖嶌傪孞傝曉偡偲偒丄嵟屻傑偱巆傞僇乕僪偺斣崋
丂丂丂幚嵺偵丄侾丂俀丂俁丂係丂俆丂俇丂俈丂俉丂俋丂侾侽丂侾侾丂侾俀丂侾俁丂侾係丂侾俆丂侾俇
丂丂丂仺俁丂係丂俆丂俇丂俈丂俉丂俋丂侾侽丂侾侾丂侾俀丂侾俁丂侾係丂侾俆丂侾俇丂俀
丂丂丂仺俆丂俇丂俈丂俉丂俋丂侾侽丂侾侾丂侾俀丂侾俁丂侾係丂侾俆丂侾俇丂俀丂係
丂丂丂仺俈丂俉丂俋丂侾侽丂侾侾丂侾俀丂侾俁丂侾係丂侾俆丂侾俇丂俀丂係丂俇
丂丂丂丂丒丒丒丒丒
丂丂丂仺俀丂係丂俇丂俉丂侾侽丂侾俀丂侾係丂侾俇
丂丂丂仺俇丂俉丂侾侽丂侾俀丂侾係丂侾俇丂係
丂丂丂仺侾侽丂侾俀丂侾係丂侾俇丂係丂俉
丂丂丂仺侾係丂侾俇丂係丂俉丂侾俀
丂丂丂仺係丂俉丂侾俀丂侾俇
丂丂丂仺侾俀丂侾俇丂俉
丂丂丂仺俉丂侾俇
丂丂丂仺侾俇丂丒丒丒丂埲忋偐傜丄嵟屻傑偱巆傞僇乕僪偼丄侾俇
丂丂丂丂 仜惓俉妏宍偺俁偮偺捀揰傪寢傫偱偱偒傞嶰妏宍偺偆偪偱丄俀摍曈嶰妏宍偱傕捈妏嶰妏
丂丂丂丂丂宍偱傕側偄傕偺偺屄悢
丂丂丂幚嵺偵丄侾偮偺捀揰傪屌掕偟丄嵟抁曈偵傛傞応崌暘偗偱媮傔傞丅
丂丂丂捀揰俙傪屌掕偟偰峫偊傞偲丄嵟抁曈AB偺応崌丄奩摉偡傞嶰妏宍偼丄仮ABD偲仮ABG
丂丂丂嵟抁曈AC偺応崌偼丄奩摉偺嶰妏宍偼側偄
丂丂丂丂傛偭偰丄捀揰偼丄俙乣俫偺俉捠傝偁傞偺偱丄媮傔傞応崌偺悢偼丄丂俀亊俉亖侾俇乮屄乯
丂丂丂乮暿夝乯嶰妏宍偺屄悢 8俠3亖俆俇(屄乯偺偆偪丄
丂丂丂丂俀摍曈嶰妏宍偱偁傞傕偺偼丄丂俉亄俉亄俉亖俀係乮屄乯
丂丂丂丂捈妏嶰妏宍偱偁傞傕偺偼丄丂係亊俇亖俀係乮屄乯
丂丂丂丂捈妏俀摍曈嶰妏宍偱偁傞傕偺偼丄丂係亊俀亖俉乮屄乯
丂丂丂側偺偱丄媮傔傞応崌偺悢偼丄丂俆俇亅乮俀係亄俀係亅俉乯亖侾俇乮屄乯
丂丂丂丂 仜侾屄係侽墌偺彜昳俙偲侾屄俇侽墌偺彜昳俛傪崌傢偣偰俆侽屄峸擖傪梊掕偟偰偄偨偲偙傠丄
丂丂丂丂丂彜昳俙丄彜昳俛偺峸擖梊掕屄悢傪庢傝堘偊偰偟傑偄丄摉弶梊掕傛傝俁俇侽墌埨偔側偭偨丅
丂丂丂丂丂傕偲傕偲偺彜昳俙偺峸擖梊掕悢
丂丂丂幚嵺偵丄侾屄庢傝堘偊傞偲丄俀侽墌嵎側偺偱丄俁俇侽亐俀侽亖侾俉屄庢傝堘偊偨偙偲偵側傞丅
丂丂丂傛偭偰丄乮俆侽亄侾俉乯亐俀亖俁係 傛傝丄摉弶偺彜昳俙偺峸擖梊掕悢偼丄俁係亅侾俉亖侾俇屄
丂丂丂乮暿夝乯摉弶偺彜昳俙偺峸擖屄悢傪倶屄偲偡傞偲丄彜昳俛偺峸擖屄悢偼俆侽亅倶屄
丂丂丂丂乮係侽倶亄俇侽乮俆侽亅倶乯乯亖俇侽倶亄係侽乮俆侽亅倶乯亄俁俇侽丂偐傜丄係侽倶亖俇係侽 傛傝丄倶亖侾俇
侾俈丒丒丒仜俀^3亄俁^2偺抣
丂丂丂幚嵺偵丄梌幃亖俉亄俋亖侾俈
丂丂丂丂 仜帺慠悢値偵懳偟偰丄俇値2亄俀俆値亄侾係偑暯曽悢偲側傞嵟彫抣偺惓偺暯曽崻
丂丂丂幚嵺偵丄値亖侾丄俀丄丒丒丒丄俆丄丒丒丒丂傪戙擖偟偰丄
丂丂丂丂値亖俆偺偲偒丄俇値2亄俀俆値亄侾係亖俀俉俋亖侾俈2
丂丂丂丂 仜慺悢倫丄倯傪梡偄偰丄倫q亄倯p 偲昞偝傟傞慺悢
丂丂丂幚嵺偵丄慺悢倫丄倯偑偲傕偵婏悢偲偡傞偲丄倫q亄倯p 偼嬼悢偲側傝丄嬼悢偺慺悢偼俀偺傒
丂丂丂丂偟偐傞偵丄倫q亄倯p亖俀丂偲側傞慺悢倫丄倯偼懚嵼偟側偄丅傛偭偰丄倫亖俀丄倯偼俁埲忋偺慺
丂丂丂丂悢偲偟偰傛偄丅倫亖俀丄倯亖俁丂偺偲偒丄俀3亄俁2亖俉亄俋亖侾俈 偼慺悢偱偁傞丅
丂丂丂丂倫亖俀丄倯亖俀値亄侾丂乮値偼俀埲忋偺帺慠悢乯丂偺偲偒丄俀q亖俀丒係値佭俀丂乮倣倧倓丂俁乯
丂丂丂丂傑偨丄倯2亖係値2亄係値亄侾亖係値乮値亄侾乯亄侾丂偵偍偄偰丄
丂丂丂丂値亖俁倠丂乮倠偼帺慠悢乯丂偺偲偒丄倯2亖侾俀倠乮俁倠亄侾乯亄侾佭侾丂乮倣倧倓丂俁乯
丂丂丂丂値亖俁倠亄侾丂乮倠偼帺慠悢乯丂偺偲偒丄倯亖俁乮俀倠亄侾乯丂偲側傝丄倯偼慺悢偲側傜側偄
丂丂丂丂値亖俁倠亄俀丂乮倠偼帺慠悢乯丂偺偲偒丄
丂丂丂丂丂倯2亖係乮俁倠亄俀乯乮俁倠亄俁乯亄侾亖侾俀乮倠亄侾乯乮俁倠亄俀乯亄侾佭侾丂乮倣倧倓丂俁乯
丂丂丂丂埲忋偐傜丄俀q亄倯2佭俀亄侾佭侽丂乮倣倧倓丂俁乯丂傛傝丄俀q亄倯2 偼慺悢偲側傝偊側偄丅
丂丂丂丂偟偨偑偭偰丄倫q亄倯p 偲昞偝傟傞慺悢偼丄侾俈
侾俉丒丒丒仜壓恾偺撌巐妏宍偺柺愊
丂丂丂丂丂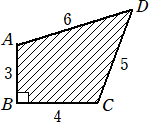
丂丂丂幚嵺偵丄俙偲俠傪寢傃丄俠偐傜俙俢偵悅慄傪壓傠偟丄崌摨側俁偮偺捈妏嶰妏宍偵暘妱偟偰丄
丂丂丂乮俁亊係亐俀乯亊俁亖侾俉
丂丂丂丂 仜佢C偑捈妏偱偁傞捈妏嶰妏宍ABC偱丄幬曈AB忋偵揰D丄E 傪庢傝乮D偺曽偑A偵嬤
丂丂丂丂丂偄乯丄曈AC忋偵揰F傪庢傞丅AD亖DF亖FE亖EC亖CB 偱偁傞偲偒偺佢BAC偺戝偒偝
丂丂丂幚嵺偵丄俀摍曈嶰妏宍偺惈幙偐傜丄俆佢俛俙俠亖俋侽亱側偺偱丄丂佢俛俙俠亖侾俉亱
丂丂丂丂 仜暯柺忋偵俙俛亖俇偲側傞俀掕揰俙丄俛傪偲傞丅崱丄摦揰俹偼丄俹俙亄俹俛亖侾俀傪枮偨偡
丂丂丂丂丂傛偆偵丄捈慄俙俛偺忋懁傪摦偔丅偝傜偵丄捈慄俙俛偺壓懁偵俙偍傛傃俛傪拞怱偲偟偰敿
丂丂丂丂丂宎俁偺敿墌忋傪摦偔揰俻丄俼偑偁傞丅
丂丂丂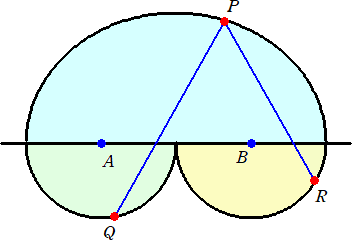
丂丂丂丂偙偺偲偒偺愜傟慄俹俻亄俹俼偺挿偝偺嵟戝抣
丂丂丂幚嵺偵丄壓恾偺傛偆偵丄俁揰俹丄俙丄俻偍傛傃俹丄俛丄俼偑堦捈慄偵暲傇偲偒丄
丂丂丂愜傟慄俹俻亄俹俼偺挿偝偼嵟戝偱丄嵟戝抣偼丄侾俀亄俁亄俁亖侾俉
丂丂丂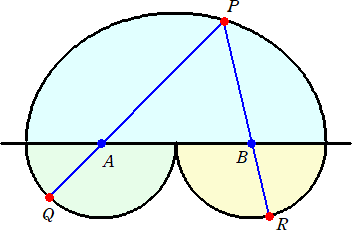
丂丂丂丂 仜倫亖俀亄 偺彫悢晹暘傪 倯 偲偡傞偲偒偺 倫2亄倯2 偺抣
偺彫悢晹暘傪 倯 偲偡傞偲偒偺 倫2亄倯2 偺抣
丂丂丂幚嵺偵丄倫亖俀亄 偺惍悢晹暘偼係側偺偱丄倯亖俀亄
偺惍悢晹暘偼係側偺偱丄倯亖俀亄 亅係亖
亅係亖 亅俀
亅俀
丂丂丂傛偭偰丄倫2亄倯2亖乮俀亄 乯2亄乮
乯2亄乮 亅俀乯2亖侾俉
亅俀乯2亖侾俉
丂丂丂丂 仜悢楍 侾丆俁丆係丆俈丆俇丆侾俀丆俉丆侾俆丆侾俁丆乮丂丂乯 偵偍偄偰丄嬻強乮丂丂乯偵揔偡傞悢
丂丂丂幚嵺偵丄戞値崁偼丄値偺惓偺栺悢偺憤榓側偺偱丄侾侽偺惓栺悢偼丄侾丄俀丄俆丄侾侽 側偺偱丄
丂丂丂丂崌寁偟偰 侾俉
丂丂丂丂 仜挿曽宍俙俛俠俢偵偍偄偰丄懳妏慄俙俠忋偵揰俹傪偲傝丄曈俙俢丄俛俠偵悅慄傪壓偟丄偦
丂丂丂丂丂偺懌傪偦傟偧傟俵丄俶偲偍偔丅
丂丂
丂丂丂丂仮俙俹俵亖侾丄仮俹俠俶亖係丂偺偲偒偺挿曽宍俙俛俠俢偺柺愊
丂丂丂幚嵺偵丄仮俙俹俵佷仮俹俠俶丂偱丄仮俙俹俵亖侾丄仮俹俠俶亖係丂傛傝丄
丂丂丂仮俙俹俵 丗 仮俹俠俶亖侾 丗 係丂偐傜丄丂俙俵2 丗 俶俠2亖侾 丗 係 傛傝丄丂俙俵 丗 俶俠亖侾 丗 俀
丂丂丂傛偭偰丄丂俶俠亖俵俛丂傛傝丄丂俙俵 丗 俵俛亖侾 丗 俀丂偡側傢偪丄丂俙俵 丗 俙俢亖侾 丗 俁
丂丂丂偟偨偑偭偰丄丂仮俙俹俵 丗 仮俙俠俢亖侾2 丗 俁2亖侾 丗 俋 偐傜丄丂仮俙俠俢亖俋仮俙俹俵亖俋
丂丂丂傛傝丄丂挿曽宍俙俛俠俢亖俀仮俙俠俢亖侾俉
侾俋丒丒丒仜丂俋/倢倧倗10俁亙侾俋
丂丂丂幚嵺偵丄悢楍 乷乮侾亄侾/値乯値乸偼扨挷憹壛偱丄帺慠懳悢偺掙 倕乮亙俁乯偵廂懇偡傞偐傜丄
丂丂丂丂乮侾亄侾/値乯値亙俁丂偑惉傝棫偮丅値亖俋傪戙擖偟偰丄丂乮侾侽/俋乯9亙俁丂偡側傢偪丄
丂丂丂侾侽9亙俁丒俋9亖俁19丂偑惉傝棫偮丅椉曈偺侾侽傪掙偲偡傞懳悢傪偲偭偰丄俋亙侾俋丒倢倧倗10俁
丂丂丂傛偭偰丄俋/倢倧倗10俁亙侾俋丂偑惉傝棫偮丅
乮僐儊儞僩乯丂忋婰偱梡偄偨晄摍幃丂乮侾亄侾/値乯値亙俁丂傪尩枾偵徹柧偟偰偍偙偆丅
丂俀崁掕棟傛傝丄丂乮侾亄侾/値乯値亖儼k=0n 値俠k乮侾/値乯k亖侾亄儼k=1n 値俠k/値k
丂丂偙偙偱丄丂値俠k/値k亖値乮値亅侾乯丒丒丒乮値亅倠亄侾乯/乮値k丒倠両乯亝侾/倠両亝侾/俀k-1 側偺偱丄
丂丂乮侾亄侾/値乯値亝侾亄儼k=1n 乮侾/俀乯k-1亖侾亄俀乮侾亅乮侾/俀乯値乯亖俁亅乮侾/俀乯値-1亙俁
丂偑惉傝棫偮丅
乮嶲峫乯丂偙偺栤戣偺椶戣偑丄暯惉俀係擭搙偺怴妰戝妛慜婜棟宯偱弌戣偝傟偨丅
丂丂丂丂 仜 侾曈偑俁偺棫曽懱偐傜侾曈偑俀偺棫曽懱傪愗傝庢偭偨屻偺巆偭偨晹暘偺懱愊
丂丂丂幚嵺偵丄丂俁3亅俀3亖侾俋
丂丂丂丂 仜摨偠戝偒偝偺晄摟柧側棫曽懱俀俈屄偑俁亊俁亊俁偵愊傫偱偁傞丅偙傟傪僇儊儔偱嶣塭
丂丂丂丂丂偡傞偲偒丄嵟戝偱壗屄偺棫曽懱傪侾枃偺幨恀偵廂傔傞偙偲偑偱偒傞偐丅偨偩偟丄嬀側
丂丂丂丂丂偳傪巊偭偰娫愙揑偵幨偡偺偼擣傔傜傟側偄丅
丂丂丂幚嵺偵悢偊偰丄侾俋屄
乮捛婰乯丂椷榓俇擭俆寧俀俋擔晅偗
丂丂丂丂 仜侾俈係俉1919 傪侾俋侾俋偱妱偭偨梋傝
仈偙偺栤戣傪丄WolframAlpha愭惗偵乽侾俈係俉1919 倣倧倓 侾俋侾俋乿偲栤偆偲丄弖帪偵丄乽侾俋乿偲
丂曉偟偰偔傟傞偑丄偪傚偭偲枴婥側偄丅庤寁嶼偵挧愴偟偰傒偨丅
丂丂丂幚嵺偵丄侾俈係俉亖俀2丒侾俋丒俀俁丂丄侾俋侾俋亖侾俋丒侾侽侾丂偵拲堄偟偰丄
丂侾俈係俉1919 亖俀3838丒侾俋1919丒俀俁1919 傛傝丄
丂侾俈係俉1919 亖俀3838丒侾俋1919丒俀俁1919亖侾俋丒侾侽侾倠亄俼乫丂偲偍偔偲丄
丂嵍曈偼侾俋偺攞悢丄侾俋丒侾侽侾傕侾俋偺攞悢側偺偱丄丂俼乫偼丄侾俋偺攞悢偲側傞丅
偦偙偱丄丂俼乫亖侾俋俼丂偲偍偔偲丄丂俀3838丒侾俋1918丒俀俁1919亖侾侽侾倠亄俼 偲彂偗傞丅
丂慺悢侾侽侾偲俀偼屳偄偵慺側偺偱丄丂俀100佭侾丂乮倣倧倓丂侾侽侾乯丂偐傜丄
丂俀3838佭俀38丂乮倣倧倓丂侾侽侾乯丂偱丄俀10佭侾係丂乮倣倧倓丂侾侽侾乯丂偐傜丄
丂俀30佭侾係3亖俀俈係係佭侾俈丂乮倣倧倓丂侾侽侾乯
傛偭偰丄丂俀3838佭俀38佭侾俈丒俀8亖係俁俆俀佭俋丂乮倣倧倓丂侾侽侾乯
摨條偵偟偰丄丂慺悢侾侽侾偲侾俋偼屳偄偵慺側偺偱丄丂侾俋100佭侾丂乮倣倧倓丂侾侽侾乯丂偐傜丄
丂侾俋1918佭侾俋18丂乮倣倧倓丂侾侽侾乯 偱丄丂侾俋3亖俇俉俆俋佭俋俀丂乮倣倧倓丂侾侽侾乯
丂侾俋6亖俋俀2亖俉係俇係佭俉侾丂乮倣倧倓丂侾侽侾乯
傛偭偰丄丂侾俋1918佭侾俋18佭俉侾3亖俆俁侾係係侾佭俉侽丂乮倣倧倓丂侾侽侾乯
傑偨丄丂慺悢侾侽侾偲俀俁偼屳偄偵慺側偺偱丄丂俀俁100佭侾丂乮倣倧倓丂侾侽侾乯丂偐傜丄
丂俀俁1919佭俀俁19丂乮倣倧倓丂侾侽侾乯丂偱丄俀俁3亖侾俀侾俇俈佭係俈丂乮倣倧倓丂侾侽侾乯丂偐傜丄
丂俀俁9亖係俈3亖侾侽俁俉俀俁佭俋俇丂乮倣倧倓丂侾侽侾乯
傛偭偰丄丂俀俁1919佭俀俁19亖俀俁9丒俀俁9丒俀俁佭俋俇丒俋俇丒俀俁亖俀侾侾俋俇俉佭俈侽丂乮倣倧倓丂侾侽侾乯
埲忋偐傜丄丂俀3838丒侾俋1918丒俀俁1919佭俋丒俉侽丒俈侽亖俆侽係侽侽佭侾丂乮倣倧倓丂侾侽侾乯丂傛傝丄
丂俀3838丒侾俋1918丒俀俁1919亖侾侽侾倠亄侾丂偲彂偗傞偙偲偑暘偐偭偨丅
丂偦偙偱丄椉曈偵侾俋傪妡偗偰
丂侾俈係俉1919亖俀3838丒侾俋1919丒俀俁1919亖侾俋乮侾侽侾倠亄侾乯亖侾俋侾俋倠亄侾俋
偟偨偑偭偰丄丂侾俈係俉1919傪侾俋侾俋偱妱偭偨梋傝偼丄侾俋丂偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂庤傕偲偵偁傞揹戩偱偼僆乕僶乕僼儘乕偱寁嶼偑晄壜擻側偺偱偡偑丄忋婰偺傛偆
丂丂丂丂丂偵丄僼僃儖儅乕偺彫掕棟傪忋庤偔妶梡偡傟偽丄庤寁嶼偱媮傑傞傫偱偡偹両
俀侽丒丒丒仜敧妏宍偺懳妏慄偺杮悢
丂丂丂幚嵺偵丄丂俉亊俆亐俀亖俀侽
丂丂丂丂 仜巐妏宍ABCD偵偍偄偰丄AD乤BC丄佢ABC=佢BDC=佢ACB/2偱偁傝丄捈慄BD偼
丂丂丂丂丂佢ABC偺俀摍暘慄偵側偭偰偄傞偲偒丄佢ABC偺戝偒偝
丂丂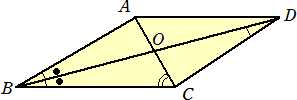
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂 仜壓恾偺傛偆側仮俙俛俠偵偍偄偰丄佢倶 偺戝偒偝傪媮傔傛丅
丂丂丂丂丂偨偩偟丄俵偼曈俛俠偺拞揰丄俶偼曈俙俛偺拞揰丄俫偼俙傛傝曈俛俠偵壓傠偟偨悅慄偺懌
丂丂丂丂丂偲偡傞丅
丂丂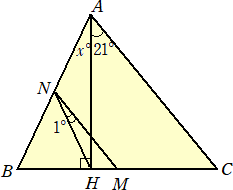
丂丂丂幚嵺偵丄俠亖俇俋亱偱丄拞揰楢寢掕棟傛傝丄俵俶偲俙俠偼暯峴側偺偱丄佢俫俵俶亖俇俋亱
丂丂丂丂傛偭偰丄佢俛俫俶亖俈侽亱傛傝丄佢俙俫俶亖俀侽亱偱丄俶偼捈妏嶰妏宍偺奜愙墌偺拞怱偱
丂丂丂丂偁傞偺偱丄俶俫亖俶俙丂傛傝丄佢倶 亖佢俙俫俶亖俀侽亱
丂丂丂丂 仜俈n 乮値偼帺慠悢)傪侾侽恑朄昞帵偟偨偲偒丄侽偑俀屄楢懕偱暲傇嵟彫偺値偺抣
丂丂丂幚嵺偵丄俀楢懕偺侽傪娷傓嵟彫偺俈n丗 値亖俀侽丂乮仺丂嶲峫丗乽庤寁嶼丠乿乯
俀侾丒丒丒仜暯柺偵偍偄偰丄俋杮偺捈慄偱弌棃傞嶰妏宍偺嵟戝悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 丂 仜廫恑朄偱婰偝傟偨偁傞悢傪丄岆偭偰暿偺掙偲偟偰撉傫偱偟傑偭偨偲偙傠丄惓偟偄抣
丂丂丂丂丂丂偺挌搙侾/俁偵側偭偨丅偙偺悢偼壗偐丅
丂丂丂幚嵺偵丄廫恑朄偱俀侾偼丄俁恑朄偱丄俈丂偙傟偼挌搙侾/俁偵側偭偰偄傞丅
丂丂丂 丂 仜俆偮偺揰俙丄俛丄俠丄俢丄俤偑偙偺弴偵堦偮偺捈慄忋偵偁傝丄師偺忦審傪枮偨偡丅
丂丂丂丂丂丂侾丏俛偼AC傪俀丗侾偵撪暘偡傞揰
丂丂丂丂丂丂俀丏俠偼俙俢傪俀丗俁偵撪暘偡傞揰
丂丂丂丂丂丂俁丏俤偼俙俠傪俈丗俆偵奜暘偡傞揰
丂丂丂丂丂丂俠俢偺挿偝偑俋們倣偺偲偒偺俙俤偺挿偝
丂丂丂幚嵺偵丄俛俠亖侾偲偡傞偲丄俙俛亖俀偱丄俠俢亖俁亊乮俁/俀乯亖俋/俀
丂丂丂偙偺偲偒丄俠俤亖俁亊乮俆/俀乯亖侾俆/俀 傛傝丄俙俤亖俁亄侾俆/俀亖俀侾/俀
丂丂丂傛偭偰丄乮俀侾/俀乯亐乮俋/俀乯亖俈/俁 側偺偱丄俙俤亖俋亊乮俈/俁乯亖俀侾乮們倣乯
丂丂丂 丂 仜侾侾丱乮俀俀丱俁俁乯丂偺壓俀寘偺悢
丂丂丂幚嵺偵丄侾侾n佭侾侽値亄侾丂乮倣倧倓丂侾侽侽乯丂偱丄俀俀m丂偺壓侾寘偼丄俀丄係丄俉丄俇丄俀丄丒丒丒
丂丂丂偲廃婜揑偵曄壔偡傞偺偱丄俁俁斣栚偼俀偱偁傞丅傛偭偰丄侾侾丱乮俀俀丱俁俁乯丂偺壓俀寘偼丄俀侾
俀俀丒丒丒仜侾寘偺俀偮偺惍悢偺愊偱昞偣側偄嵟彫偺崌惉悢
丂丂丂幚嵺偵丄俀亊侾侾亖俀俀
丂丂丂 丂 仜俀偮偺慺悢偺榓偲偟偰俁偮偺昞尰傪帩偮嵟彫偺悢
丂丂丂幚嵺偵丄丂俀俀亖俁亄侾俋亖俆亄侾俈亖侾侾亄侾侾
丂丂丂 丂 仜惓値妏宍偺撪妏偺戝偒偝偑惍悢偲側傞傛偆側値偺屄悢
丂丂丂幚嵺偵丄惓値妏宍偺侾偮偺撪妏偺戝偒偝偼丄侾俉侽亱乮値亅俀乯/値亖侾俉侽亱亅俁俇侽亱/値
丂丂丂傛偭偰丄惍悢偲側傞偺偼丄
丂丂丂値亖俁丄係丄俆丄俇丄俉丄俋丄侾侽丄侾俀丄侾俆丄侾俉丄俀侽丄俀係丄俁侽丄俁俇丄係侽丄係俆丄俇侽丄俈俀丄
丂丂丂俋侽丄侾俀侽丄侾俉侽丄俁俇侽丂偺俀俀屄偁傞丅
丂丂丂乮暿夝乯丂俁俇侽亖俀3丒俁2丒俆丂傛傝丄栺悢偺屄悢偼丄乮俁亄侾乯乮俀亄侾乯乮侾亄侾乯亖俀係
丂丂丂偙偺偆偪丄栺悢偺侾偲俀偼彍奜偝傟傞偺偱丄媮傔傞屄悢偼丄丂俀係亅俀亖俀俀乮屄乯
丂丂丂丂 仜僴儞僶乕僌僗僥乕僉侾枃傪丄僼儔僀僷儞傪巊偭偰1柺從偔偺偵丄俈暘偐偐傞丅棤曉偟
丂丂丂丂丂偰丄傕偆侾柺從偔偺偵峏偵俈暘偐偐傞丅椉柺從偗偨傜丄偦偺僴儞僶乕僌僗僥乕僉傪僷
丂丂丂丂丂儞偵偼偝傒丄僆乕僽儞僩乕僗僞乕偱從偔丅偙傟偑侾暘偐偐傞丅乮仺僴儞僶乕僈乕偺姰惉乯
丂丂丂丂丂偙偺庤弴偱丄僴儞僶乕僌僗僥乕僉偑俀枃偟偐偺偣傜傟側偄僼儔僀僷儞侾偮偲丄僷儞偑
丂丂丂丂丂俀屄偟偐擖傟傜傟側偄僆乕僽儞僩乕僗僞乕傪侾戜巊偭偰丄僴儞僶乕僈乕傪俁屄嶌傞偺
丂丂丂丂丂偵嵟掅壗暘偐偐傞偐丅偨偩偟丄棤曉偡帪娫傗僷儞偵偼偝傓帪娫側偳偼柍帇偡傞丅
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂乮俽侾昞丆俽俀昞乯偱俈暘丄乮俽侾棤丆俽俁昞乯偱俈暘丄乮俽俀棤丆俽俁棤乯偲摨帪恑峴偱俽侾偵
丂丂丂丂侾暘乮偙偺帪娫偼僇僂儞僩偝傟側偄乯丄乮俽俀棤丆俽俁棤乯偱俈暘偱丄俽俀丄俽俁偵侾暘
丂丂丂丂埲忋偐傜丄丂俈亄俈亄俈亄侾亖俀俀乮暘乯
丂丂丂丂 仜挿曽宍俙俛俠俢偵偍偄偰丄俤俫偲俥俧偼暯峴偱偁傞丅偙偺偲偒偺俆妏宍俛俥俧俫俤偺柺愊
丂丂丂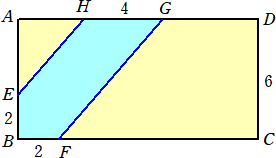
丂丂丂幚嵺偵丄俙俢偵暯峴偵俤傪捠傞慄暘偱俀偮偺恾宍偵暘妱偟偰丄
丂丂丂丂乮俀亄係乯亊俀亐俀亄係亊係亖俇亄侾俇亖俀俀
丂丂丂(暿夝乯丂係亊俇亅俀亊俀亐俀亖俀俀
丂丂丂丂 仜悢楍 侾丆俀丆係丆俉丆侾俇丆乮丂丂乯丆俀俇丆俁俉丆俇俀丆俈係丆丒丒丒 偵偍偄偰丄嬻強乮丂丂乯偵揔
丂丂丂丂丂偡傞悢
丂丂丂幚嵺偵丄戞値崁偼丄慜偺崁偵丄慜偺崁偱搊応偡傞悢帤偺愊傪壛偊偰摼傜傟傞偺偱丄俀俀
丂丂丂丂 仜暯柺忋偵丄AB丗BC=2丗1 偺挿曽宍ABCD偑偁傝丄偦偺撪晹偵丄堦曈偑25cm偺傂偟
丂丂丂丂丂宍偑愙偡傞丅
| 丂 |
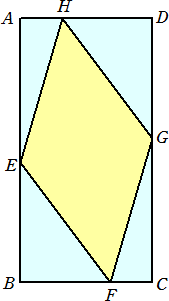 |
丂丂AB丄BC丄CD丄DA 偲偺偦傟偧傟偺愙揰傪 E丄F丄G丄H 偲
丂偡傞丅
丂丂AE丗EB亖俇丗俆丄EF丗EB亖俆丗係 偺偲偒偺BC偺挿偝 |
丂丂丂幚嵺偵丄EF丗EB亖俆丗係偱丄俤俥亖俀俆丂傛傝丄俤俛亖俀侽丄俛俥亖侾俆丂偱偁傞丅AE丗EB亖俇丗俆
丂丂丂傛傝丄俙俤亖俀係丄俙俫亖俈丂傑偨丄俥俠亖俙俫丂傛傝丄俥俠亖俈丂側偺偱丄丂俛俠亖侾俆亄俈亖俀俀
俀俁丒丒丒仜 倶2亄倶亄俀亖侽丂偺偲偒丄倶10亄倶9亄丒丒丒亄倶亄侾偺抣
丂丂丂幚嵺偵丄倶10亄倶9亄丒丒丒亄倶亄侾
丂丂丂丂丂丂丂丂丂亖乮倶2亄倶亄俀乯乮倶8亅倶6亄俀倶5亄倶4亅係倶3亄俁倶2亄俇倶亅侾侾乯亄俀俁
丂丂丂丂傛傝丄2亄倶亄俀亖侽丂偺偲偒丄倶10亄倶9亄丒丒丒亄倶亄侾亖俀俁
丂丂丂丂 仜奿巕揰傪俀怓偱揾傝暘偗傞曽朄偺悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂 仜俙乣俧偺俈恖偵擭楊偵偮偄偰暦偄偨偲偙傠丄師偺傛偆側曉摎傪摼偨丅
丂丂丂丂丂丂俙丗乽俢偼巹傛傝俈嵨擭忋偱偡丅巹偺壓傕偄傑偡丅乿
丂丂丂丂丂丂俛丗乽巹偼俥傛傝俆嵨擭壓偱偡丅乿
丂丂丂丂丂丂俠丗乽巹偼俥偲俀嵨嵎偱偡丅乿
丂丂丂丂丂丂俢丗乽巹偼俧偲俀嵨嵎偱偡丅乿
丂丂丂丂丂丂俤丗乽巹偼俙偲俁嵨嵎偱偡丅乿
丂丂丂丂丂丂俥丗乽巹偼俢偲係嵨嵎偱偡丅乿
丂丂丂丂丂丂偙偺俈恖偺拞偱丄俠偑俁斣栚偵擭楊偑崅偔丄俀俉嵨偺偲偒偺俙偺擭楊
丂丂丂幚嵺偵丄擭楊偑掅偄弴偵丄婲偙傝摼傞応崌傪楍嫇偡傞偲丄
丂丂丂俤俛俙俠俥俧俢丄俤俛俙俠俥俢俧丄俤俛俙俥俠俢俧丄俤俙俧俛俢俠俥丄俤俙俧俛俢俥俠丄俤俙俛俢俧俥俠
丂丂丂偙偺偆偪丄俠偑俁斣栚偵擭楊偑崅偄偺偼丄俤俛俙俥俠俢俧丂偺応崌偱丄俙偲俠偼俆嵨嵎側偺
丂丂丂偱丄俠偑丄俀俉嵨偺偲偒丄俙偼俀俁嵨偲側傞丅
丂丂丂丂 仜0亙兛亙兾/2丄0亙兝亙兾/2 偱丄cos兛亖倎/98丄cos兝亖71/98 偺側偡妏 兛亄兝
丂丂丂丂丂偑 2兾/3 偱偁傞偲偒偺惍悢 倎 偺抣
丂丂丂幚嵺偵丄戣堄傛傝丄丂倱倝値兛亖併乮9604亅倎2乯/98丄倱倝値兝亖39 /98丂側偺偱丄
/98丂側偺偱丄
丂丂丂們倧倱乮兛亄兝乯
丂丂丂亖們倧倱兛們倧倱兝亅倱倝値兛倱倝値兝亖71倎/9604亅39 併乮9604亅倎2乯/9604亖亅1/2丂傛傝丄
併乮9604亅倎2乯/9604亖亅1/2丂傛傝丄
丂丂丂71倎亄4802亖39 併乮9604亅倎2乯丂椉曈傪暯曽偟偰丄
併乮9604亅倎2乯丂椉曈傪暯曽偟偰丄
丂丂丂5041倎2亄681884倎亄23059204亖43823052亅4563倎2丂偲側傞偺偱丄
丂丂丂9604倎2亄681884倎亅20763848亖0丂偡側傢偪丄丂倎2亄71倎亅2162亖0
丂丂丂傛偭偰丄倎亖乷亅71亇併13689乸/2亖乷亅71亇117乸/2亖23丄亅94
丂丂丂倎亜0丂側偺偱丄倎亖23
丂丂丂丂 仜A偝傫偼堦擔偵200儁乕僕丄B偝傫偼300儁乕僕偺撉彂傪幚峴偡傞丅崱丄10嶜偺杮偑
丂丂丂丂丂偁傝乮奺杮偼200儁乕僕埲壓傗300儁乕僕埲忋偲偄傠偄傠側庬椶偑偁傞乯丄偦偺10嶜
丂丂丂丂丂偺僩乕僞儖偺儁乕僕悢偑10000儁乕僕偲偡傞丅偨偩偟丄擇恖偲傕偦偺儁乕僕悢偵枮偨
丂丂丂丂丂側偔偰傕堦嶜偺杮偑撉傒廔傢傞偲丄偦偺擔偺撉彂偼廔椆偡傞丅
丂丂丂丂丂乮偨偲偊1儁乕僕撉傫偱廔椆偟偰傕偦偺擔偼偦傟埲忋撉傑側偄丅乯
丂丂丂丂丂偨偩偟丄擇恖偼摨偠侾侽嶜偺杮傪岲偒側弴斣偱嵟弶偺儁乕僕偐傜撉傒恑傔偰偄偔傕
丂丂丂丂丂偺偲偡傞丅
丂丂丂丂丂偙偺偲偒偺擇恖偑慡晹偺杮傪撉傒廔傢傞擔悢偺嵎偲偟偰峫偊傜傟傞嵟戝悢
丂丂丂幚嵺偵丄杮偺儁乕僕悢偑壗儁乕僕偱偁偭偰傕丄
丂丂丂(A偑撉傓梊掕偺暸悢傛傝彮側偐偭偨暸悢)亅(B偑撉傓梊掕偺暸悢傛傝彮側偐偭偨暸悢)
丂丂丂偼丄昁偢100偐0偐-100偐-200偺偳傟偐偵側傝傑偡丅
丂丂丂廬偭偰丄10嶜偱偺偙傟偺崌寁偼嵟戝1000丄嵟彫-2000偱偡偐傜丄擔悢偺嵎偼丄
丂丂丂[ ] 傪僈僂僗偺婰崋偲偟偰丄[(10000+200-1+兛+1000)/200]-[(10000+300-1+兛)/300]
丂丂丂乮兛=(B偑撉傓梊掕偺暸悢傛傝彮側偐偭偨暸悢偺崌寁)乯
丂丂丂嵟戝偵側傞偺偼丄忋幃偱兛偑嵟戝偺偲偒偱丄兛+1000亝199亊10 偐傜 兛亝990 側偺偱
丂丂丂嵟戝抣偼丄[(10000+200-1+990+1000)/200]-[(10000+300-1+990)/300]=23(擔)埲壓丅
丂丂丂偲偙傠偱丄220丄220丄220丄220丄220丄220丄220丄220丄220丄8020 偺帪嵟戝偲側傝丄A=59丄
丂丂丂B=36丂傛傝丄擔悢偺嵎偼丄23乮擔乯偲側傝丄23擔偱偁傞夝偑偁傞偺偱丄偙傟偑嵟戝悢丅
俀係丒丒丒仜係恖傪堦楍偵暲傋傞曽朄偺悢
丂丂丂幚嵺偵丄係両亖係丒俁丒俀丒侾亖俀係乮捠傝乯
丂丂丂丂 仜侾丄俁丄係丄俇 偲亄丄亅丄亊丄亐丄乮丂丄乯丂傪梡偄偰丄俀係傪昞偣丅
丂丂丂幚嵺偵丄俇亐乮侾亅俁亐係乯亖俀係
丂丂丂丂 仜侾丄係丄俆丄俇 偲亄丄亅丄亊丄亐丄乮丂丄乯丂傪梡偄偰丄俀係傪昞偣丅
丂丂丂幚嵺偵丄俇亐乮俆亐係亅侾乯亖俀係
丂丂丂丂 仜愒媴丄惵媴丄墿媴偺壗傟偐係屄傪墌宍偵暲傋傞応崌偺悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂 仜係怓偺僐乕僸乕僇僢僾丒僜乕僒乕丒僗僾乕儞偺僙僢僩偑係媞偁傞丅
丂丂丂丂 丂丂丂丂丂丂 丂丂丂丂丂丂 丂丂丂丂丂 丂丂丂丂丂 丂丂丂丂丂 丂丂丂丂丂 |
| 丂 |
丂丂 丂丂丂 丂丂丂 丂丂丂 丂丂丂 丂丂丂 丂丂丂 |
| 丂 |
丂丂丂丂 丂丂丂丂丂丂丂 丂丂丂丂丂丂丂 丂丂丂丂丂丂丂 丂丂丂丂丂丂丂 丂丂丂丂丂丂丂 丂丂丂丂丂丂丂 |
丂丂丂丂摨怓偱偼偮傑傜側偄偺偱丄慡偰堘偆怓偱僙僢僩傪係媞偮偔傞偙偲偵偟偨丅椺偊偽丄
丂丂 |
丂丂丂丂偺傛偆偵偱偁傞丅偙偺嶌傝曽偺憤悢
丂丂幚嵺偵丄僐乕僸乕僇僢僾傪弴偵丄俙丄俛丄俠丄俢 偲偟丄偦傟偲摨怓偺僜乕僒乕傪彫暥帤偱丄
丂丂丂倎丄倐丄們丄倓丄偦傟偲摨怓偺僗僾乕儞傪弴偵悢帤偱丄侾丄俀丄俁丄係丂偲昞偡傕偺偲偡傞丅
丂丂丂偙偺偲偒丄僐乕僸乕僇僢僾偵懳偟偰丄僜乕僒乕偺暲傋曽偼丄係屄偺姰慡弴楍偺悢偵摍偟
丂丂丂偔丄俋捠傝偁傞偑丄幚嵺偵丄偦傟傪彂偒壓偣偽埲壓偺昞偺傛偆偵側傞丅
|
| 俙 |
俛 |
俠 |
俢 |
| 倐 |
倎 |
倓 |
們 |
| 倓 |
倎 |
倐 |
們 |
| 們 |
倎 |
倓 |
倐 |
|
|
| 俙 |
俛 |
俠 |
俢 |
| 們 |
倓 |
倎 |
倐 |
| 倓 |
們 |
倎 |
倐 |
| 倐 |
倓 |
倎 |
們 |
|
|
| 俙 |
俛 |
俠 |
俢 |
| 倓 |
們 |
倐 |
倎 |
| 們 |
倓 |
倐 |
倎 |
| 倐 |
們 |
倓 |
倎 |
|
丂丂丂忋婰偺昞偱愒帤偺応崌偼懠偺応崌偲堎側傝丄俀偮偺暥帤偱帺屓姰寢偟偰偄傞丅
丂丂丂椺偊偽丄師偺昞偐傜丄偦偺堘偄偑棟夝偝傟傞丅
|
| 俙 |
俛 |
俠 |
俢 |
| 倐 |
倎 |
倓 |
們 |
| 俁 |
係 |
侾 |
俀 |
| 俁 |
係 |
俀 |
侾 |
| 係 |
俁 |
侾 |
俀 |
| 係 |
俁 |
俀 |
侾 |
|
|
| 俙 |
俛 |
俠 |
俢 |
| 倓 |
倎 |
倐 |
們 |
| 俀 |
俁 |
係 |
侾 |
| 俁 |
係 |
侾 |
俀 |
|
|
| 俙 |
俛 |
俠 |
俢 |
| 們 |
倎 |
倓 |
倐 |
| 俀 |
係 |
侾 |
俁 |
| 係 |
俁 |
俀 |
侾 |
|
丂丂丂懠偺応崌傕摨條偱丄媮傔傞応崌偺悢偼丄丂俉亊俁亖俀係乮捠傝乯
丂丂丂 丂 仜堦曈偺挿偝偑侾們倣偺棫曽懱傪壓恾偺傛偆偵愊傒忋偘偨棫懱恾宍傪峫偊傞丅
丂丂丂丂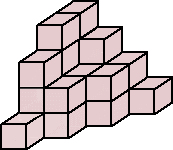
丂丂丂丂偙偺偲偒偺棫懱恾宍偺懱愊
丂丂丂幚嵺偵丄楻傟側偔廳暋側偔悢偊傞偨傔偵丄嵟忋抜偵偦傟埲壓偺屄悢傪婰擖偟偰丄
丂丂丂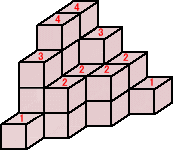
丂丂丂偙偺偲偒丄丂係亊俀亄俁亊俀亄俀亊係亄侾亊俀亖俀係乮屄乯丂傛傝丄懱愊偼丄俀係乮們倣3乯
丂丂丂 丂 仜堦曕偱丄侾抜丄俀抜丄傑偨偼丄俁抜傪搊傟傞恖偑丄俇抜偺愇抜傪搊傞曽朄偺悢
丂丂丂丂丂丂偨偩偟丄搑拞偱壓傝偨傝懌摜傒偟偨傝偼偟側偄傕偺偲偡傞丅
丂丂丂幚嵺偵丄値 抜偺愇傪搊傞曽朄偺悢傪丄倎値捠傝偲偡傞偲丄婣擺揑偵丄
丂丂丂 倎1亖侾丄倎2亖俀丄倎3亖係丄倎4亖倎3亄倎2亄倎1亖係亄俀亄侾亖俈丄
丂丂丂 倎5亖倎4亄倎3亄倎2亖俈亄係亄俀亖侾俁丄倎6亖倎5亄倎4亄倎3亖侾俁亄俈亄係亖俀係
丂丂丂 丂 仜俙丄俛偺俀柤偱憅屔惍棟傪峴偆丅惍棟傪俙偩偗偱峴偆偲丄俀柤偱峴偆偲偒偺擔悢傛傝係
丂丂丂丂丂擔懡偔偐偐傝丄俛偩偗偱峴偆偲侾俇擔懡偔偐偐傞偲偄偆丅偙偺偲偒丄俛偩偗偱惍棟傪峴偭
丂丂丂丂丂偨応崌偵梫偡傞擔悢丅偨偩偟丄俙丄俛偦傟偧傟偺侾擔摉偨傝偺巇帠検偼堦掕偲偡傞丅
丂丂丂幚嵺偵丄慡懱偺巇帠検傪侾偲偟丄俀恖偱傗傞偲丄値擔娫偐偐傞傕偺偲偡傞丅俙偩偗偱峴偆偲丄
丂丂丂俀柤偱峴偆偲偒偺擔悢傛傝係擔懡偔偐偐傞偺偱丄俙偺堦擔摉偨傝偺巇帠検偼丄侾/乮値亄係乯
丂丂丂偲側傞丅傑偨丄俛偩偗偱峴偆偲丄俀柤偱峴偆偲偒偺擔悢傛傝侾俇擔懡偔偐偐傞偺偱丄俛偺堦擔
丂丂丂摉偨傝偺巇帠検偼丄侾/乮値亄侾俇乯偲側傞丅
丂丂丂丂傛偭偰丄俙丄俛俀恖偺堦擔摉偨傝偺巇帠検偼丄侾/乮値亄係乯亄侾/乮値亄侾俇乯偲側傞丅値擔娫
丂丂丂偐偐傞偺偱丄値/乮値亄係乯亄値/乮値亄侾俇乯亖侾
丂丂丂丂暘曣傪暐偭偰丄丂値乮値亄侾俇乯亄値乮値亄係乯亖乮値亄係乯乮値亄侾俇乯丂傛傝丄丂値2亖俇係
丂丂丂偟偨偑偭偰丄丂値亖俉丂偲側傞丅偙偺偲偒丄俛偺堦擔摉偨傝偺巇帠検偼丄侾/俀係偲側傞偺偱丄
丂丂丂俛偩偗偱惍棟傪峴偭偨応崌偵梫偡傞擔悢偼丄俀係擔偲側傞丅
丂丂丂丂 仜偁傞巇帠傪俙丄俛偑堦弿偵庢傝慻傓丅搑拞偱丄俙偑俇擔媥傓偲丄巇帠傪廔偊傞偺偵丄
丂丂丂丂丂俀俈擔偐偐傞丅搑拞偱丄俛偑俀擔媥傓偲丄巇帠傪廔偊傞偺偵丄俀俆擔偐偐傞丅俀恖偲傕
丂丂丂丂丂媥傑偢偵巇帠偵庢傝慻傔偽丄巇帠偼壗擔偱廔傢傞偐丅
丂丂丂幚嵺偵丄俙丄俛偺侾擔摉偨傝偺巇帠検傪偦傟偧傟 倎丄倐 偲偍偔偲丄戣堄傛傝丄
丂丂丂俀侾倎亄俀俈倐亖侾丂丄俀俆倎亄俀俁倐亖侾丂側偺偱丄倎亖倐丂偑惉傝棫偮丅
丂丂丂偙偺偲偒丄丂俀侾倎亄俀俈倐亖係俉倐亖侾丂傛傝丄丂倐亖侾/係俉丂偱丄倎亖侾/係俉
丂丂丂傛偭偰丄俀恖堦弿偺堦擔摉偨傝偺巇帠検偼丄侾/係俉亄侾/係俉亖侾/俀係丂偲側傞偺偱丄
丂丂丂侾亐侾/俀係亖俀係 偐傜丄俀恖偲傕媥傑偢偵巇帠偵庢傝慻傔偽丄俀係擔偱廔傢傞丅
丂丂丂丂 仜偁傞巇帠傪廔偊傞偺偵丄俙偩偗偩偲侾俀擔丄俙偲俛偺俀恖偱傗傞偲丄俉擔偐偐傞丅俛堦
丂丂丂丂丂恖偱傗傞偲壗擔偐偐傞偐丅
丂丂丂幚嵺偵丄俙丄俙亄俛偺堦擔摉偨傝偺巇帠検偼丄侾/侾俀丄侾/俉側偺偱丄俛偺堦擔摉偨傝偺
丂丂丂巇帠検偼丄侾/俉亅侾/侾俀亖侾/俀係偱偁傞丅傛偭偰丄俛偑巇帠傪廔偊傞偺偵丄
丂丂丂侾亐侾/俀係亖俀係乮擔乯偐偐傞丅
俀俆丒丒丒仜俆恖傪俁偮偺僌儖乕僾偵暘偗傞曽朄偺悢
丂丂丂幚嵺偵丄乮俁5亅俁丒俀5亄俁乯/俁両亖乮俀係俁亅俋俇亄俁乯/俇亖侾俆侽/俇亖俀俆乮捠傝乯
丂丂丂 丂 仜侾侽杮偺捈慄偱嶌傜傟傞嶰妏宍偺嵟戝屄悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂 丂 仜俁庬偺偍傕傝俙丄俛丄俠偑偁傞丅俙侾屄偼丄俛俀屄偲俠侾屄偱掁傝崌偆丅俛俁屄偼丄俙侾屄
丂丂丂丂丂丂偲俠侾屄偱掁傝崌偆丅俛偑侾侽倗偺偲偒偺俙偺廳偝
丂丂丂幚嵺偵丄俙亖俛俛俠丄俙俠亖俛俛俛丂側偺偱丄俛俛俠俠亖俛俛俛丂傛傝丄俠俠亖俛亖侾侽倗 偐傜
丂丂丂丂俠亖俆倗丂傛偭偰丄俙亖侾侽亊俀亄俆亖俀俆乮倗乯
丂丂丂 丂 仜倎丄倐丄們丄倓丄倕 偺俆恖偑侾乣侾侽傑偱偺偦傟偧傟堎側傞斣崋偺僇乕僪傪傕偭偰偄傞丅
丂丂丂丂丂丂倎 偺斣崋偼丄倕 偺斣崋傛傝丄係彫偝偄丅倐 偺斣崋偼丄倓 偺斣崋傛傝丄俇彫偝偄丅們 偲
丂丂丂丂丂丂倐 偺斣崋偼俀偮堘偄偱偁傞丅倓 偲 倕 偺斣崋偺榓偼丄侾俇偱偁傞丅倕 偺斣崋偼丄倓 偺
丂丂丂丂丂丂斣崋傛傝丄俀戝偒偄丅偙偺偲偒丄俆恖偺帩偮僇乕僪偺斣崋偺崌寁
丂丂丂幚嵺偵丄倓亄倕亖侾俇丄倕亖倓亄俀丂傛傝丄倓亖俈丄倕亖俋丂偙偺偲偒丄倎亖俆丄倐亖侾丂傛偭偰丄
丂丂丂們亖俁丂偲掕傑傞偺偱丄俆恖偺帩偮僇乕僪偺斣崋偺崌寁偼丄侾亄俁亄俆亄俈亄俋亖俀俆
丂丂丂 丂 仜俁俇恖傪俀偮偺僌儖乕僾俙丄俛偵暘偗偰丄偁傞嶌嬈傪峴偭偨丅傑偢丄僌儖乕僾俙偑
丂丂丂丂丂侾帪娫嶌嬈偟慡懱偺敿暘傪廔偊丄師偵丄僌儖乕僾俛偑俀係暘娫嶌嬈偟慡懱偺侾/俈傪
丂丂丂丂丂廔偊丄嵟屻偵巆偭偨暘傪俁俇恖慡堳偱峴偄慡懱偺嶌嬈傪廔偊偨丅俁俇恖偦傟偧傟偺
丂丂丂丂丂堦掕帪娫摉偨傝偺嶌嬈検偼摨偠傕偺偲偟偰丄俁俇恖慡堳偱峴偭偨嶌嬈偼壗暘偐丠
丂丂丂幚嵺偵丄侾帪娫摉偨傝偺嶌嬈検偼丄僌儖乕僾俙偼侾/俀丄
丂丂丂僌儖乕僾俛偼丄乮侾/俈乯亊乮俇侽/俀係乯亖俆/侾係
丂丂丂俁俇恖慡堳偱峴偭偨嶌嬈検偼丄侾亅乮侾/俀亄侾/俈乯亖俆/侾係丂偱丄昁梫側帪娫傪俿偲偡傞偲丄
丂丂丂乮侾/俀乯俿亄乮俆/侾係乯俿亖俆/侾係丂傛傝丄俿亖俆/侾俀丂側偺偱丄俀俆暘娫嶌嬈傪偟偨丅
丂丂丂 丂 仜侾侽侽埲壓偺慺悢偺屄悢
丂丂丂幚嵺偵丄俀丄俁丄俆丄俈丄侾侾丄侾俁丄侾俈丄侾俋丄俀俁丄俀俋丄俁侾丄俁俈丄係侾丄係俁丄係俈丄俆俁丄俆俋丄
丂丂丂丂俇侾丄俇俈丄俈侾丄俈俁丄俈俋丄俉俁丄俉俋丄俋俈丂偺俀俆屄
丂丂丂 丂 仜俁曈偺挿偝偑惍悢偱丄俀捠傝偵昞尰偝傟傞幬曈偺嵟彫抣
丂丂丂幚嵺偵丄俀俆2亖俈2亄俀係2亖侾俆2亄俀侽2
俀俇丒丒丒仜嬻娫撪偺俀捈慄 倶亅侾俇亖乮倷亅俇乯/侾俀亖乮倸亅俀侽乯/侾俀丂丄
丂丂丂丂丂倶亄俉亖乮倷亅俉乯/俇亖乮倸亅俇乯/係 偺嵟抁嫍棧
丂丂丂幚嵺偵丄倶亅侾俇亖乮倷亅俇乯/侾俀亖乮倸亅俀侽乯/侾俀亖倲丂偲偍偔偲丄
丂丂丂丂俹乮倲亄侾俇丆侾俀倲亄俇丆侾俀倲亄俀侽乯
丂丂丂倶亄俉亖乮倷亅俉乯/俇亖乮倸亅俇乯/係亖倱丂偲偍偔偲丄
丂丂丂丂俻乮倱亅俉丆俇倱亄俉丆係倱亄俇乯
丂丂丂傛偭偰丄俹俻亖乮倱亅倲亅俀係丆俇倱亅侾俀倲亄俀丆係倱亅侾俀倲亅侾係乯
丂丂丂俹俻偑嵟彫偲側傞偲偒丄丂俹俻佦乮侾丆侾俀丆侾俀乯丄俹俻佦乮侾丆俇丆係乯
丂丂丂傛偭偰丄俹俻丒乮侾丆侾俀丆侾俀乯亖侾俀侾倱亅俀俉俋倲亅侾俇俉亖侽
丂丂丂丂俹俻丒乮侾丆俇丆係乯亖俆俁倱亅侾俀侾倲亅俇俉亖侽
丂丂丂楢棫曽掱幃傪夝偄偰丄丂倱亖倲亖亅侾丂側偺偱丄俹俻亖乮亅俀係丆俉丆亅俇乯
丂丂丂傛偭偰丄俹俻亖俀亊併乮侾俀2亄係2亄俁2乯亖俀俇
丂丂丂丂 仜暯曽悢偲棫曽悢偵偼偝傑傟偨惓偺惍悢
丂丂丂幚嵺偵丄俆2亙俀俇亙俁3
丂丂丂丂 仜嶲壛椏偑丄幮夛恖俀侽侽墌丄戝妛惗侾俆侽墌丄崅峑惗侾侽侽墌偺僎乕儉偵丄幮夛恖丄
丂丂丂丂丂戝妛惗丄崅峑惗崌傢偣偰侾俁侽柤偑嶲壛偟偨丅嶲壛椏崌寁偼丄侾俉俋侽侽墌偱丄幮夛
丂丂丂丂丂恖偺嶲壛幰偼戝妛惗傛傝俀侽柤懡偐偭偨偲偄偆丅偙偺偲偒偺戝妛惗偺嶲壛幰悢
丂丂丂幚嵺偵丄戝妛惗偺嶲壛幰悢傪 倶 偲偡傞偲丄
丂丂丂丂俀侽侽乮倶亄俀侽乯亄侾俆侽倶亄侾侽侽乮侾侾侽亅俀倶乯亖侾俉俋侽侽丂傛傝丄倶亖俀俇
丂丂丂丂 仜侾侽墌偑俀枃丄俆侽墌偑俀枃丄侾侽侽墌偑俁枃偁傞丅偪傚偆偳暐偊傞嬥妟偺応崌偺悢
丂丂丂幚嵺偵丄侾侽侽亊俁亄俆侽亊俀亖係侽侽丂傛傝丄丂係侽侽亐俆侽亄侾亖俋丂側偺偱丄
丂丂丂丂俋亊俁亅侾亖俀俇乮捠傝乯
丂丂丂丂乮暿夝乯幚嵺偵暐偊傞嬥妟傪抧摴偵寁嶼偟偰傒傞偲丄
丂丂丂丂侾侽丄俀侽丄俆侽丄俇侽丄俈侽丄侾侽侽丄侾侾侽丄侾俀侽丄侾俆侽丄侾俇侽丄侾俈侽丄俀侽侽丄俀侾侽丄俀俀侽丄
丂丂丂丂俀俆侽丄俀俇侽丄俀俈侽丄俁侽侽丄俁侾侽丄俁俀侽丄俁俆侽丄俁俇侽丄俁俈侽丄係侽侽丄係侾侽丄係俀侽
丂丂丂丂偺俀俇捠傝
丂丂丂丂 仜AB亖俀係丄AD亖俁俇偺挿曽宍ABCD偑偁傞丅AB忋偵EB亖俆偲側傞揰俤偲俙俢忋偵揰
丂丂丂丂丂俧傪偲傝丄慄暘EG偱挿曽宍傪愜傝曉偟丄岎揰F偵懳偟偰丄俛俥亖侾俀丄俥俙亖俇偲偡傞丅
丂丂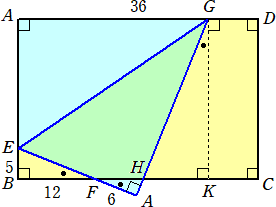
丂丂丂丂偙偺偲偒丄慄暘俧俫偺挿偝
丂丂丂幚嵺偵丄俫俲亖俀係亊乮俆/侾俀乯亖侾侽丂傛傝丄
丂丂丂俧俫2亖俫俲2亄俧俲2亖侾侽侽亄俆俈俇亖俇俈俇亖俀俇2丂傛傝丄俧俫亖俀俇
俀俈丒丒丒仜侾曈偺挿偝係偺惓嶰妏宍偺奺曈偑係摍暘偝傟丄暯峴慄偑堷偐傟偰偄傞偲偒偵弌棃
丂丂丂丂丂傞惓嶰妏宍偺屄悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂 丂丂丂 仜俙俛亖俋丄俛俠亖侾俀偺挿曽宍俙俛俠俢偺奜懁偵俠俢丄俢俙傪侾曈偲偡傞惓嶰妏宍俠俤俢丄
丂丂丂丂丂俢俥俙傪偦傟偧傟昤偔偲偒丄仮俢俤俥偺柺愊
丂丂丂幚嵺偵丄仮俢俤俥亖乮侾/俀乯丒俋丒侾俀丒倱倝値侾俆侽亱亖俀俈
丂 丂丂丂 仜俋5偺奺埵偺悢偺榓
丂丂丂幚嵺偵丄俋5亖俆俋侽係俋丂傛傝丄奺埵偺悢偺榓偼丄俆亄俋亄侽亄係亄俋亖俀俈
丂丂 丂丂 仜惍棟偺巇帠傪俆恖偱巒傔偨丅弶傔偺侾俆擔娫偼弴挷偵恑傫偩偑丄侾俇擔栚偐傜俁恖
丂丂丂丂丂偟偐摥偔偙偲偑偱偒側偔側傝丄梊掕傛傝俉擔抶傟偰巇帠偑廔傢偭偨丅 摉弶偺巇帠偑廔
丂丂丂丂丂傢傞擔悢丅偨偩偟丄俆恖偺侾擔摉偨傝偺巇帠検偼摍偟偄傕偺偲偡傞丅
丂丂丂幚嵺偵丄慡懱偺巇帠検傪侾偲偟丄俆恖偱傗傞偲丄値擔娫偐偐傞傕偺偲偡傞丅偙偺偲偒丄堦恖
丂丂丂偺堦擔摉偨傝偺巇帠検偼丄侾/俆値丂偲側傞丅
丂丂丂傛偭偰丄侾俆亊俆亊乮侾/俆値乯亄乮値亄俉亅侾俆乯亊俁亊乮侾/俆値乯亖侾丂偡側傢偪丄
丂丂丂俈俆亄俁値亅俀侾亖俆値丂傛傝丄俀値亖俆係丂丂屘偵丄値亖俀俈
丂 丂丂丂 仜俙丄俛丄俠偺俁偮偺戃偵偦傟偧傟俀俈偺攞悢偺屄悢偺僐僀儞偑擖偭偰偄傞丅俙偺戃偺
丂丂丂丂丂僐僀儞偺侾/俁偢偮傪俛偲俠偵暘偗擖傟偨丅俙偵偼尦乆偁偭偨僐僀儞偺侾/俁偑巆偭偰偄
丂丂丂丂丂傞丅摨條偵偟偰丄崱搙偼丄俛偺戃偺僐僀儞偺侾/俁偢偮傪俙偲俠偵暘偗擖傟偨丅偝傜偵丄
丂丂丂丂丂俠偺戃偺僐僀儞偺侾/俁偢偮傪俙偲俛偵暘偗擖傟偨丅偙偺偲偒丄俙偲俛偵擖偭偰偄傞僐僀
丂丂丂丂丂儞偺悢傪寁嶼偟偨傜丄嵎偑偪傚偆偳俋屄偵側偭偰偄偨丅偙偺偲偒丄尦乆俙偺戃偵擖偭偰
丂丂丂丂丂偄偨僐僀儞偺屄悢
丂丂丂幚嵺偵丄俙丄俛丄俠偵擖偭偰偄偨僐僀儞偺悢傪偦傟偧傟 俀俈倶丄俀俈倷丄俀俈倸 偲偍偔偲丄
丂丂丂乮俙乯丂俙丗丂俋倶丂丂俛丗丂俀俈倷亄俋倶丂丂俠丗丂俀俈倸亄俋倶
丂丂丂乮俛乯丂俙丗丂俋倶亄乮俋倷亄俁倶乯丂丂俛丗丂俋倷亄俁倶丂丂俠丗丂俀俈倸亄俋倶亄乮俋倷亄俁倶乯
丂丂丂俠偺僐僀儞偺暘攝偼丄俙丄俛偺僐僀儞偺嵎偵偼柍娭學側偺偱峫偊側偔偰傛偄丅
丂丂丂偙偺偲偒丄丂俋倶亄乮俋倷亄俁倶乯亅乮俋倷亄俁倶乯亖俋倶亖俋丂傛傝丄倶亖侾偲側傝丄尦乆俙偺戃偵偼
丂丂丂僐僀儞偑俀俈屄擖偭偰偄偨偙偲偵側傞丅
俀俉丒丒丒仜俀斣栚偵彫偝偄姰慡悢
丂丂丂幚嵺偵丄姰慡悢偼丄丂俇丂丄俀俉丂丄係俋俇丂丄俉侾俀俉丂丄丒丒丒
丂丂 丂丂 仜侾俀偺栺悢偺憤榓
丂丂丂幚嵺偵丄侾亄俀亄俁亄係亄俇亄侾俀亖俀俉
丂丂丂乮暿夝乯丂侾俀亖俀2丒俁丂傛傝丄媮傔傞榓偼丄乮侾亄俀亄俀2乯乮侾亄俁乯亖俀俉
丂 丂丂丂 仜偁傞悢偐傜偦偺悢偺係/俈傪堷偄偨悢偑侾俀偱偁傞偲偒偺偁傞悢
丂丂丂幚嵺偵丄偁傞悢傪俈偲偡傞偲丄堷偄偨悢偼 俁偵側傞偺偱丄偙傟傪侾俀偵偡傞偵偼丄係攞偡
丂丂丂傟偽傛偄丅傛偭偰丄偁傞悢偼丄俈亊係亖俀俉
丂丂 丂丂 仜栺悢傪偡傋偰懌偡偲俆俇丄栺悢偺媡悢傪偡傋偰懌偡偲丄俀偲側傞帺慠悢
丂丂丂幚嵺偵丄偁傞悢傪俶偲偡傞偲丄戣堄傛傝丄俆俇/俶亖俀 側偺偱丄俶亖俀俉
丂丂 丂丂 仜佺0亣 乮倶4亄倶3亅倶2乯倕-x倓倶 偺抣
丂丂丂幚嵺偵丄梌幃亖[亅乮倶4亄倶3亅倶2乯倕-x]0亣亄佺0亣 乮係倶3亄俁倶2亅俀倶乯倕-x倓倶
丂丂丂亖佺0亣 乮係倶3亄俁倶2亅俀倶乯倕-x倓倶
丂丂丂亖[亅乮係倶3亄俁倶2亅俀倶乯倕-x]0亣亄佺0亣 乮侾俀倶2亄俇倶亅俀乯倕-x倓倶
丂丂丂亖佺0亣 乮侾俀倶2亄俇倶亅俀乯倕-x倓倶
丂丂丂亖[亅乮侾俀倶2亄俇倶亅俀乯倕-x]0亣亄佺0亣 乮俀係倶亄俇乯倕-x倓倶
丂丂丂亖亅俀亄佺0亣 乮俀係倶亄俇乯倕-x倓倶
丂丂丂亖亅俀亄[亅乮俀係倶亄俇乯倕-x]0亣亄俀係佺0亣 倕-x倓倶
丂丂丂亖亅俀亄俇亄俀係[亅倕-x]0亣
丂丂丂亖亅俀亄俇亄俀係亖俀俉
俀俋丒丒丒仜侾侽斣栚偵彫偝偄慺悢
丂丂丂幚嵺偵丄慺悢傪彫偝偄弴偵暲傋傞偲丄丂俀丄俁丄俆丄俈丄侾侾丄侾俁丄侾俈丄侾俋丄俀俁丄俀俋丄丒丒丒
丂丂丂 丂 仜{(俁亄侾)/俀}2亄{(俆亄侾)/俀}2亄{(俈亄侾)/俀}2丂偺抣
丂丂丂幚嵺偵丄丂梌幃亖俀2亄俁2亄係2亖俀俋
丂丂 丂丂 仜弶崁1丄岞斾2丄崁悢300偺摍斾悢楍偺拞偵丄廫恑朄偱彂偔偲愭摢偺悢帤偑4偱偁傞
丂丂丂丂丂傕偺偼偄偔偮偁傞偐丅偨偩偟丄2^299偼91寘偺悢偱丄偦偺愭摢偺悢帤偼1偱偁傞偙偲傪
丂丂丂丂丂梡偄偰傛偄丅
丂丂丂幚嵺偵丄乽WolframAlfa乿愭惗偵庤揱偭偰傕傜偭偰丄愭摢偺悢帤偑4偱偁傞傕偺偼丄俀値偱
丂丂丂値亖俀丄侾俀丄俀俀丄俁俀丄係俀丄俆俀丄俇俀丄俈俀丄俉俀丄俋俀丄侾侽俆丄侾侾俆丄侾俀俆丄侾俁俆丄侾係俆丄
丂丂丂侾俆俆丄侾俇俆丄侾俈俆丄侾俉俆丄侾俋俉丄俀侽俉丄俀侾俉丄俀俀俉丄俀俁俉丄俀係俉丄俀俆俉丄俀俇俉丄俀俈俉丄
丂丂丂俀俉俉丂偺俀俋屄
丂丂 丂丂 仜俁/俉亙倶/俈俀亙俀侾/俆侽丂傪枮偨偡傛偆偵 倶 偺抣傪媮傔傛丅偨偩偟丄倶 偲俈俀偼屳偄偵
丂丂丂丂丂慺偲偡傞丅
丂丂丂幚嵺偵丄俁/俉亙倶/俈俀亙俀侾/俆侽丂傛傝丄丂俀俈/俈俀亙倶/俈俀亙乮侾俆侾俀/俆侽乯/俈俀丂側偺偱丄
丂丂丂丂俀俈亙倶亙侾俆侾俀/俆侽亖俁侽丏俀係丂偙偺幃傪枮偨偡帺慠悢 倶 偼丄俀俉丄俀俋丄俁侽
丂丂丂丂偙偺偆偪丄俈俀偲屳偄偵慺側悢偼丄倶亖俀俋
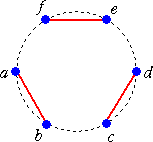
俁侽丒丒丒仜俇怓偡傋偰傪梡偄偰棫曽懱偺柺偵怓晅偗偡傞曽朄偺悢
丂丂丂幚嵺偵丄丂俆亊乮係-1乯両亖俁侽乮捠傝乯
丂丂丂丂 仜係亊係偺奿巕揰偑廲丄墶偺慄偱寢偽傟偰偄傞偲偒偵弌棃傞惓曽宍偺屄悢
丂丂丂幚嵺偵丄偙偪傜傪嶲徠
丂丂丂丂 仜侾曈係偺惓曽宍偺廲丄墶偑係摍暘偝傟暯峴慄偑堷偐傟偰偄傞偲偒丄惓曽宍偼戝彫
丂丂丂丂丂崌傢偣偰偄偔偮偁傞偐丠
丂丂丂幚嵺偵丄柺愊侾偺傕偺丒丒丒侾俇屄丂丄柺愊俀偺傕偺丒丒丒俋屄丂丄柺愊俁偺傕偺丒丒丒係屄
丂丂丂丂柺愊係偺傕偺丒丒丒侾屄丂側偺偱丄丂侾俇亄俋亄係亄侾亖俁侽乮屄乯
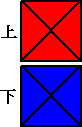
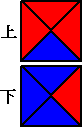
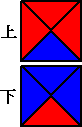
丂丂丂丂 仜惓榋柺懱偺奺柺偵侾偐傜俇傑偱傪偦傟偧傟杽傔傞傗傝曽偼壗捠傝偁傞偐丅
丂丂丂幚嵺偵丄忋柺傪堦偮偺悢帤偱屌掕偟偰丄掙柺偺杽傔曽偼俆捠傝
丂丂丂偦偺侾捠傝偵懳偟偰懁柺偺杽傔曽偼丄乮係亅侾乯両亖俇乮捠傝乯丂傛偭偰丄俆亊俇亖俁侽乮捠傝乯
丂丂丂丂 仜巐妏宍俙俛俠俢偺奺曈偺拞揰傪壓恾偺傛偆偵寢傫偱係偮偺巐妏宍偵暘妱偟偨偲偙
丂丂丂丂丂傠丄恾偺傛偆側柺愊偲側偭偨丅偙偺偲偒偺巐妏宍俙俹俷俽偺柺愊
丂丂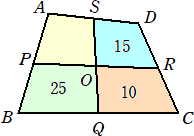
丂丂丂幚嵺偵丄壓恾傛傝丄巐妏宍俙俹俷俽亄侾侽亖俀俆亄侾俆丂側偺偱丄丂巐妏宍俙俹俷俽亖俁侽
丂丂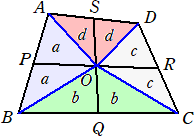
丂丂丂丂 仜壓恾偵偍偄偰丄佢俙俢俛亖倶亱偺戝偒偝
丂丂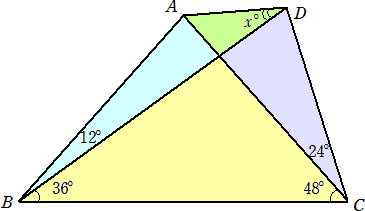
丂丂丂幚嵺偵丄仮俙俛俢傪俙俛偵娭偟偰懳徧堏摦偝偣偰惓嶰妏宍俤俛俠傪嶌傞丅
丂丂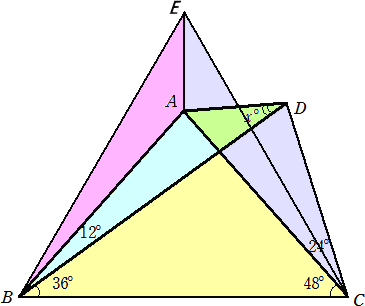
丂丂丂佢俠俛俢亖俁俇亱丄佢俛俠俢亖俈俀亱側偺偱丄佢俛俢俠亖侾俉侽亱亅俁俇亱亅俈俀亱亖俈俀亱
丂丂丂傛偭偰丄仮俛俠俢偼丄俛俠亖俛俢偺俀摍曈嶰妏宍
丂丂丂惓嶰妏宍俤俛俠偺嶌傝曽偐傜丄俛俢亖俛俤丂偱丄佢俙俛俠亖係俉亱丄佢俙俠俛亖係俉亱傛傝丄
丂丂丂仮俙俛俢偼俙俛亖俙俠偺俀摍曈嶰妏宍偲側傞丅偙偺偲偒丄仮俤俙俠佭仮俢俙俛佭仮俤俙俛丂側
丂丂丂偺偱丄俀倶亖俇侽亱傛傝丄倶亖俁侽亱
丂丂丂乮暿夝乯AB偵娭偟偰C偲懳徧側揰C乫傪偲傞偲丄仮ABC佭仮ABC乫側偺偱丄AB=AC乫
丂丂丂丂BD=BC=BC乫丄佢C乫BD=60亱偐傜丄仮BDC乫偼惓嶰妏宍側偺偱丄BD=C乫D
丂丂丂丂廬偭偰丄A傕D傕BC乫偺悅捈擇摍暘慄忋偵偁傝丄佢ADB=30亱
丂丂丂丂 仜悢楍 侾俀丆侾俆丆俀侾丆俀係丆乮丂丂乯丆俁俁丆俁俋丆俆侾 偵偍偄偰丄嬻強乮丂丂乯偵揔偡傞悢
丂丂丂幚嵺偵丄乮慜偺崁乯亄乮慜偺崁偺堦偺埵乯亄乮慜偺崁偺堦偺埵乯偑乮師偺崁乯偵側傞偺偱
丂丂丂丂乮丂丂乯亖俀係亄係亄俀亖俁侽
丂丂丂丂 仜惓曽宍俙俛俠俢偵偍偄偰丄俛俠丄俠俢偺拞揰傪偦傟偧傟俵丄俶偲偍偔丅慄暘俵俢偲慄暘
丂丂丂丂丂俶俙偺岎揰傪俹偲偡傞丅
丂丂
丂丂丂丂仮俢俹俶偺柺愊偑 俆 偺偲偒偺仮俙俵俹偺柺愊
丂丂丂幚嵺偵丄俢俶亖倎丂偲偍偔偲丄俙俢亖俀倎丂丄俙俶亖 倎丂偲側傞丅傑偨丄俙俶佦俵俢丂偱丄捈妏
倎丂偲側傞丅傑偨丄俙俶佦俵俢丂偱丄捈妏
丂丂丂嶰妏宍俙俢俶佷捈妏嶰妏宍俢俹俶丂傛傝丄俢俹亖俀倎/ 丂丄俹俶亖倎/
丂丄俹俶亖倎/
丂丂丂傛偭偰丄丂捈妏嶰妏宍俢俹俶偺柺愊偼丄丂乮侾/俀乯丒乮俀倎/ 乯丒乮倎/
乯丒乮倎/ 乯亖倎2/俆亖俆丂傛傝丄
乯亖倎2/俆亖俆丂傛傝丄
丂丂丂倎亖俆丂偲側傞丅偙偺偙偲偐傜丄惓曽宍俙俛俠俢偺侾曈偺挿偝偼丄侾侽偱丄柺愊偼丄侾侽侽偲側傞丅
丂丂丂仮俙俛俵亖仮俢俠俵亖仮俙俢俶亖俀俆丂側偺偱丄
丂丂丂仮俙俵俹亖惓曽宍俙俛俠俢亅乮仮俙俛俵亄仮俢俠俵亄仮俙俢俶亅仮俢俹俶乯
丂丂丂亖侾侽侽亅乮俀俆亄俀俆亄俀俆亅俆乯亖俁侽
俁侾丒丒丒仜俀師曽掱幃 倶2亅倶亅俀亖侽丂偺俀偮偺夝傪兛丄兝偲偡傞偲偒偺兛5亄兝5偺抣
丂丂丂幚嵺偵丄兛亄兝亖侾丄兛兝亖亅俀丂傛傝丄
丂丂丂丂兛5亄兝5亖乮兛2亄兝2乯乮兛3亄兝3乯亅兛2兝2乮兛亄兝乯
丂丂丂丂亖乮乮兛亄兝乯2亅俀兛兝乯乮乮兛亄兝乯3亅俁兛兝乮兛亄兝乯亅兛2兝2乮兛亄兝乯
丂丂丂丂亖乮侾亄係乯乮侾亄俇乯亅係亖俁侾
丂丂丂乮暿夝乯丂倶2亅倶亅俀亖乮倶亅俀乯乮倶亄侾乯亖侽丂偺俀偮偺夝偼丄俀偲亅侾側偺偱丄
丂丂丂丂丂丂丂兛5亄兝5亖俁侾丂偲偟偨曽偑堈偟偐偭偨偱偡偹丅
丂丂丂丂 仜儼k=1乣5 俀k-1 偺抣
丂丂丂幚嵺偵丄梌幃亖俀5亅侾亖俁侾
丂丂埲壓丄岺帠拞両








 丂
丂






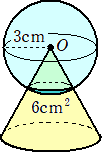

 丂
丂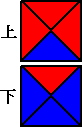





















 丂丂丂丂丂丂
丂丂丂丂丂丂 丂丂丂丂丂
丂丂丂丂丂 丂丂丂丂丂
丂丂丂丂丂








