
半径 r の円Oがあり、その中心で互いに直交する2つの直線 L、M が円と交わる点を、
A、B、C、D とおく。
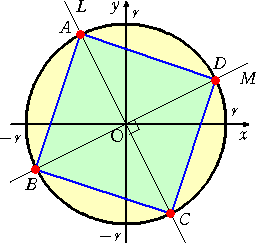
このとき4点を結んで出来る図形は正方形で、直線の傾きがどのように変化しても、その
面積は一定値 2r2 をとる。
そこで、同じような問題を楕円でも考えてみよう。
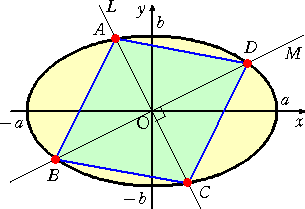
このとき4点を結んで出来る図形は平行四辺形で、その面積が一定ということは期待で
きない。
実際に、 D(a・cosθ,b・sinθ) ( 0≦θ≦π/2 ) とすると、
A(−a・sinθ,b・cosθ) で、平行四辺形ABCDの面積 S(θ) は、
で与えられる。
このとき、
S2(θ)=4(a2cos2θ+b2sin2θ)(a2sin2θ+b2cos2θ)
=(a4+b4)sin22θ+4a2b2(cos4θ+sin4θ)
=(a4+b4)sin22θ+4a2b2(1−2sin2θcos2θ)
=(a4+b4)sin22θ+a2b2(4−2sin22θ)
=(a2−b2)2sin22θ+4a2b2
0≦θ≦π/2 より、 0≦2θ≦π なので、 0≦sin2θ≦1
このことから、 θ=π/4 のとき、 S(θ) は最大で、最大値 a2+b2
θ=0、π/2 のとき、 S(θ) は最小で、最小値 2ab
従って、面積 S(θ) の取り得る値の範囲は、2ab ≦ S(θ) ≦ a2+b2 となる。
(コメント) 最大値が a2+b2 で最小値が 2ab とは...なかなか美しい組合せになる
んですね!
上記では、楕円の中心で直交する2直線を考えたが、2直線のそれぞれが異なる焦点を
通り、互いに直交するとしたら、四角形の面積の取り得る値の範囲はどうなるだろうか?
若干恐いもの見たさに、具体的な楕円の方程式を与えて計算してみよう。
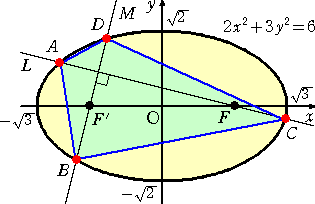
焦点 F、F’の座標がそれぞれ F( 1 , 0 ) 、 F’( −1 , 0 ) で与えられるので、
実数 m に対して、 直線 L の方程式は、 mx−y=m
直線 M の方程式は、 x+my=−1
とおける。 A( α , mα−m ) 、C( β , mβ−m ) とおくと、 α、β は、
2次方程式 2x2+3(mx−m)2=6 すなわち、(3m2+2)x2−6m2x+3m2−6=0
の解である。よって、解と係数の関係から、
α+β=6m2/(3m2+2)、 αβ=(3m2−6)/(3m2+2)
このとき、 線分ACの長さの平方 AC2 は、
AC2=(α−β)2+(mα−mβ)2=(m2+1)(α−β)2
=(m2+1){(α+β)2−4αβ}
=(m2+1){36m4/(3m2+2)2−4(3m2−6)/(3m2+2)}
=48(m2+1)2/(3m2+2)2
となるので、AC=4
同様にして、 B( −mγ−1 , γ ) 、D( −mδ−1 , δ ) とおくと、 γ、δ は、
2次方程式 2(−my−1)2+3y2=6 すなわち、
(2m2+3)y2+4my−4=0
の解である。よって、解と係数の関係から、
γ+δ=−4m/(2m2+3)、 γδ=−4/(2m2+3)
このとき、 線分BDの長さの平方 BD2 は、
BD2=(−mγ+mδ)2+(γ−δ)2=(m2+1)(γ−δ)2
=(m2+1){(γ+δ)2−4γδ}
=(m2+1){16m2/(2m2+3)2+16/(2m2+3)}
=48(m2+1)2/(2m2+3)2
となるので、BD=4
よって、求める四角形ABCDの面積 S は、
S=AC×BD/2=24(m2+1)2/{(3m2+2)(2m2+3)}
ここで、 m2=t (t≧0) とおいて、分母を払って式を整理すると、
(6S−24)t2+(13S−48)t+6S−24=0 ・・・・・ (*)
この方程式が、0 以上の解を少なくとも一つ持つように、S の値の範囲を定めればよい。
6S−24=0 即ち、 S=4 のとき、 13S−48≠0 で、方程式は、t=0 という解を
持つので、S=4 は、求める S の値の範囲に含まれる。
よって、以下では、S≠4 として、2次方程式 (*) が、少なくとも一つの正の解を持つよ
うなS の値の範囲を求めればよい。
そこで、2次方程式 (*) から、2次関数
F(t)=(6S−24)t2+(13S−48)t+6S−24
を考える。このとき、軸の方程式は、t=−(13S−48)/(12S−48)
−(13S−48)/(12S−48)<0 即ち、 0<S<48/13 、4<S のとき、
(6S−24)×F(0)<0
であればよいが、 (6S−24)2<0 は起こり得ない。
−(13S−48)/(12S−48)=0 即ち、S=48/13 のとき、F(t)=(6S−24)(t2+1)
は、t 軸と共有点を持たないから不適。
−(13S−48)/(12S−48)>0 即ち、 48/13<S<4 のとき、
判別式を D とすると、
D=(13S−48)2−4(6S−24)2
=(13S−48+12S−48)(13S−48−12S+48)=(25S−96)S≧0
であればよい。
このとき、 S≧96/25 かつ 48/13<S<4 から、 96/25≦S<4
従って、 S=4 も含めて、求める S の値の範囲は、96/25≦S≦4 となる。
(コメント) 直線 L の傾きが 0 のときに、四角形の面積は最大になるんですね!
それでは、四角形の面積が最小のときの直線の位置関係がどうなっているのか、興味が
あったので調べてみた。
簡単な計算から、それは、 t=1 即ち、 m=±1 であることが分かる。
図示すれば、下図を得る。
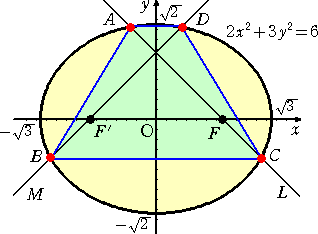
台形のときに面積が最小なんだ...。
上記の問題を一般化し、公式を作ってみよう。
楕円の方程式を
とする。
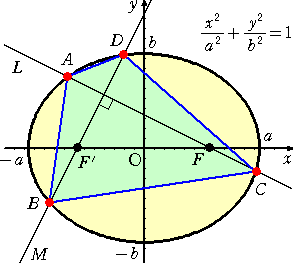
このとき、焦点 F、F’の座標は、それぞれ F( c , 0 ) 、 F’( −c , 0 ) で与えられる。
ただし、
実数 m に対して、 直線 L の方程式は、 mx−y=mc
直線 M の方程式は、 x+my=−c
とおける。 A( α , mα−mc ) 、C( β , mβ−mc ) とおくと、 α、β は、
2次方程式 b2x2+a2(mx−mc)2=a2b2 すなわち、
(a2m2+b2)x2−2a2m2cx+a2m2c2−a2b2=0
の解である。よって、解と係数の関係から、
α+β=2a2m2c/(a2m2+b2)、 αβ=(a2m2c2−a2b2)/(a2m2+b2)
このとき、 線分ACの長さの平方 AC2 は、
AC2=(α−β)2+(mα−mβ)2=(m2+1)(α−β)2
=(m2+1){(α+β)2−4αβ}
=(m2+1){4a4m4c2/(a2m2+b2)2−4(a2m2c2−a2b2)/(a2m2+b2)}
=4a2b2(m2+1)(a2m2−m2c2+b2)/(a2m2+b2)2
=4a2b4(m2+1)2/(a2m2+b2)2
となるので、AC=2ab2(m2+1)/(a2m2+b2)
同様にして、 B( −mγ−c , γ ) 、D( −mδ−c , δ ) とおくと、 γ、δ は、
2次方程式 b2(−my−c)2+a2y2=a2b2 すなわち、
(b2m2+a2)y2+2b2cmy+b2c2−a2b2=0 より、
(b2m2+a2)y2+2b2cmy−b4=0
の解である。よって、解と係数の関係から、
γ+δ=−2b2cm/(b2m2+a2)、 γδ=−b4/(b2m2+a2)
このとき、 線分BDの長さの平方 BD2 は、
BD2=(−mγ+mδ)2+(γ−δ)2=(m2+1)(γ−δ)2
=(m2+1){(γ+δ)2−4γδ}
=(m2+1){4b4c2m2/(b2m2+a2)2+4b4/(b2m2+a2)}
=4a2b4(m2+1)2/(b2m2+a2)2
となるので、BD=2ab2(m2+1)/(b2m2+a2)
よって、求める四角形ABCDの面積 S は、
S=AC×BD/2=2a2b4(m2+1)2/{(a2m2+b2)(b2m2+a2)}
ここで、 m2=t (t≧0) とおいて、分母を払って式を整理すると、
(a2b2S−2a2b4)t2+{(a4+b4)S−4a2b4}t+a2b2S−2a2b4=0 ・・・・・ (*)
この方程式が、0 以上の解を少なくとも一つ持つように、S の値の範囲を定めればよい。
a2b2S−2a2b4=0 即ち、S=2b2 のとき、a4S−4a2b4+b4S=2b2(a2−b2)2≠0
で、方程式は、t=0 という解を持つので、S=2b2 は求める S の値の範囲に含まれる。
よって、以下では、S≠2b2 として、2次方程式 (*) が、少なくとも一つの正の解を持つ
ようなS の値の範囲を求めればよい。
そこで、2次方程式 (*) から、2次関数
F(t)=(a2b2S−2a2b4)t2+{(a4+b4)S−4a2b4}t+a2b2S−2a2b4
を考える。このとき、軸の方程式は、
t=−{(a4+b4)S−4a2b4}/{2a2b2(S−2b2)}
不等式 −{(a4+b4)S−4a2b4}/{2a2b2(S−2b2)}<0 において、
2b2−4a2b4/(a4+b4)=2b2(a4+b4−2a2b2)/(a4+b4)
=2b2(a2−b2)2/(a4+b4)>0
より、 4a2b4/(a4+b4)<2b2 なので、
0<S<4a2b4/(a4+b4) 、2b2<S のとき、(a2b2S−2a2b4)×F(0)<0 であれば
よいが、 (a2b2S−2a2b4)2<0 は起こり得ない。
−{(a4+b4)S−4a2b4}/{2a2b2(S−2b2)}=0 即ち、S=4a2b4/(a4+b4) のとき、
F(t)=(a2b2S−2a2b4)(t2+1)は、t 軸と共有点を持たないから不適。
−{(a4+b4)S−4a2b4}/{2a2b2(S−2b2)}>0 即ち、
4a2b4/(a4+b4)<S<2b2 のとき、判別式を D とすると、
D={(a4+b4)S−4a2b4}2−4(a2b2S−2a2b4)2
=((a4+b4)S−4a2b4+2a2b2S−4a2b4)((a4+b4)S−4a2b4−2a2b2S+4a2b4)
=((a2+b2)2S−8a2b4)(a2−b2)2S≧0
であればよい。
このとき、 S≧8a2b4/(a2+b2)2 かつ 4a2b4/(a4+b4)<S<2b2 において、
8a2b4/(a2+b2)2−4a2b4/(a4+b4)=4a2b4(a2−b2)2/(a2+b2)2>0
2b2−8a2b4/(a2+b2)2=2b2(a2−b2)2/(a2+b2)2>0
から、4a2b4/(a4+b4)<8a2b4/(a2+b2)2<2b2
に注意して、S の値の範囲は、8a2b4/(a2+b2)2≦S<2b2
従って、 S=2b2 も含めて、求める S の値の範囲は、
となる。
(コメント) 一応、公式らしきものが得られたが、計算が煩雑と息子が宣う。もう少し易しい
計算が可能かどうか、研究してみる価値はありそうだ。
一般の場合も多分同様に出来るので、楕円の方程式が、 2x2+3y2=6 である場合を
考える。

焦点 F、F’の座標は、それぞれ F( 1 , 0 ) 、 F’( −1 , 0) で与えられる。
このとき、離心率 e=1/
F’を極とする極方程式は、
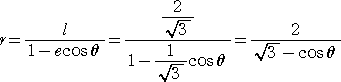
となるので、
また、Fを極とする極方程式は、

であり、さらに、FAの偏角は、 (π/2)+θ から、
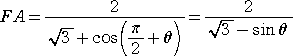
となる。 よって、求める四角形ABCDの面積 S =AC×BD/2 は、
S=(FA+FC)(F’B+F’D)/2
となるので、式を整理すると、
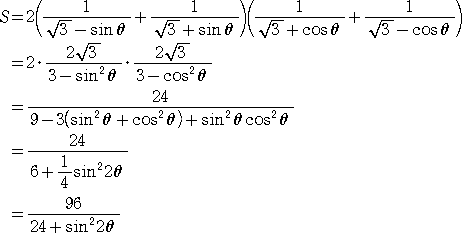
0≦θ≦π としてよいので、 0≦2θ≦2π より、 0≦sin2θ≦1
このとき、求める S の値の範囲は、96/25≦S≦4 となる。
(コメント) 少しは計算が楽になったのかな...?
以下、工事中