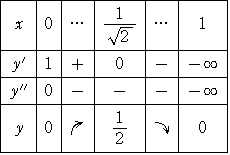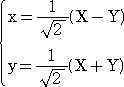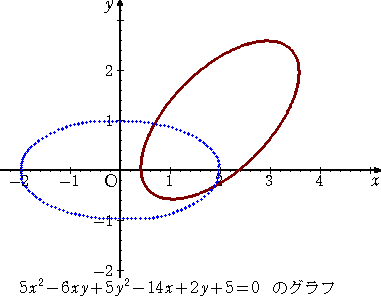いろいろな曲線 
私の高校時代(ほとんど、はるか昔かな?!)、高校数学が、数学Ⅰ、数学ⅡB、数学Ⅲ
と分かれていた頃、高校数学の最大の目標は、微分・積分を駆使して、いろいろな曲線を
描画することであった。
今でこそ、コンピュータソフトが充実し、数式を入力すれば、たちどころにディスプレイに
表示されるようになったが、当時は計算機すらなく、あるのは対数尺。結局腕力が頼りで、
計算を推し進めるほかなかった。おかげで相当に計算力が鍛えられたような気がする。
今の時代の高校では、「計算の仕方のみを簡単に扱い、計算は計算機におまかせ」状
態になっており、途中計算の微妙な綾を経験する機会を失い、計算を巧妙に工夫しようと
する意欲を抑制させているような気がする。
このページでは、いろいろな曲線を紹介しつつ、迫力ある計算の一端が紹介できればと
考えている。紹介する曲線は、下記の通り。
グラフ描画についての指針
グラフを調べる場合、次のことを念頭において計算を進めればよい。
(1) 曲線の存在範囲(Existence)や座標軸に対する対称性(Symmetry)
(2) 座標軸との交点(Intersection)や曲線上の特殊な点の座標(Special point)
(3) 関数の増減と極値(One)
(4) 関数の凹凸と変曲点(Two)
(5) 漸近線(Straight line)
私の高校時代、上記手順を覚えるために頭文字をつなぎ合わせて、
SESIOTS(セシオッツ)
などという語呂合わせを考案したものだ。
例 曲線 Y2=X2(1-X2) のグラフを描いてみよう。
式の特徴から、曲線は、X軸に関して対称、Y軸に関して対称、原点に関して対称である
ので、計算する範囲を、X≧0、Y≧0 としてよい。さらに、Y2≧0 であるので、 0≦X≦1
としてよい。このとき、与えられた関数は、
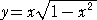
となる。この関数について考察すれば十分である。
まず、関数の増加・減少の状態を調べるために、第1次導関数を求める。
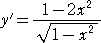
Y’=0 を解いて、0≦x≦1 を満たす x は、
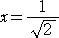
x=0 のとき、Y=0 かつ Y’=1 なので、曲線は原点において、直線 Y=Xと接する。
次に、曲線の凹凸、変曲点を調べるために、第2次導関数を求める。
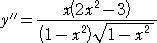
Y”=0 を解いて、0≦x≦1 を満たす x は、 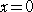
以上の計算から、次のような増減表が得られる。このとき、グラフは右図となる。
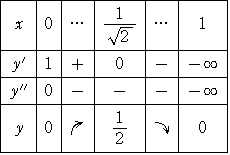
極大 |
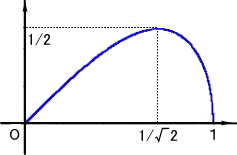 |
上で得られたグラフを、両軸に関して折り返して、求めるグラフが得られる。
明らかに、原点 ( 0 ,0 ) が変曲点である。
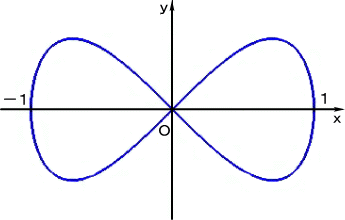
[曲線 Y2=X2(1-X2) のグラフ]
ところで、曲線 Y2=X2(1-X2) のグラフを描画する場合、いちいち関数を微分しなけ
れば、その概形がわからないのかというと、そうでもない。次のような方法でも曲線の概
形は、おおよそつかむことができる。
曲線 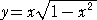 において、
において、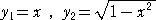 とおけば、関数の値は、
とおけば、関数の値は、
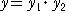 により、求められる。このことを利用して、グラフを描画することができる。
により、求められる。このことを利用して、グラフを描画することができる。
 |
左図において、y1のグラフは、
原点を通り、傾き1の直線であ
り、y2のグラフは、原点中心、
半径1の四分円である。
|
極座標について
いろいろな曲線を方程式の形に表す場合、Y=F(X) のような陽関数だけでは表現しきれ
ない。媒介変数表示の方法は万能ではあるが、式自体に美しさが感じられない。極座標を
用いると、美しく簡潔に表現されることが多い。
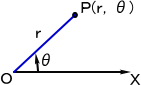 |
極座標は、平面上の定点OとOから出る半直線OXからなる。
平面上の点Pに対して、
OP=r 、∠XOP=θ (OXから反時計回りに測った角)
のとき、(r ,θ) を、点Pの極座標といい、P(r ,θ) と書く。 |
このとき、Oを極座標の極、半直線OXを始線、OPを動径、θを偏角という。
極座標においては、r<0 ということもあり得る。
(r ,θ)に対して、極Oと点対称な点 (r ,θ+π) を、(-r ,θ)
と表現する。
極座標で表された方程式を、極方程式という。
極方程式の美しさは、次の例を見れば明らかであろう。
例(三葉線)
直交座標系では、(X2+Y2)2=aY(3X2-Y2) という非常に覚えにくい式になるが、これが
極方程式だと、すっきり美しく、
r=asin3θ
と表される。
例(直線)
極を通る直線の極方程式は、 θ=α ( α は、直線と始線とのなす角)
極を通らない直線の極方程式は、 rcos(θ-α)=p
(極から直線に下ろした垂線の長さを p 、垂線と始線とのなす角を
α とする。)
例(円)
極を中心とする半径 R の円の極方程式は、 r=R
中心が(a ,α)で、半径Rの円の極方程式は、 r2+a2-2arcos(θ-α)=R2
例(2次曲線の統一的定義)
2次曲線は、定点Fと、点Fを通らない定直線Lからの距離の比が一定な点Pの軌跡と定
義される。
今、点Fから直線Lに下ろした垂線の足をHとし、その垂線の長さ(FH)を、k
とおく。右図
のように、Fを極とし、HFの方向に始線を定める。
点Pより直線Lに下ろした垂線の足をQとするとき、
定義より、
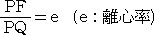
である。
右図より、 PQ=k+rcosθ なので、この式に、
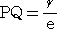
を代入して整理すれば、次のような極方程式が得ら
れる。 |
|
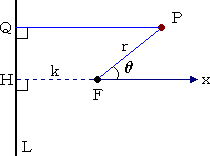 |
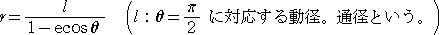
ここで、0<e<1 のとき、楕円、e=1 のとき、放物線、e>1 のとき、双曲線を表す。
また、定点Fを焦点、定直線Lを準線という。
準線は、放物線に限らず、楕円や双曲線にも存在する。一時期、高校の教科書で楕円や
双曲線の準線が扱われたが、今は消えてしまっている。
知っていると、図形上の長さの計算などが簡明に表されるので便利である。
例 放物線 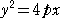 の離心率 e は、1 である。
の離心率 e は、1 である。
焦点の座標は、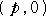 準線の方程式は、
準線の方程式は、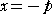
であるので、x 座標が x1 である放物線上の点Pと焦点との距離は、簡単に
|x1+p|
と表される。
例 楕円
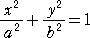 (ただし、
(ただし、 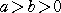 とする)
とする)
の離心率は、
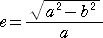
で与えられ、焦点 F、F’の座標は、F(ae,0)、F’(-ae,0) と書ける。
このとき、焦点 Fに対する準線の方程式は、 x=a/e
焦点 F’に対する準線の方程式は、 x=-a/e
であるので、x 座標が x1 である楕円上の点Pと焦点Fとの距離は、簡単に
a-ex1
と表される。同様にして、x 座標が x1 である楕円上の点Pと焦点F’との距離は、
a+ex1
と表される。
(追記) 平成24年10月16日付け
何年ぶりかでこのページを見直してみて、離心率についての記述が結果のみに終わり、詳
細な計算が省かれていることに大いに不満を感じた。できるだけ分かりやすく説明を試みた
いと思う。
まずは、楕円から。証明のポイントは次の図にある。
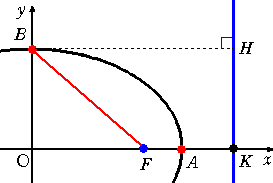 |
楕円
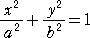 (ただし、 (ただし、 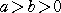 ) )
において、頂点A、Bの座標は、
A(a,0) 、B(0,b)
であり、焦点Fの座標は、F(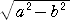 ,0) ,0)
|
このとき、三平方の定理より、 BF=a となる。
(以下の計算からも分かるように、この事実はとても重要である。)
離心率の定義から、 BF/BH=e なので、 BH=a/e となる。
すなわち、準線の方程式は、 x=a/e で与えられる。
同様にして、焦点F’(-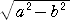 ,0)に対する準線の方程式は、 x=-a/e で与えら
,0)に対する準線の方程式は、 x=-a/e で与えら
れる。
また、 AF/AK=e より、 a-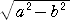 =e(a/e-a)=a-ea なので、離心率 e は、
=e(a/e-a)=a-ea なので、離心率 e は、
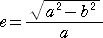
で与えられる。このとき、焦点F、F’の座標は、 F(ae,0) 、F’(±ae,0) となる。
さらに、 離心率 e=OF/OA が成り立ち、中心からどれくらい離れているのかという離
心率の雰囲気が如実に醸し出される。準線を用いた離心率の定義では味わえない感覚で
ある。
また、x 座標が x1 である楕円上の点Pと焦点Fとの距離は、
PF=e・PQ (QはPから準線に下ろした垂線の足) より、
PF=e・(a/e-x1)=a-ex1
同様にして、x 座標が x1 である楕円上の点Pと焦点F’との距離は、
PF’=e・PQ (QはPから準線に下ろした垂線の足) より、
PF’=e・(x1+a/e)=a+ex1
と表される。
例 双曲線
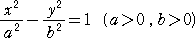
の離心率は、
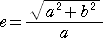
で与えられ、焦点 F、F’の座標は、F(ae,0)、F’(-ae,0) と書ける。
このとき、焦点 Fに対する準線の方程式は、 x=a/e
焦点 F’に対する準線の方程式は、 x=-a/e
であるので、x 座標が x1 である双曲線上の点Pと焦点Fとの距離は、
x1>a のとき、 ex1-a
x1<-a のとき、 a-ex1
と表される。
同様にして、x 座標が x1 である双曲線上の点Pと焦点F’との距離は、
x1>a のとき、 ex1+a
x1<-a のとき、 -a-ex1
と表される。
極座標による接線とその性質
曲線 r=F(θ) 上の1点 P(r,θ) における接線の方程式は、
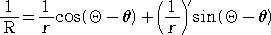
(ただし、(R,Θ)は流通座標とする。)
実際に、
直交座標系において、原点を通らない直線の方程式は、aX+bY=1 (a、b
は定数)と
おける。
このとき、流通座標(R,Θ)を用いて、X=RcosΘ 、 Y=RsinΘ と書けるので、
上式に代入して、a・RcosΘ+b・RsinΘ=1
よって、直線の方程式は、
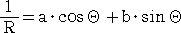
いま、この直線が、2点 (r,θ)、(r+Δr,θ+Δθ) を通るものとする。
このとき、
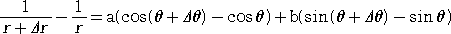
なので、両辺を Δθ で割って、Δθ→ 0 とすると、

また、直線は、 (r,θ)を通るので、
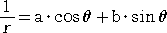
この2式から、a、b を求めると、
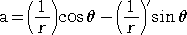
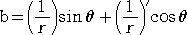
| これらを、 |
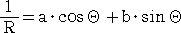 |
に代入して、公式を得る。 |
また、下図のように、曲線 r=F(θ) 上の1点 P(r,θ) における接線と始線のなす角を α 、
動径とのなす角を β とすると、次の式が成り立つ。
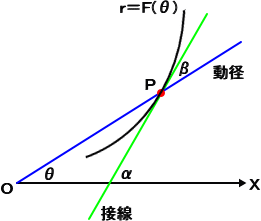 |
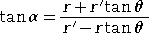
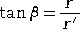
実際に、前半は、
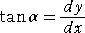
から明らか。後半は、β=α-θ と、加法定理か
ら容易に導かれる。 |
漸近線について
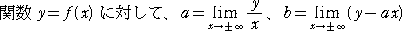
が存在し、かつ有限なとき、直線 y=ax+b は漸近線となる。
x → a のとき、 y → ±∞ ならば、直線 x=a は漸近線となる。
合同変換について
一般の曲線の方程式に対して、適当な合同変換(平行移動や回転移動)を施すと、より簡
単な方程式になり、曲線の持つ幾何学的性質が把握され易くなる。
曲線のグラフそのものを変換する場合と座標系そのものを変換する場合の2つの方法が
ある。
曲線のグラフの合同変換・・・変換前の座標を、(x ,y) 変換後の座標を、(X ,Y) とする。
平行移動
X軸方向に p 、Y軸方向に q だけ平行移動するとき、変換式は、X=x+p、Y=y+q
回転移動
原点中心に角θだけ回転させるとき、変換式は、
X=xcosθ-ysinθ Y=xsinθ+ycosθ
行列を用いて表現すれば、
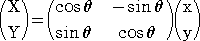
ここで、
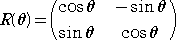
とおくと、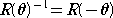 が成り立つ。
が成り立つ。
座標変換・・・変換前の座標を、(x ,y) 変換後の座標を、(X ,Y) とする。
平行移動
座標軸を、X軸方向に p 、Y軸方向に q だけ平行移動するとき、変換式は、
X=x-p、Y=y-q
回転移動
座標軸を、原点中心に角θだけ回転させるとき、変換式は、
X=xcosθ+ysinθ Y=-xsinθ+ycosθ
この変換式は、行列を用いても表される。
例 方程式 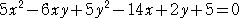 で表される曲線のグラフを書け。
で表される曲線のグラフを書け。
(解) 曲線を、X軸方向に -2 、Y軸方向に -1 だけ平行移動する。
変換前の座標を、(x ,y) 変換後の座標を、(X ,Y) とすると、
X=x-2、Y=y-1 すなわち、x=X+2、y=Y+1
この変換式を、方程式に代入して整理すると、5X2-6XY+5Y2-8=0
すなわち、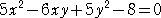 という方程式に変換される。
という方程式に変換される。
さらに、この曲線を、原点中心に角-45°回転させる。
変換前の座標を、(x ,y) 変換後の座標を、(X ,Y) とすると、
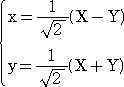
この変換式を、方程式に代入して整理すると、X2+4Y2=4
| すなわち、 |
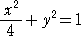 |
という方程式に変換される。 |
これは、楕円の方程式である。このグラフは容易に描画できて、上記の平行移動、回転移
動の逆の変換を施すことにより、もとのグラフが描画できる。
求めるグラフは下図の様になる。
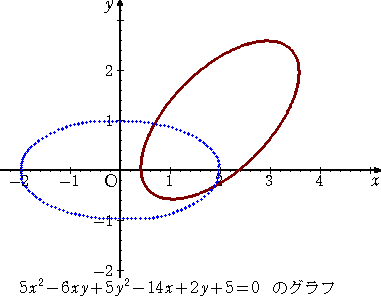
(参考文献:問谷 力、森本清吾 著 袖珍 数学公式要覧(山海堂出版部)
大槻富之助 著 数Ⅲの研究(旺文社)
佐々木重夫・和田秀三・寺田文行 著 微分積分学(廣川書店))