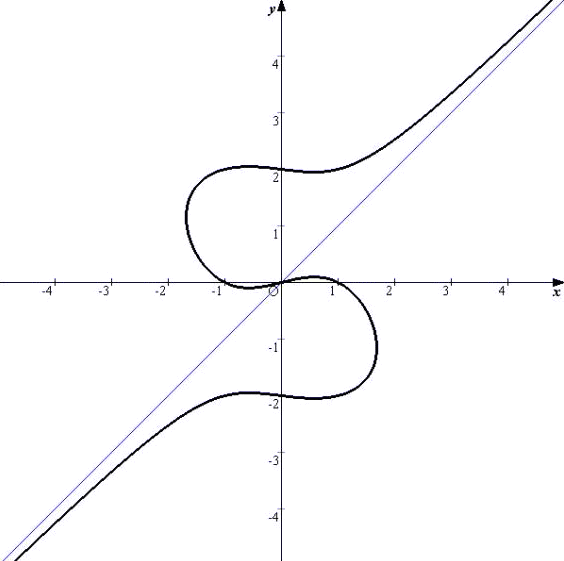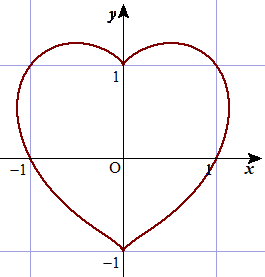その他の曲線 
このページでは、関数が多少複雑であるが形的に面白い曲線のいくつかを紹介する。
| (1) |
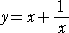 |
この関数は、相加平均と相乗平均の関係を視覚的に示してくれる。
|
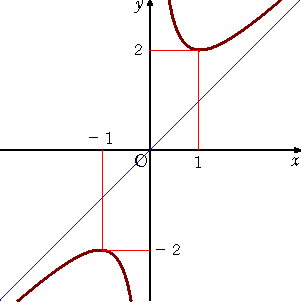 即ち、
即ち、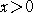 のとき、
のとき、
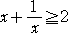
が成り立つ。
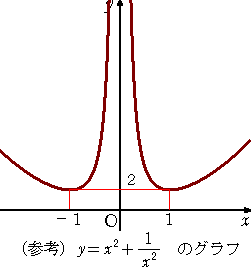
| (2) |
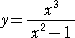 |
この関数は、漸近線を求める練習問題として、最適である。 |
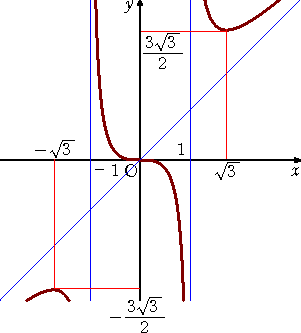
| (3) |
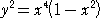 |
この関数とこちらの関数のグラフを比較すると面白い。 |
(5)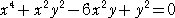
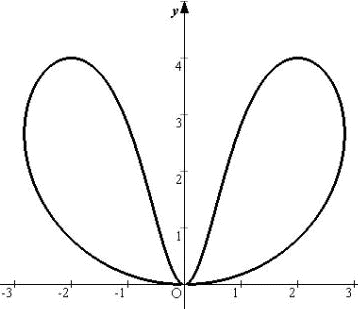
(6)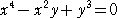
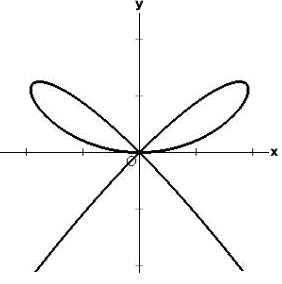
(7)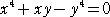
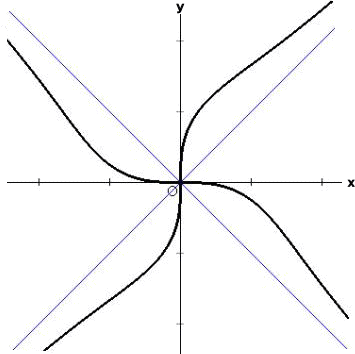
(追記)
(8) 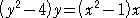
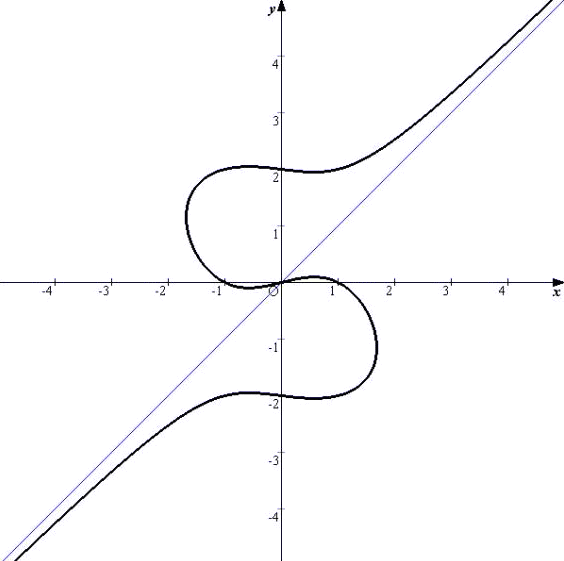
(再追記)
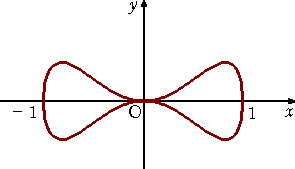
(9) チルンハウゼンの3次曲線(1680年): Y2-X3-X2=0
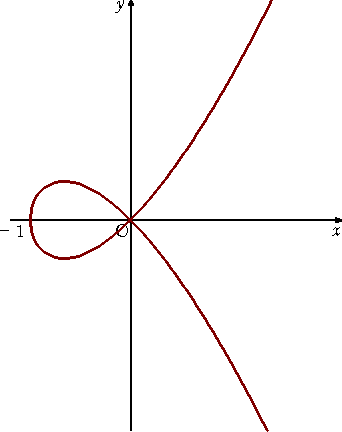
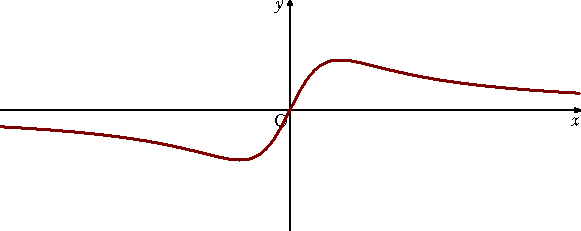
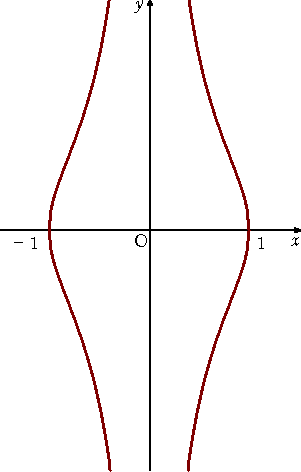
(10) ニュートンの蛇形 : X2Y+Y-X=0
(参考文献:森口繁一・宇田川銈久・一松 信 著 数学公式(岩波書店))
当HPがいつもお世話になっているHN「K.S.」さんより、2つの図形を頂きました。K.S.
さんに感謝します。また、掲載が遅れましたこと、お詫びいたします。
(11) ハート型 : (x2+y2-1)3=x2y3 (平成25年3月31日付け)
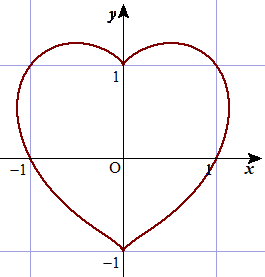
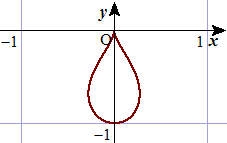
(12) 涙の形(平成25年4月11日付け)
放物線 y+x2+1=0 において、円の反転式 X=x/(x2+y2)、Y=y/(x2+y2)
により、 y(x2+y2)+x2+(x2+y2)2=0
 即ち、
即ち、

![]()

![]()

![]()

![]()