ら　し せん
螺獅線

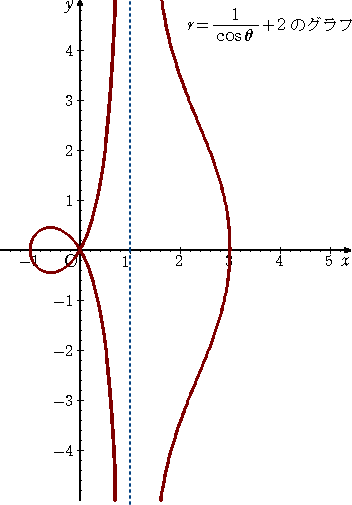
極方程式は、

　この曲線は、コンコイドともいわれる。


　　　作図の原理

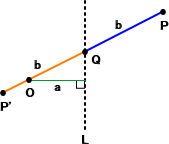定直線Ｌと距離 ａ だけ離れた 　定点Ｏが与えられている。直線 　Ｌ上に動点Ｑがあり、さらに、直 　線ＯＱ上に、ＱＰ＝ＱＰ’＝ｂ とな 　る２点Ｐ、Ｐ’をとる。点Ｑが直線 　Ｌ上を動くとき、点Ｐ、Ｐ’の軌跡 　が求める螺獅線を与える。

　角の３等分の作図について、定規・コンパスだけを用いては不可能であるが、その条件を
はずせば、角の３等分はいろいろな方法で作図される。

　例えば、蝸牛線（リマソン）の特別な場合を用いる方法、折り紙を用いる方法（１枚、２枚）、
角の ｎ 等分方程式を利用する方法など多彩である。

　ここでは、螺獅線を用いて、角を３等分する方法を考えてみよう。

　　　　　　　　

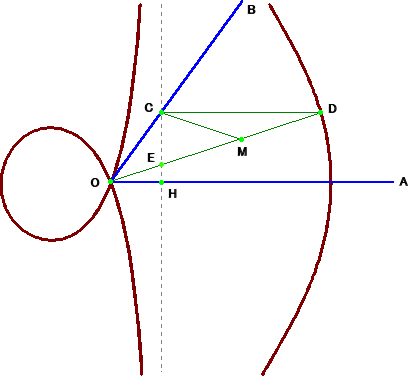
　上図において、∠ＡＯＢ　が与えられた角である。ＯＡ上任意の点Ｈで垂線を引き、ＯＢ と

の交点を Ｃ とする。このとき、ＯＨ＝ａ、２・ＯＣ＝ｂ　として螺獅線を描く。そして、この曲線

と、点ＣからＯＡ に平行な線を引き、その交点をＤとする。このとき、∠ＡＯＤが角の３等分

になっている。

　（証明）　ＯＤとＨでの垂線との交点を Ｅ とし、ＤＥの中点を Ｍ とする。螺獅線の性質から、

　ＯＣ＝ＭＤ　また、∠ＤＣＥ＝∠Ｒで、ＭがＤＥの中点であることから、ＭＤ＝ＭＣである。

　よって、　△ＭＣＤ、△ＣＯＭは二等辺三角形となり、明らか。

（注意）　直交座標系での方程式は、次のようにして求められる。

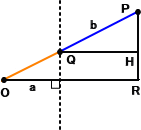　　　左図において、△ＰＯＲ∽△ＰＱＨ より、ＯＰ：ＯＲ＝ＱＰ：ＱＨ が

　　成り立つ。従って、Ｏ(０，０)、Ｐ(Ｘ，Ｙ) とすれば、

　　　　　　　ＯＰ＝Ｘ^２＋Ｙ^２、ＯＲ＝Ｘ、ＱＰ＝ｂ、ＱＨ＝Ｘ−ａ

　　であるから、これを比例式に代入して計算すればよい。