角の３等分方程式　　　　　　　　　　　　　　　　　　　　　

　作図問題において許される作業は、次の２つである。

（１）　定木を用いて、任意に与えられた２点を結ぶ直線を引くこと
（２）　コンパスを用いて、任意に与えられた中心と半径を持つ円を描くこと

　所要の線分が、定木とコンパスを用いて作図できるということは、代数的には、その線分
の長さが、有限回の、＋−×÷といった四則演算と平方根の計算により、求められること
を意味する。

　このページでは、角の３等分を可能にする線分の長さが満たす、角の３等分方程式を求
め、その解析を行うつもりである。

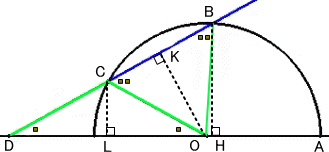アルキメデスによれば、∠AOB の３ 　等分を求めるには、 　　　　　　　　OB＝OC＝CD 　となる直線BDが作図できればよい。 　（参考：作図問題における円の役割） 　即ち、OD＝Ｘ となる点D が直線AL上 　に作図できればよい。

　この Ｘ の満たす方程式が、角の３等分方程式といわれるものである。

　それでは、実際にその角の３等分方程式を求めてみよう。ただし、OA＝１　として考える。

　OH＝ａ、CK＝BK＝Y とおくと、

　　　　△DCL∽△DOK∽△DBH なので、 　　DL ： DC ＝ DK ： DO ＝ DH ： DB

　　よって、Ｘ/２ ： １ ＝ １＋Ｙ ： Ｘ ＝ Ｘ＋ａ ： １＋２Ｙ が成り立つ。

　　　　　　　即ち、　　１＋Ｙ＝(１/２)Ｘ² 　、　　Ｘ＋ａ ＝(１/２)Ｘ＋ＸＹ

　この２式より、Ｙ を消去して、次の角の３等分方程式を得る。

　　　　　　　　　　　Ｘ³−３Ｘ−２ａ＝０

　∠AOB＝３θ を与えるということは、ａ を与えることに等しいので、上式を満たす解 Ｘ が代
数的に求まれば、角の３等分は可能となる。
　（参考）　任意の角を３等分することが不可能であることは、１８３７年に　Ｗａｎｔｚｅｌ　により証明されている。

　ところで、ａ＝ｃｏｓ３θ＝４ｃｏｓ³θ−３ｃｏｓθなので、方程式は、

　　　　　　　　　Ｘ³−３Ｘ−８ｃｏｓ³θ＋６ｃｏｓθ＝０
と書ける。

　上図より、(１/２)Ｘ＝ｃｏｓθ　即ち、Ｘ＝２ｃｏｓθ なので、上式の左辺は、Ｘ−２ｃｏｓθ　で割り
切れる。

　従って、左辺は因数分解されて、

　　　　　　　　　　（Ｘ−２ｃｏｓθ)(Ｘ^２＋２ｃｏｓθ・Ｘ＋４ｃｏｓ^２θ−３）＝０
となる。

　解の公式により、　　 Ｘ^２＋２ｃｏｓθ・Ｘ＋４ｃｏｓ^２θ−３＝０　の解は、

　　　　　　Ｘ＝

となる。ここで、三角関数における単振動の合成の公式を用いると、

　　　　　　Ｘ＝２ｃｏｓ（１２０°±θ）

と表されるので、角の３等分方程式の解は、

　　　　　　　　　　　　　２ｃｏｓθ　、　２ｃｏｓ（１２０°±θ）

で与えられる。

　例えば、∠AOB＝６０°のとき、ａ＝１/２ で、角の３等分方程式は、Ｘ³−３Ｘ−１＝０ とな
る。この方程式の３つの解は、２ｃｏｓ２０°、−２ｃｏｓ４０°−２ｃｏｓ８０°であるが、Ｘ＞０
より、求める Ｘ は、２ｃｏｓ２０°となる。
　この値は近似値しか求めることができないので、角の３等分は不可能となる。
　（参考）　Ｘ＝ｃｏｓ２０°とおくと、Ｘ は、３次方程式　８Ｘ^３−６Ｘ−１＝０ の解である。ところが、この方程式は、
　　　　　　整数係数の範囲では因数分解できない。このとき、代数学の体の拡大理論により、このような方程
　　　　　　式の実数解は、自然数に対して四則演算（＋−×÷）と開平（√）の操作を有限回行って得ることは
　　　　　　できないことが示される。したがって、Ｘ＝ｃｏｓ２０°の値を作図することは不可能である。

　※　角の３等分が不可能であることの詳細は、こちらを参照。

　角の ｎ 等分方程式については、数研出版のホームページの中の数研通信のコーナーに
ある
　　　　龍山一郎　著 　「正１７角形の代数的解法および幾何的解法」
が詳しい（一部ミスプリ有り）。是非参考にしてみて下さい。

（参考文献：鈴木晋一　山下正勝　著　作図問題の代数化（啓林館））
　　　　　　　 龍山一郎　著　正１７角形の代数的解法および幾何的解法（数研出版））


（追記）　平成１６年１０月２０日 Margulis　様の掲示板への書き込みで、放物線を用いた任
　　　　　意角の３等分の作図方法があるということを知った。楕円や双曲線でもいいらしい。

　　　このことについて、次のホームページ　：　Ｚｅｉｔｒａｕｂｅｒｓｈａｕｓ〜時間泥棒の館
　　の中で詳しく述べられている。（このページ作成中何故かＨＰにアクセス出来なかった？）

　ここでは、上記のホームページを参考にして、作図方法を確認したい。

　角 ３θ が与えられているものとして、角 θ を作図するには、上記で述べた角の３等分方
程式
　　　　　　　　Ｘ³−３Ｘ−２ａ＝０　　　（ただし、　ａ＝ｃｏｓ３θ　）

を解かなければならない。この解法に、放物線が巧妙に利用される。

　いま、放物線　Ｙ＝Ｘ² が与えられているものとし、この放物線と円：

　　　　　　　　（Ｘ−ｐ）²＋（Ｙ−ｑ）²＝ｒ²

が交わる場合を考える。放物線の式を円の式に代入して整理すると、

　　　　　　　　Ｘ⁴＋（１−２ｑ）Ｘ²−２ｐＸ＋ｐ²＋ｑ²−ｒ²＝０

となる。

　このとき、　Ｘ³−３Ｘ−２ａ＝０　の３つの解 α 、 β 、 γ が上記の４次方程式の解となるよう

に円の中心（ ｐ ， ｑ ）と半径 ｒ が求まればよい。

　第４の解を δ とすると、解と係数の関係から、

　　　　　　　　α ＋ β ＋ γ ＝ ０　　、　　α ＋ β ＋ γ ＋ δ ＝ ０

よって、そのような条件を満たすとき、　δ ＝ ０　であることが分かる。

したがって、４次式は次のように因数分解される。

　　Ｘ⁴＋（１−２ｑ）Ｘ²−２ｐＸ＋ｐ²＋ｑ²−ｒ² ＝ Ｘ（Ｘ³−３Ｘ−２ａ）

両辺の係数を比較して、　１−２ｑ＝−３　、　−２ｐ＝−２ａ　、　ｐ²＋ｑ²−ｒ²＝０

これより、　ｐ＝ａ　、　ｑ＝２　、　ｒ²＝ａ²＋４　　となる。

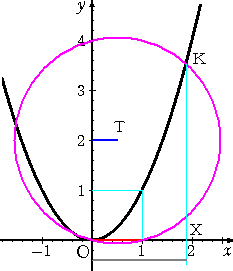
　以上から、放物線　Ｙ＝Ｘ² に対して、円 （Ｘ−ａ）²＋（Ｙ−２）²＝ａ²＋４　を描けば、その交

点のＸ座標が角の３等分を求めるための候補となる。

　ところで、角の３等分の方程式は、簡単なグラフの解析から分かるように、正の解を１個と

負の解を２個持つ。

　したがって、上記の放物線と円との交点で、Ｘ座標が正のものはただ一つ存在する。

この値が求めるものとなる。

　以上を踏まえて、実際に作図してみよう。

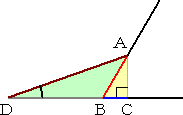<<　作図の手順　>>

（１）　∠ＡＢＣ＝３θ　は与えられた角度である。ただし、ＡＢ＝１　とする。

（２）　このとき、ＢＣ＝ｃｏｓ３θ＝ａ　となる。これにより、円の中心 Ｔ が定まる。この点を中心
　　　として原点を通る円を描き、所要の放物線との交点を Ｋ とおく。

（３）　Ｋ より、ｘ 軸に垂線を下ろし、X の位置が求められる。

（４）　ＯＸ の長さと等しい長さを持つ線分ＢＤを、ＣＢの延長線上に定める。

（５）　Ａ と Ｄ を結ぶと、∠ＡＤＣ＝ θ　となる。


（注意）　上記では、放物線　Ｙ＝Ｘ² が用いられたが、実は任意の放物線で構わないことが、
　　　　上述のＨＰで述べられている。（この事実には、とても感動しました！）

　　　　原点を頂点とする任意の放物線は、Ｙ＝ａＸ²　と書ける。そこで、長さ １/ａ を単位の
　　　長さ（１）と考えることにより、上記の作図方法がそのまま適用される。
　　　（このことは、放物線の相似性と関連がある。）