放物線の相似性 　　　　　　　　　　　　　　　　　　　　　　　　　　　

　このページは、当ＨＰをご覧になられた「Gnomon＠杉井」様から頂いた問題について考え
たものである。これは、相当に昔の立教大学の入試問題にもなっている。

　　　　　　 【　全ての放物線は互いに相似形である　】

　「Gnomon＠杉井」様によれば、名詞サイズほどの空間でその証明が出来たとのことなの
で、恐らく、次のような証明ではなかったかと推察される。

　放物線 ｙ＝ａｘ²＋ｂｘ＋ｃ　は、ｙ＝ａ（ｘ＋ｂ/(２ａ)）²−(ｂ²−４ａｃ)/(４ａ)　により、平行移動
して、放物線 ｙ＝ａｘ² と合同になる。ここで、ｙ 軸方向の拡大・縮小（相似の中心が無限遠
点の相似変換！）　Ｘ＝ｘ 、Ｙ＝(１/ａ)ｙ　を行えば、放物線 ｙ＝ａｘ² は、Ｙ＝Ｘ² に変換され
る。したがって、放物線 ｙ＝ａｘ²＋ｂｘ＋ｃ　と放物線 ｙ＝ｘ²　は相似である。

　この問題に付随する問題として、放物線を平行移動させないで、直接的に相似の中心を
求めたいという場合がある。

　少し、用語の復習をしよう。
　　　　　　　　

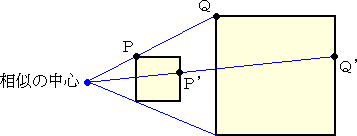
　２つの図形（上図では、正方形とした！）において、対応する２点（上図では、ＰとＱ）を結
ぶ直線がすべて１点で交わり、交点から対応点までの距離の比が常に一定であるとき、２
つの図形は相似の位置にあるといい、相似の位置における２つの図形は相似であるとい
う。ここで、交点を、相似の中心、一定な比の値を、相似比という。

　放物線を平行移動させないで、放物線 ｙ＝ａｘ²＋ｂｘ＋ｃ　と　放物線 ｙ＝ｘ²　が相似であ
ることを示すには、相当な計算力が必要である。

　ここでは、具体的な場合について、その方策を記録に留めようと思う。

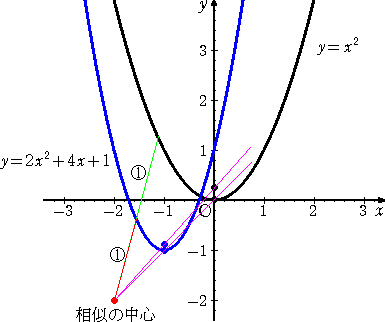
練習問題　　放物線 ｙ＝２ｘ²＋４ｘ＋１　は、放物線 ｙ＝ｘ²　と相似であることを証明し、相
　　　　　　　似の中心と相似比を求めよ。

（解）　ｙ＝２ｘ²＋４ｘ＋１＝２（ｘ＋１）²−１　より、頂点の座標は、Ａ（−１，−１）

　　　また、（ｘ＋１）²＝(１/２)（ｙ＋１）　より、焦点の座標は、Ｆ（−１，−７/８）

　　　同様にして、

　　　放物線 ｙ＝ｘ²　の頂点の座標は、Ｂ（０，０）　で、焦点の座標は、Ｇ（０，１/４）

　　　２つの放物線の頂点と頂点、焦点と焦点を結ぶ直線の方程式は、それぞれ、

　　　　　　　　　　　　ｙ＝ｘ　　、　　ｙ＝(９/８)ｘ＋１/４

　　　となる。この２直線の交点の座標は、　Ｓ（−２，−２）　である。
　　　　　　　　　　　　　　　　　　　　　　　　　（実は、この交点が、相似の中心となる！）
　　　この点 Ｓ を通り、ｘ 軸と角 θ をなす直線の方程式は、媒介変数表示を用いて、

　　　　　　　ｘ＝−２＋ｔ・ｃｏｓθ　　、　　ｙ＝−２＋ｔ・ｓｉｎθ

　　　と書ける。この式を、 ｙ＝ｘ²　に代入して整理すると、

　　　　　　　ｔ²・ｃｏｓ²θ−ｔ・（４ｃｏｓθ＋ｓｉｎθ）＋６＝０　　・・・・・　（＊）

　　　同様に、ｙ＝２ｘ²＋４ｘ＋１　に代入して整理すると、

　　　　　　　２ｔ²・ｃｏｓ²θ−ｔ・（４ｃｏｓθ＋ｓｉｎθ）＋３＝０

　　　２式の定数項をともに６にするために、両辺を２倍して、次の式を得る。

　　　　　　　（２ｔ）²・ｃｏｓ²θ−（２ｔ）・（４ｃｏｓθ＋ｓｉｎθ）＋６＝０　　・・・・・　（＊＊）

　　　（＊）の ｔ の値は、点 Ｓ から放物線 ｙ＝ｘ²　までの距離を表し、（＊＊）の ｔ の値は、

　　　点 Ｓ から放物線 ｙ＝２ｘ²＋４ｘ＋１　までの距離を表す。

　　　このとき、（＊）、（＊＊）より、点 Ｓ から放物線 ｙ＝ｘ²　までの距離は、点 Ｓ から放

　　　物線 ｙ＝２ｘ²＋４ｘ＋１　までの距離の２倍に等しいことが分かる。

　　　したがって、相似の中心は、Ｓ（−２，−２）　で、相似比は、２ ： １ であることが分か

　　　る。（終）

　上記の２つの放物線と相似の中心を図示すれば、下図のようになる。

　　　　　　


（追記）　「Gnomon＠杉井」様から、【　全ての放物線は互いに相似形である　】ことの大変
　　　　簡明な証明を頂戴した。

　　任意の放物線は、平行移動により、放物線 ｙ＝ａｘ² と合同である。放物線 ｙ＝ａｘ² と、

　直線 ｙ＝ｋｘ の交点を求めると、（０　，０）、（ｋ/ａ　，ｋ²/ａ）である。（前者が相似の中心）

　この２点の距離 Ｌ（ａ） を求めると、　Ｌ（ａ）＝ (ｋ/ａ) √(１＋ｋ²）　となる。

　　同様にして、放物線 ｙ＝ｘ² と、直線 ｙ＝ｋｘ の交点を求めると、（０　，０）、（ｋ　，ｋ²）な

　ので、この２点の距離 Ｌ（１） は、　Ｌ（１）＝ ｋ √(１＋ｋ²）　となる。

　　このとき、　Ｌ（ａ）/Ｌ（１）＝１/ａ　は、直線の傾き ｋ に無関係な定数である。

　よって、放物線 ｙ＝ａｘ² は放物線 ｙ＝ｘ² に相似で、相似比は、ａ ： １ となる。（証終）

（注意）　相似比を、「元の図形 ｙ＝ｘ² 」 ： 「相似の図形 ｙ＝ａｘ² 」 の形で表している。

　　私の想定した解法とは違い、とても基本に忠実に解かれたもので分かりやすい。今まで
　私自身、この問題に対する解答の方針として、ｙ 軸の拡大・縮小でとらえてきたが、上記
　の解答の方が自然であることに気づかされた。

　　　　　

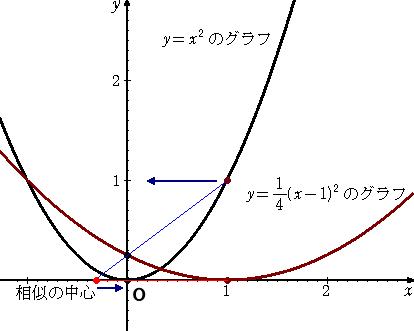
　上図からも分かるように、放物線 ｙ＝(1/4)(ｘ−１)² のグラフが、ｘ 軸に沿って原点にだん
だん近づくとき、相似の中心も、だんだんと原点に近づく。したがって、２つの放物線の頂点
がともに原点であるとき、相似の中心も原点であるということは、とても自然なことである。

　視点の転換をお教えいただいた「Gnomon＠杉井」様に感謝したい。


（追々記）　Margulis 様より上記問題の別解を頂戴した。


　　　　　　ａ≠０　のとき、 ｙ＝ａｘ² は、　 ａｙ＝（ａｘ）² 　　と書ける。

　　　　　この式で、　Ｘ＝ａｘ　、　Ｙ＝ａｙ 　とおくと、　 Ｙ＝Ｘ² 　となる。

　　　　　このことは、相似比 ａ の相似変換
　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　　により、放物線　 ｙ＝ａｘ²　が、放物線　ｙ＝ｘ²　に変換されることを意味する。

　　　　　簡単に言えば、これは座標平面を原点を中心として、全体のスケールを ａ 倍にして

　　　　　みると、放物線　ｙ＝ｘ²　 と合同形になるということである。

　　　　　　したがって、
　　　　　　　　　　　　　　「元の図形 ｙ＝ａｘ² 」 ： 「相似な図形 ｙ＝ｘ² 」＝ １ ： ａ
　　　　　である。

　　　　（コメント）　とてもスッキリした証明ですね。Margulis 様に感謝！