不可能の証明 　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　　　　解けることを証明するには、解いてみせればいいのだが
　　　解けないことを証明するには、どうするのだろうと思って
　　　日がたつほどそれが不思議でたまらなかった
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　−　岡　潔　−

　これは、日本を代表する数学者の言である。天才 岡 潔 をも困らせる「不可能の証明」
は如何にあるべきかについて、「任意の角の３等分は不可能である」という古代ギリシャ
の３大作図不能問題の一つを題材に整理してみようと思う。

　このページをおこすために、次の講演会に参加した。

	平成１８年８月５日（土）に 　日本大学文理学部（京王線 　「下高井戸駅」下車、徒歩10 　分）で、サマースクールが開 　かれた。今年で十年目にな 　るという。 　　これは、世田谷区の 　 「Do Math．Do Science」 　活動の一環でもあり、区内に 　ある東京農業大学農学部や 　武蔵工業大学工学部も日を 　変えて参加している催しであ 　る。 　（写真は、正門を入って直ぐ 　の１号館・・・校舎の配置が 　美しい！）
	サマースクールは当初区 　内の中学生が対象であった 　が、最近は多くの数学愛好 　家に門戸を開いている。今 　年は老若男女合わせて多分 　２００名近い方が集まったよ 　うに思う。 　　お昼には豪華なお弁当も 　出され、しかもケーキやお菓 　子がたくさん並ぶお茶会もあ 　って、本当にいたれりつくせ 　りだった！来年も是非参加 　したい．．．。 　（写真は、サマースクールが 　開かれた図書館・・・玄関前 　では縄跳びのアクロバット技 　の練習に励む学生達）

　サマースクールでは、森　真　先生の「 π の話」、茂手木公彦　先生の「可能？それとも不
可能？」という２つの講演があった。どちらの話題も当ＨＰのコンテンツと関係があり、終日
興味を持って拝聴することが出来た。両先生に感謝したい。

　このページでは、そのうちの茂手木先生の話された話題を私なりに理解したものをまとめ
ていきたいと思う。

　１９９５年、ワイルズ（Andrew Wiles　（1953〜））によって証明されたフェルマーの予想：

　自然数 ｎ (ｎ≧３) について、　ｘ^ｎ＋ｙ^ｎ＝ｚ^ｎ　を満たす自然数解 (ｘ，ｙ，ｚ) はない

　　（　今は、この事実は、フェルマー・ワイルズの定理と呼ばれる。）

もある意味では不可能の証明（解が存在することは不可能という意味で！）と言えるだろう。

　証明のあらましは次のようであるらしい。

　　自然数解が存在したとすると、ある特別な性質を持つ楕円曲線が存在することになるが、
　楕円曲線は決してそのような性質は持たない。よって、自然数解は存在しない。

　たった２行で人類３５０年の努力の結晶を表すのはとてもおこがましいが、その２行の行間
を埋めるために貢献した日本人数学者のことを考えると、とても感動的である。

　茂手木先生の話された話題「角の３等分は不可能」も、基本的な証明の方針は、上記と同
じで、「角の３等分は可能」とすると、何やら変なことが起こるぞ！というものである。

　いくつか基礎知識を準備しよう。

　これから考えることは一つの平面上の話であるので、座標平面で考えることはごく自然な
ことである。

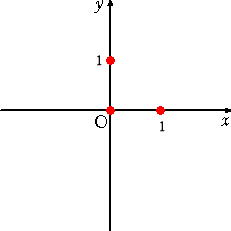
　座標平面は、平面上の任意の１点 Ｏ で直交する直線と、それぞれの直線上の単位点が
与えられたものである。（下図参照）

これらの３点を出発点として、定木とコンパスを用 　いて作図できる点をどんどん書き加えていこう。 　　茂手木先生の言葉を借りれば、これらの作図でき 　る点のことを作図可能点という。 　　定木とコンパスの役割を、この「作図可能」という 　キーワードを用いて表すと、 　　定　　木＝作図可能な２点を結ぶ直線が引ける 　　コンパス＝中心が作図可能点で、半径が作図可能 　　　　　　　　 点を結ぶ線分の長さの円が描ける 　となる。

　定木・コンパスを用いて、下図のように作図可能点を無限に作ることが出来る。

　　　　　　　　　　　　

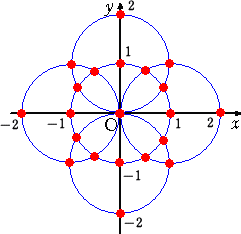
　以上をまとめると、次の操作で得られる新しい点も作図可能点となる。

（１）　作図可能点同士を結ぶ直線（作図可能直線という）同士の交点
（２）　中心が作図可能点で、半径が作図可能点を結ぶ線分の長さの円（作図可能円という）
　　　同士の交点
（３）　作図可能直線と作図可能円との交点

　座標平面上の作図可能点の ｘ 座標（または、 ｙ 座標）のことを、作図可能値という。

数直線（実数全体 Ｒ と一対一に対応）上の作図可能値全体の集合を、Ｋ とおく。

　集合 Ｋ には、どんな数が含まれているだろうか？

（１）　整数（　・・・，−２，−１，０，１，２，・・・　）を含むことは、上図から明らかだろう。

（２）　有理数（　１/２，２/３，・・・・　）を含むことも、例えば、下図から明らかだろう。

　　　　　　　　　　　　

（３）　作図可能値 ｎ の平方根 が作図可能値であることも、例えば、下図から明らか
　　　だろう。
　　　　　　　　

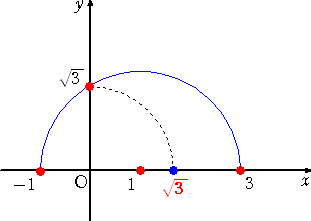
　このようにして得られる集合 Ｋ に、自然に代数学で言うところの「体」の構造が入ることは
下図から明らかだろう。

和と差は、．．．

　　　

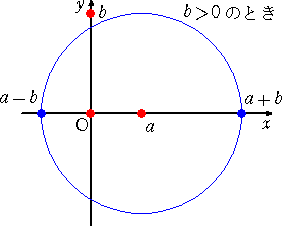
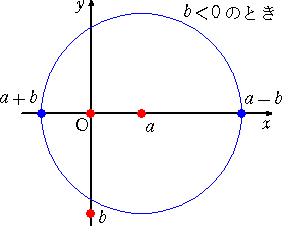
積は、．．．．

　　　　　　　　


　　　　　　　　　　

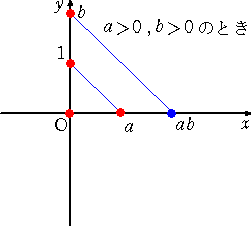
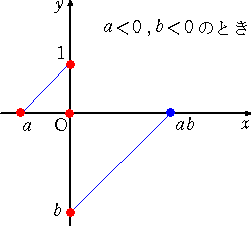
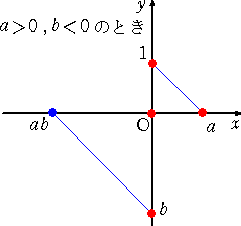
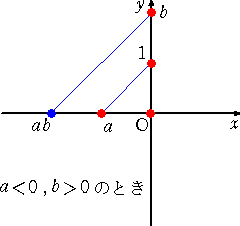
商は、．．．．

　　　　　　　　


　　　　　　　　　　

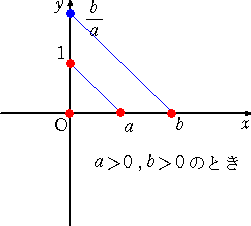
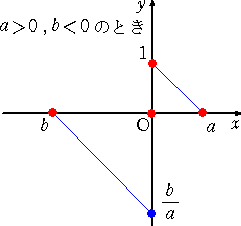
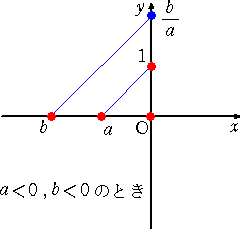
　さて、体 ｋ を一つ定める。（ ｋ を有理数全体からなる体 Ｑと思ってもいいだろう。）上記
で述べたことから、「作図可能値 ｎ の平方根 も作図可能値」であった。

　そこで、　ｎ∈ｋ　（ただし、ｎ＝ｍ² となる ｍ∈ｋ は存在しないものとする。）に対して、集合

　　　　　　　ｋ（）＝｛ ａ＋ｂ ｜　ａ∈ｋ　、ｂ∈ｋ　｝　

は、ｋ の２次の拡大体になる。通常、拡大次数は、　［ ｋ（） ： ｋ ］＝２　と表される。

　このような操作を続けると、ｋ に属さない作図可能値 ｐ　に対して次のことが言える。

　ある自然数 ｎ に対して、 ｋ の拡大体の列　Ｋ₁、Ｋ₂、・・・、Ｋ_ｎ　が存在して、

　　　　Ｑ＝ｋ⊂Ｋ₁⊂Ｋ₂⊂・・・⊂Ｋ_ｎ⊂Ｒ　　かつ　　ｐ∈Ｋ_ｎ　、　ｐ Ｋ_ｎ-1

が成り立つ。

　このとき、拡大次数に注目すれば、　［ Ｋ_ｎ ： Ｑ ］＝２^ｎ　が成り立つ。

　この事実を活用して、「任意の角の３等分は不可能である」ことが次のようにして示される。
それには、決して３等分され得ない角を与えれば十分だろう。

　いま、１２０°の角をなす２つの直線があり、この角度を３等分するような２つの半直線が
作図可能であると仮定する。

　　　　　　　　

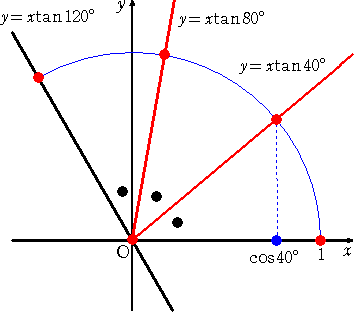
　すると、上図から、作図可能円との交点の ｘ 座標 ｃｏｓ４０°は作図可能値となる。

したがって、　ｃｏｓ４０°∈Ｋ_ｎ　となる有理数体 Ｑ の拡大体 Ｋ_ｎ が存在して、

　　　　　　　　　［ Ｋ_ｎ ： Ｑ ］＝２^ｎ

となる。　

　ところで、　θ＝４０°とおくと、　３θ＝１２０°なので、

　ｃｏｓ３θ＝４ｃｏｓ³θ−３ｃｏｓθ　より、　　　８ｃｏｓ³θ−６ｃｏｓθ＋１＝０

　２ｃｏｓθ＝Ｘ　とおくと、　Ｘ³−３Ｘ＋１＝０　で、　２ｃｏｓ４０°はこの３次方程式の解となる。

ところで、この３次方程式は、有理数の解を持たない。

　もし、有理数解 ｍ/ｎ （ｍ、ｎ は整数で、ｎ＞０、ｍ と ｎ は互いに素）を持つとすると、

　　　　　ｍ³/ｎ³−３ｍ/ｎ＋１＝０　すなわち、　ｍ³/ｎ＝３ｍｎ−ｎ²

　右辺は整数なので、　ｍ³ すなわち ｍ は、ｎ で割り切れる。

　ｍ と ｎ は互いに素なので、　ｎ＝１　でなければならない。

　よって、解は整数となり、　１＝Ｘ（３−Ｘ²）　から、１の約数でなければならない。

　すなわち、　解は、１　または　−１。　しかし、何れも、Ｘ³−３Ｘ＋１＝０　を満たさない。

　以上から、　３次方程式　Ｘ³−３Ｘ＋１＝０　は有理数の解を持たない。

このことから、　１ と Ｘ はＱ上１次独立であることが分かる。

　実際に、　Ｑ上１次独立でないと仮定すると、　ｍ−ｎＸ＝０　となるような少なくとも一つは

０ でない　ｍ、ｎ∈Ｑ　が存在する。　Ｘ³−３Ｘ＋１＝０　なので、

　Ｘ³−３Ｘ＋１＝（ｍ−ｎＸ）（２次式）　と因数分解され、方程式 Ｘ³−３Ｘ＋１＝０　は、有理

数の解 ｍ/ｎ　を持つ。これは、矛盾である。

　よって、　１ と Ｘ はＱ上１次独立である。

同様にして、　１ と Ｘ と Ｘ² はＱ上１次独立である。

ところで、　Ｘ³−３Ｘ＋１＝０　から、　１ と Ｘ と Ｘ² と Ｘ³ はＱ上１次独立にはならない。

このことから、　［ Ｑ（Ｘ） ： Ｑ ］＝３　であることが分かる。

　このとき、　ｃｏｓ４０°∈Ｋ_ｎ　となる有理数体 Ｑ の拡大体 Ｋ_ｎ と Ｑ（Ｘ） の交わりを Ｈ

とおくと、Ｈは、　Ｑ⊂Ｈ⊂Ｋ_ｎ　、Ｑ⊂Ｈ⊂Ｑ（Ｘ）　を満たす体で、

　　　　［ Ｈ ： Ｑ ］［ Ｋ_ｎ ： Ｈ ］＝２^ｎ　　、　［Ｈ ： Ｑ ］［ Ｑ（Ｘ） ： Ｈ ］＝３

であることから、　拡大次数 ［ Ｈ ： Ｑ ］ は、　２^ｎ　および　３　の約数となる。

　したがって、　［ Ｈ ： Ｑ ］＝１　でなければならないが、これは、　Ｈ＝Ｑ　を意味し、

　２ｃｏｓ４０°∈Ｑ　となる。

２ｃｏｓ４０°は、方程式　Ｘ³−３Ｘ＋１＝０　の解で、方程式　Ｘ³−３Ｘ＋１＝０　は有理数解

を持たないので、これは矛盾である。

　したがって、１２０°の角をなす２つの直線に対して、この角度を３等分するような２つの

半直線を作図することは不可能である。

（コメント）　平成１８年９月３０日に、このページを書き始めて、ようやく年内にまとめを行う
　　　　　　ことができてホッとしている。
　　　　　　　当ＨＰではこれまで、角の３等分方程式　や　３次方程式と作図の問題　で角
　　　　　　の３等分を話題にしてきたが、あまりスッキリとしたものではなかった。
　　　　　　　今回、茂手木先生のお話しを伺って、これまでモヤモヤしていた部分が一気に
　　　　　　解消されてスッキリした気分である。茂手木先生にこの場を借りて感謝したい。


（追記）　令和３年１０月２８日付け

　当ＨＰの「クイズ＆パズル」には、いくつかの埋め込みパズルが掲載されている。

　図形の埋め込み　、図形の埋め込み２　、図形の埋め込み４　、図形の埋め込み５

　これらは、埋め尽くすことが可能な場合で、解を一つ見つければ、それで終わりである。

　これに対して、次の問題はどうだろうか？

問題　　４×４の正方形から対角線上に向かい合う２隅を切り落とした図形を考える。

　　　　　　　

　これを、２×１のタイル

　　　　　　　

で埋め尽くせるか？（タイルは、縦にも横にも使ってよいものとする。）

　このとき、どのような埋め込み方をしても埋め尽くすことは出来ないだろうということが分か
る。

　埋め込みが不可能を証明するには、埋め尽くす方法を全て列挙して確かめればいいのだ
が、それは大変な労力を要する。

　最善の方法は、埋め尽くせると仮定して、何かしらの矛盾を示すという方法だろう。

　与えられた図形とタイルを次のように色分けする。

　与えられた図形で、白は６個、黒は８個である。ところが、２×１のタイルで埋め尽くされた
とき、白と黒は同数の筈である。これは、矛盾である。

　よって、２×１のタイルで、図形を埋め尽くすことは不可能である。


（追記）　令和３年１０月３０日付け

問題　　５×５の正方形から、右上隅の２×２の正方形を切り落とした図形を考える。

　　　　　　　

　これを、３×１のタイル

　　　　　　　

で埋め尽くせるか？（タイルは、縦にも横にも使ってよいものとする。）

　この場合は、埋め尽くしが可能で、実際の埋め尽くしの状態を示せば十分である。

　　　　　　　

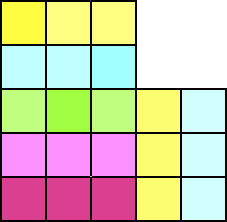
　これに対して、次の問題はどうだろうか？

問題　　７×７の正方形から、右上隅の２×２の正方形を切り落とした図形を考える。

　　　　　　　

　これを、３×１のタイル

　　　　　　　

で埋め尽くせるか？（タイルは、縦にも横にも使ってよいものとする。）

　この場合は、どんなに頑張っても埋め尽くすことは不可能である。

　３×１のタイルに、次のように３つの数字（１、２、３）を割り当てる。（ただし、順不同）

　　　　　　　

　与えられた図形にも、下図のように数字を割り当てる。

　　　　　　　

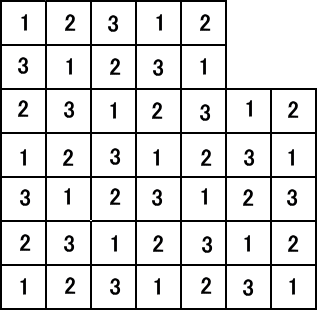
　３×１のタイルをどのように配置しても、必ず３×１のタイル上には、数字（１、２、３）が割り
当てられる。

　与えられた図形で、１：１６個、２：１５個、３：１４個である。ところが、３×１のタイルで埋め
尽くされたとき、数字の１と２と３は同数の筈である。これは、矛盾である。

　よって、３×１のタイルで、図形を埋め尽くすことは不可能である。

＃当初、６×６の図形で出題していましたが、６×６−２×２＝３２は３の倍数ではないので
　そもそも問題として不適切ではというご指摘を、当ＨＰ読者のＨＮ「tetsu」様より、いただき
　ました。確かに問題として自明だったということで、上記のように、より難しい３の倍数にな
　る形に修正しました。tetsu様に感謝いたします。（令和３年１１月２日付け）



　　以下、工事中！