図形の埋め込み５　 　　　　　　　　　　　　　　　　　　　　　　　　　

１×２のタイル

を用いて、次の３×２の図形

　　　　

を埋め尽くすことを考える。１×２のタイルは、縦にも横にもしてよいものとする。

　このとき、埋め尽くす方法は、明らかに ３通りある。（ただし、色は区別しないものとする。）

　　　　　　　　　　　　　　　

　同様にして、３×４の図形

　　　　

を埋め尽くす方法は、全部で１１通りある。

　　　　　　

　　　　　　

　　　　

　そこで、問題です。

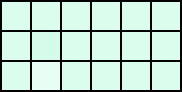
（１）　３×６の図形

　　　　

　を埋め尽くす方法は、全部で何通りあるか？


（２）　３×８の図形

　　　　

　を埋め尽くす方法は、全部で何通りあるか？
























（答）（１）　４１通り　　（２）　１５３通り

　３×４の図形

　　　　

を埋め尽くす方法の数は、上記では漏れなく重複なく数え上げたが、その１１通りは、

　　　　　　

　　　　　　



のように、

　　

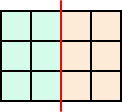
と、真ん中でくっきり分断される場合と

　　

のように、真ん中でくっきりとは分断されない場合に場合分けされる。

　分断される場合は、３×２の図形の埋め尽くす方法の数 ３ 通りを用いて、

　　　３×３＝９（通り）

分断されない場合は、上図のように２通りあるので、

従って、求める場合の数は、　９＋２＝１１（通り）　と求められる。

　このような見方、考え方をすれば、３×６の図形の場合も、全てを数え上げなくても計算で
求めることが可能である。

（１）（イ）　分断線が２箇所ある場合

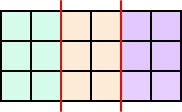３×２の図形が３連の場合なので、この条件で 　　　埋め尽くされる方法の数は、 　　　　　３×３×３＝２７（通り）

（ロ）　分断線が１ヶ箇所のみの場合

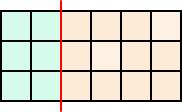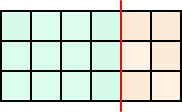３×２＋２×３ 　　＝１２（通り）

（ハ）　分断線がない場合

　　　　

　この場合の埋め尽くす方法は、次の２通りしかない。

　　　　　　　

　以上から、３×６の図形を埋め尽くす方法の数は、

　　　３×３×３＋３×２＋２×３＋２＝２７＋１２＋２＝４１（通り）

となる。

（２）　（１）と同様に分類して、

３×３×３×３＋３×３×２＋２×３×３＋３×２×３＋３×２＋２×２＋２×３＋２＝１５３（通り）

であることが分かる。


（追記）　令和３年１０月１０日付け

　上記で

１×２のタイル

を用いて、

　３×２の図形を埋め尽くす方法の数は、　３通り

　３×４の図形を埋め尽くす方法の数は、　１１通り

　３×６の図形を埋め尽くす方法の数は、　４１通り

　３×８の図形を埋め尽くす方法の数は、　１５３通り

であることを知った。

　３×１の図形を埋め尽くす方法の数は、明らかに、　１通り　であるので、

数列　１，３，１１，４１，１５３，・・・　が得られる。

　この数列を「オンライン整数列大辞典」に問い合わせると、「A001835」や「A079035」が
ヒットした。

　それらのページでは、「ドミノを用いて、３×２ｎの長方形を埋め尽くす方法の数 ａ_ｎ」が調
べられている。（ドミノ＝２つの正方形をつなげた形）

　数列｛ａ_n｝ について、漸化式

　　ａ₁＝１、ａ₂＝３、ａ_n+2＝４ａ_n+1−ａ_n　（ｎ＝１，２，３，・・・）

が成り立つという。

例　ａ₃＝４ａ₂−ａ₁＝４×３−１＝１１

　　 ａ₄＝４ａ₃−ａ₂＝４×１１−３＝４１

　　 ａ₅＝４ａ₄−ａ₃＝４×４１−１１＝１５３

で、確かに、これまでの結果と一致する。


　果たして、この漸化式は、どうやって作ったのだろうか？


（追記）　令和３年１０月１１日付け

　３×２ｎの図形を１×２のタイルで埋め尽くす方法の数をａ_ｎ通りとおく。

　漸化式を考えるために、まず、３×２の図形

　　　　　

を埋め尽くす方法

　　　　　　　　　　　　　　　

を、次の２つの場合に分類する。

・　３つの１×２のタイルがすべて縦１列に並ぶ場合

　　　　

・　その他の場合

　　　　　　　　　　

　同様にして、３×４の図形

　　　　

を埋め尽くす方法を、次の２つの場合に分類する。

・　左端の３つの１×２のタイルがすべて縦１列に並ぶ場合

　　　　　　　　

・　その他の場合で、真ん中でくっきり分断される場合

　　　　　　　　

　　　　　　　　

　　真ん中でくっきりとは分断されない場合

　　　　　　

　そこで、

　左端の３つの１×２のタイルがすべて縦１列に並ぶときの埋め尽くす方法の数をｘ_ｎ通り

それ以外のときの埋め尽くす方法の数を、ｙ_ｎ通りとおくとき、上図の場合から、

　３×２の図形について、　ａ₁＝３　、ｘ₁＝１　、ｙ₁＝２　　から、ａ₁＝ｘ₁＋ｙ₁　である。

　３×４の図形について、　ａ₂＝１１　、ｘ₂＝３　、ｙ₂＝８　から、　ａ₂＝ｘ₂＋ｙ₂　である。

　このとき、　ｘ₂＝１×ａ₁＝ｘ₁＋ｙ₁　で、　ｙ₂＝（２ｘ₁＋２ｙ₁）＋ｙ₁＝２ｘ₁＋３ｙ₁　である。

　このことから、一般的に、

　　　ｘ_ｎ+1＝ａ_ｎ＝ｘ_ｎ＋ｙ_ｎ　、ｙ_ｎ+1＝２ｘ_ｎ＋３ｙ_ｎ

が成り立つ。　ｙ_ｎ＝ｘ_ｎ+1−ｘ_ｎ　を代入して、　ｘ_ｎ+2−ｘ_ｎ+1＝２ｘ_ｎ＋３（ｘ_ｎ+1−ｘ_ｎ）　から、

漸化式　ｘ_ｎ+2＝４ｘ_ｎ+1−ｘ_ｎ　を得る。


　DD++ さんからのコメントです。（令和３年１０月１２日付け）

　分断線の考え方で、一番右の分断線がどこなのを考えれば、

　a[n] = 3*a[n-1] + 2*a[n-2] + 2*a[n-3] + …… + 2*a[1] + 2

　添字をずらして、

　a[n-1] = 3*a[n-2] + 2*a[n-3] + …… + 2*a[1] + 2

　これらの差をとると、　a[n] - a[n-1] = 3*a[n-1] - a[n-2]　から、

　　a[n] = 4*a[n-1] - a[n-2]

ですかね。


（コメント）　DD++ さん、ありがとうございます。左端の３×２の部分を除いて、分断されない
　　　　　　部分の埋め尽くす方法の数が、いつも２通りというのが急所かな？そうすれば、
　　　　　　連立の漸化式を立てるまでもなかったですね。


（追記）　令和３年１０月１７日付け

冒頭の問題で、すぐ気がつくことは、１×２のタイル

の面積は２、偶数なので、

この１×２のタイルを用いて、３×（２ｎ＋１）の図形を埋め尽くすことは絶対に不可能だとい
うことである。

　また、３×２ｎの図形を１×２のタイルで埋め尽くす方法の数をａ_ｎ通りとおくと、数列｛ａ_n｝

　　１，３，１１，４１，１５３，・・・　

から、すべての自然数 ｎ に対して、ａ_ｎ は奇数であることが推測されるが、漸化式

　　ａ₁＝１、ａ₂＝３、ａ_n+2＝４ａ_n+1−ａ_n　（ｎ＝１，２，３，・・・）

から、明らかなことだろう。

　実際に、ａ₁＝１、ａ₂＝３　は奇数で、漸化式より、ａ₃ も奇数となる。以下、帰納的に、

すべての自然数 ｎ に対して、ａ_ｎ は奇数であることが分かる。

（厳密には、数学的帰納法による）



　　以下、工事中！