作図問題における円の役割　　　　　　　　　　　　　　戻る

　いろいろな図形の問題を考えていると、円という制約が、いかに大きなものであるかに気が
つく。一方で、円なくして語れない問題も数多い。新学習指導要領で、今まで中学で学習して
いた円の性質が高校に移行し、しかも、数学Aという科目の性質から、日本の高校生の全員
が必ず学ぶということもなくなる。中学生段階で、円のおもしろい性質に気がつき、幾何にお
ける深遠なる謀略を楽しむことが、その後の数学の学習に多大な影響を与えると思うのだが、
それもまた難しい時代になってしまった。

　このページでは、巧妙に、円の性質が使われている例をいくつか紹介したいと思う。

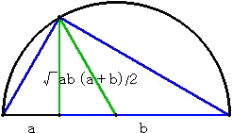
例１（相加平均と相乗平均の関係）

　　相加平均は、相乗平均以上、即ち、　
　このことは、次の図から明らかである。

　　　　　　　　

（追記）　平成２２年２月１８日付け

　ＨＮ「Ｈ．Ｉ．」さんより、相加平均・相乗平均・調和平均等の大小関係を一目で把握できる
図をご紹介いただいた。

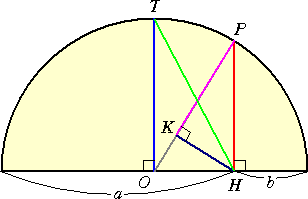　　ＯＴは相加平均　（ａ＋ｂ）/２

　　ＰＨは相乗平均　√（ａｂ）

　　ＰＫは調和平均　２ａｂ/（ａ＋ｂ）

　　ＴＨは二乗平均　√｛（ａ2＋ｂ2）/２｝

　　になるとのことである。




　高校の問題としてよく出てくる相加相乗平均について、２数 ａ、ｂ の和を直径とする円で、
その関係を表す有名な図があるが、二乗平均や調和平均についても同様に表現できない
ものかと考えられたとのこと.。調和平均や二乗平均の図示はさほど有名ではないとのこと
で、特に興味を引きました！

　たとえば、ＰＫが調和平均になることは、　ＰＫ＝ＰＨ・ＰＨ/ＯＰ　から分かるのかな．．．。

　上図を見ると、

　　　　　　　　二乗平均≧相加平均≧相乗平均≧調和平均

であることが本当に明白ですね！

　また、ａ＋ｂ が定数、つまり直径が一定で円の形が変わらないとして、ａ が ｂ の値に限り
なく近づくとき、二乗平均、相乗平均、調和平均が相加平均に近づく様子も確かに実感でき
ますね。

（コメント）　とても印象的な図ですね。Ｈ．Ｉ．さんに感謝します。


（追記）　平成２３年９月２３日付け

　当ＨＰの読者のＳさんより、「相加平均と相乗平均の関係」について、平成２３年９月２２日
付けでメールを頂いた。

　相加相乗の図形的証明の中で、台形による方法で相乗平均の部分がなかったので考え
てみました。また、円の場合も添付しました。

　相加相乗平均の図形的証明

　 ≧ 　⇔　ａ2＋ｂ2≧２ａｂ　なので、ａ2、ｂ2　（ａ≧ｂ）　を正方形の面積とする。

　　　　　　　　

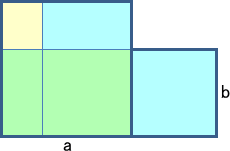
　上図より、２つの正方形の和の方が、長方形２つ分（緑と水色部分）よりも小正方形（黄色

部分）の分大きい。すなわち、　ａ2＋ｂ2≧２ａｂ　が成り立つ。また、等号成立は、小正方形

の面積が ０ のときで、つまり、ａ−ｂ＝０　より、ａ＝ｂ のとき。

　次に、円利用の場合について考える。

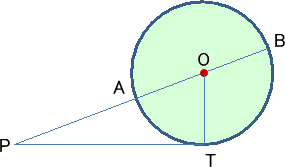　　　左図において、円Ｏの外部の点Ｐからの

　　長さを考える。

　　　　ＰＯ＝（ＰＡ＋ＰＢ）/２　である。

　　また、接線ＰＴについて、方べきの定理より、

　　　　ＰＴ2＝ＰＡ・ＰＢ


　したがって、相加平均と相乗平均の関係が成り立つ。ＯとＴが近づいて円が限りなく小さく

なるとき、等号が成立し、ＰＡ＝ＰＢのときである。

（コメント）　美しく簡明な証明ですね！Ｓさんに感謝します。


例２（２次方程式の解の作図）

　　２次方程式 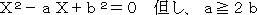　の解α、βは次のような長さで
　与えられる。
　　　　　　　　
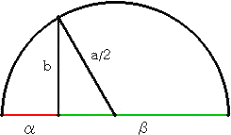
　　　このとき、図から
　　　　　　　　　　　　　　　α＋β＝ａ、αβ＝ｂの２乗　（解と係数の関係）
　　が成り立つことも分かる

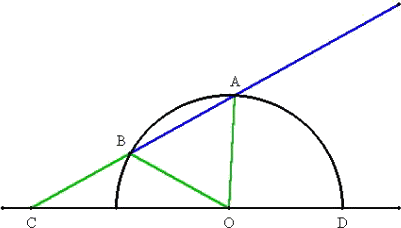
例３（角の３等分の作図）

　　直線ACを、OA＝OB＝BC となるように引く。（実は、これを引くのが一番難しい！）
　このとき、∠ＢOＣは、∠AODの３等分を与える。
　この作図は、ギリシヤ数学の黄金時代であったＢ．Ｃ．３世紀頃、アルキメデスにより発見
されたものである。さらに、この方法は、１６世紀後半ヴィエタにより、再発見された。
　　

　　　　（追記）　角の３等分の実用的な方法

　　　　　　目盛りのない定規とコンパスを用いて、角の３等分が出来ないことは既に証明さ
　　　　　れている（ワンツェル　１８３７年）ことであるが、目盛りのある定規とコンパスを用い
　　　　　ると、角の３等分が可能であることを最近知る機会があった。

　　　　　　２箇所に目盛りのついた定規を、アルキメデスの定規というそうだ。

　　　　　　アルキメデスの定規の使い方と角の３等分の方法については、下図と、じっと睨
　　　　　めっこして、悟ってください。
　　　　　　（ちょっと、定規の当て方に微妙に神経を使いますが．．．。）

　　　　　　　　　　　　　

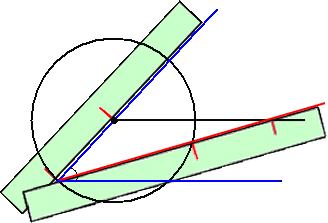
　　　　　（参考文献：星野敏司さんのホームページ：Ｍｅｔａ2ｍａｔｈｅｍａｔｉｃｉａｎ’ｓ　ＨＰ）

例４（正三角形と円の割線）

　　正三角形と円が与えられた場合、次の事実は、とても興味深い。


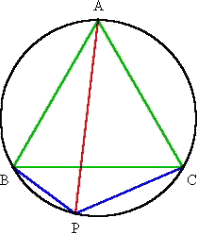
　　正三角形ABCが円に内接しているとき、
　弧BC上の点Pに対して、
　　　　　　　AP＝BP＋PC
　が成り立つ。
　
　（証明）　ＰＣの延長線上に、ＢＰ＝ＣＰ’となる点Ｐ’をとる。
　　　　　このとき、△ABP≡△ACP’である。
　　　　　従って、△APP’は正三角形となり、
　　　　　AP＝BP＋PC が成り立つ。






（参考文献：鈴木晋一、山下正勝　著　代数演算と作図（啓林館））