
丂僥僗僩偑曉偝傟傞偲丄惗搆偨偪偼桭恖偨偪偲揰悢偺崌寁揰偱嫞偄崌偄丄堦婌堦桱偡傞丅懳
偟偰丄嫵偊傞懁偼丄僋儔僗偵傛偭偰恖悢偑堘偆偺偱丄僋儔僗偺暯嬒揰傪寁嶼偟偰丄偙傟傑偱偺
巜摫偺惉壥偵偮偄偰帺屓昡壙偡傞丅
丂傕偪傠傫丄暯嬒揰偩偗偱偼曣廤抍偺摿挜偑偮偐傔側偄偺偱昗弨曃嵎傗暘晍偺忬懺傕嶲
峫偵偡傞丅昞寁嶼僜僼僩偺偍偐偘偱丄偦傟傜偺寁嶼偑堦弖偺偆偪偵偱偒偰偟傑偆偺偱戝偄偵
彆偐偭偰偄傞丅
丂悽偺拞偱丄暯嬒偲偄偊偽嶼弍暯嬒傪偄偆偑丄暯嬒偵偼懠偵傕婔壗暯嬒偲偐挷榓暯嬒側偳
偑偁傝丄偦傟偧傟梡搑偑堎側傞丅
偄傠偄傠側暯嬒丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂僥僗僩偑曉偝傟傞偲丄惗搆偨偪偼桭恖偨偪偲揰悢偺崌寁揰偱嫞偄崌偄丄堦婌堦桱偡傞丅懳
偟偰丄嫵偊傞懁偼丄僋儔僗偵傛偭偰恖悢偑堘偆偺偱丄僋儔僗偺暯嬒揰傪寁嶼偟偰丄偙傟傑偱偺
巜摫偺惉壥偵偮偄偰帺屓昡壙偡傞丅
丂傕偪傠傫丄暯嬒揰偩偗偱偼曣廤抍偺摿挜偑偮偐傔側偄偺偱昗弨曃嵎傗暘晍偺忬懺傕嶲
峫偵偡傞丅昞寁嶼僜僼僩偺偍偐偘偱丄偦傟傜偺寁嶼偑堦弖偺偆偪偵偱偒偰偟傑偆偺偱戝偄偵
彆偐偭偰偄傞丅
丂悽偺拞偱丄暯嬒偲偄偊偽嶼弍暯嬒傪偄偆偑丄暯嬒偵偼懠偵傕婔壗暯嬒偲偐挷榓暯嬒側偳
偑偁傝丄偦傟偧傟梡搑偑堎側傞丅
| 丂嶼弍暯嬒丒丒丒丂俀悢 倎丄倐 偵懳偟偰丄 | 丂乮憡壛暯嬒偲傕偄傢傟傞丅乯 |
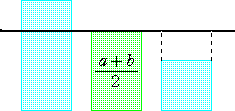 |
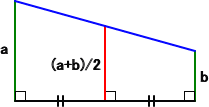
丂丂嶼弍暯嬒偼丄嵍恾偐傜傕暘偐傞傛偆偵丄偱偙傏偙 丂偺傕偺傪側傜偡摥偒偑偁傞丅 丂丂俀悢 倎丄倐 偵懳偟偰丄偦偺嶼弍暯嬒偼師偺傛偆偵 丂嶌恾偟偰丄婔壗揑偵媮傔傞偙偲偑偱偒傞丅 |
||
| 丂丂丂丂 |
 |
||
丂俁偮偺悢 倎丆們丆倐 偑偙偺弴偵摍嵎悢楍傪側偡偲偒丄們 偼摍嵎拞崁偲尵傢傟傞丅
丂丂們亖乮倎亄倐乯/俀
偑惉傝棫偮丅偡側傢偪丄摍嵎拞崁 們 偼丄俀悢 倎丄倐 偵懳偟偰丄嶼弍暯嬒偲側傞丅
丂幚嵺偵丄丂們亅倎亖倐亅們丂偐傜丄們亖乮倎亄倐乯/俀丂偱偁傞丅
乮捛婰乯丂椷榓俈擭俉寧侾係擔晅偗
丂師偺搶杒戝妛丂屻婜暥宯乮侾俋俋俈乯偺栤戣偼丄摍嵎拞崁偵娭偡傞栤戣偱偁傞丅
栤戣丂丂弶崁 倎丄岞斾 倰 乮倰亗侾乯 偺摍斾悢楍 倎n亖倎倰n-1 乮値亖侾丄俀丄俁丄丒丒丒乯傪峫偊傞丅偙偺
丂丂悢楍偺嵟弶偺俁崁 倎1丄倎2丄倎3 偼師偺惈幙乮鶣乯丄乮鶤乯傪傕偮偲偡傞丅
乮鶣乯丂倎1亄倎2亄倎3亖俇
乮鶤乯丂倎1丄倎2丄倎3 偺弴彉傪揔摉偵擖傟姺偊傞偲摍嵎悢楍偵側傞丅
丂偙偺偲偒丄弶崁 倎 偲岞斾 倰 偺慻傪偡傋偰媮傔傛丅
乮夝乯丂乮鶣乯傛傝丄丂倎亄倎倰亄倎倰2亖倎乮侾亄倰亄倰2乯亖俇丂偐傜丄丂倎亗侽
丂倎丄倎倰丄倎倰2 偑摍嵎悢楍偺偲偒丄 俀倎倰亖倎亄倎倰2
丂倎亗侽丂側偺偱丄丂俀倰亖侾亄倰2丂偐傜丄丂倰亖侾丂偱丄忦審偐傜丄晄揔
丂倎倰丄倎丄倎倰2 偑摍嵎悢楍偺偲偒丄丂俀倎亖倎倰亄倎倰2
丂倎亗侽丂側偺偱丄丂俀亖倰亄倰2丂偐傜丄丂乮倰亄俀乯乮倰亅侾乯亖侽丂偱丄倰亗侾丂傛傝丄倰亖亅俀
丂偙偺偲偒丄丂倎亖俀
丂倎倰丄倎倰2丄倎 偑摍嵎悢楍偺偲偒丄丂俀倎倰2亖倎倰亄倎
丂倎亗侽丂側偺偱丄丂俀倰2亖倰亄侾丂偐傜丄丂乮俀倰亄侾乯乮倰亅侾乯亖侽丂偱丄倰亗侾丂傛傝丄倰亖亅侾/俀
丂偙偺偲偒丄丂倎亖俉
埲忋偐傜丄丂乮倎丆倰乯亖乮俀丆亅俀乯丄乮俉丆亅侾/俀乯丂丂乮廔乯
丂婔壗暯嬒丒丒丒丂俀偮偺惓悢 倎丄倐 偵懳偟偰丄![]() 丂乮憡忔暯嬒偲傕偄傢傟傞丅乯
丂乮憡忔暯嬒偲傕偄傢傟傞丅乯
丂丂嶼弍暯嬒偼丄榓丂倎亄倐丂偺抣偑丄偁傞悢傪俀夞懌偟偨傕偺偵側傞偲偒偺偁傞悢偺偙偲傪偄
丂偆丅悢捈慄忋偱峫偊傟偽丄俀揰俹乮倎乯丄俻乮倐乯偺拞揰偺嵗昗偲偄偆惈奿傪帩偭偰偄傞丅
丂丂偙傟偵懳偟偰丄婔壗暯嬒偼丄愊丂倎倐丂偺抣偑丄偁傞悢傪俀夞妡偗偨傕偺偵側傞偲偒偺偁傞
丂悢偺偙偲傪偄偆丅
丂丂偨偲偊偽丄晛捠偺恏偝偺僇儗乕偵懳偟偰丄僇儗乕俙偼俀攞恏偔丄僇儗乕俛偼俉攞恏偄偲偡傞丅
丂偙偺恏偝偺暯嬒傪峫偊傞偲偒丄俲亊俲亖俀亊俉丂傛傝丄俲亖係丂偲側傝丄暯嬒偺恏偝偼係攞偲側
丂傞丅
丂乮偟偐偟丄偙傟偵偼堎榑偑偁傞偐傕偟傟側偄丅悇應偱偁傞偑丄俀攞恏偄偲偼丄晛捠傛傝俀攞搨
丂恏巕偑懡偔擖偭偰偄傞丄俉攞恏偄偲偼丄晛捠傛傝俉攞搨恏巕偑懡偔擖偭偰偄傞偲偡傞偲丄俀偮
丂傪暯嬒偡傞偲偄偆偙偲偼丄搨恏巕偺検偑俆攞偲偄偆偙偲偱丄俆攞恏偄僇儗乕偑偱偒偰偟傑偆偲
丂巚偆偺偩偑丄娫堘偭偰偄傞偩傠偆偐丠僇儗乕偵徻偟偄曽丄惀旕偍嫵偊偔偩偝偄両両乯
丂俁偮偺悢 倎丆們丆倐 偑偙偺弴偵摍斾悢楍傪側偡偲偒丄們 偼摍斾拞崁偲尵傢傟傞丅
丂丂們亖![]()
偑惉傝棫偮丅偡側傢偪丄摍斾拞崁 們 偼丄俀悢 倎丄倐 偵懳偟偰丄婔壗暯嬒偲側傞丅
丂幚嵺偵丄丂們/倎亖倐/們丂偐傜丄們亖![]() 丂偱偁傞丅
丂偱偁傞丅
丂丂俀悢 倎丄倐 偵懳偟偰丄偦偺婔壗暯嬒傕娙扨偵嶌恾偡傞偙偲偑偱偒傞丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮嶲峫丗嶌恾栤戣偵偍偗傞墌偺栶妱乯
丂摉俫俹偺撉幰偺俽偝傫傛傝丄憡忔暯嬒偺嶌恾曽朄傪偛嫵帵捀偄偨丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俁擭俋寧俀俀擔晅偗乯
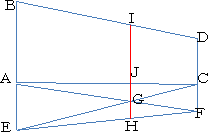
丂丂丂嵍恾偵偍偄偰丄俙俛亖倎丄俠俢亖倐丂偲偟丄俙俤亖併倎丄
丂丂俠俥亖併倐丂偲偡傞丅懳妏慄偺岎揰俧傪捠傝丄俙俠佦俬俫
丂丂偲偡傞偲偒丄俬俰亖![]() 丂偱偁傞丅
丂偱偁傞丅
乮徹柧乯丂揰俙傪嵗昗幉偺尨揰偲偟丄俙俠傪 倶 幉偺惓偺岦偒偲偡傞丅俙俠亖倣丂偲偡傞偲偒丄
丂捈慄俛俢偺曽掱幃偼丄丂倷亖乷乮倐亅倎乯/倣乸倶亄倎丂偱丄揰俰偺嵗昗偼丄憡帡斾傛傝
丂丂乮 乷併倎/乮併倎亄併倐乯乸倣 丆侽 乯
丂偙偺偲偒丄丂俬俰亖乷乮倐亅倎乯/倣乸丒乷併倎/乮併倎亄併倐乯乸倣亄倎
丂丂丂丂丂丂丂亖乮併倐亅併倎乯丒併倎亄倎亖![]() 丂丂乮徹廔乯
丂丂乮徹廔乯
乮僐儊儞僩乯丂俽偝傫偵姶幱偟傑偡丅
丂挷榓暯嬒丒丒丒丂俀悢 倎丄倐 偵懳偟偰丄媡悢偺嶼弍暯嬒偺媡悢 |
||
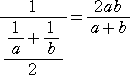 |
丂丂挷榓暯嬒偺椺偲偟偰偼丄師偑桳柤偱偁傞丅
丂乽峴偒偑帪懍係倠倣丄婣傝偑帪懍俇倠倣偱曕偄偨偲偒丄暯嬒偺懍偝偼偄偔傜偐丠乿
丂側傫偲側偔丄帪懍俆倠倣偲摎偊偑偪偱偁傞偑丄幚嵺偼丄帪懍係丏俉倠倣丂偱偁傞丅
丂乮懍偝乯亊乮帪娫乯亖乮嫍棧乯偺岞幃傪梡偄偰寁嶼偡傞偲丄帺慠偲挷榓暯嬒偺寁嶼岞幃偵摫
丂偐傟傞丅
丂丂俀悢 倎丄倐 偵懳偟偰丄偦偺挷榓暯嬒偺幃偐傜庴偗傞僀儊乕僕偼暋嶨偦偆偱偁傞偑丄嶌恾
丂偡傞偙偲偼娙扨偱偁傞丅壓恾偺傛偆偵嶌恾偡傟偽傛偄丅
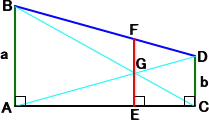
| 丂丂嵍恾偵偍偄偰丄仮ABG佷仮DCG丂傛傝丄 丂丂丂丂丂丂AG丗GD亖BG丗GC亖 倎 丗 倐 丂丂仮AEG佷仮ACD丂傛傝丄GE亖倎倐/乮倎亄倐乯 丂丂仮BFG佷仮BDC丂傛傝丄FG亖倎倐/乮倎亄倐乯 丂丂偟偨偑偭偰丄 |
||
| 丂丂丂丂丂丂EF亖 | 偲側傝丄俤俥偑挷榓暯嬒傪梌偊傞丅 | |
乮嶲峫暥專丗拞懞媊嶌丒垻绮宐堦丂挊丂戙悢傪恾宍偱夝偔乮島択幮僽儖乕僶僢僋僗乯乯
乮捛婰乯丂婔壗暯嬒偵偮偄偰丄師偺傛偆側惈幙偑偁傞偙偲傪忋婰彂愋偵傛傝抦偭偨丅尨棟偼
丂丂丂丂扨弮偱偁傞偑丄偲偰傕嫽枴怺偄帠幚偱偁傞丅
 丂丂丂丂嵍恾偺挿曽宍俙俛俠俢偵偍偄偰丄
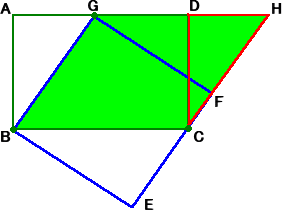
丂丂丂丂嵍恾偺挿曽宍俙俛俠俢偵偍偄偰丄
丂丂丂俙俛亖倎丄俙俢亖倐丂偲偡傞丅
丂丂丂偄傑丄俀悢倎丄倐丂偺婔壗暯嬒傪堦曈偲偡傞
丂丂丂惓曽宍俛俤俥俧乮俧偼俙俢忋乯傪嶌恾偡傞丅
丂丂丂丂偙偺偲偒丄挿曽宍偺侾捀揰俠偼丄偙偺惓
丂丂丂曽宍偺曈俤俥忋偵偁傞丅
丂丂丂丂徹柧偼丄嵍恾傪傒傟偽柧傜偐偱偁傠偆丅
丂丂乮挿曽宍偐傜惓曽宍傊偺摍愊曄宍偱偁傞丅乯
乮捛婰乯丂暯惉俀俁擭俆寧俉擔晅偗
丂暯嬒偲偄偆偲丄廳偝傗挿偝丄揰悢摍偑暘偐傝堈偄戣嵽偱偁傞偑丄柺愊偺暯嬒偲偼偳傫側傕
偺偩傠偆丅
丂柺愊偲偄偆扨側傞悢検偺暯嬒偵偼嫽枴偼側偄丅恾宍偺宍傕峫椂偵擖傟偨暯嬒偺曽偑堄
枴偑偁傞偩傠偆丅偡側傢偪丄憡帡側恾宍摨巑偺柺愊偺暯嬒偱偁傞丅
椺丂俀侾僀儞僠偺TV偲俁俀僀儞僠偺TV偺夋柺偺柺愊偺暯嬒偼壗僀儞僠偺TV偱偁傞偐丅
丂TV夋柺偺戝偒偝偼丄懳妏慄偺挿偝乮俀侾僀儞僠丄俁俀僀儞僠乯偱掕傑傞丅俀偮偺TV夋柺偼偲傕
偵丄係丗俁 偺夋柺偲偡傞丅
丂偙偺偲偒丄丂俀侾僀儞僠偺TV夋柺偺廲偺挿偝偼丄丂俀侾亊俁/俆亖俇俁/俆
丂墶偺挿偝偼丄丂俀侾亊係/俆亖俉係/俆
丂傛偭偰丄俀侾僀儞僠偺TV夋柺偺柺愊偼丄丂俇俁/俆亊俉係/俆亖俆俀俋俀/俀俆丂偲側傞丅
丂丂摨條偵偟偰丄丂俁俀僀儞僠偺TV夋柺偺廲偺挿偝偼丄丂俁俀亊俁/俆亖俋俇/俆
丂墶偺挿偝偼丄丂俁俀亊係/俆亖侾俀俉/俆
丂傛偭偰丄俀侾僀儞僠偺TV夋柺偺柺愊偼丄丂俋俇/俆亊侾俀俉/俆亖侾俀俀俉俉/俀俆丂偲側傞丅
丂丂俀偮偺夋柺偺戝偒偝偺暯嬒偼丄丂乮俆俀俋俀/俀俆亄侾俀俀俉俉/俀俆乯/俀亖俉俈俋侽/俀俆
丂偙偺偲偒丄媮傔傞TV夋柺偑 俙僀儞僠偱偁傞偲偡傞偲丄
丂廲偺挿偝偼丄丂俙亊俁/俆丂丄墶偺挿偝偼丄丂俙亊係/俆
側偺偱丄偦偺柺愊偼丄丂俙2亊侾俀/俀俆丂偱偁傞丅
丂傛偭偰丄丂俙2亊侾俀/俀俆亖俉俈俋侽/俀俆丂傛傝丄丂俙2亖俉俈俋侽/侾俀亖俀俋俁侽/係丂側偺偱丄
丂俙亖俆係丏侾俀俋係俈係係侾丒丒丒/俀亖俀俈丏侽俇係俈俁俈俀侾丒丒丒
丂埲忋偐傜丄丂偍傛偦俀俈僀儞僠偺俿倁夋柺偑俀偮偺俿倁夋柺偺暯嬒偲側傞丅
丂扨偵丄乮俀侾亄俁俀乯/俀亖俀俇丏俆乮僀儞僠乯偺俿倁偱側偄偲偙傠偑柺敀偄丅
丂忋婰偺寁嶼偼丄師偺傛偆偵堦斒壔偱偒傞丅
丂懳妏慄偺挿偝偑偦傟偧傟 倎丄倐 偺憡帡側挿曽宍偑偁傞丅懳妏慄偲墶偺側偡妏傪
兤 偲偡傞丅
偙偺偲偒丄俀偮偺挿曽宍偺柺愊偼丄偦傟偧傟丂丂倎2倱倝値兤們倧倱兤丂丄丂倐2倱倝値兤們倧倱兤丂側偺偱丄
丂柺愊偺暯嬒偼丄丂乮倎2倱倝値兤們倧倱兤亄倐2倱倝値兤們倧倱兤乯/俀亖乮倎2亄倐2乯倱倝値兤們倧倱兤/俀
傛偭偰丄媮傔傞挿曽宍偺懳妏慄偺挿偝偑 俙偱偁傞偲偡傞偲丄
丂丂丂丂丂廲偺挿偝偼丄丂俙倱倝値兤丂丄墶偺挿偝偼丄丂俙們倧倱兤
側偺偱丄偦偺柺愊偼丄丂俙2倱倝値兤們倧倱兤丂偱偁傞丅
丂偟偨偑偭偰丄丂俙2倱倝値兤們倧倱兤亖乮倎2亄倐2乯倱倝値兤們倧倱兤/俀丂傛傝丄
丂![]()
偲側傞丅
丂摨條偵丄嵟挿懳妏慄偺挿偝偑丄偦傟偧傟 倎丄倐 偱偁傞俀偮偺憡帡側捈曽懱偵偮偄偰傕丄椉
幰偺暯嬒偱偁傞捈曽懱偺嵟挿懳妏慄偺挿偝 俙 偼丄師幃偱梌偊傜傟傞丅
丂![]()
丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽俧俙俬乿偝傫偐傜丄乽暯嬒偺悢妛揑峔憿乿偲偄偆偙偲偱丄
師偺傛偆側娭學偑偁傞偙偲傪偛嫵帵偄偨偩偄偨丅乮暯惉俀俁擭俆寧俋擔晅偗乯
丂倎亜侽丄倐亜侽丂偵懳偟偰丄
丂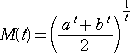
偲偍偔偲丄
丂俙亖俵乮侾乯亖乮倎亄倐乯/俀丂偲側傝丄憡壛暯嬒傪昞偡丅
丂偝傜偵丄倲 仺 侽丂偺偲偒丄丂俵乮倲乯 仺 俧亖![]() 丂偲側傝丄憡忔暯嬒傪昞偡丅
丂偲側傝丄憡忔暯嬒傪昞偡丅
幚嵺偵丄丂乮倢倧倗乮倎倲亄倐倲乯亅倢倧倗俀乯/倲丂偼丄侽/侽偺晄掕宍偺嬌尷偱丄儘僺僞儖偺掕棟傪梡偄偰丄
倲
仺 侽丂偺偲偒丄丂乮倎倲倢倧倗倎亄倐倲倢倧倗倐乯/乮倎倲亄倐倲乯 仺 乮倢倧倗倎亄倢倧倗倐乯/俀亖倢倧倗![]()
丂傛偭偰丄丂俵乮倲乯 仺 俧亖![]() 丂偱偁傞丅
丂偱偁傞丅
丂傑偨丄丂俫亖俵乮亅侾乯亖俀倎倐/乮倎亄倐乯丂偲側傝丄挷榓暯嬒偑尰傟傞丅
乮僐儊儞僩乯丂慄暘偐傜挿曽宍丄捈曽懱偲憡帡側恾宍娫偺暯嬒傪峫偊偰傒偨偺偱偡偑丄俧俙俬 偝
丂丂丂丂丂丂傫偐傜偛嫵帵偄偨偩偄偨偄傠偄傠側暯嬒偺娭學偐傜丄幚偼摑堦揑偵婰弎偱偒傞悢
丂丂丂丂丂丂幃偑偁傞偙偲偵嬃偐偝傟傑偟偨丅俧俙俬 偝傫偵姶幱偄偨偟傑偡丅
丂俹俽俹偝傫偐傜偺僐儊儞僩偱偡丅乮暯惉俀俈擭俁寧俇擔晅偗乯
丂俀忔暯曽榓暯嬒丄憡壛暯嬒丄憡忔暯嬒丄挷榓暯嬒偺嶌恾偵扙朮偟傑偟偨丅壛廳暯嬒傕壛偊
偰丄嶌恾僜僼僩傪嶌惉偟偰傒傑偟偨丅乮仺丂嶌恾僜僼僩偲嶲峫恾乯
乮捛婰乯丂暯惉俁侾擭俀寧侾俋擔晅偗
丂倶1丄倶2丄倶3 傪惓偺悢偲偡傞丅偙偺偲偒丄
丂倶1丄倶2 偺憡壛暯嬒偼丄乮倶1亄倶2乯/俀丂偱偁傝丄憡忔暯嬒偼丄併乮倶1倶2乯丂偱偁傞丅
丂倶1丄倶2丄倶3 偺憡壛暯嬒偼丄乮倶1亄倶2亄倶3乯/俁丂偱偁傝丄憡忔暯嬒偼丄丂3併乮倶1倶2倶3乯丂偱偁傞丅
丂偙傟傜偺暯嬒偵偮偄偰丄嫗搒巗嵼廧偺塱揷弐栫偝傫偑
丂悢妛僙儈僫乕丂乫侾俋丂俁寧崋乮擔杮昡榑幮乯
偵偍偄偰丄師偺傛偆側娭學偑偁傞偙偲傪帵偝傟偰偄傞丅乮忋婰偱偼堦斒揑偵帵偝傟偰偄傞丅乯
丂丂俀乮乮倶1亄倶2乯/俀亅併乮倶1倶2乯乯亝俁乮乮倶1亄倶2亄倶3乯/俁亅3併乮倶1倶2倶3乯乯
丂偁傞堄枴偱偺乽扨挷惈乿偩偲偄偆丅
乮徹柧乯丂倷倠亖倶倠丱(1/6)丂偲偍偒丄摿偵丄倷1亖倲丂偲偍偔偲丄倲 偺娭悢倄偼丄
丂倄亖塃曈亅嵍曈亖乮俀倷23乯倲3亅乮俁倷22倷32乯倲2亄倷36
丂倲 偱旝暘偟偰丄丂倄乫亖乮俇倷23乯倲2亅乮俇倷22倷32乯倲亖侽丂傛傝丄丂倲亖侽丂丄倷32/倷2
丂倲亞侽丂偺斖埻偱丄倄偼丄倲亖倷32/倷2 偱嬌彫偐偮嵟彫偱丄嵟彫抣 侽 偱偁傞丅
丂偟偨偑偭偰丄倄亞侽 偱丄
丂俀乮乮倶1亄倶2乯/俀亅併乮倶1倶2乯乯亝俁乮乮倶1亄倶2亄倶3乯/俁亅3併乮倶1倶2倶3乯乯
偑惉傝棫偮丅