| かぎゅうせん | |
| 蝸牛線 |
極方程式は、 
この曲線は、パスカルの蝸牛線(別名リマソン（1650年))といわれる。
ａ＞ｂ、ａ＝ｂ、ａ＜ｂ の各場合でグラフの形状が異なる。
特に、ａ＝ｂのときは、心臓形（Cardioid)といわれる。
ａ＞ｂ のとき |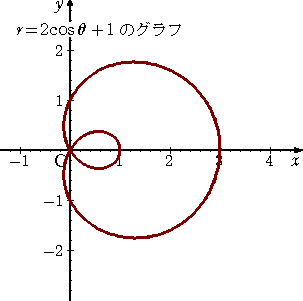
ａ＜ｂ のとき |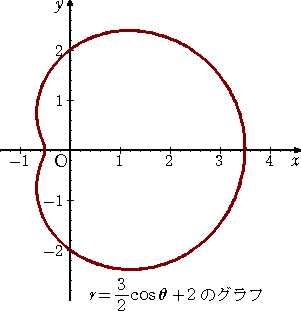
ａ＝ｂのとき
 |
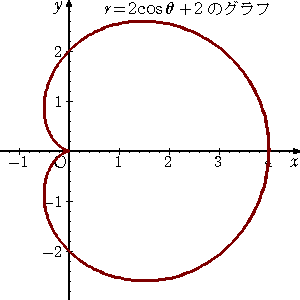作図の原理 |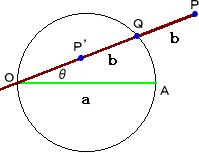
| 直径ＯＡ(＝ａ) の円周上を動く点Ｑがある。 Ｏを始点とし、直線ＯＱ上に、ＰＱ＝Ｐ’Ｑ＝ｂ となる点Ｐ、Ｐ’をとる。 このときの点Ｐ、Ｐ’の描く軌跡が蝸牛線と いわれる曲線である。 この曲線は螺獅線の一種である。螺獅線 における定直線が、定円となった場合が、こ の蝸牛線である。 |
蝸牛線のうち、特に、曲線 ｒ＝２ｃｏｓθ＋１ は、角を３等分する作図に用いられる。
それでは、角を３等分する方法を考えてみよう。
 |
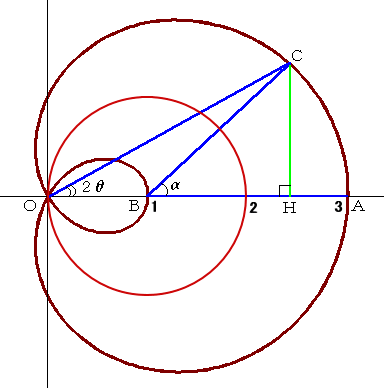左図において、△ＯＢＣに余弦 定理を用いて、 ＢＣ＝２ｃｏｓθ であることが分かる。 さらに、 BH＝ＯＨ−１ ＝ＯＣｃｏｓ２θ−１ ＝(２ｃｏｓ２θ＋１)ｃｏｓ２θ−１ ＝ｃｏｓ４θ＋ｃｏｓ２θ ＝２ｃｏｓ３θｃｏｓθ 従って、 ｃｏｓα＝２ｃｏｓ３θｃｏｓθ÷２ｃｏｓθ ＝ｃｏｓ３θ より、 α＝３θ |
よって、∠ＯＣＢ＝θ となり、∠ＯＣＢ が ∠ＡＢＣ の３等分を与えている。
以上、計算により示したが、あまり美しい解答とはいえない。幾何的に示すには、次のよう
にすればよい。
 |
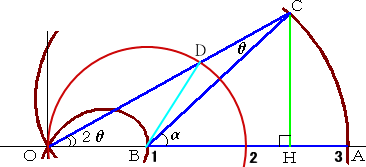（追記） 令和７年１０月３０日付け
次の東北大学 後期理系（２００１）の問題は、蝸牛線に関する問題である。
問題 ０＜ａ＜１ であるような定数 ａ に対して、次の方程式で表される曲線Ｃを考える。
Ｃ： ａ2（ｘ2＋ｙ2）＝（ｘ2＋ｙ2−ｘ）2
（１） Ｃの極方程式を求めよ。
（２） Ｃと ｘ 軸および ｙ 軸との交点の座標を求め、Ｃの概形を描け。
（３） ａ＝１/
とする。Ｃ上の点の ｘ 座標の最大値と最小値および ｙ 座標の最大値と最
小値をそれぞれ求めよ。
（解）（１） ｘ＝ｒｃｏｓθ、ｙ＝ｒｓｉｎθ とおくと、 ａ2ｒ2＝（ｒ2−ｒｃｏｓθ）2 から、
ｒ＝０ 、ａ2＝（ｒ−ｃｏｓθ）2 すなわち、 ｒ＝０ 、ｒ＝ｃｏｓθ±ａ
ここで、ｒ＝ｃｏｓθ−ａ は、ｒ＝ｃｏｓθ＋ａ に、θにπ＋θ、ｒ に−ｒ を代入して得られる。
また、０＜ａ＜１ より、 ｃｏｓθ＝−ａ となるθを定めれば、ｒ＝０ となる。
以上から、求める極方程式は、 ｒ＝ｃｏｓθ＋ａ となる。
（２） ｘ＝０ を代入して、 ａ2ｙ2＝ｙ4 から、ｙ＝０ 、ｙ＝±ａ
よって、ｙ 軸との交点は、 （０，０）、（０，±ａ）
次に、ｙ＝０ を代入して、 ａ2ｘ2＝（ｘ2−ｘ）2＝ｘ2（ｘ−１）2 から、 ｘ＝０ 、ｘ＝１±ａ
よって、ｘ 軸との交点は、 （０，０）、（１±ａ，０）
以上から、Ｃの概形は下図。
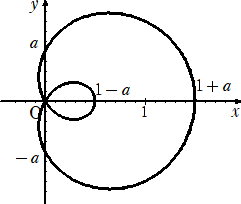
（３） ａ＝１/ とすると、 ｒ＝ｃｏｓθ＋１/ から、 ｘ＝（ｃｏｓθ＋１/）ｃｏｓθ
よって、 ｘ＝ｃｏｓ2θ＋（１/）ｃｏｓθ＝（ｃｏｓθ＋１/（２））2−１/１２
−１≦ｃｏｓθ≦１ なので、 ｃｏｓθ＝１ のとき、ｘ は最大で、最大値 １＋１/ をとる。
ｃｏｓθ＝−１/（２） のとき、ｘは最小で、最小値 −１/１２ をとる。
同様に、 ｙ＝（ｃｏｓθ＋１/）ｓｉｎθ より、
ｙ’＝−ｓｉｎ2θ＋（ｃｏｓθ＋１/）ｃｏｓθ＝２ｃｏｓ2θ＋（１/）ｃｏｓθ−１
＝（１/）（２ｃｏｓ2θ＋ｃｏｓθ−）
＝（１/）（２ｃｏｓθ＋）（ｃｏｓθ−１）＝０ とおくと、
θ＝５π/６、７π/６、α、２π−α （ただし、ｃｏｓα＝１/）
α＜５π/６＜７π/６＜２π−α に注意して、
ｙ は、θ＝α、７π/６ で極大で、θ＝５π/６、２π−α で極小となる。
θ＝α のとき、 ｃｏｓα＝１/ から、 ｓｉｎα＝
/３ なので、
極大値は、 （２/）（/３）＝２
/３
θ＝７π/６ のとき、 ｃｏｓ（７π/６）＝−/２ 、ｓｉｎ（７π/６）＝−１/２ なので、
極大値は、 （−/２＋１/）（−１/２）＝/１２
このとき、 ２/３＞/１２ なので、ｙ の最大値は、２/３ となる。
同様にして、
θ＝５π/６ のとき、 ｃｏｓ（５π/６）＝−/２ 、ｓｉｎ（５π/６）＝１/２ なので、
極小値は、 （−/２＋１/）（１/２）＝−/１２
θ＝２π−α のとき、 ｃｏｓα＝１/ から、 ｓｉｎα＝−/３ なので、
極小値は、 （２/）（−/３）＝−２/３
このとき、 −２/３＜−/１２ なので、ｙ の最小値は、−２/３ となる。 （終）
（コメント） かなりハードな計算でした。
以下、工事中！