| 偼偄偣傫 |
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂 |
| 澆慄 |
| 丂丂丂丂攠夘曄悢昞帵偼丄 |
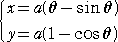 |
丂丂 |
丂偙偺嬋慄偼丄僒僀僋儘僀僪偲晛捠偄傢傟傞丅
丂掕捈慄偵増偭偰墌偑妸傜偢偵夞揮偡傞偲偒偺丄墌廃忋偺掕揰偺婳愓偱偁傞丅
丂壓恾偼丄倎亖侾 偲偟偨偲偒偺僒僀僋儘僀僪偱偁傞丅
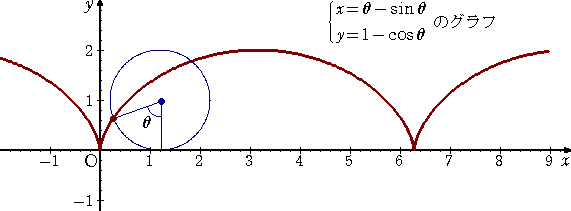
丂僒僀僋儘僀僪傪庤彂偒偱尩枾偵昤偔偙偲偼擄偟偄偑丄偦偺嬤帡宍偼師偺傛偆偵偟偰媮傔傜傟
傞丅
丂傑偢丄倎亖侾 偺偲偒丄敿宎侾偺墌廃偺挿偝偼丄丂俀兾佮俇丏俀俉丂偱偁傞偺偱丄偙偺挿偝傪俉摍
暘偡傞丅乮俉摍暘偡傞偙偲偼丄梕堈偱偁傞乯
丂敿宎侾偺墌廃傪俉摍暘偟丄忋婰偺俉摍暘揰偱愙偡傞墌傪昤偒丄弴師丄墌廃偺俉摍暘揰傪妸
傜偐偵寢傫偱偄偔偲丄僒僀僋儘僀僪傪嬤帡揑偵昤偔偙偲偑偱偒傞丅
丂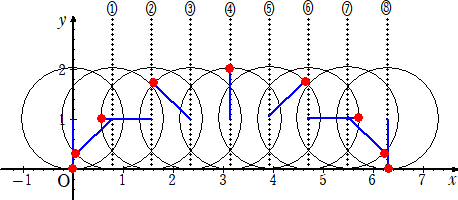
惈幙丂侾丏墌偑侾夞揮偟偰偱偒傞屖偺挿偝偼丄墌偺捈宎偺係攞
丂丂丂丂丂丂丂丂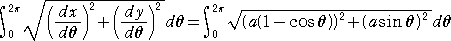
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂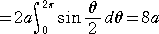
丂 丂丂俀丏墌偑侾夞揮偟偰偱偒傞屖偲倃幉偱埻傑傟偨晹暘偺柺愊偼丄墌偺柺愊偺俁攞
丂丂丂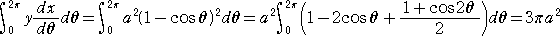
乮捛婰乯丂忋婰偱偼掕愊暘傪梡偄偰柺愊傪媮傔偨偑丄僇償傽儕僄儕偺尨棟傪梡偄傞偲娙扨偵媮
丂丂丂丂丂傔傜傟傞丅拀攇戝妛晬懏嬵応崅峑偺峏壢愭惗丄楅栘愭惗偐傜偛嫵庼偄偨偩偄偨曽
丂丂丂丂丂朄偱偁傞丅椉愭惗偵姶幱偟偨偄丅乮暯惉俀俋擭俀寧俀俈擔晅偗乯
丂丂丂丂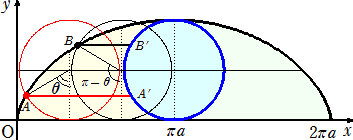
丂忋恾偺嵍懁偺晹暘乮墿怓乯傪 倶 幉偵暯峴側慄暘俙俙乫偱愗偭偨偲偒丄丂俙俙乫亖乮兾亅兤乯倎
摨條偵丄倶 幉偵暯峴側慄暘俛俛乫偱愗偭偨偲偒丄丂俛俛乫亖乮兾亅乮兾亅兤乯乯倎亖兤倎
丂傛偭偰丄嵍懁偺晹暘乮墿怓乯偺柺愊偼丄僇償傽儕僄儕偺尨棟傛傝丄
丂丂俙俙乫亊倎亄俛俛乫亊倎亖乮俙俙乫亄俛俛乫乯亊倎亖兾倎亊倎亖兾倎2
丂埲忋偐傜丄僒僀僋儘僀僪偲 倶 幉偱埻傑傟偨晹暘偺柺愊偼丄
丂丂兾倎2亄兾倎2亄兾倎2亖俁兾倎2
偲側傞丅
惈幙丂丂俁丏僒僀僋儘僀僪偺弅暵慄傕傑偨僒僀僋儘僀僪偱偁傞乮仺丂嶲峫乯
乮捛婰乯丂僒僀僋儘僀僪偼丄1501擭僔儍儖儖丒僽償僃儖偑墌愊栤戣偵娭楢偟偰弎傋偨偺偑嵟弶
丂丂丂丂丂偱偁傞丅偦偺屻丄僈儕儗僆傜偑尋媶偟丄嫶偺傾乕僠偲偟偰偦偺巊梡朄偑帵嵈偝傟偨丅
丂僒僀僋儘僀僪偺傾乕僠偼丄寶抸妛忋懠偺偳傫側嬋慄傛傝傕桪傟偰偄傞偲偄偆丅儂僀僿儞僗
乮1629乣1695乯偼丄僒僀僋儘僀僪傪忋壓媡偵偟偨嬋慄偑摍帪崀壓慄偵側傞偙偲傪帵偟丄怳巕
帪寁偺惢嶌偵梡偄偨丅
丂摍帪崀壓慄ゥ葠鼜銈處繐_偑廳椡偺傒偵傛偭偰嬋慄忋傪崀壓偡傞偲偒丄嬋慄忋偳偙偵偁偭偰傕摨偠帪娫偱嵟壓揰
丂丂丂丂丂丂丂丂丂丂丂偵摓払偡傞偲偄偆嬋慄
丂僒僀僋儘僀僪偼丄偦偺摿庩側旤偟偝丒桪夒側惈幙偐傜亀婔壗妛偺僿儗儞亁偲傕屇偽傟傞偦偆
偩丅
丂丂丂僿儗儞ゥg儘僀偺僿儗儞偼丄愴憟偑婲偙偭偰偟傑偆傎偳偺楌巎忋偵巆傞旤彈偱偁傞丅
乮嶲峫暥專丗俤丏俿丏儀儖丂挊丂揷拞丂桬丒嬧椦丂峗丂栿丂悢妛傪偮偔偭偨恖乆乮嘥乯丂乮搶嫗恾彂乯乯
乮捛婰乯丂暯惉侾俋擭係寧侾擔晅偗
丂俁寧俁侾擔丄壗偲偼側偟偵俿倁傪尒偰偄偨傜丄乽悽奅堦庴偗偨偄庼嬈両両俽俹乿乮NTV宯乯偱柺敀
偄栤戣傪徯夘偟偰偄偨丅
丂丂丂丂丂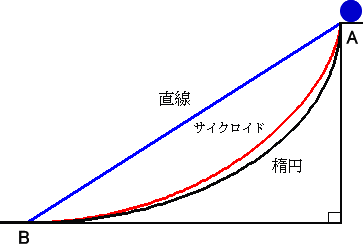
丂捈慄丄僒僀僋儘僀僪丄懭墌偺偦傟偧傟偺嬋慄忋偵増偭偰丄揰俙偐傜惵媴傪揮偑傝棊偲偡偲
偒丄偳偺応崌偑嵟傕懍偔揰俛偵摓払偡傞偩傠偆偐丠
丂僒僀僋儘僀僪偑嵟懍崀壓慄偲偄偆帠幚傪抦偭偰偄傞曽偼壗偱傕側偄栤戣偱偁傞偑丄抦傜側
偄曽偼偐側傝柪偆偩傠偆丅乮捈慄偺応崌偼嵟傕嫍棧偑抁偄偟丄懭墌偺応崌偼揰俙偐傜媫崀
壓偟偰偄偰懍偦偆偵尒偊傞偟丄丏丏丏丅乯
仈僒僀僋儘僀僪偼丄乽僽儔僸僗僩僋儘乕僱乿偲偄偆暿柤傪帩偮丅僊儕僔傾岅偱丄僽儔僸僗僩乮嵟抁偺乯
丂僋儘乕僱乮帪娫乯偲偄偆堄枴偱偁傞丅
丂俙偐傜俛傑偱偺嵟抁嫍棧偼丄傕偪傠傫丄乽捈慄俙俛乿偱偁傞偑丄栤戣偼丄俙偐傜俛傑偱偺嵟抁
帪娫偱丄惵媴偺懍偝偑娭學偟偰偔傞丅
丂嵟弶偺晹暘偱媫崀壓偝偣傟偽丄嵟屻偺晹暘偱偼丄偳偆偟偰傕備傞傗偐側孹幬偲側偭偰偟傑偆丅
偦偺偄偄墫攡偺嬋慄偑丄僒僀僋儘僀僪偲側傞丅
丂僒僀僋儘僀僪偑嵟懍崀壓慄偱偁傞偙偲傪弶傔偰徹柧偟偨偺偼丄僗僀僗偺悢妛幰儀儖僰乕僀
孼掜乮儎僐僽丒儀儖僰乕僀丄儓僴儞丒儀儖僰乕僀乯偱偁傞乮侾俇俋俈擭乯丅
| 丂丂丂丂僒僀僋儘僀僪偺攠夘曄悢昞帵丂 |
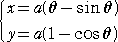 |
丂丂 |
偐傜丄僒僀僋儘僀僪忋偺擟堄偺揰偵偍偗傞懍搙儀僋僩儖偼丄丂兤亖冎倲丂偲偟偰丄
丂丂丂丂乮 倓倶/倓倲丂丆丂倓倷/倓倲 乯 亖乮 倎冎乮侾亅們倧倱兤乯丂丆丂倎冎倱倝値兤
乯
偱梌偊傜傟傞偐傜丄愙慄偲 倶 幉偺惓偺岦偒偲側偡妏傪 兛 偲偡傞偲丄
丂丂丂丂丂倲倎値 兛 亖 倓倷/倓倶 亖倱倝値兤/乮侾亅們倧倱兤乯亖們倧倲乮兤/俀乯亖倲倎値乮兾/俀亅兤/俀乯
丂傛偭偰丄丂兛亖兾/俀亅兤/俀丂偑惉傝棫偮丅
丂偙偺偲偒丄丂倷 亖 倎乮侾亅們倧倱兤乯 亖 俀倎倱倝値2乮兤/俀乯 亖 俀倎們倧倱2兛丂偲側傞偺偱丄
丂丂丂丂丂丂丂丂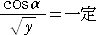
偑惉傝棫偮丅丂偙偺幃偙偦偑丄僒僀僋儘僀僪偑撪柺偱帩偮惈幙傪摿挜偯偗偰偄傞丅
丂忋恾偵偍偄偰揰俙傪尨揰偲偟丄悈暯曽岦嵍岦偒偵 倶 幉傪庢傝丄墧捈壓岦偒偵
倷 幉傪庢傞丅
弶懍搙偑 侽 偱丄幙揰偵摥偔椡偑廳椡偺傒偺応崌丄幙揰偺懍偝 倴 偼丄幙揰偺
倷 嵗昗傪 倷 偲
偟偰丄椡妛揑僄僱儖僊乕曐懚偺朄懃偐傜丄丂倴2 亖 俀倗倷丂乮 倗 偼丄廳椡壛懍搙乯 偵傛傝梌偊
傜傟傞丅
丂偄傑丄幙揰傪乽岝乿偲峫偊丄岝偺懍偝偑丂倴2 亖 俀倗倷丂偱梌偊傜傟傞傛偆側攠幙偺拞傪恑傓傕
偺偲偡傞偲丄岝偼丄岝妛揑偵嵟抁偺宱楬傪恑傒丄孅愜偺朄懃偐傜丄
丂丂丂丂丂丂丂丂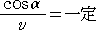
偑惉傝棫偮丅偲偙傠偱丄丂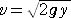 丂傪忋幃偵戙擖偡傞偲丄
丂傪忋幃偵戙擖偡傞偲丄
丂丂丂丂丂丂丂丂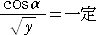
偑惉傝棫偪丄岝偼丄僒僀僋儘僀僪偵増偭偰恑傓偙偲偵側傞丅
丂偙偺偙偲偼丄僒僀僋儘僀僪偑嵟懍崀壓慄偱偁傞偙偲傪帵偟偰偄傞丅
乮僐儊儞僩乯丂忋婰偼尩枾偲偼尵偊側偄偑丄偩偄偨偄偺暤埻婥偼偁偭偰偄傞偺偐側丠
乮捛婰乯丂忋恾偱僠儔僢偲尒偨懭墌偲僒僀僋儘僀僪偺埵抲娭學傪扵媶偟偰傒傛偆丅
丂僒僀僋儘僀僪丂倶亖兤亅倱倝値兤丄倷亖侾亅們倧倱兤丂乮侽亝兤亝俀兾乯丂偺奣宍
丂丂丂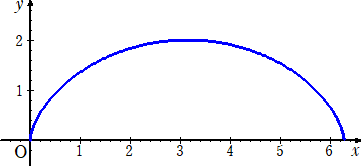
偲丄懭墌丂乮倶亅兾乯2/乮係兾2乯亄倷2/係亖侾丂乮倷亞侽乯丂偺奣宍
丂丂丂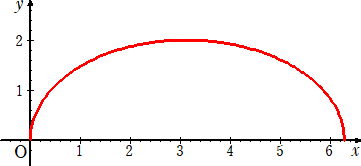
偼忋恾偺傛偆偱偁傞丅
丂偳偭偪偑偳偭偪偐暘偐傜側偄傎偳丄杮摉偵偦偭偔傝偝傫偱偡偹両婥帩偪揑偵懭墌偺椉抂偑
彮偟傆偭偔傜偟偨姶偠側偺偐側丏丏丏丅
丂椉幰傪堦偮偺嵗昗宯偵彂偒崬傫偱傒傞偲丄堘偄偑傛偔暘偐傞丅偙傟偼僷僜僐儞偺昤夋僜僼僩
偵彂偐偣偨傕偺偱丄偙傟傪庤彂偒偱彂偔偺偼帄擄偺媄偱偟傚偆丅
丂丂丂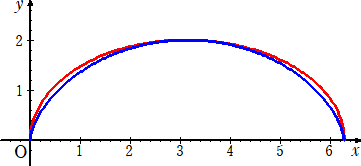
丂僒僀僋儘僀僪偲倶幉偱埻傑傟偨柺愊偼丄俁兾丄懭墌偲倶幉偱埻傑傟偨柺愊偼丄兾2丂偱偁傞偙偲
偐傜丄
丂丂丂丂丂丂丂兾2亜俁兾
側偺偱丄懭墌偺曽偑彮偟傆偭偔傜偟偰偄傞偙偲偼悇嶡偝傟傞丅
丂幚嵺偵丄倶亖兤亅倱倝値兤丄倷2亖侾亅們倧倱兤丂乮侽亝兤亝俀兾乯
丂丂丂丂丂丂倶亖兾亄兾們倧倱倲丄倷1亖俀倱倝値倲丂乮侽亝倲亝兾乯
偵偍偄偰丄丂兤亖俀兾亅俀倲丂偵拲堄偟偰丄
丂倷1亅倷2亖俀倱倝値倲亅侾亄們倧倱兤亖俀倱倝値倲亅侾亄們倧倱俀倲亖亅俀倱倝値2倲亄俀倱倝値倲
丂偙偙偱丄倱倝値倲亖倃 偲偍偔偲丄丂侽亝倲亝兾丂傛傝丄丂侽亝倃亝侾
丂偙偺偲偒丄丂倷1亅倷2亖亅俀倃2亄俀倃亖亅俀乮倃亅侾/俀乯2亄侾/俀丂側偺偱丄
丂丂丂侽亝倷1亅倷2亝侾/俀丂偡側傢偪丄丂倷1亞倷2
丂偙偺偙偲偐傜丄懭墌偼俁偮偺嫟桳揰傪彍偄偰丄偄偮傕僒僀僋儘僀僪偺忋曽偵偁傞偙偲偑暘偐
傞丅
丂丂埲壓丄岺帠拞両
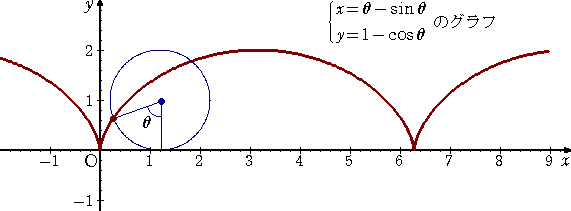

![]()
![]()
![]()


![]()
![]()
![]() 丂傪忋幃偵戙擖偡傞偲丄
丂傪忋幃偵戙擖偡傞偲丄![]()


