カヴァリエリの原理
 |
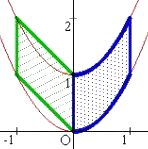
左図において、 Ｙ軸の右側には、 放物線 Ｙ＝Ｘ２、Ｙ＝Ｘ２＋１ （０≦Ｘ≦１）で囲まれた図形 Ｙ軸の左側には、 直線 Ｙ＝−Ｘ、Ｙ＝−Ｘ＋１ （−１≦Ｘ≦０）で囲まれた図形 がある。 |
一見して明らかに両者の面積は等しいが、詳しくは、次の原理による。 （→ 参考：「数学感動秘話」） |
|
カヴァリエリ（Cavalieri）の原理
２つの平面図形を、平行な直線で切ったときの切り口の長さがいつも等しければ、２つ
の図形の面積は等しい。
この原理は、立体においても成立する。すなわち、
２つの立体を、平行な平面で切ったときの切り口の面積がいつも等しければ、２つの立
体の体積は等しい。
練習問題
１． 半径ａ の円をＬだけ平行移動したとき、円が辿った跡の面積を求めよ。
（答） ２ａＬ
２． 幅ｄ、長さＬの２つの図形の面積は等しいか？
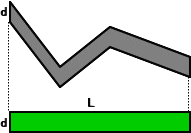
（答） 面積は同じで、ｄＬ
３． 道幅ａ の通路を距離Ｌだけ歩いたとき、歩いた通路の面積を求めよ。
（答） ａＬ
３．では直線的な図形を考えたが、曲線的な図形においても同様の性質が成り立つ。
４． 道幅ａ の通路を距離Ｌだけ歩いたとき、歩いた通路の面積を求めよ。
（答） ａＬ
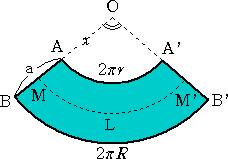
この考え方は、直円錐台の側面積、ひいては回転体の表面積の公式に応用される。
上図は、上面が半径 ｒ の円、底面が半径 Ｒ の円である直円錐台の側面の展開図であ
る。 いま、扇形の角の大きさを、θ （ラジアン）とすると、
ｘθ＝２πｒ 、 （ｘ＋ａ）θ＝２πＲ
が成り立つ。２式より、 （Ｒ−ｒ）ｘ＝ｒａ であることが分かる。
直円錐台の側面積＝（１/２）（ｘ＋ａ）・２πＲ−（１/２）・ｘ・２πｒ
＝（ｘ＋ａ）・πＲ−ｘ・πｒ
＝πｘ・（Ｒ−ｒ）＋πａＲ
＝πｒａ＋πａＲ
＝πａ（Ｒ＋ｒ）
＝２π｛（Ｒ＋ｒ）/２｝ａ
ＡＢの中点をＭとすると、２π｛（Ｒ＋ｒ）/２｝は、上図の曲線の長さ Ｌ に等しい。
よって、直円錐台の側面積は、 ａＬ で与えられる。
カヴァリエリ（Cavalieri）の原理を用いて、球の体積は、次のようにして求められる。
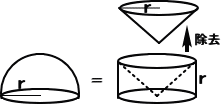
下図において、
「半径 ｒ の半球」
と、
「半径 ｒ、高さ ｒ の円柱から半径 ｒ、高さ ｒ の円錐を取り除いた立体」
のそれぞれの体積は等しい。
 |
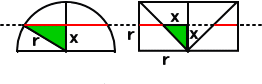実際に、それぞれの立体を、底面に平行な 平面（点線）で切断したときの断面積は、２つ とも π (ｒ２−Ｘ２) に等しい。 |
従って、球の体積は、 ２×（πｒ3−（1/3)πｒ3）＝(4/3) π ｒ3
（円錐の体積の公式は、カヴァリエリ（Cavalieri）の原理より、角錐の体積の公式から求め
られ、角錐の体積の公式は角柱の公式より求められる。（参考：角錐の体積）
（追記） 広島工業大学の大川研究室よりアドバイスを頂戴した。（平成１７年１月１８日付）
カヴァリエリ（Cavalieri）の原理では、次の事実も成立するとのことである。
２つの平面図形を、同心円で切ったときの切り口の長さがいつも等しければ、２つの図
形の面積は等しい。
立体の場合は、
２つの立体を、同心球で切ったときの切り口の面積がいつも等しければ、２つの立体の
体積は等しい。
２つの立体を、中心軸が同一の円柱で切ったときの切り口の面積がいつも等しければ、
２つの立体の体積は等しい。
前にあげた原理と上記の原理を交互に利用すると、一見して面積（体積）が求められな
いような図形に変形できるそうだ。
機会があれば、そのような図形を構成したいものだ。
（追記） カヴァリエリ（Cavalieri）の原理を用いると、積分計算をすることなく、放物線 ｙ＝ｘ2
と ｘ 軸、直線 ｘ＝１ で囲まれた図形の面積が求められることを最近知ることができ
た。（平成２６年１２月２１日付け）
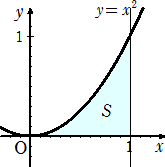
積分を用いれば、左図の図形の面積Ｓが１/３であることは
周知のことだろう。
この面積を、カヴァリエリ（Cavalieri）の原理で求めるために、
次のような工夫を行う。
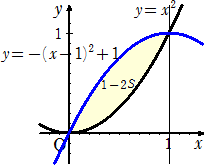左図において、放物線 ｙ＝ｘ2 と合同な放物線
ｙ＝−（ｘ−１）2＋１＝−ｘ2＋２ｘ
を用いる。２つの放物線に囲まれた図形の面積は、
１−２Ｓ である。
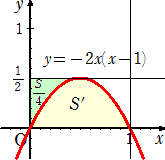左図において、放物線 ｙ＝−２ｘ（ｘ−１） は、
放物線 ｙ＝−ｘ2＋２ｘ をｘ軸、ｙ軸方向に１/２倍に縮小した
ものである。
従って、左図の薄緑色の部分の面積は、Ｓ/４となり、面積
Ｓ’は、 Ｓ’＝１/２−（Ｓ/４）×２＝１/２−Ｓ/２ となる。
ところで、 （−ｘ2＋２ｘ）−ｘ2＝−２ｘ（ｘ−１） なので、カヴァリエリ（Cavalieri）の原理より、
１−２Ｓ＝１/２−Ｓ/２ すなわち、 Ｓ＝１/３ が成り立つ。
また、次のような見方で求めることも可能である。
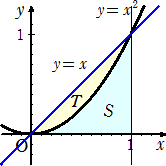
左図において、直線 ｙ＝ｘ と放物線 ｙ＝ｘ2 で囲まれた図形
の面積Ｔは、カヴァリエリ（Cavalieri）の原理より、下図の図形
の面積Ｔに等しい。
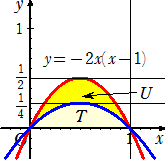放物線 ｙ＝−ｘ（ｘ−１） を ｙ軸方向に２倍に拡大した放物線
が、ｙ＝−２ｘ（ｘ−１） となる。
放物線 ｙ＝−２ｘ（ｘ−１） と ｘ軸で囲まれた図形の面積をＵ
とおくと、
Ｕ＝２Ｔ＝２（１/２−Ｓ） かつ Ｕ＝１/２−Ｓ/２
よって、 ２（１/２−Ｓ）＝１/２−Ｓ/２ より、 Ｓ＝１/３ が成り立つ。
３つの放物線 ｙ＝ｘ2 、ｙ＝（ｘ−１）2 、ｙ＝−２ｘ（ｘ−１） について、その和を考えると、
ｘ2＋（ｘ−１）2−２ｘ（ｘ−１）＝１
となる。この性質を利用すると、次のような別解が得られる。
Ｓ＋Ｓ＋（１/２−Ｓ/２）＝１ より、 Ｓ＝１/３
（コメント） この別解は、筑波大学附属駒場高校の三井田先生に伺ったものである。筑駒
では、２次関数の指導は中学３年〜高校１年に行われ特段先取り学習は行って
いないとのことであるが、中学３年で２次関数は半年以上の時間を使って、原点
頂点の放物線に関するありとあらゆることを扱い、内容を深化させているのだそ
うだ。関数どうしを足したり、引いたり、自由な発想を指導されているので上記の
ような別解もそれほど苦労なく導き出せるのだろう。
以下、工事中！