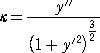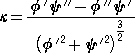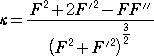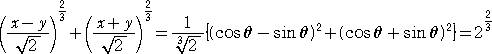包絡線　　　　 　 　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　曲線 Ｅ が、媒介変数 ｍ を含む曲線群 Ｆ＝｛ Ｆ（ ｘ，ｙ，ｍ ）＝０ ｝の包絡線であるとは、

　Ｅの各点が、どれかの曲線 Ｆ（ ｘ，ｙ，ｍ ）＝０ 上にあり、かつ、その点で２曲線が
互いに接している

ときを言う。（　→　参考　）

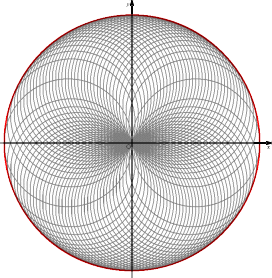
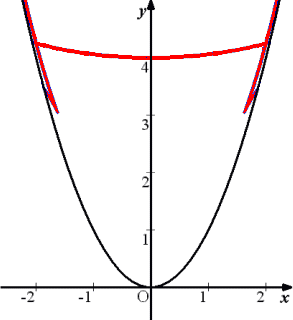
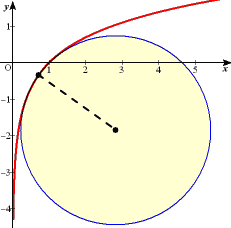
例　曲線群 Ｆ＝｛ ｙ＝ｍｘ＋ｍ²　（ ｍ は実数） ｝の包絡線を求めよ。

　以前は、手作業でいくつかの曲線を描き、その包絡線らしきものを想像していたが、最
近は、パソコンで簡単に残像つきのグラフが描けるようになったので、包絡線そのものが
視覚的にはっきりと認識できるようになった。


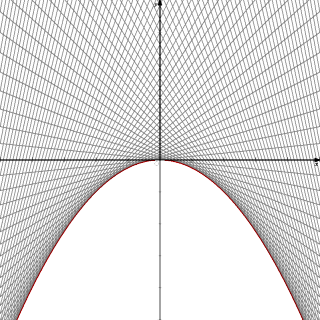
　　　　左図においては、放物線（赤色！）

　　　　　　ｙ＝−(１/４)ｘ²

　　　が包絡線となる。














　上記のように、グラフ（幾何）的に求めた包絡線を、代数的、解析的に求めようとするの
が、このページの主テーマである。

　包絡線の理論を整理しておこう。

　Ｆ（ ｘ ， ｙ ， ｍ ）＝０　が包絡線を持つとする。このとき、この曲線と包絡線との接点の座

標は、ｍ の関数で、　ｘ＝φ（ｍ）、ｙ＝ψ（ｍ）　と書ける。

　このとき、曲線　ｘ＝φ（ｍ）、ｙ＝ψ（ｍ）　が包絡線の方程式である。

　曲線　Ｆ（ ｘ ， ｙ ， ｍ ）＝０　と包絡線　ｘ＝φ（ｍ）、ｙ＝ψ（ｍ）　は接点で共通接線を持

つことから、その点で、Ｆ_ｘ 、Ｆ_ｙ は同時に０になることはない。

　そこで、　Ｆ_ｙ≠０ としても一般性を失うことはない。

　曲線 Ｆ（ ｘ ， ｙ ， ｍ ）＝０　上の接点における微分係数は、ｍ は定数として、

　　　　　Ｆ_ｘ ＋Ｆ_ｙ （ｄｙ/ｄｘ）＝０　より、　　ｄｙ/ｄｘ＝−Ｆ_ｘ/Ｆ_ｙ

また、包絡線　ｘ＝φ（ｍ）、ｙ＝ψ（ｍ）　上の接点における微分係数は、

　　　　　ｄｙ/ｄｘ＝（ｄｙ/ｄｍ）/（ｄｘ/ｄｍ）

この両者が一致するので、　−Ｆ_ｘ/Ｆ_ｙ＝（ｄｙ/ｄｍ）/（ｄｘ/ｄｍ）　から、

　　　　Ｆ_ｘ （ｄｘ/ｄｍ）＋Ｆ_ｙ （ｄｙ/ｄｍ）＝０

が成り立つ。一方、Ｆ（ ｘ ， ｙ ， ｍ ）＝０　を ｍ で偏微分すると、

　　　　Ｆ_ｘ （ｄｘ/ｄｍ）＋Ｆ_ｙ （ｄｙ/ｄｍ）＋Ｆ_ｍ＝０

が得られる。

　このとき、　Ｆ_ｘ （ｄｘ/ｄｍ）＋Ｆ_ｙ （ｄｙ/ｄｍ）＝０　なので、　Ｆ_ｍ＝０　が成り立つ。

　以上から、

　包絡線の方程式を求めるには、Ｆ（ ｘ ， ｙ ， ｍ ）＝０　、Ｆ_ｍ（ ｘ ， ｙ ， ｍ ）＝０　

から、 ｍ を消去すればよい。


　　上記のような計算を理解すれば、偏微分が出ることの必然性は疑う余地はないが、初
学者にとっては突拍子もないことと感じるかもしれない。

　別な視点で、このいわれをのぞいておこう。

　いま、円群　（ｘ−α）²＋ｙ²＝ｒ²　を考え、その包絡線を求めたい。

　包絡線を求めるために、ごく近い２つの円を考える。

　　　　（ｘ−α）²＋ｙ²＝ｒ²　　、　（ｘ−α＋ε）²＋ｙ²＝ｒ²

これらの交点を求めるには、この連立方程式を解けばよい。

　すなわち、　（ｘ−α）²＋ｙ²＝ｒ²　　、　２ε（ｘ−α）＋ε²＝０

　ε≠０　としてよいので、　（ｘ−α）²＋ｙ²＝ｒ²　　、　２（ｘ−α）＋ε＝０

　ここで、　εを限りなく０に近づけると、２つの円の交点は、包絡線上の点に近づく。

すなわち、包絡線上の点は、連立方程式

　　　　　（ｘ−α）²＋ｙ²＝ｒ²　　、　２（ｘ−α）＝０

を満たす。

　この式は、　Ｆ（ ｘ ， ｙ ， α ）＝（ｘ−α）²＋ｙ²−ｒ²＝０　として、

　　　　　　　　Ｆ_α（ ｘ ， ｙ ， α ）＝２（ｘ−α）＝０

としたものに等しい。

　このように考えれば、包絡線を求めるのに偏微分が用いられることが実感できることと
思われる。

　因みに、円群の包絡線の方程式は、　第２式から、ｘ＝α で、これを第１式に代入して

　　ｙ＝±ｒ　で、円群を頭の中で「ググ〜ッ！」と動かして得られるイメージと一致する。


　さて、包絡線の公式を用いて、先の例における包絡線を求めてみよう。

（解）　　Ｆ（ ｘ ， ｙ ， ｍ ）＝ｍｘ−ｙ＋ｍ²　とおくと、　Ｆ_ｍ（ ｘ ， ｙ ， ｍ ）＝ｘ＋２ｍ　なので、

　　　ｍ＝−ｘ/２　を、　ｍｘ−ｙ＋ｍ²＝０　に代入して、　（−ｘ/２）ｘ−ｙ＋（−ｘ/２）²＝０

　　　　よって、　包絡線の方程式は、　ｙ＝−(１/４)ｘ²　となる。　（終）


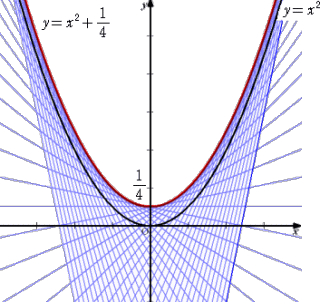
　ところで、曲線群 Ｆ＝｛ ｙ＝ｍｘ＋ｍ²　（ ｍ は実数） ｝の包絡線は、ｙ＝−(１/４)ｘ²　であ
ることが示されたが、この式は、ｍ の２次方程式　ｍ²＋ｍｘ−ｙ＝０　が重解を持つ、すな
わち、判別式 Ｄ＝０　を計算しても得られることに気づかされる。

　実際に、Ｆ が ｍ についての多項式関数のとき、

　　　「 Ｆ＝０　、Ｆ_ｍ＝０　」が成り立つということは、

　　　ｍ の方程式として、「 Ｆ＝０ 」が重解を持つことに等しい

ので、特に、２次関数 Ｆ については、偏微分というものを表に出さずとも、高校数学風に判
別式を利用して包絡線の方程式を求める方が簡明だろう。
（平成２０年１２月１８日付けで、Ｓ（Ｈ）さんから、「判別式を求めるのに偏微分を用いているのでは？」
　というご指摘を頂きました。正にその通りで、「高校数学風に」と文言を修正させていただきました。）

例　曲線群 Ｆ＝｛ （ｘ−ｍ）²＋（ｙ−ｍ）²＝ｍ²　（ｍは実数） ｝の包絡線の方程式を
　求めよ。

（解）　ｍ²−２（ｘ＋ｙ）ｍ＋ｘ²＋ｙ²＝０　の判別式をＤとすると、

　　　　　Ｄ/４＝（ｘ＋ｙ）²−（ｘ²＋ｙ²）＝２ｘｙ＝０

　　　よって、包絡線の方程式は、　ｘ＝０　または　ｙ＝０　　（終）

　　　　　　

例　曲線群 Ｆ＝｛ ｙ＝ｍｘ−（１＋ｍ²）ｘ²　（ｍは実数） ｝の包絡線の方程式を求めよ。

（解）　ｘ²ｍ²−ｘｍ＋ｘ²＋ｙ＝０　は、ｘ＝０　のとき重解を持たないので、ｘ≠０　としてよい。

　　このとき、判別式をＤとすると、　Ｄ＝ｘ²−４ｘ²（ｘ²＋ｙ）＝０　より、　ｙ＝−ｘ²＋１/４

　　　よって、包絡線の方程式は、　ｙ＝−ｘ²＋１/４

　　　　　　　　　　　　ただし、点（ ０ ， １/４ ）は省く。　　（終）

　　　　　　　　　


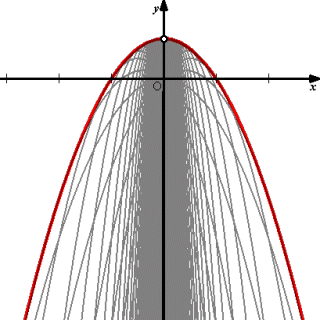
　曲線群 Ｆ＝｛ Ｆ（ ｘ ， ｙ ， α ， β ）＝０　　（ α 、 β は実数 ） ｝を表すパラメータが２個
あって、２つのパラメータ間に拘束条件　Ｇ（ α ， β ）＝０　がある場合は、１パラメータと
同様の公式が成り立つ。

　すなわち、

　　曲線群が、２つの方程式　Ｆ（Ｘ，Ｙ，α，β）＝０　、Ｇ（α，β）＝０　で与えられる

とき、包絡線上の全ての点は、次の方程式 ：

　　Ｆ（Ｘ，Ｙ，α，β）＝０　、Ｇ（α，β）＝０　、

　　Ｆ_αＧ_β−Ｇ_αＦ_β＝０　　（ただし、Ｆ_αは、Ｆのαに関する偏微分を表す。他も同様）

からパラメーターα，βを消去して得られる方程式を満たす。

　実際に、　Ｇ（ α ， β ）＝０　より、　β を α の関数 β＝ｇ（α）　と見て、

　　　Ｈ（ ｘ ， ｙ ， α ）＝Ｆ（ ｘ ， ｙ ， α ， ｇ（α） ）

と書ける。（必要があれば、α を β の関数と思って式を作ってもよい。）

　このとき、包絡線上の点は、方程式　Ｈ（ ｘ ， ｙ ， α ）＝０　、　Ｈ_α（ ｘ ， ｙ ， α ）＝０

を満たす。ここで、　Ｆ_ｘ（ｄｘ/ｄα）＋Ｆ_ｙ（ｄｙ/ｄα）＝０　であることに注意して、

　　Ｈ_α＝Ｆ_α＋Ｆ_β（ｄβ/ｄα）＝０　・・・　（*）

　ところで、　Ｇ（ α ， β ）＝０　の両辺を α で偏微分すると、

　　　　　　Ｇ_α＋Ｇ_β（ｄβ/ｄα）＝０　・・・　（**）

　このとき、　（*）、（**）から、（ｄβ/ｄα）を消去すれば、

　　　　　　Ｆ_αＧ_β−Ｇ_αＦ_β＝０

が得られる。

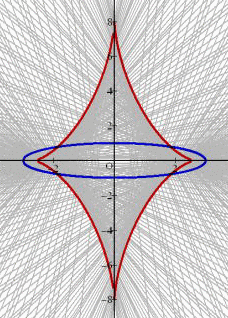
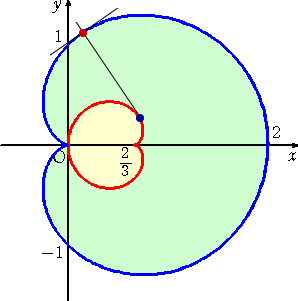
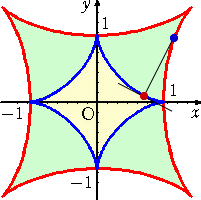
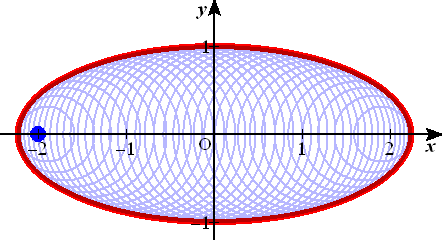
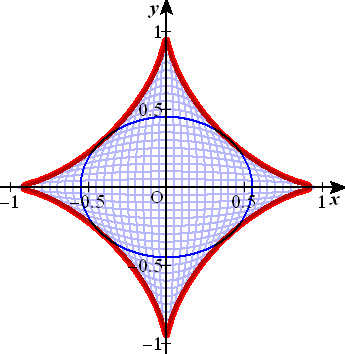
例　 α²＋β²＝Ｌ²　のとき、直線群 βｘ＋αｙ＝αβ の包絡線の方程式を求めよ。

（解）　Ｆ（ ｘ ， ｙ ， α ， β ）＝βｘ＋αｙ−αβ　、Ｇ（α，β）＝α²＋β²−Ｌ²　とおく。

　　Ｆ_αＧ_β−Ｇ_αＦ_β＝（ｙーβ）（２β）−（２α）（ｘ−α）＝０　より、

　　　β（ｙ−β）−α（ｘ−α）＝０

　以上から、連立方程式　αｘ−βｙ＝α²−β²　、　βｘ＋αｙ＝αβ　が得られる。

　これを解いて、　Ｌ²ｘ＝α³　、Ｌ²ｙ＝β³　となる。

　これらを、α²＋β²＝Ｌ²　に代入して、
　　　　　　　　　　　　　　　　　　　　　　　　　　　（終）

（ → 参考 ： 「星芒形」、「直角に曲がる通路の通過問題」）

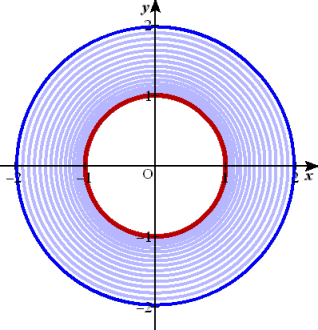
例　 α²＋β²＝Ｌ²　のとき、円群 ｘ²＋ｙ²＋２αｘ＋２βｙ＝０ の包絡線の方程式を
　　求めよ。

（解）　Ｆ（ ｘ ， ｙ ， α ， β ）＝ｘ²＋ｙ²＋２αｘ＋２βｙ　、Ｇ（α，β）＝α²＋β²−Ｌ²　とおく。

　　Ｆ_αＧ_β−Ｇ_αＦ_β＝（２ｘ）（２β）−（２α）（２ｙ）＝０　より、　βｘ−αｙ＝０

　このとき、実数 ｍ を用いて、　α＝ｍｘ　、　β＝ｍｙ　　とおける。

　α²＋β²＝Ｌ²　に代入して、　ｍ²ｘ²＋ｍ²ｙ²＝Ｌ²　より、

　　　　　　　

　これらを、　ｘ²＋ｙ²＋２αｘ＋２βｙ＝０　に代入して整理すると、　ｘ²＋ｙ²＝４Ｌ²　　（終）

　　　　　　　　　

（コメント）　上記の場合、原点も包絡線に含まれるとしていいんですよね？

　当ＨＰがいつもお世話になっているＳ（Ｈ）さんから次のような問題が提起された。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２０年１２月１３日付け）

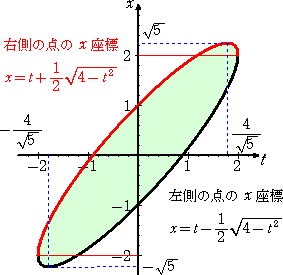
例　 放物線　ｙ＝ｘ²　上の２点Ａ（ α ， α² ）、Ｂ（ β ， β²）　（ただし、α＜β）が、
　　ＡＢ＝Ｌ（＝一定）という条件を満たしながら動く。このとき、線分ＡＢの包絡線の方
　　程式を求めよ。

　Ｓ（Ｈ）さんによれば、Ｌ＝４ のときに、特異点を有する包絡線が出現するという。

　Ｌ＝４　の場合を考えてみよう。

　直線 ＡＢ の方程式は、明らかに、　ｙ＝（α＋β）ｘ−αβ　である。

このとき、拘束条件は、　（α−β）²＋（α²−β²）²＝１６

　すなわち、　（α−β）²｛１＋（α＋β）²｝＝１６　である。

ここで、　α＋β＝ｍ　、　αβ＝ｎ　とおくと、

　直線 ＡＢ の方程式は、　ｙ＝ｍｘ−ｎ

　拘束条件は、　（ｍ²−４ｎ）（１＋ｍ²）＝１６

となる。このことから、
　　　　　　　　　　　　　　

このとき、　ｘ²＝ｍｘ−ｎ　すなわち、　ｘ²−ｍｘ＋ｎ＝０　において、解の公式により、

　　　　　

であるので、
　　　　　　　　

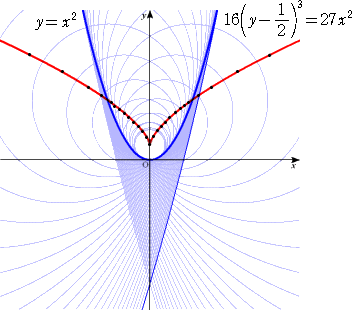
の範囲にある線分ＡＢを変化させると、下図が得られる。（一部手書き補正！）

　　　　　　

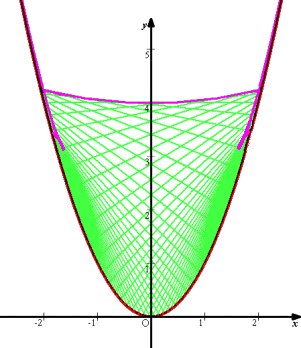
（コメント）　あ〜、本当だ！特異点っぽい所がありますね。予想では、線分が滑らかに変化
　　　　　　していくので特異点は出そうにないと思っていましたが、予想が外れました．．．。
　　　　　　拘束条件が意外にきついのと放物線の傾きが滑らかに変化することの障害にな
　　　　　　っているんでしょうね？

　　　　　　　Ｓ（Ｈ）さんによれば、 ｙ＝ｘ⁴ に対しては、Ｌ＝７ のときに、特異点を有する包絡
　　　　　　線が出現するという。

　　　　　　（追記）平成２１年１２月２６日付け

　　　　　　　　　ＨＮ「Ｂｏｏ」さんから、この話題についてご教示いただいた。

　　　　　　　　　　計算したり、グラフを描いてみたりしたところ、

　　　　　　　　　　　・　ｙ＝ｘ²　では、線分の長さＬが２より大きい場合

　　　　　　　　　　　・　ｙ＝ｘ⁴　では、線分の長さＬが２の場合

　　　　　　　　　　でも特異点が出そうな気がします。

　　　　　　　　　とのこと。

　　　　　　　（コメント）　ＨＮ「Ｂｏｏ」さん、ありがとうございます。今後検証したいと思います。


　上記では包絡線の様子を視覚的に眺めたが、その方程式はどのように記述されるのだろ
うか？特異点が出現しているので、このことも大いに興味があるところである。

　Ｓ（Ｈ）さんからは、「描写された包絡線では見えがたい微妙な代数曲線の部分があるので、
その包絡線の代数方程式を明記し、具体的に、特異点の状況を調べた方がよい。」というア
ドバイスを頂いた。（平成２０年１２月１５日付け）

　まさにその通りで、上記の関数の真実を探りたいと思う。

　上記の計算から、包絡線上の点は、次の方程式を満たす。

　　　Ｆ（ ｘ ， ｙ ， ｍ ， ｎ ）＝ｍｘ−ｙ−ｎ＝０

　　　Ｇ（ ｍ ， ｎ ）＝ｍ⁴＋（１−４ｎ）ｍ²−４ｎ−１６＝０

　　　Ｆ_ｍＧ_ｎ−Ｇ_ｍＦ_ｎ＝４ｍ³−４ｍ²ｘ＋２（１−４ｎ）ｍ−４ｘ＝０

　ｎ＝ｍｘ−ｙ　を他の２式に代入して式を整理すると、

　　　　ｍ⁴−４ｘｍ³＋（４ｙ＋１）ｍ²−４ｘｍ＋４ｙ−１６＝０

　　　　２ｍ³−６ｘｍ²＋（４ｙ＋１）ｍ−２ｘ＝０

　これらの方程式は、共通解 ｍ を持っているので、シルベスターの消去法を用いて、ｍ
を消すことにより、包絡線上の点が満たす方程式を求めることができる。

　すなわち、

　　　

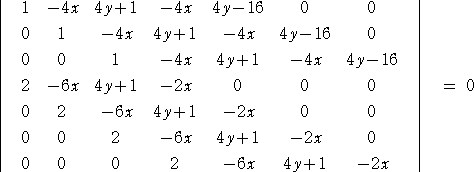
　行列式の性質を用いて、左辺を計算（手計算 ．．． ｆ(^^;) ）すると、

−１０２４ｘ⁶＋（−２０４８ｙ²＋３８９１２ｙ−１１３７９２）ｘ⁴

　　＋（−１０２４ｙ⁴＋７１６８ｙ³−５１５８４ｙ²＋１５５５８４ｙ−１３２５２）ｘ²

　　　　＋１０２４ｙ⁵−５１２０ｙ⁴＋１２６７２ｙ³−３８４６４ｙ²＋３３５４０ｙ−６７６００＝０

となる。

（コメント）　平成２０年１２月２１日付けのＳ(Ｈ)さんからの正しい計算結果の提示がなかっ
　　　　　　たら、手計算ゆえに計算結果には全く自信がなく、係数の大きさから不安に煽
　　　　　　られ、ただ恐れおののくだけだったろう。Ｓ(Ｈ)さんからのアドバイスが神々しく
　　　　　　感じられた。Ｓ(Ｈ)さんに感謝します。

　　　　　　　それにしても、上記の手計算は、とてもハードでした．．．！

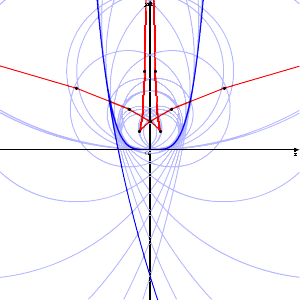
　確認のために、上記の方程式のグラフをグラフ描画ソフトに描かせてみると、

　　　　　　

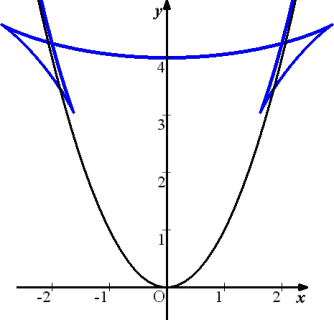
　もっとも、上図は直線群 ＡＢ の包絡線である。問題では、線分群 ＡＢ なので、実際の包
絡線は下図のようになるであろうか？

　 　　　　　　

　当ＨＰがいつもお世話になっているＳ（Ｈ）さんから包絡線に関わる新しい問題が提起され
た。（平成２０年１２月２７日付け）

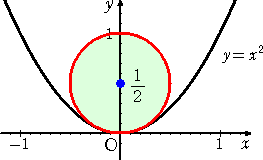
例　 放物線　ｙ＝ｘ²　において、放物線の上方の１点を、Ｐ（ ａ ， ｂ ） とおく。点Ｐを
　　通る直線が放物線と交わる２点をＡ（ α ， α² ）、Ｂ（ β ， β²） とする。　（た
　　だし、α＜β）　このとき、次の問いに答えよ。

　　　（１）　放物線と直線ＡＢで囲まれた図形の面積の最小値 Ｓ（ ａ ， ｂ ） を求めよ。

　　　（２）　曲線 Ｓ（ ａ ， ｂ ）＝ｋ　（ｋ は実数の定数）は、ある直線群の包絡線とな
　　　　　　ることを示せ。

（１）　直線ＡＢの方程式は、傾きを ｍ として、　ｙ＝ｍ（ｘ−ａ）＋ｂ　とおける。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（ → 参考 ： 「放物線で掛け算」）

　　放物線の方程式　ｙ＝ｘ²　と連立して、　ｘ²−ｍｘ＋ｍａ−ｂ＝０

　　解と係数の関係から、　α＋β＝ｍ　、　αβ＝ｍａ−ｂ

　　放物線と直線ＡＢで囲まれた図形の面積は、　（β−α）³/６　で与えられる。

　　　よって、

　　　　（β−α）²＝（α＋β）²−４αβ＝ｍ²−４（ｍａ−ｂ）＝（ｍ−２ａ）²−４ａ²＋４ｂ

　　より、求める面積は、ｍ＝２ａ　のとき最小で、最小値 Ｓ（ ａ ， ｂ ） は、

　　　　　　　　　　　
　　となる。

（２）　ｋ＝（４/３）ｎ³ を満たす実数 ｎ はただ１つ存在して、曲線 Ｓ（ ａ ， ｂ ）＝ｋ　は、放物

　　線　ｂ＝ａ²＋ｎ²　を表す。

　　　（１）より、　ｍ＝２ａ　のとき、面積は最小なので、そのときの直線ＡＢの方程式は、

　　ｙ＝２ａｘ−２ａ²＋ｂ　となる。このとき、面積は、

　　　　（β−α）³/６＝ｋ＝（４/３）ｎ³　より、　β−α＝２ｎ　となる。

　　このとき、（α＋β）²−４αβ＝４ｎ²　に、α＋β＝２ａ　、αβ＝２ａ²−ｂ　を代入して、

　　　　４ａ²−４（２ａ²−ｂ）＝４ｎ²　　すなわち、　−ａ²＋ｂ＝ｎ²

　　そこで、拘束条件　Ｇ（ａ，ｂ）＝−ａ²＋ｂ−ｎ²＝０　のもとに、直線群

　　　　Ｆ（ ｘ ， ｙ ， ａ ， ｂ ）＝２ａｘ−ｙ−２ａ²＋ｂ＝０

　　を考えると、

　　　Ｆ_ａＧ_ｂ−Ｇ_ａＦ_ｂ＝（２ｘ−４ａ）・１−（−２ａ）・１＝２ｘ−２ａ＝０

　　より、　ａ＝ｘ　となる。このとき、　ｂ＝ａ²＋ｎ²＝ｘ²＋ｎ²

　　　これらを、　Ｆ（ ｘ ， ｙ ， ａ ， ｂ ）＝２ａｘ−ｙ−２ａ²＋ｂ＝０　に代入して、

　　　　２ｘ²−ｙ−２ｘ²＋ｘ²＋ｎ²＝０　より、　ｙ＝ｘ²＋ｎ²

　　よって、直線群の包絡線の方程式は、ｙ＝ｘ²＋ｎ²　となる。

　　したがって、求める直線群は、　ｙ＝２ａｘ−ａ²＋ｎ²　（ただし、ａ は実数）　である。

（コメント）　拘束条件が包絡線そのものですが、これは勇み足？

　ｋ＝１/６　のとき、　ｎ＝１/２　で、　直線群は、　ｙ＝２ａｘ−ａ²＋１/４　となる。

この場合を図示してみよう。

　　　　　　　　　　

　上記の計算で、
　　　　　　　　　　　Ｓ＝（β−α）³/６

の最小値を求めるために、　（β−α）²＝（ｍ−２ａ）²−４ａ²＋４ｂ　という２次関数を利用し
たが、この種の問題の一般的解法のため次のような解法を確認しておくことも大切だろう。

（別解その１）　放物線　ｙ＝ｘ² の上方にある点（ ａ ， ｂ ） を通る直線と放物線との交点の

　　ｘ 座標を α、β （α＜β） とすると、直線の方程式は、　ｙ＝（α＋β）ｘ−αβ

　　と書ける。このとき、　ｂ＝（α＋β）ａ−αβ　であるので、

　　　　　　　　　　　　　　　

　　を、Ｓの式に代入して、βを消去し、整理すると、

　　　　　　　　　　　　

　　ここで、　ａ−α＞０　、　ｂ−ａ²＞０　に注意して、相加平均と相乗平均の関係から、

　　求める最小値は、
　　　　　　　　　　　　　　

　　となることが分かる。　（終）

（コメント）　この（別解その１）の解法も、Ｓの特殊な形に依存しているので、「一般的」とは
　　　　　　言えないかも．．．？

（別解その２）　放物線　ｙ＝ｘ² の上方にある点（ ａ ， ｂ ） を通る直線と放物線との交点の

　　ｘ 座標を α、β （α＜β） とすると、直線の方程式は、　ｙ＝（α＋β）ｘ−αβ

　　と書ける。このとき、　ｂ＝（α＋β）ａ−αβ　であるので、

　　　　　　　　　　　　　　　

　　を、Ｓの式に代入して、βを消去し、整理すると、

　　　　　　　　　　　　

　　　ここで、　ｘ＝α−ａ （＜０）、ｍ＝ｂ−ａ² （＞０）　とおくと、

　　　　　　　　　　　　

　　　両辺を ｘ で微分して、
　　　　　　　　　　　　　　　　　

　　　Ｓ’＝０　を解いて、　　で、このとき、Ｓは極小かつ最小となり、

　　　最小値は、
　　　　　　　　　　　

　　　となる。　（終）

　上記の計算で、陰関数の微分法を用いてもよいだろう。

（別解その３）
　　　　　　　

　　の分母を払って、ｘ の降べきの順に式を整理すると、

　　　　　　　ｘ⁶＋３ｍｘ⁴＋６Ｓｘ³＋３ｍ²ｘ²＋ｍ³＝０　・・・　(*)

　　両辺を ｘ で微分して、

　　　　　　　６ｘ⁵＋１２ｍｘ³＋６Ｓ’ｘ³＋１８Ｓｘ²＋６ｍ²ｘ＝０

　　ｘ＜０　なので、　ｘ⁴＋２ｍｘ²＋Ｓ’ｘ²＋３Ｓｘ＋ｍ²＝０

　　　ここで、Ｓ’＝０　として、　ｘ⁴＋２ｍｘ²＋３Ｓｘ＋ｍ²＝０　・・・　(**)

　　(*)(**)　より、Ｓを消去すると、　ｘ⁶＋ｍｘ⁴−ｍ²ｘ²−ｍ³＝０

　　よって、　ｘ²（ｘ⁴−ｍ²）＋ｍ（ｘ⁴−ｍ²）＝０　より、　（ｘ²＋ｍ）²（ｘ²−ｍ）＝０

　　これを解いて、　　より、Ｓの最小値

　　　　　　

　　を得る。　（終）

　上記では極値を与える候補（この場合、最小値を与えることは幾何学的に自明としていいだろう）
を求めてから最小値を求めたが、シルベスターの消去法を用いれば、そういった遠回りを
しなくても直接的に最小値は求められる。当ＨＰがいつもお世話になっているＳ（Ｈ）さんは
その方法で最小値を求められた。（平成２０年１２月２９日付け）

（Ｓ（Ｈ）さんの計算）　Ｓ＝(β−α）³/６　、　ｂ−ａα−ａβ＋αβ＝ ０　からβを消去し

　−６Ｓａ³＋ｂ³＋１８Ｓａ²α−６ａｂ²α−１８Ｓａα²＋１２ａ²ｂα²＋３ｂ²α²
　　　　　　　　　　＋６Ｓα³−８ａ³α³−１２ａｂα³＋１２ａ²α⁴＋３ｂα⁴−６ａα⁵＋α⁶＝０

また、上式を α で微分して、Ｓ’＝０　とおくと、

　 １８Ｓａ²−６ａｂ²−３６Ｓａα＋２４ａ²ｂα＋６ｂ²α＋１８Ｓα²−２４ａ³α²
　　　　　　　　　　　　　　　　　　　−３６ａｂα²＋４８ａ²α³＋１２ｂα³−３０ａα⁴＋６α⁵＝０

　シルベスターの消去法により、（←　ここの部分は手計算だと大変そう．．．！）

　　　−３７７９１３６Ｓ⁴（ａ²−ｂ）⁶（９Ｓ²＋１６ａ⁶−４８ａ⁴ｂ＋４８ａ²ｂ²−１６ｂ³）＝０

　　　　　−３７７９１３６Ｓ⁴（ａ²−ｂ）⁶（９Ｓ²＋１６（ａ²−ｂ）³）＝０

　よって、　９Ｓ²＝１６（ｂ−ａ²）³　より、
　　　　　　　　　　　　　　　　　　　　　　　　
　を得る。　（終）

　Ｓ（Ｈ）さんの解法を意識して、ここでは、互除法の考えを用いて手計算してみよう。
このような機会を与えていただいたＳ（Ｈ）さんに感謝します。

（別解その４）
　　　　　　　

　　の分母を払って、ｘ の降べきの順に式を整理すると、

　　　　　　　ｘ⁶＋３ｍｘ⁴＋６Ｓｘ³＋３ｍ²ｘ²＋ｍ³＝０　・・・　(*)

　　両辺を ｘ で微分して、

　　　　　　　６ｘ⁵＋１２ｍｘ³＋６Ｓ’ｘ³＋１８Ｓｘ²＋６ｍ²ｘ＝０

　　ｘ＜０　なので、　ｘ⁴＋２ｍｘ²＋Ｓ’ｘ²＋３Ｓｘ＋ｍ²＝０

　　　ここで、Ｓ’＝０　として、　ｘ⁴＋２ｍｘ²＋３Ｓｘ＋ｍ²＝０　・・・　(**)

　　極値を与える候補の ｘ は、(*)(**)　の２式を同時に満たす。

　このとき、　ｘ⁶＋３ｍｘ⁴＋６Ｓｘ³＋３ｍ²ｘ²＋ｍ³

　　　　　　　＝（ｘ⁴＋２ｍｘ²＋３Ｓｘ＋ｍ²）（ｘ²＋ｍ）＋３Ｓｘ³−３ｍＳｘ

　なので、極値を与える候補の ｘ は、

　　　　　　　ｘ⁴＋２ｍｘ²＋３Ｓｘ＋ｍ²＝０　、　ｘ³−ｍｘ＝０

　の２式を同時に満たす。

　このとき、　ｘ⁴＋２ｍｘ²＋３Ｓｘ＋ｍ²＝（ｘ³−ｍｘ）ｘ＋３ｍｘ²＋３Ｓｘ＋ｍ²

　なので、極値を与える候補の ｘ は、

　　　　　　　ｘ³−ｍｘ＝０　、　３ｍｘ²＋３Ｓｘ＋ｍ²＝０

　の２式を同時に満たす。シルベスターの消去法により、

　　　　　

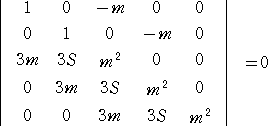
　すなわち、
　　　　　　　

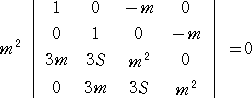
　これより、　ｍ²｛ｍ⁴−９Ｓ²ｍ＋３ｍ⁴＋３ｍ（３ｍ³＋ｍ³）｝＝０　なので、

簡約すると、　ｍ³（−９Ｓ²＋１６ｍ³）＝０　となる。

　よって、求める面積の最小値は、

　　　　　　

で与えられることが分かる。　（終）

　シルベスターの消去法を用いると、どうしても高次の行列式の計算が必須になる。手計算
をする身にとっては、これは避けなければならない由々しき事態である。

　現在当面している問題設定において、放物線との囲まれた面積が最小となる直線群の包
絡線が求める曲線であるという事実を知れば、次のような別解も可能となる。この解法につ
いては、平成２０年１２月３１日付けでＳ（Ｈ）さんが取り組まれた。

（別解その５）

　放物線と直線ＡＢで囲まれた図形の面積は、　（β−α）³/６　で与えられる。そこで、

面積の最小値　Ｓ（ ａ ， ｂ ）＝ｋ　とし、　とおくと、　β＝α＋Ｋ　となる。

　このとき、直線ＡＢの方程式　ｙ＝（α＋β）ｘ−αβ　が、点（ ａ ， ｂ ） を通るので、

　　ｂ＝（２α＋Ｋ）ａ−α（α＋Ｋ）　すなわち、　α²＋（Ｋ−２ａ）α＋ｂ−Ｋａ＝０

　そこで、　Ｆ（ ａ ， ｂ ， α ）＝α²＋（Ｋ−２ａ）α＋ｂ−Ｋａ＝０　とすると、

　　　　　　　Ｆ_α（ ａ ， ｂ ， α ）＝２α＋（Ｋ−２ａ）＝０

　シルベスターの消去法により、

　　　　　

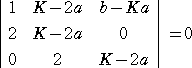
　よって、　（Ｋ−２ａ）²＋４（ｂ−Ｋａ）−２（Ｋ−２ａ）²＝０　すなわち、　Ｋ²＝４（ｂ−ａ²）

　　したがって、
　　　　　　　　　　　　（終）

（コメント）　十分手計算の範疇まで落ちてきましたね！でも、Ｆ_α＝０　が１次方程式なので、

　　　　　　α＝−（Ｋ−２ａ）/２　を、Ｆ＝０　に代入して、

　　　　　　　　（Ｋ−２ａ）²/４−（Ｋ−２ａ）²/２＋ｂ−Ｋａ＝０　より、　Ｋ²＝４（ｂ−ａ²）

　　　　　　としたい誘惑が．．．．。

　　　　　　ちょうど、代入による消去とシルベスターの消去法の端境期ですね！


　ｘ 、ｙ の多項式 Ｆ（ ｘ ， ｙ ， ｍ ） または　Ｆ（ ｘ ， ｙ ，α，β）　によって定義される方程
式　Ｆ（ ｘ ， ｙ ， ｍ ）＝０　または　Ｆ（ ｘ ， ｙ ，α，β）＝０　を満たす点（ ｘ ， ｙ ）全体の集
合は、幾何学的には「代数曲線」と呼ばれる。

　高校で扱う曲線、例えば、直線、円、放物線、楕円、双曲線などは、もちろん代数曲線で
ある。

　ここで、Ｆｘ ＝０　かつ　Ｆｙ＝０　であるような曲線 Ｆ＝０ 上の点 Ｐを Ｆ の特異点という。

　代数曲線は、特異点を全く持たないか、有限個の特異点（結節点、尖点、孤立点）を持
つの何れかである。

　特異点の種類の判定には、ヘシアンの符号が用いられる。ヘシアンは、ヘッセの行列
式（ヤコビの行列式）とも言われる。

　曲線　Ｆ（ ｘ ， ｙ ）＝０　が、点Ｐ（ ａ ， ｂ ）で特異点を持つとすると、その近くの曲線上

の点Ｑ（ ａ＋ｈ ，ｂ＋ｋ ）に対して、

　　　　　　Ｆ（ ａ ， ｂ ）＝０　、　Ｆｘ（ ａ ， ｂ ）＝０　、Ｆｙ（ ａ ， ｂ ）＝０

であることに注意して、Ｔａｙｌｏｒ の定理より、

　　Ｆ（ ａ＋ｈ ，ｂ＋ｋ ）≒ （1/2）｛ Ｆ_ｘｘ（ａ，ｂ）ｈ²＋２Ｆ_ｘｙ（ａ，ｂ）ｈｋ＋ Ｆ_ｙｙ（ａ，ｂ）ｋ² ｝

　　Ｆ（ ａ＋ｈ ，ｂ＋ｋ ）＝０　なので、

　　　　　Ｆ_ｘｘ（ａ，ｂ）ｈ²＋２Ｆ_ｘｙ（ａ，ｂ）ｈｋ＋ Ｆ_ｙｙ（ａ，ｂ）ｋ²≒０

　そこで、　Ａ＝Ｆ_ｘｘ（ａ，ｂ）　、　Ｂ＝Ｆ_ｘｙ（ａ，ｂ）　　、　Ｃ＝ Ｆ_ｙｙ（ａ，ｂ）　　とおき、

　　　ヘシアン(Hessian)　：　Ｈ＝ＡＣ−Ｂ²　を考える。

　ヘシアンは、関数　Ｆ（ ｘ ， ｙ ） に対して、（ ａ ， ｂ ） におけるヘッセ行列

　　　　　　　　

の行列式として得られる。ヘシアンは、行列 Ｈ の固有値の積に等しい。

特異点の判定公式

（１）　Ｈ＜０　のとき、　特異点Ｐは、結節点である。

　　実際に、Ｈ＜０　だと、　Ｆ_ｘｘ（ａ，ｂ）ｈ²＋２Ｆ_ｘｙ（ａ，ｂ）ｈｋ＋ Ｆ_ｙｙ（ａ，ｂ）ｋ²　は一次式の積
　に分解できるので、点Ｐの近くでは曲線は近似的に２直線となる。

（２）　Ｈ＝０　のとき、　特異点Ｐは、尖点である。

　　実際に、Ｈ＝０　だと、　Ｆ_ｘｘ（ａ，ｂ）ｈ²＋２Ｆ_ｘｙ（ａ，ｂ）ｈｋ＋ Ｆ_ｙｙ（ａ，ｂ）ｋ²　は一次式の平
　方に分解できるので、点Ｐの近くでは曲線は近似的に２接線が一致した１直線となる。

（３）　Ｈ＞０　のとき、　特異点Ｐは、孤立点である。

　　実際に、Ｈ＞０　だと、　Ｆ_ｘｘ（ａ，ｂ）ｈ²＋２Ｆ_ｘｙ（ａ，ｂ）ｈｋ＋ Ｆ_ｙｙ（ａ，ｂ）ｋ²　は定符号とな
　り、点Ｐの近くには曲線上の点はない。


　特異点の具体例をあげて、その感覚を磨いておこう。

例（結節点）　ｒ²＝８ｃｏｓ２θ　すなわち、　（ｘ²＋ｙ²）²＝８（ｘ²−ｙ²）

　　この曲線は、連珠形（レムニスケート）と言われる。（ → 参考 ： 「二葉線」 ）

　　　　

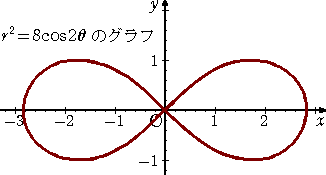
　　Ｆ（ ｘ ， ｙ ）＝（ｘ²＋ｙ²）²−８（ｘ²−ｙ²）　とおくと、

　　　　　Ｆｘ＝２（ｘ²＋ｙ²）・２ｘ−１６ｘ＝４ｘ（ｘ²＋ｙ²−４）＝０

　　　　　Ｆｙ＝２（ｘ²＋ｙ²）・２ｙ＋１６ｙ＝４ｙ（ｘ²＋ｙ²＋４）＝０

　　よって、原点（ ０ ， ０ ）で、曲線 Ｆ（ ｘ ， ｙ ）＝０ は特異点を持つ。

　ヘシアン　Ｈ＝Ｆ_ｘｘＦ_ｙｙ−Ｆ_ｘｙＦ_ｙｘ＝（１２ｘ²＋４ｙ²−１６）（４ｘ²＋１２ｙ²＋１６）−８ｘｙ・８ｘｙ

　において、　Ｈ（ ０ ， ０ ）＝−２５６＜０　なので、特異点は結節点である。

例（尖点）　　ｙ²＝ｘ⁴

　 　　　　　　

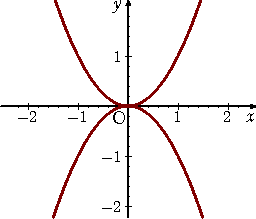
　　Ｆ（ ｘ ， ｙ ）＝ｘ⁴−ｙ²　とおくと、

　　　　　Ｆｘ＝４ｘ³＝０

　　　　　Ｆｙ＝−２ｙ＝０

　　よって、原点（ ０ ， ０ ）で、曲線 Ｆ（ ｘ ， ｙ ）＝０ は特異点を持つ。

　ヘシアン　Ｈ＝Ｆ_ｘｘＦ_ｙｙ−Ｆ_ｘｙＦ_ｙｘ＝１２ｘ²・（−２）−０＝−２４ｘ²

　において、　Ｈ（ ０ ， ０ ）＝０　なので、特異点は尖点である。

例（孤立点）　　ｘ⁴＋ｙ⁴−６ｘ²−８ｙ²＝０

　 　　　　　　 　　

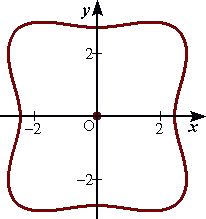
　　Ｆ（ ｘ ， ｙ ）＝ｘ⁴＋ｙ⁴−６ｘ²−８ｙ²　とおくと、

　　　　　Ｆｘ＝４ｘ³−１２ｘ＝４ｘ（ｘ²−３）＝０

　　　　　Ｆｙ＝４ｙ³−１６ｙ＝４ｙ（ｙ²−４）＝０

　　よって、原点（ ０ ， ０ ）で、曲線 Ｆ（ ｘ ， ｙ ）＝０ は特異点を持つ。

　ヘシアン　Ｈ＝Ｆ_ｘｘＦ_ｙｙ−Ｆ_ｘｙＦ_ｙｘ＝（１２ｘ²−１２）（１２ｙ²−１６）−０

　　　　　　　　　　　　　　　　　　　＝（１２ｘ²−１２）（１２ｙ²−１６）

　において、　Ｈ（ ０ ， ０ ）＝１９２＞０　なので、特異点は孤立点である。


　包絡線の計算で注意しなければいけないことは、

　　　Ｆ（ ｘ ， ｙ ， ｍ ）＝０　、Ｆ_ｍ（ ｘ ， ｙ ， ｍ ）＝０　

　　　または、

　　　Ｆ（ ｘ ， ｙ ， α ， β）＝０　、Ｇ（ α ， β ）＝０　、　Ｆ_αＧ_β−Ｇ_αＦ_β＝０

からパラメーター　ｍ　または、α，βを消去して得られる方程式によって定義される曲線
には、包絡線の他に、包絡線上にはない他の点が含まれることもありうるという点だあろ
う。

　すなわち、パラメータを消去して得られる曲線は、

　　　　　包絡線　および　曲線の特異点の軌跡

を含む。

　この事情は、先に述べた視点で考えれば当然のことと理解できる。すなわち、

　　ごく近い位置にある２つの曲線の交点の極限点として、包絡線上の点を捉えたが、
　特異点、例えば、結節点Ｐの近くでも２つの曲線の交点Ｑが存在する。
　　このとき、 Ｑ → Ｐ なので、パラメータを消去して得られる曲線に点Ｐが含まれる
　ことになる。

　したがって、特異点を１つも持たない曲線群の包絡線は、パラメータを消去して得られる
曲線そのものであると言える。

　次に、包絡線の話題の応用として、縮閉線と伸開線の話題を取り上げたい。

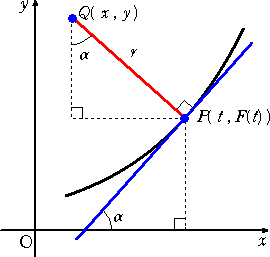
　曲線　ｙ＝Ｆ（ｘ）　において、２点Ｐ（ ａ ， Ｆ（ａ） ）、Ｑ（ ａ＋ｈ ， Ｆ（ａ＋ｈ） ）を考える。
２点 Ｐ 、Ｑ において接線を引き、２接線の ｘ 軸の正の向きとのなす角をそれぞれ、
　　　θ　、　θ＋Δθ　　（Δθは、点Ｐ における接線から点Ｑにおける接線へ測った角）
とする。

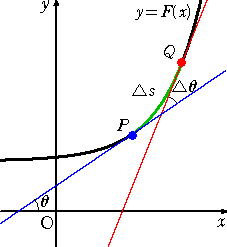　　　このとき、点Ｐから歩き始めて道のりΔｓだけ歩い
　　て点Ｑに達するとき、Δθは感覚的に曲線の曲がり
　　具合を示す。

　　　そこで、単位長さ当たりの曲がり具合

　　　　　

　　　を点Ｐにおける曲線の曲率（ｃｕｒｖａｔｕｒｅ）と言う。

　　　曲率の絶対値の逆数は、曲率半径と言われる。




定　理　　曲線　ｙ＝Ｆ（ｘ）　上の点Ｐ（ ａ ， Ｆ（ａ） ）における曲率 κ は、

　　　　　　　　　

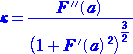
（略証）　　ｔａｎθ＝Ｆ’（ａ）　、　ｔａｎ（θ＋Δθ）＝Ｆ’（ａ＋ｈ）　なので、平均値の定理より、

　　　　　　Δθ＝ｔａｎ^-1Ｆ’（ａ＋ｈ）−ｔａｎ^-1Ｆ’（ａ）＝ｈＦ”（ｃ）/（１＋Ｆ’（ｃ）²）

　　　　　　　　　　　　　ただし、　ｃ は、ａ　と　ａ＋ｈ　の間の数

　　　　また、　Δｓ＝ｈ（１＋Ｆ’（ｄ）²）^1/2　　　ただし、　ｄ は、ａ　と　ａ＋ｈ　の間の数

　　　　　よって、　（Δθ）/（Δｓ）は、　ｈ→０　のとき、κ に近づく。　（略証終）

例　原点中心、半径 ｒ の円では、その曲率の絶対値は、　１/ｒ　に等しい。

　　実際に、　ｘ²＋ｙ²＝ｒ²　より、　２ｘ＋２ｙｙ’＝０　なので、　ｙ’＝−ｘ/ｙ　、ｙ”＝−ｒ²/ｙ³
　このとき、　曲率κの絶対値は、　１/ｒ　となる。　　　　　　　　　　　　　　　　　　　　　　　　　　　　

例　曲線 ｙ＝ｌｏｇ ｘ　の曲率半径の最小値を求めよ。
曲率半径を ｒ とすると、　ｙ＝１/ｘ　、　ｙ”＝−１/ｘ2　より、
	このとき、		なので、
		のとき最小で、最小値は、

　特別な場合として、原点で ｘ 軸に接する曲線の曲率 κ は、

　　　　　　　　

で与えられる。

　実際に、　曲線　ｙ＝Ｆ（ｘ）　が、原点で ｘ 軸に接するので、　Ｆ’（０）＝０

　　　　よって、原点における曲率 κ＝Ｆ”（０）　である。

　　ところで、ロピタルの定理より、

　　　　

　　よって、上記の公式が成り立つ。


例　ｙ＝ｘ²　は、原点において、ｘ 軸に接する。

　　したがって、　ｙ＝ｘ²　から、　ｙ’＝２ｘ　、　ｙ”＝２　なので、　κ＝２　となる。

　このとき、曲率半径は、１/２　で、曲率円の中心の座標は、（ ０ ， １/２ ）となる。

　　　　　　　　　

　上図からも気がつくように、曲率円は曲線の凹の側にとる。このときの曲率円の中心は
曲率中心と言われる。

　上記の放物線　ｙ＝ｘ²　の原点に対する曲率中心は、（ ０ ， １/２）で、この点は、放物線
の原点における法線上にある。

　曲率中心の軌跡のことを、縮閉線といい、もとの曲線のことを伸開線と言う。

　曲線　ｙ＝Ｆ（ｘ）上の点Ｐ（ ｔ ， Ｆ（ｔ） ）に対して、縮閉線上の点Ｑ（ ｘ ， ｙ ）の座標は、

　　　　　　　　

で与えられる。

　実際に、点Ｐにおいて、法線と接線は垂直なので、　ｙ’・｛ ｙ−Ｆ（ｔ）｝/（ｘ−ｔ）＝−１

　　また、　ＰＱは曲率半径なので、　（ｘ−ｔ）²＋｛ ｙ−Ｆ（ｔ）｝²＝（１＋ｙ’²）³/ｙ”²

　　これより、　｛ ｙ−Ｆ（ｔ）｝²＝（１＋ｙ’²）²/ｙ”²

　　曲率中心は曲線の凹の側にとるので、 ｙ−Ｆ（ｔ）　と　ｙ”　は同符号。

　　よって、　ｙ−Ｆ（ｔ）＝（１＋ｙ’²）/ｙ”　より、　ｙ＝Ｆ（ｔ）＋（１＋ｙ’²）/ｙ”

　　このとき、　ｘ＝ｔ−ｙ’｛ ｙ−Ｆ（ｔ） ｝＝ｔ−ｙ’（１＋ｙ’²）/ｙ”　である。

例　ｙ＝ｘ²　上の点Ｐ（ ｔ ，ｔ² ）に対して、　ｙ’＝２ｔ　、　ｙ”＝２　なので、

　　縮閉線上の点Ｑ（ｘ ， ｙ ）の座標は、

　　　ｘ＝ｔ−２ｔ（１＋４ｔ²）/２＝−４ｔ³　　　ｙ＝ｔ²＋（１＋４ｔ²）/２＝３ｔ²＋１/２

　　したがって、放物線　ｙ＝ｘ²　の縮閉線のグラフを図示すると、

　　　

　上図において、縮閉線は、点（ ０ ， １/２）で特異点（尖点）を持つことが分かる。

平成２１年１月９日付けで、Ｓ（Ｈ）さんは次の問題を提起された。

　曲線 ｙ＝ｘ⁴　の法線群に対する包絡線の方程式を多様な発想で求めよ。また、放
物線 ｙ＝ｘ²　との相違点に留意して特異点を求め、特異点と曲線 ｙ＝ｘ⁴　との最短
距離を求めよ。

　この問題提起を意識しながら、曲線 ｙ＝ｘ⁴　の縮閉線の方程式を求めたいと思う。

　　ｙ＝ｘ⁴　上の点Ｐ（ ｔ ， ｔ⁴ ）に対して、　ｙ’＝４ｔ³　、　ｙ”＝１２ｔ²　なので、

　　縮閉線上の点Ｑ（ｘ ， ｙ ）の座標は、

　　　ｘ＝（２ｔ−１６ｔ⁷）/３　　　ｙ＝（２８ｔ⁶＋１）/（１２ｔ²）

　　したがって、放物線　ｙ＝ｘ⁴　の縮閉線のグラフを図示すると、

　　　

　上図において、縮閉線は、２個の特異点（尖点）を持つことが分かる。（ｔ≒±０．５？）

　Ｓ（Ｈ）さんのアドバイスと上図を鑑みると、上記で求めた縮閉線（曲率中心の軌跡）は、
与えられた曲線の法線群の包絡線と一致していることに気がつく。

　実は、次の定理が成り立つ。

定　理　　曲線　ｙ＝Ｆ（ｘ）　上の点Ｐ（ ｔ ， Ｆ（ｔ） ）における法線は、その曲率中心

　　　　Ｑ（ｘ ， ｙ ）で、縮閉線に接する。さらに、縮閉線上の２点間の弧の長さは、

　　　　その両端における曲率半径の差に等しい。

（証明）　
　　　　　　　　

　　より、
　　　　　　　　　

　　よって、
　　　　　　　

　　このことから、曲率中心Ｑにおける接線の傾きと点Ｐにおける法線の傾きが一致する
　ことが分かる。

　　また、縮閉線上の２点間の弧の長さを ｓ とすると、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

　である。さらに、　（ｘ−ｔ）²＋｛ ｙ−Ｆ（ｔ） ｝²＝ｒ²　　（　ただし、ｒ は曲率半径　）　の両辺を
　ｔ で微分して、
　　　　　　　　　　
　ここで、
　　　　　　　　
　を代入して、
　　　　　　　　　　
　また、法線の方程式から、
　　　　
　これらの２式より、
　　　　　　　　　　　　　　　　　
　なので、結局
　　　　　　　　　　

　が成り立つ。そこで、曲率半径が増加するように弧の長さを測ることにすると、

　　　　　　　　　　

　すなわち、　ｓ＝ｒ＋（定数）　である。

　　このとき、縮閉線上の２点間の弧の長さは、その両端における曲率半径の差に等しい

　と言える。　（証終）

　この定理から、縮閉線は、曲率中心の軌跡と言っても良いし、または、曲線の法線群の
包絡線と言っても良いことになる。さらに、もとの曲線が伸開線と呼ばれる理由も頷ける。

　伸開線と縮閉線との関係を図示すると下図のようになるであろうか．．．。

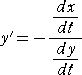
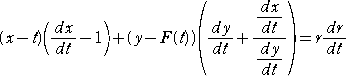
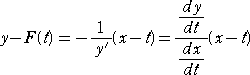
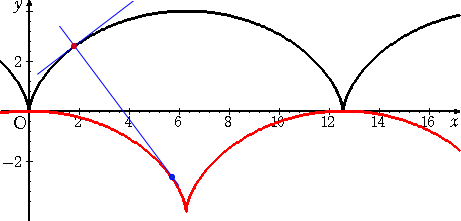
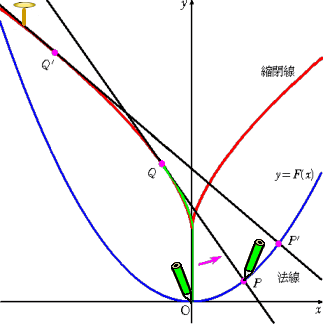　　　　左図において、縮閉線上の任意

　　　の点で紐を画鋲で止め、縮閉線に

　　　沿わせた紐の先端Ｏを鉛筆に固定

　　　して紐をピンと張ったまま移動させ

　　　る。このとき、鉛筆の先端Ｐは曲線

　　　ｙ＝Ｆ（ｘ）　上にあり、弧ＱＱ’の長さ

　　　は、ちょうど、　Ｐ’Ｑ’−ＰＱ　に等し

　　　い。

　　（まさしく、縮閉線に巻き付けた紐がちょ
　　　うど解けていくように．．．。）



　上記の定理で述べたことは、次のように直観的に考えた方が、す〜っと頭の中に刻まれ
るかもしれない。

　曲線 ｙ＝Ｆ（ｘ） 上の２点Ｐ、Ｐ’はごく近い場所にあるものとする。２本の法線ＰＱ、Ｐ’Ｑ’
の交点をＲとおく。

　このとき、△ＲＰＰ’は、ほとんど２等辺三角形の形をしているので、　ＲＰ≒ＲＰ’　として
よい。

　また、縮閉線上の２点Ｑ、Ｑ’を結ぶ弧の長さ ｓ について、　ｓ≒ＲＱ＋ＲＱ’　としてよい。

　よって、　ｓ≒ＲＱ＋ＲＱ’＝（ＲＰ−ＰＱ）＋（Ｐ’Ｑ’−ＲＰ’）≒Ｐ’Ｑ’−ＰＱ

（コメント）　上記の定理のスゴイところは、「２点Ｐ、Ｐ’はごく近い場所にある」と仮定しなく
　　　　　　ても、キッチリと「　ｓ＝Ｐ’Ｑ’−ＰＱ　」が成り立つことですね！

　さらに、この定理から気がつくことは、曲線 ｙ＝Ｆ（ｘ） に対して縮閉線はただ一つ存在す
るが、逆に、与えられた曲線を縮閉線として持つ伸開線は、無数に存在しうるということだ。

　縮閉線の媒介変数表示を見れば、第１次導関数や第２次導関数が含まれるので、この
ことは自然に納得されるし、上図を見ても、紐の長さを変えれば、また違った曲線が得ら
れるだろうことは十分推測される。

　種々の曲線に対して、興味深い縮閉線の幾つかを計算してみよう。

例　楕円
　　　　　　　　

　　　に対して、その縮閉線の方程式は、（ α ， β ）を楕円上の点として、

　　　α²＋９β²＝９　のとき、法線群 ９βｘ−αｙ−８αβ＝０ の包絡線の方程式

　　　に一致する。

　　　　そこで、　Ｆ（ ｘ ， ｙ ， α ， β ）＝９βｘ−αｙ−８αβ　、

　　　　　　　　　　Ｇ（α，β）＝α²＋９β²−９

　　　とおくと、

　　　　Ｆ_αＧ_β−Ｇ_αＦ_β＝（−ｙー８β）（１８β）−（２α）（９ｘ−８α）＝０　より、

　　　　　　　９β（ｙ＋８β）＋α（９ｘ−８α）＝０

　以上から、

　　　連立方程式　９αｘ＋９βｙ＝８α²−７２β²　、　９βｘ−αｙ＝８αβ

　が得られる。　これを解いて、

　　　　８１ｘ＝８α³　、ｙ＝−８β³　となる。

　これらを、α²＋９β²＝９　に代入して、
　　　　　　　　　　　　　　　　　　　　　　　　

　このグラフを図示すると、下図のようになる。

　　　　　　

（コメント）　何となく宇宙の神秘を眺めているような気分にさせてくれますね！

　曲線　ｙ＝Ｆ（ｘ）　上の点Ｐ（ ｔ ， Ｆ（ｔ） ）における法線上の曲率中心Ｑ（ｘ ， ｙ ）の座標は、

　　　　　　　　　　

により与えられた。さらに、このときの、曲率 κ は、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　
であった。

　それでは、曲線が　Ｘ＝φ（ｔ）　、　Ｙ＝ψ（ｔ）　と媒介変数表示されている場合の曲率中
心の座標と曲率は、どのように表されるだろうか？興味あることなので計算してみた。

　結論から言えば、

　　　　　　　

　　　

が成り立つ。

　これらは、
　　　　　　　　ｙ’＝ψ’/φ’　　、　　ｙ”＝（φ’ψ”−φ”ψ’）/（φ’）³

などの媒介変数表示の場合の微分の公式から明らかだろう。

例　サイクロイド　　Ｘ＝ｒ（ ｔ−ｓｉｎ ｔ ） 、　Ｙ＝ｒ（ １−ｃｏｓ ｔ ）　に対して、

　　　　Ｘ’＝ｒ（ １−ｃｏｓ ｔ ）　、　Ｙ’＝ｒ・ｓｉｎ ｔ　、　Ｘ”＝ｒ・ｓｉｎｔ　、　Ｙ”＝ｒ・ｃｏｓ ｔ

　　なので、　Ｘ’Ｙ”−Ｘ”Ｙ’＝ｒ（ １−ｃｏｓ ｔ ）・ｒ・ｃｏｓ ｔ−ｒ・ｓｉｎｔ・ｒ・ｓｉｎ ｔ

　　　　　　　　　　　　　　　　＝ｒ²（ ｃｏｓ ｔ −１ ）

　　　また、　Ｘ’²＋Ｙ’²＝ｒ²（ １−ｃｏｓ ｔ ）²＋（ ｒ・ｓｉｎ ｔ ）²＝２ｒ²（ １−ｃｏｓ ｔ ）

　　よって、縮閉線上の点（ ｘ ， ｙ ）は、

　　　　ｘ＝ｒ（ ｔ＋ｓｉｎ ｔ ）　　、　ｙ＝−ｒ（ １−ｃｏｓ ｔ ）

　　ここで、　ｔ＝π＋θ　と置換すれば、

　　　　ｘ＝ｒ（ θ−ｓｉｎ θ ）＋πｒ　　、　ｙ＝−ｒ（ １＋ｃｏｓ θ ）＝ｒ（ １−ｃｏｓ θ ）−２ｒ

　　となり、やはり、サイクロイドである。

　　　ｒ＝２　として、そのグラフ達を眺めておこう。

　　　

（コメント）　もとのサイクロイドのどの部分が新しいサイクロイドのどの部分に対応するのか
　　　　　　想像するのも楽しいですね！

　曲線の方程式を扱う場合、媒介変数表示の場合を押さえておけば十分だろうが、極座標
による場合も時として必要になるので、公式として、まとめておこう。

　極座標で曲線の方程式が、　Ｒ＝Ｆ（θ）　と表されるものとする。

　このとき、直交座標系に変換して、曲線の方程式が、

　　　　　　　Ｘ＝Ｆ（θ）ｃｏｓθ　、　Ｙ＝Ｆ（θ）ｓｉｎθ

と媒介変数表示されることに気がつけば、後は容易だろう。

　結論から言えば、曲線上の点Ｐ（ Ｆ（θ）ｃｏｓθ ， Ｆ（θ）ｓｉｎθ ）における法線上の曲率

中心Ｑ（ｘ ， ｙ ）の座標と曲率 κ について、

　　　　　　　　　　　

　　　　　　　　　　　

　　　　　　　　　　　
が成り立つ。

　　実際に、　Ｘ’＝Ｆ’ｃｏｓθ−Ｆｓｉｎθ　、　Ｙ’＝Ｆ’ｓｉｎθ＋Ｆｃｏｓθ　で、さらに、

　　　Ｘ”＝Ｆ”ｃｏｓθ−Ｆ’ｓｉｎθ−Ｆ’ｓｉｎθ−Ｆｃｏｓθ＝Ｆ”ｃｏｓθ−２Ｆ’ｓｉｎθ−Ｆｃｏｓθ

　　　Ｙ”＝Ｆ”ｓｉｎθ＋Ｆ’ｃｏｓθ＋Ｆ’ｃｏｓθ−Ｆｓｉｎθ＝Ｆ”ｓｉｎθ＋２Ｆ’ｃｏｓθ−Ｆｓｉｎθ

　このとき、

　　　Ｘ’²＋Ｙ’²＝（Ｆ’ｃｏｓθ−Ｆｓｉｎθ）²＋（Ｆ’ｓｉｎθ＋Ｆｃｏｓθ）²＝Ｆ²＋Ｆ’²

　　　Ｘ’Ｙ”−Ｘ”Ｙ’＝（Ｆ’ｃｏｓθ−Ｆｓｉｎθ）（Ｆ”ｓｉｎθ＋２Ｆ’ｃｏｓθ−Ｆｓｉｎθ）

　　　　　　　　　　　　　　　　　−（Ｆ”ｃｏｓθ−２Ｆ’ｓｉｎθ−Ｆｃｏｓθ）（Ｆ’ｓｉｎθ＋Ｆｃｏｓθ）

　　　　　　　　　　　＝Ｆ²＋２Ｆ’²−ＦＦ’

　となり、これらの結果を媒介変数表示の場合の公式に代入して、上記の公式を得る。


例　心臓形　Ｒ＝Ｆ（θ）＝１＋ｃｏｓθ　に対して、Ｆ’＝−ｓｉｎθ　、Ｆ”＝−ｃｏｓθ　なので、

　　　Ｆ²＋Ｆ’²＝（１＋ｃｏｓθ）²＋ｓｉｎ²θ＝２（１＋ｃｏｓθ）

　　　Ｆ²＋２Ｆ’²−ＦＦ”＝（１＋ｃｏｓθ）²＋２ｓｉｎ²θ−（１＋ｃｏｓθ）（−ｃｏｓθ）

　　　　　　　　　　　　　＝３（１＋ｃｏｓθ）

　　よって、縮閉線上の点（ ｘ ， ｙ ）は、

　　　　　　ｘ＝（１＋ｃｏｓθ）ｃｏｓθ−（2/3）｛（１＋ｃｏｓθ）ｃｏｓθ−ｓｉｎ²θ｝

　　　　　　　＝（1/3）｛（１＋ｃｏｓθ）ｃｏｓθ＋２ｓｉｎ²θ｝

　　　　　　　＝（1/3）（１＋ｃｏｓθ＋ｓｉｎ²θ）

　　　　　　ｙ＝（１＋ｃｏｓθ）ｓｉｎθ−（2/3）｛（１＋ｃｏｓθ）ｓｉｎθ＋ｓｉｎθｃｏｓθ｝

　　　　　　　＝（1/3）｛（１＋ｃｏｓθ）ｓｉｎθ−２ｓｉｎθｃｏｓθ｝

　　　　　　　＝（1/3）（１−ｃｏｓθ）ｓｉｎθ

　ここで、　（１−ｃｏｓθ）ｃｏｓθ＝ｃｏｓθ−ｃｏｓ²θ＝−１＋ｃｏｓθ＋ｓｉｎ²θ　なので、

　　　　　　ｘ−２/３＝（1/3）（−１＋ｃｏｓθ＋ｓｉｎ²θ）＝（1/3）（１−ｃｏｓθ）ｃｏｓθ

　このとき、　求める曲線は、やはり（？）心臓形　Ｒ＝（１−ｃｏｓθ）/３　を、 ｘ 軸方向に

２/３　だけ平行移動したものになる。

　　　　　　　　　　　

　因みに、心臓形　ｒ＝１＋cosθ　の代数曲線表示は、

　ｘ＝ｒ・ｃｏｓθ　、　ｙ＝ｒ・ｓｉｎθ　で、　ｒ²＝ｘ²＋ｙ²　に注意して展開すると、

　　　ｘ⁴−２ｘ³＋２ｘ²ｙ²−２ｘｙ²＋ｙ⁴−ｙ²＝０

と与えられる。

　この形で縮閉線を求めることは、あまり得策ではないように感じるが、Ｓ（Ｈ）さんは、この
代数曲線表示の形での縮閉線の計算に何か意味を見い出されているようだ。

（コメント）　上記の２例では、偶然にも、サイクロイドの縮閉線はサイクロイド、心臓形の縮
　　　　　　閉線も心臓形と同種の曲線となった。この話題について、当ＨＰがいつもお世話
　　　　　　になっているＳ（Ｈ）さんも指摘されている。平成２１年１月１８日付けでＳ（Ｈ）さん
　　　　　　は、「縮閉線を反復して計算しても名前が不変な曲線の他の事例は？」と問いか
　　　　　　けておられる。

　　　　　　　そのような例としては、アステロイドが一番面白いのではないだろうか？

　　　　　　もとのアステロイド曲線を、　Ｘ＝ｃｏｓ³θ　、　Ｙ＝ｓｉｎ³θ　とおくと、

　　　　　　縮閉線上の点（ ｘ ， ｙ ）は、　ｘ＝ｃｏｓ³θ＋３ｓｉｎ²θｃｏｓθ

　　　　　　　　　　　　　　　　　　　　　　　　ｙ＝ｓｉｎ³θ＋３ｃｏｓ²θｓｉｎθ


　　　　　　　この曲線は、もとのアステロイド曲線を、原点中心に４５°回転し、２倍に相似
　　　　　　拡大した、やはり、アステロイド曲線である。

　　　　　　　　実際に、　ｘ−ｙ＝ｃｏｓ³θ＋３ｓｉｎ²θｃｏｓθ−ｓｉｎ³θ−３ｃｏｓ²θｓｉｎθ

　　　　　　　　　　　　　　　　　＝（ｃｏｓθ−ｓｉｎθ）³

　　　　　　　　　　　　　　ｘ＋ｙ＝ｃｏｓ³θ＋３ｓｉｎ²θｃｏｓθ＋ｓｉｎ³θ＋３ｃｏｓ²θｓｉｎθ

　　　　　　　　　　　　　　　　　＝（ｃｏｓθ＋ｓｉｎθ）³
　　　　　　　　　よって、
　　　　　　　　

　　　　　　　から明らかだろう。

　　　　　　　　　　　　　

　　　　　　構成法から、縮閉線を求める操作を繰り返しても、常にアステロイドが得られるこ
　　　　　とが見て取れる。（とても美しい結果ですね！）

　上記では、陽関数表示、媒介変数表示、極座標表示の各場合について、

　　　　曲線上の点Ｐ（ ｔ ， Ｆ（ｔ） ）における法線上の曲率中心Ｑ（ｘ ， ｙ ）の座標

を求めたが、それらの公式の構造を簡単化すれば、次のようになる。

　曲線上の点Ｐにおける接線が ｘ 軸の正の向きとなす角を α とし、曲率半径を ｒ とすると、

曲率中心Ｑ（ｘ ， ｙ ）の座標は、

　　　　　ｘ ＝ ｔ−ｒ・ｓｉｎα　　　、　　ｙ ＝ Ｆ（ｔ）＋ｒ・ｃｏｓα

と表される。

　ｔａｎα＝Ｆ’　なので、これより、　ｓｉｎα　、ｃｏｓα　は容易に求められるだろう。

　　　　　　　　　　

（コメント）　考えてみれば当たり前の公式だが、グチャグチャだった公式がスッキリして覚
　　　　　　えやすくなりましたね！

　上記の公式の簡単化について、Ｓ（Ｈ）さんから、ご教示を頂いた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２１年１月２１日付け）

　曲線　Ｘ＝φ（ｔ）、Ｙ＝ψ（ｔ） 上の点Ｐ（φ（ｔ），ψ（ｔ））に対する曲率中心をＱ（ｘ ， ｙ ）とす

ると、曲率中心は点Ｐにおける法線上にあり、しかも、その曲率中心の軌跡は、法線群の

包絡線として得られることを用いれば、

　　　無理して公式を覚えなくても、次の連立方程式

　　　ベクトルの内積　Ｆ（ｘ，ｙ，ｔ）＝（φ’，ψ’）・（ｘ−φ，ｙ−ψ）＝０　および

　　ｔ に関する偏導関数 Ｆ_ｔ（ｘ，ｙ，ｔ）＝０

　　を解くという基本方針に従えば、曲率中心の媒介変数表示が「自然に」導かれる

という。

　確かに、原理は上記の通りなのだが、曲線のいろいろな表示方法によって、その結果が
どのような形になるのかをまとめてみることも捨てがたいという気持ちもある。（ちょっと、受
験数学に毒されているかな？）

　実際に問題に対処する場合は、Ｓ（Ｈ）さんの仰るような基本方針で臨んで解決に至ると
いう流れも数学的に美しいものがある。

例　放物線 ｙ＝ｘ²　について、以前公式を用いて、その縮閉線を求めたが、上記の考えに
　　従えば、公式を特段意識することなく確かに自然に縮閉線の媒介変数表示が得られ、
　　感動的である。

　　　　ｙ＝ｘ²　の媒介変数表示は、　ｘ＝ ｔ 　、　ｙ＝ ｔ² 　なので、

　　　Ｆ（ ｘ ， ｙ ， ｔ ）＝（ １ ， ２ｔ ）・（ ｘ−ｔ ， ｙ−ｔ² ）＝ｘ−ｔ＋２ｔｙ−２ｔ³＝０

　　　このとき、　Ｆ_ｔ（ ｘ ， ｙ ， ｔ ）＝−１＋２ｙ−６ｔ²＝０

　　　これより、　ｙ＝３ｔ²＋１/２　で、　ｘ＝−４ｔ³　となり、縮閉線の媒介変数表示が自然に

　　導かれた。

（追記）　平成２１年１月２５日付け

　この包絡線の定義に関連して、平成２１年１月２４〜２５日付けで、当ＨＰがいつもお世話
になっているＳ（Ｈ）さんに、ご教示いただいた。Ｓ（Ｈ）さんに感謝します。

　包絡線を定義する場合、当初当ＨＰでは、

　　　「媒介変数 ｍ を含む曲線群 Ｆ＝｛ Ｆ（ ｘ，ｙ，ｍ ）＝０ ｝のすべてに接して、

　　　しかもその接点の軌跡となる曲線のことを、曲線群の包絡線」

としていたが、どうもこの定義は勇み足らしい。（冒頭の定義は修正済み）

　このことを考える材料として、Ｓ（Ｈ）さんから、次の問題に取り組むことを勧められた。

問　題　　曲線群　（ｘ−ｔ）²＋ｙ²＝１−ｔ²/４　の包絡線の方程式を求めよ。

（解）　Ｆ（ ｘ ， ｙ ， ｔ ）＝（ｘ−ｔ）²＋ｙ²−１＋ｔ²/４＝０　とおくと、

　　　　Ｆ_ｔ（ ｘ ， ｙ ， ｔ ）＝−２（ｘ−ｔ）＋ｔ/２＝０

　　　よって、　ｘ＝５ｔ/４　で、　ｙ²＝１−５ｔ²/１６＝１−ｘ²/５　より、

　　　包絡線は、　楕円　ｘ²/５＋ｙ²＝１　となる。

　　　

（コメント）　上記の計算で、今まで気づかなかったことに気づかされた。
　　　　　　曲線群の中には、例えば、　ｔ＝−２　すなわち　点（ −２ ， ０ ）も含まれるので、
　　　　　「曲線群のすべてに接する」という定義では、包絡線が存在しなくなってしまう。
　　　　　　この事情は、ｔ＝２　のときも同様である。

　上図で、点（ −２ ， ０ ）の周辺の様子をもう少し精査してみよう。　

　１−ｔ²/４≧０　より、−２≦ｔ≦２　なので、円の中心（ ｔ ， ０ ）は、点（ −２ ， ０ ）から ｘ 軸
に沿って、点（ ２ ， ０ ）まで移動する。この際、円の半径は０より単調に増加し、ｔ＝０　のとき
最大値 １ のあと単調減少に転じ、０に至る。

　このときの円と ｘ 軸との交点のうち左側の交点の ｘ 座標は、

　　　　　　

であり、右側の交点の ｘ 座標は、

　　　　　　

である。この両者のグラフを描くと、下図のようになっている。

　　　　　

　上図から、ｘ の取り得る値の範囲は、　で、円達の大きくなっていく様子が
想像できる。

　また、この範囲は、楕円　ｘ²/５＋ｙ²＝１　における ｘ の変域にも一致する。（当然！）

このことから、曲線群　（ｘ−ｔ）²＋ｙ²＝１−ｔ²/４　のうち、

　　　　、　

の範囲にある ｔ の値で定まる円達は、包絡線とは全く接していない。

　サッカーの試合でオフサイドの位置にあっても、プレーに全く関係していない場合はオフサイドになら
ないのと同じような感覚だ！

　この件について、平成２１年１月２７日付けで、当ＨＰがいつもお世話になっている、らすか
るさんは、「接しないような ｔ の値を除外して、ｔ の定義域を限定して『包絡線』と呼べば問題
ない」と述べておられる。

　そうすると、曲線群を最初から制限された形で与えればいいわけだが、それは数学の問題
として美しさが損なわれることに等しい。

　包絡線上の点は必ず、「ある」曲線上の点でもあり、かつ両者はその点で接するとすれば、
特別に曲線群を制限することもなくなると思うのだが．．．。

　包絡線の「包」は「包む」、「絡」は「絡む」ということで、曲線群を包み絡める存在として「包
絡線」がイメージできる。このページの冒頭の例のように、包絡線は、曲線群の通過領域の
境界線という認識に立てば、包絡線に接しない曲線が存在してもいいような．．．そんな雰囲
気。こう考えた方が私としては、包絡線のイメージがスッキリする。

例　曲線群　ｘ²＋ｙ²＝１＋ｔ²　の包絡線を求めよ。

　　ｔ を実数とすると、全ての曲線群に接するような曲線は存在しない。実際に、同心円の集
まりであることから明らかだろう。

　　　　　　

　しかし、包絡線は、現実のものとして確かに存在する。

　曲線群　ｘ²＋ｙ²＝１＋ｔ²　の通過領域の境界線という立場に立てば、包絡線は、原点中心
で半径１の円 ： ｘ²＋ｙ²＝１　である。

　この曲線は、包絡線を求める公式からも得られる。実際に、

　　Ｆ（ ｘ ， ｙ ， ｔ ）＝ｘ²＋ｙ²−１−ｔ²＝０　とおくと、Ｆ_ｔ（ ｘ ， ｙ ， ｔ ）＝−２ｔ＝０　なので、

両者を連立すれば、包絡線の方程式　ｘ²＋ｙ²＝１　が得られる。

　また、包絡線　ｘ²＋ｙ²＝１　上の任意の点（ ｘ ， ｙ ）に対して、その点を共有する曲線群
の中の曲線（ｘ²＋ｙ²＝１）が存在し、しかもその点で両者が接することは明らかである。

　したがって、曲線　ｘ²＋ｙ²＝１　は、曲線群　ｘ²＋ｙ²＝１＋ｔ²　の包絡線であると言える。

　この話題に関連して、平成２１年１月２８日付けで、Ｓ（Ｈ）さんから次の問題を解いてみる
ことを勧められたので解いてみた。

問　題　　曲線群　ｘ²/ｔ²＋ｙ²/（１−ｔ）²＝１　の包絡線の方程式を求めよ。

（解）　Ｆ（ ｘ ， ｙ ， ｔ ）＝（１−ｔ）²ｘ²＋ｔ²ｙ²−ｔ²（１−ｔ）²＝０　とおくと、

　　　　Ｆ_ｔ（ ｘ ， ｙ ， ｔ ）＝−２（１−ｔ）ｘ²＋２ｔｙ²−２ｔ＋６ｔ²−４ｔ³＝０

　　　連立方程式を解くと、　ｘ²＝ｔ³　、　ｙ²＝（１−ｔ）³　となる。

　　　　この計算から、包絡線が存在するためには、必然的に、　０＜ｔ＜１　と媒介変数 ｔ の

　　　値が制限される。

　　　　このとき、包絡線は、　アステロイド　となる。

　　　　　　　　

（コメント）　ｔ の制限がないと、曲線群はほとんど平面を埋め尽くしてしまって包絡線が見え
　　　　　　てこない。このように、ｔ に制限をつける方が包絡線の定義としてはベストだろうと
　　　　　　思った。


（追記）　平成２７年３月２日付け

　平成２７年度入試　東京大学　前期理系　で次のような問題が出題された。包絡線問題の
適当な練習となろう。

問題　正の実数ａに対して、座標平面上で次の放物線を考える。

　　Ｃ ： ｙ＝ａｘ²＋（１−４ａ²）/（４ａ）

　ａが正の実数全体を動くとき、Ｃの通過する領域を図示せよ。

（解）　両辺を４ａ倍して整理すると、　４（ｘ²−１）ａ²−４ａｙ＋１＝０

　題意より、このａに関する２次方程式が少なくとも一つ正の解を持つ条件を求めればよい。

　ｘ²−１＝０　すなわち、　ｘ＝±１　のとき、　４ａｙ＝１　が正の解を持つためには、ｙ＞０

　ｘ²−１≠０　のとき、　Ｆ（ａ）＝４（ｘ²−１）ａ²−４ａｙ＋１　とおくと、Ｆ（０）＝１＞０　なので、

　題意を満たすためには、

　ｘ²−１＞０　のとき、　放物線の軸について、　ｙ/｛２（ｘ²−１）｝＞０　すなわち、　ｙ＞０

　　　　　　　　　　　　　　判別式について、　４ｙ²−４（ｘ²−１）≧０　すなわち、　ｘ²−ｙ²≦１

　ｘ²−１＜０　のときは必ず正の解を持つ。

　以上から、Ｃの通過する領域を図示すれば下図を得る。







　　ただし、境界線は実線部分は含み、点（±１，０）
　および点線部分は含まない。







（コメント）　受験問題集に必ず載っているような典型問題で、合格のためには絶対落とせな
　　　　　　い問題ですね。それにしても河合塾や駿台予備校が発表している解答例は随分と
　　　　　　難しく解いているような雰囲気。その点が大いに気になりました。



　　　　　以下、工事中