ベルヌーイのレムニスケート曲線(1694年)といわれる。
極方程式は、
例 a=2 のとき、
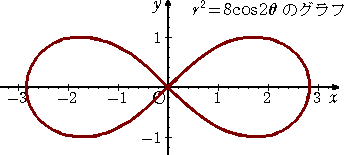
楕円や双曲線、放物線と同様に、2定点からの距離を用いて、連珠形を定義することが
できる。
連珠形(レムニスケート)は、
同一平面上の2定点F、F’までの距離の積が一定な平面上の点Pの描く曲線
である。レムニスケートは、ギリシャ語で「リボン状の」という意味である。
FF’=2a (ただし、a>0) とおく。F、F’を結ぶ線分の中点を座標平面の原点Oとする。
このとき、 F(a,0)、F’(−a,0) となる。
このとき、 OF・OF’=a2 となる。そこで、P(x,y)とおいて、 PF・PF’=a2 を満たす
曲線の方程式を求める。
PF2・PF’2=a4 なので、 {(x−a)2+y2}{(x+a)2+y2}=a4
これを展開して、 (x2−a2)2+2(x2+a2)y2+y4=a4
すなわち、 x4−2a2x2+a4+2(x2+a2)y2+y4=a4 より、
(x2+y2)2=2a2x2−2a2y2=2a2(x2−y2)
ここで、 x=r・cosθ 、y=r・sinθ とおくと、 x2+y2=r2 で、
x2−y2=r2(cos2θ−sin2θ)=r2cos2θ から、 r4=2a2r2cos2θ
r=0 は、r2=2a2cos2θ に含まれるので、媒介変数表示は、
r2=2a2cos2θ
となる。
例 上記の式変形から、曲線 (x2+y2)2=8(x2−y2)のグラフ
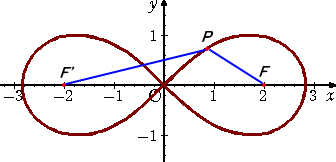
において、2定点F、F’の座標が、F(2,0)、F’(−2,0) であることが分かる。
連珠形において、線分FF’を両側に延長し、交点をA(b,0)、A’(−b,0)とすると、
bの値は、aの値を用いて表すことができる。
すなわち、 (b−a)(b+a)=a2 から、 b2=2a2 よって、 b=
連珠形 (x2+y2)2=2a2(x2−y2) と、原点を通る直線 y=mx を考える。
2式を連立して、 (1+m2)2x4=2a2(1−m2)x2 より、
x=0 、 x2=2a2(1−m2)/(1+m2)2
このとき、もし交点が存在すれば、 1−m2>0 すなわち、 −1<m<1 でなければ
ならない。
m≦−1 、m≧1 のときには、原点以外に交点は存在しない。
次に、連珠形 (x2+y2)2=2a2(x2−y2) の極値を計算しよう。
両辺を微分して、 2(x2+y2)(2x+2yy’)=2a2(2x−2yy’) から、
(x2+y2)(x+yy’)=a2(x−yy’)
ここで、 y’=0 とすると、 (x2+y2)x=a2x
x≠0 として、 x2+y2=a2
このとき、 x2−y2=a2/2 と連立して、 x=±(
図形的に考えて、極値を与える点は4個あり、その座標は、
(±(
である。
連珠形が囲む図形の面積Sを求めてみよう。
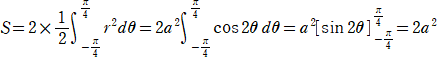
(コメント) 連珠形の定義式
なるんですね!とても美しい関係です。
連珠形の曲線の長さLを求めてみよう。こちらは、面積の場合と比べて、それほど美しいと
は思われない。
r2=2a2cos2θ の両辺をθについて微分して、 2rr’=−4a2sin2θ より、
rr’=−2a2sin2θ なので、 r2r’2=4a4sin22θ となる。
すなわち、 r’2=2a2sin22θ/cos2θ
よって、 r2+r’2=2a2/cos2θ である。
このとき、
ここで、 tanθ=t とおくと、 θ=0 のとき、t=0 、θ=π/4 のとき、t=1 で、
dθ/cos2θ=dt より、 dθ=dt/(1+t2)
また、 cos2θ=cos2θ(1−tan2θ)=(1−t2)/(1+t2) なので、
これは、楕円積分で、初等関数では表せないし、値を具体的に求めることは出来ない。
具体的な値は求まらないが、いろいろな表現を眺めてみよう。
t4=x とおくと、 t=0 のとき、x=0 、t=1 のとき、x=1 で、
4t3dt=dx より、 dt=(1/4)dx/x^(3/4) なので、
と書ける。これは、「特殊関数の応用」から、ベータ関数を用いて、
L=
と表される。ここで、ガンマ関数を用いて、
B(1/4,1/2)=Γ(1/4)Γ(1/2)/Γ(3/4)=
と書けることから、
L=
とも表せる。
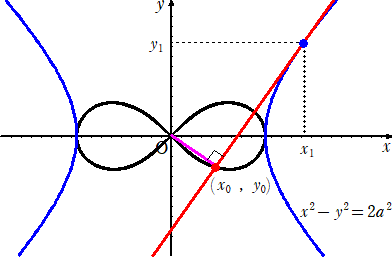
次に、直角双曲線との面白い関係を眺めることにしよう。
直角双曲線 x2−y2=2a2 上の点P(x1,y1)で接線Lを引く。x12−y12=2a2 である。
接線の傾きは、m1=x1/y1 なので、接線の方程式は、 y=(x1/y1)x−2a2/y1
接線上に点Q(x0,y0)をとると、原点OとQを結ぶ線分の傾きは、 m0=y0/x0
ここで、L⊥OQ の場合を考えると、m1・m0=−1 なので、 (x1/y1)(y0/x0)=−1
すなわち、 x1/y1=−(x0/y0) である。
このとき、 y0=(x1/y1)x0−2a2/y1=−(x0/y0)x0−2a2/y1 より、
(x02+y02)/y0=−2a2/y1 すなわち、 y1=−2a2y0/(x02+y02)
また、 x1=−(x0/y0)y1 より、 x1=2a2x0/(x02+y02)
これらを、x12−y12=2a2 に代入して、
4a4x02/(x02+y02)2−4a4y02/(x02+y02)2=2a2
よって、 (x02+y02)2=2a2(x02−y02) となる。
これは、点Qが連珠形 (x2+y2)2=2a2(x2−y2) 上の点であることを示す。
図示すれば、
上記では割と煩雑な計算をして結果を得たが、次のように簡便に計算する方法もある。
直角双曲線 x2−y2=2a2 上の点P(x1,y1)における接線の方程式は、
x1・x−y1・y=2a2 ・・・ (*)
この接線に垂直で原点を通る直線の方程式は、
y1・x+x1・y=0 ・・・ (**)
(*)×x+(**)×y より、 x1・(x2+y2)=2a2x
(**)×x−(*)×y より、 y1・(x2+y2)=2a2y
よって、 x12・(x2+y2)2−y12・(x2+y2)2=4a4x2−4a4y2 より、
(x12−y12)(x2+y2)2=4a4(x2−y2)
ここで、 x12−y12=2a2 なので、 (x2+y2)2=2a2(x2−y2)
以上から、直角双曲線 x2−y2=2a2 上の点Pにおける接線に原点Oから下ろした垂線
の足の軌跡の方程式は、連珠形 (x2+y2)2=2a2(x2−y2) となる。
上記では、直角双曲線 x2−y2=2a2 から連珠形 (x2+y2)2=2a2(x2−y2) が構成
されたが、逆に、連珠形 (x2+y2)2=2a2(x2−y2) から直角双曲線を構成してみよう。
連珠形 (x2+y2)2=2a2(x2−y2) 上の点P(x1,y1)に対して、OP・OQ=1 となる直線
OP上の点Q(x0,y0)を考える。これは、円 x2+y2=1 による反転である。
題意より、 (x1,y1)=k(x0,y0) (kは実数) とおける。
OP・OQ=1 より、 k√(x02+y02)・√(x02+y02)=1 なので、 k=1/(x02+y02)
このとき、 x1=x0/(x02+y02) 、y1=y0/(x02+y02)
これらを、(x12+y12)2=2a2(x12−y12) に代入して、
(x02+y02)2/(x02+y02)4=2a2(x02−y02)/(x02+y02)2
すなわち、 x02−y02=1/(2a2) となる。
以上から、点Q(x0,y0)は、直角双曲線 x2−y2=1/(2a2) 上の点である。
直角双曲線 x2−y2=1/(2a2) の焦点の座標は、G(1/a,0)、G’(−1/a,0) である。
連珠形 (x2+y2)2=2a2(x2−y2) の焦点の座標が、F(a,0)、F’(−a,0) であった
ことを考えると、当然ながら、
OG=1/OF 、OG’=1/OF’
が成り立つ。
例 a=2 のとき、連珠形と直角双曲線のグラフを描いてみよう。
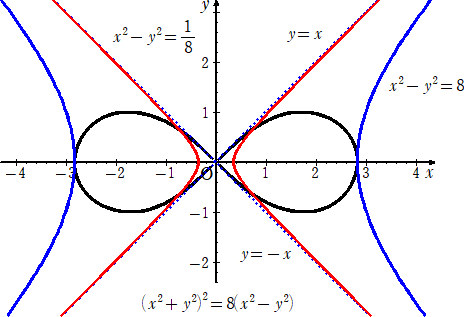
(追記) 令和4年5月26日付け
上記では、FF’=2a (ただし、a>0) とし、線分FF’の中点が原点Oのとき、
OF・OF’=a2 ということから、 PF・PF’=a2 を満たす点P(x,y)の軌跡を考え、その方
程式 (x2+y2)2=2a2(x2−y2) を導き、横にした8の字の連珠形のグラフを得た。
そこで、今度は、PF・PF’の値をいろいろ変えてみて、連珠形のグラフの変化の様子を鑑
賞してみよう。
a=2 として、 F(2,0)、F’(−2,0) とする。P(x,y)とおいて、 PF・PF’=c2 を満
たす曲線の方程式を求める。c=2 のときが、連珠形 (x2+y2)2=8(x2−y2) である。
PF2・PF’2=c4 なので、 {(x−2)2+y2}{(x+2)2+y2}=c4
これを展開して、 (x2−4)2+2(x2+4)y2+y4=c4
すなわち、 x4−8x2+16+2(x2+4)y2+y4=c4 より、
(x2+y2)2=8(x2−y2)+c4−16
となる。曲線の方程式に未知変数があるときのグラフ描画では、「GRAPES」が活躍する。
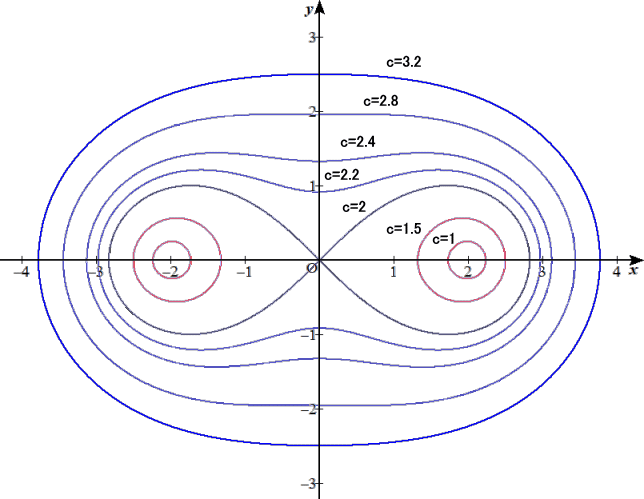
上図において、
c<2 のとき、 F(2,0)、F’(−2,0) の周りに卵形ができる。
c=2 のとき、 横にした8の字形
c>2 のとき、 原点での交わりは消失し、だんだんへこみも少なくなる。
(コメント) 何となく、お猿さんの顔に見えるのは私だけ...?
上記では、2焦点F(2,0)、F’(−2,0)を考えてグラフを描いたが、焦点がもう少しあっ
たら、どんな曲線となるのだろうか?興味は尽きない。
例 焦点F(2,0)、F’(−2,0)、G(0,2)、G’(0,−2)に対して、
PF・PF’・PG・PG’=c2
を満たす点P(x,y)の軌跡の方程式
{(x−2)2+y2}{(x+2)2+y2}{x2+(y−2)2}{x2+(y+2)2}=c4
を考え、そのグラフを描いてみた。
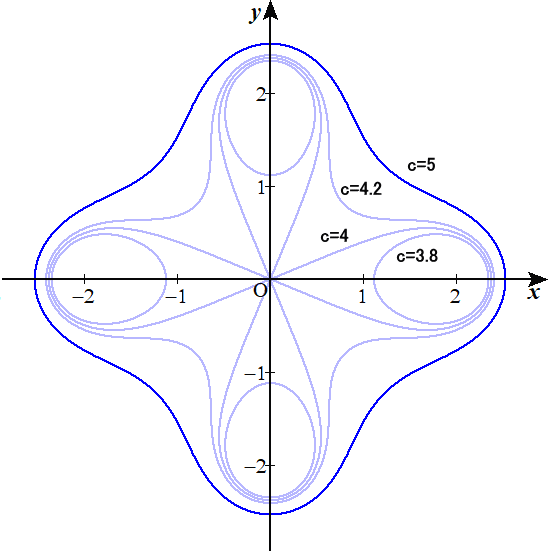
例 焦点F(2,0)、F’(−2,0)、G(0,2)、G’(0,−1)に対して、
PF・PF’・PG・PG’=c2
を満たす点P(x,y)の軌跡の方程式
{(x−2)2+y2}{(x+2)2+y2}{x2+(y−2)2}{x2+(y+1)2}=c4
を考え、そのグラフを描いてみた。
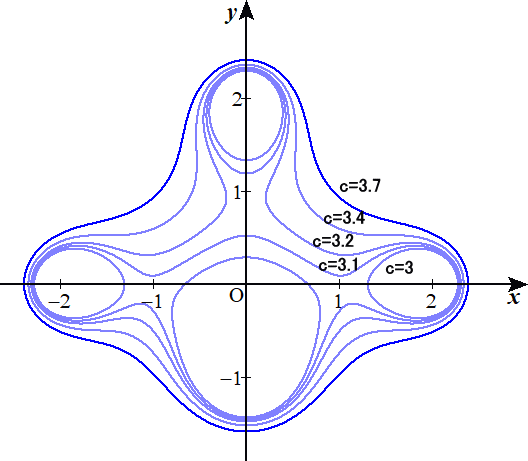
例 焦点F(2,0)、F’(−2,0)、G(0,2)、G’(0,−1)、H(1,1)、H’(−1,1)に対して、
PF・PF’・PG・PG’・PH・PH’=c2
を満たす点P(x,y)の軌跡の方程式
{(x−2)2+y2}{(x+2)2+y2}{x2+(y−2)2}{x2+(y+1)2}
×{(x−1)2+(y−1)2}{(x+1)2+(y−1)2}=c4
を考え、そのグラフを描いてみた。
(コメント) 焦点の個数や配置、c の値をいろいろ工夫すると、面白そうな図形が描けそう
ですね!
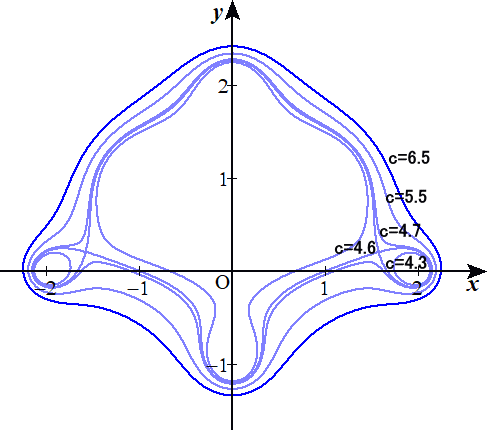
例 焦点F(3,0)、F’(−3,0)、G(0,1)、G’(0,0)、H(1,−1)、H’(−1,−1)、
I(2,3)、I’(−2,3)に対して、
PF・PF’・PG・PG’・PH・PH’・PI・PI’=c2
を満たす点P(x,y)の軌跡の方程式
{(x−3)2+y2}{(x+3)2+y2}{x2+(y−1)2}{x2+y2}{(x−1)2+(y+1)2}
×{(x+1)2+(y+1)2}{(x−2)2+(y−3)2}{(x+2)2+(y−3)2}=c4
を考え、そのグラフを描いてみた。
(コメント) カエルさんかな...?
(追記) kuiperbelt さんからのコメントです。(令和6年8月8日付け)
連珠形(レムニスケート)で、焦点の数と配置を変えたものをいくつか描画してみました。
焦点(2,0)、(-1,
c=1.5、1.9、2、2.1、2.5、3 の場合を描画してみると、
c<2 のとき、各焦点の周りに卵形ができる(赤色の曲線)。
c=2 のとき、原点で交わる三つ葉型(緑色の曲線)。
c>2 のとき、原点での交わりが消失し、cが大きくなると凹みが少なくなる(青色の曲線)。

焦点(2,0)、(1,
{(x-2)^2+y^2}{(x-1)^2+(y-
×{(x+1)^2+(y-
c=1.9、1.98、2、2.02、2.1、2.6 の場合を描画してみると、
c<2 のとき、各焦点の周りに卵形ができる(赤色の曲線)。
c=2 のとき、原点で交わる六つ葉型(緑色の曲線)。
c>2 のとき、原点での交わりが消失し、cが大きくなると凹みが少なくなる(青色の曲線)。

焦点(2,0)、((-1+
((-1-
{(x-2)^2+y^2}{(x-(-1+
×{(x-(-1-
c=1.9、1.98、2、2.03、2.1、2.6 の場合を描画してみると、
c<2 のとき、各焦点の周りに卵形ができる(赤色の曲線)。
c=2 のとき、原点で交わる五つ葉型(緑色の曲線)。
c>2 のとき、原点での交わりが消失し、cが大きくなると凹みが少なくなる(青色の曲線)。

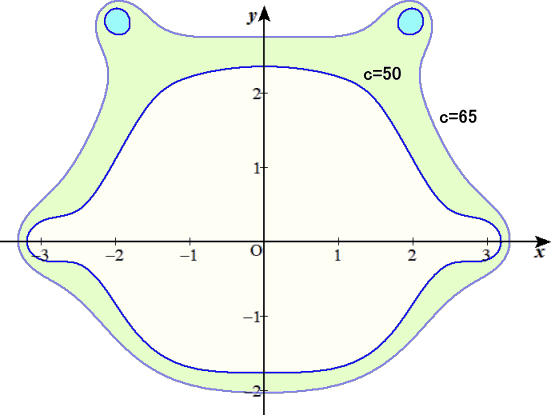
焦点(2,0)、(0,0)、(-2,0)で、{x^2+y^2}{(x-2)^2+y^2}{(x+2)^2+y^2}=c^6
c=1.3、1.4、(256/27)^(1/6)=1.4548…、1.5、1.6、1.7 の場合を描画してみると、
c<(256/27)^(1/6) のとき、各焦点の周りに卵形ができる(赤色の曲線)。
c=(256/27)^(1/6) のとき、(√(4/3),0),(-√(4/3),0)で交差する閉曲線(緑色の曲線)。
c>(256/27)^(1/6) のとき、交差が消失し、cが大きくなると凹みが少なくなる(青色の曲線)。

焦点(3,0)、(1,0)、(-1,0)、(-3,0)で、{(x-1)^2+y^2}{(x+1)^2+y^2}{(x-3)^2+y^2}{(x+3)^2+y^2}=c^8
c=1.6、
c<
c=
c=2 のとき、(
c>2 のとき、交差が消失し、cが大きくなると凹みが少なくなる(青色の曲線)。

以下、工事中!