
以前、大学の教養学部で学ぶ数学と言えば、「微分積分学」と「線形代数学」と相場が決
まっていた。将来、文系方面・理系方面の何れに進むにせよ、学問研究のバックボーンと
しての重要性から伝統的に教えられてきたように思う。
大学で学ぶ微分積分は、高校で学ぶ微分積分とは大きく異なる。決定的に違うところは、
実数論や極限論に習熟し、厳密な理論展開になる点だろう。しかも、扱える関数も膨大に
増える。
大学では、高校で学んだ微分積分の限界を知り、被積分関数が特異点を持つ場合や積
分区間が有界でない場合の処理を学び、ゆくゆくは、リーマン積分とは異なる発想の、測度
論に根ざしたルべーグ積分へと導かれる。
このような新しい積分法の出現は、方程式の解による基礎体の拡大に似ている。ルべー
グ積分では、リーマン積分では可積分でなかった関数が可積分となり、積分できる関数が
飛躍的に増大する。
この途中過程で、ベータ関数やガンマ関数などの特殊関数が目の前に表れ、幾ばくかの
性質を示して、消え去っていく。ベータ関数やガンマ関数については、そのような認識しか
なかった。
しかし、最近、当HPがいつもお世話になっている A’z さんから、ガンマ関数の魅力的な
応用例をご教示いただいた。今まで、ベータ関数やガンマ関数というと、具体的な値が分
かるのは本当に特殊な場合だけで、実際は、数値解析により所要の精度まで求める手法
が奔流であろうということで、あまり顧みなかった。
久しぶりに、ベータ関数やガンマ関数などの特殊関数の名前を聞き、懐かしく思った。記
憶を呼び戻すべく、基本に立ち返って、特殊関数の性質をまとめてみようと思う。
ベータ関数(Beta function)は、次式で定義される。
p>0 、q>0 に対して、
いくつか具体例を計算してみよう。
例
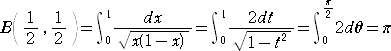
ガンマ関数(Gamma function)は、次式で定義される。
s>0 に対して、
ガンマ関数については、 Γ(1)=1 は明らかだが、次の例が最も有名であろう。
例
ここで、
とおくと、
よって、
ベータ関数は次のような性質を持つ。
(1) B( p , q )=B( q , p ) ・・・・・ 定義から明らかだろう。
(2) B( p , q )=B( p+1 , q )+B( p , q+1 )
1=x+(1−x) から明らかだろう。
(3) B( p+1 , q )={p/(p+q)}・B( p , q )
部分積分法により、 B( p+1 , q )=(p/q)・B( p , q+1)
ここで、 (1−x)q=(1−x)q-1・(1−x) を用いて、
B( p+1 , q )=(p/q)・{B( p , q )−B( p+1, q )}
よって、 {(p+q)/q}・B( p+1 , q )=(p/q)・{B(p , q ) より、
B( p+1 , q )={p/(p+q)}・B( p, q )
が成り立つ。
(4) B( p , q+1 )={q/(p+q)}・B( p , q )
(3)と同様にして示される。
(5) B( p , q )={(q−1)/p}・B( p+1 , q−1 )
(4)より、 B( p , q )={(q−1)/(p+q−1)}・B(p , q−1 )
(3)より、 B( p+1 , q−1 )={p/(p+q−1)}・B(p , q−1 ) なので、
B( p , q−1 )={(p+q−1)/p}・B( p+1 ,q−1 )
よって、 B( p , q )={(q−1)/p}・B( p+1 , q−1) が成り立つ。
(6) 自然数 m、n に対して、
(5)より、 B( m , n )={(m−1)/(m+n−1)}・B( m−1, n )
={(m−1)!n!/(m+n−1)!}・B(1 , n )
ここで、 B( 1 , n )={(n−1)/n}・B( 1 , n−1 )
={(n−1)!/n!}・B( 1 , 1 )
=(n−1)!/n!
よって、与式は成り立つ。
ガンマ関数は次のような性質を持つ。
(1) Γ( s+1 )=sΓ( s )
(2) 自然数 n に対して、 Γ( n ) = (n−1)!
(この性質から、ガンマ関数は自然数における階乗の一般化になっている。)
(1)と(2)の証明は、「階乗の一般化」を参照。
(3)
p , q が自然数ならば、ベータ関数の性質(6)とガンマ関数の性質(2)から100%自
明だろうが、同様の性質が、p、q>0 としても成り立つところがエライところである。
よく知られた証明をなぞっておこう。
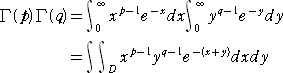
(ただし、 D={ ( x , y ) | x ≧0 、 y≧0 } とする。)
ここで、置換を施す。 x=u2 、y=v2 ( u ≧0 、 v≧0 )とおくと、
Jacobian は、 4uv より、 dxdy=4uvdudv
なので、 (← 参考:「重積分の計算」)
さらに、置換を施す。 u=r・cosθ 、v=r・sinθ ( r ≧0 、 0≦θ≦π/2 )とおくと、
Jacobian は、 r より、 dudv=rdrdθ
なので、
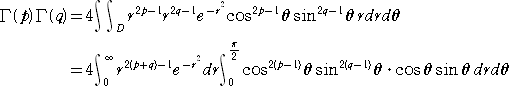
ここで、 r2 = x とおくと、 2rdr = dx より、
で、さらに、 cos2θ = x とおくと、 −2cosθsinθdθ=dx より、
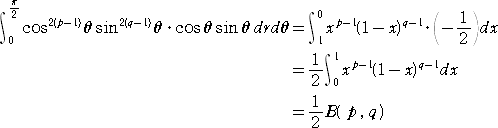
なので、
が成り立つ。
(コメント) 置換積分の手頃な練習問題ですね!でもこの証明方法を初めて考えた人はエ
ライです。多分初見では、まずどうしたらよいか途方に暮れてしまうようなタイプの
問題なので...。
(4)
(5)
(6)
この証明はすこぶる難しいが、この結果を用いると、
は直ちに得られる。
(追記) 令和7年10月21日付
次の東北大学 前期理系(2001)の問題は、ガンマ関数が出題の背景にある。
問題 (1) nを正の整数とする。t≧0 のとき、不等式 et>tn/n! が成り立つことを数
学的帰納法で示せ。
(2) 極限 Im=limt→∞∫0t xme-xdx (m=0、1、2、・・・) を求めよ。
(解)(1) n=1 のとき、 F(t)=et−t とおくと、 F’(t)=et−1
t≧0 のとき、F’(t)=et−1≧0 なので、F(t)は単調に増加する。F(0)=1>0 なので、
t≧0 のとき、F(t)>0 から、et>t が成り立つ。よって、n=1のとき、命題は成り立つ。
n=k(k≧1)のとき成り立つと仮定する。すなわち、et>tk/k!
n=k+1 のとき、 F(t)=et−tk+1/(k+1)! とおくと、 F’(t)=et−tk/k!>0
よって、F(t)は単調に増加し、F(0)=1>0 なので、t≧0 のとき、F(t)>0 すなわち、
et>tk+1/(k+1)!が成り立つ。よって、n=k+1のときも、命題は成り立つ。
以上から、すべての正の整数nに対して、 et>tn/n! が成り立つ。
(2) Jm=∫0t xme-xdx とおくと、m≧1 のとき、
Jm=[−xme-x]0t+m∫0t xm-1e-xdx=−tme-t+mJm-1
両辺を m!で割って、 Jm/m!=−tme-t/m!+Jm-1/(m−1)!
すなわち、 Jm/m!−Jm-1/(m−1)!=−tme-t/m! より、
Jm/m!−J0=−Σk=1m tke-t/k!
ここで、J0=∫0t e-xdx=[−e-x]0t=1−e-t なので、
Jm/m!=1−Σk=0m tke-t/k! すなわち、 Jm=m!(1−Σk=0m tke-t/k!)
ここで、(1)より、nを正の整数とする。t≧0 のとき、不等式 et>tn/n! が成り立つので、
tke-t/k!=tk+1e-t/(k+1)!・(k+1)/t<(k+1)/t
よって、 Σk=0m tke-t/k!<Σk=0m (k+1)/t=(m+1)(m+2)/2・(1/t) → 0 より、
Jm → m! すなわち、 Im=m! となる。 (終)
以下、工事中