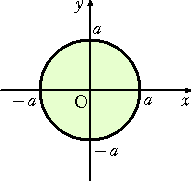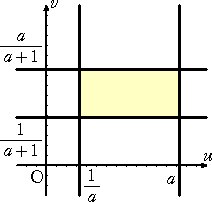重積分の計算 
高校では、1変数の関数の定積分を考えるが、唯一2変数の関数の定積分を教える機会
がある。それは、正規分布曲線の面積が 1 であることを示すときである。普通は結果だけ
示して通り過ぎるところであるが、雰囲気だけだったら説明しても害はないと思われる。
(→参考:無限の拡がりをもつ面積1の図形について)
大学で重積分を学んでいる頃、NHKだったか、中国の英才教育の実態を紹介する番組
が放映された。そこでは、小学生くらいの児童が難しそうな重積分の問題をスラスラ解いて
いた。それがとてもショックだったことを今でも覚えている。ある意味で、それは私自身の中
におけるスプートニク・ショックであった。もっとも日本でも公文式というものがあって、小学
生くらいで微分積分まで到達する者がいるらしいので、日本も捨てたものではない。
ある意味で、重積分に限らず微分積分の計算問題は、型にはまった定型的な問題が多
く比較的計算力がある方だったら、そこそこのレベルに到達することは可能である。
このページでは厳密さをある程度無視して雰囲気で重積分およびその応用を紹介しよう
と思う。高校生の方々に理解して欲しいので、予備知識も高校程度の微分積分とするつも
りである。
z=F(x,y) を領域 D を含むある範囲で定義された連続関数とする。
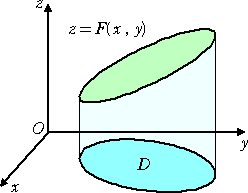 |
このとき、
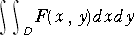
を、F(x,y) の D における定積分(二重積分)
と呼ぶ。
1変数の関数 y=f(x) (f(x)≧0)において、
 |
は、区間[a,b]を細分化し、無数の長方形の面積の和という意味があった。
(→詳しくは、区分求積法)
二重積分の式も、F(x,y)≧0 と仮定すれば、無数の直方体の体積の和という意味があ
る。
重積分の計算で、次の性質は基本的である。
| (1) |
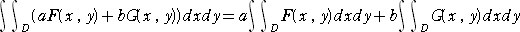 |
| (2) |
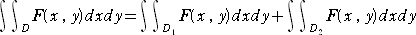 |
ただし、a、b は定数で、D は2つの有界閉領域 D1とD2に分けられるものとする。
体積ということを念頭におけば、上記の性質は明らかだろう。
特に、
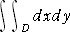
は、領域 D の面積を表す。
二重積分の計算では、次の公式が基本的である。
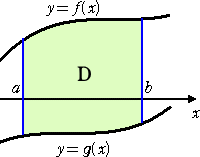
(逐次積分法)
右図のような領域 D において、
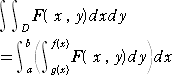
|
 |
例 正方形の面積
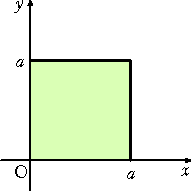 |
左図において、1辺が a の正方形の面積は、
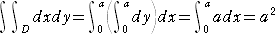
である。
|
逐次積分の計算例1
円の内部及び周 x2+y2≦1 を領域 D とするとき、
二重積分
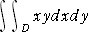
を計算せよ。
(解)
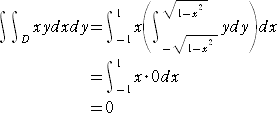 (終)
(終)
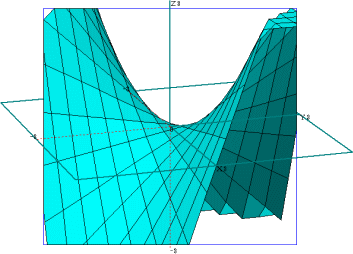
値が 0 になることは、グラフからも推察される。
逐次積分の計算例2
三角形の内部及び周 x+y≦1 、x ≧ 0 、 y ≧ 0 を領域 D とするとき、
二重積分
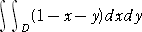
を計算せよ。
(解)
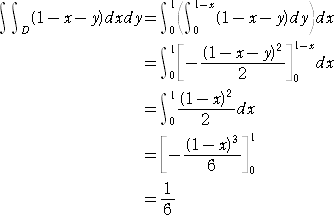 (終)
(終)
この二重積分は、実は下図の三角錐の体積を求めている。
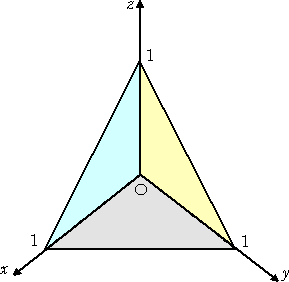 |
計算しようとする積分の意味が分かれば、
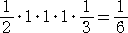
とした方が易しいだろう。
これは、1変数関数における
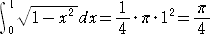
という計算(半径 1 の四分円の面積)に似
ている。
|
二重積分と同様にして、三重積分
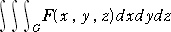
も定義される。
三重積分を用いれば、領域 G を x+y≦1 、x ≧ 0 、 y ≧ 0 、z ≦1−x−y として、
上図の三角錐の体積は、
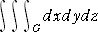
で表される。
1変数関数における定積分の計算で置換積分という方法により積分計算が容易になった
ことを覚えていると思う。
重積分(二重積分、三重積分、・・・)においても、その方法は重要である。
一変数関数の場合を復習しておこう。
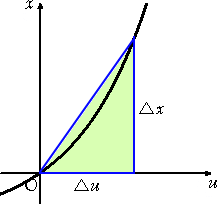
x=F(u) という置換を考える。このとき、u → u+Δu における x
の微小な変位を Δx と
おく。すなわち、 Δx = F(u+Δu)−F(u)
平均値の定理から、 F(u+Δu)−F(u) = Fu(v)Δu ( v は、u と u+Δu の間の値)
となる v が存在する。ただし、Fu(u) は、F(u)の u に関する微分を表すものとする。
したがって、 Δx = Fu(v)Δu が成り立つ。
Δu → 0 のとき、 Fu(v) → Fu(u) なので、
十分小さい Δu においては、 Fu(v) ≒ Fu(u)
と考えられる。そこで、上記の関係を、 dx = Fu(u)du と表すことにする。
この2つの関係式の違いは、下図を見れば明らかだろう。
 |
|
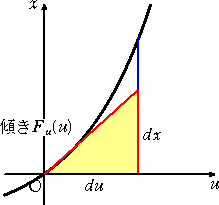 |
すなわち、Δx を近似するのに、十分小さいΔuにおいては、左図の三角形を用いないで
右図の三角形を用いようというわけである。
この話を、二変数の場合に拡張してみよう。
いま、 x = F( u , v ) という置換を考える。このとき、 u → u+Δu 、v
→ v+Δv に
おける x の微小な変位を Δx とおく。
すなわち、 Δx = F( u+Δu , v+Δv )−F( u , v )
上式は、
Δx = F( u+Δu , v+Δv )−F( u , v+Δv )+F( u , v+Δv )−F( u , v )
と変形される。
そこで、十分小さい Δu 、Δv においては、一変数関数の場合と同様にして、
dx=Fu( u , v )du+Fv( u , v )dv
と表される。ただし、Fu( u , v )、Fv( u , v )はそれぞれ u 、 v に関する微分である。
上記の関係式は簡単に、 dx=Fudu+Fvdv と表される。
同様にして、 y = G( u , v ) という置換であれば、 dy=Gudu+Gvdv なる。
ここで、 x = F( u , v ) 、y = G( u , v ) という置換を考えるとき、
dx=Fudu+Fvdv
dy=Gudu+Gvdv
という2つの式は何を意味するのだろうか?このことを考えると二変数関数における置換
積分の公式が得られる。
実は、上式は、ベクトル(du,dv)からベクトル(dx,dy)への一次変換の式とみなせる。
(新学習指導要領では「一次変換」という言葉はないので点の移動の式と思ってもよい。)
その変換を表す行列が
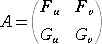
で、変換式は、
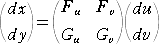
となる。行列 A の行列式は通常、函数行列式(Jacobian)と呼ばれ、
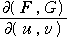
すなわち、
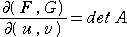
である。
突然、行列式が出てきた事情は、次の図を考えれば明らかだろう。
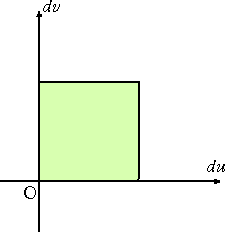 |
|
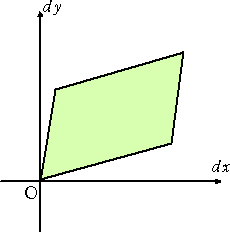 |
一次変換により、左図の長方形は右図の平行四辺形に移される。
このとき、長方形の面積 dudv と平行四辺形の面積 dxdy の間には、
dxdy=|det A|dudv
という関係が成り立つ。
これが、変数変換の公式である。
(専門家の方が読まれたら、ハチャメチャな論理展開にあきれかえられることだろう。一応その雰囲気で
も味わってもらおうという趣旨で厳密さは完璧に無視している!ので悪しからず。)
それでは、いくつかの代表的な置換の例を見てみることにしよう。
例1 x=r・cosθ 、 y=r・sinθ (r≧0) とおくとき、
xr=cosθ 、 xθ=−r・sinθ
yr=sinθ 、 yθ=r・cosθ
よって、
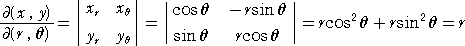
したがって、 dxdy=rdrdθ が成り立つ。
変数の変換の中で、この例1の置換が最も利用度が高い!
例2 x=a・u 、 y=b・v (a、b は正の定数) とおくとき、
dxdy=abdudv
が成り立つ。
例3 x+y=u 、 x=u・v (u>0、v>0) とおくとき、
dxdy=ududv
が成り立つ。
このような置換は、ただ闇雲に行うものではなく、確固たる目的がある。
逐次積分の計算例1では、 y の変域が少し煩雑であった。できるだけ逐次積分がやりや
すいように領域の変更を意識するのはおそらく自然な流れだと思う。
上記の例1〜3であげた置換により、特徴ある領域が、ごく単純な領域に変わる。
例1 の「 x=r・cosθ 、 y=r・sinθ (r≧0) 」という置換では、例えば、円の内部及
び周 x2+y2≦a2 (a>0) の領域 D が長方形の内部及び周 0≦r≦a、0≦θ≦2π と
いう領域に変わる。(長方形の領域の方が逐次積分しやすい!)
(注意) 変換式においては、長方形が円に変換されるという意味であるが...。
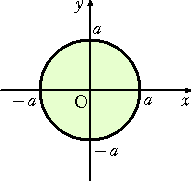 |
|
 |
この置換により、逐次積分の計算例1で行った計算は、次のようにもできる。
逐次積分の計算例1(置換による方法)
円の内部及び周 x2+y2≦1 を領域 D とするとき、
二重積分
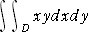
を計算せよ。
(解) x=r・cosθ、y=r・sinθ とおくと、 0 ≦ r ≦ 1 、
0 ≦ θ ≦ 2π で、 dxdy=rdrdθ
このとき、 xy=r2・sinθcosθ=(r2/2)sin2θ であるので、
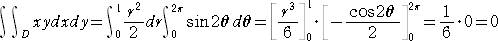 (終)
(終)
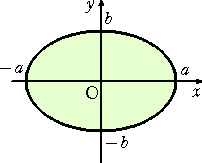
例2 の「 x=a・u 、 y=b・v (a、b は正の定数) 」という置換では、例えば、
楕円の内部及び周 x2/a2+y2/b2≦1 の領域 D が円の内部及び周 u2+v2≦1 とい
う領域に変わる。
例3 の「 x+y=u 、 x=u・v (u>0、v>0) 」という置換では、例えば、
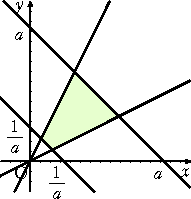
台形の内部及び周 1/a≦x+y≦a 、x/a≦y≦ax (a>0) の領域
D が長方形の内部
及び周 1/a≦u≦a 、1/(a+1)≦v≦a/(a+1) という領域に変わる。
これはまず、 1/a≦x+y≦a に x+y=u を代入して、 1/a≦u≦a
また、 y=u−x=u−uv 、 x=uv を x/a≦y≦ax に代入して、
uv/a≦u−uv≦auv より、u>0 に注意して、 v/a≦1−v≦av
よって、 v/a≦1−v より、 v≦a/(a+1) かつ、 1−v≦av より、 1/(a+1)≦v
すなわち、 1/(a+1)≦v≦a/(a+1) となる。
さて、読者のみなさんの、これまでの理解度を確認するための練習問題です。ぜひ、挑戦
してみてください。
練習問題 4つの放物線 y=2x2 、y=3x2 、y2=2x 、y2=3x で囲まれた図形 D
の面積を求めよ。
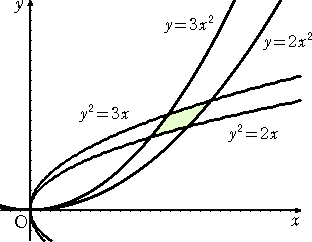
パッ!と見て、計算が大変そうな雰囲気...。
でも、次のように解けることを知ると楽しい!?
(解) x2=uy 、y2=vx (u>0、v>0) とおくと、 2x2≦y≦3x2 から、 2uy≦y≦3uy
y>0 としてよいので、 2u≦1≦3u すなわち、 1/3≦u≦1/2
同様にして、 (1/3)y2≦x≦(1/2)y2 から、 (1/3)vx≦x≦(1/2)vx
x>0 としてよいので、 (1/3)v≦1≦(1/2)v すなわち、 2≦v≦3
また、 x4=u2y2=u2vx より、 x3=u2v 同様にして、 y3=uv2
すなわち、変数の変換
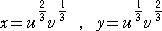
により、領域 D は、長方形の内部及び周 1/3≦u≦1/2 、2≦v≦3 という領域に変わる。
ところで、

なので、この変数変換の Jacobian は、
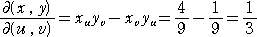
となる。
したがって、求める面積は、 (1/3)(1/2−1/3)(3−2)=1/18 である。 (終)
以下、工事中!


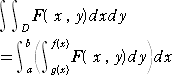

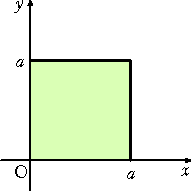
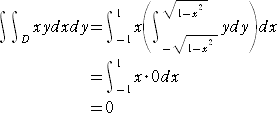 (終)
(終)
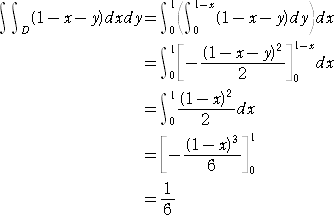 (終)
(終)