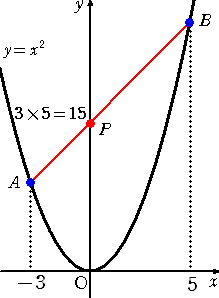
の2点を結ぶ直線が y 軸と交わる点を P とする。
この点Pの y 座標が、求める積の値を知らせる。
一般に、2点A( −a , a2 ) 、 B( b , b2 )を結ぶ
直線が y 軸と交わる点の y 座標が積 a×b の値を
示す。
実際に、2点を通る直線の方程式が、
y=(b−a)x+ab
であることから明らかだろう。
・ 放物線で掛け算 GAI 氏
放物線 y=x2 の思わぬ利用で、2つの数のかけ算の結果を、次のような作図で求めら
れることを知った。
例 3×5=15
 |
放物線上に2点A(−3,9) 、 B(5,25)を取り、こ の2点を結ぶ直線が y 軸と交わる点を P とする。 この点Pの y 座標が、求める積の値を知らせる。 一般に、2点A( −a , a2 ) 、 B( b , b2 )を結ぶ 直線が y 軸と交わる点の y 座標が積 a×b の値を 示す。 実際に、2点を通る直線の方程式が、 y=(b−a)x+ab であることから明らかだろう。 |
生徒達に、このグラフを書かせることはしばしばあるが、このグラフでこのかけ算をやら
せるとまた違った見方ができるだろうと感じた。私にとって、このグラフは今まで何度も目
にしてきたにも関わらず、計算での確認をとるまでは気がつかなかった。
放物線での掛け算は、「123×45」のような場合でも、2点 A(−1.23,1.232) 、
B(4.5,4.52)を結ぶ直線が y 軸と交わる点( y 切片)を読み取り、これを、1000倍
すればよい。
すなわち、 −10<x<10 でのグラフさえ準備しておけば、どんな桁数での積の値でも
計算尺よろしく算出できる。
この現象をコンピュータを利用して表現(グラフィック的に見せる!)できたら、無味乾燥
と大方の人が感じるグラフがもう少し身近な道具として存在することを知らせることができ
るのではないだろうか。
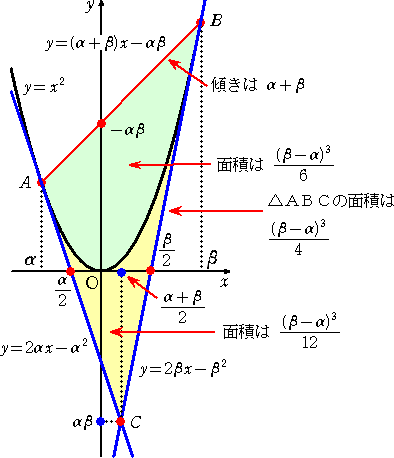
(塾長より、補足) 放物線上の2点に関わる直線には、いろいろな数が見て取れますね!