| 媒介変数表示は、 | |
この曲線は、円をX軸方向、または、Y軸方向に一定倍率で、拡大・縮小することにより得られる。
![]() の場合と
の場合と ![]() の場合がある。
の場合がある。
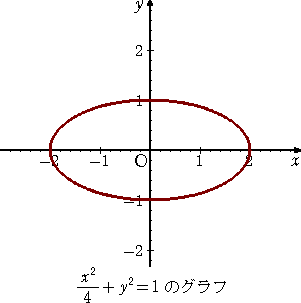
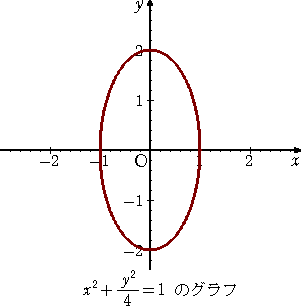
楕円は、2つの定点F、F’からの距離の和が一定な点Pの軌跡である。
このときの2つの定点を、焦点という。
![]() のとき、焦点の座標は、
のとき、焦点の座標は、![]()
![]() のとき、焦点の座標は、
のとき、焦点の座標は、![]()
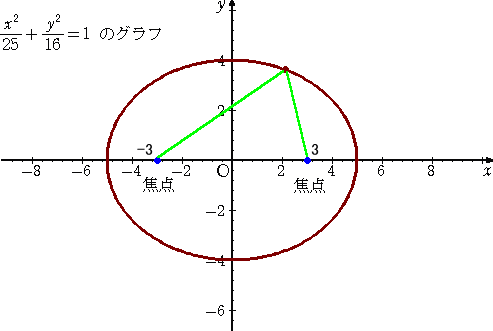
上記の楕円の定義を用いて実際に作図する場合、よく教科書等では、一定の長さの紐の
両端を画鋲でとめ、紐が緩まないように鉛筆を走らせる絵が描かれている。
しかし、この作画方法は一般の人を説得するには十分であるが、だいぶ誤差が伴う方法
で厳密性に乏しい。
そこで、次のように作画する方法があることを最近知ったので、紹介したい。
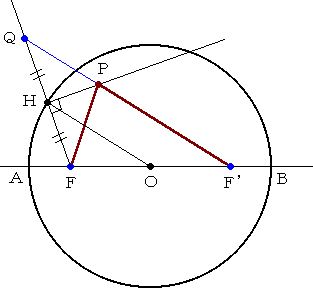 |
2つの定点F、F’からの距離の和を 2a とする。 線分FF’の中点Oを中心とし、半径 a の 円を描く。 点Fを通る任意の直線と円との交点をH とし直線上に、FH=HQとなる点Qをとる。 点Hを通り直線FQと垂直な直線と直線 F’Qとの交点をPとする。 このとき、点Pは楕円上の点である。 |
実際に、中点連結定理を用いて、 PF+PF’=PQ+PF’=QF’=2OH=2a
したがって、点Pは楕円上の点である。
さらに詳しくいえば、直線PHは、楕円の接線になっている。(→参考:楕円に接する円)
楕円は、円を一定方向に拡大縮小したものであるが、多少形は変わるものの円と同様
の性質が成り立つ。(→参考:「方べきの定理」)
円 O において、円外の1点 P から円に引いた2つの接線のなす角は、直線
OP により
2等分される。
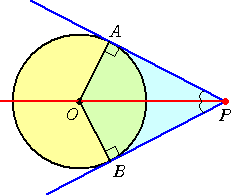 |
証明は明らかだろう。 直角三角形OPAと直角三角形OPBが合同なので、 ∠OPA=∠OPB が成り立つ。 |
このことと同様のことは、楕円では期待できないだろうと思いきや、次のように文言を修正
すれば、やはり成り立つというのは驚きである。
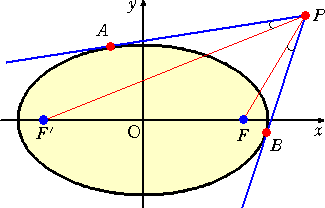 |
左図のように、楕円外の1点 Pから、 2点 F、F’ を焦点とする楕円に引いた 接線の接点を A、Bとするとき、 ∠F’PA=∠FPB が成り立つ。 |
#F=F’ の場合が円なので、上記の事実は、円の場合の一般化になっている。
(証明)
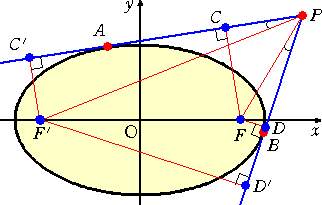 |
左図のように、焦点 F、F’ から接線 に垂線を下ろし、その足を、C、C’、D、 D’ とするとき、 FC×F’C’=FD×F’D’(=一定) である。 |
実際に、上図において、楕円
![]() (ただし、
(ただし、 ![]() とする)
とする)
の離心率を
![]()
とすると、焦点 F、F’の座標は、F(ae,0)、F’(−ae,0) と書ける。
点 P の座標を、(x1,y1)とおくと、楕円の準線は、 x=a/e 、x=−a/e なので、
−a/e<x1<a/e すなわち、 a−ex1>0 、 a+ex1>0 が成り立つ。
このことから、点と直線の距離の公式を用いて、
FC=k(a−ex1) 、 F’C’=k(a+ex1)
ただし、
![]()
と書ける。 よって、
FC×F’C’=k2(a−ex1)(a+ex1)=a2b4(a2−e2x12)/(b4x12+a4y12)
ここで、 b2x12+a2y12=a2b2 が成り立つので、
FC×F’C’=b4(a4−(a2−b2)x12)/{b2(a4−(a2−b2)x12)}=b2
同様にして、 FD×F’D’=b2 が成り立つので、FC×F’C’=FD×F’D’ である。
(コメント) 解析的には上記のように示されるが、もっと幾何学的に示すことは出来ないのだ
ろうか?もし、幾何学的な証明を見いだされた方は、こちらまでご教示下さい。
上記では、離心率や点と直線の距離など解析幾何の知識を用いたが、もう少し易しく解こ
うと思えば次のようになるであろうか?
楕円上の接点Pにおける接線に垂線を下ろしたとき、その足は楕円の補助円 x2+y2=a2
上の点であるという事実がある。(→参考:楕円の作図)
楕円
![]()
において、傾き m の接線の方程式は、 ![]() で与えられる。
で与えられる。
実際に、楕円 b2x2+a2y2=a2b2 に、y=mx+k を代入して整理すると、
(a2m2+b2)x2+2kma2x+a2(k2−b2)=0
この2次方程式が重解をもつので、
判別式 D/4=k2m2a4−(a2m2+b2)a2(k2−b2)=0
これより、 k2=a2m2+b2 なので、求める公式が得られる。
いま、この接線に垂直で焦点を通る直線は、
![]()
2つの直線の交点の座標を、(X,Y)とおくと、
(Y−mX)2+(mY+X)2=a2m2+b2+a2−b2=(m2+1)a2
(m2+1)(X2+Y2)=(m2+1)a2 から、 X2+Y2=a2
以上から、 2つの直線の交点は、円 X2+Y2=a2 上の点である。
|
![]()
よって、 OF2=a2−b2=OF’2 なので、(FC2+b2)F’C’=(F’C’2+b2)FC
(FC×F’C’−b2)(FC−F’C’)=0
FC−F’C’=0 すなわち、 FC=F’C’ のとき、FC=F’C’=b なので、
FC×F’C’=b2 が成り立つ。
FC−F’C’≠0 のとき、 FC×F’C’=b2 が成り立つ。
以上から、何れにしても、 FC×F’C’=b2 が成り立つ。
(コメント)計算量はそれほど変わらないかな?
さて、証明の本題に戻ろう。
 |
左図において、 FP=L、F’P=L’、∠F’PA=α、 ∠FPF’=β、∠FPB=γ とおく。 FC×F’C’=FD×F’D’ なので、 |
Lsin(α+β)×L’sinα=Lsinγ×L’sin(β+γ)
すなわち、 −2sin(α+β)×sinα=−2sinγ×sin(β+γ)
三角関数における積和の公式により、
cos(2α+β)−cosβ=cos(β+2γ)−cosβ
よって、 cos(2α+β)=cos(β+2γ) より、 cos(2α+β)−cos(β+2γ)=0
三角関数における和積の公式により、 −2sin(α+β+γ)sin(α−γ)=0
明らかに、 0<α+β+γ<π 、−π<α−γ<π なので、 α−γ=0 である。
したがって、 α=γ より、 ∠F’PA=∠FPB が成り立つ。 (証終)
(コメント) この性質は、名古屋工大の入試問題で問われた。
上記では、「∠F’PA=∠FPB」であることを解析的に示したわけであるが、初等幾何学的
証明を当HP読者のM.S.さんよりメールで頂いた。(平成25年2月23日付け)
(証明) Fの接線PBに関して対称な点をF0、F’の接線PAに関して対称な点をF0’とおく。
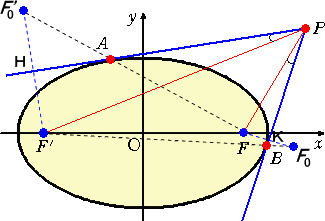
このとき、次のことが成り立つ。
(1) 3点F、A、F0’および3点F’、B、F0は同一線上にあり、F’F0=FF0’=(長軸の長さ)
実際に、点Aは楕円上の接点なので、∠PAF=∠HAF’
また、△AHF’≡△AHF0’なので、∠HAF’=∠HAF0’
よって、 ∠PAF=∠HAF0’から、3点F、A、F0’は同一線上にある。
このとき、 FF0’=FA+AF0’=FA+AF’=(長軸の長さ)
同様に、3点F’、B、F0は同一線上にあり、F’F0=(長軸の長さ)であることも示される。
(2) 対称な点なので、PF=PF0 、PF’=PF0’
(1)(2)より、 △PF0F’≡△PFF0’(3辺相等) なので、 ∠F0PF’=∠FPF0’
従って、 ∠F’PF0’=∠FPF0’−∠FPF’=∠F0PF’−∠FPF’=∠FPF0 より、
∠F’PA=(1/2)∠F’PF0’=(1/2)∠FPF0=∠FPB (証終)
(コメント) 鮮やかな初等幾何的証明ですね!とても分かりやすいです。M.S.さんに感謝
します。因みに、平成25年2月19日に証明されたそうです。
楕円の持つ次の性質も面白い。
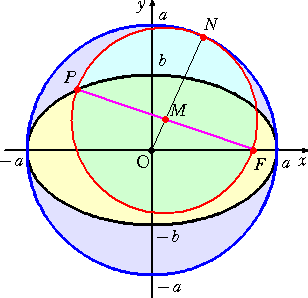 |
楕円 上の点 P と焦点 F を結ぶ線分 PF の 中点 M を中心とし、MPを半径とする 円は、楕円の補助円 x2+y2=a2 に 内接する。 |
(証明) 楕円の離心率を、 e とすると、、焦点 F の座標は、F(ae,0)
と書ける。
点 P の座標を、(x1,y1)とおくと、 M((x1+ae)/2,y1/2) である。
このとき、 OM2={(x1+ae)2+y12}/4 で、
(ae)2=a2−b2 、y12=(a2b2−b2x12)/a2
より、
OM2=(x12+2x1ae+(ae)2+y12)/4
=(x12+2x1ae+a2−b2+(a2b2−b2x12)/a2)/4
=(x12+2x1ae+a2−b2x12/a2)/4=((ex1)2+2x1ae+a2)/4=(ex1+a)2/4
ex1+a>0 なので、 OM=(ex1+a)/2 より、 MN=(a−ex1)/2
また、
PF2
=(x1−ae)2+y12
=x12−2x1ae+(ae)2+(a2b2−b2x12)/a2
=x12−2x1ae+a2−b2+b2−b2x12/a2=(ex1)2−2x1ae+a2=(ex1−a)2
a−ex1>0 なので、 PF=a−ex1=2MN
よって、M を中心としMPを半径とする円は楕円の補助円 x2+y2=a2 に内接する。
(証終)
(追記) 当HP読者のHN「DS」さんから、上記の性質が幾何学的に証明出来るとのメール
を頂いた。(平成27年7月26日付け)
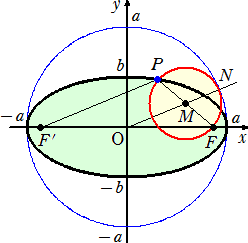
上図のように点を取れば、△FOM∽△FF’P であり、FP+PF’=2a より、FM+MO=a
また、FM=MN なので、ON=OM+MN=OM+MF=a
よって、題意は示された。
(コメント) Nが、Mを中心とする半径aの円周上にあり、かつ、補助円 x2+y2=a2 上にも
あることが示されたが、それが接していることの証明にはなっていないような...。
例 楕円 x2/8+y2/4=1 上の点P(0,2)と焦点F(2,0)を結ぶ線分PFの中点M(1,1)
を中心とし、半径![]() の円の方程式は、(x−1)2+(y−1)2=2 となり、楕円の補助円
の円の方程式は、(x−1)2+(y−1)2=2 となり、楕円の補助円
x2+y2=8 に対して、確かに接する。
実際に、円 x2+y2=8 と直線 y=x との交点Nは(2,2)で、Nにおける
円 x2+y2=8 の接線の方程式は、2x+2y=8 すなわち、x+y=4
円 (x−1)2+(y−1)2=2 の接線の方程式は、x−1+y−1=2 すなわち、x+y=4
となり、直線 x+y=4 は2円の共通接線となり、2円は接する。
接することを初等幾何的に示すには、どうすればいいのだろうか?それとも、上記の証明
で言い尽くされていることなのだろうか?今ひとつ自信が持てない。
DD++さんからのコメントです。(平成27年7月30日付け)
一言足りないだけで、言い尽くされていると思いますよ。「上図のように」と書いてしまってい
るところでNは何を仮定して何を仮定しないのか明記すべきでした。NはOMの延長に取るこ
とを仮定しているようなので、両中心を通る直線上に共有点があるということで接することに
なりますね。
DSさんからの続報です。(平成27年7月30日付け)
上記の証明についての補足です。
点Nは半直線OMの延長線上かつ円Mの周上の点です。よって円Mの円周上でOから最も
離れている点はNです。よって、円Mの円周上の他の点は補助円よりも内側にあります。
つまり、補助円と円Mは一点Nのみを共有することになり、これは接しているということと同じ
です。これでどうでしょうか?
(コメント) DSさん、ありがとうございます。合点しました。私の考えは杞憂だったようです。
(追記) 令和元年10月14日付け
BC=p、CA=q の直角三角形ABCに長軸の長さが2a、短軸の長さが2bの楕円を内接
させる。
与えられた直角三角形を横方向にb/a倍に縮小させた直角三角形AB’Cを考える。このと
き、楕円も長軸、短軸の長さがともに2b(=直径)の円となる。
円外の1点から引いた接線の長さは等しいので、 AB’−B’C+2b=AC
ここで、 B’C=bp/a 、AC=q 、AB’=√((bp/a)2+q2) を代入して整理すると、
a=p(q−2b)/(2q−2b)
このことから、例えば、BC=12、CA=6の直角三角形ABCに内接する楕円の短軸の長
さを4とするとき、長軸の長さは、6となることが分かる。
上記の手順を作図してみた。
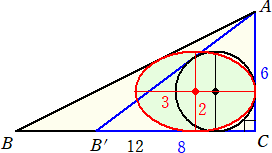
(参考) → 「三角形に内接する楕円」
以下、工事中!