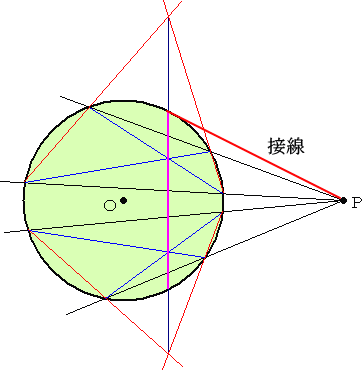
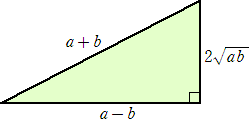��{�̍�}�@ �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�����g�A�ȑO�͒�E�R���p�X��p���āA���낢��Ȑ}�`����}�E�`�悵�����̂����A�`
��\�t�g���g���悤�ɂȂ��āA���֗̕�������A��K�E�R���p�X��p����@��͂قƂ�ǂȂ�
�Ȃ��Ă��܂����B
�@�`��\�t�g�͊m���ɑ����Y��ɐ��m�Ɋ�]����}��`�悵�Ă���邪�A���g�ŏ����Ă���
���������S�����悻�悻�����B�d�쓯�l�A�����������������Ă���l���g���Ύ��Ԃ̒Z
�k�ɂȂ�d�邪�A����������������Ȃ��Ă��`���Ă��܂��Ƃ���ɗ��n�̌��ɂȂ�댯
�����͂��ł���B
�@�����ŁA���̃y�[�W�ł́A��{�̍�}�����������グ�āA���̌��������m�����A
�܂Ƃ߂Ă݂邱�Ƃɂ����B
�@�`��\�t�g�ō�}���w���オ�A�u�Ȃ��A���̂悤�ȍ�}���\�Ȃ̂��H�v�Ƃ����^���
�����ꂽ�Ƃ��̓��W�ɂł��Ȃ�K���ł���B
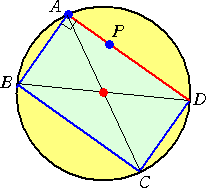
�����̓�����
 |
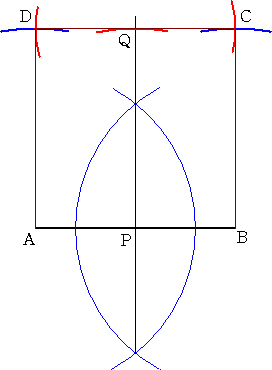
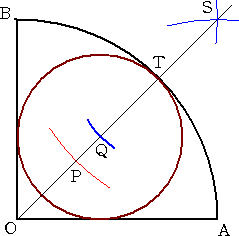
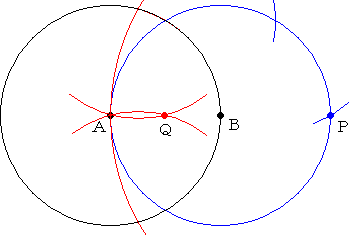
�@�@�����������������`�a�ɑ��āA���}�̂悤��
�@�����`�b�������B�R���p�X���g�p���āA�����`�b��
�@��C�ӂ̒����œ���������B |
�@�����a�c�����сA�e�����_��������a�c�ɕ��s�Ȑ����������A�����`�a�Ƃ̌�_�����߂�B
�@���ꂪ�A���߂铙���_�ł���B
�i�NjL�j�@�����Q�S�N�Q���Q�U���t��
�@�Вc�@�l���{���w��A���������S�W��w�̂T�X�R�S�l��Ώۂɍs�����e�X�g�̌��ʁA
�@�@�u���ς̈Ӗ��v�@�E�E�E�@�������@�V�U��
�@�@�u��Ƌ����𑫂��Ɗ�ɂȂ闝�R�v�@�E�E�E�@�������@�R�S��
�@�@�u��ƃR���p�X���g���Đ������R����������@�v�@�E�E�E�@�������@�W��
�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�Ƃ������ʂł������Ƃ����B�������W���́u�����̂R�����v���A���@���P��o�����Ă���ΈՂ�
���Ǝv���̂����A�o�����Ă��Ȃ���A��L�̔��z���l�̗͂ŔP�o����͓̂��������
��Ȃ��B
�����`
 |
�@�@�@�����`�̈�ӂ`�a���^�����Ă���B�_�a
�@�@�𒆐S�ɔC�Ӕ��a�̉~��`���A���� �`�a ��
�@�@�̌�_���o�Ƃ���B���̉~�Ɠ��������̔��a
�@�@�ło�𒆐S�Ƃ���~�ʂœ_�p�A�_�p�𒆐S��
�@�@����~�ʂœ_�q�����ꂼ���߂�B�C�ӂ�
�@�@�����ŁA�_�p�A�q�𒆐S�Ƃ��ĉ~�ʂ�`���A�_
�@�@�r���߂�B�����a�r��ɂ`�a���a�b�ƂȂ��
�@�@���ɓ_�b���߂�B |
�@�����`�a�̒����a�A�_�`�A�b�𒆐S�Ƃ��ē_�c���߂�B
�@���̂Ƃ��A�l�p�`�`�a�b�c�����߂鐳���`�ł���B
�@�i�����̒[�_�Ő����������Ƃ��A���O�p�`�̐������I���Ɏg���Ă���B�j
��L�̕��@�ɔ�ׂăG���K���g���Ɍ����邩������Ȃ����A���̂悤�ȍ�}�菇���̂ē�B
 |
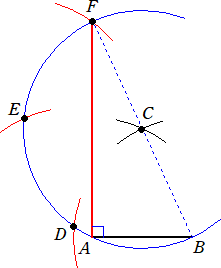
�@�@�@�����`�̈�ӂ`�a���^�����Ă���B����
�@�@�`�a�̐���������`���A�`�a���o�p�ƂȂ�
�@�@�悤�ɓ_�p�������B�_�p�𒆐S�ɔ��a�`�o�̉~
�@�@�ʂ�`���B���̉~�ʂƓ_�a�𒆐S�A���a�`�a��
�@�@�~�ʂƂ̌�_���b�Ƃ���B���l�ɂ��āA�_�c��
�@��߂�B
�@�@���̂Ƃ��A�l�p�`�`�a�b�c�����߂鐳���`��
�@����B
�@�i������������A������̕��������̕����v����
�@ �������@�ł͂Ȃ����Ɛ��@�����B�j |
�i�NjL�j�@�ߘa�S�N�P�O���Q�O���t��
�@�^����ꂽ�����`�a�ɑ��āA�[�_�`�Ő����𗧂Ă��}�́A��{�I�Ȗ�肾�낤�B�ŋ߁A
��L�Ƃ͈قȂ�����������邱�Ƃ�m�����B
�i���@�P�j
 |
�@�@�����`�a�̐����Q��������ɔC�ӂɓ_�b���Ƃ�B�b��
�@���S�Ƃ��āA���a�b�a�̉~�ʂ�`���B�a�𒆐S�Ƃ��āA��
�@�a�b�a�̉~�ʂ�`���A�_�c���߂�B���l�ɂ��āA�_�d�A
�@�e���߂�Ƃ��A�����`�e�����傤�ǐ����`�a�̐����ƂȂ�B |
�i�ؖ��j�@�a�e�́A�~�b�̒��a�Ȃ̂ŁA�@�ڂa�`�b���X�O���ƂȂ�B�@�@�i�؏I�j
�i���@�Q�j
 |
�@�@�a�𒆐S�Ƃ��Ĕ��a�a�`�̉~�ʂ�`���A���̎���
�@�ɔC�ӂɓ_�b���Ƃ�B�b�𒆐S�Ƃ����a�b�`�̉~��
�@��`���A�~�a�Ƃ̌�_���c�Ƃ����B
�@�`�𒆐S�Ƃ����a�`�c�̉~�ʂ�`���A�~�b�Ƃ̌�_
�@���d�Ƃ����B
�@���̂Ƃ��A�`�d�����߂鐂���ł���B |
�i�ؖ��j�@���b�`�c�́A�b�`���b�c�̂Q���ӎO�p�`�Ȃ̂ŁA�@�ڂb�`�c���ڂb�c�`
�@�܂��A�`�c���`�d �ŁA�b�͉~�̒��S�Ȃ̂ŁA�@�ڂb�`�c���ڂb�`�d
�@�ȏォ��A�@�ڂb�c�`���ڂb�`�d�@�Ȃ̂ŁA�ڌ��藝���A�����`�d�́A�_�`��ړ_�Ƃ���~�a
�̐ڐ��ƂȂ�B���������āA�`�a�ۂ`�d�@�������ꂽ�B�@�@�i�؏I�j
��_�ʉ߂̕��s��
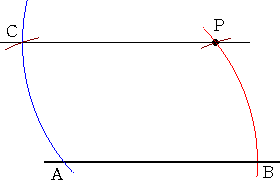 |
�@�@�@�����Ɠ_�o���^�����Ă���B�_�o�𒆐S��
�@�@�C�Ӕ��a�̉~��`���A�����Ƃ̌�_���`�Ƃ�
�@�@��B���̉~�Ɠ��������̔��a�ł`�𒆐S�Ƃ���
�@�@�~��`���A�����Ƃ̌�_���a�Ƃ���B |
�@�_�`�𒆐S�Ƃ��Ĕ��a�a�o�̉~��`���A��̉~�Ƃ̌�_���b�Ƃ���B
�@���̂Ƃ��A�����o�b�����߂���̂ł���B
�@�i���s�l�ӌ`�̐������I���Ɏg���Ă���B�j
�l���~�̓��ډ~
 |
�@�l���~�n�`�a���^�����Ă���B�ڂ`�n�a
�̓����n�r��`���A�ʂ`�a�Ƃ̌�_���s
�Ƃ���B�s���ڐ���`���A�����n�`�̉���
���Ƃ̌�_���o�Ƃ���B�ڂn�o�s�̓���
�Ɛ����n�r�Ƃ̌�_�p�����߂�~�̒��S��
����B |
�i�����ڕ��ʂŕ`���Ă��āA�K���Ɍ떂�����Ă��܂����l�D�D�Df(^_^)�@�j
�@��L�ł͉~�̒��S�����߂邽�߂ɁA�p�̓������Q�{��}���ꂽ���A�U��Ԃ��Ă݂�
�ƁA���܂茫���ȕ��@�Ƃ͌����Ȃ��B���̂悤�ɍ�}���邱�Ƃ��\�ł���B
 |
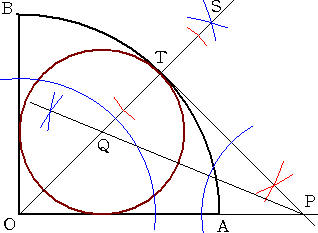
�@�@�@�l���~�n�`�a���^�����Ă���B�_�`�𒆐S�Ƃ���
�@�@�a�n�`�̉~�ʂ�`���B���l�ɓ_�a�𒆐S�Ƃ����a�n�`
�@�@�̉~�ʂ�`���A��_���r�Ƃ���B�_�r�𒆐S�Ƃ����a
�@�@�n�`�̉~�ʂ�`���A�����n�r�Ƃ̌�_���o�Ƃ���B��
�@�@���n�r�ƌʂ`�a�̂̌�_���s�Ƃ��A�s�𒆐S�ɔ��a�n�o
�@�@�̉~�ʂ�`���B�����n�r�Ƃ̌�_���p�Ƃ���B |
�@���̂Ƃ��A�_�p�����߂�~�̒��S�ł���B
�i�菇�������Ԃ�X�b�L�����܂����l�D�D�Df(^_^)�@�j
�@���̉�@��ɂ́A��}�ɂ���������p����B���߂�~�̔��a�́A�i �|�P�j�n�`
�|�P�j�n�`
�ł���B
���^
 |
�@�@�@�~�n���^�����Ă���B���a�`�a�Ƃ��̐����n�b��
�@�@��}����B�n�a�̒��_�l�𒆐S�Ƃ����a�b�l�̉~��
�@�@��`���A�n�`�Ƃ̌�_���m�Ƃ���B
�@�@�@�b�𒆐S�Ƃ����a�b�m�̉~�ʂ�`���A�~�n�Ƃ̌�_
�@�@���o�Ƃ���B�ʂb�o�̒����ŁA�~�����T��������B |
�@���̂Ƃ��A�T�����_�o�A�p�A�q�A�r�A�b�����ׂA���^��������B
�@���̍�}�̗��_�I�w�i�́A���������Q�ƁB
�~�ʂ̘A���Ȑ�
 |
�@�@���g�o�̌f���ɁA�g�m�u����v����Ƃ���
�@�����珑�����݂��������B
�@�@�@�q�̏o�����ɂ��Ă̎���ł��B�Ⴆ
�@�@�A�q�T�Ƃ����̂̓ӂP�O �̔����ƕ�����
�@�@�����B�Ȃ����̂悤�ȕ\���̂�����������
�@�@�̂���������܂���B �܂��A�ɂ��̂q
�@�@�T�̋Ȑ��𐍁i����j���g���č��ꍇ�A
�@�@���ӂ̐��ō������̂ł��傤���H
�@�@���w�I�ɕ� ����₷���ؖ��ł������
�@�@�ł��傤���H
�@�����g���Ĕ����Ƃ������Ƃ��z���ł�
�܂���i���͌��������铹��H�j���A�Ȑ���
�������̉~�ʂ̏W�܂�ƍl����A���}
�̂悤�Ȍ`�ō�}�ł���Ǝv���܂��B |
�@�q�́A�p��́@Radius�@�i���a�j�̓��������Ƃ������́B�q�̐��l�̑傫�������J�[�u�`��
�͐Ȃ�܂��B���H�W���ł��p�����A�^�]�҂ɂ̓J�[�u�̂������������ďd�܂��B
�@��L�̂悤�Ȑ����ŁA�g�m�u����v����̎���̎�|�ɍ��v���Ă��邩�ǂ����S�����M������
�܂���B
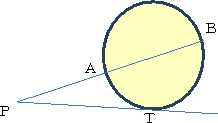
�~�̐ڐ�
�@�~����̔C�ӂ̓_�Őڐ��������ꍇ�A�ŏ��Ɏv�������@�́A�ړ_�ƒ��S�����Ԕ��a��
�����Ȓ�����`���Ƃ������̂ł��낤�B
�@����ɑ��āA���̕��@�͂ƂĂ��a�V�ł���B
 |
�g�ɂ�����ڐ����^�����Ă�����̂Ƃ���B
���a�j�g��̓_�j�Ɖ~����̔C�ӂ̓_�`����
�сA���̉������Ƃg�ɂ�����ڐ��̌�_���o
�Ƃ���B
�@�����g�o�̒��_���l�Ƃ���A�����`�l����
�߂�ڐ��ƂȂ�B |
�i�ؖ��j�@�ڂg�`�j���ڂq�@���A�ڂg�`�o���ڂq�@�@����āA�_�l�͂R�_�g�A�`�A�o ��ʂ�~�̒��S
�@�@�@�@�ƂȂ�B���̂Ƃ��A�ڂl�`�g���ڂl�g�`�@�����藧�B�ڌ��藝���A�ڂl�g�`���ڂg�j�`
�@�@�@�@�@�䂦�ɁA�ڂl�`�g���ڂg�j�`�@�ƂȂ�A�ڌ��藝�̋t�ɂ��A�l�`�͂`�ɂ�����ڐ��Ƃ�
�@�@�@�@��B
�@�@�@�@�@���ۂɁA���p�O�p�`�k�g�`�ɂ����āA�ڂg�j�`���ڂg�k�`�A�ڂg�k�`�{�ڂg�`�k���ڂq
�@�@�@�@�@����āA�ڂl�`�g�{�ڂg�`�k���ڂq�@���A���a�n�`�ۂl�`�@�Ȃ̂Őڐ��Ƃ�����B
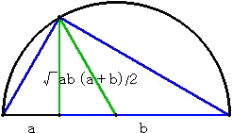
���������m�̎O�p�`
�@�R�ӂ̗^����ꂽ�O�p�`����}���邱�Ƃ́A�O�p�`�����݂������A�Ղ����B����ł͔�
�z��ς��āA�^����ꂽ�����������Ƃ���O�p�`����}����ɂ͂ǂ�������悢�ł��낤���H
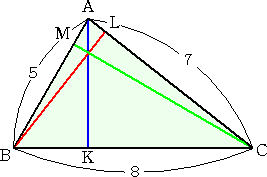 |
�@�@���A�^����ꂽ�������A�T�A�V�A�W�@�Ƃ��A���̒�����
�@�R�ӂƂ���O�p�`��`���B���`�a�b�̖ʐςɒ��ӂ���
�@�@(1/2)�`�j�E�a�b��(1/2)�a�k�E�b�`��(1/2)�b�l�E�`�a
�@���Ȃ킿�A�a�b�F�b�`�F�`�a���P/�`�j�F�P/�a�k�F�P/�b�l
�@�@����āA�����ƕӂ̒����͔���Ⴗ��B |
 |
�@�@���������āA���߂遢�o�p�q�́A
�@���}�̂悤�ɍ�}������܂�B
�@�@�����ŁA�f�g�͂p�g�̐����ł���A
�@�f�g���T�@�Ƃ���B�Ԑ���̓_�o��
�@���āA�o�f�Ƃp�g�͕��s�ŁA��
�@���݂��ɕ��s�Ƃ���B |
�~�̂S����
 |
�@�@�@�����ł́A�~�̒��S���^�����Ă�����̂Ƃ��čl����B
�@�@�i���@�Q�l �F �~�̒��S�i�R���p�X�݂̂ł̍�}�j�j
�@�@�@��ƃR���p�X��p���āA�~���S�������邱�Ƃ͈Ղ����B����
�@�@�ł́A�R���p�X�݂̂��g���ĉ~���S����������@���l����B
�@�i���̖��́A�n���h���l�[�� tappon ����Ƃ��������炢����
�@ �������̂ł���B�j |
�@�܂��A�^����ꂽ�~����ɁA�C�ӂɂP�_ �` ���Ƃ�B�` �𒆐S�Ƃ��āA�~����ɔ��a�n�`�ɓ���
���_ �b�A�c���Ƃ�B���x�́A�b�A�c�𒆐S�Ƃ��āA�~����ɔ��a�n�`�ɓ������_���Ƃ�B���̑���
�𑱂��āA�~������U��������B
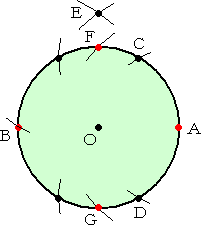 |
�@�@�`�A�a �𒆐S�Ƃ��āA���� �b�c �̒����ɓ������~�ʂ�`���A
�@���̌�_�� �d �Ƃ���B
�@�@����ɁA�` �𒆐S�Ƃ��āA���� �n�d �̒����ɓ������~�ʂ�
�@�`���A���̌�_�� �e�A�f �Ƃ���B
�@�@���̂Ƃ��A�S�_ �`�A�a�A�e�A�f �����傤�lj~�����S�������Ă�
�@��B
�i�R�����g�F�@�R���p�X�݂̂ŁA�~�����S�����ł���Ȃ�Ď���
�@�@�@�@�@�@�����ł��I�j |
�����`�̕ӂ̒��_
 |
�@�@�@��ƃR���p�X��p���āA�����`�̕ӂ̒��_����}
�@�@���邱�Ƃ͈Ղ����B
�@�@�@�����ł́A��݂̂��g���Ē����`�̕ӂ̒��_����
�@�@�}������@���l����B
�@�@�@�i���̖��́A�n���h���l�[�� tappon�@����Ƃ�����
�@�@�@�@���炢�����������̂ł���B�j
|
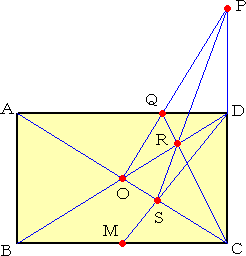 |
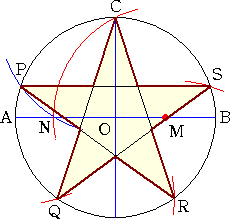
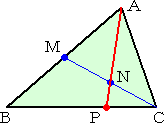
�@�@�ӂb�c��K�X�������A�_�o���Ƃ�A�Ίp���`�b�Ƃa�c
�@�̌�_�n�ƌ��сA�ӂ`�c�Ƃ̌�_���p�Ƃ���B����
�@�b�p�ƑΊp���a�c�Ƃ̌�_���q�Ƃ��A�����o�q�̉���
�@���ƑΊp���`�b�Ƃ̌�_���r�Ƃ���B���̂Ƃ��A����
�@�c�r�̉������ƕӂa�b�̌�_�l���A�ӂa�b�̒��_��
�@�Ȃ�B |
�@������ƁA��}�̕��@�����G�Ȃ̂ŁA��}�̉�͂����Ă����܂��B
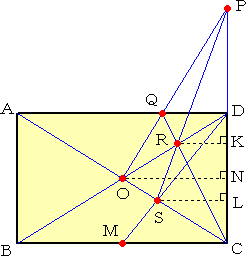 |
�@�@�����`�`�a�b�c�ɂ����āA��ʐ����������ƂȂ��A
�@�`�a���Q�A�a�b���Q���@�Ƃ��Ă悢�B
�@�@�܂��A���}�ɂ����āA
�@�@�@�@�@�o�c�����@�A�@�p�c�����@�A�@�q�j�����@�A
�@�@�@�@�@�r�k�����@ �A�@�c�j�����@�A�@�k�b����
�@�@�Ƃ����B |
�@�܂��A���o�p�c �� ���o�n�m �ɂ����āA�@�� �F �� �� �� �F ���{�P�@�Ȃ̂ŁA�@��
�� ����/�i���{�P�j
���c�q�j �� ���c�n�m �ɂ����āA�@�� �F �� �� �� �F �P�@�Ȃ̂ŁA�@�� ��
����
���b�q�j �� ���b�p�c �ɂ����āA�@�� �F �� �� �Q�|�� �F �Q�@�Ȃ̂ŁA�@�Q��
�� ���i�Q�|���j
�@�� �� ����/�i���{�P�j�@�A �� �� �����@�������Đ�������ƁA�@�����Q��/�i�R���{�Q�j�@�ŁA
�@�����Q����/�i�R���{�Q�j�@�ƂȂ�B
�܂��A���b�r�k �� ���b�n�m �ɂ����āA�@�� �F �� �� �� �F �P�@�Ȃ̂ŁA�@��
�� ����
���o�q�j �� ���o�r�k �ɂ����āA�� �F �� �� ���{�� �F ���{�Q�|���@�Ȃ̂ŁA�i���{�Q�|���j�� �� ���i���{���j
�@�����Q��/�i�R���{�Q�j�@�A�����Q����/�i�R���{�Q�j�@�A�� �� �����@�������Đ�������ƁA
�����Q/�R�@�ŁA�����i�Q/�R�j���@�ƂȂ�B
�@���̂Ƃ��A�����c�r�̌X���́A�@�i�Q�|���j/�����Q/���@�ƂȂ�A���̌��ʁA�����l�b�̒����́A��
�ɓ������Ȃ�B
�@����āA�_�l�́A�����a�b�̒��_�ƂȂ�B
�i�R�����g�F������ł͕s�\�ł́H�Ǝv�����̂ł����A�ӊO�ɂ���}���o�����ł��ˁI
�@�@�@�@�@�@�{���ɋ����ł��B�j
�i�����P�U�N�P�P���P�T���NjL�j�@��L�̍�}�ł́A�V�����g���Ă��邪�Atappon�@�����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���A�킸���T�����g�������ŏ\���Ƃ̂��Ƃł���B
�@�ȉ��̍�}���@�́Atappon�@����ɂ����������������B
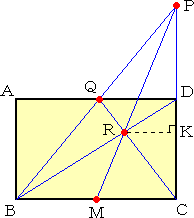 |
�@�@�@�ӂb�c��K�X�������A�_�o���Ƃ�A�_�a�ƌ��сA�ӂ`�c��
�@�@�̌�_���p�Ƃ���B�����b�p�ƑΊp���a�c�Ƃ̌�_���q��
�@�@���A�����o�q�̉������ƕӂa�b�̌�_���l�Ƃ���ƁA�_�l
�@�@���ӂa�b�̒��_�ƂȂ�B |
�@�i�R�����g�j�@�ƂĂ��Ȗ��ȕ��@�ŁA�����I�ł��B�ŏ��M�����Ȃ����@�������̂ŁA���ɏ�
�@�@�@�@�@�@�@���Ċm���߂Ă݂��Ƃ���A�܂��ɒ��_�����܂��Ă��܂����B
�@��}�̉�͈͂ȉ��̂悤�ɂȂ�܂��B
�@�@�����`�`�a�b�c�ɂ����āA��ʐ����������ƂȂ��A�@�`�a���Q�A�a�b���Q���@�Ƃ��Ă悢�B
�@�܂��A��}�ɂ����āA�@�o�c�����@�A�@�p�c�����@�A�@�q�j�����@�A�@�j�b�����@�@�Ƃ����B
�@�܂��A���o�p�c �� ���o�a�b �ɂ����āA�@�� �F �Q�� �� �� �F ���{�Q�@�Ȃ̂ŁA�@�� �� �Q����/�i���{�Q�j
���c�q�j �� ���c�a�b �ɂ����āA�@�� �F �� �� �Q�|�� �F �Q�@�Ȃ̂ŁA�@��
�� ���i�Q�|���j/�Q
���b�q�j �� ���b�p�c �ɂ����āA�@�� �F �� �� �� �F �Q�@�Ȃ̂ŁA�@�� ��
����/�Q
�@�� �� �Q����/�i���{�Q�j�@�A �� �� ���i�Q�|���j/�Q�@�A �� �� ����/�Q�@���A�@�����i���{�Q�j/�i���{�P�j�@�ŁA
�@��������/�i���{�P�j�@�ƂȂ�B
�@���̂Ƃ��A�����o�q�̌X���́A�@�i���{�Q�|���j/�����i���{�Q�j/���@�ƂȂ�A���̌��ʁA�����l�b��
�����́A���@�ɓ������Ȃ�B�@����āA�_�l�́A�����a�b�̒��_�ƂȂ�B
�@�܂��Atappon�@����ɂ��A��L�ł͒����`�̊O����L���Ɏg���č�}���Ă��邪�A��
���萔����������̂̒����`�̓���������p���č�}���邱�Ƃ��\�Ƃ̂��Ƃł���B
�@�ȉ��̍�}���@���Atappon�@����ɂ��������������܂����B
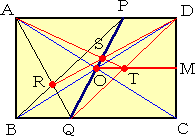 |
�@�@�Ίp���`�b�Ƃa�c�̌�_���n�Ƃ��A�n��ʂ�C�ӂ̐����o�p
�@��`���B�l�p�`�`�a�p�o�̑Ίp���̌�_���q�Ƃ��A�����c�q��
�@�����o�p�̌�_���r�Ƃ����B�����`�r�Ɛ����p�c�̌�_���s��
�@���A�����n�s�ƕӂb�c�̌�_���l�Ƃ����B
�@�@���̂Ƃ��A�_�l�́A�ӂb�c�̒��_�ł���B |
�@������ƁA��}�̕��@�����G�Ȃ̂ŁA���W�̍l���ō�}�̉�͂����Ă����܂��B
�@�n�i�O�C�O�j�A�`�i�|���C�P�j�A�a�i�|���C�|�P�j�A�b�i���C�|�P�j�A�c�i���C�P�j�@�Ƃ����B
�܂��A�o�i���C�P�j�A�p�i�|���C�|�P�j�Ƃ����ƁA�����`�p�̎��́A�����i�Q/(���|��)�j�i���{���j�{�P
�����a�o�̎��́A�����i�Q/(���{��)�j�i���{���j�|�P�@�Ȃ̂ŁA�_�q�i�|�i��2�{��2)/�i�Q���j�C�|��/���j
�����c�q�̎��́A�����i�Q�i���{���j/(��2�{�R��2)�j�i���|���j�{�P�@�Ȃ̂ŁA
�_�r�i�|���i��2�|�Q�����{��2)/�i��2�{�Q�����|�R��2�j�C�|�i��2�|�Q�����{��2)/�i��2�{�Q�����|�R��2�j�j
���������āA�����`�r�̎��́A�����i�Q/(���|�R��)�j�i���{���j�{�P�@�ƂȂ�A
�����p�c�̎��́A�����i�Q/(���{��)�j�i���|���j�{�P�@�ł���̂ŁA���҂�A�����āA�_�s�� �� ��
�W�����߂�ƁA�O �ƂȂ�B
�@���̂��Ƃ́A�����n�s�ƕӂb�c�̌�_�l���A�ӂb�c�̒��_�ɂȂ邱�Ƃ������B
�i�R�����g �F�@�ؖ��͂ł��Ă��A�ǂ����Ă��̂悤�ȍ�}���@���v�����̂��A�S����������
�@�@�@�@�@�@�@�܂���ˁI�u�X�S���I�v�̈��ɐs���܂��B�j
�i�NjL�j�@��L�̍�}�ł́A�X�����g���Ă��邪�A�킸���U�����g�������ŏ\���ł�
�@�@�@�@�邱�Ƃ��m�F���ꂽ�̂ŁA���̕ł��B �i�����P�U�N�P�P���P�V���t���j
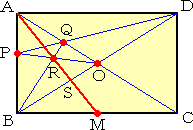 |
�@�@�Ίp���`�b�Ƃa�c�̌�_���n�Ƃ��A�ӂ`�a��̔C�ӂ̓_�o��
�@�_�c�����сA�Ίp���`�b�Ƃ̌�_���p�Ƃ����B�����a�p�Ɛ���
�@�o�n�̌�_���q�Ƃ��A�����`�q�ƕӂa�b�̌�_���l�Ƃ����B
�@�@���̂Ƃ��A�_�l�́A�ӂa�b�̒��_�ł���B |
�@��}�̉�͈͂ȉ��̂悤�ɂȂ�܂��B
�@�`�F�o�̒藝�ɂ��A
�@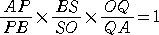
���l���E�X�̒藝�ɂ��A
�@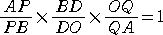
����āA
�@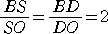
�@���̂��Ƃ���A�r�͐����a�n���A�Q �F �P �ɓ�������_�ł���B
�@���`�a�b�ɂ����āA�_�n�͕ӂ`�b�̒��_�ł���̂ŁA�r�́��`�a�b�̏d�S�ƂȂ�B
���������āA�����`�r�ƕӂa�b�̌�_�ł���l�́A�ӂa�b�̒��_�ƂȂ�B
���s��
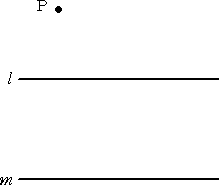 |
�@�@��ƃR���p�X��p���āA�����O�̂P�_���璼���ɕ�
�@�s�Ȓ�������}���邱�Ƃ͈Ղ����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i����_�ʉ߂̕��s���j
�@�@�����ł́A��݂̂��g���āA���s�� �� �� �� ���^��
�@��ꂽ�Ƃ��A�����O�̂P�_�o���璼���ɕ��s�Ȓ�������
�@�}������@���l����B
�@�i���̖��́A�n���h���l�[���utappon�v����Ƃ�������
�@ �炢�����������̂ł���B�j |
�@�_�o��ʂ�A���s�� �� �A�� �ƂQ�_�a�A�b�Ō���钼����C�ӂɈ����A���̒�����̔C�ӂ�
�_���`�Ƃ����B
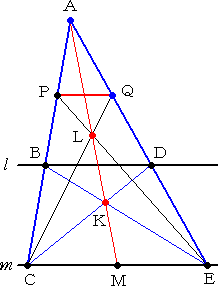 |
�@�@����ɁA�_�`��ʂ�A���s�� �� �� �� �ƂQ�_�c�A�d�Ō���
�@�钼����C�ӂɈ����B
�@�@���̂Ƃ��A�����a�d�Ɛ����b�c�̌�_���j�Ƃ��A�����`�j
�@�ƒ����� �Ƃ̌�_���l�Ƃ���ƁA�l�͐����b�d�̒��_��
�@����B
�@�@�����`�l�Ɛ����o�d�̌�_���k�Ƃ��A�����b�k�Ɛ����`�d
�@�̌�_���p�Ƃ����ƁA�����o�p�́A���� �� �ɕ��s�ƂȂ�B |
�@������ƁA��}�̕��@�����G�Ȃ̂ŁA��}�̉�͂����Ă����܂��B
�@�`�F�o�̒藝���A
�@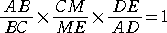
�ŁA�Q������ �� �� �́A���s������A
�@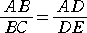
�����藧���A���������āA
�@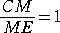
�ƂȂ�B�@������A�b�l���l�d�@�ŁA�l�́A�����b�d�̒��_�ƂȂ�B
�@����ɁA�`�F�o�̒藝���A
�@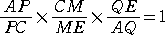
�����藧���A
�@
�Ȃ̂ŁA
�@
�����藧�B�@���̂��Ƃ���A�����o�p�́A���� �� �@���Ȃ킿�@���� ���@�ɕ��s�ƂȂ�B
�i�NjL�j�@Dengan kesaktian Indukmu �����L�Ɋ֘A����������������܂����B
�@�@�i�ߘa�V�N�U���P�P���t���j
�@��L�ł́A�_�o�����s���ɋ��܂�Ă��Ȃ��̈�ɒu����Ă���ꍇ�̍�}���@�ł������B
�ł́A���s���ɂ͂��܂�Ă���̈�̂Ƃ��ɂ͂ǂ�������悢�̂ł��傤���H
�@���̌��ɂ��Ĉ��̉������@������������ɂȂ�܂����̂ŁA�ȉ��ɎZ�z�Ƃ��Ă���
���������܂��B
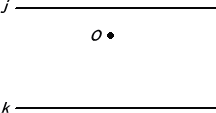
�y�Z�z�z�@���s�� j �� k �Ƃ��A�^�����Ă��܂��B�܂��A�����ɂ͂��܂��̈���ɁA�_ O ��
�@�@�@�@�^�����Ă��܂��B�R���p�X���g�킸�ɒ�݂̂ŁA�_ O ��ʂ� ���� j �ɕ��s�Ȓ���
�@�@�@�@h ����}�����������B
�@�@
�����̃A�C�f�A�ł́AO �� j �Ƃ̊Ԃ̋����ƁAO �� k �Ƃ̊Ԃ̋����Ƃ��������ƁA��}�ɂЂ�
�@��ԗ]�v�ɂ������Ă��܂��܂��B�����Ɨǂ��A�C�f�A������̂ł͂Ɗ��҂��Ă��܂��܂��B
�@�܂��A��}�����܂��������Ƃ��������߂̕��̏ؖ����A�x�N�g����͂��g�����S���S���v�Z
�@�ɂ����̂ł��āA�G���K���g�ł͂���܂���ł����B������������{�������Ă��Ȃ��\
�@��������܂��B
�@�@�F�l�������f���炵����}�����҂��Ă���܂��B
�@DD++ ����̃R�����g�ł��B�i�ߘa�V�N�U���P�Q���t���j
�@�O�ɂ���ꍇ�ƑS���������@���g����悤�Ɏv���̂ł����A�����_���ȗ��R�������ł��������H
�@Dengan kesaktian Indukmu ����̃R�����g�ł��B�i�ߘa�V�N�U���P�Q���t���j
�@���� DD++ ����A���̃{�[���w�b�h�ł������c�c�B�O�ɂ���ꍇ�ɂ́A�قڂQ�{�̎萔
��������Ƃ���v������ł��܂����B���͏o��ł��̂ŁA���ƂŊm�F���܂��B
�@DD++���炲�w�E���������́A�͕s���̂��ߎ��ɂ͂܂��܂������Ɏ��Ԃ������肻����
���B������������̕����{���Ŗ{�������Ă��邱�Ƃ͊ԈႢ�Ȃ����ƂƎv���܂��B
�@�܂��͑��߂ɋ؈��ȋ��Ă����}���@�݂̂�����I���邱�ƂƂ������܂��B���}����������
�����B
�@�@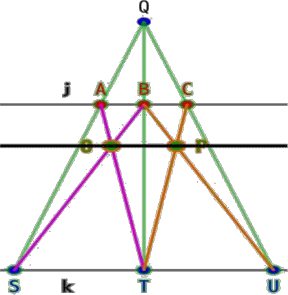
�@ ���s�� j, k �ɂ͂��܂ꂽ�_ O ���^�����܂��BO �́Aj �̕��ɂ��߂����̂Ƃ��܂��B
�A O ��ʂ���� AT, BS ����}���܂��B
�B ���� AS, BT �̌�_�� Q �Ƃ��܂��B
�C Q ���璼�� CU �������܂��B C �� j �Ƃ̌�_�AU �� k �Ƃ̌�_�Ƃ��܂��Bj ��� A,B,C ��
�@���̏��ɕ��Ԃ��̂Ƃ��܂��B
�D ���� BU �Ɛ��� CT �Ƃ̌�_�� P �Ƃ��܂��B
�E ���� OP �ɖ��O������ h �Ƃ��܂��Bh �� �� �ƕ��s�ƂȂ�܂��B
( ����͍�}�݂̂̂��ē��ł� )
�� O �� j, k �̂ǐ^�ɂ���ꍇ�ɂ́AQ �̍�}���ł��܂���B�������ɂȂ�܂��B���ꂪ
���̍�}�̌��_�ł��B�����Ƃ��āAO �Ƃ͕ʂ� O' �� j, k �̊Ԃ̗̈�A�������A�ǐ^��
�Ȃ��悤�Ƀ_�~�[�Ŕz�u���AO' ��ʉ߂��� j �ɕ��s�Ȓ��� j' �����������}���܂��Bj' �� k ��
�̑g�݂Ȃ�AO ��ʉ߂��镽�s���������܂��B�y�Q�{�̎菇��������܂��z
�@�����͂����܂łƂ����Ă��������B
�@�ǂ��ł��ǂ����ł����A�����قǂ̐}�́A����AI �ɍ�点�� HTLM�ɕ\�����������̂ł��B
canvas�v�f�� JavaScript ����тɁA���߂Č����`��̂��߂̃��C�u�������g���Ă���悤�ł��B
�@Gemini �Ɂu����Ȃ̂̐}�����v�Ǝw�����o���܂����B�s����Ȃ́t�͈ȉ��̉p���ł��B����AI
�ɗ����ł���悤�ɉp���������ق����A���ʂɃc�[���ō�}����������Ԃ������邱�Ɛ�����
���ł��B
Let two parallel lines j and k be given. Consider a point Q located on
the same side of both
lines, such that line j is closer to Q than line k.From point Q, draw three distinct lines a, b,
and c, each intersecting both j and k, in such a way that each line intersects
j before it
intersects k as we move away from Q.
�@Specifically, let line a intersect j at point A and k at point S; line b intersect j at point B
and k at point T; and line c intersect j at point C and k at point U.
�@Assume that the points A, B, and C appear in this order along line j,
as we move along j in
a fixed direction.
�@Let O be the point of intersection of segments AT and BS, and let P be
the point of
intersection of segments BU and CT.
�@Define line h as the line passing through points and P.
�@Dengan kesaktian Indukmu ����̃R�����g�ł��B�i�ߘa�V�N�U���P�S���t���j
�@j �� k �Ƃ��A�͂Ȃ�����͕��s�ł͂Ȃ������Ƃ��܂��B������}������ƁAj, k, h �͂P�_�Ō�
��邻���ł� (���_)�B
���]
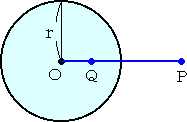 |
�@�@���a �� �̉~�n�ɑ��āA�@�n�o�~�n�p����2�@�����藧�Ƃ��A
�@�_�p�́A�~�n�Ɋւ��āA�_�o�ƑΏ̂ł���Ƃ����B
�@�@���̂Ƃ��A�_�o�ɓ_�p��Ή������邱�Ƃ��A���]�Ƃ����B
�@�~�n���A���]�~�A���S�n�]�̒��S�A��2 �]�x�Ƃ����B
�@�@�u���]�v�̕����ʂ�̈Ӗ��́A�u�u�������v�Ƃ������Ƃł���B |
�@�_�o���~�n�̊O���ɂ���Ƃ��A�_�p���R���p�X�݂̂�p���č�}���邱�Ƃ͈Ղ����B
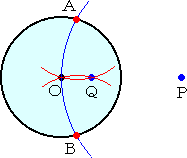 |
�@�@�_�o�𒆐S�Ƃ��Ĕ��a�n�o�̉~�ʂ�`���A�~�n�Ƃ̌�_��
�@�`�A�a�Ƃ���B
�@�@�Q�_�`�A�a�̂��ꂼ��𒆐S�Ƃ��Ĕ��a �� �̉~�ʂ�`���Ƃ��A
�@���̌�_�����߂�_�p��^����B |
�@�����ŁA��}�̉�͂����Ă������B
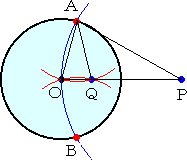 |
�@�@�@���o�`�n�Ɓ��`�n�p�͓ӎO�p�`�ŁA�����ł���B
�@�@����āA�@�n�o �F �n�` �� �n�` �F �n�p�@�����藧�B
�@�@�@���������āA�@�n�o�~�n�p���n�`2����2�@�Ȃ̂ŁA
�@�@�_�p�́A�~�n�Ɋւ��āA�_�o�ƑΏ̂ɂȂ�B |
�@��L�ł́A�_�o���~�n�̊O���ɂ���Ƃ����l�������A�_�o���~�n�̓����ɂ���Ƃ��͎���
�悤�ɍ�}����悢�B
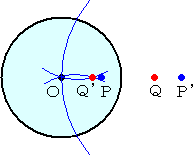 |
�@�@�n�o�f�����E�n�o�i�o�f�͉~�̊O���̓_�j�ƂȂ�悤�ɁA�� ��K
�@�X���߂�B
�@�@��L�̍�}���@�ɂ��A�p�f�����߁A�@�n�p�����E�n�p�f�@��
�@���_�p �����߂�A�_�p�����߂�_�ƂȂ�B
�@�@���ۂɁA�n�o�E�n�p��(1/��)�n�o�f�E���E�n�p�f���n�o�f�E�n�p�f
�@���疾�炩�ł��낤�B |
�@�P�X���I�̏I��荠�A�A�E�A�h���[�ɂ��A�R���p�X�݂̂�p����Ƃ�����}���ɁA���]��
���p���ꂽ�B�Ⴆ�A�[�_�݂̂��^����ꂽ�����̒��_�����߂�ꍇ�A
�@
�ꌩ����ƁA��E�R���p�X��p���Ȃ��ƍ�}�ł��Ȃ����̂悤�ȋC�����邪�A���]��p����
�ƁA��Ȃ��ŃR���p�X�݂̂Œ��_����}���邱�Ƃ��\�ƂȂ�B
�@
�@����́A�@�`�o���Q�`�a�@�A�`�o�~�`�p���`�a2�@���A�`�p���i1/2�j�`�a�@�����藧���Ƃ��疾��
���ł��낤�B
�i�Q�l�����F�R�X�g�t�X�L�[�@���@����@���@��@�R���p�X�ɂ���}�@�i�����}���j�j
�~�̐ڐ��Q
 |
�@�@�@��ƃR���p�X��p���āA�~�O�̂P�_�o����~�n��
�@�@�ڐ�����}���邱�Ƃ͈Ղ����B
�@�@�@��}�̕��@���m�F���Ă������B |
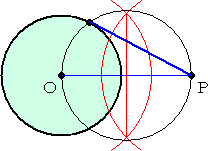 |
�@�@�n�o�a�Ƃ���~��`���A�~�n�Ƃ̌�_�����߂�B
�@���̌�_�Ɠ_�o�����ׂA���ꂪ���߂�ڐ��ƂȂ�B |
�@��L�̕��@�ł́A�R���p�X���L���ɗp����ꂽ���A�R���p�X�𗘗p�����}���@����
��݂̂𗘗p�����}�̕������p���ł���B
�@�����ŁA��L�̐ڐ��̍�}���A��݂̂�p�����ꍇ�ɂ��čl�@�����悤�Ǝv���B
�@���܁A���}�̂悤�ɁA�ڐ������������̂Ƃ���B
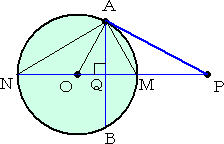 |
�@�@���̂Ƃ��A���`�n�p �� ���o�n�`�@�ŁA
�@�@�@�@�n�o�~�n�p���n�`2
�@�����藧�̂ŁA�_�p�́A�_�o�Ɖ~�n�Ɋւ��đΏ̂�
�@����B�i ���@�Q�l �F ���] �j |
�@���̐����ɒ��ڂ���A���]�̗��_������ڐ������߂邱�Ƃ͉\�ł���B
�@��}�ɂ́A�����Ƒ�Ȑ������B��Ă���B
�@���`�p�o�ɂ����āA�`�l�́ڂo�`�p�̓����ł���A�`�m�́ڂo�`�p�̊O�p�̓�����
�Ȃ��Ă���B
�@���̂Ƃ��A�@�`�p �F �`�o �� �p�l �F �l�o�@�A�@�`�p �F �`�o �� �m�p �F
�m�o�@ �����藧�B
���Ȃ킿�A�@�p�l �F �l�o �� �m�p �F �m�o�@ ���A
�@�m�p �F �p�l �� �m�o �F �o�l�@
�����藧�B
�@���̂悤�ȊW�����P������̓_�� �o�C�p �G �l�C�m �����a�_���ł���Ƃ����B
���̂Ƃ��A���̎������m���Ă���B
�@�~�n�ɉ~�O�̂P�_�o���璼���k�������A���̌�_���l�A�m�Ƃ����B�l�C�m �G
�o �ƒ��a�_��Ƃ�
��_���p�Ƃ����B�_�o�𒆐S�Ƃ��āA�����k����]������ƁA�_�p�̋O�Ղ́A�����ƂȂ�B
�@���̒����k���~�n�Ɋւ���_�o���ɐ��Ƃ����A�_�o���ɓ_�Ƃ����B
����ɁA���̎������m���Ă���B
�@�~�n�Ɋւ���_�o�̋ɐ��́A�o�Ƃn�����Ԓ����ɐ����ł���B
���������āA��}�ɂ����āA�_�� �o�C�p �G �l�C�m �͒��a�_��ł���A�n�o�Ƃ`�a�͐����Ȃ̂ŁA
�����`�a���~�n�Ɋւ���_�o�̋ɐ��ƂȂ�B
�@����āA���̂悤�ȋɐ����݂̂ō�}���邱�Ƃ��\�ł���A�ڐ��̍�}���\��
�Ȃ�B
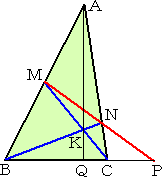 |
�@�Ƃ���ŁA���}�ɂ����āA�`�F�o�̒藝�ƃ��l���E�X�̒藝��p
���āA
�@�@�@�@ �@�@�a�p �F �p�b �� �a�o �F �o�b
�����藧���A�S�_�o�C�p �G �b�C�a �͒��a�_��ƂȂ�B
�@���}�ɂ��A���̍�}���@�����������B |
�@
�@��}�ł́A�f�p�ȕ��@�Őڐ�����}���Ă��邪�A�}�����������悤�ɁA�����ƊȒP�ȍ�
�}���@�����݂���B�i�ǎ҂̊F����́A�}�������ƒ��߂āA�l���Ă݂Ă��������B�j
�i�Q�l�����F�X���S���W�F�t�X�L�[�@���@�������b�E��h��@��@��ɂ���}
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����}���j�j
�i�NjL�j�@�����Q�R�N�X���Q�S���t��
�@���g�o�̓ǎ҂̂r������A�֘A����b������[���Œ������B
 |
�@�@�@�~�n�̊O���̓_�o���A���S��ʂ钼���������A
�@�@�o�`���P�A�o�a�����@�Ƃ���B��L�̕��@�ŁA�ڐ��o�s
�@�@����}�o����Ƃ��A�@�o�s���め�@�����藧�B
�@�@�i�ؖ��́A���ׂ��̒藝��薾�炩���낤�B�j |
�@�^����ꂽ�����̒����i���j���A�め����}������@�́A���낢��l�����邪�A
�@
�@��}�ɂ����āA�����P�@�ƍl����A��}���@�͖��炩���낤�B
�����̒��_
 |
�@�@��ƃR���p�X��p���āA�����̒��_�����߂邱�Ƃ͈�
�@�����B�i���Q�l�F�����̓������j
�@�@����ł́A���}�̂悤�ȉ~���^����ꂽ�Ƃ��A�����`�a��
�@���_���݂̂�p���č�}���邱�Ƃ͂ł��邾�낤���H
�@�@�i���̖��́A�n���h���l�[�� tappon�@����Ƃ���������
�@�@�@�������������̂ł���B�j
�@�@�@�����́A�\�ł���B
�@�@�@�~�̒��S�͒��a���Q�������邱�Ƃ𗘗p���āA���a��
�@�@���s�Ȓ�������}�ł��邱�ƂɋC�����悢�B
�@�~�n�̔C�ӂ̒��a���o�p�Ƃ��A�����o�a��ɔC�ӂɓ_�q��
�Ƃ�B |
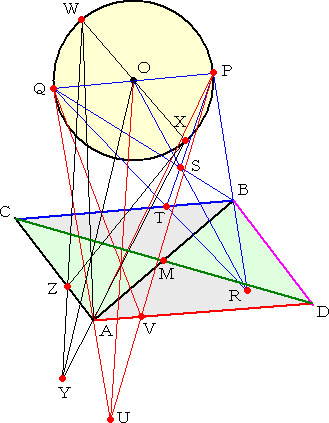 |
�����a�p�Ɛ����q�n�̌�_���r�Ƃ��A��
���o�r�Ɛ����p�q�̌�_���s�Ƃ���ƁA
�����a�s�́A���a�o�p�ɕ��s�ł���B
�@���l�ɂ��āA���a�o�p�ɑ��āA����
�p�`��̔C�ӂ̓_�t����_�u����}��
����B
�@���̂Ƃ��A�����`�u�́A���a�o�p�ɕ��s
�ł���B
�@�܂��A�~�n�̔C�ӂ̂o�p�Ƃ͕ʂ̒��a
���v�w�Ƃ��A�����w�`��̔C�ӂ̓_�x����
�_�y����}�ł���B
�@���̂Ƃ��A�����`�y�́A���a�v�w�ɕ��s
�ł���B
�@�@���l�ɂ��āA�_�a��ʂ�A���a�v�w��
�@���s�Ȓ�������}�ł���B
�@���̂Ƃ��A���߂�_�l�͕��s�l�ӌ`
�`�c�a�b�̑Ίp���̌�_�ł���B |
�Q�F�P�̕��_
�@���̒��ɁA��}�̌��ʁA�Q�F�P�ɕ�����_�ƂȂ�ꍇ�͂�������B�����A�Ƃ����Ɂu���̂�
���ȓ_����}����B�v�ƌ���ꂽ��A���̑����̐l�́A�������R�������āA�Q�F�P�ɓ�������_
���w���������Ƃ��낤�B�i�Q�l�F�����̓������j
�@�������Ȃ���A��ԗL���ȁu�Q�F�P�ɕ�����_�v�́A�����A�O�p�`�̏d�S�ł���B
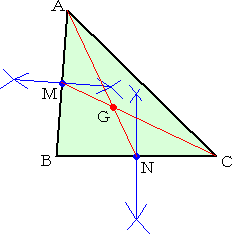 |
�@�@���`�a�b�ɂ����āA
�@�ӂ`�a�A�a�b�̒��_�����ꂼ��l�A�m�Ƃ���Ƃ��A
�@�����`�m�Ƃb�l�̌�_���A�d�S�f�ł���B
�@�@�d�S�f�́A�����`�m���A�Q�F�P�ɓ�������B
�@�@���}�ł́A��E�R���p�X��p���āA���_����}��
�@�Ă��邪�A�������A�R���p�X�݂̂�p���č�}�\
�@�ł���B���������āA�d�S�f���R���p�X�݂̂ō�}��
�@�\�ł���B�i ���@�Q�l �F ���] �j |
�@�d�S�ȊO�ɁA�u�Q�F�P�ɕ�����_�v�̍�}����܂Ƃ߂Ă݂悤�B
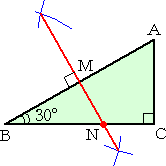 |
�@�@�@�a���R�O���̒��p�O�p�`�`�a�b�ɂ����āA�Εӂ`�a�̐�����
�@�@���������ӂa�b�ƌ����_���m�Ƃ����ƁA
�@�@�@�m�́A�ӂa�b���A�Q�F�P�ɓ�������B |
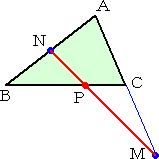 |
�@�@�@���`�a�b�ɂ����āA
�@�@�ӂ`�b�̉�����ɁA�`�b���b�l�ƂȂ�_�l���Ƃ�B
�@�@�@�ӂ`�a�̒��_�m�Ƃl�����сA�ӂa�b�Ƃ̌�_���o�Ƃ����B
�@�@�@���̂Ƃ��A�o�́A�ӂa�b���A�Q�F�P�ɓ�������B
|
 |
�@�@�@���`�a�b�ɂ����āA
�@�@�ӂ`�a�̒��_���l�Ƃ��A�����l�b�̒��_���m�Ƃ����B
�@�@�@�����`�m�ƕӂa�b�Ƃ̌�_���o�Ƃ����B
�@�@���̂Ƃ��A�o�́A�ӂa�b���A�Q�F�P�ɓ�������B |
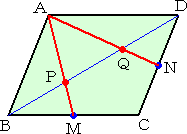 |
�@�@�@���s�l�ӌ`�`�a�b�c�ɂ����āA
�@�@�ӂa�b�A�b�c�̒��_�����ꂼ��l�A�m�Ƃ����B
�@�@�@�����`�l�A�`�m�ƑΊp���a�c�Ƃ̌�_���A���ꂼ��o�A�p��
�@�@�����B
�@�@���̂Ƃ��A�o�A�p�́A�Ίp���̂R�����_�ł���B |
�����̓��{
�@�~�̂S�����ŗp����ꂽ���@�����p����A�����̓��{���R���p�X�݂̂ō�}���邱��
���ł���B
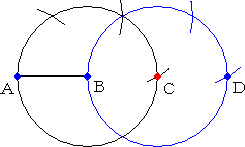 |
�@�@���}�߂�A���炩�ł��낤�B
�@�@�_�a�𒆐S�Ƃ��Ĕ��a�`�a�̉~��`���A�~�����U��
�@��������@�ɂ��_�b�����߂���B
�@�@���̂Ƃ��A�����`�b�͐����`�a�̂Q�{�ɂȂ��Ă���B
�@���l�ɂ��āA�����`�a�̂R�{�ɂȂ�_�c����}�ł���B |
�~�̒��S
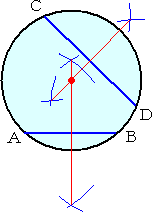 |
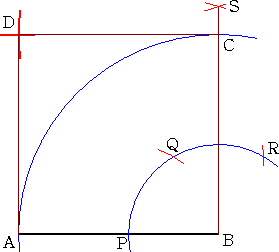
�@�@�@��ƃR���p�X��p���āA�~�̒��S�����߂邱�Ƃ͈Ղ����B
�@�@�@�C�ӂɒ��p���āA���`�a�A�b�c�������A�e�����̐�����
�@�@��������}����悢�B
�@�@�@���̂Ƃ��̌�_���A���߂�~�̒��S�ƂȂ�B
�@�����ł́A�R���p�X�݂̂��g���ĉ~�̒��S�����߂���@���l����B |
 |
�@�@�@�~����ɔC�ӂɂP�_�`���Ƃ�B�_�`�𒆐S�Ƃ���C
�@�@�Ӕ��a�̉~��`���A���̌�_���o�A�p�Ƃ���B
�@�@�@�Q�_�o�A�p�𒆐S�Ƃ����a�`�o�̉~�ʂ����ꂼ��`
�@�@���A���̌�_���a�i������́A�`�j�Ƃ���B
�@�@�@���̂Ƃ��A�~�`�Ɋւ��āA�_�a�ƑΏ̂ȓ_�n����}
�@�@����A�_�n�����߂�~�̒��S�ƂȂ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i���@�Q�l �F ���] �j
|
�@�����ŁA��}�̉�͂����Ă������B
�@��}���@����A�`�n�E�`�a���`�o2 �Ȃ̂ŁA���炩�ɁA���`�o�n �� ���`�a�o�@�ł���B
���̂Ƃ��A���`�a�o�ɂ����āA�`�o���a�o �Ȃ̂ŁA�n�`���n�o �ƂȂ�B
���l�ɂ��āA���`�p�n �� ���`�a�p�@�Ȃ̂ŁA�n�`���n�p �ƂȂ�B
���������āA�_�n�́A�~����̂R�_�`�A�o�A�p���瓙�����ɂ���_�Ȃ̂ŁA�~�̒��S�ƂȂ�B
�i�NjL�j�@�����Q�O�N�T���P�X���t���ŁA���g�o�̌f���u�o��̐�v�ɁA�g�m�u�ق��ق��v����
�@�@�@�@�@���玟�̂悤�ȏ������݂��������B
�@���w�l�N�̑��q�̎Q�ϓ��́A�u���ȏ��t�^�̎��̉~�ՂƓ����傫���̉~���R���p�X�ŕ`
���v�Ƃ������Ƃ������B�����ł́A�~�̔��a�����߂邽�߂ɁA���̉~�Ղ��l���~�ɐ܂��Ē�
�S�����߁A��������~���܂ł̋����a�Ƃ��āA�~��`���Ă����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�ӂ����Ȃ���A�͔����炵���D�D�D(^^;)
�j
�����ŋ^��B���ꂪ���łȂ��܂�Ȃ��S�Ƃ��̉~�Ղ�������A�ǂ�����̂��낤�A�Ƃ������ƁB
���w�l�N�Ȃ̂ŁA�܂����s�̊T�O�������������K���ĂȂ����D�D�D�B�Ȃɂ��������@
�͂���̂��낤���H
�@���̖₢�����ɑ��āA���g�o�����������b�ɂȂ��Ă���A�炷���邳��́A�T���Q�O��
�t���Ōf���ɁA
�@�u���钼���̂���_��ʂ肻�̒����Ɛ����Ȓ����v�̍�}���\�Ȃ�A�~���ɒ����`
���`���āA�Ίp���̌�_�����߂�~�̒��S�ł���B
�Ə������܂�Ă���B�����A�炷���邳��̈Ӗ�����Ƃ���͉��}�̒ʂ肩�ȁH
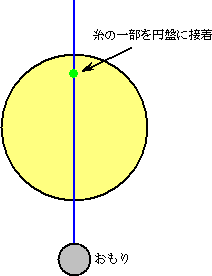
�@
�@���́u���w�l�N���v�����ɍl�������@�́A�d�͂𗘗p������́B�C���[�W�}�͉��}�B����
�Ő��m�ɒ��S�����߂���̂��Ɠ˂����܂��A���ƂȂ������������邵���Ȃ���@��
���D�D�D�B
�i�ق��ق�����̑��q����́A�u�R�łƂ߂�̂͌��������ĂȂ��Ɠ����Ȃ��H�v��
�c�b���܂�Ă��܂��������ł���B�i���n���D�D�D�B�j�u�Z���e�[�v���g�������Ƒ��v�v�ƃt�H
���[���Ă��������������Ŋ��ӂ��܂��B�G�`�ƁA���̏ꍇ�̑z��́A�A�����A���t�@�Ȃǂ̏u
�Ԑڒ��܂�A�������ʂ̔S���������g�����̂ł��D�D�D�B�j
�@
�@�@���̑�����A�~���̕ʂȓ_�ł��s���A�Q�̒����̌�_���~�̒��S�ƂȂ�B
�@���w�l�N�������Ƃ������ƂȂ̂ŁA�u���]�v��p���邱�Ƃ���������A�u�ق��ق��v����̖�
�������Ɍ����ɓ�����Ƃ���A��L�ŏq�ׂ��u���]�ɂ��~�̒��S�̍�}�v�������菇
�ƂȂ邾�낤�B
�i�NjL�j�@�����Q�O�N�T���Q�Q���t��
�@���̌ア�낢��ȕ�����A�C�f�A�Ղ����̂ł܂Ƃ߂Ă��������B
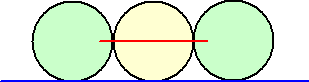
�@�o��҂́u�ق��ق��v����D�D�D�D
�@�F�B����~�Ղ���Ă��ĉ��}�̂悤�ɒ�����ɕ��ׁA���a�����߂�B����������A�~��
������]�����čs���B�Q�̒��a�̌�_���~�̒��S�ƂȂ�B
�@
�@���g�o�����������b�ɂȂ��Ă���u�j�������v�����v����D�D�D�D
�@�O�p��K�̒��p�̕������~���ɂ��Ă����A�ΕӈȊO�̂Q�ӂƉ~���Ƃ̌�_�����Ԃƒ��a
��������B���̑�������Ă����ꏊ��ς��čs���A�Q�̒��a�̌�_���~�̒��S�ƂȂ�B
�@
�@���g�o�����������b�ɂȂ��Ă���u�J���s�X�v����D�D�D�D
�@�~����ɈقȂ�R�_���Ƃ��āA�O�p�`�̊O�ډ~�̒��S��ӂ̐����Q�������������ċ���
��B
�i�R�����g�j�@��������`���l�̗\���m���ɉ��������@�ŁA�u�A���v���낤�B
�~�̐ڐ��R�@�i�~�̒��S��p���Ȃ��ŁA�~����̔C�ӂ̓_�Őڐ��������j
�@�����P�V�N�T���Q�O���A���g�o�����������b�ɂȂ��Ă���g�m�u�炷����v������A���[��
�Ղ����B�����ɂ́A�a�V�ȉ~�̐ڐ��̍�}���@��������Ă����B
�@��T�Ԓ��O�i�T���P�S���j�ɉ~�̐ڐ��������ʔ������@���l����ꂽ�Ƃ̂��ƂŁA���̕��@
�𑽂��̕��ɖ��ɗ��悤�ɋL�^�Ƃ��Ďc���Ăق����Ƃ����炷���邳��̎v�������g�o�̂�
�̃y�[�W�ɑ����ꂽ�B
�@���g�o�́u�~�̐ڐ��v�ł́A�~�̒��S���{���I�Ȗ������ʂ����Ă����B�炷���邳��̍l
�Ă��ꂽ���@�́A�~�̒��S��������Ȃ��Ă���}���\�ŁA�������A�������Q��R���p�X��
���p���邾���ł���B
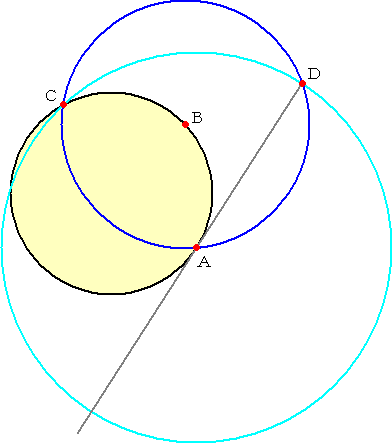 |
�i��}���@�j
�@�@�^����ꂽ�~�n�Ƃ��̎���
�@�̓_���`�Ƃ���B
�@�i�P�j �~�n�̉~����̔C�ӂ�
�@�@�@�_�a�𒆐S�Ƃ��ē_�`���
�@�@�@��~��`���A�~�n�Ƃ̂���
�@�@�@��̌�_���b�Ƃ���B
�@�i�Q�j �_�`�𒆐S�Ƃ��ē_�b��
�@�@�@�ʂ�~��`���A�~�a�Ƃ̂�
�@�@�@����̌�_���c�Ƃ���B
�@�i�R�j �_�c�Ɠ_�`�����Ԓ�����
�@�@�@���߂�ڐ��ƂȂ�B |
�@�����ŁA�m���ɐڐ��ƂȂ邱�Ƃ��m�F���Ă݂悤�B�i�ؖ��͈Ղ����I�j
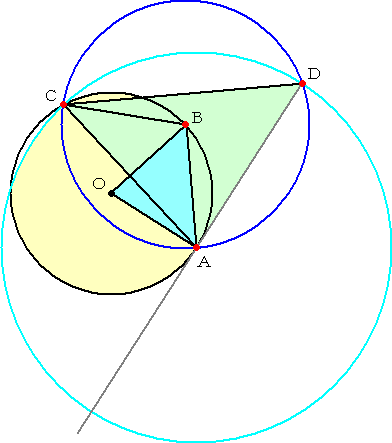 |
�ڂa�b�`���� �Ƃ����ƁA
�ڂa�n�`���Q�Ɓ@�ł���B
�@�܂��A���`�a�b�͓ӎO�p
�`�Ȃ̂ŁA�ڂa�`�b���Ƃł���B
�@����āA
�@�@�ڂ`�a�b���P�W�O���|�Q��
���A�@�ڂ`�c�b���X�O���|��
�@�@�����ŁA���`�c�b�͓ӎO
�@�p�`�Ȃ̂ŁA
�@�@�@�ڂ`�b�c���X�O���|��
�@����āA�ڂc�`�b���Q�ƂƂȂ�B
�ڂa�`�b���Ɓ@�Ȃ̂ŁA
�@�@�ڂa�`�c���Q�Ɓ|�Ɓ���
�@�ȏォ��A�ڂa�b�`���ڂa�`�c
�����藧���A�ڌ��藝�ɂ��A
�����`�c�́A�~�n�̓_�`�ɂ���
��ڐ��ƂȂ�B |
�i�R�����g�j�@�ƂĂ��X�b�L��������}���@�ł��ˁI�Ƃ���ŁA�ؖ��ɂ͎g���Ă��܂��A
�@�@���n�`�a�Ɓ��`�c�b�������ɂȂ邱�Ƃɂ��A���͐S�䂩�����̂�����܂����B���������
�@�@�V���肪��ꂻ���ł��B���̂悤�ȋ@���^���Ă����������A�炷���邳��Ɋ��ӂ���
�@�@���܂��B
�������̏œ_�E��
 |
�@�@�@��ƃR���p�X��p���āA�C�ӂɗ^����ꂽ��������
�@�@�œ_�Ǝ�����}������@���l����B
�@�@�@�i���̕��@�́A�n���h���l�[�� tappon�@����Ƃ�������
�@�@�@�������������������̂ł���B�j
|
�@�������ɑ��āA�C�ӂɕ��s�ȂQ���� �`�a�A�b�c
�������B�����̒��_�� �l�A�m �Ƃ��A�����l�m�ƕ�
�����Ƃ̌�_�� �d �Ƃ���B
�@�_ �d �ɂ����āA�����`�a�ƕ��s�Ȓ����d�w������
�ƁA����́A�_ �d �ɂ�����ڐ��ƂȂ�B
�@�����l�m�ɐ����Ȑ����o�p��C�ӂɈ����A����
�����Q�������q�x�́A�������̎��ƂȂ�B
�@�_ �d �ɂ�����ڐ��Ɋւ��āA�����l�m�ƑΏ̂�
�����������A�����q�x�Ƃ̌�_���A�e �Ƃ����ƁA�_�e
�́A�������̏œ_�ƂȂ�B |
�@�@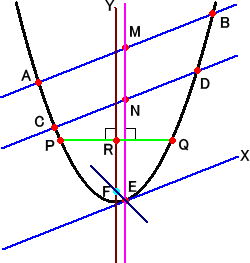 |
�i��́j�@�ȒP�̂��߁A�������̕��������@������2�@�Ƃ���B
�@�@���̕������ɔC�ӂɒ��� �� �� ���� �{ ���@�������B���̂Ƃ��́A��_�� �� ���W�́A�Q����
�@�����@��2 �| ���� �| �� �� �O�@�̉��ƂȂ�B���̂Q�̉����A���A�� �Ƃ����ƁA���ƌW���̊�
�@�W����A�@�� �{ �� �� ���@�ƂȂ�B
�@�@���������āA�����`�a�A�b�c�̒��_�l�A�m�� �� ���W�́A�Q�����`�a�A�b�c�����s�Ȃ�A����
�@�l�ƂȂ�A�����l�m�́A�������̎��ɕ��s�ƂȂ�B
�@�@�_ �d �̎�������A�����d�w�͕������̐ڐ��ƂȂ�B
�@���ɕ��s�Ȓ����l�m�ɐ����Ȑ����o�p�̐����Q�������́A���炩�ɁA�������̎��ƂȂ�B
�@���ɕ��s�ȓ��ˌ����l�d�́A�������̐�������A�_ �d �Ŕ��˂��āA�œ_ �e��ʂ�B����
�@�����𗘗p���āA�������̏œ_����}�����B
�Q�_�����Ԑ���
�@�Q�_�����Ԑ������ň����Ƃ��A�����^��Ɏv�����Ƃ�����B�^����ꂽ��Ƃ���
�̂́A�ǂ�Ȃɉ����ɗ��ꂽ�Q�_�ł��P��̑���Œ����������Ă��܂��قǂ̂��̂Ȃ̂�
�ƁB�i�����A�w�̐��E�̒�̒�`���炷��ƁA��Ƃ������̂͂����������̂Ȃ�
���낤�I�j
�@�^����ꂽ�Q�_�����т����̂ɁA��̒���������Ȃ��Ƃ������Ƃ́A�����̐��E�ł́A
�����Β��ʂ��邱�Ƃł���B���ʂ�������A�K���ɂQ�_�Ԃɒ�������āA�ڕ��ʂň�
���Ă��܂��Ă�����������Ǝv���邪�A�����ł́A�R���p�X�����p���Ĉ������Ǝv���B
�@�P��̑���Ő����������Ȃ��قǁA������x���ꂽ�Q�_�`�A�a���^�����Ă�����̂�
����B
�@�����ŗp����R���p�X�́A�w�ɂ������`���炷��A�C�Ӕ��a�̉~�ʂ�������
�͂��ł��邪�A����������I�ł͂Ȃ��B�Q�̏ꍇ�ɕ����čl���悤�B
�@�Q�_�`�A�a�𒆐S�Ƃ���~�ʂ������ꍇ �F �R���p�X�ŕ`����~�ʂ̔��a�������`�a�̔���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�ȏ�̏ꍇ
�@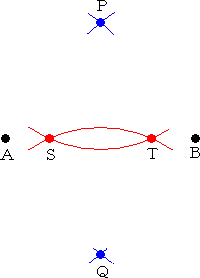 |
�@�@�@�Q�_�`�A�a�𒆐S�Ƃ���~�ʁi���ꔼ�a�j�̌�_���A
�@�@�o�A�p �Ƃ���B
�@�@�@���ɁA�Q�_�o�A�p�𒆐S�Ƃ���~�ʁi���ꔼ�a�j�̌�
�@�@�_���A�r�A�s �Ƃ���B
�@�@�@�����r�s�ƒ����`�a�͓���̒����ł���B
�@�@�@�Q�_�r�A�s���A�P��̑���Ő����������Ȃ��Ƃ��́A
�@�@��L�̑�����J��Ԃ��āA�P��̑���Ő�����������
�@�@�܂ŁA�Q�_�Ԃ̋������k�߂邱�Ƃ��o����B
�@�@�@���̂悤�ɁA�����`�a��ɕ��_����������}���āA��
�@�@�������Ԃ��Ƃɂ��A�����`�a����}���邱�Ƃ��ł���B |
�@�Q�_�`�A�a�𒆐S�Ƃ���~�ʂ������Ȃ��ꍇ
�F �R���p�X�ŕ`����~�ʂ̔��a�������`�a�̔�����菬�����ꍇ
�@���̏ꍇ�́A��L�̂悤�ȍ�}���s�\�Ȃ̂ŕʂȕ��K�v�ƂȂ�B
�@ |
�@�@�@�Q�_�`�A�a��������Q������C�ӂɈ����A��_���A
�@�@�o �Ƃ���B
�@�@�@���ɁA�`�o�A�a�o �̒��_���A�l�A�m �Ƃ���B
�@�@�@�����l�m�������A����ƕ��s�ɒ����`�a��������
�@�@�悢�B
�@�@�@�����l�m�������Ȃ��ꍇ�́A�R�����_�A�S�����_�D�D�D
�@�@���l����悢�B
�@�@�@�����`�o�A�a�o�������Ȃ��ꍇ�́A�Q�_�`�i�a�j�A�o�ɑ�
�@�@���āA��L�̑�����s���悢�B |
�����̐���
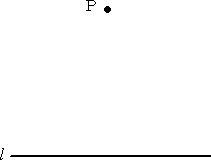 |
�@��ƃR���p�X��p���āA�����O�̂P�_���璼���ɐ���
���������Ƃ͈Ղ����B
�@�����ł́A��݂̂��g���āA�����O�̂P�_�o���璼��
�ɐ��������낷���@���l����B
�@�������A������ɒ��S�����~���^�����A�_�o�́A�~
�̊O���ɂ�����̂Ƃ���B |
�@�^����ꂽ�~�̒��a���`�a�Ƃ��A�����o�`�A�o�a�Ɖ~
�Ƃ̌�_���A���ꂼ�� �r�A�s �Ƃ���B
�@�Q�_�`�Ƃs�A�a�Ƃr�����сA���̌�_���p�Ƃ����B
�@���̂Ƃ��A�����o�p�́A�^����ꂽ���� �� �̐���
�ƂȂ�A�_�g�́A���̂Ƃ��̐����̑��ł���B |
�@�@�@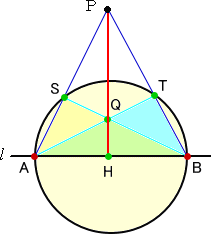 |
�@���̍�}�@�́A�O�p�`�̂R�����͂P�_�Ō����Ƃ��������𗘗p���Ă���B
�@��L�ł́A�_�o�́A�~�̊O���ɂ�����̂Ƃ������A�����ɂ���ꍇ�͎��̂悤�ɍl�����
�悢�B
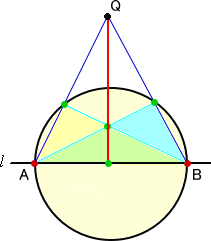 |
�@�@�~�O�ɔC�ӂɓ_�p���Ƃ�A��L�̂悤�ɐ�������������
�@���o����B
�@�@���l�ɂ��āA�����P�{�������������Ƃ��o����B |
�@���̂Ƃ��A���s���ŏq�ׂ����@�ɂ��A�~����
�_�o��萂�����������Ƃ��o����B |
�@�@�@�@�@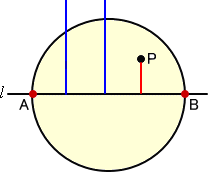 |
�i�R�����g�j�@���������b�ɂȂ��Ă���炷���邳��A���̘b��ɂ��ă��[�������B
�@�@�i�����P�V�N�V���U���t���j
�@��L�ł́A�^����ꂽ�������~�̒��a��ɂ�����̂Ɖ��肵�����A�炷���邳��ɂ��A
�~���ǂ��ɗ^�����Ă��Ă������������邻�����B(���@�͌��\���G�炵���B)����ǂ��납�A
�~�Ƃ��̒��S���ǂ����Ɉ�^�����Ă��邾���ŁA�R���p�X�ƒ�ō�}�o������̂͑S
�āA������ō�}�o����Ƃ̂��Ƃł���B
�@����ɂ��ẮA����̌����ۑ�Ƃ��悤�B�i���@�Q�l�F�u��ɂ���}�v�j
�p�̈ړ�
�@��A�R���p�X��p���āA�^����ꂽ�p���A�C�ӂ̈ʒu�Ɉڂ����Ƃ͈Ղ����B
�@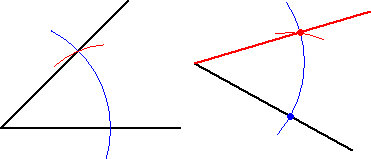
�@����ł́A�R���p�X�݂̂�p���č�}����ɂ́A�ǂ�������悢�̂��낤���H
���܁A���ʏ�ɂR�_�`�A�a�A�b���^�����Ă��āA�ڂa�`�b��C�ӂ̈ʒu�Ɉړ����������B
�@
�@���ʏ�̔C�ӂ̓_���A�`�f�Ƃ��A����ɁA�`�f�a�f���`�a�ƂȂ�_���^�����Ă�����̂Ƃ���B
���̂Ƃ��́A���}�̂悤�ɍ�}����悢�B
�@
�@��L�̍�}�̍����́A�@���`�a�b�߁��`�f�a�f�b�f�@�ł���B
�@��L�ł́A�`�f�a�f���`�a�ƂȂ�_�a�f�����炩���߉��肵�����A�a�f���C�ӂ̈ʒu�ɂ���Ƃ�
�́A�ǂ���}����悢�̂��낤���H
�~�ɐڂ���~
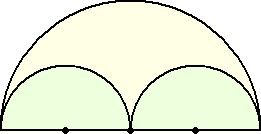 |
�@�@�@���}�̂悤�ɁA���~�̒��ɓ����a�̔��~��
�@�@�ڂ��Ă���B
�@�@�@���̂Ƃ��A�Q�̏����~�ɊO�ڂ��A�唼�~��
�@�@���ڂ���~�́A���̂悤�ɍ�}�����B |
�@�唼�~�̒��a���P�ӂƂ��鐳���`��`���A
�����`�̒��_�ƂQ�̏����~�̒��S�`�A�a
�����Ԑ����̌�_���b�Ƃ���B
�@���̂Ƃ��A�_�b�����߂�~�̒��S�ƂȂ�B |
�@�@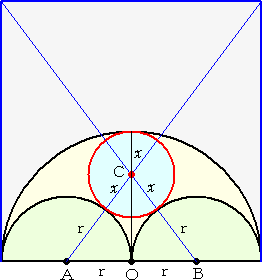 |
�@�����ŁA��}�̉�͂����Ă������B
�@���߂�~���E��}�̂悤�ɍ�}�ł������̂Ƃ���B
�@���p�O�p�`�b�`�n�ɂ����āA�O�����̒藝���A�@��2�{�i�Q���|���j2���i���{���j2
�@����āA�����Q��/�R�@�ƂȂ�B���̂Ƃ��A�@�`�n�����A�b�n���S��/�R�A�b�`���T��/�R�@�Ȃ̂ŁA
���p�O�p�`�b�`�n�́A�ӂ̔䂪�A�R�F�S�F�T�@�̎O�p�`�ƂȂ�B
���l�ɁA���p�O�p�`�b�a�n���A�ӂ̔䂪�A�R�F�S�F�T�@�̎O�p�`�ƂȂ�B
�@�ȏォ��A���߂�~�̒��S�́A��}�̂悤�ȍ�}�œ�����B
�@�Ƃ���ŏ�L�ł͏����~�̔��a�͓������Ɖ��肵������ʂ̏ꍇ�͂ǂ��Ȃ�ł��낤���H
�@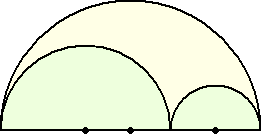
�@���߂�~�̔��a�́A��͓I��@�ŋ��߂���B
 |
���b�`�n�Ɓ��b�a�n�ɂ����ė]���藝��p���āA
�@�@�@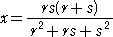
�@�@���A���߂�~�̔��a�ł���B |
�@���ۂɁA���b�`�n�ɂ����āA�b�`�����{���@�A�`�n�����@�A�n�b�����{���|���@�Ȃ̂ŁA
�@�������ڂ`�n�b���i�i���{���|���j2�{��2�|�i���{���j2�j/�i�Q�i���{���|���j���j
���l�ɁA���b�a�n�ɂ����āA�b�a�����{���@�A�a�n�����@�A�n�b�����{���|���@�Ȃ̂ŁA
�@�������ڂa�n�b���i�i���{���|���j2�{��2�|�i���{���j2�j/�i�Q�i���{���|���j���j
�ڂ`�n�b�{�ڂa�n�b���@�Ȃ̂ŁA�@�������ڂ`�n�b���|�������ڂa�n�b
����āA�@�@���i�i���{���|���j2�{��2�|�i���{���j2�j���|���i�i���{���|���j2�{��2�|�i���{���j2�j
�@���i���{���j2�|�Q�����i���{���j�{����2�{����2�|��3�|�Q��2���|����2
���|���i���{���j2�{�Q�����i���{���j�|����2�|����2�{��3�{�Q��2���{����2
�@�Q���i���i���{���j�{��2�{���i���{���j�{��2�j�����i���{���j2�{����2�|��3�{���i���{���j2�{����2�|��3
���������āA
�@�S���i��2�{�����{��2�j���i���{���j3�|�i���|���j�i��2�|��2�j
���i���{���j�i�i���{���j2�|�i���|���j2�j���S�����i���{���j
�@������A
�@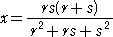
�����藧�B
�@���̉�͓I��@�ŋ��߂��~���I�ɍ�}������@�͂���̂��낤���H
�@���̌��Ɋւ��āA���g�o�����������b�ɂȂ��Ă���g�m�F�炷���� ����A��L�̍�}
���@�����������|�A���[���������������B�i�����P�V�N�W���X���t���j
�@������������}���@�́A��L�̏ꍇ�̎��R�Ȉ�ʉ��ɂȂ��Ă���A�ƂĂ��N�₩�Ȃ���
�ŁA�v�킸�������Ă��܂����I�炷���邳��Ɋ��ӂ������܂��B
 |
�@�@�@���}�̂悤�ɁA�唼�~�̒��a���P�ӂ�
�@�@���鐳���`���Q�`���A�����̐����`��
�@�@�ӂ̒��_���o�Ƃ���B
�@�@�@�����o�a�Ɛ����`�Ƃ̌�_���p�Ƃ����B
�@�@�@�܂��A�����`�p�ƒ����o�e�Ƃ̌�_���b
�@�@�Ƃ���B
�@�@�@���̂Ƃ��A�_�b�����߂�~�̒��S�ƂȂ�B
�@�@�i�R�����g�j�@���������ł������悤�ɁA����
�@�@�@�@�@�@�@�@�ǎ҂̕����A���̂悤�ȒP����
�@�@�@�@�@�@�@�@��}�Ŗ{���ɏ��v�̂��̂���
�@�@�@�@�@�@�@�@���Ă��邩�ǂ����A���M���^
�@�@�@�@�@�@�@�@���낤�Ǝv���B
�@�@�@�@�@�@�@�@�i�炷���邳��A����I�j
�@�@�@�@�����ŁA��}�̉�͂����āA�{���ɋ�
�@�@�@�߂�_�������邱�Ƃ��m�F���悤�B
�@�@�i��́j�@�@���߂�~�����}�̂悤�ɍ�}
�@�@�@�@�@�@�@�ł������̂Ƃ��A�����`�b�̉���
�@�@�@�@�@�@�@�Ɛ����`�Ƃ̌�_���p�Ƃ���B
�@�@�@�@���`�a�b�ɂ����āA�]���藝���A
�@�@�@�@�@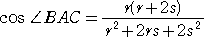
|
�ƂȂ�̂ŁA
�@�@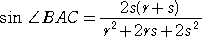
���Ȃ킿�A
�@�@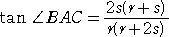
���̂Ƃ��A
�@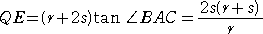
���A
�@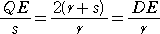
�����藧�B
�@�����ŁA�n�a�� �� �ɒ��ӂ��ď�}�̂悤�ɁA�c�d���n�o �ł���悤�ɓ_�o���Ƃ�A�㎮�́A
�@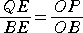
�����藧���Ƃ��Ӗ�����B
�@����āA�Q�̒��p�O�p�`�a�d�p�Ƃa�n�o�ɂ����āA�@���a�d�p�䁢�a�n�o
�ƂȂ�A
�R�_�o�A�a�A�p �͂P������ɂ��邱�Ƃ�������B
�@�܂��A��L�̎O�p��̒l��p���āA
�@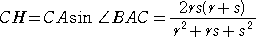
�@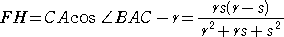
�ł���̂ŁA
�@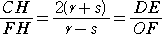
�����藧�B
�@����āA
�@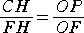
�����藧���Ƃ���A�Q�̒��p�O�p�`�e�g�b�Ƃe�n�o�ɂ����āA�@���e�g�b�䁢�e�n�o
�ƂȂ�A
�R�_�o�A�e�A�b �͂P������ɂ��邱�Ƃ�������B
�@�ȏォ��A��L�̍�}���@���Ƃ�A���v�̂��̂������邱�Ƃ����������B�i�I�j
�i�NjL�j�@�����P�X�N�T���Q�O���t��
�@�T���P�X���t���ōL���ݏZ�̂r���畽���P�U�N�X���Q�R���ȗ��̃��[�������B����
�Ƃ��́AVISUAL�@BASIC���c�[���ɂ��ăv���O����������Ă���Ƃ̂��Ƃł��������A���A
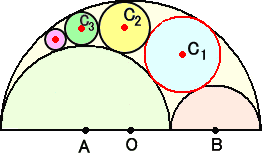
�~�̃O���t�ɊS�������Ă�����Ƃ̂��ƂŁA���̂悤�Ȗ����N���ꂽ�B
�P�D�@�傫�ȉ~������A���̒��ɓ��ډ~��`���Ă����B��̏ꍇ�͓��S�~�œ������a�̂�
�@�@�̂�`���������A��A�O�̏ꍇ���ł���B�l�̏ꍇ���ǂ��ɂ��ł���B
�@�@�@�����ŁA�C�ӂ̌��̉~��`���ꍇ�ɁA���ꂼ��̉~�̒��S���W�ƒ��S�̍��W�̈�
�@�@�ʎ��͂���̂��낤���H����Ƃ���ǂ��Ȃ�̂��낤�H
�Q�D�@���~�̒��a��ɒ��S�����Q�̓��ډ~��`���A���̌�A���̌��Ԃɓ��ډ~�����X
�@�@�ƕ`���Ă����ꍇ�̂��ꂼ��̉~�̒��S���W�ƒ��S�̍��W�̈�ʎ��͂ǂ��Ȃ�̂���
�@�@�����H
�i�R�����g�j�@�P�D�Q�D�ɂ��ẮA�]�ˎ���̘a�Z�Ɓi�֍F�a�⌚�����O�Ȃǁj�����Ȃ茤��
�@�@�@�@�@�@���Ă��āA����������T���ƎQ�l�ɂȂ�L�q������Ǝv���܂��B�����Ƃ��ẮA
�@�@�@�@�@�@�u���{�̊@��������܂����v���L���ł��傤�B
�@�@�@�@�@�@�@���ɁA�Q�D�ɂ��ẮA�m�ڂ̓��ډ~��`�����Ƃ��A���̒��S������Ƃ̔��~
�@�@�@�@�@�@�̒��a�ɉ��낵�������̒������m�ڂ̓��ډ~�̒��a�̂m�{�ɂȂ�Ƃ�������
�@�@�@�@�@�@����肭�g���ƁA�r����̊�]�����������ł��ˁI
�@��L�Ōv�Z�����悤�ɁA�P�ڂ̉~�̔��a �� �́A
�@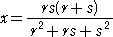
�ł������B���̉~�̒��S�b���璼�a�ɉ��낵�������̒��� �x �ɂ���
�@�x���Q���@�@�i�������̒��������ډ~�̒��a�ɓ������j
�ɂȂ��Ă��邩�ǂ������ۂɒ��ׂĂ݂悤�B
�@�w�����̌�����p���āA
�@�i���`�a�b�j2���������i���{���{���j�����i�i��2�{�����{��2�j���{�������j����2�i���{���j2
�܂��A�@���`�a�b���i���{���j�x/�Q�@�ł�����̂ŁA�@�x2���S��2�@�@���Ȃ킿�A�@�x���Q��
�����藧�B
�@�P�ڂ̉~�ɂ��ẮA��L�̂悤�Ƀw�����̌�����p���ĊȒP�Ɏ������Ƃ��ł������A
�Q�ȏ�̏ꍇ�͏�������悤�Ɏv���B�i���l�̎�@���g���Ȃ��I�j
 |
�@�@�@���}�̂悤�ɁA�~���������ڂ���Ƃ��A����
�@�@���ډ~�̔��a���L�̐������ؖ�����ɂ́A
�@�@�u���]�v�̐����𗘗p����Ɣ�r�I���ՂȌv�Z
�@�@�ŋ��߂���B
�@�@�@���]��p�����ɁA���̌v�Z����v�Z�ōs��
�@�@���Ƃ͔��ɐh���I�I�܂��A���W�ɂ��v�Z
�@�@���c�傷���Ď�ɕ����Ȃ��D�D�D�\���I |
�@�~ �b�� �̔��a�́A
�@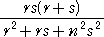 �@�@�@�i���@�Q�l�F�u�ȗ��̐^���i���]�j�v�j
�@�@�@�i���@�Q�l�F�u�ȗ��̐^���i���]�j�v�j
�@�~ �b�� ���璼���`�a�ɉ��낵�������̒����́A��L�̔��a�� �Q�� �{�ł���B
�i���@�Q�l�F�u�ȗ��̐^���i�C���̃i�C�t�j�v�j
�i�⑫�j�@���}�̂悤�Ȑ}�`�́A�A���L���f�X�ɂ��A�A���x���X�i�C���̃i�C�t�j�ƌĂꂽ�B
 |
�@�@�A���L���f�X�́A�~ �b1 �̔��a�����߂Ă���B
�@�@�܂��A�����̒����ƒ��a�̊W�́A�p�b�|�X��
�@��蔭�����ꂽ�B
|
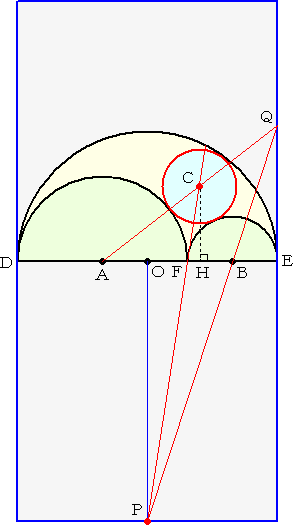
�i�NjL�j�@�����P�X�N�P�P���P�W���t��
�@�P�P���P�V���t���ōL���ݏZ�̂r���烁�[�������B
�@��L�œ���ꂽ���ʂ��A�~ �b �̒��S �i �� �C �� �j �̍��W�́A
�@�����i�Q��3�{�T��2���{�S����2�j/�i��2�{�Q�����{�Q��2�j
�@�����Q���i���{���j2/�i��2�{�Q�����{�Q��2�j
�ŗ^������B�������A�����`�a�� �� ���Ƃ��A���~�̒��a�̂`���̒[�_�����_�Ƃ���B
�@���̂Ƃ��A�p�\�R����p���āA���̉~��`�悳����Ɣ����ɃY���Ă��܂��Ƃ����B
�@�ǂ��ɊԈႢ������̂��낤���H�Ƃ������Ƃ������B
�@���ۂɁA�O���t�`��\�t�g��p���ĕ`�����Ă݂����̂����}�ł���B�����Q�A�����P�@�Ƃ��āA
�@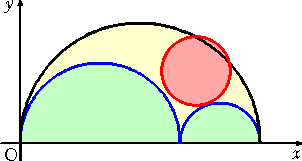
�@�m���ɁA�Y���Ă��܂��ˁI�D�D�D�ł��A����́A�p�\�R���̌v�Z�̌덷���炭����̂Ǝ���
���f�����̂ł����A�^���͔@���ɁH
�i�NjL�j�@�l������������̃R�����g�ł��B�i�����Q�W�N�R���P�T���t���j
�@���v���Ԃ�ł��B�u����ɑ����(18)�v�Ɋւ��铊�e�ȗ��A�R�N�Ԃ�ƂȂ�܂��B
�@���āA��L�́u�Y���̐^���͔@����?�v�Ƃ̂��Ƃł����A�~C�̒��S�̍��W�Ɍ�肪���邽
�߁A�Y���������Ă��܂��B
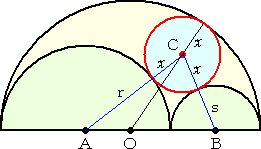
<x���W>�@����̐����`���Q�A�Ȃ����}�𗘗p����ƁADH�ɑ������܂��B
�@DH=DF+FH=2r+\frac{rs(r-s)}{r^2+rs+s^2}=\frac{r(r+s)(2r+s)}{r^2+rs+s^2}
���Ȃ킿�A�@�����i�Q��3�{�R��2���{����2�j/�i��2�{�����{��2�j
< y���W>�@���}��CH�ɑ������ACH=\frac{2rs(r+s)}{r^2+rs+s^2}
���Ȃ킿�A�@�����Q�����i���{���j/�i��2�{�����{��2�j
�ƂȂ�܂��B�}�̏�desmos����}���Ă݂܂����B�ꏕ�ƂȂ�K���ł��B
�i�R�����g�j�@���S�̍��W������Ă����Ƃ́D�D�D�B�l������������Ɋ��ӂ��܂��B
�����`�Q
�@�����`�̖ʐςƓ��ς̐����`����}���邱�Ƃ́A����قǎ��v�͂Ȃ���������Ȃ����A
���̍�}�Ɏ�����@�_�ɂ͂ƂĂ�����������B
�@���g�o�́u��}���ɂ�����~�̖����v�ɂ����āA�~��p�����������ςƑ��敽�ς̊�
�W�̏ؖ��ŁA���}�𗘗p�����B
 |
�@�@���̐}����͂���ƁA�����`�̖ʐςƓ��ς̐�
�@���`����}����ɂ́A���̂悤�ɍs���悢����
�@��������B |
�����`�`�a�b�c�ɑ��āA���_�`�𒆐S�Ƃ��A
���a�`�a�̉~�ʂ�`���A�ӂ`�c�̉����Ƃ̌�
�_���d�Ƃ���B
�����d�c�̒��_���n�Ƃ��A�n�𒆐S�A�n�c��
�a�Ƃ���~��`���A�����`�a�Ƃ̌�_���e�A�o
�Ƃ���B
���̂Ƃ��A�`�e���P�ӂƂ��鐳���`��`���A
���̐����`�����߂���̂ł���B |
 |
�@�ؖ��́A��}�̏㔼�~�}��������炩�ł��낤���A���ׂ��̒藝��p������@������B
�@�����`�`�a�b�c�̖ʐς́A�`�a�~�`�c�i�������j�@�ł���B
���ׂ��̒藝���A�`�d�~�`�c���`�e�~�`�o�@�����藧�B
�Ƃ���ŁA�@�`�a���`�d�@�A�@�`�e���`�o�@�ł���B
�@����āA�@�`�a�~�`�c���`�d�~�`�c���`�e�~�`�o���`�e2�@�����藧�B
�ȏォ��A�����`�`�e�g�f�̖ʐςƒ����`�`�a�b�c�̖ʐς͓������B
�i�NjL�j�@�����Q�R�N�X���Q�S���t��
�@���g�o�̓ǎ҂̕��A�r������֘A����b������[���Œ������B
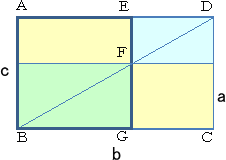 |
�@�@�@���}�ɂ����āA�`�a�����A�a�b�����A�e�f�����@�Ƃ���B
�@�@�l�p�`�`�a�f�d�𐳕��`�Ƃ���Ƃ��A��������2�@�ł���B
�@�@�@���̐����𗘗p����ƁA�Q���̑��敽�ς�����
�@�@�̐�����}������@��������B
|
�@���A�� ���^����ꂽ�ꍇ�� ���� ���i�����j �̍�}���@
�@�@�a�e�̉����Ƃ`�d�̉����̌�_���c�Ƃ���A�`�c���� �ł���B
�@���A�� ���^����ꂽ�ꍇ�� ���� ���i�����j �̍�}���@
�@�@�`�d�̉�����ɂ`�c���� �ƂȂ�悤�ɓ_�c���Ƃ�A�a�c�Ƃd�f�̌�_���e�Ƃ���A�e�f���� ��
�@����B
�����`�R
�@���E�c�̒��������ꂼ�� ���A�� �i�������A�������Ƃ���B�j�̒����`�̖ʐςƓ��ς̐����`
����}����ɂ́A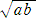 �̒�������}�ł���悢�B�����`�Q�ɂ����ẮA���ׂ��̒藝
�̒�������}�ł���悢�B�����`�Q�ɂ����ẮA���ׂ��̒藝
��p���Ă�������߂��B
�@�����ł́A���̎��ό`�𗘗p���č�}������@���l����B
�@�i���{���j2�|�i���|���j2���S����
�@���̎���}�`�I�ɍl����A���̂悤�ȂR�ӂ������p�O�p�`���l���邱�Ƃ��ł���B
�@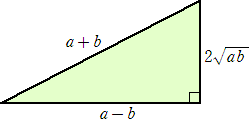
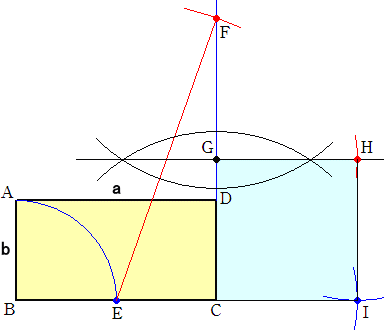
�@���̒��p�O�p�`�̍�}��ڕW�ɍl����ƁA���̂悤�ȍ�}���@��������B
�@
�@�a�𒆐S�Ƃ������a �� �̉~�ʂ�`���A�ӂa�b�Ƃ̌�_���d�Ƃ����B����ɁA�d�𒆐S�Ƃ�����
�a ���{�� �̉~�ʂ�`���A�ӂb�c�̉����Ƃ̌�_���e�Ƃ����B�����b�e�̒��_���f�Ƃ���ƁA��
���b�f�̒��������傤�Nj��߂鐳���`�̈�ӂ̒����ƂȂ�B��́A�g�A�h ����}����悢�B
���̒����Q���̎O�p�`
�@���̒����� �Q�� �œ��p�̈����p�ł���O�p�`�̍�}���l���Ă݂悤�B����́A�u�~
�O�̂P�_����̐ڐ��̒����͓������v�Ƃ���������p���ĉ��������B
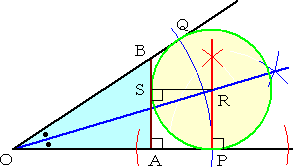 |
�@�@�@�@�_�n�𒆐S�Ƃ��āA���a �� �̉~��`
�@�@�@���A�Q�����Ƃ̌�_���o�A�p�Ƃ����B
�@�@�@�@�_�o�ł̐����Ɓڂn�̂Q�������Ƃ�
�@�@�@��_���q�Ƃ���B�q���A�n�o�̕��s��
�@�@�@�������~�Ƃ̌�_���r�Ƃ���B
�@�@�@�@�r�ɂ�����~�̐ڐ��ƂQ�̐����n�o�A
�@�@�@�n�p�Ƃ̌�_�����ꂼ��`�A�a�Ƃ����B |
�@�@�@�@�@�@�@�@�@�@�@���̂Ƃ��A���n�`�a�̎��̒����́A�Q�� �ŁA���߂�O�p�`������ꂽ�B |
���ۂɁA�@�Q�����n�o�{�n�p���i�n�`�{�`�o�j�{�i�n�a�{�a�p�j
�@�@�@�@�@���i�n�`�{�`�r�j�{�i�n�a�{�a�r�j���n�`�{�`�a�{�n�a�@�ł���B
�ȉ~�ɐڂ���~
�@�~�ɐڂ���~����}���邱�Ƃ͈Ղ����B
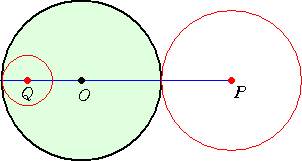 |
�@�@�@���}�̂悤�ɁA��~ �n �ɑ��ĉ~�O
�@�@�̓_ �o ����щ~���̓_ �p �ɑ��āA
�@�@�_ �n ��ʂ钼���������Ƃ��A�~ �n �Ƃ�
�@�@��_����܂�̂Ŕ��a����܂�B
�@�@�@���̂��Ƃ��獶�}�̂悤�ɍ�}�ł���B
�@�@�@����ɑ��āA�ȉ~�ɐڂ���~����}
�@�@����ɂ͂ǂ������炢���̂��낤�B
|
�@�~�̂悤�ɊȒP�ɂ͕`���Ȃ��Ɨ\�z�����̂ŁA�܂���͂����Ă݂悤�B
�@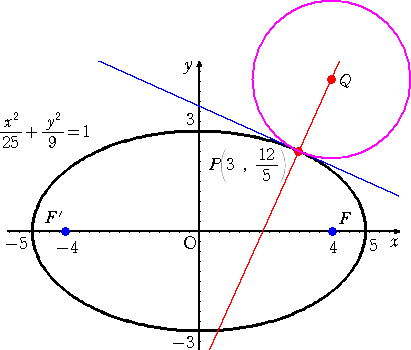
�@��}�̂悤�ɑȉ~��̓_�o�ɂ����Đڐ��������A���̐ڐ��ɐ����Őړ_��ʂ钼���i�@
���j��������A���̒�����̔C�ӂ̓_����ȉ~�ɐڂ���~����}���邱�Ƃ͈Ղ����B
�@�������A�����ł������̖��_����������B
�@�i�P�j�@�ȉ~��̔C�ӂ̓_�Őڐ��͍�}�ł���̂��낤���H
�@�i�Q�j�@�ȉ~��̐ړ_�o��^���Ă���_�p��_���Ă��邪�A����͍l���鏇�Ԃ��t�ł͂�
�@�@�@�����H�i���Ȃ킿�A�ȉ~�O�̔C�ӂ̓_�p����_�o�����߂Ă͂��Ȃ��I�j
�@�i�P�j�̖��_�́A���̂悤�ȑȉ~�̋����ׂ������ɂ����������B
�@�@�@�@�@�@
�@�ȉ~�̏œ_ �e�A�e�f�̈ʒu���������Ă���ꍇ�A�� ����ɂ͂Ȃ��ȉ~��̔C�ӂ�
�_�o�ɂ�����@���́A�ڂe�o�e�f�̂Q�������ł���B
�@�������A�_ �o �ɂ�����ڐ��́A�ڂe�o�e�f�̊O�p�̂Q�������ł�����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i���Q�l�F���낢��ȋȐ��̒����ȉ~�̍��j
�@���̎�������A�œ_�̈ʒu��������ΐڐ����������Ƃ͈Ղ����B
�@��L�̎������ؖ����Ă݂悤�B
�i�ؖ��j
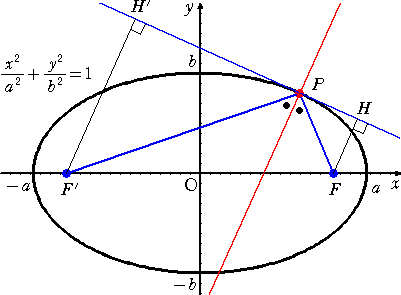 |
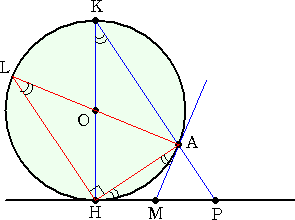
�@�@���}�̂悤�ɁA�_ �o �ɂ�
�@����ڐ��ɂQ�̏œ_ �e�A
�@�e�f��萂�������낵�A����
�@�������ꂼ�� �g�A�g�f�Ƃ���B
�@�@�ȉ~�̗��S���� �� �Ƃ��āA
�@�œ_ �e�A�e�f�̍��W�́A
�@�@�e�i�����C�O�j�A�e�f�i�|�����C�O�j
�@�Ə�����B
�@�@�_ �o �̍��W���A�i��1�C��1�j
�@�Ƃ����B |
�@���̂Ƃ��A�ȉ~�̏����́A�@������/���@�A�����|��/���@�Ȃ̂ŁA�@�|��/������1����/���@���Ȃ킿�A
�@�@�@�@�@�@�@���|����1���O�@�A�@���{����1���O
�����藧�B���̂��Ƃ���A�_�ƒ����̋����̌�����p���āA
�@�@�@�e�g�����i���|����1�j�@�A�@�e�f�g�f�����i���{����1�j�@�@�i�������A�� �͒萔�j
�Ə�����B�Ƃ���ŁA
�@�@�@�o�e2���i��1�|�����j2�{��12���i���|����1�j2�@�@�Ȃ̂ŁA�@�o�e�����|����1
�܂��A�@�o�e�{�o�e�f���Q���@���A�@�o�e�f�����{����1�@�ƂȂ�B
�@�ȏォ��A�@�@�o�e �F �o�e�f�� �e�g �F �e�f�g�f�@�@�����藧�B
���p�O�p�` �o�e�g �ƒ��p�O�p�` �o�e�f�g�f �ɂ����āA�Ή�����Q�ӂ̔䂪�������̂ŁA
�@�@�@�@�@�@�@�@���p�O�p�` �o�e�g �� ���p�O�p�` �o�e�f�g�f
�ƂȂ�B�@����āA�@�ڂe�o�g���ڂe�f�o�g�f�@�ƂȂ�A�_ �o �ɂ�����@���́A�ڂe�o�e�f���Q������
�邱�Ƃ������ꂽ�B�@�i�؏I�j
�i�NjL�j�@�����P�X�N�V���T���t��
�@��L�ł́A��͊I�ɏؖ��������A���̂悤�ɏ����I�ɂ��ؖ��ł���悤���B
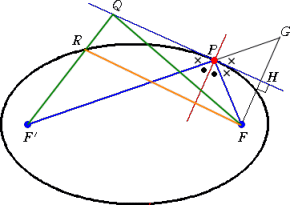 |
�@�@���}�ɂ����āA
�@�@�e�o�{�e�f�o���e�q�{�e�f�q���e�p�{�e�f�p
�@�@���������́A�o���p�@�̂Ƃ��Ɍ���B
�@����āA�_�o�́A�e�p�{�e�f�p �̒����̍ŏ��l
��^����B
�@���̂Ƃ��A�ڐ��Ɋւ��Ăe�ƑΏ̂ȓ_�f�Ƃe�f��
���Ԓ�����ɓ_�o������B |
�@���̂��Ƃ���A�ڂe�o�g���ڂe�f�o�p�@�����藧���A�_ �o �ɂ�����@���́A�ڂe�o�e�f���Q����
���邱�Ƃ������ꂽ�B
�@���āA�ȉ~�̕�����
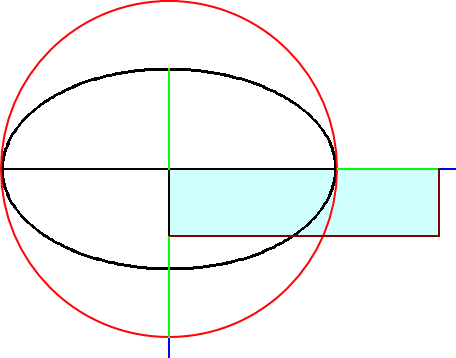
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@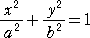
���^������Ή�͓I�ɏœ_ �e�A�e�f�̍��W�͋��߂���B�]���āA�� �A��
����}�\�Ȓl
�Ȃ�A���̏œ_����}�\�ł���B
�@����ł́A�ȉ~�̃O���t�������^�����Ă��āA���̕��������^�����Ă��Ȃ��ꍇ�ɁA
�ȉ~�̏œ_����}���邱�Ƃ͉\�ł��낤���H�@�������A�����A�Z���͗^������̂Ƃ���B
�@
�@���̂悤�ɍ�}����A����͗e�Ղ��낤�B
�@
�@��}�̂悤�ɁA�@��2�|��2���i���{���j�i���|���j�@��ʐςɎ������`�i���F�j����}�����B
�@���̂Ƃ��A�ȉ~�̏œ_�� �� ���W�́A���̒����`�̖ʐς̕������ł���̂ŁA�����`�Q��
��������@�ɂ�蒷���`�Ɠ����ʐς��������`����}����A���߂�ȉ~�̏œ_�� �� ���W
�́A���̐����`�̑Ίp���̒����ƂȂ�B���̒�����p���āA�Q�̏œ_����}�����B
�@
�@�ȏ�ŁA���_�i�P�j�͊��S�ɉ��������B
�i�R�����g�j�@�����ł́A�ȉ~��ɔC�ӂ̓_��^���āA���̓_��ړ_�Ƃ���ڐ�����}�����
�@�@�@�@�@�@���A�œ_�����߂邱�Ƃɂ��l�������A�������œ_���ӎ������ɐڐ�����}����
�@�@�@�@�@�@���@�����݂���B���̕��@�́A�ȉ~�̐ڐ��ŏq�ׂ���B
�@���āA���_�i�Q�j�̉����Ɍ����ď��������悤�B
�@���̋����ׂ��������m���Ă���B���̐��������p����ƁA���_�i�Q�j�������ł��������B
�@���}�̂悤�ɁA�ȉ~
�@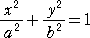
��̂Q�_ �o�A�p �ŕ��s�Ȑڐ��������B���̂Ƃ��A���̂Q�ڐ��Ɛڂ��A���A�ȉ~�ɂ��ڂ���~
�̒��S�� �b �Ƃ���Ƃ��A
�@�n�b �� �� �{ ��
�����藧�B
�@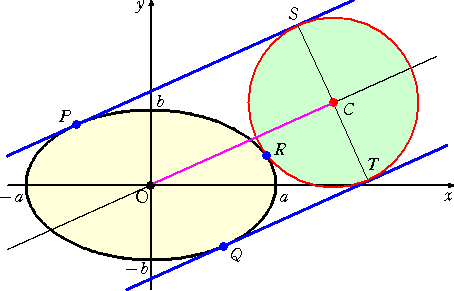
�i�ؖ��j�@���}�̂悤�ɁA�ڐ��o�r�� �� ���Ƃ̌�_���`�A�����b�q�� �� ���Ƃ̌�_���a�Ƃ��A�_
�@�@�@�@�n����ڐ��o�r�ɉ��낵�������̑����g�A�_�q���� �� ���ɉ��낵�������̑����j�A�_
�@�@�@�@�b���� �� ���ɉ��낵�������̑����k�Ƃ���B
�@
�@���̂Ƃ��A�@��AOH �� ���n�b�k�@���A�@�`�n �F �n�g �� �n�b �F �b�k�@�Ȃ̂ŁA
�@�n�b���`�n�~�b�k/���@�@�i�����ŁA�� �͉~�b�̔��a�ŁA�n�g�����@�ł��邱�Ƃɒ��Ӂj
�܂��A�@���q�a�j �� ���b�a�k�@���A�@�q�a �F �q�j �� �b�a �F �b�k�@�Ȃ̂ŁA�q�a�����@�Ƃ��āA
�@�b�k���i�i���{���j/���j�q�j
����āA�@�n�b���i�i���{���j/�����j�`�n�~�q�j�@�����藧�B
�@�����ŁA
�@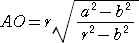 �@�@�@�@
�@�@�@�@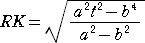
�����藧�B�@���ۂɁA�ȉ~
�@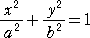
��̓_�o�i���C���j�ɂ�����ڐ��̕������́A�@����/��2�{����/��2���P�@�Ȃ̂ŁA
�@�`�i��2/���C�O�j�@�@�i�������A�@��2��2�{��2��2����2��2�@�j
�ł���B�܂��A���̐ڐ��ƌ��_�Ƃ̋����́A�� �ɓ���������A
�@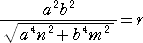
���ӂ����āA��������ƁA�@��4�i��2�|��2�j����2��2�i��2�|��2�j
����āA�@�@��4/��2����2�i��2�|��2�j/�i��2�|��2�j�@�ł���B
������A
�@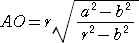
���l�ɁA�_�q�i���C���j�ɂ�����@���̕������́A�@��2�����|��2�������i��2�|��2�j�����@�Ȃ̂ŁA
�@�a�i�i��2�|��2�j��/��2�C�O�j�@�@�i�������A�@��2��2�{��2��2����2��2�@�j
�ł���B�ȉ~�ɓ��ڂ���~�̐�������A
�@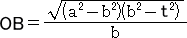
����āA�i��2�|��2�j�i��2�|��2�j/��2���i��2�|��2�j2��2/��4
���A�@��2��2����4�i��2�|��2�j/�i��2�|��2�j�@�Ȃ̂ŁA�@��2���i��2��2�|��2��2�j/��2�@�ɑ�����āA
�@��2���i��2��2�|��4�j/�i��2�|��2�j
������A
�@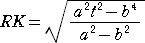
���������āA�������A�n�b���i�i���{���j/�����j�`�n�~�q�j�@�ɑ�����Đ�������ƁA
�@�n�b2���i�i���{���j/���j2�i��2��2�|��4�j/�i��2�|��2�j�@�E�E�E�E�E�i���j
�Ƃ���ŁA���p�O�p�`�n�k�b�ɂ����āA�O�����̒藝���A�@�@�n�b2���n�k2�{�b�k2
�����ŁA�@�n�k���n�a�{�a�k���n�a�{�i�i���{���j/���j�a�j�@�Ȃ̂ŁA
�@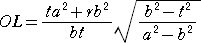
�܂��A
�@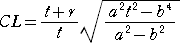
����āA�@�n�b2���n�k2�{�b�k2�@�ɑ�����Đ�������ƁA�i�����Ȃ�v�Z����ρI�j
�@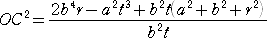
��L�́i���j���㎮�ɑ�����Đ�������ƁA�i�����Ȃ�v�Z����ρI�j
�@��2��2�i��4�{�Q��2�����{��2��2�j����2��2�i��4�{�Q��2�����{��2��2�j�@���A�@����������
���̂Ƃ��A�@��������/���@���i���j�ɑ�����Đ�������ƁA�@�n�b2���i���{���j2
�@���Ȃ킿�A�@�n�b�����{���@�����藧�B�@�@�i�؏I�j
�i�R�����g�j�@���ʂ͊Ȗ��Ȃ̂ɁA�����Ɏ���܂ł̌v�Z���ƂĂ��n�[�h�ł��ˁI�����Ə���
�@�@�@�@�@�@�I�Ƃ������Ȗ��ȏؖ����Ȃ����̂ł��傤���H�i�Ȗ��ȏؖ������ꂽ���́A
�@�@�@�@�@�@�������܂ł��������������B�j
�@����ɂ��Ă��A�ؖ��r���œ���ꂽ��Ꭾ�@�����������@���Ȃ킿�A
�@�i���ډ~�̔��a�j�F�i�O�ډ~�̔��a�j���i�Z���̒����j�F�i�����̒����j
�́A�ƂĂ��������W�ł��ˁI
�i�Q�l�����F�[��p�r�A�_���E�y�h�[�@���@���{�̊|��������܂����H�@�i�X�k�o�Łj�j
�@���̎�����p���āA���_�i�Q�j�͔������x���������B
 |
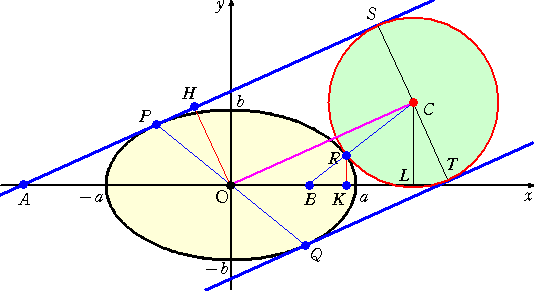
�@�@���}�ɂ����āA�ȉ~
�@�@�@�@�@�@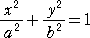
�@�̒��S�n���甼�a ���{�� ��
�@�~��`���A���̉~����̔C
�@�ӂ̓_���p�Ƃ���B
�@�@�_�p�Ɠ_�n�����ёȉ~�Ƃ�
�@��_���`�Ƃ��A�_�`��ʂ� ��
�@���̐����ƕ⏕�~
�@�@�@�@ ��2�{��2��a2�@ |
�Ƃ̌�_���a�Ƃ���B���a�n�a�ɐ����Ȓ��a���b�A�c�Ƃ��A���̓_�ň������ڐ���
�� ���Ƃ̌�
�_�����ꂼ��d�A�e�Ƃ���B�Q�_�b�A�c��肻�ꂼ�� �� ���ɐ����������A�ȉ~�Ƃ̌�_���f�A�g
�Ƃ���B���̂Ƃ��A�����d�f�A�e�g�͐����n�p�ɕ��s�ȑȉ~�̐ڐ��ƂȂ�B�_�p�𒆐S�Ƃ��āA
�Q�̐ڐ��ɐڂ���~��`���ƁA���̉~�͑ȉ~�Ɠ_�o�Őڂ���B
�i�R�����g�j�@�ȉ~�O�̔C�ӂ̓_�����߂�~�̒��S�Ƃ������������A��L�ł́A�n�p�����{��
�@�@�@�@�@�@�Ƃ�������t���̔C�ӂ̓_�ł���B���̈Ӗ��ŁA�������x�̉����Ɣ��f�����B
�i�⑫�j�@�����P�X�N�V���R���t��
�@
�@�ȉ~�̕��������A�@��2/�Q�T�{��2/�X���P�@�Ƃ��A�ړ_ �o�i�|�S�C�X/�T�j�Ƃ���B
�@���̂Ƃ��A�ڐ��̕������́A�@�����i�S/�T�j���{�T�@�Ȃ̂ŁA�ڐ��� �� ���̐��̌����ƂȂ��p
�� �� �i�O���Ɓ���/�Q�j�Ƃ����ƁA
�@�������Ɓ��S/�T
�����藧���A�ȒP�Ȍv�Z����A�@�@�������Ɓ��T/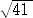 �@�A�@�������Ɓ��S/
�@�A�@�������Ɓ��S/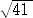 �@�ł���B
�@�ł���B
�@�Ƃ���ŁA�@��L�ŋ��߂������ɑ�����āA�@�����Q�T/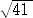 �@�A�@�����P�T/
�@�A�@�����P�T/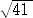 �@���A
�@���A
�@�n�a���P�U/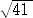 �@�A�@�a�j���X/
�@�A�@�a�j���X/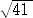 �@�Ȃ̂ŁA�@�n�j���Q�T/
�@�Ȃ̂ŁA�@�n�j���Q�T/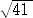
�@�܂��A�@�q�j���P�Q/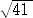 �@�Ȃ̂ŁA�~ �b �Ƒȉ~�̐ړ_ �q �̍��W�́A
�@�Ȃ̂ŁA�~ �b �Ƒȉ~�̐ړ_ �q �̍��W�́A
�@�q�i�Q�T/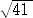 �C�P�Q/
�C�P�Q/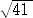 �j
�j
�ƂȂ�B���̂��Ƃ́A�@�q�i ���E�������� �C ���E�������� �j�@�Ə����邱�Ƃ��Ӗ�����B
�@���̎����́A��ʓI�ɐ��藧�炵���B
�i�I�[�X�g�����A�̃N�B�[���Y�����h��w�̃J�y�����m���������ꂽ�I�j
�@���ۂɁA��}�ɂ����āA
�@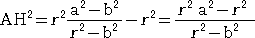
�Ȃ̂ŁA
�@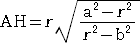
����āA�@��OAP���Ɓ@�Ƃ���ƁA
�@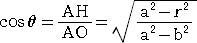 �@�@�@�@�@
�@�@�@�@�@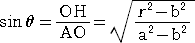
�ł���B���܁A�_�q�i �� �C �� �j�Ƃ���ƁA�@�� �� �n�a�{�a�j
�@�����ŁA
�@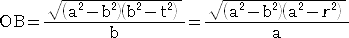
�ŁA�܂��A
�@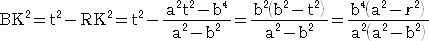
���A
�@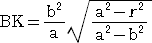
���������āA
�@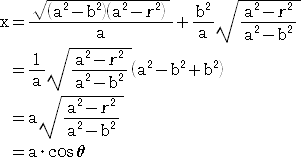
�܂��A
�@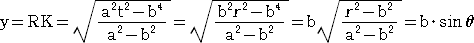
�@�ȏォ��A�ڐ��� �� ���̐��̌����Ƃ̂Ȃ��p�� �� �Ƃ���ƁA
�@���s�ȂQ�ڐ��Ɖ~�ɐڂ���ȉ~��̐ړ_�̍��W�́A�q�i���Ecos�ƁC���Esin�Ɓj
�Ə����邱�Ƃ������ꂽ�B
�i�R�����g�j�@���̎�����p����ƁA���s�����^������A�u���ɐړ_�q�����߂��A�_�q
�@�@�@�@�@�@�Ŗ@����`���A�ȒP�ɉ~����}�ł��܂��ˁI
�@���ۂɁA�ړ_�̍��W�̌`����A���̂悤�ɏ��v�̉~����}�����B
�@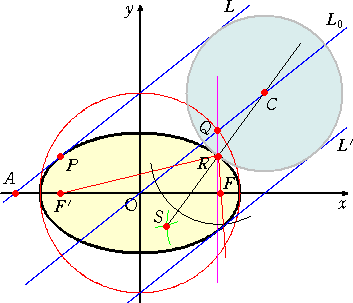
�@�ȉ~��̔C�ӂ̓_ �o �ɂ�����ڐ� �k �� �� ���ƌ����_�� �` �Ƃ���B���_��ʂ�A�k��
���s�Ȓ����� �k0 �Ƃ���B���� �k0 �Ƒȉ~�̕⏕�~�Ƃ̌�_���p �Ƃ��A�p���� �� ���ɉ���
���������Ƒȉ~�Ƃ̌�_���q �Ƃ���B�i���̓_ �q �����߂�ړ_�ƂȂ�B�j
�@�ȉ~�̏œ_ �e�A�e�f�ɂ��āA�ڂe�o�e�f�̂Q���������r�q �Ƃ��A���� �k0 �Ƃ̌�_�� �b �Ƃ�
��B�i���̓_ �b �����߂�~�̒��S�ƂȂ�B�j
�@�_ �b �𒆐S�Ƃ��A���a�b�q �̉~��`���A���ꂪ���߂�~�ƂȂ�B
�ȉ~�̐ڐ�
�@�ȉ~�ɐڐ���`�����Ƃ͓�����Ɏv���邪�A�~�̐ڐ��Ɠ��l�ɔ�r�I�ȒP�ł���B����
���@�́A�ȉ~�ɐڂ���~�ł��p����ꂽ�B
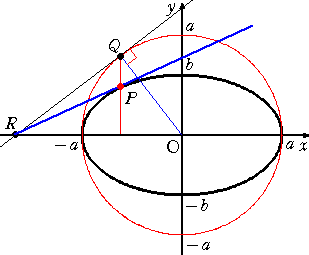 |
�@�@�@���}�̂悤�ɁA�ȉ~
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@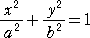
�@�@�̕⏕�~ ��2�{��2��a2�@����}�����B
�@�@�@�ȉ~��̔C�ӂ̓_ �o �ɑ��āA�⏕
�@�@�~��̓_ �p ����܂�B
�@�@�@���a �n�p �ɐ����ȉ~�̐ڐ��������A
�@�@�� ���Ƃ̌�_�� �q �Ƃ���B
�@���̂Ƃ����� �o�q �͋��߂�ڐ��ƂȂ�B |
�@�� �������̏k���ϊ����l����A���̎����͖��炩�����A��͓I�ȏؖ���^���Ă������B
�i�ؖ��j�@�_ �o�i���C���j�Ƃ����ƁA�@��2��2�{��2��2����2��2�@�����藧�B
�@�܂��A�_ �p�i���C���f�j�Ƃ����ƁA�@��2�{���f2����2�@�����藧�B
�@�_ �p �ɂ�����ڐ��̕������́A�@�����{���f������2�@�ł���B�@����āA�q�i��2/���C�O�j
�@�Q�_ �o�A�q ��ʂ钼���̕������́A�@�����|�i���|��2/���j���|��2��/�����O
���Ȃ킿�A�@�������|�i��2�|��2�j������2��
�@�����ŁA�@��2��2�{��2��2����2��2�@���A�@��2�i��2�|��2�j���|��2��2�@�Ȃ̂ŁA
�@��2�������|��2�i��2�|��2�j������2��2��
����āA�@�@��2�������{��2��2������2��2���@�@���Ȃ킿�A�@��2�����{��2��������2��2
�@����́A�_�o�i���C���j�ɂ�����ڐ��̕������@����/��2�{����/��2���P�@��^���Ă���B�i�؏I�j
�@���̌����̉��p�Ƃ��āA���̖����l���Ă݂悤�B
��@���@�@���ʏ�̂Q�_�`�i �P �C �O �j�A�a�i �Q �C �O �j���œ_�Ƃ���ȉ~�ɁA���_��ʂ�
�@���� �k �F ���������@���ڂ���Ƃ��A�ȉ~�̕������́A�� ��p���Ăǂ������邾�낤���B
�@����������Ȃ̂ŁA�v�Z���Ă݂��B�Ώ̐�����A�����O�@�Ƃ��čl���邱�Ƃɂ���B
�@�ȉ~�̒��S�́A�_�i �R/�Q �C �O �j�Ȃ̂ŁA�S�̂� �� �������� �|�R/�Q �������s�ړ����čl
����B�@���̂Ƃ��A�n�f�i �|�R/�Q �C �O �j�A�`�f�i �|�P/�Q �C �O �j�A�a�f�i
�P/�Q�C �O �j�@�ƂȂ�B
�@���߂�ȉ~�̒����̒����� �j�i���Q���j�Ƃ���ƁA�ȉ~�̕������́A
�@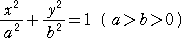
�Ə�����B�������A�S��2�|�S��2���P�@�ł���B
�@���̑ȉ~�̕⏕�~�̕������́A�@��2�{��2����2�@�ł���B
�@�_�n�f�i �|�R/�Q �C �O �j��ʂ钼�����A�~ ��2�{��2����2�@�ɐڂ���Ƃ��A���̐ړ_�̍��W
�i ��1 �C ��1 �j�́A�A���������@�i�|�R/�Q�j��1����2�@�A�@��12�{��12����2�@���������Ƃɂ�蓾���
��B���ۂɉ����ƁA
�@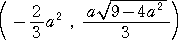
�ł���B���̓_�� �� �������� ��/��
�{�����_���A���� �k �Ƒȉ~�Ƃ̐ړ_�ƂȂ�B���Ȃ킿�A
�@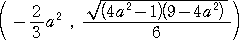
���̂Ƃ��A���� �k �̌X�� �� �ɂ��āA
�@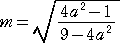
�ƂȂ�B����� �� �ɂ��ĉ��������A
�@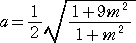
�ƂȂ�B���̂Ƃ��A
�@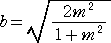
�@���̂��Ƃ���A�� �̒l��������Αȉ~�̕������͊m�肷��B
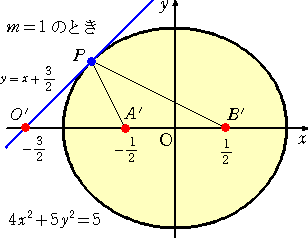
�@�Ⴆ�A�����P �ɑ��āA���̑ȉ~�����߂Đ}������Ɖ��}�̂悤�ɂȂ�B
�@
�@�ړ_ �o �̍��W�� �� �̊��Ƃ��ĕ\�����B���ۂɁA��L�̌��ʂ���A
�@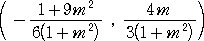
�ƂȂ�B
�@�܂��A��L�̓_�o�� �� �������ɂR/�Q�������s�ړ�������A�����̐ړ_�i
�� �C�� �j�̍��W
�@
��������B
�@�ȉ~�ɐڂ��钼���̏����Ƃ��āA���̌������m���Ă���B
�@���� �F �`���{�a���{�b���O�@���A�ȉ~ �F ��2/��2�{��2/��2���P�@�ɐڂ��邽�߂�
�K�v�\�������́A
�@��2�`2�{��2�a2���b2
�ł���B
�i�ؖ��j�@�����Ƒȉ~�� �� �������� ��/�� �{�̊g��k�����s���āA
�@�����@���`���{���a���{���b���O�@�@�Ɓ@�~�@��2�{��2����2�@��B
�@����炪�ڂ��邽�߂̕K�v�\�������́A
�@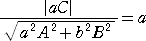
������A��2�`2�{��2�a2���b2�@�@�i�؏I�j
�@���̂Ƃ��A���̂悤�Ȗʔ����������������B
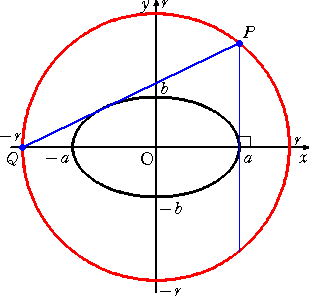 |
�ȉ~
�@�@�@�@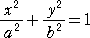
�ɑ��āA���_�𒆐S�Ƃ����a �� �̉~���l
���A���̉~����ɁA�Q�_
�@�@�o�i �� �C ��0 �j �A �p�i �|�� �C �O �j�@���Ƃ�B
�@�@���̂Ƃ��A
�����o�p���ȉ~�ɐڂ��邽�߂̏����́A
�@�@�@�@�@�@�� �� �� �{ ��
�@�ł���B
|
�i�ؖ��j�@�����o�p�̕������́A�@��0���|�i���{���j���{��0�����O�@�Ȃ̂ŁA�ȉ~�ɐڂ��邽�߂ɂ́A
�@��2��02�{��2�i���{���j2����02��2
�@��2����2�{��02�@�Ȃ̂ŁA�@��2�i���{���j2����04
����āA�@���i���{���j����02����2�|��2���i���|���j�i���{���j�@���A
�@�������|���@�@���Ȃ킿�A�@�������{���@�@�i�؏I�j
���~�ɓ��ڂ���~
 |
�@�@���܂œK���ɏ����Ă������̂ƌ����A����
�@�����́u���ʁv����������������悤�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�Q�l�F�M���ɂ����j
�@�@����Ɠ��l�̂��̂Ƃ��āA���~�ɓ��ڂ���~
�@�������ł͂Ȃ����낤���H�Ȃ������獡�܂Ō�
�@���ɍ�}���悤�Ƃ����C���N���Ȃ������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�D�D�D�s�v�c�I�H�j |
�@���g�o�́u�ӊO�ȏ��ɂQ���ӎO�p�`�v�ɂ����鐫����p����ƁA�����ɓ��ډ~���`�����B
�@���~����ɔC�ӂɓ_�o���Ƃ�A�_�`�𒆐S�Ƃ��Ĕ��a�`�o�̉~�ʂ�`���B���a�`�a�Ƃ̌�_
���p�Ƃ���B�����`�q�g�p�r����}���邱�Ƃɂ��A���ډ~�̒��S�r�����߂���B
���� ��/�� �̍�}
�@���g�o�̌f���u�o��̐�v�ɁA�����Q�O�N�W���R���t���ŁA�g�m�u�n�������v����������
�ꂽ�b����A�ꕔ���e���C���E�⑫���āA�܂Ƃ߂����Ǝv���B
 |
�@�@���� �� �A�� ����� �P �̐������^�����Ă������
�@�Ƃ���B
�@�@���̂Ƃ��A�����̒��� ��/�� �́A�����a�q����A
�@�@�@�@�@�@�@�@�����̒��� ��/�� �́A�����b�p����A
�@���߂���B�����O�p�`�̐������疾�炩���낤�B
�@�@���̘b��ɂ��Ďc���ꂽ�ۑ�́A���� �� �A�� �̐�
�@��������^���āA���� �P �̐��������߂��Ȃ����Ƃ�
�@�����Ƃł���B
�@�@�ʂ����āA���̂��Ƃ͉\�Ȃ̂��낤���H |
�����̘a���Ϗ�
�@���g�o�̌f���u�o��̐�v�ɁA�e�m�����̂悤�ȏ������݂����ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�Q�N�S���Q�R���t���j
�@�u�R���p�X�ƒ�ō�}�ł�����̂́A���ׂăR���p�X�݂̂ō�}�ł���v�Ƃ������[���E�}
�X�P���[�j�̒藝������B�������A�Ⴆ�ΐ������������Ƃ͂ł��Ȃ�����A�[�_������ł�
��ΐ��������������̂Ƃ݂Ȃ��̂ł��傤�B
�@�����ł́A�R���p�X�݂̂�p���Ă̍�}���@���l���邱�Ƃɂ���B
�@�^����ꂽ�����̂Q�{����������@�i�`�a����`�o�j�Ɠ��l�ɂ��āA�R�{�A�S�{�A�E�E�E�E�͍�}��
���A���]�ɂ���Ă��̋t���{����}�ł���B�]���ėL�����{�͍�}�ł���B
�@���R�� �� �ɑ��āA�ゎ �{�͂ǂ�����č�}����̂��낤���B���O�p�`�̍�}����A
�̍�}�͗e�ՂŁA�u��{�̍�}�v�́u�~�̂S�����v�̎�@��p���āA �̍�}���ł���B
�̍�}���ł���B
�����T �����l�ɂł������ŁA���ׂĂ� �� �ɂ��Ăł������D�D�D�B
�@�����Ɗ�{�I�Ȃ̂��A
�@�P�@���� �� �A�� ���^����ꂽ�Ƃ��A ���{�� ����}���邱��
�@�Q�@���� �� �A�� �A�� ���^����ꂽ�Ƃ��A ����/�� ����}���邱��
�ł��邪�A�ȒP�ɂ͂ł������ɂȂ��B�ǂ���������̂��낤���H
�@���̖₢�����ɑ��āA�e�m�����g����̃��|�[�g�ł��B�i�����Q�Q�N�S���Q�S���t���j
�@��L�̖₢�����������킯�ł͂Ȃ����A������ �̂Ƃ��A���|�� �̍�}���ł���ǂ����
�ł��邱�Ƃ����������B�ȉ��ł́A���̍�}���\�Ƃ��čl�������̂ł���B
�@���� �� ���^����ꂽ�Ƃ��A���̗L�����{�͍�}�ł���B�i�m�F�ς݁j
�P�@������ �̂Ƃ��́A�Q�� ������A������ �Ƃ��Ă���ʐ�������Ȃ��B
�@
�@���̂Ƃ��A�L���� �� ���Ƃ��āA�������� �Ƃł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@(��/���������P �ƂȂ�L���� k ���Ƃ�悢�j
�@������������������ ������A�����|���A���|���� �͍�}�ł���B
�@����āA���̍�����}�ł���B
�@�����A�@�����|���|�i���|�����j���i���|�P�j�i���{���j �͍�}�ł���B
�@�]���āA���̗L�����{�ł��� ���{�� ����}�ł���B
�Q�@�܂��A��i�����j ����}�ł��邱�Ƃ������B
�@���|�� ����}�ł��邩��A�Q�i���|���j ����}�ł��A���̒��_����}�ł���B
�@�]���āA�`�A�a�Ƃ��̒��_�l�������āA�`�l���a�l�����|�� �Ƃł���B
�@�`�A�a���甼�a ���{�� �̉~�������Č�_���b�Ƃ���B���`�l�b�͒��p�O�p�`�ɂȂ邩��O��
�@���̒藝���A�@�i���|���j2�{�b�l2���i���{���j2�@�Ȃ̂ŁA�b�l���Q��i�����j
�@
�@�]���āA��i�����j ����}�ł���B�܂��A���]�ɂ���āA�� �� �� ���� ��2/�� ����}�ł���B
�@����āA�� �� ��i�����j ����A����/�� ����}�ł���B
�@���Ȃ��A�Q����A���� ���A���A�P ���^����ꂽ�Ƃ��A
�@�@�@�@���~���@�́A����/�P�@�Ƃ��āA�@�������@�́A���E�P/���@�Ƃ��č�}�ł���B
�@�e�m����̖₢�����ɑ��āA���g�o�����������b�ɂȂ��Ă���g�m�u�炷����v���A
�u���|�� �̍�}���@�v���l����ꂽ�B�i�����Q�Q�N�S���Q�U���t���j
���O �F �Q�_�̒��_�͍�}�\
�@�g���]�h�ɂ��\�ł���B
���P �F �~�O�̓_����~�ւ̐ڐ����������Ƃ͉\�i�ړ_����}�ł���Ƃ����Ӗ��I�j
�@�~�̒��S�Ɖ~�O�̓_�Ƃ̒��_���Ƃ��āA���̒��_�𒆐S�Ƃ��ĉ~�O�̓_��ʂ�~��`��
�A���̉~�Ƃ̌�_���ړ_�ƂȂ�B
���Q �F ���钷���� �{�̒����͍�}�\
�{�̒����͍�}�\
 |
�@�@�@���O�p�i�q�͍���̂ŁA�~�̊O���ɂ����āA�~�ɍł���
�@�@�����O�p�i�q�_����~�ɐڐ��������A�ړ_�܂ł̋����́A
�@�@�~�̔��a�� �{�ɂȂ�B �{�ɂȂ�B |
���R �F �~���̂S�����͉\
�@���Q�ō�������a�� �{�̒������g���Ή\�ł���B
�{�̒������g���Ή\�ł���B
�{���@�E�E�E�@�������₷���悤�ɍ��W���ʏ�ōl���邱�Ƃɂ���B
�@���_�𒆐S�Ƃ���P�ʉ~��`���A�_�`�i �� �C �O �j ���Ƃ�ƁA���]�ɂ��A�_�a�i�P/
�� �C �O �j
���Ƃ��B���_�Ɠ_�a����A�_�b�i�|�P/ �� �C �O �j���Ƃ��B�_�`�Ɠ_�b�̒��_���Ƃ��āA�Q�_�`
�Ƃb��ʂ�~��`���A�P�ʉ~�Ƃ̌�_�̈�͓_�c�i �O �C �P �j�ƂȂ�B
�@���R�ɂ��A�_�c����_�d�i �P �C �O �j���Ƃ��B
�@�ȏ�̑���ɂ��A�u����~�̒��S�ƊO���̓_�����Ԑ����Ɖ~�Ƃ̌�_�v����}�ł�����
�ŁA���|�� ����}�ł��邱�ƂɂȂ�B�@�i�I�j
�@��L�ɂ��āA�e�m����̕⑫�ł��I�i�����Q�Q�N�S���Q�U���t���j
�@�n�`���� �Ƃ��A�n �𒆐S�Ƃ��Ĕ��a �� �̉~�b1�Ɋւ��āA�`�]�����_���a�A�n�Ɋւ���a
�̑Ώ̓_���b�A�`�b�a�Ƃ���~�Ɖ~�b1�̌�_���c�Ƃ���B���̂Ƃ��A�n�c���`�b�Ɛ����ł�
��B�i�����ꂪ�|�C���g�ł��ˁI�j
�@�����A���R�ɂ��A���� �� �̐����Ɛ����ȕ����ɒ��� �� �̐������Ƃ邱�Ƃ��ł���B
�@�]���āA���|�� ����}�ł���B�i�t�����ɉA���{�� ����}�ł���B�j
���n�c�ۂ`�b���ȒP�Ɏ�����悤�ɁA�����P �Ƃ������W�ŏ����Ă������悤�ł��ˁB�ŏ��́A
�@�� �͂ǂ��ɂ���낤�Ƃ��v���Ă��܂��܂����B
�@����ŁA���� ���A�� ���璷�� ���{���A���|���A��i�����j �������āA����
���A���A�P ���� �����A��/��
��������B��ƃR���p�X�ŕ`����}�`�Ɋւ����{�I�Ȓ藝��F�߂�A�R���p�X����
�ŏ�����}�`���A��ƃR���p�X�ŕ`����}�`�Ɠ����ɂȂ邱�Ƃ̏ؖ��͂���Ȃɓ����
�������ł��B
�i�R�����g�j�@�e�m����A�炷���邳��Ɋ��ӂ��܂��B
�@�e�m���ʉ����l�����܂����B�i�����Q�Q�N�T���V���t���j
�i�ꕔ���������C�������Ă��������܂����B�j
�@���� �� �̐���(�������[�_�̂�)�̂Q�{�͍�}�\�Ȃ̂ŁA�`�a�̒��_��M�Ƃ��āA
�`�l���a�l���� �Ƃł���B�`�A�a���甼�a �� �̉~��`���āA���̌�_���b�Ƃ���B
���`�l�b�͒��p�O�p�`�ł��邩��A�O�����̒藝���A�b�l����i��2�|��2�j�@�ƂȂ�B
����  �� ���`����̂ŁA��L�̑���Ɠ��l�ɂ��āA��i�Q��2�|��2�j ���`�����Ƃ��ł���B
�� ���`����̂ŁA��L�̑���Ɠ��l�ɂ��āA��i�Q��2�|��2�j ���`�����Ƃ��ł���B
�b�l����i��2�|��2�j�@��`�����}�ɂ����āA�b�𒆐S�Ƃ��Ĕ��a ��i�Q��2�|��2�j �̉~��`���A
����ɁA�l�𒆐S�Ƃ��Ĕ��a �� �̉~��`���B���̂Q�̉~�̌�_�̂��������b�l�Ɋւ��Ă`
�̑��ɂ���_���c�Ƃ���B
�@���̂Ƃ��A���b�c�l�ɂ����āA
�@�@�@�b�c����i�Q��2�|��2�j�A�@�b�l����i��2�|��2�j�@�A�@�c�l����
�Ȃ̂ŎO�����̒藝�����藧���A�ڂb�l�c���X�O���ł���B
�]���āA�c�A�`�A�l�A�a�͈꒼����ɂ���A�`�c�����|���@�A�a�c�����{���@�ł���B
�@�@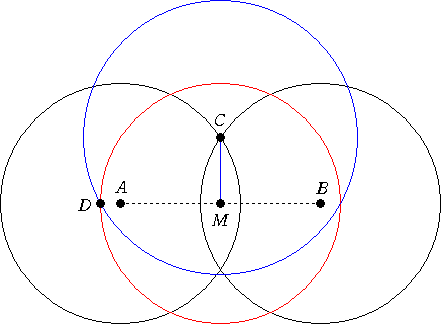
�i�R�����g�j�@�Ȃ�قǁI�Ȗ��ł��ˁB�e�m����Ɋ��ӂ��܂��B
���ڂ��鐳�O�p�`
�@���g�o�ǎ҂̂j�D�r�D������A�C�ӂ̎O�p�`�i�����`�j�ɓ��ڂ��鐳�O�p�`�̍�}���@��
�����������܂����B�i�����Q�R�N�P�O���T���t���j
�@�C�ӂ́��`�a�b�̂Q�ӂ̏�ɂQ���_�q�A�p�����A���`�a�b�ɓ��ڂ��鐳�O�p�`���o�p�q����
��B�����b�o�ƕӂ`�a�Ƃ̌�_�c���Ƃ�A�c�e���o�q�ɕ��s�A�c�d���o�p�ɕ��s�ɂƂ�A���c�d�e
�͓��ڂ������O�p�`�ƂȂ�B�i�����`���O�p�`�ɓ��ڂ��邱�Ƃ����l�ɉ\�ł��B�j
�@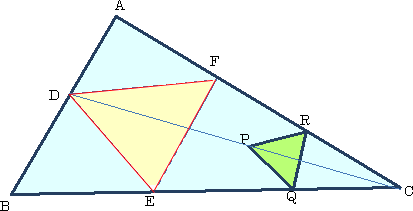
�i�R�����g�j�@�����g��𗘗p������}�ł��ˁI�j�D�r�D����Ɋ��ӂ��܂��B
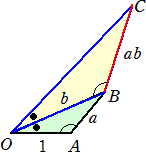
���� ���� �̍�}
�@���� �� �A�� ����� �P �̐������^�����Ă�����̂Ƃ���B���̂Ƃ��A�����̒���
���� �́A
���̂悤�ɍ�}�ł���B�����O�p�`�̐������疾�炩���낤�B
�@
�����`�̕���
�@���ʏ�ɂS�_�`�A�a�A�b�A�c������A�����͂��鐳���`�̂S�ӂ̂��ꂼ��̏�ɂ���P�_��
����B���̂Ƃ��A���̐����`�����邱�Ƃ͑傢�ɋ��������������ނƌ����邾�낤�B
�@�o�T�F�f���[�h�j�[�@�u����I�ȃp�Y���v�i�P�X�Q�U�N�j
�@�@�@
�@��}�̃|�C���g�́A�����Ȓ��p�O�p�`�������������Ƃł���B
�@�@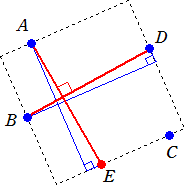
�@��ӂ��A�S�_�`�A�a�A�b�A�c�́A���鐳���`�̕ӏ�ɂ���̂ŁA�a�c���`�d�A�a�c�ۂ`�d �ƂȂ�
�悤�ɓ_�d���Ƃ�A�d���܂������`�̕ӏ�̓_�ł���B
�@��́A�����b�d�������A�����b�d�ɕ��s�œ_�`��ʂ钼���������B����ɁA�����b�d�ɐ����ŁA
�_�a�A�c��ʂ钼�������ꂼ������A�����`�������ł���B�����͑S�Ē�A�R���p�X
�ō�}�\�ł���B
�@���g�o�ǎ҂̂g�m�u�t�h�m�v����̃R�����g�ł��B�i�����Q�W�N�P���P�R���t���j
�@�}�̓_E���_�b�Əd�Ȃ鎞�͕����ł���̂ł����H���������O��������������Ă����
���ł����A�����ɕ`�������͕����ƍl����̂ł��傤���H
�i�R�����g�j�@�m���ɁA�S�_�̈ʒu�W�ɂ���ẮA�u�_E���_�b�Əd�Ȃ鎞�v�����蓾�܂��ˁB
�@�@�@�@�@�@���̂Ƃ��͐����`�̕����͏o���Ȃ��悤�ł��B
�ȉ~�̒��S�Ǝ�
�@�~�̒��S�́A�݂��ɕ��s�łȂ��Q�̌��̐����Q�������̌�_�Ƃ��ċ��߂���B�ȉ~
�ɑ��ē������Ƃ�����Ă��ȉ~�̒��S�͋��߂��Ȃ��B
�@�@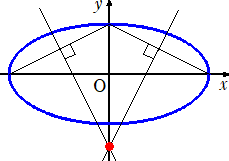
�@�ȉ~�̒��S�����߂�ɂ́A�ǂ���������̂��낤���H
�@�ȉ~�̌��ŕ��s�Ȃ��̂��Q�`���A���̒��_�����Ԍ��������A���̒��_���ȉ~�̒��S��
�Ȃ�B
�@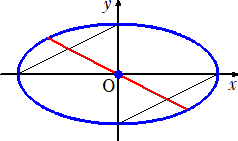
�@��L�ł́A���W�������L����Ă������A�ȉ~�������L���ꂢ�āA���W�������L����Ă�
�Ȃ��Ƃ��͂ǂ����낤�B�ȉ~�̒��S�́A��L�̂悤�ɂ��ċ��߂���B
�@�@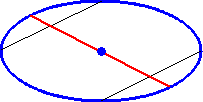
�@���̂Ƃ��A�ȉ~�̒��S�𒆐S�Ƃ��đȉ~�ƂS�_�Ō����~��`���B�����̌�_�Ƒȉ~��
���S�����ԂQ�ׂ̗荇�������̊p�̂Q��������`���ƁA���ꂪ���x�A����\���B
�@�@
�������̖@��
�@�������̔C�ӂ̓_�o�Őڐ��������A���̐ڐ��ɐړ_�o�Œ������钼���������A���ꂪ
�@���ƂȂ�B
�@����āA�@���̍�}���l����ꍇ�A���̈Ӗ���������A�ڐ����܂��`���āA���ꂩ��@��
��`���ƁA���ʍl���邩������Ȃ����A���́A�ڐ���`���K�v�͂Ȃ��A�@������}���邱�Ƃ�
�o����B
�@���̂��߂ɂ́A���̕������̐�����p����B���̐����́A�z�C�w���X�ɂ�蒍�ڂ��ꂽ
���̂Ƃ��Ēm���Ă���炵���B
�@������ ��������2 ��̓_�o(X�C���w2�j�ɂ�����@���̕�����
�@�@�@�����|�i�P/�i�Q���w�j�j���{���w2�{�P/�i�Q���j
�ƁA�����Ƃ̌�_�p�̍��W�́A
�@�@�@�p�i�O�C���w2�{�P/�i�Q���j�j
�ƂȂ�B���̂��Ƃ́A�������̔C�ӂ̓_�Ƃ��̓_�ɂ�����@���Ƃ����Ƃ̌�_�Ƃ̍��፷��
�� �̒l�ɂ�炸�A���i���P/�Q���j�ɂȂ邱�Ƃ������B
�@���̐����𗘗p���āA�������̖@������}���Ă݂悤�B
��@�����P/�Q�@�Ƃ��āA������ ����(�P/�Q�j��2 ��̓_�o(�|�Q�C�Q�j�ɂ�����@���͎��̂悤�ɍ�
�@�@�}�ł���B
�@�@�@���̏ꍇ�̂Q�_�o�A�p�̍��፷�́A�P�ƂȂ�̂ŁA
�@
�@��}�̐F�̎������_�o�ɂ�����@���ł���B���፷���������Ă���̂ŁA�@���̍�}
�͔��ɊȒP�Ȃ��̂ɂȂ�B
�����`�S
�@�ߘa�S�N�P���R�P���t���ŁA���g�o�����������b�ɂȂ��Ă���g�m�u�r�i�g�j�v����A�ʔ�
���T�C�g�����Љ���������B���̒��ŁA�x���[�X���C������́y�����`���z�ɋ������������B
�@�ǂ�ȎO�p�`������ʐς������������`����}�ł���
�i��}���@�j�@�@���`�a�b�̒�ӂa�b�̒����� �� �A������ �� �Ƃ���B�ӂa�b�̂b�����ɁA
�@�b�c����/�Q �ƂȂ�_�c���Ƃ�A�����a�c�̒��_���l�Ƃ����B
�@����ɁA�l�𒆐S�Ƃ��Ĕ��a�a�l�̉~�ʂ�`���A�b�ɂ���������a�c�̐����Ƃ̌�_���d��
�����B
�@��́A�����b�d���P�ӂƂ��鐳���`��`���ƁA���̐����`�̖ʐς́A���`�a�b�̖ʐςƓ���
�ɂȂ�B
�@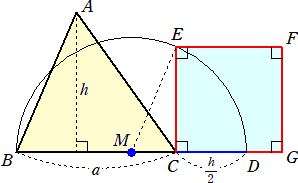
�i��́j�@���`�a�b������/�Q�@�ł���B
�@���d�l�b�ɂ����āA�@�l�d���i���{��/�Q�j/�Q�@�Ȃ̂ŁA�O�����̒藝����A
�@�d�b2���o�i���{��/�Q�j/�Q�p2�|�o�i���{��/�Q�j/�Q�|��/�Q�p2������/�Q
�@���̂��Ƃ���A�O�p�`�̖ʐςƐ����`�̖ʐς͓������B
�@�@�ȉ��A�H����