定木による作図 
当HPの「基本の作図」では、定木・コンパスを用いたり、コンパスのみを用いたりと、いろ
いろな条件で基本と思われる作図題に挑戦している。 (参考 → 「線分の垂線」)
平成22年8月30日付けで、当HPの掲示板「出会いの泉」に、HN「ぽっぽ」さんから次の
ような書き込みがあった。
作図で、1つの円と任意の点の集合から垂直2等分線や正96角形など様々な形が作図
できる、つまり、正96角形をコンパスを一回使えば作図できることが分かりました。
このことについて、当HPがいつもお世話になっているHN「らすかる」によれば、「一つ円
が描かれていれば、あとは定木だけで、通常作図できるもの(円弧自体を除いて)はすべ
て作図できる」ことは証明されているとのことである。Wikipediaにもそのことは書かれて
いるとのこと。(平成22年8月30日付け)
ぽっぽさんによれば、この事実は、「ポンスレー-スタイナーの定理」というらしい。
(平成22年8月30日付け)
当HPがいつもお世話になっているHN「FN」さんからの詳報です。
(平成22年8月31日付け)
ポンスレー-スタイナーの定理
定木とコンパスで作図できる図形は、1つの円とその中心が与えられていれば、定
木だけですべて作図できる。
上記の定理が成り立つとはいうものの、定木だけでは何もできそうな気がしません。まず、
ごく基本的なところから、次の作図はどうすればできるのでしょうか。
(1)直線Lと点Pが与えられたとき、点Pを通って直線Lに平行な直線を引く。
(2)直線Lと点Pが与えられたとき、点Pを通って直線Lに垂直な直線を引く。
ただし、円(と中心)が一つ与えられていることは使っていいとします。
私の感じとしては、円と中心が与えられていることは、(1)を示す段階では使えないのでは
ないかという気がします。
(1)ができれば、線分でできた図形の平行移動ができるようになるので、与えられた円の
所に平行移動して、円を使って作図をして、平行移動で元に戻すというようなことをするのか
なと思っています。
そもそも定木だけでの作図で許されることが何なのかもわかりません。
与えられた2点を結ぶ線分(直線)を引く。
与えられた線分を両側に延長する。
この2つは当然できるのでしょうが、他にどのようなことができるのでしょうか。
与えられた長さの線分を引く。
これは許されるのでしょうか。例えば、線分ABの延長上に、AB=BCとなる点Cをとるの
は許されるのでしょうか。普通はコンパスを使って点Cをとりますね。だから許されないと考
えるべきなのでしょう。
FNさんの疑問について、らすかるさんからのコメントです。(平成22年8月31日付け)
与えられた長さの線分を引く。
これは、もちろん許されません。これも、円を用いて作れることを示す必要があります。
他にできることは、
直線上、与えられた円の周上、あるいは円の近く、直線の近くなどの適当なところ
に点をとる
ぐらいでしょうか。基本の作図一つを達成するだけで手数が相当多くなります。
例えば、「円周上のある点を通る円の接線を引く」という作図は、次のようになります。
(私が自分で考えたものですので、最短ではないかも知れませんが...。)
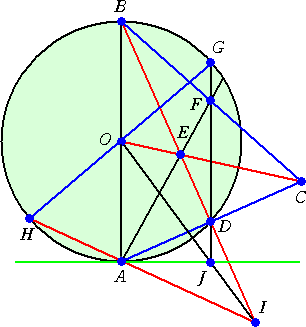 |
円Oとその円周上の点Aが与えられてい
るとする。
(1)半直線AO(線分AB)を引く。BはAOと円
Oとの新しい交点。三角形CABの辺CAと
辺CBが円周との交点を持つように点Cを
円Oの外部にとる。
(2)線分CAを引き、円Oとの交点をDとする。
(3)線分COを引く。
(4)線分CBを引く。
(5)半直線BDを引き、COとの交点をEとす
る。
(6)半直線AE(線分AF)を引く。FはAEとCB
の交点。 |
(7)直線DFを引き、円Oとの新しい交点をGとする。 ※DFはABと平行
(8)半直線GO(線分GH)を引く。Hは円Oとの新しい交点。 ※AD=BG=AH
(9)半直線HA(線分HI)を引く。IはHAとBDの交点。
(10)線分IOを引き、FDとの交点をJとする。 ※Jは「AIとDJの交点」とDとの中点
(11)直線AJを引くと、これが点Aにおける接線。 |
らすかるさんによる参考図→ http://www10.plala.or.jp/rascalhp/image/tan2.gif
他に「円外のある点から円に接線を引く」という作図もメモが残っていますが、こちらは17
ステップです。
「(2)直線Lと点Pが与えられたとき、点Pを通って直線Lに垂直な直線を引く。」は、
「私的数学塾」−「私の備忘録」−「基本の作図」−「線分の垂線」
に記録がありますので、以前自分で考えたはずですが、この作図方法はメモが見当たりま
せんでした。頭の中では出来ていてもステップが多すぎて、まとめる気にならなかったのか
も知れません。
今、ちょっと考えてみましたが、
「(1)直線Lと点Pが与えられたとき、点Pを通って直線Lに平行な直線を引く。」
は以下の手順で出来ると思います。
(補題0)
円周上のある点を通る円の接線が引ける。
円外の点から円に接線が引ける。
(証)
略。
(補題1)
円外の任意の直線に対し、円の中心に関して点対称な直線(つまり円を真ん
中に挟むような平行線)が描ける。
(証)
直線上に任意の点をとり、円に接線を引いて、接点と円の中心を結んで反対側の交点
をとり、その点における接線を引く。描いた平行線と元の直線との2交点と円の中心をそ
れぞれ結んで平行線との交点をとると平行四辺形が作れるので平行線が描ける。
(補題2)
直線上に2点A,Bがあるとき、ABの中点が作図できる。
(証)
補題1のようにして直線の平行線を描き、平行線の向こう側に適当な点をとって、上で
書いた「円の接線」の直線AB、直線DF、点Cの考え方でAF、BD、CEを結びOを求める。
(本題)
直線l上に等間隔に並ぶ3点A,B,Cをとり、APの先に適当な点Dをとって、BD、
CDを結び、BDとCPの交点をE、AEとCDの交点をFとすれば、PFは求める直線。
(関連)
直線上に2点A,Bがあるとき、A,B,Cの順に並びAB=BCとなる点Cがとれる。
(証)
直線の「反対側の平行線」を描き、補題2により等間隔に並ぶ3点D,E,Fを(DE<ABとな
るように間隔を狭く)作図し、AD、BEの交点をGとしてGFと元の直線の交点をとれば、そ
れが求める点。
このように積み重ねていけば、すべて証明できるのでしょうね。
「(2)直線Lと点Pが与えられたとき、点Pを通って直線Lに垂直な直線を引く。」
も考えたら出来ました。(平成22年9月1日付け)
(1) 円の中心をOとし、直線L上に適当な点Aをとり、線分AOと円の交点をBとする。
(2) Bを通り直線Lと平行な直線mを引く。
(3) 直線mと円とのもう一つの交点をCとする。
(4) 直線OCと直線Lとの交点をDとする。△ODAは、OA=ODの二等辺三角形。
(5) ADの中点Mをとる。
(6) Pを通りOMと平行な直線を引けば、これは直線Lに垂直。
※このとき、直線OM上に等間隔に並ぶ3点をとらなければなりませんが、前の証明では
円外の直線にしかとれません。しかし、この場合は円との交点と中心が等間隔に並ぶ3
点となっているので大丈夫です。
(コメント) コンパスがないだけでこんなに長手順になるんですね!コンパスの偉大さがヒ
シヒシと伝わってきました。らすかるさんに感謝します。

