曲率の真実 
曲率は曲線の曲がり具合を表す。一般社会では曲率半径(曲率の逆数)の方が馴染み
があるかもしれない。車を運転する人だったら、「R=300」などという標識を見て、これか
ら通過するであろうカーブのきつさを判断する。Rの値が大きければ大きいほど「ゆるやか
な」カーブだといえる。直線の曲率は、0 である。(→参考:「正方形を彫る」)
微分幾何で曲率を学んで以来、曲率そのものにはあまり関心がなかったが、いま考えて
いる問題と曲率が大いに関係があるということに、最近、気づかされた。
「基本の作図」の中の「円に接する円」において、
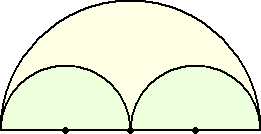 左図のように、半円の中に同半径の半円が
左図のように、半円の中に同半径の半円が
接しているとき、2つの小半円に外接し、大半
円に内接する円は、次のように作図される。
大半円の直径を1辺とする正方形を描き、
正方形の頂点と2つの小半円の中心A、B
を結ぶ線分の交点をCとする。
このとき、点Cが求める円の中心となる。 |
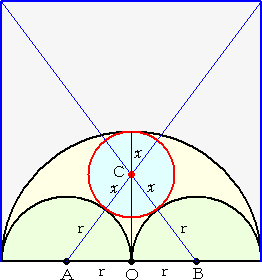 |
このとき、直角三角形CAOにおいて、三平方の定理より、 r2+(2r−x)2=(r+x)2
よって、上図のように接する円(赤)の半径は、 x=2r/3 となる。
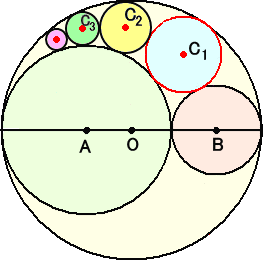
ところで上記では小半円の半径は等しいと仮定したが一般の場合はどうなるであろうか?
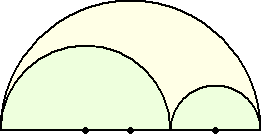
これに対して、求める円の半径は容易に求められる。
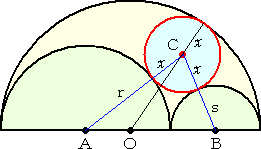 △CAOと△CBOにおいて余弦定理を用いて、
△CAOと△CBOにおいて余弦定理を用いて、
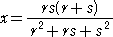
が、求める円の半径である。(→求め方)
このように、互いに接する3つの円に接する第4の円の半径を求める場合、上記では、
三平方の定理やその一般化である余弦定理を活用した。
この場面に、まさか曲率が使えるとは誰も思いつかないだろう。
(歴史的には、今から100〜200年前位には知られていた事実らしい。)
1921年のノーベル化学賞授賞者 フレデリック・ソディ(英国 1877〜1956)は、次のよ
うな公式を遺している。
平面上に、4つの円があり、どの2円もただ1点でのみ接するものとする。このとき、
4円の半径を a、b、c、d とし、その逆数(曲率!)をそれぞれ A、B、C、D とおくと、
2(A2+B2+C2+D2)=(A+B+C+D)2
が成り立つ。(ソディの公式)
ただし、左下図のような関係のときは、Dの符号は正とし、右下図のような関係のと
きは、Dの符号は負として考えるものとする。他の符号は正である。
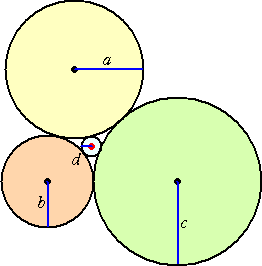
例 a=r 、b=x 、c=r 、d=2r で右上図のような位置関係にある場合、D=−1/2r
と考えて、ソディの公式より、
2((1/r)2+(1/x)2+(1/r)2+(−1/2r)2)=(1/r+1/x+1/r−1/2r)2
これより、 x=2r/3 が得られる。これは、今までの結果と一致する。
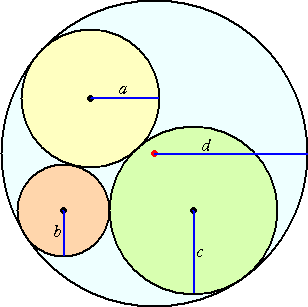
例 a=s 、b=x 、c=r 、d=r+s で右上図のような位置関係にある場合、
D=−1/(r+s) と考えて、ソディの公式より、
2((1/s)2+(1/x)2+(1/r)2+(−1/(r+s))2)=(1/s+1/x+1/r−1/(r+s))2
これより、
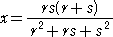
が得られる。
これは、今までの結果と一致する。
(コメント) ソディの公式は、デカルトの円定理とも言われる。とても興味ある公式である。
デカルトの円定理
 左図において、互いに外接する3つの円に
左図において、互いに外接する3つの円に
外接する第4の円の半径 d は、
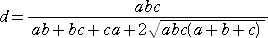
で与えられる。
(参考文献:深川英俊、ダン・ペドー 著
日本の幾何−何題解けますか?
(森北出版))
この式もそれなりに調和のとれた美しい形を
しているが、
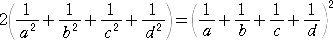
と書き直した方が、より均整のとれた美しい公式になると思う。この形が、互いに外接する
場合のソディの公式である。
さて、デカルトの円定理を確認するために、次の事実をまず証明しよう。
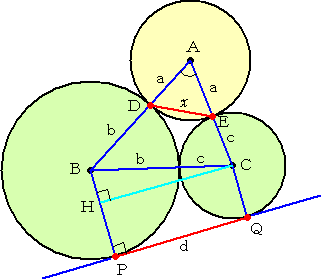 左図において、半径 a の円Aに、半径
左図において、半径 a の円Aに、半径
b の円B、半径 c の円Cがそれぞれ点
D、Eで互いに外接している。
(左図では、円B、Cが外接しているよう
に見えるが、その必要はなく、離れてい
てもよい!)
このとき、線分DEの長さ x について、
共通接線の長さPQ=d を利用して、
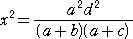
が成り立つ。
(証明) △ADEにおいて、余弦定理より、 cosA=(2a2−x2)/(2a2)
同様に、△ABCにおいて、余弦定理より、
cosA=((a+b)2+(a+c)2−(b−c)2−d2)/(2(a+b)(a+c))
=(2a2+2ab+2bc+2ca−d2)/(2(a+b)(a+c))
=1−d2/(2(a+b)(a+c))
よって、 (2a2−x2)/(2a2)=1−d2/(2(a+b)(a+c)) より、
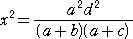
が、直ちに成り立つ。(証終)
この事実を用いて、デカルトの円定理は、次のように示される。
(証明)
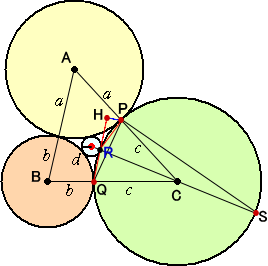 左図において、半径 a の円A、半径 b の円B、
左図において、半径 a の円A、半径 b の円B、
半径 c の円Cが互いに外接している。
円A,Bと円Cの接点を、それぞれP,Qとする。
3つの円に外接する第4の円の半径を d とし、
円Cとの接点をRとする。RSを円Cの直径とす
る。
直線QRに点Pより垂線PHを下ろす。
このとき、明らかに、
△PRS ∽ △HPQ
が成り立つ。
よって、 PR : RS = HP : PQ より、 HP=PR・PQ/(2c) である。
いま、直角三角形PHRにおいて、∠PRH=θ とおくと、 cosθ=RH/PR
△PQRにおいて、余弦定理より、
cos(180°−θ)=(PR2+QR2−PQ2)/(2PR・QR)
cos(180°−θ)=−cosθ なので、
(PR2+QR2−PQ2)/(2PR・QR)=−RH/PR
すなわち、 PR2+QR2−PQ2=−2QR・RH が成り立つ。
ただし、 RH2=PR2−HP2=PR2(1−PQ2/(4c2)) であることに注意する。
ここで、上記で証明した事実を用いると、
PQ2=c2((a+b)2−(a−b)2)/((b+c)(c+a))=4abc2/((b+c)(c+a))
QR2=c2((b+d)2−(b−d)2)/((b+c)(c+d))=4bc2d/((b+c)(c+d))
PR2=c2((a+d)2−(a−d)2)/((c+a)(c+d))=4ac2d/((c+a)(c+d))
である。これより、
RH2=4ac2d/((c+a)(c+d))・(1−ab/((b+c)(c+a)))
=4ac3d(a+b+c)/((c+a)2(b+c)(c+d))
となる。
これらを、 PR2+QR2−PQ2=−2QR・RH に代入して、
4ac2d/((c+a)(c+d))+4bc2d/((b+c)(c+d))−4abc2/((b+c)(c+a))
=−8c2d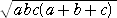 /((c+a)(b+c)(c+d))
/((c+a)(b+c)(c+d))
両辺を 4c2 で割って、さらに分母を払うと、
ad(b+c)+bd(c+a)−ab(c+d)=−2d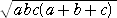
となるので、
d(ab+bc+ca+2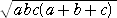 ) = abc
) = abc
すなわち、
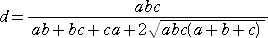
が成り立つ。(証終)
上述のソディの公式を見て分かるように、半径そのものを扱うよりも、その逆数を扱うと
公式が簡明になる。このページでは、円の半径の逆数ということで、曲率という言葉で表
現したが、詳しくは、「反転」と関係があるようだ。(→参考:「反転」)
反転において大切な性質を確認しておこう。
(1) 半径 r の円Oに関して、2点P、Qの反転を、P’、Q’とすると、
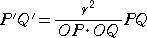
が成り立つ。
(証明) OP・OP’=r2 、OQ・OQ’=r2 より、 OP/OQ=OQ’/OP’
よって、△OPQ ∽ △OQ’P’ なので、 PQ : P’Q’=OP
: OQ’
したがって、 PQ : P’Q’=OP : r2/OQ より、明らか。(証終)
(2) 反転の中心Oを通る直線の反転は、Oを通る直線である。
反転の中心Oを通らない直線の反転は、Oを通る円である。
反転の中心Oを通る円の反転は、Oを通らない直線である。
反転の中心Oを通らない円の反転は、Oを通らない円である。
(3) 2つの円の接点を反転の中心とすると、平行な2直線に反転される。
2つの円の接点が反転の中心でないとき、互いに接する2つの円に反転される。
(4) 半径 a の円Aが、半径 b の円Bに反転されるものとする。
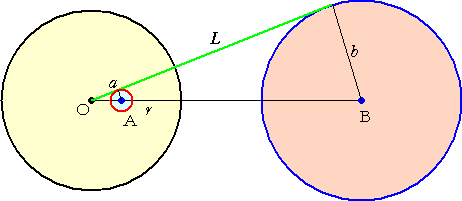
反転の中心Oから円Bに引いた接線の長さを、L とすると、
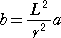
が成り立つ。
(証明) 円Aと線分OBとの交点を左側より、P、Qとし、その反転を、P’、Q’とする。
このとき、
2b=OP’−OQ’
=r2/OP−r2/OQ
=2ar2/(OP・OQ)
=2ar2・OP’/r2・OQ’/r2
=2a・OP’・OQ’/r2
方べきの定理より、 OP’・OQ’=L2 なので、
2b=2aL2/r2
よって、
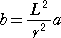
が成り立つ。(証終)
反転を用いて、円の半径を求めてみよう。
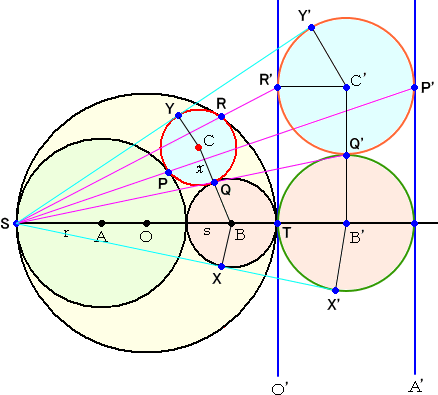
円Oと円Aの接点Sを反転の中心とし、反転度を、4(r+s)2 とする。
このとき、反転の性質(2)(3)から、円Oと円Aはそれぞれ平行な2直線O’、A’に反転さ
れ、また、円Bと円Cは2直線O’、A’に接し、互いに接する2円B’、C’に反転される。
反転の性質(4)から、 C’Y’=SY’2/(4(r+s)2)・CY すなわち、
x =CY=4(r+s)2・C’Y’/SY’2
が成り立つ。 ここで、 C’Y’=B’X’ なので、
x =4(r+s)2・B’X’/SY’2=(4(r+s)2/B’X’)・(B’X’/SY’)2
ところで、
SY’2=SC’2−C’Y’2=SB’2+B’C’2−B’X’2=SB’2+(2B’X’)2−B’X’2
より、 SY’2=SB’2+3B’X’2 である。
このとき、
(SY’/B’X’)2=(SB’/B’X’)2+3(B’X’/B’X’)2=(SB’/B’X’)2+3
となる。
ここで、 △SBX ∽ △SB’X’ なので、 SB’/B’X’=SB/BX=(2r+s)/s
よって、 (SY’/B’X’)2=((2r+s)/s)2+3=4(r2+rs+s2)/s2 より、
(B’X’/SY’)2=s2/(4(r2+rs+s2))
また、SB : SB’ = BX : B’X’ より、 (2r+s)B’X’=(2(r+s)+B’X’)s なので、
2r・B’X’=2s(r+s) すなわち、 B’X’=s(r+s)/r
以上から、
x =4r(r+s)2/(s(r+s))・s2/(4(r2+rs+s2))
これより、
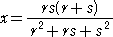
が成り立つ。
(補足) 上記の計算を精査すれば、下図のように順次円が内接する場合の円
Cn の半径
を求めることは容易だろう。
 左図において、円 Cn の半径は、
左図において、円 Cn の半径は、
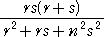
により与えられる。
上記の計算で、
SY’2=SB’2+3B’X’2 の部分を
SY’2=SB’2+(4n2−1)B’X’2
に変えれば同様に証明される。
(コメント) 反転を用いて、円の半径を計算してはみたものの、そんなに計算が簡略化され
たとは感じられなかった。円がすべて同半径の円に反転されるので、円の個数が
もっとたくさんあるときに多分その御利益にあずかれるのだろう。
上記の解と比較するためにも、余弦定理を用いた解法を書いておこう。
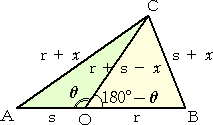 左図において、
左図において、
cos(180°−θ)=−cosθ
の両辺に、余弦定理の結果を代入して、
{s2+(r+s−x)2−(r+x)2}/(2s(r+s−x))
=−{r2+(r+s−x)2−(s+x)2}/(2r(r+s−x))
分母を払って、r{2s2+2rs−2(2r+s)x}=−s{2r2+2rs−2(r+2s)x}
よって、 4(r2+rs+s2)x=4rs(r+s) より、
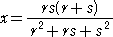
が得られる。
 さて、次の関心は左図において、4つの円の
さて、次の関心は左図において、4つの円の
半径が全て整数となる場合があるだろうかと
いうことである。このことは、問題作成をする場
合の最大の関心事であろう。
これについて、次のような公式が知られているようだ。
任意の整数 α>β≧γ>0 に対して、
λ=2αβγ(α+β)−αβ(αβ−γ2)−γ2(α+β)2
|
とおくと、
a=λα(αβ−γ2)
b=λβ(αβ−γ2)
c=λγ2(α+β)
d=αβγ2(αβ−γ2)(α+β)
である。
(参考文献:深川英俊、
ダン・ソコロフスキー 著
日本の数学−何題解けますか?[上]
(森北出版))
|
 |
例 α=2、β=γ=1 とすると、 λ=1 で、 a=2 、b=1 、c=3 、d=6
このとき、下図のような配置になる。
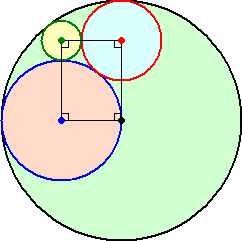
(コメント) 4つの円の中心を結ぶと長方形になって、しかも辺の長さが、3 と 4 。
何かしらの問題ができそうな予感...。
例 α=3、β=γ=1 とすると、 λ=2 で、 a=12 、b=4 、c=8 、d=24
これは、上記の例の図を4倍に拡大したものになっている。
例 α=4、β=γ=1 とすると、 λ=3 で、 a=36 、b=9 、c=15 、d=60
このとき、下図のような配置になる。
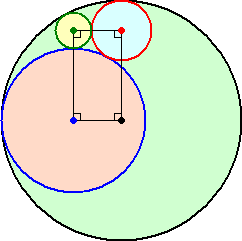
(コメント) この場合も、4つの円の中心を結ぶと長方形になって、しかも辺の長さが、
24 と 45 。 4つの円の中心を結ぶと長方形になるのは偶然?
さて、冒頭で考えた右図の図形(半円を除い
た黄色い部分は、「靴屋のナイフ」と呼ばれる
らしい!)について、面白い定理が存在する。
これは、4世紀アレキサンドリアの数学者パッ
プスによるものといわれる。 |
 |
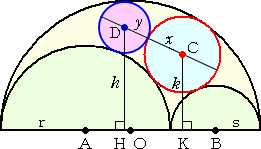
左図のように互いに接する円C、Dより、直線
ABに垂線CK、DHを下ろす。
このとき、円の直径と垂線の長さについて、
k = 2x 、 h = 2・2y
が成り立つ。
直接計算で、「 k = 2x 」であることを強引に証明してみよう。
(証明) △ABCにおいて、余弦定理より、
cosA={r2+rs+(r−s)x}/{2(r+x)(r+s)}
よって、 sin2A=1−cos2A
=4sx{r2+rs+rx}/{(r+x)2(r+s)2}
このとき、 k2=(r+x)2sin2A
=4sx{r2+rs+rx}/(r+s)2
上式に、
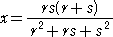
を代入して計算すると、
k2=4rs2(r+s)/(r2+rs+s2)・r(r+s)3/{(r2+rs+s2)(r+s)2}
=4r2s2(r+s)2/(r2+rs+s2)2
=4x2
よって、 k = 2x が成り立つ。(証終)
多分、上記の計算は、反転の考えを用いると、もう少し見通しよくなると思う。
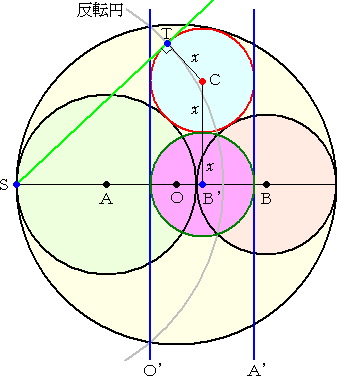
上図において、Sを反転の中心とし、Sより円Cに接線STを引き、線分STの長さを反転
度とする。
このとき、反転の性質(2)(3)から、円Oと円Aはそれぞれ平行な2直線O’、A’に反転さ
れ、また、円Bと円Cは2直線O’、A’に接し、互いに接する2円B’、C’に反転される。
この場合、円Cと点Sを通る直線との交点P、Qについて、方べきの定理より、
SP×SQ=ST2
が成り立つので、2点P、Qは互いに反転の関係にあり、円Cと円C’は重なる。
上図から、 k = 2x が成り立つことは明瞭であろう。
同様の作図を施せば、 h = 2・2y も示される。
一般に、直径 dλ の円 Cλ (ただし、C1=C)から直線ABに下ろした垂線の長さを hλ と
すると、
hλ = λ・dλ
が成り立つ。(パップスの定理)
この定理も、反転の考えから自明と言える。
(コメント:上記の円について、当初アップしたものが誤りであることに気づき訂正しました。
接点Tを通る円を反転円に据えるのがポイントのようです。
−2005.8.27 18:22記−)
(参考文献: ガードナー 著 高山 宏 訳 ガードナーの数学サーカス (東京図書))

 左図のように、半円の中に同半径の半円が
左図のように、半円の中に同半径の半円が

 △CAOと△CBOにおいて余弦定理を用いて、
△CAOと△CBOにおいて余弦定理を用いて、

 左図において、半径 a の円Aに、半径
左図において、半径 a の円Aに、半径 左図において、半径 a の円A、半径 b の円B、
左図において、半径 a の円A、半径 b の円B、

 左図において、円 Cn の半径は、
左図において、円 Cn の半径は、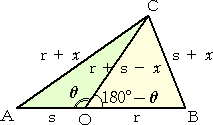 左図において、
左図において、


