「角の2等分」と聞いて、直ぐに、その作図方法が頭に描ける人は、かなり幾何が好きな人
である。
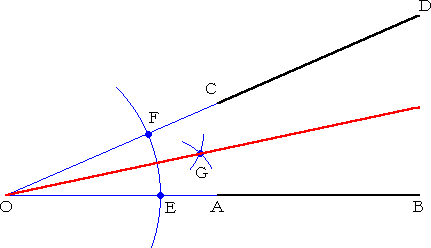
中学・高校で習う「角の2等分」は、上図のように、頂角O が分かっている場合に限られて
いる。
(作図方法)
頂角Oを中心として、適当な半径で円弧を描き、2直線との交点を、E、F とする。次に、2
点E、F を中心として、適当な同じ半径で円弧を描き、その交点をGとする。
このとき、2点O、G を結ぶ直線が求めるものである。
ところが、最近、次のような問題に遭遇した。
問題 頂角を持たない角を2等分せよ。
・角の2等分 S.H氏
「角の2等分」と聞いて、直ぐに、その作図方法が頭に描ける人は、かなり幾何が好きな人
である。

中学・高校で習う「角の2等分」は、上図のように、頂角O が分かっている場合に限られて
いる。
(作図方法)
頂角Oを中心として、適当な半径で円弧を描き、2直線との交点を、E、F とする。次に、2
点E、F を中心として、適当な同じ半径で円弧を描き、その交点をGとする。
このとき、2点O、G を結ぶ直線が求めるものである。
ところが、最近、次のような問題に遭遇した。
問題 頂角を持たない角を2等分せよ。
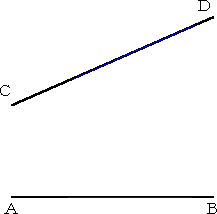 |
「頂角を持たない」という条件なので、上図のように、 AB、CDを延長して頂角を作図してから、通常の「角 の2等分」の作図をするのは邪道であろう。 この問題に対して、次のような作図方法があること を、最近知った。 結果が分かれば、その証明は容易である。 「作図の心構え」に従って、作図すればよい。 |
(作図方法) 2つの線分AB、CDに交わる直線を適当に引き、交点を、P、Q
とする。
解析 ・・・ 角の2等分線が引けたものとする。このとき、この2等分線上には、△OPQ の
内心と傍心が存在する。よって、この2点を作図すれば、求める直線が得られる。
作図 ・・・ 2点P、Q において、角の2等分線を引き、それらの交点を、R、Sとおく。このと
き、2点R、S を結ぶ直線を引けばよい。
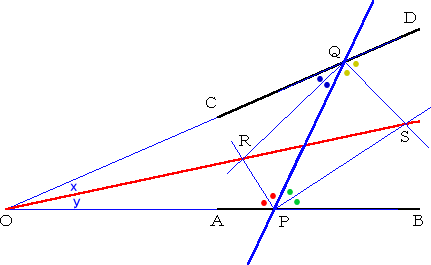
証明 ・・・ 四角形PSQR は、∠SPR=∠SQR=90°なので、円に内接する四角形である。
三角形の外角の性質と、円周角の定理により、
x+∠OQR=∠SRQ=∠SPQ 、 y+∠OPR=∠SRP=∠SQP
よって、 x =∠SPQ−∠OQR=∠SPQ−∠PQR
y =∠SQP−∠OPR=∠SQP−∠QPR
したがって、
x − y =(∠SPQ−∠PQR)−(∠SQP−∠QPR)
=(∠SPQ+∠QPR)−(∠PQR+∠SQP)
=∠SPR−∠SQR= 0 (∠SPR=∠SQR=90°より)
よって、 x = y
以上から、2点R、S を結ぶ直線RSは、2つの線分AB、CDのなす角を2等分する。
(参考文献:野口健助 著 平面画法入門(日刊工業新聞社))
(追記) 令和6年12月9日付け
上記では、直線PQを引き、それぞれの内角、外角の2等分線の交点から内心、外心を作
図し、その2点を通る直線が、求める角の2等分線であることを示している。
同様に、直線AC、BDを用いれば、内心と内心、内心と傍心、傍心と内心、傍心と傍心の
作図からも得られる。内心・傍心については高校レベルの話であろう。
頂角Oなしで、内心・傍心によらない直接的に求める方法も考えられる。
 |
線分AB上に任意に点Pをとり、Pより線分CDに垂線 PHを下ろす。Pにおける線分ABの垂線と線分CDの交 点をKとおく。∠KPHの2等分線と線分CDの交点をM 遠く。Mにおける線分CDの垂線と線分PKとの交点を Qとおくと、Qは、線分AB、CDのなす角の2等分線上に ある。 同様の操作を線分AB上の点P’で行い、点Q’を得れ ば、直線QQ’が求める角の2等分線となる。 (単に、∠PQMの2等分線を引いてもよい。) |
(コメント) △PMQが2等辺三角形になるところが面白いですね!しかも、点Qは、線分AB、
CDに接する円の中心になります。
次のように、直接、角の2等分線を得る方法もある。
 |
線分AB上に任意に点Pをとり、Pより線分CDに平行 線PQを引く。 ∠BPQの2等分線上に任意に点Hをとり、PHに垂直 な直線を引き、線分AB、CDとの交点をそれぞれN、M とおく。 線分MNの中点をKとおき、Kにおいて線分MNに垂 直な直線を描けば、これが求める角の2等分線となる。 |
もちろん、素朴に頂角Oを作図して、角の2等分線を引いてもよい。
 |
線分AB、CD上に任意に点P、Qをとり、P、Qにおけ る垂線上に等距離にP’、Q’をとる。 P’、Q’において、線分AB、CDに平行な直線m、n を引き、その交点をRとする。 Rにおける角の2等分線が求めるものである。 |
また、2等辺三角形を巧妙に用いて求める方法もある。
 |
線分AB上に任意に点Pをとり、Pにおける垂線が線 分CDと交わる点をQとする。Qにおける線分CDの垂 線上に、QP=QRとなる点Rをとる。 線分PRと線分CDの交点をSとおき、Sにおける垂 線が線分PQと交わる点をMとおく。 このとき、Mは求める角の2等分線上の点となる。 同様の操作を線分AB上の点P’で行い、点M’を得 れば、直線MM’が求める角の2等分線となる。 |
次の作図方法も面白い。
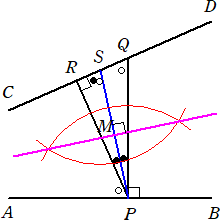 |
線分AB上に任意に点Pをとり、Pにおける垂線が線 分CDと交わる点をQとする。また、点Pから線分CDに 垂線PRを引く。 ∠QPRの2等分線が線分CDと交わる点をSとおく。 このとき、∠APS=∠CSPなので、線分PSの垂直2 等分線を引けば、これが求める角の2等分線となる。 |