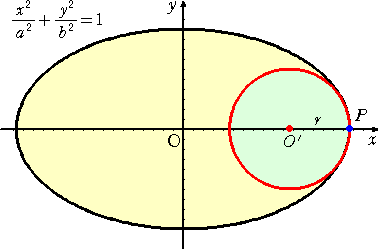
楕円に内接する円　 　　　　　　　　　　　　　　　　　　　

　楕円のグラフは、円のグラフを横方向に一定倍率で拡大縮小したものである。
（楕円の方程式については、こちらを参照）

　

　このグラフに、下図のような半径 ｒ の円を内接させたい。

　

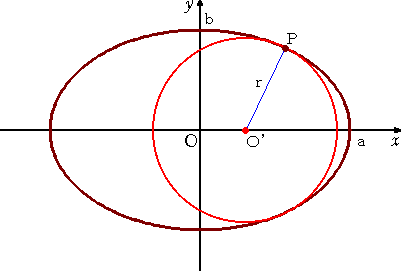
　中心をどこにおいたら、正しく作図できるのだろうか？

これについて、次の公式が知られている。

　

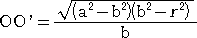
（証明）　点Ｐ（ｍ，ｎ）における楕円の接線の方程式は、

　

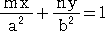
すなわち、　ｂ²ｍｘ＋ａ²ｎｙ＝ａ²ｂ²

　また、Ｏ’（ｃ，０）とすると、点Ｐ（ｍ，ｎ）における円の接線の方程式は、

　（ｍ−ｃ)(ｘ−ｃ）＋ｎｙ＝ｒ²

すなわち、　（ｍ−ｃ)ｘ＋ｎｙ＝ｒ²＋（ｍ−ｃ)ｃ

　２つの接線の方程式は一致するから、

　ｂ²ｍ/（ｍ−ｃ)＝ａ²ｎ/ｎ＝ａ²ｂ²/（ｒ²＋（ｍ−ｃ)ｃ）

すなわち、　ｂ²ｍ/（ｍ−ｃ)＝ａ²＝ａ²ｂ²/（ｒ²＋（ｍ−ｃ)ｃ）

後者の等式から、ｂ²＝ｒ²＋（ｍ−ｃ)ｃ　より、ｍｃ＝ｂ²−ｒ²＋ｃ²

同様に、前者の等式から、ｂ²ｍ＝ａ²（ｍ−ｃ)

よって、 ｂ²（ｂ²−ｒ²＋ｃ²）＝ａ²（ｂ²−ｒ²＋ｃ²−ｃ²)＝ａ²（ｂ²−ｒ²)　より、

　ｂ²ｃ²＝ａ²（ｂ²−ｒ²)−ｂ²（ｂ²−ｒ²）＝（ａ²−ｂ²)(ｂ²−ｒ²)

これより、

　

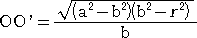
が示された。

（別解）　楕円　ｂ²ｘ²＋ａ²ｙ²＝ａ²ｂ²　と　円　(ｘ−ｃ）²＋ｙ²＝ｒ²　を連立して、ｙ を消去すると、

　（ａ²−ｂ²）ｘ²−２ｃａ²ｘ＋ａ²（ｃ²＋ｂ²−ｒ²）＝０

２次方程式が重解を持てばよいので、判別式をＤとすると、

Ｄ/４＝ｃ²ａ⁴−（ａ²−ｂ²）ａ²（ｃ²＋ｂ²−ｒ²）

　＝ａ²ｂ²ｃ²−（ａ²−ｂ²）ａ²（ｂ²−ｒ²）＝０

より、　ｂ²ｃ²−（ａ²−ｂ²）（ｂ²−ｒ²）＝０

したがって、

　


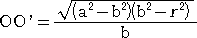
（コメント）　Ｓ（Ｈ）さんが示された指針を参考に、別解を得ました。双対曲線を用いた解法で
　　　　　はありませんが、高校生レベルの解法としては最善かつ自然と思われます。解答の
　　　　　ヒントを与えていただいたＳ（Ｈ）さんに感謝します。上記の共通接線による解法は少
　　　　　し遠回りでした！


（追記）　令和６年１２月１０日付け

　ＨＰ読者のＨＮ「Ｋ．Ｏ．」さんより、本ページについてご意見をいただいた。具体的な問題
について考察し、その返答としたい。

　楕円 ｘ²/４＋ｙ²＝１ の内部に接する ｘ 軸上に中心を持つ円を作図したい。

　円の半径を ｒ とすると、上記の公式から、円の中心の ｘ 座標は、√（３（１−ｒ²））　で与え
られる。ｒ＝０．９ の場合にＧｒａｐｅｓ で描画させたものが下図である。接しているかな？

　　

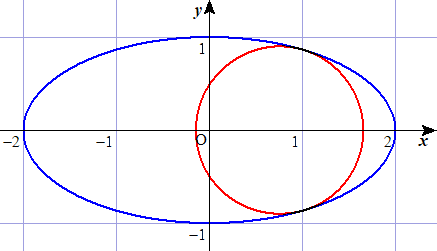
例　楕円 ｘ²/１６＋ｙ²/９＝１ の内部に接する ｘ 軸上に中心を持つ円を作図したい。

　円の半径を ｒ とすると、上記の公式から、円の中心の ｘ 座標は、√（７（１−ｒ²/９））　で
与えられる。ｒ＝２．９ の場合にＧｒａｐｅｓ で描画させたものが下図である。接しているかな？

　　

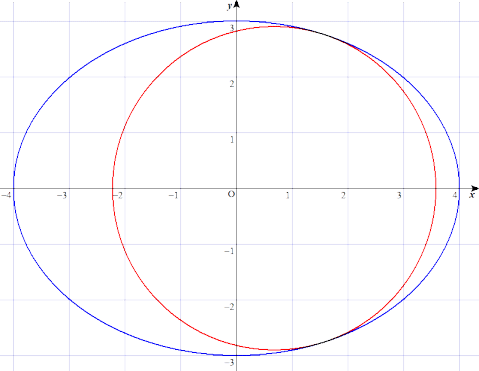
　楕円に内接する円の特別な場合として曲率円が考えられる。（→参考：日常の中の曲率）

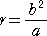
この場合について、上記の公 　式を当てはめれば、次の美しい 　公式が得られる。 　　曲率円の半径 ｒ は、 　　　　　 　で与えられる。

　証明は明らかであろう。ＯＯ’＝ａ−ｒ　なので、平方して整理すると、　（ａｒ−ｂ²）²＝０　が

得られる。　よって、　ａｒ−ｂ²＝０　から、上式が求められる。


（追記）　令和６年１２月１１日付け

　ＨＮ「Ｋ．Ｏ．」さんから、本ページの問題の類題が平成２５年度の東京工業大学で出題され
ている旨、ご教示いただいた。（令和６年１２月１０日付け）

問題５　　ａ、ｂ を正の実数とし、円Ｃ₁：（ｘ−ａ）²＋ｙ²＝ａ²　と楕円Ｃ₂：ｘ²＋ｙ²/ｂ²＝１ を考
　　える。

（１）　Ｃ₁がＣ₂に内接するための ａ、ｂ の条件を求めよ。

（２）（３）は（略）

　曲率円の半径は、　ａ＝ｂ²　で与えられ、また、公式　

　

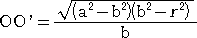
から、　ａ²ｂ²＝（１−ｂ²）（ｂ²−ａ²）　より、　ａ²＝ｂ²（１−ｂ²）　が成り立つ。

　ａ＝ｂ²　を代入して、　２ｂ²＝１　から、　ｂ＝１/　となる。

　したがって、　０＜ｂ＜１/　のとき、　ａ²＝ｂ²（１−ｂ²）

　幾何的に考えて、　ｂ≧１/　のとき、　ａ＝１/２

が求める ａ、ｂ の条件となる。


（コメント）　「幾何的に考えて」が少し気持ち悪いので、代数的にきちんと計算してみよう。

（解）　（ｘ−ａ）²＋ｙ²＝ａ²　に ｘ²＋ｙ²/ｂ²＝１ を代入して、（１−ｂ²）ｘ²−２ａｘ＋ｂ²＝０

　ｂ＝１　のとき、ａ＝１/２　で、（ｘ−１/２）²＋ｙ²＝１/４　は、 ｘ²＋ｙ²＝１ に点（１，０）で内
接する。

　ｂ≠１　とすると、２次方程式 （１−ｂ²）ｘ²−２ａｘ＋ｂ²＝０ が得られる。

軸の方程式は、　ｘ＝ａ/（１−ｂ²）

判別式をＤとおくと、Ｄ/４＝ａ²−ｂ²（１−ｂ²）＝０　から、軸の方程式は、ｘ＝ｂ²/ａ　となる。

Ｆ（ｘ）＝（１−ｂ²）ｘ²−２ａｘ＋ｂ²　とおくと、　Ｆ（０）＝ｂ²＞０　である。

軸の位置で場合分けをする。

・　０＜ｂ²/ａ＜１　のとき、解が　０＜ｘ＜１　にある。このとき、Ｆ（１）＝１−２ａ＞０　である。

このとき、　ｂ²＜ａ＜１/２　から、　０＜ｂ＜１/　で、　ａ²＝ｂ²（１−ｂ²）　である。

・　ｂ²/ａ＝１　のとき、解が ｘ＝１ となるためには、Ｆ（１）＝１−２ａ＝０

このとき、ａ＝１/２　で、ｂ²＝ａ＝１/２　から、ｂ＝１/

　ｂ＞１/　のとき、（ｘ−ａ）²＋ｙ²＝ａ²　が ｘ＝１ で ｘ²＋ｙ²/ｂ²＝１ に接することから、

ａ＝１/２　となる。

以上から、　０＜ｂ＜１/　のとき、　ａ²＝ｂ²（１−ｂ²）

　ｂ≧１/　のとき、　ａ＝１/２　　（終）

が求める ａ、ｂ の条件である。


（コメント）　楕円　ｂ²ｘ²＋ａ²ｙ²＝ａ²ｂ²　に　円　(ｘ−ｃ）²＋ｙ²＝ｒ²　が内接するとき、

　連立して、ｙ を消去すると、（ａ²−ｂ²）ｘ²−２ｃａ²ｘ＋ａ²（ｃ²＋ｂ²−ｒ²）＝０

　軸の方程式は、　ｘ＝ｃａ²/（ａ²−ｂ²）　なので、楕円と円が２点で接するためには、

　０＜ｃａ²/（ａ²−ｂ²）＜ａ　すなわち、　ｃａ＜ａ²−ｂ²　のとき、

判別式Ｄ＝０　から、　ｂ²ｃ²＝（ａ²−ｂ²）（ｂ²−ｒ²）　が成り立つ。

ｃａ≧ａ²−ｂ²　のとき、楕円と円は１点（ａ，０）で接する。

このとき、　ｃａ²/（ａ²−ｂ²）＝ａ　から、　ｃａ＝ａ²−ｂ²

（ａ²−ｂ²）ｘ²−２ｃａ²ｘ＋ａ²（ｃ²＋ｂ²−ｒ²）＝０　の ｘ に ａ を代入して、

　（ａ²−ｂ²）ａ²−２ｃａ³＋ａ²（ｃ²＋ｂ²−ｒ²）＝０

すなわち、　ａ²−ｂ²−２ｃａ＋ｃ²＋ｂ²−ｒ²＝０　から、　ｒ²＝（ａ−ｃ）²　より、　ｒ＋ｃ＝ａ　が

成り立つ。



　　以下、工事中！