・　日常の中の曲率　　　 　　　　　　　　　　　　　Ｓ．Ｈ氏

　日常生活で数学を意識することはあまりないが、車を運転する人は否応にも数学を意識
する瞬間がある。それは、急カーブを曲がるときだ。

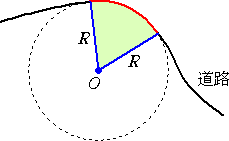
　カーブのある瞬間は、半径が Ｒ の円周上を動いている。その半径を曲率半径という。曲
率半径の逆数は、曲率と言われる。

　　　　　　　　　　　

　急なカーブの前では、下記のような標識が立っていて運転者に速度の減速を促す。

　　　　　　　　　　　　　　　　　

　日本の道路は、道路構造令に基づいて造られている。その第１５条には曲線半径（数学
でいう曲率半径のこと）のことが述べられている。（一部抜粋）

　車道の屈曲部のうち緩和区間を除いた部分（以下「車道の曲線部」という。）の中心
線の曲線半径は、当該道路の設計速度に応じ、次の値以上とするものとする。

　この表によれば、一般道路（最高速度６０ｋｍ/ｈ）では、曲線半径１５０ｍ以上、高速道路
（最高速度１００ｋｍ/ｈ）では、曲線半径４６０ｍ以上で設計されているということである。た
だ、地形によっては、「Ｒ＝３００」ということもあり、その場合は、「かなりの急カーブ」という
ことで、８０ｋｍ/ｈ程度に減速しないと、安全にカーブを曲がるのも辛いことになる。

　乾いた道路とタイヤの摩擦係数を、０．５ として、「Ｒ＝３００」のカーブで、どれくらいまで
スピードが可能か計算してみよう。

　公式　　（速度）²＝（重力加速度）×（曲線半径）×（摩擦係数）　に代入して、

　　　　　　　

　これを時速に直すと、大体　１３８ｋｍ/ｈ　くらい。これは臨界速度なので、これよりスピー
ドを出すとカーブを曲がりきれず道路外に飛び出すことも考えられる。

　曲線半径からどれくらいの時速でカーブを曲がればよいのか、上記の表は一つの指針を
与えてくれる。日本では、曲線半径でカーブのきつさを表しているが、外国の標識では「速
度の上限」を示しているものもあるようだ。