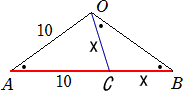惓俆妏宍偺嶌恾偲愜傝巻丂丂丂丂丂丂丂丂丂丂丂丂 
丂侾俈俋俇擭俁寧俁侽擔偺挬丄侾俋嵨偺僈僂僗惵擭偼丄栚妎傔偨弖娫偵丄惓侾俈妏宍偺嶌恾
乮掕栘偲僐儞僷僗偺傒傪梡偄傞乯傪巚偄偮偄偨偲偄偆丅
丂惓俁妏宍丄惓係妏宍丄惓俆妏宍丄惓侾俆妏宍傗偦偺曈偺悢傪師乆偵俀攞偟偰偱偒傞惓俇妏
宍丄惓俉妏宍丄惓侾侽妏宍丏丏丏丏丏側偳偺嶌恾偼丄屆偔儐乕僋儕僢僪偺帪戙偵偼暘偐偭偰偄
偨丅儐乕僋儕僢僪埲棃丄堦斒偵弶摍婔壗偱偼丄嶌恾偱偒傞惓懡妏宍偼丄偦傟埲忋側偄偩傠
偆偲挿偔怣偠傜傟偰偄偨丅
丂偦偺拞偱偺偙偺敪尒偼丄旕忢偵嬃偔傋偒傕偺偑偁傞丅徻偟偄撪梕偵偮偄偰丄偙偙偱怗傟
傞偵偼丄偁傑傝偵榖偑崅搙偡偓傞偺偱丄杮偺徯夘偵棷傔偨偄丅
乮偱傕丄偪傚偭偲嫽枴偑偁傞恖偼丄偙偪傜傪嶲徠乯
丂惓侾俈妏宍偺嶌恾偺壜擻惈偺徹柧偵偮偄偰偼丏丏丏
丂丂崅栘掑帯丂挊丂丂嬤悽悢妛巎択乮嫟棫慡彂乯
丂幚嵺偺惓侾俈妏宍偺嶌恾偵偮偄偰偼丏丏丏
丂丂崅栘掑帯丂挊丂丂弶摍惍悢榑島媊丂戞俀斉乮嫟棫弌斉乯丂俹丏侾侾侾乣俹丏侾侾俀
丂
丂俀侽侽侾擭偼丄僈僂僗偺乽惍悢榑乿偑姧峴偝傟偰挌搙俀侽侽擭偲偄偆愡栚偺擭偱偁傞丅僈僂
僗偺摿廤偑悢妛僙儈僫乕丂俀侽侽俀亅侾寧崋乮擔杮昡榑幮乯偱慻傑傟偰偄傞丅
丂偙偺儁乕僕偱偼丄僈僂僗偵偼墦偔媦偽側偄偑丄惓俆妏宍偺嶌恾偵偮偄偰丄傑偲傔偰傒偨
偄偲巚偆丅
 |
丂丂丂惓俆妏宍嶌恾偺億僀儞僩偼丄
丂丂仮俙俠俢佷仮俢俥俠偵婥偑晅偔偙偲偱偁傞丅
丂丂丂惓俆妏宍偺堦曈偺挿偝傪俀偲偡傞偲丄
丂丂丂丂丂俙俥亖俥俢亖俠俢亖俀丂偱偁傞丅
丂丂丂偦偙偱丄俥俠傪倃偲偡傞偲丄斾椺幃
丂丂丂俀亄倃丂丗丂俀丂亖丂俀丂丗丂倃丂偑惉傝棫偮丅
丂丂偙傟傪夝偔偲丄倃亖 亅侾偲側傞丅 亅侾偲側傞丅
丂丂丂廬偭偰丄俙俠亖 亄侾丂偱偁傞偙偲偑暘 亄侾丂偱偁傞偙偲偑暘
丂丂偐傞丅
丂丂丂埲忋偺峫嶡偐傜丄惓俆妏宍偺嶌恾偼丄
丂丂 偺嶌恾偑偱偒傟偽壜擻偲側傞丅 偺嶌恾偑偱偒傟偽壜擻偲側傞丅 |
丂丂場傒偵丄惓侾俈妏宍偺嶌恾偺偨傔偵偼丄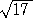 傪偼偠傔偲偟偨偄傠偄傠側悢偺暯曽崻偺
傪偼偠傔偲偟偨偄傠偄傠側悢偺暯曽崻偺
丂嶌恾偵婣拝偝傟傞偙偲偑抦傜傟偰偄傞丅
丂惓俆妏宍偺嶌恾朄偼壓婰偺捠傝偱偁傞丅
 |
丂嵍恾偺傛偆偵丄俠俢偺拞揰俫偐傜悅捈擇摍暘慄傪堷
偒丄俧俫亖俀 偲側傞傛偆偵丄俧傪偲傞丅
丂偙偺偲偒丄丂俠俧亖 偱偁傞丅 偱偁傞丅
丂俠俧偺俧曽岦偺墑挿慄忋偵俧俲亖侾偲側傞傛偆偵俲傪
偲傞偲丄
丂丂丂丂丂俠俲亖 亄侾 亄侾
偱偁傞丅偙偺挿偝傪丄僐儞僷僗傪梡偄偰俙偵堏偡丅
丂偙偺惓俆妏宍偺捀揰俙偑寛傑傟偽丄俙丄俠傪梡偄偰
俛偑寛傑傝丄俙丄俢傪梡偄偰俤偑寛傑傞丅
丂埲忋偱丄惓俆妏宍偺嶌恾偼姰惉偱偁傞丅 |
丂丂崱偐傜侾侽擭掱慜乮暯惉俁擭崰乯偵丄巹帺恎愜傝巻偵嫮偄嫽枴傪帩偭偨帪婜偑偁偭偨丅
丂掕栘偲僐儞僷僗偩偗偱偼丄妏偺俁摍暘偼晄壜擻偱偁傞偑丄愜傝巻傪梡偄傞偲偦傟偼壜
丂擻偱偁傞偙偲傪抦偭偨丅愜傝巻偺帩偮恄旈偝丄帺桼惈偵怱傂偐傟偨巚偄弌偑偁傞丅
丂丂忋婰偺傛偆偵丄惓俆妏宍偼丄巻柺偵掕栘偲僐儞僷僗傪梡偄偰彂偔偙偲偑偱偒傞偑丄幚偼丄
丂愜傝巻偱惓俆妏宍傪嶌傞偲偄偆帋傒傕旕忢偵嫽枴怺偄丅
丂丂偙偺帋傒偵偮偄偰偼丄杧堜梞巕丂挊丂乽愜傝巻偲悢妛乿丂乮柧帯恾彂乯丂俹丏係俁乣俹丏係係
丂偵徻偟偔弎傋傜傟偰偄傞丅
丂忋婰偺寁嶼傛傝丄惓俆妏宍偺堦曈偺挿偝傪俀偲偡傞偲丄懳妏慄偺挿偝偼丄侾亄 偱偁傞丅
偱偁傞丅
廬偭偰丄媡偵懳妏慄偺挿偝傪 俀 偲偡傞偲丄堦曈偺挿偝偼丄亅侾亄 偲側傞丅愜傝巻偱惓俆
偲側傞丅愜傝巻偱惓俆
妏宍傪愜傞応崌丄偙偺挿偝傪偄偐偵幚尰偡傞偐偑億僀儞僩偲側傞丅
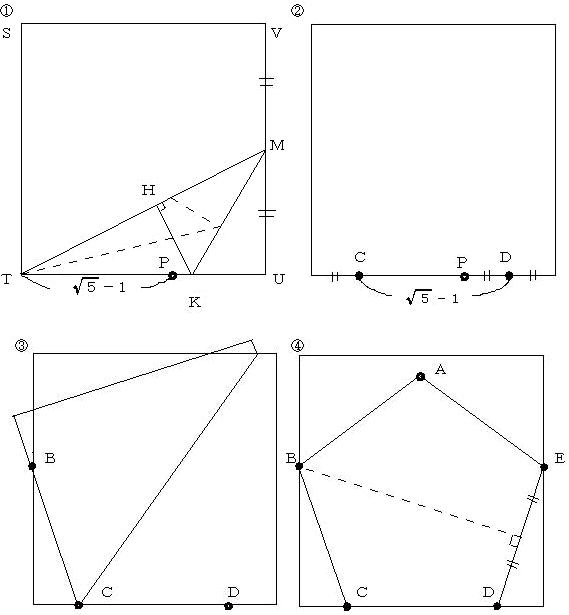
丂嘆丂愜傝巻偺堦曈倀倁乮倀倁亖俀乯偺拞揰俵偲俿傪寢傇慄偱愜傝丄愜傝栚傪偮偗傞丅俵倀偑
丂丂丂俿俵偵廳側傞傛偆偵愜傝丄偝傜偵丄俿俲偑俿俵偵廳側傞傛偆偵愜傞丅偙偺偲偒丄俿俫亖俿俹
丂丂丂偲側傞傛偆偵俿倀忋偵俹傪懪偮丅
丂嘇丂俹倀偺拞揰俢傪偲傝丄俿俠亖俢倀偲側傞傛偆偵俿倀忋偵俠傪懪偮丅
丂嘊丂俠傪屌掕偟偰丄俢偑俽俿忋偵偔傞傛偆偵愜傝嬋偘丄俽俿忋偵俛傪懪偮丅
丂嘋丂摨條偵偟偰丄倀倁忋偵俤傪懪偪丄偝傜偵丄俢偑俤偵廳側傞傛偆偵愜傝嬋偘傞丅俠偲廳側傞
丂丂丂揰俙傪懪偪丄俙俛丆俙俤偱愜傝嬋偘傞丅
丂丂埲忋偱丄愜傝巻偵傛傞惓俆妏宍偺姰惉偱偁傞丅
乮捛婰乯丂惓俆妏宍偺嶌恾偵偮偄偰丄忋婰偱偼丄侾曈傪梌偊偰嶌恾偟偨丅偟偐偟丄忬嫷偵傛偭
丂丂丂丂偰偼丄惓俆妏宍偺懳妏慄偺挿偝偲偐惓俆妏宍偑撪愙偡傞墌偺敿宎傪傕偲偵丄惓俆妏
丂丂丂丂宍傪嶌恾偟側偗傟偽側傜側偄偲偒傕偁傞丅偙偙偱偼丄偦偺傛偆側応崌偵偮偄偰丄嶌恾
丂丂丂丂偺幚嵺傪尒偰傒偨偄偲巚偆丅
乮侾乯丂懳妏慄偺挿偝偑暘偐偭偰偄傞応崌
丂丂丂惓俆妏宍偺侾曈偺挿偝傪丄俀 偲偡傞偲丄懳妏慄偺挿偝偼丄 亄侾 偱偁傞丅偟偨偑偭偰丄
亄侾 偱偁傞丅偟偨偑偭偰丄
丂丂媡偵丄懳妏慄偺挿偝傪 俀 偲偡傞偲丄堦曈偺挿偝偼丄 亅侾 偲側傞丅
亅侾 偲側傞丅
丂丂丂偟偨偑偭偰丄梌偊傜傟偨懳妏慄偺挿偝偑丂俀倃丂偺偲偒丄侾曈偺挿偝丂乮 亅侾乯倃丂傪嶌
亅侾乯倃丂傪嶌
丂丂恾偡傟偽傛偄丅
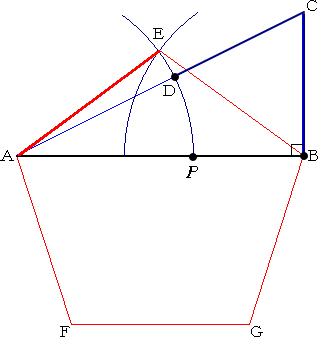 |
丂丂侾乯梌偊傜傟偨懳妏慄傪俙俛偲偡傞丅
丂丂丂俛偵偍偄偰丄俙俛偺挿偝偺敿暘偺悅
丂丂丂慄 俛俠傪偐偔丅
丂丂俀乯俙俠忋偵俠俢亖俠俛偲側傞揰俢傪偲傞丅
丂丂俁乯俙俢偺挿偝偱丄俀揰俙丄俛傛傝丄揰俤傪
丂丂丂寛傔傞丅
丂丂係乯俙俛丄俙俤偺挿偝傪梡偄偰丄巆傝偺捀
丂丂丂揰丂俥丄俧 傪寛傔傞丅
丂嵍恾偵偍偄偰丄揰俹偼慄暘俙俛傪墿嬥暘
妱偡傞揰偱偁傞丅
丂傛偭偰丄慄暘偺墿嬥暘妱揰偑嶌恾偱偒
傟偽丄偦偺慄暘傪懳妏慄偵帩偮惓俆妏宍
傪嶌恾偡傞偙偲偑偱偒傞丅 |
乮俀乯丂撪愙偡傞墌偺敿宎偑暘偐偭偰偄傞応崌
丂丂丂惓俆妏宍偑撪愙偡傞墌偺敿宎傪 俀 偲偟偰峫偊傞丅乮堦斒偺応崌偼丄掕悢攞偡傟偽傛偄丅乯
丂丂傑偢丄偙偺偲偒偺惓俆妏宍偺侾曈偺挿偝傪媮傔偰傒傞丅惓俆妏宍傪拞怱偱俆暘妱偟丄師偺
丂丂嶰妏宍偱峫偊傞丅
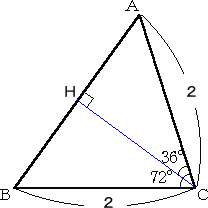 |
丂丂兤亖俁俇亱偲偡傞偲丄俆兤亖侾俉侽亱
丂傛偭偰丄倱倝値俀兤亖倱倝値乮侾俉侽亱亅俁兤乯
丂丂丂丂丂丂丂丂丂亖倱倝値俁兤
丂丂丂丂丂丂丂丂丂亖俁倱倝値兤亅係倱倝値3兤
丂丂俀倱倝値兤們倧倱兤亖俁倱倝値兤亅係倱倝値3兤丂偺椉曈傪倱倝値兤偱妱偭偰丄
丂丂丂丂丂丂俀們倧倱兤亖俁亅係倱倝値2兤
丂丂丂丂丂丂丂丂丂丂亖俁亅係乮侾亅們倧倱2兤乯
丂丂丂丂傛偭偰丄係們倧倱2兤亅俀們倧倱兤亅侾亖侽丂傛傝丄
丂丂丂丂丂丂丂丂丂丂丂丂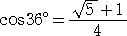 |
丂偙傟傛傝丄
丂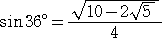
偟偨偑偭偰丄惓俆妏宍偺侾曈偺挿偝偼丄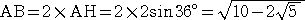
乮捛婰乯丂椷榓尦擭侾侾寧係擔晅偗
丂忋婰偱偼丄嶰妏娭悢偺俀攞妏偺岞幃丄俁攞妏偺岞幃傪梡偄偰夝偄偰偄傞偑丄偦偆偄偆崅媺
媄傪梡偄側偔偰傕丄嶰暯曽偺掕棟傪梡偄偰傕偭偲弶摍揑偵夝偔偙偲偑偱偒傞丅丂
| 乮暿夝乯 |
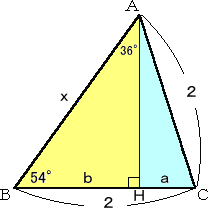 |
丂丂丂撪愙墌偺敿宎傪俀偲偟丄偦偺偲偒偺惓俆妏宍偺
丂丂侾曈偺挿偝傪倶偲偍偔丅
丂丂丂惓俆妏宍偺侾曈偺挿偝偑侾偺偲偒丄懳妏慄偺挿
丂丂偝偼丄乮侾亄 乯/俀 側偺偱丄斾椺幃 乯/俀 側偺偱丄斾椺幃
丂丂丂丂俀丗乮侾亄 乯倶/俀亖倎丗倶/俀 乯倶/俀亖倎丗倶/俀
丂丂傛傝丄丂乮侾亄 乯倎倶/俀亖倶 乯倎倶/俀亖倶
丂傛偭偰丄丂倎亖俀/乮侾亄 乯亖乮 乯亖乮 亅侾乯/俀 亅侾乯/俀 |
丂嶰暯曽偺掕棟傛傝丄
倶2亖乮俀亅乮 亅侾乯/俀乯2亄係亅乮乮
亅侾乯/俀乯2亄係亅乮乮 亅侾乯/俀乯2亖俉亅俀乮
亅侾乯/俀乯2亖俉亅俀乮 亅侾乯亖侾侽亅俀
亅侾乯亖侾侽亅俀 丂側偺偱丄
丂側偺偱丄
丂倶亖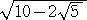 丂丂乮廔乯
丂丂乮廔乯
丂傛偭偰丄挿偝 俀 偐傜丄挿偝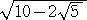 偑嶌恾偱偒傟偽傛偄偙偲偵側傞丅
偑嶌恾偱偒傟偽傛偄偙偲偵側傞丅
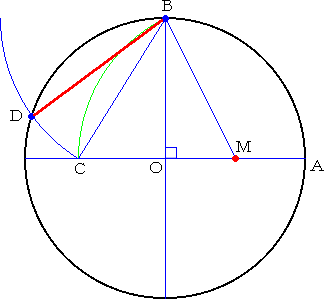 |
丂嵍恾偵偍偄偰丄俵偼敿宎俷俙偺拞揰
側偺偱丄俷俵亖侾
丂傛偭偰丄俛俵亖
丂俙傪抂揰偲偡傞捈宎忋偵丄俵俠亖俵俛
偲側傞揰俠傪偲傞丅
丂偙偺偲偒丄俷俠亖 亅侾丂側偺偱丄 亅侾丂側偺偱丄
丂丂丂丂丂俛俠亖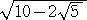
偲側傞丅
丂傛偭偰丄俛傪拞怱偲偟丄敿宎俛俠偺墌傪
昤偒丄墌俷偲偺岎揰傪俢偲偡傟偽丄慄暘
俛俢偑媮傔傞惓俆妏宍偺侾曈偲側傞丅 |
乮拲乯丂偙偺嶌恾曽朄偼傑偨丄墌廃傪俆摍暘偡傞曽朄傕梌偊偰偄傞丅
乮嶲峫暥專丗栰岥寬彆丂挊丂暯柺夋朄擖栧乮擔姧岺嬈怴暦幮乯乯
乮捛婰乯丂忋婰偱偼丄捈愙揑偵惓俆妏宍偺堦曈傪嶌恾偟偨偑丄惓侾侽妏宍偺嶌恾偐傜惓俆妏宍
丂丂丂偺堦曈傪嶌恾偡傞曽朄偑偁傞偙偲傪嵟嬤抦傞偙偲偑偱偒偨丅
丂敿宎俀偺墌偵撪愙偡傞惓侾侽妏宍偺堦曈偺挿偝傪 俴 偲偍偔偲丄梋尫掕棟偐傜丄
丂俴2亖俀2亄俀2亅俀丒俀丒俀丒們倧倱俁俇亱亖俉亅俉丒們倧倱俁俇亱
偙偙偱丄
丂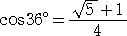
側偺偱丄丂丂俴2亖俇亅俀 丂丂傛傝丄丂丂俴亖
丂丂傛傝丄丂丂俴亖 亅侾丂偲側傞丅
亅侾丂偲側傞丅
丂偙偺偙偲偐傜丄師偺傛偆側嶌恾曽朄偑峫偊傜傟傞丅
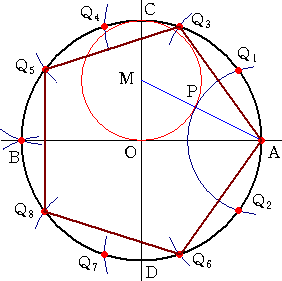 |
丂丂俷俠偺拞揰俵傪拞怱偲偡傞敿宎侾偺墌傪
丂昤偔丅
丂丂偙偺墌偲慄暘俙俵偲偺岎揰傪俹偲偡傞丅
丂丂偙偺偲偒丄丂俙俹亖 亅侾丂丂偱偁傞丅 亅侾丂丂偱偁傞丅
丂丂偦偙偱丄揰俙傪拞怱偲偟丄俙俹傪敿宎偲偡傞
丂墌屖傪昤偒丄墌俷偲偺岎揰傪丄俻1丄俻2 偲偡
丂傞丅
丂丂偁偲偼丄慄暘俙俻1 偺挿偝偱丄墌俷偺廃忋
丂傪嬒摍偵暘妱偟丄揰俻3丄俻4丄俻5丄俻6丄俻7丄
丂俻8 傪栚惙傟偽傛偄丅
丂丂偦偟偰丄堦偮旘傃偵揰傪寢傫偱偄偔偲丄惓
丂俆妏宍傪嶌恾偡傞偙偲偑偱偒傞丅 |
乮捛婰乯丂暯惉侾俉擭俆寧係擔晅偗
丂忋婰偱丄愜傝巻偵傛傞惓俆妏宍偺嶌恾朄傪庢傝忋偘偨偑丄彮偟崬傒擖偭偰偄傞偐側丠偲
偄偆報徾偑巹帺恎偵偼偁偭偨丅傕偆彮偟弶摍揑側愜傝曽偑朷傑偟偄偲巚偭偰偄偨偲偙傠丄師
偺傛偆側愜傝曽偑偁傞偙偲傪嵟嬤抦偭偨丅
| 乮侾乯 |
|
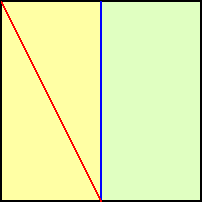
乮俀乯 |
|
 |
仺 |
 |
仺 |
|
|
|
|
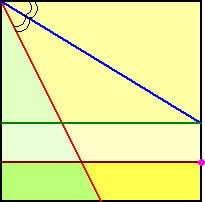
| 乮俁乯 |
|
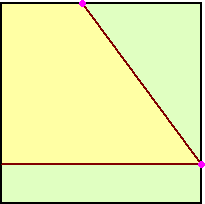
乮係乯 |
|
 |
仺 |
 |
仺 |
|
|
|
|
| 乮俆乯 |
|
乮俇乯 |
|
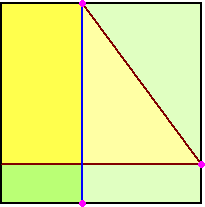 |
仺 |
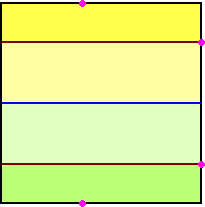 |
仺 |
|
|
|
|
| 乮俈乯 |
|
|
|
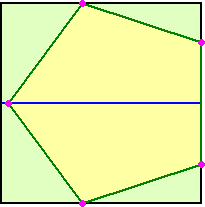 |
|
|
|
乮僐儊儞僩乯丂尨棟揑偵偼丄慜偺傕偺偲摨偠偐側丠両
乮嶲峫暥專丗嬍栘塸旻丂挊丂丂彫妛惗偵僺僞僑儔僗丂乮傒偡偢彂朳乯乯
乮捛婰乯丂暯惉俀侽擭俆寧俁侽擔晅偗偱丄摉俫俹偺宖帵斅乽弌夛偄偺愹乿偵丄乽倠侽俁俇乿偝傫偐傜
丂丂丂丂彂偒崬傒偑偁偭偨丅
丂乽巹偺旛朰榐乿偺惓俆妏宍偺嶌恾傪尒傑偟偨丅巹傕偙偺嶌恾偺惓摉惈傪徹柧偟傛偆偲
俀擭慜偵挧愴偟傑偟偨丅偦偟偰丄壓婰傪尒偮偗傑偟偨丅
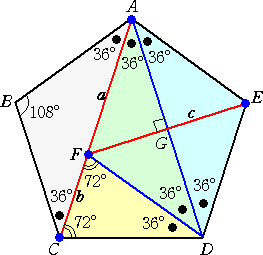 |
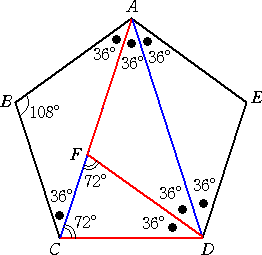
丂丂丂嵍恾偺傛偆偵丄
丂丂丂俥俙亖倎丂丄丂俥俠亖倐丂丄丂俥俤亖們
丂丂偲偍偔偲丄丂倎2亄倐2亖們2丂偑惉傝棫偮丅
乮僐儊儞僩乯丂偙傟偼惓偵僺僞僑儔僗偺掕棟偵弌偰偔傞
丂丂丂丂傛偆側娭學幃偱偡偹両 |
丂乽倠侽俁俇乿偝傫偵傛傟偽丄偙傟偼乽儐乕僋儕僢僪尨榑乿乮仺嶲峫丗嶳岥戝妛嫵堢妛晹懖嬈尋媶乯偺戞侾俁
姫偵偁傞柦戣俋偲柦戣侾侽丗
柦戣 俋丂 摨偠墌偵撪愙偡傞丄惓俇妏宍偺曈偲惓侾侽妏宍偺曈偑彂偐傟偨偲偒丄捈慄慡懱偼
丂丂丂丂丂奜拞斾偵暘偗傜傟丄偦偟偰丄偦偺傛傝戝偒偄晹暘偼惓俇妏宍偺曈偲側傞丅
丂乮嶲峫丗丂徹柧丂仺丂嶳岥戝妛丂搉绯丂惓丂尋媶幒偺俫俹乯
柦戣侾侽丂惓俆妏宍偑墌偵撪愙偡傞偲偒丄惓俆妏宍偺曈偺忋偺惓曽宍偼丄摨偠墌偵撪愙偡
丂丂丂丂丂傞惓俇妏宍偺曈偲惓侾侽妏宍偺曈偺忋偺惓曽宍偺榓偲摍偟偄丅
丂乮嶲峫丗丂徹柧丂仺丂嶳岥戝妛丂搉绯丂惓丂尋媶幒偺俫俹乯
傪娙扨偵愢柧丒徹柧偡傞偙偲偵側傞偦偆偱偁傞丅
丂偡側傢偪丄椺偊偽丄尨榑丂戞侾俁姫丂柦戣侾侽 偺撪梕偼丄
丂摨堦偺墌偵撪愙偡傞惓侾侽妏宍丄惓俇妏宍丄惓俆妏宍偺曈挿偵偮偄偰丄
丂乮惓俆妏宍偺曈挿乯2亖乮惓俇妏宍偺曈挿乯2亄乮惓侾侽妏宍偺曈挿乯2
偲偄偆偙偲傪堄枴偡傞丅
丂惓俆妏宍丄惓俇妏宍丄惓侾侽妏宍偺攝抲恾偼師偺傛偆偵昤偔偲暘偐傝傗偡偄丅
乮乽倠侽俁俇乿偝傫偵傛傞傕偺傪丄側偧傜偣偰偄偨偩偒傑偟偨両乯
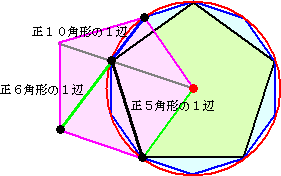
丂乽 倎 丗 倐 乿偑墿嬥斾偱偁傞偙偲偼丄傛偔抦傜傟偰偄傞偑丄偝傜偵丄 倎 丄
倐 丄 們 偵偮偄偰丄僺僞
僑儔僗偺掕棟偵弌偰偔傞傛偆側娭學幃偑惉傝棫偮偙偲偼弶尒偱偟偨丅
丂戝偄偵嫽枴偑偁偭偨偺偱丄乽倠侽俁俇乿偝傫偵傛傞徹柧傪嶲峫偵傑偲傔偝偣偰偄偨偩偄偨丅偙
偺傛偆側婡夛傪梌偊偰偄偨偩偄偨乽倠侽俁俇乿偝傫偵姶幱偄偨偟傑偡丅
丂朻摢偱寁嶼偟偨傛偆偵丄惓俆妏宍偺侾曈偺挿偝傪 俀 偲偡傞偲丄丂倎亖俀丂丄丂倐亖 亅侾丂偱
亅侾丂偱
偁傞丅傑偨丄
丂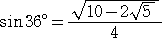
側偺偱丄丂們亖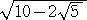
偲側傞丅丂偙偺偲偒丄柧傜偐偵丄丂倎2亄倐2亖們2丂偑惉傝棫偮丅
丂忋婰偱偼嶰妏斾偺抣傪媮傔偰徹柧偟偨偑丄偁傑傝弶摍揑偲偼尵偊側偄丅乽倠侽俁俇乿偝傫偵
傛傞師偺傛偆側徹柧偑廫暘弶摍揑偱暘偐傝傗偡偄丅
乮倠侽俁俇偝傫偵傛傞徹柧丒丒丒堦晹廋惓偝偣偰偄偨偩偒傑偟偨両乯
 |
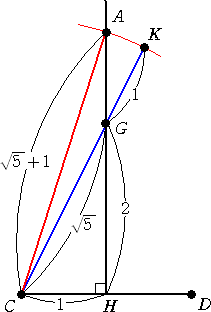
丂丂丂嵍恾偵偍偄偰丄仮俙俠俢佷仮俢俠俥丂側偺偱丄
丂丂丂丂丂丂丂丂丂倎亄倐 丗 倎 亖 倎 丗 倐
丂丂丂傛偭偰丄丂倎倐亖倎2亅倐2丂偑惉傝棫偮丅
丂丂丂丂傑偨丄丂捈妏嶰妏宍俙俥俧偵偍偄偰丄
丂丂丂丂丂俙俥亖 倎 丄俥俧亖們/俀 丄 俙俧亖乮倎亄倐乯/俀
丂丂丂側偺偱丄僺僞僑儔僗偺掕棟傛傝丄
丂丂丂丂丂倎2亖乮們/俀 乯2亄乷乮倎亄倐乯/俀乸2
丂丂丂偡側傢偪丄
丂丂丂丂丂丂丂丂丂丂們2亖俁倎2亅俀倎倐亅倐2
丂傛偭偰丄忋幃偵丄倎倐亖倎2亅倐2丂傪戙擖偟偰丄
丂丂丂們2亖俁倎2亅俀倎倐亅倐2亖倎2亄倐2 |
乮僐儊儞僩乯丂堄奜側偲偙傠偵丄堄奜側娭學幃偱戝曄柺敀偄偲巚偄傑偡丅
乮捛婰乯丂摉俫俹偑偄偮傕偍悽榖偵側偭偰偄傞俫俶乽俧俙俬乿偝傫偐傜偺僐儊儞僩偱偡丅
丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂乮暯惉俀俆擭俉寧俀侽擔晅偗乯
丂掕婯偲僐儞僷僗偱惓屲妏宍傪嶌恾偡傞怓乆側曽朄傪傒傞偙偲偑偁傞偑丄偲偰傕僔儞僾儖偱
妎偊傗偡偄曽朄偑丄
丂晄巚媍偍傕偟傠婔壗妛帠揟乮俢丏僂僃儖僘丂挊丂媨嶈嫽擇丂懠栿丂乮挬憅彂揦乯乯
偺俈俈暸偵徯夘偝傟偰偄傞丅嶲峫傑偱偵丄
侾丏堦偮偺墌撪偵丄屳偄偵捈岎偡傞俀杮偺捈宎俴丄俴乫傪昤偔丅
俀丏俴忋偱丄敿宎偺拞揰傪俵偲偡傞丅
俁丏捈宎俴乫偑墌偲岎傢傞揰偺堦曽傪俙偲偟丄俵傪拞怱偲偡傞敿宎俙俵偺墌偑捈宎俴偲岎傢傞
丂揰傪俶偲偡傞丅
係丏揰俙傪拞怱偲偟偰敿宎俙俶偺墌傪昤偒丄尦偺墌偲偺岎揰傪俛丆俤偲偡傞丅
俆丏俁揰俙丄俛丄俤偼惓俆妏宍偺俁偮偺捀揰偲側傞丅
丂愢柧偟偰偄傞偲傗傗偙偟偔姶偠傑偡偑丄幚嵺嶌恾偡傟偽偙傫側偵娙扨偵嶌恾偱偒傞傫偩偲
巚偭偨傕偺偱偡丅乮懠偺曽朄傕偄傠偄傠彂偐傟偰偄傞偑丄偳傟傕偡偖偵朰傟偰偟傑偆丅乯
丂偙偺杮偼儁乕僕悢乮俀係俁儁乕僕乯偺妱偵偼崅壙乮惻崬傒偱俆侾係俆墌丏丏丏倖(^^;) 乯側偺偱偡
偑丄捠忢偺杮偱偼尒傜傟側偄怓乆側婔壗揑栤戣偑偁傞傾儅僠儏傾婔壗妛幰偲柤偺傞挊幰
乮DAVID WELLS)偑廤傔偰偄偨傕偺傪栿偟偨傕偺偱偁傞丅悽奅偵偼偙傫側晽曄傢傝側恖暔偑
偄傞偍堿偱丄杽傕傟偰偟傑偭偰偄傞巚偭偰傕偄側偄栤戣偑昞偵尰傟偰偔傞丅儅乕僠儞丒僈乕僪
僫乕傕傃偭偔傝嬃偒丄嫽枴捗乆偺悢乆偵弌夛偊傑偡丅
乮僐儊儞僩乯丂俧俙俬 偝傫偑姶摦偝傟偨曽朄偼丄偙偺暸偺
丂乮俀乯撪愙偡傞墌偺敿宎偑暘偐偭偰偄傞応崌
偱徯夘偝傟偰偄傑偡丅傑偨丄乽婎杮偺嶌恾乿偺拞偺乽惎宆乿傕偛嶲徠偔偩偝偄丅
乮捛婰乯丂暯惉俀俈擭俀寧侾俉擔晅偗
丂師偺栤戣傪丄惓俆妏宍偺栤戣偲偲傜偊傞曽偼偳傟偔傜偄偄傞偺偩傠偆丅
丂壓恾偼丄掙柺偺墌偺敿宎俁丄曣慄偺挿偝侾侽偺捈墌悕偺揥奐恾偱偁傞丅偙偺偲偒丄慄暘俙俛
偺挿偝傪媮傔傛丅
丂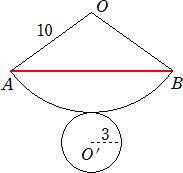
乮夝乯丂拞怱妏佢俙俷俛偺戝偒偝偼丄俁俇侽亱亊俇兾/俀侽兾亖侾侽俉亱側偺偱丄媮傔傞挿偝俙俛偼
侾曈偺挿偝偑侾侽偺惓俆妏宍偺懳妏慄偺挿偝偱偁傞丅侾曈偺挿偝偑俀偺惓俆妏宍偺懳妏慄偺
挿偝偼丄侾亄 側偺偱丄丂俙俛亖俆亄俆
側偺偱丄丂俙俛亖俆亄俆 丂偲側傞丅丂丂乮廔乯
丂偲側傞丅丂丂乮廔乯
乮僐儊儞僩乯丂崅峑惗側傜偽丄偙偺栤戣偼恀偭愭偵梋尫掕棟傪巚偄偮偔偩傠偆偑丄寁嶼偑偲偰傕
丂丂丂丂丂丂斚嶨偲側傞丅
丂忋婰偺夝偺傛偆偵丄惓俆妏宍偺侾曈偺挿偝侾偵懳偟偰丄懳妏慄偺挿偝乮乮侾亄 乯/俀乯偑墿
乯/俀乯偑墿
嬥斾偵側傞偲偄偆帠幚傪抦傜側偔偰傕丄朻摢偺峫偊曽偲摨條偵偟偰丄憡帡側嶰妏宍傪尒偮偗
傟偽丄屻偼俀師曽掱幃偺寁嶼偲側傞丅
丂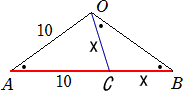
丂忋恾偵偍偄偰丄俀摍曈嶰妏宍俷俙俛偼俀摍曈嶰妏宍俠俛俷偵憡帡偱偁傞丅
傛偭偰丄丂侾侽 丗 倶 亖 侾侽亄倶 丗 侾侽丂偑惉傝棫偮丅偡側傢偪丄丂倶2亄侾侽倶亅侾侽侽亖侽
偙偺偲偒丄丂倶亖亅俆亄俆 丂側偺偱丄丂俙俛亖俆亄俆
丂側偺偱丄丂俙俛亖俆亄俆 丂偲側傞丅
丂偲側傞丅
乮僐儊儞僩乯丂俁俇亱丄俈俀亱偺恾宍偺埖偄偵姷傟偰偄側偄偲擄偟偄偐傕丏丏丏丅
乮捛婰乯丂暯惉俁侽擭俈寧俈擔晅偗
丂嵟嬤丄惓俆妏宍偺嶌恾傪怳傝曉傞婡夛偑偁傝丄偦偺惉壥傪傑偲傔偰偍偒偨偄丅
乮侾乯丂捀妏俁俇亱偺擇摍曈嶰妏宍傪棙梡偡傞曽朄
丂丂掙曈偺挿偝傪俀偲偡傞偲丄摍曈偺挿偝偼丄 亄侾偱偁傞丅偟偨偑偭偰丄
亄侾偱偁傞丅偟偨偑偭偰丄 丄傂偄偰偼
丄傂偄偰偼
 亄侾偺嶌恾偑億僀儞僩偲側傞丅
亄侾偺嶌恾偑億僀儞僩偲側傞丅
丂丂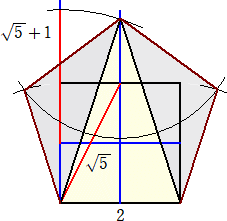
乮俀乯丂暋慺悢暯柺傪棙梡偡傞曽朄乮僈僂僗暯柺偲偄偭偨曽偑彮偟偐偭偙偄偄偐側丠乯
丂丂曽掱幃丂倸5亖侾 偺夝偑惓俆妏宍偺捀揰傪梌偊傞丅
丂倸亖cos兤亄倝丒倱倝値兤丂偲偍偔偲丄僪丒儌傾僽儖偺掕棟偐傜丄丂cos俆兤亄倝丒倱倝値俆兤亖侾
丂傛偭偰丄丂俆兤亖俀倠兾丂乮倠亖侽丄侾丄俀丄俁丄係乯丂傛傝丄
丂兤亖侽丄俀兾/俆丄係兾/俆丄俇兾/俆丄俉兾/俆
丂偙偺偲偒丄曽掱幃丂倸5亖侾 偺俆偮偺夝偼丄
丂倸1亖侾丄倸2亖cos(俀兾/俆)亄倝丒倱倝値(俀兾/俆)丄倸3亖cos(係兾/俆)亄倝丒倱倝値(係兾/俆)丄
丂倸4亖cos(俇兾/俆)亄倝丒倱倝値(俇兾/俆)丄倸5亖cos(俉兾/俆)亄倝丒倱倝値(俉兾/俆)
丂偙偙偱丄倸4亖cos(俇兾/俆)亄倝丒倱倝値(俇兾/俆)亖cos(俀兾亅係兾/俆)亄倝丒倱倝値(俀兾亅係兾/俆)
丂亖cos(係兾/俆)亅倝丒倱倝値(係兾/俆)丂乮仼丂倸3 偺嫟栶暋慺悢乯
倸5亖cos(俉兾/俆)亄倝丒倱倝値(俉兾/俆)亖cos(俀兾亅俀兾/俆)亄倝丒倱倝値(俀兾亅俀兾/俆)
丂亖cos(俀兾/俆)亅倝丒倱倝値(俀兾/俆)丂乮仼丂倸2 偺嫟栶暋慺悢乯
傑偨丄倸4亄倸3亄倸2亄倸亄侾亖侽丂偐傜丄丂乮倸亄侾/倸乯2亄乮倸亄侾/倸乯亅侾亖侽
傛偭偰丄丂倸亄侾/倸亖乮亅侾亇 乯/俀
乯/俀
丂侾/倸偼丄倸偺嫟栶暋慺悢側偺偱丄丂倸2亄倸5亖乮亅侾亄 乯/俀丂丄倸3亄倸4亖乮亅侾亅
乯/俀丂丄倸3亄倸4亖乮亅侾亅 乯/俀
乯/俀
偡側傢偪丄丂cos(俀兾/俆)亖乮亅侾亄 乯/係丂丄cos(係兾/俆)亖乮亅侾亅
乯/係丂丄cos(係兾/俆)亖乮亅侾亅 乯/係
乯/係
傛偭偰丄乮亅侾亄 乯/係傗乮亅侾亅
乯/係傗乮亅侾亅 乯/係偑嶌恾偱偒傟偽丄惓俆妏宍偑嶌恾偱偒傞丅
乯/係偑嶌恾偱偒傟偽丄惓俆妏宍偑嶌恾偱偒傞丅
丂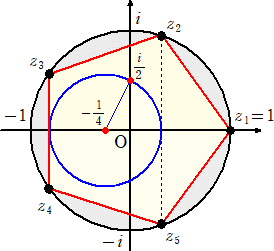
乮僐儊儞僩乯丂暋慺悢暯柺偱丄亅侾/係傪拞怱偲偟丄敿宎 /係偺墌傪嶌恾偡傞偙偲偵傛傝丄惓俆
/係偺墌傪嶌恾偡傞偙偲偵傛傝丄惓俆
丂丂丂丂丂丂妏宍偑嶌恾偱偒傞傫偱偡偹両偡偛偔扨弮壔偝傟傑偟偨丏丏丏丅