３次方程式と作図の問題　　　　　　　　　　　　　　　　

　ギリシアの古代から有名な問題：任意の角を３等分する作図はできるか？
がある。

　この問題については既に、作図不可能ということで決着していることは周知の通りである。
しかしながら、角の３等分ができる場合があることも事実で、その場合に、どのような方法で
３等分されるのかを考えることも、一つの数学であろう。

　当ＨＰの「私の備忘録」に掲載の「角の３等分方程式」において、角の３等分を可能にする
線分の長さが満たす方程式を、アルキメデスの方法を用いて求めた。別解として、次のよう
にして求める方法もある。

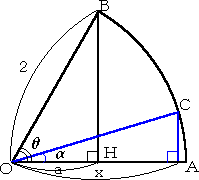左図において、θ＝３α　である。三角関数の、３倍角の 　公式から、 　　 　ここで、左図より、 　　 　 なので、上式に代入して整理すると、

　ｘ³−3ｘ−ａ＝０

という方程式が得られる。この解が作図可能ならば、角の３等分は作図可能となる。

　このページでは、どのような解が作図可能となるのか、また、作図可能な図形はどのよう
な代数的意味を持つのかについて、まとめてみたい。

定理　＋、−、×、÷、√ を用いて表される数は、定木・コンパスを用いて作図可能

（加法・減法の作図方法）

　正数 ａ、ｂ （ａ＞ｂ）　を与えられた数とする。このとき、ａ＋ｂ、ａ−ｂ は、次のように作図さ
れる。

　

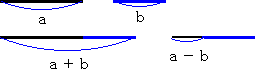
（乗法・除法の作図方法）

　正数 ａ、ｂ を与えられた数とする。このとき、ａ×ｂ、ａ÷ｂ は、次のように作図される。

　

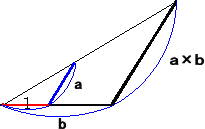
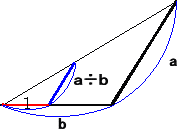
（平方根の作図方法）

　正数 ａ を与えられた数とする。このとき、√ａ は、次のように作図される。
（参考：作図問題における円の役割）

　　


　若き日のガウスは、正１７角形が作図可能であることを示した。それは、正１７角形の頂
点 Ｚ が満たす方程式　Ｚ¹⁷−１＝０　の一つの解 Ｚ が、次の形で与えられるからである。

　

ただし、ａ は、次の値である。



　式の形から、作図可能であることは明らかであるが、この数を実際に作図するのは、多分
大変で、作図しようという気が全く起こらないのは私だけじゃないですよね！？（塾長）


　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんから作図法をご教示いただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２９年５月３１日付け）

　正１７角形の作図は、半径1の円を描いておき、一つ分の開きに相当するcos(2*Pi/17)を
作図で作り出せればよい。

gp > cos(2*Pi/17)
%10 = 0.93247222940435580457311589182156338626258777794512

一方
gp > (-1+sqrt(17)+sqrt(34-2*sqrt(17))+2*sqrt(17+3*sqrt(17)
　　　　-sqrt(34-2*sqrt(17))-2*sqrt(34+2*sqrt(17))))/16
%12 = 0.93247222940435580457311589182156338626258777794512

と平方根だけで表せるため理屈では作図可能は示せる。

ちなみに、正７角形は、

gp > cos(2*Pi/7)
%25 = 0.62348980185873353052500488400423981063227473089640

一方
gp > -1/6+sqrtn(7*(1+3*sqrt(3)*I)/2,3)/6+sqrtn(7*(1-3*sqrt(3)*I)/2,3)/6
%26 = 0.62348980185873353052500488400423981063227473089640 + 0.E-58*I

より、３乗根と虚数単位Iが入り込む。

　しかし、実際に、これを定規とコンパスだけで忠実に再現していくことは困難を極める。

　ガウスが１９歳の（1796年)時、朝目覚めて起きようとした時に忽然と（いかにも天才らしい
セレンディピティ）思い付いてから約100年後の1893年にリッチモンドなる人物が、以下のよ
うな手順を発表した。（他の方法も見たことあるが、これは簡潔！）

＜手順＞

[1]　中心Ｏとして任意の大きさの円を描く。

[2]　直交する２つの直径ＡＯＰ[0]、ＢＯＣを引く。

[3]　ＯＢ/4の点ＪをＯＢ上にとる。

[4]　∠ＯＪＰ[0]/4=∠ＯＪＥなる点ＥをＯＰ[0]上にとる。
　　（角の２等分線は作図可能なので、２度繰り返せば可能）

[5]　∠ＥＪＦ=45°となる点ＦをＯＡ上にとる。

[6]　ＦＰ[0]を直径とする円を描き、これがＯＢと交わる点をＫとする。

[7]　Ｅを中心としＫを通る円がＡＰ[0]と交わる点をＧ（Ａ側）、Ｈ（Ｐ[0]側）とする。

[8]　ＡＰ[0]に垂直で、Ｇ、Ｈを通る線を引き、元の円と交わる点をそれぞれＰ[5]、Ｐ[3]とする。

[9]　２点Ｐ[5]、Ｐ[3]での垂直２等分線を引き、円と交わる点をＰ[4]とする。

[10]　これで正１７角形分の一辺Ｐ[3]Ｐ[4]（又はＰ[4]Ｐ[5]）が採れる。

＃すべての作業を慎重に進めないと、なかなか正確な図になっていかないので注意のこと。


　ガウスは、さらに次の驚くべき事実も証明している。

定理　正ｎ角形が定木とコンパスで作図できるとき、
　　　　　　　　　
　　　と素因数分解される。

（追記）　通りすがりさんからのコメントです。（平成２７年２月２２日付け）

　正65537角形は円とコンパスで作図可能。しかし、作図方法(の計算要旨)は、200ページを
超える。

（コメント）　６５５３７＝２¹⁶＋１　で作図できるんですね！


　さて、話を３次方程式に戻そう。四則計算と開平で作られた数は、必ず作図可能であった。
そこで、次の定理が成り立つ。

定理　３次方程式が有理数解をもち、他に実数解を持てば、解は全て作図可能である。

　また、２次方程式の理論と因数定理によれば、次の定理が成り立つ。

定理　３次方程式が作図可能な解を持つとき、解のうち少なくとも一つは有理数解である。

　上の定理の対偶を考えて、次の定理を得る。

定理

角の３等分方程式が有理数解を持たなければ、解は全て幾何学的に作図不能である。

（例）　角６０°の ３等分方程式は、ａ＝１　を代入して、ｘ³−3ｘ−１＝０
　　　この方程式が、有理数解　α　を持つと仮定すると、α　は −１ の約数となるから、
　　　α ＝ −１ 、１ である。しかるに、この何れも上記方程式の解にはなり得ない。
　　　これは、矛盾である。よって、方程式は、有理数解を持たない。
　　　よって、６０°の３等分の角を作図することは不可能である。

　また、定木・コンパスを用いて作図するということは、次のような代数的意味を持つ。

直線を引くこと
・・・・・　２点 ( ａ ，ｂ )、( ｃ ，ｄ ) を通る直線の方程式　ｐＸ＋ｑＹ＋ｒ＝０　の係数 ｐ、ｑ、ｒ は、
　ａ、ｂ、ｃ 、ｄ の有理式で表される。

２直線の交点を求めること
・・・・・　連立一次方程式を解くこと。その解は、係数の有理式で表される。

円を描くこと
・・・・・　中心 ( ａ ，ｂ ) とその半径の一端 ( ｃ ，ｄ )　が与えられたとき、円の半径は、四則計
　算（＋−×÷）と平方根の計算により求められる。

直線と円、円と円の交点を求めること
・・・・・　一次と二次、二次と二次の連立方程式を解くこと。これらの実数解は、四則計算
　（＋−×÷）と平方根の計算により求められる。

　このように、幾何学における作図問題は、代数における整式の問題・整方程式の解の性質
と密接に関係していることが分かった。そして、角の３等分問題が古代ギリシアで提出され、代
数の力を借りて、「作図できない！」という形で解決されたのは、１８３７年、ドイツの Wantzel に
よってである。ここまで到達するのに多大な時間を要したことを、我々は心に留めておかなけれ
ばならないと思う。

（参考文献：遠山　啓　著　数学入門（上・下）　（岩波新書）
　　　　　　　鈴木晋一・山下正勝　著　代数演算と作図（啓林館）
　　　　　　　佐々木元太郎　著　方程式の理論と解法（科学新興社））


　kuiperbelt さんからのコメントです。（令和６年７月１４日付け）

角の三等分と正７、１３、１９角形

　円分多項式 xⁿ−１＝０ で、ｎ＝３、５、１７では根が有限回の平方根と四則演算で表すこと

ができるので、定規とコンパスで作図できますが、ｎ＝７、９、１３、１９の場合は、根に立方根

が現れるので、定規とコンパスで作図をすることができません。

　また、角の三等分方程式は三次方程式で、根に立方根が現れるので、一般の角の三等

分は定規とコンパスで作図をすることができません。

　以前、もし、定規とコンパスに加えて「角の三等分器」という道具を使用可能としたら、どの

ようにして正７、１３、１９角形を作図できるかというのを考えてみました。


　Dengan kesaktian Indukmu さんからのコメントです。（令和６年７月１５日付け）

　kuiperbelt さんのＨＰ：「作図不可能多角形の作図」を拝読いたしました。

　正11角形が作図できないこと、意外に思いました。


　DD++ さんからのコメントです。（令和６年７月１６日付け）

　角の三等分器を利用すれば開立ができるのは正しいとして、逆に、角の三等分器を利用
して新たにできるようになることは開立だけなんでしょうか？


　Dengan kesaktian Indukmu さんからのコメントです。（令和６年７月１６日付け）

　なるほど、角の３等分が許されるとき、ｍ、ｎ を非負整数として ｐ が　ｐ＝２^m・３ⁿ＋１　と
書けるならば、正ｐ角形の作図が原理的には可能と。ｐは、11にはなり得ない。興味深いこ
とです。

　上記は、ちょっと甘すぎで、認識誤り。正しくは、「ピアポント素数」の項に書かれています。


　kuiperbelt さんからのコメントです。（令和６年７月２７日付け）

　 ｍ、ｎ を非負整数として ｐ＝２^m・３ⁿ＋１　という形の素数をピアポント素数というのですね。

　k個の素数p1,p2,p3,...,pk(p1<p2<p3<...<pk)に対して、(p1^n1)*(p2^n2)*(p3^n3)*...*(pk^nk)+1
の形の素数を一般化ピアポント素数というそうです。

　ネウシス作図では、一般の角の三等分と、pがピアポント素数のときの正p角形の作図が
できて、他に正11角形の作図もできるそうですが、p=(2^n1)*(3^n2)*(5^n3)+1の一般化ピア
ポント素数のときの正p角形の作図が可能かどうかは未解決問題なのだそうです。



　　以下、工事中！