
丂嶰妏宍偺柺愊偺岞幃偲偄偊偽丄乮掙曈乯亊乮崅偝乯亐俀 偱丄偍撻愼傒偱偁傞丅婎杮揑偵丄柺
愊偺岞幃偼慡偰丄偙偺岞幃偑弌敪揰偱偁傞丅
椺侾丏乮嶰妏宍偺俀曈 倎 丄倐 偲偦偺娫偺妏 兤 偑暘偐偭偰偄傞偲偒乯
丂俽亖(侾/俀)倎倐丒sin兤丂丂丂(乮掙曈乯亖倎丄乮崅偝乯亖b sin兤)
嶰妏宍偺柺愊偺岞幃丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂丂
丂嶰妏宍偺柺愊偺岞幃偲偄偊偽丄乮掙曈乯亊乮崅偝乯亐俀 偱丄偍撻愼傒偱偁傞丅婎杮揑偵丄柺
愊偺岞幃偼慡偰丄偙偺岞幃偑弌敪揰偱偁傞丅
椺侾丏乮嶰妏宍偺俀曈 倎 丄倐 偲偦偺娫偺妏 兤 偑暘偐偭偰偄傞偲偒乯
丂俽亖(侾/俀)倎倐丒sin兤丂丂丂(乮掙曈乯亖倎丄乮崅偝乯亖b sin兤)
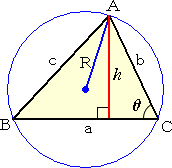 |
丂 丂椺侾丏偺曄宍僶乕僕儑儞偲偟偰偼師偺岞幃偑桳柤偩傠偆丅 丂丂仮俙俛俠 偺奜愙墌丄撪愙墌偺敿宎傪偦傟偧傟 俼 丄倰 偲偡傞偲丄 丂丂丂丂丂丂俽亖倎倐們/係俼亖倰倱 丂丂丂丂偨偩偟丄倱偼丄嶰妏宍偺廃偺挿偝偺敿暘丅 |
乮徹柧乯丂俽亖倎倐們/係俼丂傪帵偡偵偼丄惓尫掕棟傪梡偄傟偽傛偄丅
丂丂惓尫掕棟傛傝丄丂倱倝値兤亖們/俀俼丂側偺偱丄
丂俽亖(侾/俀)倎倐丒sin兤亖(侾/俀)倎倐丒乮們/俀俼乯亖倎倐們/係俼
丂俽亖倰倱丂傪帵偡偵偼丄仮俙俛俠傪撪愙墌偺拞怱傪捀揰偲偡傞俁偮偺彫嶰妏宍偵暘妱偟丄偦
偺柺愊偺憤榓傪媮傔傟偽傛偄丅
丂懄偪丄俽亖倎倰/俀亄倐倰/俀亄們倰/俀亖乮倎亄倐亄們乯倰/俀亖倰倱丂 乮徹廔乯
丂丂忋婰偱偼丄惓尫掕棟傪梡偄偰丄俽亖倎倐們/係俼丂傪帵偟偨偑丄捈愙揑偵帵偡曽朄傕抦傜
丂傟偰偄傞丅
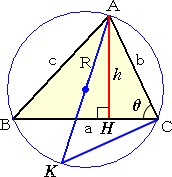 |
丂丂嵍恾偵偍偄偰丄丂仮俙俛俫佷仮俙俲俠丂側偺偱丄 丂丂丂丂丂丂俙俛 丗 俙俲 亖 俙俫 丗 俙俠 丂丂丂偡側傢偪丄丂們 丗 俀俼 亖 倛 丗 倐丂傛傝丄丂倛亖倐們/俀俼 丂丂丂傛偭偰丄丂俽亖倎倛/俀亖倎倐們/係俼 |
乮僐儊儞僩乯丂惓尫掕棟傪帵偡庤朄偲摨偠偱偡偹両
椺俀丏乮嵗昗暯柺忋偱丄俙( 倎 丆 倐 )丄俛( 們 丆 倓 )丄O( 侽 丆侽 ) 偺偲偒乯
丂俽亖(侾/俀)| 倎倓亅倐們 |丂丂丂乮|丂丂|偼愨懳抣傪昞偡乯
椺俁丏乮儀僋僩儖傪梡偄偨偲偒乯
丂椺俀丏偺俁揰偵偍偄偰丄![]() 丂偲偍偔偲丄
丂偲偍偔偲丄
丂![]()
丂椺俁丏傪梡偄偰丄椺俀丏偼娙扨偵摫偐傟傞丅
椺係丏(峴楍幃傪梡偄偨偲偒乯
丂![]()
偦偺峴楍幃丂倓倕倲乮俙乯 偼丄倓倕倲乮俙乯亖倎倓亅倐們丂側偺偱丄
丂俽亖(侾/俀)|倓倕倲(俙)|
椺俆丏乮嶰妏宍偺嶰曈 a 丄b 丄c 偑暘偐偭偰偄傞偲偒)
丂僿儘儞偺岞幃丂丂![]()
偨偩偟丄倱偼丄嶰妏宍偺廃偺挿偝偺敿暘丅
丂梋尫掕棟偲丄椺侾丏偺岞幃傪梡偄偰帵偝傟傞丅偨偩彮偟偽偐傝丄場悢暘夝偑戝曄偐傕偟傟
側偄丅
椺俇丏乮椺俆丏傪弶摍揑偵摫擖乯
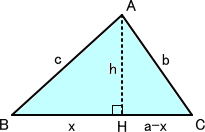 |
丂丂仮俙俛俫偱丄嶰暯曽偺掕棟傛傝丄倛2亖們2亅倶2 丂丂仮俙俫俠偱丄嶰暯曽偺掕棟傛傝丄倛2亖倐2亅(倎亅倶)2 丂 偙偺俀偮偺幃傛傝丄 丂丂丂丂丂丂丂丂丂丂丂 |
丂偙偺 倶 傪丄戞侾幃偵戙擖偟偰丄倛偑媮傑傞丅乮場悢暘夝偺抦幆傪梫偡傞丅乯
丂幚嵺偵丄
係倎2倛2亖係倎2們2亅乮們2亄倎2亅倐2乯2
亖乮俀倎們亄們2亄倎2亅倐2乯乮俀倎們亅們2亅倎2亄倐2乯
亖乷乮們亄倎乯2亅倐2乸乷倐2亅乮們亅倎乯2乸
亖乮倎亄倐亄們乯乮倎亅倐亄們乯乮倎亄倐亅們乯乮亅倎亄倐亄們乯
丂俀倱亖倎亄倐亄們丂偲偍偔偲丄
係倎2倛2亖俀倱乮俀倱亅俀倐乯乮俀倱亅俀們乯乮俀倱亅俀倎乯亖侾俇倱乮倱亅倎乯乮倱亅倐乯乮倱亅們乯丂傛傝丄
丂倎2倛2亖係倱乮倱亅倎乯乮倱亅倐乯乮倱亅們乯
偙偺寢壥傪丄俽亖(侾/俀)倎倛丂偵戙擖偟偰丄
丂僿儘儞偺岞幃丂丂![]() 丂偑摼傜傟傞丅
丂偑摼傜傟傞丅
乮嶲峫暥專丗丂愇扟丂栁丂挊丂峴楍偲峴楍幃偱妝偟傓乮尰戙悢妛幮乯乯
乮捛婰乯丂暯惉俀俆擭侾侾寧俀俆擔晅偗
丂崱傑偱僿儘儞偺岞幃偲偄偆偲丄
丂![]() 丂丂丂乮偨偩偟丄丂俀倱亖倎亄倐亄們丂乯
丂丂丂乮偨偩偟丄丂俀倱亖倎亄倐亄們丂乯
偺宍偱偟偐擣幆偟偰偄側偐偭偨偑丄傕偭偲暿側宍偑偁傞偙偲傪丄偁傞寁嶼傪偟偰偄傞偲偒偵婥
偯偐偝傟偨丅偡側傢偪丄師偺幃偑惉傝棫偮丅
丂丂侾俇俽2亖乮倎2亄倐2亄們2乯2亅俀乮倎4亄倐4亄們4乯
乮徹柧乯丂僿儘儞偺岞幃傛傝丄丂俀倱亖倎亄倐亄們丂偵懳偟偰丄
侾俇俽2亖俀倱乮俀倱亅俀倎乯乮俀倱亅俀倐乯乮俀倱亅俀們乯
亖乮倎亄倐亄們乯乮亅倎亄倐亄們乯乮倎亅倐亄們乯乮倎亄倐亅們乯
亖乷乮倐亄們乯2亅倎2乸乷倎2亅乮倐亅們乯2乸
亖亅倎4亄乷乮倐亄們乯2亄乮倐亅們乯2乸倎2亅乮倐亄們乯2乮倐亅們乯2
亖亅倎4亄俀乮倐2亄們2乯倎2亅倐4亄俀倐2們2亅們4
亖亅倎4亅倐4亅們4亄俀倎2倐2亄俀倐2們2亄俀們2倎2
亖乮倎2亄倐2亄們2乯2亅俀乮倎4亄倐4亄們4乯丂丂乮徹柧乯
(僐儊儞僩乯丂偙偺幃曄宍偵傛傝丄僿儘儞偺岞幃偵夝愅揑側庤朄偑揔梡壜偲側傞丅崱丄偦偺傛偆
丂丂丂丂側栤戣傪峫嶡拞偱偁傞丅
丂僿儘儞偺岞幃偑揔梡偝傟傞偺偼丄曈偺挿偝偑偡傋偰惍悢偺応崌偲憡応偑寛傑偭偰偄傞偑丄
忋婰偺傛偆側岞幃偺宍偱偁傟偽丄曈偺挿偝偵懡彮暯曽崻側偳偺柍棟悢偑偁偭偰傕寁嶼偺戝
曄偝偼偦傟傎偳偱傕側偄偩傠偆丅
椺丂仮俙俛俠偵偍偄偰丄俁曈偺挿偝偑丂![]() 丄
丄![]() 丄
丄![]() 偱偁傞偲偒丄仮俙俛俠偺柺愊傪媮傔傛丅
偱偁傞偲偒丄仮俙俛俠偺柺愊傪媮傔傛丅
乮夝乯丂侾俇俽2亖乮俀亄俁亄俇乯2亅俀乮係亄俋亄俁俇乯亖侾俀侾亅俋俉亖俀俁丂傛傝丄
丂俽亖乮併23乯/係丂丂乮廔乯
乮暿夝乯丂們倧倱兤亖乮俀亄俁亅俇乯/乮俀![]() 乯亖亅侾/乮俀
乯亖亅侾/乮俀![]() 乯丂傛傝丄丂倱倝値兤亖乮併23乯/乮俀
乯丂傛傝丄丂倱倝値兤亖乮併23乯/乮俀![]() 乯
乯
丂傛偭偰丄丂俽亖乮侾/俀乯![]() 丒乮併23乯/乮俀
丒乮併23乯/乮俀![]() 乯亖乮併23乯/係丂丂乮廔乯
乯亖乮併23乯/係丂丂乮廔乯
乮捛婰乯丂忋婰偵偍偄偰丄儀僋僩儖傪梡偄偨嶰妏宍偺柺愊偺岞幃乮椺俁乯偐傜丄惉暘昞帵偺
丂丂丂乮椺俀乯偼娙扨偵摫偐傟傞偲彂偄偨偑丄乮椺俀乯偦偺傕偺偼丄嬌嵗昗宯偱峫偊偨曽偑丄
丂丂丂偼傞偐偵娙扨偵摫偐傟傞丅
丂丂幚嵺偵丄壓恾偵偍偄偰丄OA亖俴丄OB亖俵丂偲偡傞偲丄仮OAB 偺柺愊偼丄
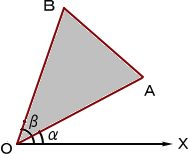 |
丂俽亖(1/2乯乥俴俵倱倝値(兝亅兛)乥 丂丂亖(1/2乯乥俴俵(倱倝値兝們倧倱兛亅們倧倱兝倱倝値兛)乥 丂丂亖(1/2乯乥俵倱倝値兝丒俴們倧倱兛亅俵們倧倱兝丒俴倱倝値兛)乥 丂偙偙偱丄俙(倎丆倐)丄俛(們丆倓) 偲偡傟偽丄 |
丂倎亖俴們倧倱兛丂丄倐亖俴倱倝値兛丂丄們亖俵們倧倱兝丂丄倓亖俵倱倝値兝
側偺偱丄俽亖(1/2乯| ad亅bc |
乮捛婰乯丂椺俇丏偵偍偄偰丄僿儘儞偺岞幃偺弶摍揑徹柧傪帵偟偨偑丄師偺傛偆側徹柧偑偁傞
丂丂丂丂偙偲傪嵟嬤抦偭偨丅
丂僿儘儞偺岞幃偵偍偗傞丂倱亅倎丄倱亅倐丄倱亅們丂偺堄枴偑暘偐偭偰丄巚傢偢歑偭偰偟傑偭偨丅
丂惓捈偵崘敀偡傞偲丄倱亅倎丂側偳偑丄恾宍揑偵偳傫側堄枴偑偁傞偺偐丄崱傑偱怺偔峫偊偨偙
偲偼側偐偭偨丏丏丏丏丏丏f(^_^)丅
丂埲壓偺徹柧偱偼丄偙偺擣幆偑僉乕億僀儞僩偵側偭偰偄傞丅
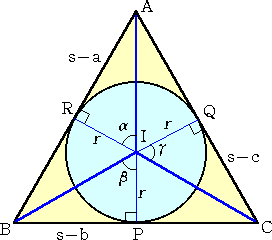 |
丂丂仮俙俛俠 偵偍偄偰丄俛俠亖倎丄俠俙亖倐丄俙俛亖們 丂偲偟丄俀倱亖倎亄倐亄們丂偵傛傝丄倱 傪掕傔傞丅 丂 丂丂仮俙俛俠 偺撪怱傪 俬 丄敿宎傪 倰 偲偡傞丅 丂丂俬 偐傜奺曈偵壓傠偟偨悅慄偺懌傪偦傟偧傟 俹丄 丂俻丄俼丂偲偡傞丅 丂丂傑偨丄嵍恾偺傛偆偵丄俀偮偺慄暘偺側偡妏傪 丂兛丄兝丄兞丂偲偡傞丅 丂丂侾偮偺捀揰偐傜堷偄偨愙慄偺挿偝偼摍偟偄偐 丂傜丄丂俛俹亄俠俻亄俙俼亖倱丂偑惉傝棫偮丅 |
丂偙偺偲偒丄俛俹亖倱亅俠俻亅俙俼亖倱亅俠俻亅俙俻亖倱亅俠俙亖倱亅倐丂偱偁傞丅
摨條偵偟偰丄丂俠俻亖倱亅們丂丄丂俙俼亖倱亅倎丂偑惉傝棫偮丅
兛亄兝亄兞亖兾丂側偺偱丄
丂
傛偭偰丄暘曣傪暐偭偰丄丂![]()
偟偨偑偭偰丄兛亄兝亄兞亖兾丂側傜偽丄丂![]()
偑惉傝棫偮丅偙偺偲偒丄
![]()
偑惉傝棫偮偺偱丄丂![]()
偟偨偑偭偰丄媮傔傞仮俙俛俠丂偺柺愊 俽 偼丄丂![]() 丂偱梌偊傜傟
丂偱梌偊傜傟
傞丅
乮拲乯丂偲偰傕僗僢僉儕偟偨徹柧偱丄僄儗僈儞僩偱偡偹両
乮嶲峫暥專丗愺尒丂斈丂挊丂僿儘儞偺岞幃傪摫偔乮孾椦丂崅悢曇丂俶倧丏205乯丂乮孾椦娰乯乯
乮捛婰乯丂丂嶰妏宍偺柺愊偺岞幃偺椺俀丗
丂乮嵗昗暯柺忋偱丄俙( 倎 丆 倐 )丄俛( 們 丆 倓 )丄O( 侽 丆侽 ) 偺偲偒乯
丂俽亖(侾/俀)| 倎倓亅倐們 |丂丂丂乮|丂丂|偼愨懳抣傪昞偡乯
偼丄儀僋僩儖傪梡偄偨傝乮椺俁乯丄嶰妏娭悢偺壛朄掕棟傪梡偄偨傝乮捛婰乯丄偄傠偄傠側徹柧朄
偑偁傞丅嵟嬤丄偙偺徹柧傪恾宍傪梡偄偰帵偟偨曽偑偍傜傟傞偙偲傪丄嬼慠師偺儂乕儉儁乕僕
偱抦偭偨丅
丂乽庢傟偨偰捠怣乿丂搈椝僒乕僋儖俀侽侽俁擭俇寧椺夛
丂婔壗揑偵慛傗偐側徹柧偱偁傞偺偱丄偙偙偱惀旕徯夘偟偨偄偲巚偆丅
嶰妏宍偺戙傢傝偵暯峴巐曈宍偱帵偡偙偲偵偡傞丅
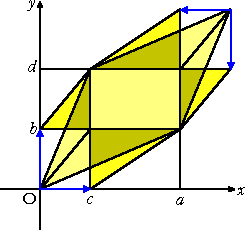 |
丂丂丂嵍恾偺傛偆偵丄暯峴巐曈宍傪愗傝暘偗丄 丂丂係偮偺嶰妏宍偵偍偄偰丄摍愊曄宍傪峴偄丄 丂丂捈妏嶰妏宍偵偡傞丅 |
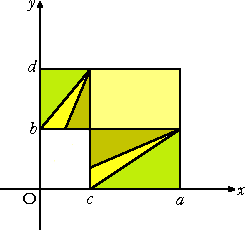 |
丂丂丂嵍恾偺傛偆偵丄嵍忋恾偺塃懁丄忋懁偵 丂丂偁偭偨捈妏嶰妏宍傪丄偦傟偧傟嵍懁丄壓 丂丂懁偵暯峴堏摦偝偣傞丅 |
丂媮傔傞暯峴巐曈宍偺柺愊偼丄嵍壓恾偵偍偄偰丄挿曽宍俁偮暘偺柺愊偵摍偟偄丅
傛偭偰丄
丂俽亖倎亊倓亅們亊倐亖倎倓亅倐們
偱偁傞丅
乮拲乯丂壗偲側偔丄倎倓亅倐們 偺堄枴偑暘偐偭偨傛偆側婥偑偟傑偡両
乮捛婰乯丒丒丒暯惉侾俉擭俀寧侾俀擔晅偗
丂忋婰偵偍偄偰丄僿儘儞偺岞幃偺徹柧傪俀偮傎偳偁偘偨偑丄師偺傛偆側徹柧傕嫽枴怺偄丅
丂仮俙俛俠丂偵偍偄偰丄俛俠亖倎丄俠俙亖倐丄俙俛亖們丂偲偟丄俀倱亖倎亄倐亄們丂偵傛傝丄倱
傪掕傔傞丅
偙偙偱傕丄傗偼傝丄丂俙俧亖倱亅倎丂丄俛俫亖倱亅倐丂偲偄偆帠幚偑桳岠偱偁傞丅
 |
乮徹柧乯丂丂偄傑丄仮俙俛俠偺曈俛俠偵愙偡傞朤愙墌 俬俙 傪峫偊丄 丂丂丂丂偦偺敿宎傪丂倰俙 偲偡傞丅 丂丂丂丂偙偺偲偒丄仮俬俙俲俛佷仮俛俫俬 側偺偱丄 丂丂丂丂丂丂丂俬俙俲 丗 俛俲亖俛俫 丗 俬俫丂偑惉傝棫偮丅 丂丂丂丂傑偨丄俙俴亖倱丂側偺偱丄丂俛俲亖俛俴亖倱亅俙俛丂偲側傝丄 丂丂丂丂丂丂丂俛俲亖倱亅們 丂丂丂丂偱偁傞丅丂傛偭偰丄丂俛俫亖倱亅倐丂側偺偱丄 丂丂 丂丂丂倰俙 丗 倱亅們 亖 倱亅倐 丗 倰丂偐傜丄 丂丂丂丂丂丂丂丂 丂丂丂丂偑惉傝棫偮丅 |
丂傑偨丄仮俙俧俬佷仮俙俴俬丂傛傝丄丂俬俧 丗 俬俙俴亖俙俧 丗 俙俴丂側偺偱丄丂倰 丗 倰俙 亖 倱亅倎 丗 倱
傛偭偰丄丂倰倱亖倰俙 乮倱亅倎乯丂偑惉傝棫偮丅
丂仮俙俛俠偺柺愊傪俽偲偡傞偲丄丂俽亖倰倱丂側偺偱丄丂俽亖倰俙 乮倱亅倎乯
偟偨偑偭偰丄丂俽2亖俽丒俽亖倰倱丒倰俙 乮倱亅倎乯亖倱(倱亅倎)(倱亅倐)(倱亅們)丂傛傝
丂僿儘儞偺岞幃丂丂![]()
傪摼傞丅乮徹廔乯
偙偺徹柧偺暃嶻暔偲偟偰丄師偺旤偟偄掕棟偑惉傝棫偮丅
丂![]()
偨偩偟丄倰俙丄 倰俛丄 倰俠 偼忋婰偲摨條偵掕傑傞朤愙墌偺敿宎偲偡傞丅
乮徹柧乯
丂![]() 丂丄
丂丄![]() 丂丄
丂丄![]()
側偺偱丄
丂侾/倰俙亄侾/倰俛亄侾/倰俠
亖倰乮侾/(倱亅倐)(倱亅們)亄侾/(倱亅們)(倱亅倎)亄侾/(倱亅倎)(倱亅倐)乯
亖倰/(倱亅倎)(倱亅倐)(倱亅們)丒乷倱亅倎亄倱亅倐亄倱亅們乸
亖倰倱/(倱亅倎)(倱亅倐)(倱亅們)
亖俽/乮俽2/倱乯
亖倱/俽
亖侾/倰
丂偑惉傝棫偮丅丂丂乮徹廔乯
乮僐儊儞僩乯丂偙偺岞幃傪挱傔偰偄傞偲丄乽撪愙墌偺偁傞惈幙 乿偱摼傜傟偨岞幃
丂丂丂丂丂丂丂丂丂丂侾/倛A亄侾/倛B亄侾/倛C亖侾/倰
乮偨偩偟丄倛A丄倛B丄倛C偼丄仮俙俛俠偺捀揰 俙丄俛丄俠 傛傝奺懳曈偵壓傠偟偨悅慄偺挿偝偱偁傞丅乯
丂偵宍偑帡偰偄傞偙偲偵婥偯偐偝傟傞丅壗偐怺墦側傞朄懃偱摑惂偝傟偰偄傞傛偆偵姶偠傞丅
乮嶲峫暥專丗丂拞懞暥懃巵乮嶥杫埉媢崅峑乯偺俫俹乽嶰妏宍偺柺愊傪傂傕夝偔乿乯
丂嶰妏宍偺撪愙墌偺敿宎偼丄嶰妏宍偺柺愊傪棙梡偟偰娙扨偵媮傔傜傟傞丅
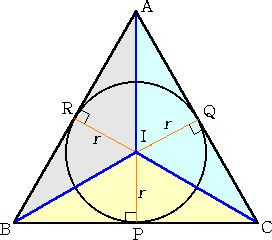 |
丂 仮俙俛俠偵偍偄偰丄撪愙墌偺敿宎傪 倰 丄嶰妏宍 偺廃偺挿偝偺敿暘傪 倫 偲偡傞偲丄 丂丂丂仮俙俛俠亖倫丒倰 偑惉傝棫偮偐傜偱偁傞丅 丂偨偩偟丄丂倫亖乮倎亄倐亄們乯/俀 |
傑偨丄 墌奜偺侾揰偐傜墌偵堷偄偨愙慄偺挿偝偼摍偟偄 偺偱丄揰俠偐傜堷偄偨愙慄偺挿偝
倶 偼丄丂倶亖乮倎亄倐亅們乯/俀丂偱媮傔傜傟傞丅
丂摿偵丄俠亖俋侽亱偺捈妏嶰妏宍偺応崌偼丄倶亖倰丂側偺偱丄柺愊傪棙梡偟側偔偰傕丄撪愙墌偺
敿宎
倰
偼丄丂倰亖乮倎亄倐亅們乯/俀丂偲媮傔傜傟傞丅
丂偙偺岞幃偼丄愙慄偺挿偝傪梡偄傞偺偑嵟懍偱偁傞偑丄仮俙俛俠亖倫丒倰丂偐傜傕媮傔傞偙偲偑
偱偒傞丅
丂俠亖俋侽亱偺捈妏嶰妏宍側偺偱丄丂仮俙俛俠亖倎倐/俀
丂傛偭偰丄丂倎倐/俀亖倰丒乮倎亄倐亄們乯/俀丂傛傝丄丂倎倐亖倰丒乮倎亄倐亄們乯
丂傑偨丄嶰暯曽偺掕棟傛傝丄丂a2亄倐2亖們2丂側偺偱丄丂乮倎亄倐乯2亅俀倎倐亖們2
丂傛偭偰丄丂俀倎倐亖乮倎亄倐乯2亅們2亖乮倎亄倐亄們乯乮倎亄倐亅們乯丂側偺偱丄
丂乮倎亄倐亄們乯乮倎亄倐亅們乯/俀亖倰丒乮倎亄倐亄們乯
丂偟偨偑偭偰丄丂倰亖乮倎亄倐亅們乯/俀丂偑惉傝棫偮丅
乮捛婰乯丂摉俫俹撉幰偺俲丏俽丏偝傫偑丄乽嶰妏宍偺柺愊偺岞幃乿傪傑偲傔傜傟偨丅
丂丂乮暯惉俀係擭俀寧俀俆擔晅偗乯
丂忋婰偵偼側偄岞幃傕娷傑傟丄嫽枴偼恠偒側偄丏丏丏丅嶲峫偵側傝傑偡丅俲丏俽丏偝傫偵姶幱偟
傑偡丅
乮侾乯丂俽亖掙曈亊崅偝亐俀丂乮彫妛惗乯
乮俀乯丂俽亖乮侾/俀乯倎倛丂乮拞妛惗乯
乮俁乯丂俽亖乮侾/俀乯倎倐倱倝値俠丂乮嶰妏斾乯
乮係乯丂俽亖倎倐們/乮係俼乯丂乮俼丗奜愙墌偺敿宎乯
乮俆乯丂俽亖乮倎亄倐亄們乯倰/俀亖倱倰丂乮倰丗撪愙墌偺敿宎乯
乮俇乯丂俽亖併乮倱乮倱亅倎乯乮倱亅倐乯乮倱亅們乯丂乮僿儘儞偺岞幃乯
乮俈乯丂俽亖併乮倰丒倰倎丒倰倐丒倰們乯丂乮倰倎丄倰倐丄倰們丗朤愙墌偺敿宎乯
乮俉乯丂俽亖乮侾/俀乯倎2倱倝値俛倱倝値俠/倱倝値乮俛亄俠乯丂乮侾曈偲椉抂妏乯
乮俋乯丂俽亖乮侾/俀乯併乮乥倎乥2乥倐乥2亅乮倎丒倐乯2乯丂乮儀僋僩儖乯
乮侾侽乯丂俽亖乮侾/俀乯乥倶1倷2亅倶2倷1乥丂乮暯柺儀僋僩儖乯
乮侾侾乯丂俽亖乮侾/俀乯乥俙俛亊俙俠乥丂乮嬻娫儀僋僩儖乯
乮侾俀乯丂俽亖乮侾/俀乯乥俬倣乮倅1倅2~乯乥亖乮侾/係乯乥倅1倅2~亅倅1~倅2乥丂乮暋慺暯柺乯
乮侾俁乯丂俽亖仮俙俛俠亖仮俹俙俛亄仮俹俛俠亄仮俹俠俙丂乮晞崋晅偒柺愊乯
乮捛婰乯丂摉俫俹撉幰偺俲丏俽丏偝傫偐傜丄乽巐妏宍偺柺愊偺岞幃乿傪儊乕儖偱捀偄偨丅
丂丂乮暯惉俀俆擭俇寧俀俀擔晅偗乯
丂摿暿側応崌偺岞幃偱偁傞偑丄巹偺崅峑帪戙丄嫵壢彂偵嵹偭偰偄偨傛偆側婥偑偡傞丅俲丏俽丏
偝傫偵姶幱偟傑偡丅
丂巐妏宍俙俛俠俢偵偍偄偰丄懳妏慄俙俠偲俛俢偺側偡妏傪兤偲偡傞偲偒丄柺愊俽偼丄
丂俽亖乮侾/俀乯俙俠丒俛俢倱倝値兤
偱梌偊傜傟傞丅
丂徹柧偼丄懳妏慄偵暯峴側暯峴巐曈宍乮捀揰俙俛俠俢傪曈忋偵傕偮乯傪嶌傞偲丄暯峴巐曈宍偺
敿暘偵側傞帠偐傜傢偐傞丅
椺俈丏乮捈妏嶰妏宍偺撪愙墌偲幬曈偺愙揰偑暘偐偭偰偄傞偲偒乯
丂俫俹僒僀僩乽悢偺晄巚媍悽奅乿偱丄俫俶乽夡傟偨斷乿偝傫偑暯惉俀俈擭俀寧侾俉擔晅偗偱柺敀偄
掕棟傪徯夘偝傟偰偄傞丅僆儕僕僫儖偱偼側偄偲偺偙偲偩偑丄徹柧偵挧愴偟偰傒偨丅
掕棟丂捈妏嶰妏宍俙俛俠偺撪愙墌偑幬曈俙俛偲愙偡傞揰傪俢偲偡傞偲丄仮俙俛俠偺柺愊俽偼丄
丂俽亖俙俢丒俛俢丂丂偱媮傔傜傟傞丅
乮徹柧乯丂仮俙俛俠偺撪愙墌偺敿宎傪 倰 偲偡傞偲丄椺侾丏傛傝丄
丂俽亖倰倱亖倰乮俙俛亄俛俠亄俠俙乯/俀
偙偙偱丄丂俙俛亖俙俢亄俛俢丂丄俛俠亖俛俢亄倰丂丄俠俙亖俙俢亄倰丂側偺偱丄
丂俽亖倰乮俙俢亄俛俢亄倰乯亖倰2亄倰乮俙俢亄俛俢乯
傑偨丄嶰暯曽偺掕棟傛傝丄丂俙俛2亖俛俠2亄俠俙2丂偑惉傝棫偮偺偱丄
丂乮俙俢亄俛俢乯2亖乮俛俢亄倰乯2亄乮俙俢亄倰乯2
丂揥奐偟偰惍棟偡傞偲丄丂俙俢丒俛俢亖倰乮俙俢亄俛俢乯亄倰2
丂埲忋偐傜丄丂俽亖俙俢丒俛俢丂偑惉傝棫偮丅丂丂乮徹廔乯
乮捛婰乯丂椷榓俁擭俇寧俀侾擔晅偗
丂仮俙俛俠 偺撪愙墌偺敿宎傪 倰 丄倱傪嶰妏宍偺廃偺挿偝偺敿暘偲偡傞偲丄
丂仮俙俛俠 偺柺愊俽偼丄丂俽亖倰倱丂偱梌偊傜傟傞丅
丂傛偔抦傜傟偨岞幃偱偁傝丄戝妛庴尡偱傕桳梡偱偁傞偺偱丄撉幰偺偨傔偵楙廗栤戣傪巆偟偰
偍偙偆丅
楙廗栤戣丂丂壓恾偺傛偆偵丄捈妏嶰妏宍俙俛俠偵惓曽宍俹俻俼俽偑撪愙偟偰偄傞丅偙偺偲偒丄
丂丂丂丂丂丂丂仮俙俻俹偺撪愙墌偺敿宎 倰 傪媮傔傛丅
丂丂丂丂丂丂丂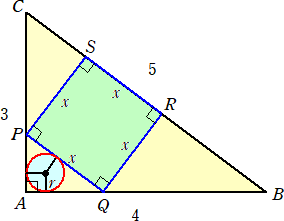
乮夝乯丂俙俹亖俁倶/俆丄俙俻亖係倶/俆丂側偺偱丄丂俁 丗 倶亖俆 丗 係亅係倶/俆
丂丂偙傟傪夝偄偰丄丂倶亖俇侽/俁俈丂側偺偱丄丂俙俹亖俁俇/俁俈丂丄俙俻亖係俉/俁俈
丂傛偭偰丄丂仮俙俻俹亖乮侾/俀乯乮俁俇/俁俈乯乮係俉/俁俈乯亖俉俇係/侾俁俇俋
丂偙偙偱丄倱亖乮俁俇/俁俈亄係俉/俁俈亄俇侽/俁俈乯/俀亖俈俀/俁俈丂側偺偱丄
丂丂乮俈俀/俁俈乯倰亖俉俇係/侾俁俇俋丂傛傝丄丂倰亖侾俀/俁俈丂丂乮廔乯
乮僐儊儞僩乯丂仮俙俛俠亖俇丂側偺偱丄仮俙俛俠偺撪愙墌偺敿宎俼偼丄丂俼亖侾
丂丂傛偭偰丄丂倰亖侾亊乮倶/俆乯亖侾俀/俁俈
丂偲偟偨曽偑娙柧偐側丠
乮捛婰乯丂椷榓俁擭俇寧俀俀擔晅偗
丂忋婰偺楙廗栤戣偱偼丄捈妏嶰妏宍偺俁曈偺挿偝傪梌偊偨偑丄撪愙墌偺敿宎傪梌偊偰丄捈
妏嶰妏宍偺曈偺挿偝傪媮傔傞栤戣傪峫偊偰傒傛偆丅
楙廗栤戣丂丂壓恾偺傛偆偵丄幬曈偺挿偝偑侾俆偺捈妏嶰妏宍俙俛俠偵惓曽宍俹俻俼俽偑撪愙偟
丂丂丂丂丂丂丂偰偄傞丅仮俛俼俻丄仮俠俹俽偺撪愙墌偺敿宎偑偦傟偧傟侾俉侽/侾侾侾丄侾俁俆/侾侾侾
丂丂丂丂丂丂丂偱偁傞偲偒丄捈妏嶰妏宍偺曈俙俛丄俙俠偺挿偝傪媮傔傛丅
丂
乮夝乯丂俙俹亖倐倶/侾俆丄俙俻亖倎倶/侾俆丂側偺偱丄丂倐 丗 倶亖侾俆 丗 倎亅倎倶/侾俆
偙傟傪夝偄偰丄丂倶亖侾俆倎倐/乮倎倐亄俀俀俆乯丂側偺偱丄
丂俙俹亖倎倐2/乮倎倐亄俀俀俆乯丂丄俙俻亖倎2倐/乮倎倐亄俀俀俆乯
傛偭偰丄丂俹俠亖倐亅倎倐2/乮倎倐亄俀俀俆乯亖俀俀俆倐/乮倎倐亄俀俀俆乯
丂俻俛亖倎亅倎2倐/乮倎倐亄俀俀俆乯亖俀俀俆倎/乮倎倐亄俀俀俆乯
捈妏嶰妏宍俙俛俠偺撪愙墌偺敿宎 倰 偼丄乮倎亅倰乯亄乮倐亅倰乯亖侾俆丂傛傝丄倰亖乮倎亄倐亅侾俆乯/俀
丂偟偨偑偭偰丄撪愙墌俷1偺敿宎偑侾俉侽/侾侾侾偱偁傞偙偲偐傜丄
丂乮倎亄倐亅侾俆乯/俀丒乮俻俛/侾俆乯亖侾俆倎乮倎亄倐亅侾俆乯/乮俀乮倎倐亄俀俀俆乯乯亖侾俉侽/侾侾侾
丂偡側傢偪丄丂侾侾侾倎乮倎亄倐亅侾俆乯亖俀係乮倎倐亄俀俀俆乯
摨條偵丄撪愙墌俷2偺敿宎偑侾俁俆/侾侾侾偱偁傞偙偲偐傜丄
丂乮倎亄倐亅侾俆乯/俀丒乮俹俠/侾俆乯亖侾俆倐乮倎亄倐亅侾俆乯/乮俀乮倎倐亄俀俀俆乯乯亖侾俁俆/侾侾侾
偡側傢偪丄丂侾侾侾倐乮倎亄倐亅侾俆乯亖侾俉乮倎倐亄俀俀俆乯
傛偭偰丄倎亖乮係/俁乯倐丂側偺偱丄戞俀幃偵戙擖偟偰惍棟偡傞偲丄係俈倐2亅俁俁俁倐亅俉侾侽亖侽
丂倐亜侽丂偵拲堄偟偰丄偙傟傪夝偔偲丄丂倐亖俋丂偱丄偙偺偲偒丄倎亖侾俀
乮拲堄乯丂倎亖乮係/俁乯倐丂偲丄倎2亄倐2亖俀俀俆丂偐傜丄丂倎亖侾俀丄倐亖俋丂傪媮傔偰傕傛偄丅
乮僐儊儞僩乯丂揔摉偵悢抣愝掕偟偨偺偱丄栤戣愝掕偑尒偊尒偊偱墭偔側偭偰偟傑偄傑偟偨両
丂DD++偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俁擭俇寧俀俁擔晅偗乯
丂枹抦悢偑 a丄b丄倶 偺 3 偮偱偁傞偺偵懳偟丄惂栺偑懡偡偓偰丄偙偺恾宍偼懚嵼偱偒側偄傫
偠傖側偄偱偟傚偆偐丅幚嵺丄婰帠偵偁傞摎偊偺悢抣偱偼丄捈妏嶰妏宍 ABC 偱嶰暯曽偺掕棟
偑惉棫偟偰偄側偄傛偆偵尒偊傑偡丅
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俁擭俇寧俀俁擔晅偗乯
丂嶰暯曽偳偙傠偐丄a=(16亇8併14)/5 偱丄(16+8併14)/5佮9.2亜(幬曈)丄(16-8併14)/5亙0丂側
偺偱偳偪傜傕晄揔偱偡偹丅
乮僐儊儞僩乯丂妋偐偵丄幬曈偺挿偝偑俉偺捈妏嶰妏宍俙俛俠偵惓曽宍俹俻俼俽偑撪愙偟丄仮俛俼俻丄
丂丂丂丂丂丂仮俠俹俽偺撪愙墌偺敿宎偑偦傟偧傟俀丄侾丂偲偄偆愝掕偱偼丄嶰暯曽偺掕棟偑惉棫
丂丂丂丂丂丂偟偰偄側偐偭偨偱偡偹両傕偭偲怲廳偵悢抣愝掕偡傋偒偱偟偨丅忋婰偱偼丄愝掕傪廋
丂丂丂丂丂丂惓偟偨傕偺偱偡丅撪愙墌偺敿宎偑傕偭偲鉟楉偵側傟偽偄偄偺偱偡偑丄偦傟偼崱屻
丂丂丂丂丂丂偺尋媶壽戣偲偟傑偡丅
丂俧俙俬 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓俁擭俇寧俀係擔晅偗乯
 |
丂嵍恾偺傛偆偵丄3丄4丄5偺嶰曈傪帩偮捈妏嶰妏 宍偱丄幬曈偵惓曽宍偺堦曈傪桳偡傞撪愙偡傞傕 偺傪峫偊偨偲偒丄俁偮偺寗娫偵偱偒傞奺捈妏嶰 妏宍 仮APQ丄仮RBQ丄仮SPC 偵撪愙偡傞撪愙 墌偺奺敿宎 r1丄r2丄r3 傪媮傔傞偲丄 丂丂r1=12/37丂丄r2=20/37丂丄r3=15/37 丂偲側傞偑丄偙傟偼丄 丂丂r1 丗 r2 丗 r3=12 丗 20 丗 15=3*4 丗 4*5 丗 5*3 |
偱傕偁傞偙偲偐傜丄崱搙偼丄5丄12丄13偺嶰曈傪帩偮捈妏嶰妏宍偱丄摨偠偔幬曈偵撪愙偡傞惓
曽宍偺堦曈傪廳偹偨偲偒丄俁偮偺寗娫偱偺奺捈妏嶰妏宍偺撪愙墌偺敿宎偺斾棪偼丄
丂丂5*12 丗 12*13 丗 5*13=60 丗 156 丗 65
偲側傞傕偺側傫偱偟傚偆偐丠
乮捛怢乯丂堦斒偵丄俁曈偺挿偝偑A丄B丄C (A2+B2=C2) 偱偁傞捈妏嶰妏宍偱偼丄拞偵堦曈偑
丂丂丂丂丂x 偺惓曽宍傪幬曈偵廳側傞條偵撪愙偟偰傞偲偒丄俁偐強偵偱偒傞捈妏嶰妏宍偱偺撪
丂丂丂丂丂愙墌偺敿宎 r1丄r2丄r3 偼丄
丂丂r1=(A*B)^2/((A+B+C)*(A*B+C^2))
丂丂r2=A^2*B*C/((A+B+C)*(A*B+C^2))
丂丂r3=A*B^2*C/((A+B+C)*(A*B+C^2))
懄偪丄丂r1 丗 r2 丗 r3亖A*B 丗 A*C 丗 B*C丂傪枮偨偡丅
丂傑偨丄忋恾偵偍偄偰丄AQ=a丄AP=b 偲偟偰
丂丂a=A*k丂丄b=B*k丂丄x=C*k
丂偨偩偟丄k=A*B/(A*B+C^2) 偵偰寁嶼偟偰偍偗偽傛偄丅
乮僐儊儞僩乯丂幬曈偺挿偝偑侾俆偱丄倎亖侾俀丄倐亖俋偺偲偒丄r2亖侾俉侽/侾侾侾丂丄r3亖侾俁俆/侾侾侾
丂丂丂丂丂丂側偺偱丄妋偐偵丄丂r2 丗 r3亖侾俉侽/侾侾侾 丗 侾俁俆/侾侾侾亖係 丗 俁亖侾俀*侾俆 丗 俋*侾俆
丂丂丂丂丂丂偑尵偊偰偄傑偡偹丅怴偟偄帇嵗偱偡偹両
乮捛婰乯丂椷榓係擭俁寧俀俀擔晅偗
丂暯惉俁侽擭搙偺撳崅峑擖帋偱丄師偺栤戣偑弌戣偝傟偨丅撪愙墌偵娭學偡傞栤戣偱丄嫽枴
偑偁傝夝偄偰傒偨丅栤戣偼庒姳夵戣偟傑偟偨丅
栤戣丂丂壓恾偺傛偆偵丄仮俙俛俠偲揰 俬 傪拞怱偲偡傞墌偑偁傝丄偙偺墌偼曈俙俛丄俛俠丄俠俙偵
丂丂丂丂愙偟偰偄傞丅偨偩偟丄俙俛亖侾俈丄俙俠亖俀俆丄俙俬亖侾侽偱丄仮俙俛俬亄仮俙俠俬亖侾俀俇偲偡傞丅
丂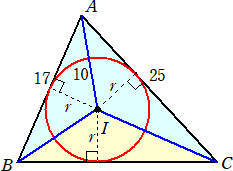
丂偙偺偲偒丄曈俛俠偺挿偝傪媮傔傛丅
乮夝乯丂仮俙俛俬亄仮俙俠俬亖侾俀俇丂偐傜丄丂侾俈倰/俀亄俀俆倰/俀亖俀侾倰亖侾俀俇丂傛傝丄丂倰亖俇
丂揰 俬 傛傝丄曈俙俛丄俙俠偵悅慄傪壓傠偟丄偦偺懌傪偦傟偧傟俫丄俲偲偍偔丅
偙偺偲偒丄丂俙俫亖俙俲亖俉丂側偺偱丄丂俛俠亖乮侾俈亅俉乯亄乮俀俆亅俉乯亖俀俇丂丂乮廔乯
乮僐儊儞僩乯丂嶰妏娭悢傪梡偄傟偽丄師偺傛偆偵傕夝偗傞偩傠偆丅
丂佢俛俙俬亖佢俠俙俬亖兤丂偲偍偔偲丄仮俙俛俬亄仮俙俠俬亖侾俀俇丂偐傜丄
丂丂乮侾/俀乯丒侾俈丒侾侽倱倝値兤亄乮侾/俀乯丒侾侽丒俀俆倱倝値兤亖俀侾侽倱倝値兤亖侾俀俇
丂傛偭偰丄丂倱倝値兤亖俁/俆丂偱丄丂們倧倱俀兤亖侾亅俀倱倝値2兤亖俈/俀俆
丂梋尫掕棟傛傝丄丂俛俠2亖俀俉俋亄俇俀俆亅俉俆侽丒乮俈/俀俆乯亖俇俈俇丂側偺偱丄丂俛俠亖俀俇
仈摉弶丄俙俛亖俉丄俙俠亖侾侽丄俙俬亖俆丄仮俙俛俬亄仮俙俠俬亖俀俈偲栤戣愝掕傪梊掕偟偰偄偨偑丄
丂専嶼偡傞偲丄柕弬偺偁傞恾宍偲側偭偰偟傑偭偨丅撳崅峑偺悢抣愝掕偵姶摦偟傑偟偨丅
丂DD++ 偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭俁寧俀俆擔晅偗乯
丂忋婰偺栤戣丄柺愊偺忣曬傪嶍彍偟偰傕嶰妏宍偑儐僯乕僋偵掕傑傝傑偡傛偹丅偡側傢偪丄埲
壓偺栤戣偼乮拞妛斖埻偵惂尷偟側偗傟偽乯偪傖傫偲夝偗傞偼偢丅
丂乽嶰妏宍 ABC 偺撪怱傪 I 偲偡傞丅AB=17, AC=25, AI=10 偺偲偒丄BC 傪媮傔傛丅乿
丂偝偰丄鉟楉側夝偒曽偼偁傞偱偟傚偆偐丠
丂傜偡偐傞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭俁寧俀俇擔晅偗乯
丂偲傝偁偊偢鉟楉偱傕壗偱傕側偄乽晛捠偺乿夝偒曽偱偡偑
丂AB=c丄BC=a丄CA=b 偲偍偔偲丄仮ABC偺柺愊S偼丄
丂丂S=(1/4)併{(a+b+c)(-a+b+c)(a-b+c)(a+b-c)}
側偺偱丄撪愙墌偺敿宎 r 偼丄
丂丂r=2S/(a+b+c)=(1/2)併{(-a+b+c)(a-b+c)(a+b-c)/(a+b+c)}
丂A偐傜撪愙墌偺愙揰傑偱偺嫍棧傪s丄B偐傜撪愙墌偺愙揰傑偱偺嫍棧傪t丄C偐傜撪愙墌偺
愙揰傑偱偺嫍棧傪u 偲偍偔偲丄
丂丂a=t+u丄b=u+s丄c=s+t丂側偺偱丄丂s=(-a+b+c)/2
丂AI=d 偲偍偔偲丄丂d^2=s^2+r^2=bc-2abc/(a+b+c)
丂偙傟傪 a 偵偮偄偰夝偔偲丄丂a=(bc-d^2)(b+c)/(bc+d^2)丂側偺偱丄b=25丄c=17丄d=10丂傪戙擖
偟偰丄丂a=26丂偱偁傞丅
(捛婰)丂偙傟傪寁嶼偟偰偄偰婥晅偄偨偺偱偡偑丄忋婰偺 s丄t丄u 傪巊偆偲丄
丂丂柺愊偼丄丂S=併{stu(s+t+u)}
丂丂撪愙墌偺敿宎偼丄丂r=併{stu/(s+t+u)}
偲偄偆鉟楉側幃偱昞偣傞傫偱偡偹丅
乮僐儊儞僩乯丂撪愙墌偺敿宎傪 倰 偲偡傞偲丄倱倝値佢俛俙俬亖倰/侾侽丄們倧倱佢俛俙俬亖併乮侾侽侽亅倰2乯/侾侽
丂墌奜偺侾揰偐傜堷偄偨愙慄偺挿偝偑摍偟偄偙偲偐傜丄丂俛俠亖係俀亅俀併乮侾侽侽亅倰2乯
丂傛偭偰丄丂仮俙俛俠亖倰乮係俀亅併乮侾侽侽亅倰2乯乯
堦曽丄仮俙俛俠亖乮侾/俀乯丒侾俈丒俀俆丒俀乮倰/侾侽乯丒乮併乮侾侽侽亅倰2乯/侾侽乯亖乮侾俈/係乯倰併乮侾侽侽亅倰2乯
側偺偱丄丂乮侾俈/係乯倰併乮侾侽侽亅倰2乯亖倰乮係俀亅併乮侾侽侽亅倰2乯乯
丂偡側傢偪丄丂併乮侾侽侽亅倰2乯亖俉丂傛傝丄丂倰亖俇丂側偺偱丄丂俛俠亖俀俇丂偲掕傑傞丅
乮拲乯丂併乮侾侽侽亅倰2乯亖倶丂偲偟偰丄丂倱倝値佢俛俙俬亖倰/侾侽丄們倧倱佢俛俙俬亖倶/侾侽
丂墌奜偺侾揰偐傜堷偄偨愙慄偺挿偝偑摍偟偄偙偲偐傜丄丂俛俠亖係俀亅俀倶
丂傛偭偰丄丂仮俙俛俠亖倰乮係俀亅倶乯
堦曽丄仮俙俛俠亖乮侾/俀乯丒侾俈丒俀俆丒俀乮倰/侾侽乯丒乮倶/侾侽乯亖乮侾俈/係乯倰倶
側偺偱丄丂乮侾俈/係乯倰倶亖倰乮係俀亅倶乯丂傛傝丄丂倶亖俉丂側偺偱丄丄丂俛俠亖俀俇丂偲掕傑傞丅
乮忋婰偺寁嶼偐傜暘偐傞傛偆偵丄併乮侾侽侽亅倰2乯偺 倰 偼媮傔傞昁梫偼側偄傛偆偱偡丅乯
仈丂柺愊偺忦審偑側偔偰傕丄乽俛俠亖俀俇乿偑暘偐傞傫偱偡偹両姶摦偟傑偟偨丅DD++ 偝傫偵姶幱
丂丂偟傑偡丅傜偡偐傞偝傫丄夝摎傪偁傝偑偲偆偛偞偄傑偡丅
丂DD++ 偝傫偺偛嫵帵傪庴偗丄柕弬偺側偄栤戣愝掕傪峫偊偰傒偨丅
丂俠俙亖倐丄俙俛亖們 偲偍偄偰丄俙俬亖俆丄倰亖俁 偲側傞傛偆偵偟偨偄丅
丂偙偺偲偒丄丂俛俠亖倐亄們亅俉丂偱丄丂倱亖倐亄們亅係丂側偺偱丄丂仮俙俛俠亖俁乮倐亄們亅係乯
丂堦曽丄丂仮俙俛俠亖乮侾/俀乯丒倐們丒俀乮俁/俆乯乮係/俆乯亖侾俀倐們/俀俆丂側偺偱丄
丂丂侾俀倐們/俀俆亖俁乮倐亄們亅係乯丂偡側傢偪丄丂係倐們亖俀俆乮倐亄們亅係乯
丂偙傟傛傝丄丂乮係倐亅俀俆乯乮係們亅俀俆乯亖俀俀俆丂偲側傞丅
丂倐丄們 乮倐亝們乯 偑惍悢偲偄偆忦審傪晅壛偟偰丄
丂乮係倐亅俀俆丆係們亅俀俆乯亖乮侾俆丆侾俆乯丄乮俁丆俈俆乯 偐傜丄丂乮倐丆們乯亖乮侾侽丆侾侽乯丄乮俈丆俀俆乯
丂偙偺偆偪丄丂倐亖俈丄們亖俀俆 傪嵦梡偡傟偽丄戣堄傪枮偨偡丅
丂偙偺偲偒丄丂仮俙俛俬亄仮俙俠俬亖係俉丂偱偁傞丅
丂傝傜傂偄偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭俁寧俀俈擔晅偗乯
丂傢偨偟傕嵟弶偼傜偡偐傞偝傫偲摨偠傛偆側曽朄偱夝偒傑偟偨丅偦偺屻丄暿偺曽朄偱傕夝偄偰
傒傑偟偨丅鉟楉側夝偒曽偵偼側傝傑偣傫偱偟偨偑丄堦墳彂偄偰傒傑偡丅
丂BC=a丄CA=b丄AB=c丄佢A=2兛丄佢B=2兝丄佢C=2兞丄AI=d 偲偍偔丅
丂佢CAI=佢BAI=兛丄佢ABI=佢CBI=兝丄佢BCI=佢ACI=兞 偲側傞丅
丂佢A+佢B+佢C=兾 傛傝丄丂兛+兝+兞=兾/2 側偺偱丄
丂佢AIB = 兾-(兛+兝) = 兾-(兾/2-兞) = 兾/2+兞
丂佢AIC = 兾-(兛+兞) = 兾-(兾/2-兝) = 兾/2+兝
丂仮AIB偵惓尫掕棟傪巊偆偲丄丂(sin兝)/d=(sin佢AIB)/c 傛傝丄sin兝=(d/c)*cos兞 側偺偱丄
丂(sin兝)^2+(cos兝)^2=1 偵戙擖偟偰丄丂(d/c)^2*(cos兞)^2+(cos兝)^2=1 乧丂嘆
丂仮AIC偵惓尫掕棟傪巊偆偲丄丂(sin兞)/d=(sin佢AIC)/b 傛傝丄sin兞=(d/b)*cos兝 側偺偱丄
丂(sin兞)^2+(cos兞)^2=1 偵戙擖偟偰丄丂(d/b)^2*(cos兝)^2+(cos兞)^2=1 乧丂嘇
嘆嘇傪楢棫偟偰夝偔偲丄
丂(cos兞)^2=c^2(b^2-d^2)/(b^2*c^2-d^4)丂丄(cos兝)^2=b^2(c^2-d^2)/(b^2*c^2-d^4)
傛偭偰丄
a= b*cos(2兞) + c*cos(2兝)
= b*(2*(cos兞)^2-1) + c*(2*(cos兝)^2-1)
= b*(2*c^2(b^2-d^2)/(b^2*c^2-d^4)-1) + c*(2*b^2(c^2-d^2)/(b^2*c^2-d^4)-1)
= (b+c)*(bc-d^2)/(bc+d^2)
側偺偱丄b=25丄c=17丄d=10 傪戙擖偟偰丄a=26丂傪摼傞丅
仈傜偡偐傞偝傫偺夝朄偺d^2偺寁嶼偱丄暘巕偺3師丄2師偺崁偑徚偊偨傝丄忋偺夝朄偺a偺寁
丂嶼偱栺暘偑偱偒偨傝偡傞偺偱丄壗偐偟傜鉟楉側夝偒曽偑偁偭偰傕傛偝偦偆側婥傕偟傑偡丅
丂僗儌乕僋儅儞偝傫偐傜偺僐儊儞僩偱偡丅乮椷榓係擭俁寧俀俈擔晅偗乯
丂寁嶼偩偗側傜丄埲壓偺傛偆偵偟偰媮傔偰傒傑偟偨 ^^丅
丂A丄俛丄俠偐傜撪愙墌偺愙揰傑偱偺嫍棧傪偦傟偧傟 s丄倲丄倳 偲偍偔丅
丂傑偨丄佢A/2=兛 偲偍偔偲丄丂sin兛=r/d丂丄cos兛=s/d
丂偙偙偱丄丂仮ABC=AB*AC*sin(2兛)/2=AB*AC*(rs/d^2)=(s+t+u)*r丂側偺偱丄
丂17*25*s=(17+25-s)*100丂傛傝丄丂17s=4(42-s)丂偡側傢偪丄21s=4*42丂傛傝丄丂s=8
丂傛偭偰丄丂t=17-8=9丂丄u=25-8=17丂側偺偱丄丂BC=t+u=9+17=26
丂偪側傒偵丄丂r=併(10^2-8^2)=6丂偱偁傞丅
乮捛婰乯丂椷榓俇擭侾侾寧俈擔晅偗
丂師偺搶杒戝妛丂暥棟嫟捠乮侾俋俉俆乯偺栤戣偼丄嶰妏宍偺柺愊偺岞幃傪媮傔偰偄傞丅
栤戣丂丂仮ABC偵偍偄偰丄CA丒AB亖倎丄AB丒BC亖倐丄BC丒CA亖們 偲偍偔丅師偺栤偵摎偊傛丅
乮侾乯丂倎倐們亖侽 偺偲偒丄仮ABC偼偳偺傛偆側嶰妏宍偲側傞偐丅
乮俀乯丂(倎亅倐)(倐亅們)(們亅倎)亖侽 偺偲偒丄仮ABC偼偳偺傛偆側嶰妏宍偲側傞偐丅
乮俁乯丂仮ABC偺柺愊偼丄乮侾/俀乯併乮倎倐亄倐們亄們倎乯偱偁傞偙偲傪徹柧偣傛丅
乮夝乯乮侾乯丂倎倐們亖侽 偺偲偒丄俙丄俛丄俠偺壗傟偐偑俋侽亱偲側傞偺偱丄仮ABC偼捈妏嶰妏宍
乮俀乯丂倎亖倐丂傑偨偼丄倐亖們丂傑偨偼丄們亖倎丂偱偁傞丅
丂倎亖倐丂偺偲偒丄CA丒AB亖AB丒BC丂偐傜丄丂俙俛丒乮俠俙亅俛俠乯亖俙俛丒乮俠俙亄俠俛乯亖侽
傛偭偰丄丂俙俛偺拞揰傪俵偲偍偔偲丄丂俙俛丒乮侾/俀乯俠俵亖侽丂傛傝丄丂俙俛佦俠俵
偟偨偑偭偰丄仮俙俛俠偼丄俠俙亖俠俛丂偺俀摍曈嶰妏宍偲側傞丅
丂倐亖們丂傑偨偼丄們亖倎丂偺偲偒傕丄摨條偵偟偰丄仮俙俛俠偼俀摍曈嶰妏宍偲側傞丅
乮俁乯丂仮俙俛俠亖乮侾/俀乯俙俛丒俙俠丒倱倝値俙
偙偙偱丄倱倝値俙亖併乮侾亅們倧倱2俙乯丂偵偍偄偰丄們倧倱俙亖俙俛丒俙俠/乮俙俛丒俙俠乯亖亅倎/乮俙俛丒俙俠乯
傛傝丄丂仮俙俛俠亖乮侾/俀乯俙俛丒俙俠丒併乮侾亅倎/乮俙俛2丒俙俠2乯乯亖乮侾/俀乯併乮俙俛2丒俙俠2亅倎2乯
偙偙偱丄倐亖AB丒BC亖俙俛丒乮俛俙亄俙俠乯丂偐傜丄丂俙俛2亖俙俛丒俙俠亅倐亖亅倎亅倐
丂們亖BC丒CA亖乮俛俙亄俙俠乯丒俠俙丂偐傜丄丂俙俠2亖亅倎亅們
傛偭偰丄丂仮俙俛俠亖乮侾/俀乯併乮乮倎亄倐乯乮倎亄們乯亅倎2乯亖乮侾/俀乯併乮倎倐亄倐們亄們倎乯丂丂乮廔乯
丂傛偍偡偗偝傫偐傜椶戣傪偄偨偩偒傑偟偨丅乮椷榓俇擭侾侾寧俉擔晅偗乯
丂忋婰偺栤戣傪尒偰丄椶戣偑庤尦偵偁傝傑偟偨丅
丂暯柺忋偺仮俙俛俠偵偍偄偰丄俙俛丒俛俠亖倫丄俛俠丒俠俙亖倯丄俠俙丒俙俛亖倰丂偲偟傑偡丅偙偺嶰妏宍
偺柺愊俽傪 倫丄倯丄倰 傪梡偄偰昞偟側偝偄丅
乮弌揟乯丂戞238夞幚梡悢妛媄擻専掕弨1媺2師 栤戣1
仸彫栤柍偟丄巊傢傟偰偄傞彫暥帤偑堎側傞埲奜偼丄搶杒戝妛乮侾俋俉俆乯偲傎傏摨偠
乮僐儊儞僩乯丂杮摉偵偦偺傑傑僘僶儕偱偡偹両摎偊偼丄俽亖乮侾/俀乯併乮倫倯亄倯倰亄倰倫乯丂偱偡偹両
丂丂丂丂丂傛偍偡偗偝傫偵姶幱偟傑偡丅
丂丂埲壓丄岺帠拞両