内接円のある性質　　 　　　　　　　　　　　　　　　　　　　戻る

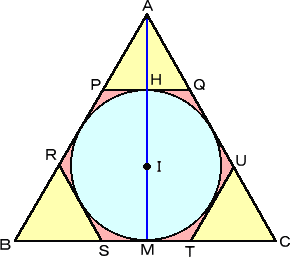
　　左図のような正三角形 ＡＢＣ において、
　円 Ｉ は、その内接円とする。

　　各辺に平行な、内接円の接線が各辺と
　交わる点を、それぞれ、
　　　 　Ｐ　、 Ｑ　、 Ｒ　、 Ｓ　、 Ｔ　、 Ｕ
　とする。

　　頂点 Ａ より、底辺 ＢＣ に下ろした垂線
　の足を、Ｍ とし、ＰＱ との交点を、Ｈ とす
　る。

　　△ＡＢＣ　の面積を Ｓ とし、△ＡＰＱ 、
　△ＢＳＲ 、△ＣＵＴ の面積を、それぞれ
　 Ｓ1 、 Ｓ2 、 Ｓ3 　とする。

　正三角形 ＡＢＣ の一辺の長さを ６ とすると、　Ｓ ＝ ９　である。

　正三角形においては、内心と重心は一致するので、　ＡＨ ： ＡＭ ＝ １ ： ３　が成り立つ。

　面積比は、相似比の２乗に等しいので、　Ｓ1 ＝ となる。

　対称性から、　Ｓ2 ＝ Ｓ3 ＝

　したがって、次の関係式　　が成り立つ。


　上記の証明の方針を検討してみると、この等式は、一般の三角形についても成り立つこ
とが予想される。

　頂点 Ａ、Ｂ、Ｃ より各対辺に下ろした垂線の長さを、それぞれ　ｈA、ｈB、ｈC　とおく。

また、ＢＣ＝ａ 、ＣＡ＝ｂ 、ＡＢ＝ｃ　に対して、ｐ＝（ａ＋ｂ＋ｃ）/２　とおき、内接円の半径を ｒ
とおく。

Ｓ1 ＝ Ｓ×（（ｈA−２ｒ）/ｈA）2　、Ｓ2 ＝ Ｓ×（（ｈB−２ｒ）/ｈB）2　、Ｓ3 ＝ Ｓ×（（ｈC−２ｒ）/ｈC）2

である。また、

　（ｈA−２ｒ）/ｈA＋（ｈB−２ｒ）/ｈB＋（ｈC−２ｒ）/ｈC＝３−２ｒ（１/ｈA＋１/ｈB＋１/ｈC）

において、　１/ｈA＋１/ｈB＋１/ｈC＝ａ/（２Ｓ）＋ｂ/（２Ｓ）＋ｃ/（２Ｓ）＝ｐ/Ｓ＝１/ｒ　なので、

　（ｈA−２ｒ）/ｈA＋（ｈB−２ｒ）/ｈB＋（ｈC−２ｒ）/ｈC＝ １

となる。したがって、一般の三角形においても、　　が成り立つ。


（応用例）　問題の設定は、冒頭と同様とする。下図の緑色の部分の面積を求めてみよう。

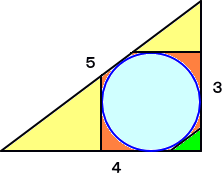　　　　内接円の半径は、明らかに、１ なので、

　　 　　　Ｓ1 ＝ （1/2）・(4/3)・１ ＝２/３

　　　　　 Ｓ2 ＝ （1/2）・２・（3/2） ＝３/２

　　　　　 Ｓ　＝ （1/2）・４・３ ＝６

　　　　よって、等式により、Ｓ3 ＝ １/６

　上記の面積は、もちろん等式を用いなくても求めることはできるが、ちょっとだけ計算は
大変かもしれない。


（追記）　平成２１年１２月１日付け

　上記の応用問題について、ＨＮ「ｚａｒｕｓａｎ」さんから等式を用いない別解を頂いた。

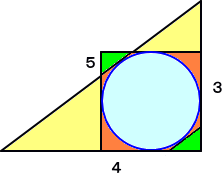　　　　内接円の半径は、明らかに、１ で、円に外接す

　　　る正方形の面積は、４。　この正方形と三角形と

　　　の重ならない部分は、Ｓ3 と合同であることから、

　　　　　　Ｓ3＝Ｓ1＋Ｓ2＋４−Ｓ＝１/６

（コメント）　この応用問題は等式を試してもらうための問題で、「ｚａｒｕｓａｎ」さんのような別
　　　　　　解も有りですね！素朴な解法で、こちらの方が本解でしょう。「ｚａｒｕｓａｎ」さんに
　　　　　　感謝します。


（追記）　令和５年７月６日付け

　冒頭の図形について、

　　

　正三角形 ＡＢＣ の一辺の長さを ６ とすると、Ｓ ＝ ９　で、

　△ＡＰＱ＝△ＢＳＲ＝△ＣＵＴ＝　であることから、

　六角形ＰＲＳＴＵＱの面積は、　９−３×＝６　となる。

　六角形ＰＲＳＴＵＱは、正しくは、等辺六角形である。この図形は、正三角形を２枚、内心が
一致するように重ねたときに出来る図形で、上図の場合が面積最小となる。

　この場合について、もう少し精査してみよう。この話題は、今から６０年以上の昔、京都大
学で出題（１９６０年）された。

　一辺の長さが ６ の正三角形 ＡＢＣ と正三角形 Ａ’Ｂ’Ｃ’ を、内心 Ｉ が一致するように重
ねる。言い換えれば、Ｉ を中心に反時計回りに正三角形 ＡＢＣ を角θだけ回転させて、正三
角形 Ａ’Ｂ’Ｃ’ を得る。辺ＡＢと辺Ａ’Ｂ’の交点をＤ、辺ＢＣと辺Ａ’Ｂ’の交点をＥとし、さらに、
辺ＡＢと辺Ａ’Ｃ’の交点をＦとおく。

　　

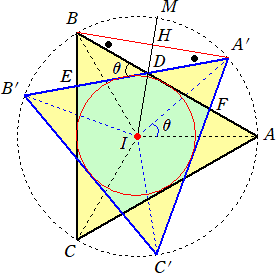
　このとき、∠ＡＢＡ’＝∠Ｂ’Ａ’Ｂ　から、△ＤＢＡ’は２等辺三角形となる。よって、ＤＡ’＝ＤＢ

△ＤＩＡ’と△ＤＩＢ において、ＤＩ 共通で、ＩＡ’＝ＩＢ、ＤＡ’＝ＤＢ　より、△ＤＩＡ’≡△ＤＩＢ

よって、　∠ＤＩＡ’＝∠ＤＩＢ　となり、ＩＤは２等辺三角形ＩＡ’Ｂの∠Ａ’ＩＢの２等分線となる。

したがって、　ＩＭ⊥Ａ’Ｂ　、Ａ’Ｈ＝ＢＨ　より、Ａ’とＢは、線分ＩＭに関して線対称である。

弧ＭＡ＝弧ＭＢ’、弧ＭＣ＝弧ＭＣ’なので、ＡとＢ’、ＣとＣ’も線分ＩＭに関して線対称である。

　以上から、正三角形 ＡＢＣ と正三角形 Ａ’Ｂ’Ｃ’ は、線分ＩＭに関して線対称である。

　このとき、ＤＥ＝ＤＦ　である。同様にして、２つの正三角形の共通部分が等辺六角形であ
ることが分かる。

　△ＢＤＥにおいて、正弦定理より、　ＢＥ/ｓｉｎθ＝ＤＥ/ｓｉｎ６０°＝ＢＤ/ｓｉｎ（１２０°−θ）

　Ａ’Ｄ＝ＢＤ　、ＢＥ＝Ｂ’Ｅ　から、　ＢＤ＋ＤＥ＋ＢＥ＝６　なので、

　｛ｓｉｎ（１２０°−θ）/ｓｉｎ６０°｝ＤＥ＋ＤＥ＋｛ｓｉｎθ/ｓｉｎ６０°｝ＤＥ＝６　より、

　ＤＥ＝６/［｛ｓｉｎ（１２０°−θ）/ｓｉｎ６０°｝＋１＋｛ｓｉｎθ/ｓｉｎ６０°｝］

　　＝６/（ｓｉｎθ＋ｃｏｓθ＋１）＝６/（２ｓｉｎ（θ＋π/６）＋１）

　０≦θ≦２π/３　より、　π/６≦θ＋π/６≦５π/６　なので、ＤＥは、θ＋π/６＝π/２

　即ち、θ＝π/３ のとき、最大である。最大値は、２　となる。

このとき、正三角形ＡＢＣの内接円の半径 ｒ は、　９ｒ＝９　より、ｒ＝　なので、

等辺六角形の面積は、

　ＤＥ・・（１/２）・６＝１８/（２ｓｉｎ（θ＋π/６）＋１）

で与えられる。

　よって、面積最小となる等辺六角形の面積は、　２・・（１/２）・６＝６　となる。

＃θ＝π/３ のとき、２つの正三角形の交わりの様子は冒頭の図になる。



　　以下、工事中！