方べきの定理　　　 　　 　　　　　　　　　　　　　　　　　　　　　　戻る　

　平面幾何で記憶に残る定理としたら、三平方の定理とこの方べきの定理だろう。他にも、
メネラウスの定理やチェバの定理などいろいろあるが、定理の簡明さを考えたら、この２つ
が筆頭だろうと思う。

方べきの定理


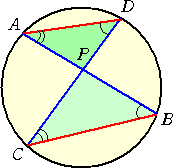
 　　円周上の４点 Ａ、Ｂ、Ｃ、Ｄ　に対して、２つの線分 ＡＢ、ＣＤ
　が円内の１点 Ｐ　で交わるとき、

　　　　　　ＰＡ・ＰＢ＝ＰＣ・ＰＤ

　が成り立つ。
（証明）　右図において、　△ＰＡＤ∽△ＰＣＢ　なので、

　　　　　　　ＰＡ：ＰＣ＝ＰＤ：ＰＢ

　　より成り立つ。　（証終）　		 　　　


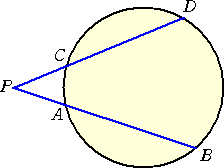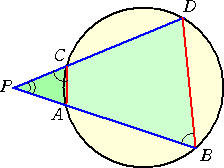
　　　円周上の４点 Ａ、Ｂ、Ｃ、Ｄ　に対して、２つの線分
　　ＡＢ、ＣＤ　が円外の１点 Ｐ　で交わるとき、

　　　　　　ＰＡ・ＰＢ＝ＰＣ・ＰＤ

　　が成り立つ。
（証明）　右図において、　△ＰＡＣ∽△ＰＤＢ　なので、

　　　　　　　ＰＡ：ＰＣ＝ＰＤ：ＰＢ

　　より成り立つ。　（証終）　

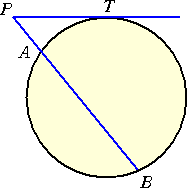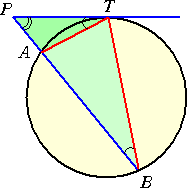
　　　円外の１点 Ｐより、接線ＰＴ　と、円と Ａ、Ｂで交わる直線
　　を引く。このとき、

　　　　　　　　　ＰＡ・ＰＢ＝ＰＴ2

　　が成り立つ。
（証明）　右図において、　△ＰＡＴ∽△ＰＴＢ　なので、

　　　　　　　ＰＡ：ＰＴ＝ＰＴ：ＰＢ

　　より成り立つ。　（証終）　		 　　　　

　方べきの定理は、円の持つ美しい性質の結果として得られるが、現行の学習指導要領で
は高校１年で通常学ぶ「数学Ａ」を待たなければいけない。日本の高校生にとって、とても不
幸なことである。

　この方べきの定理に酷似した定理が、楕円においても成り立つことを最近知ることが出来
た。

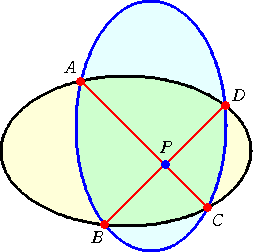　　　左図のように、長軸が互いに直交し、４点で交

　　わる２つの楕円がある。

　　　線分 ＡＣ、ＢＤ　の交点を Ｐ とおくと、

　　　　　　ＰＡ・ＰＣ＝ＰＢ・ＰＤ

　　が成り立つ。

　　　ただし、長軸、短軸の長さはともに等しいもの

　　とする。

　証明は大変そうなので、具体例で追認しておこう。

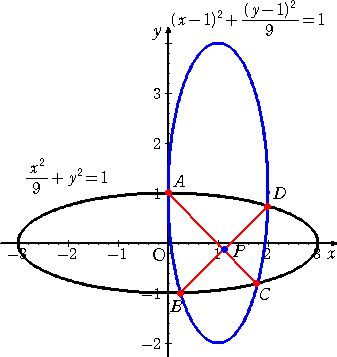　　　左図のように、２つの楕円

　　　　　

　　　

　が、４点 Ａ、Ｂ、Ｃ、Ｄ で交わっている。

　線分 ＡＣ、ＢＤ　の交点を Ｐ とおく。

　　Ａ（０，１）を通る直線を、 ｙ＝ｍｘ＋１

　とおく。３式を連立することにより、

　　ｍ＝−１　、

　が得られる。

これらを、直線と楕円の交点の座標（Ａ以外）

　　　　

に代入して、点 Ｂ、Ｃ、Ｄ の座標をそれぞれ求めると、

　　　　

　よって、直線ＡＣの方程式 ： ｙ＝−ｘ＋１　、直線ＢＤの方程式 ： ｙ＝ｘ−５/４　から、

　　　Ｐ（９/８　，　−１/８）

となる。このとき、簡単な計算から、　　ＰＡ・ＰＣ＝２４３/１６０　　、　　ＰＢ・ＰＤ＝２４３/１６０

なので、　ＰＡ・ＰＣ＝ＰＢ・ＰＤ　の成り立つことが推察される。


（コメント）　この証明を掲載した算額は現存しないという。一般的な証明を試みようとしたが
　　　　　　計算が煩雑そうで躊躇してしまった。現時点では、上記の具体例で納得すること
　　　　　　にしよう。一般的な証明に成功された方、ぜひご教示ください。（こちらへ）


（追記）　平成２０年７月１２日付け

　上記の楕円の場合の方べきの定理について、「一般的な証明を試みようとしたが、計算
が煩雑そうで躊躇してしまった」のは、直接的に交点の座標を求めてから何しようとしたた
めである。

　この件について、平成２０年７月１１日付けで、Ｈ．Ｋ．さんから、

　　　４つの交点は、実は、同一円周上にある

旨のメールを頂いた。

　次のように考えると、交点の座標を求めなくても証明されるとのことである。

　問題の条件から、２つの楕円の方程式は、　ａ＞ｂ＞０　として

　　　ｂ2（ｘ−ｐ）2＋ａ2（ｙ−ｑ）2＝ａ2ｂ2　　、　　ａ2（ｘ−ｒ）2＋ｂ2（ｙ−ｓ）2＝ａ2ｂ2

としても一般性は失われない。

　このとき、上記２つの楕円の交点は、円の方程式

　　　　ｂ2（ｘ−ｐ）2＋ａ2（ｘ−ｒ）2＋ａ2（ｙ−ｑ）2＋ｂ2（ｙ−ｓ）2＝２ａ2ｂ2

を満たし、４点は同一円周上にある。

　よって、円の場合の方べきの定理から、楕円においても成り立つことが分かる。

　Ｈ．Ｋ．さんからの情報によれば、同様のことが、互いに軸が直交する放物線においても
成り立つようだ。

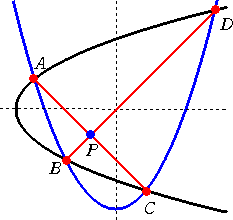　　　左図のように、軸が互いに直交し、４点で交わる

　　２つの放物線がある。このとき、

　　　線分 ＡＣ、ＢＤ　の交点を Ｐ とおくと、

　　　　　　ＰＡ・ＰＣ＝ＰＢ・ＰＤ

　　が成り立つ。

　証明は、上記と同様にして、

　２つの放物線の方程式　　（ｘ−ａ）2＝４ｐｙ＋ｂ　　、　　（ｙ−ｃ）2＝４ｑｘ＋ｄ　　の交点が、

円の方程式　（ｘ−ａ）2＋（ｙ−ｃ）2＝４ｑｘ＋４ｐｙ＋ｂ＋ｄ　を満たすことから明らかであろう。

（コメント）　このような手法の証明を昔やったことを思い出しました。図形と方程式の証明問
　　　　　　題では必須の技法でした。このような証明に気づかせていただいた Ｈ．Ｋ．さんに
　　　　　　感謝いたします。


　当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さんから、上記の話題に関する公式を投稿
して頂いた。別な視点からの方べきの定理の拡張で、大変興味深いものでした。ＧＡＩ さん
に感謝します。（平成２６年７月７日付け）

　円では、円とその円内に点Pをとり、点Pを通る２本の割線（円との共有点が２個の直線）と
円との交点を、A、B と C、D とするとき、

　　PA・PB＝PC・PD　⇔　PA・PB ： PC・PD＝１ ： １

というよく知られた方べきの定理が成立する。そこで、楕円ではいかなることになるのか？

　これに対し、楕円の中に任意の二点 P1、P2 をとる。P1 を通る異なる２本の割線をL1、M1

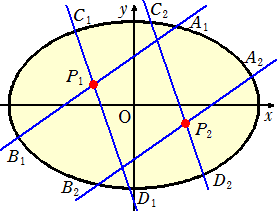　　とし、それぞれが楕円と交わる点を A1、B1 と

　　 C1、D1 で、それぞれと点P1との長さを、

　　P1A1＝a1、P1B1＝b1、P1C1＝c1、P1D1＝d1

　　としておく。一方、P2 を通り、先の直線 L1、M1

　　にそれぞれ平行な直線を L2、M2 とし、これが

　　楕円と交わる点をそれぞれ A2、B2 と C2、D2

とし、P2 との長さを、P2A2＝a2、P2B2＝b2、P2C2＝c2、P2D2＝d2 とするとき、

　　　a1・b1 ： c1・d1＝a2・b2 ： c2・d2

なる関係式が成立する。

　今まで、方べきの定理は、円の図形に限定された定理と思い込んでいた世界を、さらなる
広さの世界から見れる視座を与えられた気分でした。


　読者のために、方べきの定理を用いる練習問題を残しておこう。

練習問題　　下図のように、円と正三角形が左右対称に重なっている。正三角形の１辺の
　　　　　　　　長さを求めよ。

　　　　　　　　　

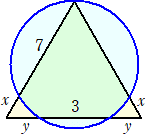
（解）　方べきの定理より、　ｘ（ｘ＋７）＝ｙ（ｙ＋３）

　　　さらに、正三角形であることから、　ｘ＋７＝２ｙ＋３

　　連立方程式を解いて、　ｘ＝２、ｙ＝３　なので、正三角形の１辺の長さは、９　　（終）


（コメント）　答えが無理数にならないように、「７」と「３」が選ばれています。答えが一番きれ
　　　　　　いかな？


（追記）　令和４年９月２１日付け

　何とはなしに数学史の本をパラパラめくっていたら、次のような事実が目に留まった。何と
なく方べきの定理っぽい感じがした。

　半径 ｒ の円Ｏに対して、中心Ｏを通る直線Ｌを考える。この直線Ｌに平行な円Ｏの接線を引
き、その接点をＰとおく。点Ｐを通り円Ｏと交わる直線を引き、直線Ｌとの交点をＡ、円Ｏとの交
点をＡ’とおく。また、直線Ｌと円Ｏとの交点を、Ｂ、Ｃとおく。

　　　　　

　このとき、　ＰＡ・ＰＡ’＝２ｒ2　が成り立つ。

（証明）
　　　　

　上図において、△ＰＡＢ∽△ＰＢＡ’なので、　ＰＡ ： ＰＢ＝ＰＢ ： ＰＡ’

　よって、　ＰＡ・ＰＡ’＝ＰＢ2＝２ｒ2　　（証終）


　方べきの定理を用いても次のように示される。

（別証）　方べきの定理より、　ＡＡ’・ＡＰ＝ＡＢ・ＡＣ　が成り立つ。すなわち、

　（ＰＡ−ＰＡ’）・ＰＡ＝（ＡＯ−ｒ）・（ＡＯ＋ｒ）＝ＡＯ2−ｒ2

　ＰＡ2−ＰＡ・ＰＡ’＝ＡＯ2−ｒ2　から、　ＰＡ・ＰＡ’＝ＰＡ2−ＡＯ2＋ｒ2＝２ｒ2　　（別証終）


（追記）　令和４年１２月１４日付け

　今日は早起きして、Ｗ杯「アルゼンチン　ｖｓ　クロアチア」戦をＴＶ観戦した。クロアチアの
モドリッチも凄い選手だが、アルゼンチンは神懸かり的なメッシの動きと絶妙に絡み合い、
３−０で勝利した。１５日は「フランス　vs　モロッコ」戦があり、また、早起きとなりそうだ。

　方べきの定理の証明でも分かるように、基本的に「方べきの定理」は相似の問題と同等で
ある。何か、方べきの定理の深遠なる原理はないのだろうか、と思い、検討してみた。

　 　

　上記で、何れも　「ＰＡ×ＰＢ＝ＰＣ×ＰＤ」を主張するのが、方べきの定理である。

即ち、　「ＰＡ×ＰＢが一定」という性質　と捉えることもできる。

　特に、ＣＤが直径に等しい場合を考える。

　Ｐから円の中心までの距離を ｄ 、円の半径を ｒ とすると、その一定値は、

　　（ｄ−ｒ）（ｄ＋ｒ）＝ｄ2−ｒ2

となる。これは、点Ｐと円の中心のみで定まる量である。

　２つの円Ｏ、Ｏ’が交わるとき、その２交点を通る直線上の任意の点Ｐについて、２つの円
Ｏ、Ｏ’に関して、

　　ｄ2−ｒ2

の値は、相等しい。

　　　

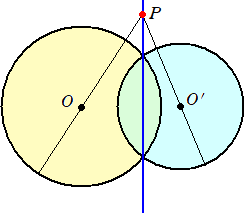
　実際に、方べきの定理から明らかだろう。

　このことを一般化すると、３円が交わるとき、２円の交点を通る３直線は１点で交わること
も明らかだろう。

　　　


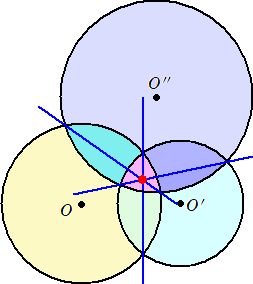
（コメント）　今まで何とはなしに描いてきた３円ですが、２円の交点を通る直線が１点で交わ
　　　　　　るという美しい性質があったんですね！方べきの定理様々です。


（追記）　令和５年７月４日付け

　７月４日は、アメリカ合衆国の建国記念日であるが、私的には、トム・クルーズ主演の映画
「７月４日に生まれて」が印象深い。

　方べきの定理を利用する問題を解いておこう。

問題　　円Ｏの直径ＡＢに、円周上の点Ｐより垂線ＰＨを下す。ＰＨ＝３、ＨＢ＝４のとき、円Ｏ
　　　　の半径 ｒ の長さを求めよ。

　　

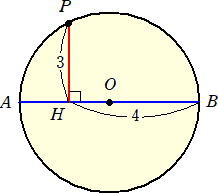
（解）　次の図に対して、方べきの定理を用いる。

　　

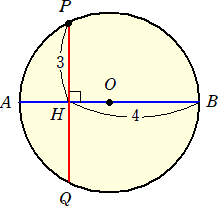
　ＡＨ・ＨＢ＝ＰＨ・ＱＨ　より、　４ＡＨ＝９　　よって、ＡＨ＝９/４

　したがって、　２ｒ ＝９/４＋４＝２５/４　より、　ｒ ＝２５/８　　（終）

＃ＡＨを経由せず、直接 ｒ を求めてもよい。

　実際に、方べきの定理より、　（２ｒ−４）・４＝９　なので、　ｒ ＝２５/８


　方べきの定理と同義であるが、三角形の相似を用いてもよい。

（別解）　次の図において、

　　

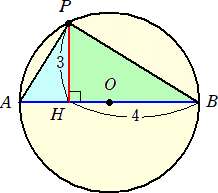
　ＰＢ＝５　で、△ＡＰＨ∽△ＰＢＨ　より、　ＡＨ ： ＨＰ＝ＰＨ ： ＨＢ なので、

　４ＡＨ＝９　から、　ＡＨ＝９/４

　したがって、　２ｒ ＝９/４＋４＝２５/４　より、　ｒ ＝２５/８　　（終）


（追記）　令和５年９月２日付け

　方べきの定理に気づけば、次の問題は容易だろう。

問題　　下図において、共通弦ＰＱと共通接線ＡＢとの交点をＭとするとき、ＡＭの長さを求
　　　　めよ。

　　

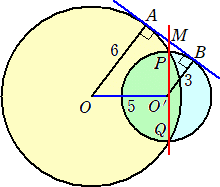
（解）　ＯＯ’＝５　なので、ＡＢ＝４　である。

　方べきの定理より、　ＡＭ2＝ＭＰ・ＭＱ＝ＢＭ2　なので、　ＡＭ＝ＢＭ

　すなわち、Ｍは線分ＡＢの中点となる。よって、　ＡＭ＝２　である。　　（終）



　　以下、工事中！