直角に曲がる通路の通過問題
 |
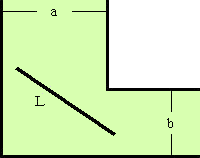
左図のように、幅ａの通路と幅ｂの通路が直角に位置し ている。この通路を、長さＬの棒が通過するときのＬの最 大値を求めたい。 通路に沿って、ぎりぎりの状態で通過しなければいけな いので、必然的に棒は通路の壁をつたって移動すること になる。 |
|
|
 |
包絡線の知識があれば、最初の問題の解答は易しい。 ｘ ＝ ａ ， ｙ ＝ ｂ のときの Ｌ が
求める最大値である。
すなわち、Ｌ の最大値は、
となる。特に、ａ＝ｂ＝Ｗ のとき、最大値は、２
Ｗ となる。
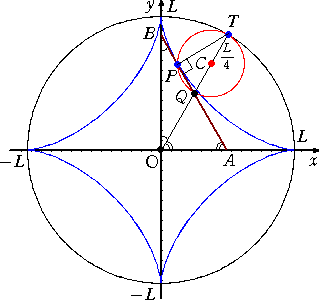
また、上記のことから、星芒形は、
その接線が座標軸の間にはさまれる長さは一定である
という美しい性質を持つことになる。
この証明は易しい。
曲線の方程式
から、点（ ｘ ， ｙ ）における微分係数は、
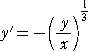
であるので、流通座標系を （ Ｘ ， Ｙ ）として、点（ ｘ ， ｙ ）における接線の方程式は、
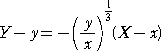
この接線と、ｘ 軸、ｙ 軸との交点をそれぞれ Ａ、Ｂ とおくと、
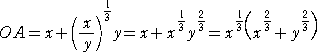
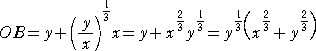
である。 よって、
であることが分かる。
星芒形を、内サイクロイドの特別な場合と考えれば、微分を用いた上記の計算は不要に
なる。
半径 Ｌ の円 Ｏ
の周上を滑ることなく転
がる半径 Ｌ/４ の小円 Ｃ がある。
小円 Ｃ の周上に固定された点を、Ｐ と
すると、点 Ｐ
の軌跡が星芒形となる。
小円 Ｃ と円 Ｏ の接点を Ｔ 、線分ＯＴと
小円 Ｃ
との交点をＱとする。
∠ＴＰＱ＝９０°であるので、直線ＰＱ
は、点Ｐにおける星芒形の接線となる。
この接線が ｘ
軸、ｙ 軸と交わる点をそ
れぞれ Ａ、Ｂ とおく。
∠ＴＯＢ＝θ とおく。
半径 Ｌ の円 Ｃ の中心角 θ
に対する弧の長さと半径 Ｌ/４ の小円 Ｃ
の弧ＴＣの長さは
等しいので、
Ｌ×θ＝（Ｌ/４）×∠ＴＣＰ より、 ∠ＴＣＰ＝４θ
となる。 よって、 ∠ＴＱＰ＝２θ で、∠ＱＢＯ＝θ となる。
したがって、△ＱＢＯは、ＱＢ＝ＱＯ
の２等辺三角形である。
また、 ∠ＱＯＡ＝∠ＱＡＯ でもあるので、△ＱＯＡ
も２等辺三角形となる。
したがって、点Ｐの位置によらず、
ＡＢ＝ＡＱ＋ＱＢ＝２ＯＱ＝２×（Ｌ/２）＝Ｌ
となるので、接線の長さ
ＡＢ は一定である。
さて、一般に、包絡線を求めるには、次の公式が用いられる。（→参考：「包絡線」）
曲線群が、２つの方程式 Ｆ（Ｘ，Ｙ，α，β）＝０ 、Ｇ（α，β）＝０ で与えられる
とき、包絡線上の全ての点は、次の方程式からパラメーターα，βを消去して得られ
る方程式を満たす。
Ｆ（Ｘ，Ｙ，α，β）＝０ 、Ｇ（α，β）＝０ 、
ＦαＧβ−ＧαＦβ＝０ （ただし、Ｆαは、Ｆのαに関する偏微分を表す。他も同様）
例 座標軸上の２点 Ａ（ α ， ０ ）、Ｂ（ ０ ， β ）に対して、 α2＋β2＝Ｌ2 という拘束条
件を満たすとき、直線群 βｘ＋αｙ＝αβ の包絡線の方程式を求めてみよう。
（解） Ｆ（Ｘ，Ｙ，α，β）＝βｘ＋αｙ−αβ 、Ｇ（α，β）＝α2＋β2−Ｌ2 とおく。
ＦαＧβ−ＧαＦβ＝（ｙーβ）（２β）−（２α）（ｘ−α）＝０ より、
β（ｙ−β）−α（ｘ−α）＝０
以上から、連立方程式 αｘ−βｙ＝α2−β2 、 βｘ＋αｙ＝αβ が得られる。
これを解いて、 Ｌ2ｘ＝α3 、Ｌ2ｙ＝β3 となる。
これらを、 α2＋β2＝Ｌ2 に代入して整理すると、
が得られる。 （終）
Ｓ（Ｈ）さんからの示唆（平成２０年１２月１３日付け）によると、上記の計算により、
半径 Ｌ の円 ： ｘ2＋ｙ2＝Ｌ2 から、星芒形（asteroid) ： への写像 φ
φ（α，β）＝（ α3/Ｌ2 ， β3/Ｌ2 ）
が与えられたことを意味するとのことである。
（コメント） 空気の一杯入った円から一気に空気が抜けて萎んでしまったような絵柄ですね！
さて、冒頭の問題は、包絡線の知識がなくても、高等学校で学ぶ微分積分の知識があれ
ば、十分解決は可能である。
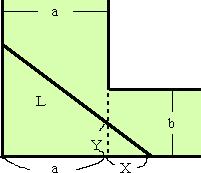左図において、Ｌ＞ａ としてよいので、Ｘ＞０ である。
このとき、相似の関係から、
である。これより、
ここで、Ｙの最大値が ｂ 以下のとき、通り抜け可能となる。つまり、
が成り立つように、Ｌの最大値を求めればよい。上式を変形して、
ここで、
とおく。
Ｘについて微分して、
よって、
のとき、Ｆは極小かつ最小で、最小値は
となる。したがって、Ｌの最大値は、
(参考文献： バケリマン、ボルチャンスキー著 北原泰彦、冨田幸子 訳
反転・包絡線 （東京図書）
佐々木重夫、和田秀三、寺田文行 著 微分積分学 （廣川書店）
谷口 勝 著 微分・積分 （旺文社））