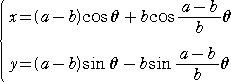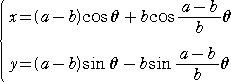内サイクロイド　　　　　　　　　　　　　　　　　　　　　　　　　　　　　

定円に沿って内接しながら円が滑らずに回転するときの、円周上の定点の軌跡である。

媒介変数表示は、

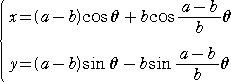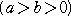　　　　　　　　　　　　　　　ここで、、である。

動円の回転角は、定円の回転角の

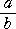倍である。

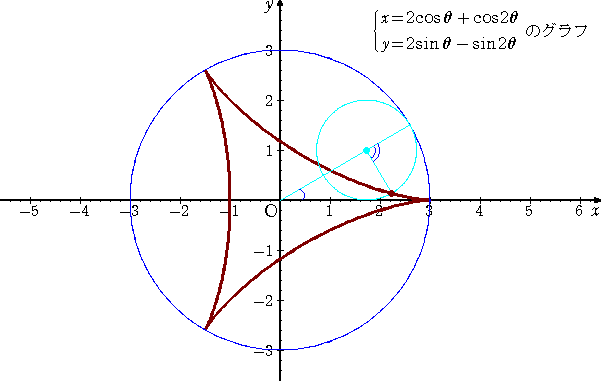
　この曲線は、オイラーのデルタ曲線(1745年)ともいわれる。

（追記）１９７０年代に、spirogragh という好奇心をそそる教育的なおもちゃが流行った。プラ
　　　　スチック製のもので、種々の大きさの回転盤(外縁が歯車)と２つの同心円からできて
　　　　いる輪(内縁・外縁が歯車)がセットになったものである。回転盤には、中心から種々
　　　　の距離で穴があけられていて、その穴に鉛筆を差し込んで、輪の内側(または外側)
　　　　に沿って動かすと、曲線が描かれるというものである。
　　　　
　　　　　このおもちゃを使うと、上のような曲線を描くことは容易であり、楽しい。内サイクロ
　　　　イドは、hypocycloid、外サイクロイドは、epicycloidと言われるが、hypo は、ギリシャ
　　　　語の接頭語「下の」、epi は、ギリシャ語の接頭語「越えた」からきている。

　　　（参考文献：エリ・マオール　著　好田順治　訳
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　素晴らしい三角法の世界　（青土社））