この曲線は、糸の両端を固定して、懸垂させたときにできる。
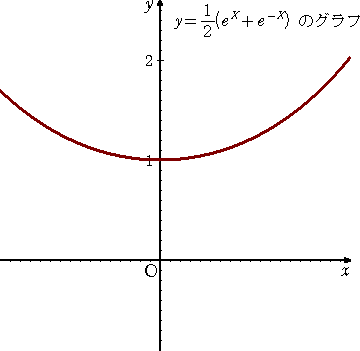
物体を投げたときに描く軌跡が放物線であるが、上記の懸垂線のグラフをみて放物線と
勘違いしたのは、どうやら私だけではないようだ。
ガリレオは、「２本の釘を壁に打ちつけ、その釘に鎖をかけると、その鎖の形が放物線に
なる」と、誤った説明をしている。
ガリレオが説明した曲線が放物線でないことは、微分方程式を用いて示される。
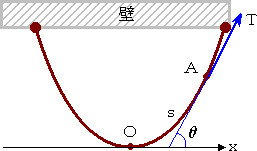曲線の最下端から曲線上の点Ａまでの曲線
の長さを ｓ 、点Ａにおける張力を Ｔ 、張力
がＸ軸となす角を θ 、鎖の単位長さに働く重
力を ｇ とすると、微分方程式
が成り立つ。
ただし、張力 Ｔ は、θ の関数で、
このＴを微分方程式に代入して、微分方程式を解くとき、原点を通るものは次式で与えら
れる。
この式は明らかに懸垂線の方程式で、鎖の形は放物線ではなく、懸垂線であることが証
明された。もっとも、この方程式は、原点の近くでは、限りなく放物線である。
上の方程式を、Ｘ＝０ のまわりでTaylor 展開（MaclLaurin 展開）すると、
４次以上の項は、０ のまわりの十分小さい近傍では無視できるので、
となる。これは、まさしく放物線の方程式である。
微分方程式がなかった時代において、上記のガリレオの誤った説明を非難することは
できない。
原点のまわりでは、ほぼ放物線なのだから・・・！むしろ、ガリレオの洞察の素晴らしさ
に感服する次第である。懸垂線が原点のまわりでは、ほぼ放物線になることを推察して
いた（？）のだから・・・。
（参考文献：遠山 啓 著 数学入門（下） （岩波新書））