クロソイド曲線

クロソイド曲線について　　　　　　　　　　　　　　　　　　

　毎日、車を片道３０km程走らせて自宅から職場に通っている。家を出る時間やその日の
気分、道路の混み具合によって、毎日走る道は変わる。自動車専用道路もその中に入る
場合があるが、高速安定走行ができるように設計されているせいか、とても走りやすい。

　それに対して、一般道は、その土地のいろいろな制約から、とても安全に走行できるよう
には設計されていない場合が多い。

　私の通勤路でも、普通に滑らかにハンドルをきっていると、そのまま左側の歩道に乗り上
げるのではないかと思われるところがある。当然急ハンドルをきると、今度はセンターライン
をオーバーしてしまう。危ない限りだ！

　円軌道は、実は危険な曲線なのに、カーブとして自然に見えるので、きっと誤った道路設
計になっているのだろう。このような道路を設計し供用させているということは、交通事故を
減らそうとする動きに逆らうものではないだろうか。

　このことに関して、１９９３年３月号数学セミナー（日本評論社）に、

　　　　　「”人間的曲線”クロソイドとは何か？」（八木一正著）

という、おもしろい特集が組まれている。

　このページでは、数学的に滑らかでも、人間的には滑らかではないということについて、
まとめてみたい。

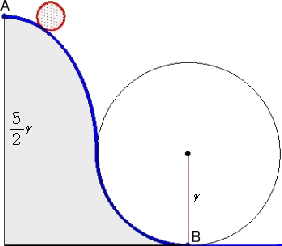　　　左の図を見てみよう。地点Ａより、赤い物
　　体が青い斜面に沿って落下し　ている。

　　　地点Ｂの周辺の青い斜面は、半径ｒの円
　　周に沿っている。

　　　地点Ａは、地点Ｂより　５ｒ/２だけ高い位置
　　にあるものとする。

　　　地点Ｂより右側は円に接する直線上を動く。

　　　円周上の点から、その接線上の点に移動
　　するので、図形的には、滑らかに移動してい
　　るように見える。

　　しかし、地点Ｂの周辺での、物体にかかる力の変化を計算すると、驚くべき結果を得るこ
とになる。

　　物体の質量をｍ、地点Ｂでの速さを V 、重力加速度を g とする。

　「地点Ａでの力学的エネルギーと地点Ｂでの力学的エネルギーが等しい」という力学的
エネルギー保存の法則を用いると、

　

　曲線部分では、速度に応じて遠心力が働くことに注意すると、地点Ｂでは、瞬間的に体重
が６０kgの人は、３００kgから６０kgに変化するわけで、身体的には非常に好ましくない。
　　　　　　　　　　　　　　　　　　　　　（実際に働く力は、この遠心力と重力との合力である。）

　このように、図形的な自然なつながりと身体的に安全なつながりとは、全く別な次元の問
題である。身体的に安全なつながりとは、体にかかる力が徐々に変化するものをいう。この
ような条件を満たす曲線が安全曲線、やさしさ曲線ともいわれる「クロソイド曲線」である。

　車が一定速度で走行している時、速度を落とさずにハンドルを一定の割合でゆっくり回し続
けるときにできる車の走行跡や家の手すりの曲がり具合、テーブルの丸みのカーブや遊園地
のジェットコースターなど、その曲線を目にすることは多い。

　しかし、この曲線の数学的な記述

　　　　　　　　　　　　　　　

をみると、その解析は、それほど易しいとはいえない。

　この曲線を書こうとしても、私の手持ちの描画ソフトでは無理みたいなので、イラストでその
雰囲気を味わってほしいと思う。

　　　　　　　　　　　

（参考）　ＨＰ：「生活の中のクロソイド曲線いろいろ」は、とても面白い題材を扱っていて、た
　　　　めになりました。感謝いたします。

（追記）　平成２０年２月１９日付け

　当ＨＰがいつもお世話になっているＨＮ：ＫｙａｍＷｅｂさんからアドバイスをいただき、こ
のクロソイド曲線をグラフ描画ソフトで書かせてみようと思い立った。
（→参考：ＫｙａｍＷｅｂさんのＨＰ）

　マクローリン展開を用いると、　ｘ＝０　の近傍において、

　　　　

　　　　

と書ける。　よって、

　　　　

　　　　

において、第６項以降を無視して、

　　　　

　　　　

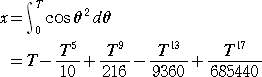
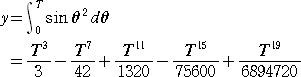
となる。

　－２．１≦Ｔ≦２．１　の範囲でグラフを描くと、下図のようなクロソイドっぽい曲線の概形を
得ることが出来る。

　　　　　

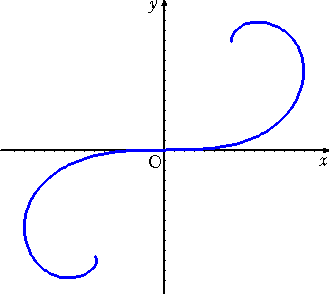
（コメント）　Ｔの範囲をもう少し広げると、曲線は「の」の字を描いて外に発散してしまいまし
　　　　　　た。第５項までだけで書かせることに無理があるようです。

　平成２０年２月２１日に、ａｋｉｒａさんという方からメールを頂戴した。

　ａｋｉｒａさんによれば、普通に数値計算して軌跡を描こうとしても、上述の式において、θ²
の強い非線形性のために、θ が大きくなると軌跡が発散してしまうとのことで、確かにこれ
は私自身上記の計算で経験したことである。

　これを回避するために、ある程度の大きさの θ までは通常の数値積分を行い、その後は
置換積分(θ² をＴとしてみる等)に積分式を変えることでうまく数値計算できる可能性があ
るとのことである。

　ａｋｉｒａさんの計算によれば、クロソイド曲線は、点

　　　　　　　　

に収束するのだという。これって、大体（±０．６２６６６，±０．６２６６６）位かな？

　この計算には、正則関数
　　　　　　　　　　　　　　　　　　
を使うといいそうだ。

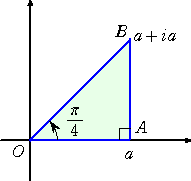　左図の積分経路Ｃ（Ｏ→Ｂ→Ａ→Ｏ）において、

　　　　　　　

であることから、

　　　　　　

が求められ、実部、虚部を比較すればよい。

　さらに、ａｋｉｒａさんから、クロソイド曲線の収束する様子を、Ｅｘｃｅｌファイルにまとめて送っ
ていただいた。

　クロソイド曲線上の点（ｘ_ｎ，ｙ_ｎ）と媒介変数 θ_ｎを次の漸化式により定義する。

　　ｘ₀ ＝０　、ｙ₀ ＝０　、　θ₀ ＝０　として、

　　　θ_ｎ＋1 ＝ θ_ｎ＋Δθ　（ただし、Δθは定められた定数）

　　　ｘ_ｎ＋1 ＝ｘ_ｎ＋Δθ・ｃｏｓθ_ｎ²

　　　ｙ_ｎ＋1 ＝ｙ_ｎ＋Δθ・ｓｉｎθ_ｎ²

　ａｋｉｒａさんの計算結果（Δθ＝０．０１）を図示すると、下記のようになる。

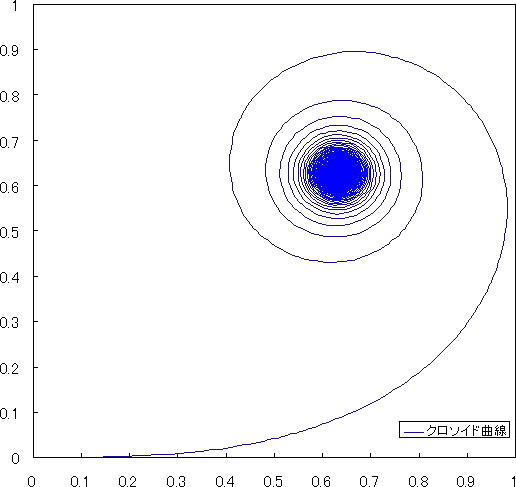
　クロソイド曲線が深遠なる世界に収束していくようで、とても神秘的ですね！

　ａｋｉｒａさんの作られたＥｘｃｅｌファイルで、Δθ＝０．００５　として、０≦θｎ≦６　の範囲で
描かせたものを合成すると下図のようになる。
　　　

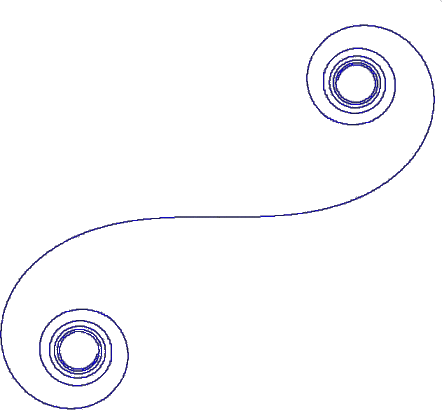
（コメント）　何か生き物のような雰囲気ですね！ａｋｉｒａさんに感謝いたします。