双曲線は、漸近線をもつ。その直線の方程式は、

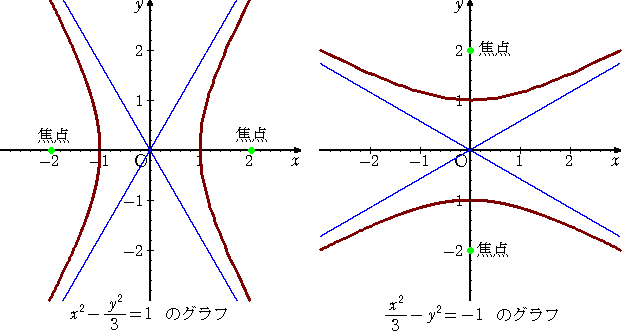
双曲線は、２つの定点Ｆ、Ｆ’からの距離の差が一定な点Ｐの軌跡である。２つの定点を、焦点

という。
　　　　　　　焦点の座標は、　　　または、　


（追記）　令和６年７月１８日付け

　東北大学　文理共通（１９７１）で、双曲線の方程式を求める問題が出題された。

第２問　　原点を中心とし、ｙ＝ｘ、ｙ＝−（１/）ｘ を漸近線とする双曲線で、点（１，０）
　　を通るものの方程式を求めよ。ただし、ｃｏｓ²（π/１２）＝（２＋）/４ である。

（解）　題意より、求める双曲線の方程式は、　（ｘ−ｙ）（ｘ＋ｙ）＝ｋ　とおける。

　点（１，０）を通ることから、　ｋ＝　なので、　（ｘ−ｙ）（ｘ＋ｙ）＝　　（終）


（コメント）　解答をみる限り、「ｃｏｓ²（π/１２）＝（２＋）/４」のヒントを使うまでもないと思
　　　　　うのだが、どんな意図があるのだろうか？


　　以下、工事中！