ら せん
螺旋(渦線）

螺旋（１６３８年）　・・・　極方程式は、　

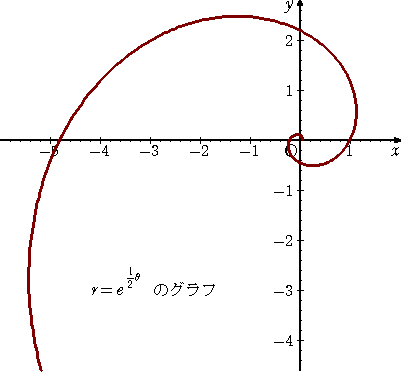
　この等角螺旋は、自然界に多く見られる曲線として大切である。

例　蜂が花に向かって飛ぶ軌跡やアンモナイト、銀河系など

　等角螺旋は、曲線の接線と中心から引いた動径とのなす角が一定になるという性質を有
する。これが、等角螺旋の命名の由来である。

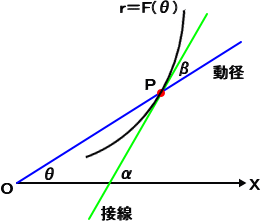
　下図のように、曲線 ｒ＝Ｆ(θ) 上の１点 Ｐ(ｒ，θ) における接線と始線のなす角を α 、動
径とのなす角を β とすると、次の式が成り立つ。



　　　


　　　







　このとき、 ｒ＝ｂｅ^ａθ　について、　ｒ’＝ａｂｅ^ａθ　より、　ｔａｎβ＝１/ａ（＝一定）　である。

このことから、中心を通る直線を引いて１８０°反対の側にある等角螺旋上の点での接線
は平行になる。
　　　

　この話題に関連して那覇在住のＹさんよりメールを頂いた。（平成２３年２月２６日付け）

　　あるカーブがあって、どうも「らせん」と思われる。(ある機械加工をすると出てくる線です)
　色々ならせんがありますが、等角らせんと思われる。問題は、中心(原点)がどこかを知る
　ことです。どうやって、この原点を求めればいいでしょうか？大体どの辺りが原点だという
　目星は付けられますが、正確な位置が知りたいです。こういう現実の問題は、どのように
　解けばいいでしょうか。

　　　　　　　　　　

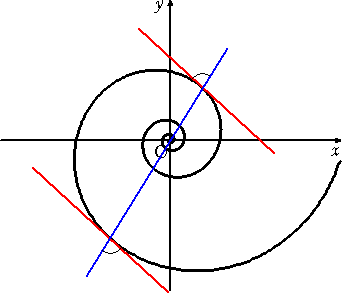
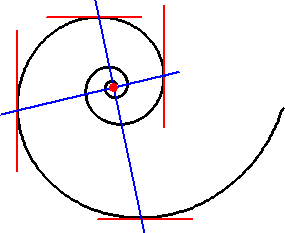
　上記の等角螺旋の性質に着目して、次のよう解いてみた。

　　１．曲線上の任意の点で接線を引く。

　　２．その反対側の曲線に、接線と平行な接線を引く。

　　３．２つの接点を結ぶ。

　　４．１．２．３．の操作を他の点で行う。

　　５．３．と４．で得られた線分の交点が等角らせんの中心である。

　　　　　　　　


　等角螺旋以外にも、たくさんの渦巻線が考えられている。

（１）　アルキメデス螺旋（B．C．２２５年)

　　　　極方程式は、　ｒ＝ａθ　（下記グラフは、ａ＝１のとき）

　　　　　　　　　　　　

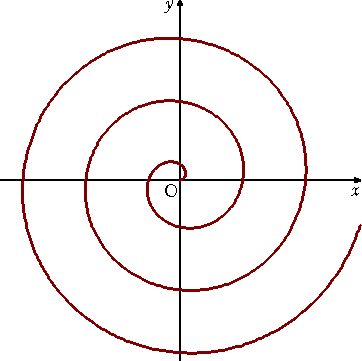
　弧と弧の間の空間がいつまでも一様なので、何故かしら人工的な感じを受ける。

アルキメデス螺旋について、興味ある事実がある。

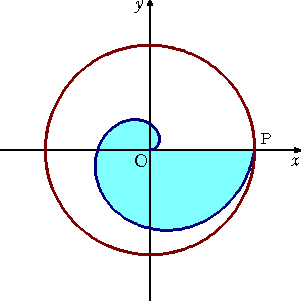
　（イ）　動径が１回転して通過する図形の面積は、１回転目の動径を半径とする円の
　　　　面積の３分の１ である。

　　実際に、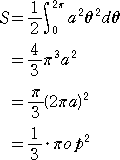
　　　　　　　　








　（ロ）　動径が１回転した点Ｐで引いた接線とＯにおけるＯＰの垂線との交点をＱとす
　　　　る。このとき、線分ＯＱの長さは、ＯＰを半径とする円周の長さに等しい。

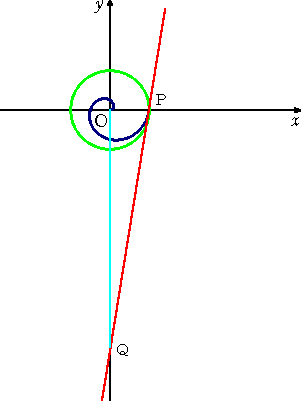　　　実際に、接線と始線とのなす角を α と
　　すると、公式より、
　　　　　　　　
　　よって、
　　　　　　　　ＯＱ＝ＯＰ×ｔａｎ α
　　　　　　　　　　 ＝２π・ＯＰ



















（参考文献：山下純一　著　数学史物語（東京図書）
　　　　　　　 佐々木重夫・和田秀三・寺田文行　著　微分積分学（廣川書店））

（２）　フェルマーの渦巻線（１６３６年）

　　　　極方程式は、　ｒ²＝θ
　　　　　　　

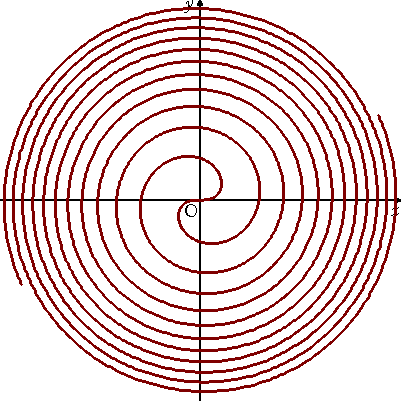
　果てしなく繰り返す陰陽の錯覚を起こさせる。

（３）　コーツのリトゥウス（１７２２年）　・・・・・　喇叭線ともいわれる。

　　　　極方程式は、　ｒ²θ＝ａ² 　（下記グラフは、ａ＝１のとき）



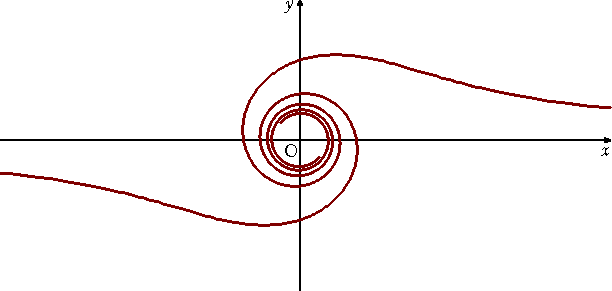
　古代ローマの占官が用いた曲がり杖に形が似ているらしい。

（４）　双曲螺旋

　　　　極方程式は、ｒθ＝ａ 　（下記グラフは、ａ＝１のとき）