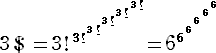・ 巨大数を作る S.H氏
世の中には手軽に意味のない巨大な数を作る方法が存在する。その一つの方法として、
1995年に Clifford Pickover によって定義された超階乗 n$ がある。
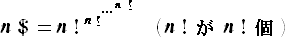
例 1$=1!=1 、 2$=2!2!=22=4
手計算で求められるのは、多分上記のものだけである。3$については、定義より
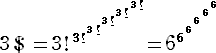
であるが、もはやその値を正確に計算することは不可能だろう。
上記の数の読み方も込み入っている。次のよう読むのだろうか?
6の〈6の〔6の{6の(6の6乗)乗}乗〕乗〉乗
これでは絶対途中で、「訳、分からん...!?」になると思う!
「冪(べき)」を表す記号「^」を用いれば、 6^〈6^〔6^{6^(6^6)}〕〉 とも書ける。
表計算ソフト Excel を用いて計算できるのは、せいぜい
619=609359740010496
までである。
3$という数は恐ろしく巨大な数で、我々人間には手が出せない神の領分に属するよう
な印象があるが、よくよく見ると、3$は驚くほど単純な構造になっていることに気がつく。
すなわち、
3$は、幾つかの「6」を単に掛け合わせたもの
に過ぎない。
このことに注目すると、3$の値を正確に求めることは困難であるが、例えば、下3桁が
どのような数になるかを求めることぐらいは出来そうである。そこで、表計算ソフト
Excel
を用いて、「6」という数を延々と掛け続けてみた。単に計算させると、直ぐに計算はオー
バーフローしてしまうので、MOD関数を使って、下3桁のみの数字の出方の様子を眺め
てみた。
すると、そこには恐ろしく美しい法則性が存在した!
1〜999までしか考えないので、「6」という数を延々と掛け続けると、鳩ノ巣原理により、
あるところから循環するだろうことは予想できる。
実際に、次のような順番で循環する。
| ・ |
・ |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| 6 |
36 |
216 |
296 |
776 |
656 |
936 |
616 |
696 |
176 |
56 |
336 |
16 |
96 |
576 |
| |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
・・・・・ |
| 456 |
736 |
416 |
496 |
976 |
856 |
136 |
816 |
896 |
376 |
256 |
536 |
216 |
・・・・・ |
166個の6の倍数のうち、出現するのはわずかに25個だけであることにも驚かされる。
ところで、 66=46656 なので、
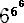
は、6を46656回掛け合わせたものである。この数の正しい値を求めることは困難である
が、その下3桁については、上記の循環しているという性質を活用すると容易に求めること
が出来る。
すなわち、 46656−2 を 25 で割った余りは、4 なので、上記の表から、
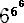
の下3桁の数は、 656 である。
この操作を続けていくと、
3$は、6を ***・・・***656回掛け合わせた数
なので、上記と同様の計算(2を引いて、25で割る)をして、余りが 4 であることから、
3$の下3桁の数は、 656
であると言える。
(コメント) 当初インターネットで調べても、この超階乗についての記述はあまりなく途方に
暮れた。しかしながら、上記のように少しずつ解きほぐして、3$の数字の並びの
一端を垣間見ることが出来て、ほっとしている。また、十分楽しむことができた!
このような計算をしたホームページを検索することはできなかったので、多分、
この世界では初めての計算かな?と思う次第である。
この超階乗について、もっとご存じの方がおられたら、是非ご教示ください。
(追記) 3$の下3桁を求めた以上、下4桁も求めてみようという気になった。
「6」という数を延々と掛け続けると、下4桁の数字は、次のように出現する。
6 、36 、216 、1296 、7776 、6656 、9936 、9616 、7696 、6176 、7056 、
2336 、4016 、4096 、4576 、7456 、4736 、8416 、496 、2976 、7856 、
7136 、2816 、6896 、1376 、8256 、9536 、7216 、3296 、9776 、8656 、
1936 、1616 、9696 、8176 、9056 、4336 、6016 、6096 、6576 、9456 、
6736 、416 、2496 、4976 、9856 、9136 、4816 、8896 、3376 、256 、
1536 、9216 、5296 、1776 、656 、3936 、3616 、1696 、176 、1056 、
6336 、8016 、8096 、8576 、1456 、8736 、2416 、4496 、6976 、1856 、
1136 、6816 、896 、5376 、2256 、3536 、1216 、7296 、3776 、2656 、
5936 、5616 、3696 、2176 、3056 、8336 、16 、96 、576 、3456 、736 、
4416 、6496 、8976 、3856 、3136 、8816 、2896 、7376 、4256 、5536 、
3216 、9296 、5776 、4656 、7936 、7616 、5696 、4176 、5056 、336 、
2016 、2096 、2576 、5456 、2736 、6416 、8496 、976 、5856 、5136 、
816 、4896 、9376 、6256 、7536 、5216 、1296 、7776 、・・・・・・・・・・・・・・・・
上記の青色の数字が循環する部分で、125個ある。
ところで、 66=46656 なので、
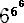
は、6を46656回掛け合わせたものである。上記の循環しているという性質を活用すると、
46656−3 を 125 で割った余りは、28 なので、上記の表から、
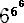
の下4桁の数は、 8656 である。
この操作を続けていくと、
3$は、6を ***・・・***8656回掛け合わせた数
なので、上記と同様の計算(3を引いて、125で割る)をして、余りが 28
であることから、
3$の下4桁の数は、 8656
であると言える。
(コメント) 3$の下3桁が求まったら、次は下4桁、そして、下5桁、・・・と興味は尽きない
が、計算の方針は全く同じなので、ここで幕引きとしたい。