鳩ノ巣原理 
高校で習う論証法としては、「背理法」や「数学的帰納法」が有名である。「平方根2
が無理
数である」ことを示すのに、背理法が使われるが、大学入試における、その他もろもろの問
題においても、背理法が登場する頻度は高い。また、自然数 n に関する命題の証明には、
数学的帰納法が活躍する。「自然数 n に対して、2n>n 」を示す場合、直接的な証明も可
能であるが、数学的帰納法による証明の方が簡明である。
結論を否定して、矛盾を導くという背理法の証明方法は、新しい数学の定理を創造するの
に有効である。いくつか具体的な事例を計算して結論の予想を立て、それを証明する場合、
背理法が主に使われる。大学院時代、同じ研究室にいらした、群論を専門とする方に論文
を見せてもらう機会があったが、ほとんど背理法一色であった。それだけ、背理法は数学的
な論証において、強力な武器となりうる。
この「背理法」や「数学的帰納法」に匹敵すると思われる、論証の武器 :「鳩ノ巣原理」は、
なぜかしら高校で教えられることはない。しかし、数学オリンピックの必須アイテムであるこ
とを考えると、世界の標準的な論証法と考えるべきだろう。鳩ノ巣原理は、存在定理を証明
するときに有効である。
鳩ノ巣原理について最初に言及したのは、ドイツの数学者ヨハン・ディリクレ(1834年)で、
「引き出し論法」という言葉を使っている。「鳩ノ巣原理」というフレーズを数学の専門誌で最
初に使ったのは、数学者のラファエル・M・ロビンソン(1940年)と言われる。
「鳩ノ巣原理」を意識するには、次の問題を考えるといいだろう。
問題 サイコロ1個を何回続けて投げるかを予め宣言する。
宣言した回数以内に同じ目が2回以上出たら、「勝ち」
そうならなかったら、「負け」
さて、あなたは何回と宣言すれば、必ず勝てるでしょうか。最小回数を答えてください。
正解は、「7回」です。これは何故?と思われた方は是非「鳩ノ巣原理」を学んでください。
そして、上記のような問題が自由に作れたら、あなたはもう鳩ノ巣原理マスターですね!
鳩ノ巣原理自体は、とても当たり前のことを主張する。
鳩ノ巣原理(・・・ディリクレの引き出し論法、部屋割り論法ともいわれる)
n 個の巣穴に n+1 羽の鳩を入れる場合、
必ずどれかの巣穴は、2 羽以上
これを一般化して、
n 個の巣穴に m 羽の鳩を入れる場合、m>kn ならば、
必ずどれかの巣穴は、k+1 羽以上
|
 |
「たくさんあるものの中で、2つ(以上)は同じ」ことを示したりする場合、鳩ノ巣原理がよく
用いられる。
上記の問題だと、サイコロの目は、1〜6の6個なので、7回と宣言すれば、必ずどれかの
目が2回以上出ることは確実なので、「勝ち」となる。
さらに、次の問題に対して、この鳩ノ巣原理を応用してみよう。
問題 実数係数の3次方程式が次の性質を持つとする。
α が解ならば、その平方 α2 も解になる
このとき、この性質を持つ3次方程式の解の絶対値は、0 または 1 である。
(解) 今 α が解ならば、α2、α4、α8 も解になる。ところが、3次方程式は、3個の解しか
もたないので、α、α2、α4、α8 のうち相等しいものが存在する。(鳩ノ巣原理)
そこで、ある m、n に対して、αm=αn (m>n)とすると、
αn(αm−n−1)=0
から、|α|n=0、|α|m−n=1 となり、|α|=0、1 が成り立つ。(終)
この問題からも分かるように、何が鳩ノ巣で、何が鳩かを把握することが、この論法のキ
ーポイントである。上記問題では、3個の解が鳩ノ巣で、4つの数 α、α2、α4、α8 が鳩に
相当する。
鳩ノ巣原理は、その単純さから、一般の人にとっても納得されやすい原理であるが、実際
に、問題解決に利用しようとする場合、相当の熟練を要する。このページでは、鳩ノ巣原理
を利用する問題をいくつか提示して、その適用の仕方を見ていこう。これらの例題をマスタ
ーすれば、無意識の内に「鳩ノ巣原理」が使えるようになるだろう。
例題1 分数を小数に直す場合、有限小数か、循環小数である。これは、どうしてか?
(解) 分子を分母で割り算したとき、割り切れれば、有限小数である。割り切れず、永
遠に割り算が繰り返される場合に、循環小数ができる。
実際に、分母 n で割ったとき、その余りの可能性は、1、2、3、・・・、n−1
の
n−1 個ある。(これが、鳩ノ巣)
今、n 回割り算を繰り返して、余りが、n 個得られたとする。(これが、鳩)
このとき、鳩ノ巣原理により、この余りのうち、少なくとも2つは同じ数である。
よって、その同じ数に対応するところから、小数は循環する。(終)
例題2 1辺が 4 の正方形の内部および辺上に、9つの点をとる。このうちの3点を結ん
で三角形を作るとき、すくなくとも一つの三角形の面積は、2 以下である。
(解) 与えられた正方形の各辺の中点を結んで、4つの合同な正方形に分割する。(こ
れが、鳩ノ巣) いま、9つの点(これが、鳩)があるので、鳩ノ巣原理により、
9>2×4 から、少なくとも一つの三角形の内部および辺上に、2+1=3
個以上
の点がある。このうちの3点で作られる三角形の面積は、2 以下である。(終)
(ものの本によると、このような三角形は、少なくとも2個あるらしい!)
例題3 1辺が 2 の正三角形の内部および辺上に、5つの点をとる。このとき、2点間の
距離が 1 以下であるような2点が存在する。
(解) 与えられた正三角形の各辺の中点を結んで、4つの合同な正三角形に分割する。
(これが、鳩ノ巣) いま、5つの点(これが、鳩)があるので、鳩ノ巣原理により、ど
れか1つの正三角形の内部および辺上に、2つ以上の点がある。このうちの2点を
結んで得られる線分の長さは、1 (正三角形の一辺の長さ)以下である。(終)
例題4 3で割って 1 余る数の数列: 1,4,7,・・・,97,100 を考える。この34個の数
から相異なる 20 個の数をどのように選んでも必ず、その 20 個の中に、2つの相
異なる数で、和が、104 となるものが存在する。
(解) 和が、104 となる数の組合せは、
4&100、7&97、10&94、・・・、49&55 の16 通りある。この各場合に使わ
れていない数は、1 と 52 である。そこで、次の 18 通りの場合を考える。
4&100、7&97、10&94、・・・、49&55、1、52 (これが、鳩ノ巣)
今、相異なる 20 個の数を任意に選ぶ。(これが、鳩)
このとき、鳩ノ巣原理により、2つの数とも選ばれている対 A&B
が存在して、
A+B=104 である。(終)
#「和が、104となる数の組合せ」に誤りがあると、Kelly Burkhard さんからご指摘いただきまし
た。(平成30年8月11日付け) 上記は修正済みです。Kelly Burkhard さんに感謝します。
例題5 1 から 1999 までの1000個の奇数がある。この中から、 501個の奇数をどの
ように選んでも必ず、その 501 個の中に、2つの相異なる数で、和が、2000
とな
るものが存在する。
(解) 和が、2000 となる数の組合せは、
1&1999、3&1997、5&1995、・・・、999&1001 の500
通りある。(これ
が、鳩ノ巣) 今、相異なる 501 個の奇数を任意に選ぶ。(これが、鳩)
このとき、鳩ノ巣原理により、2つの数とも選ばれている対 A&B
が存在して、
A+B=2000 である。(終)
例題6 任意に与えられた相異なる4つの整数から適当に2つ選ぶと、その差は、3 の倍
数になる。
(解) 4つの整数を 3 で割った余りを、それぞれ p、q、r、s とおく。(これが、鳩)
ところで、整数を 3 で割った余りは、0、1、2 のいずれか。(これが、鳩ノ巣)
よって、鳩ノ巣原理により、p、q、r、s のうちに少なくとも2つ相等しいものがある。
そのうちの2つについて差をとれば、その差は、3 の倍数になる。(終)
上記の例題6は、次のように一般化される。
例題6’ 相異なる n+1 個の整数から適当に2つ選ぶと、その差が、nの倍数になるもの
がある。(早稲田大学)
(解) 相異なる n+1 個の整数を、 a1、a2、・・・、an、an+1 とし、これらを n で割った
余りを、それぞれ
r1、r2、・・・、rn、rn+1 とおく。(これが、鳩) ところで、整数を
n
で割った余りは、0、1、2、・・・、n−1 のいずれか。(これが、鳩ノ巣)
よって、鳩ノ巣原理により、
r1、r2、・・・、rn、rn+1 のうちに少なくとも2つ相等しい
ものがある。そのうちの2つについて差をとれば、その差は、n の倍数になる。(終)
例題7 100以下の自然数から、51個の数を適当に選ぶと、互いに素となる 2つの数が
必ず存在する。
(解) 隣り合う数同士を組み合わせて、次のような 50個の対を作る。
1&2、3&4、5&6、・・・、99&100 (これが、鳩ノ巣)
この「50個の対」に対して、51個の数を選んだ(これが、鳩)ので、鳩ノ巣原理によ
り、2つの数とも選ばれている対 A&B が存在する。このとき、隣り合う数同士は、
互いに素なので、題意を満たす。(終)
例題8 19以下の自然数から、7個の数を適当に選ぶ。この7個の数の中から、いくつか
の相異なる数の組を 2 組選んで、その和を等しくすることができる。
(解) 7個の数の中から、いくつかの相異なる数を選んで組を作るとき、その作り方は、
27−1 = 127通りある。(これが、鳩)
また、そのような組の中で、
和が最大となるものは、19+18+17+16+15+14+13=112
和が最小となるものは、1
である。
したがって、和のとり得る値は、1、2、3、・・・・、112 (これが、鳩ノ巣)
よって、鳩ノ巣原理により、和が等しくなる組が少なくとも2つ存在する。
2つの組にもし、同じ数があれば、それらを取り除いても、和は等しいままで、しか
も、2つの組の数は、すべて異なるようにできる。(終)
(参考文献:ローレン・C・ラーソン 著 秋山 仁・飯田博和 訳
数学発想ゼミナール <1> (シュプリンガー・フェアラーク東京))
FNさんが、この問題を考察された。(平成23年1月22日付け)
上記の問題で、「19」を「21」に変えても全く同じ形で証明できます。「19」を「23」に変え
る場合は、少し証明を変えればできます。
例題8’ 23以下の自然数から7個の数を任意に選ぶ。この7個の数からいくつかの相異
なる数の組を2組選んでその和を等しくすることができる。
FNさんが、例題8’の解答を与えられました。(平成23年1月25日付け)
(解) 7個の数の中から、いくつかの相異なる数を選んで組を作るとき、その作り方は、
27−1=127通りある。(これが、鳩)ここまでは例題と同じ。
(最大と最小について、例題8の(解)より少しだけ正確にする。)
7個の数のうち最小なものを
a
とする。そのような組の中で、和が最大となるものは、
23+22+21+20+19+18+a=123+a
で、和が最小となるものは、a である。
したがって、和のとり得る値は、 a 、a+1 、a+2 、・・・ 、a+123 の124通りあ
る。(これが、鳩ノ巣) 以下は例題8の(解)と同じ。 (終)
例題8’では、例題8の「19」を「23」に変えましたが、まだまだ甘い結果で、もっと大きな数
で成り立ちそうです。ただ鳩の巣原理で証明できるのは、このあたりが限度かなと思います。
「43」で成り立つらしいですが、簡単には証明できないと思われます。はっきり書いてはない
のですが、「44」では反例があるのかなと思います。例題8の証明を参考に多少表現を変え
ます。(平成23年1月22日付け)
例題8” 44以下の自然数7個をうまく選んで次の条件をみたすようにせよ。
7個の中から何個かを取りだして作った和はすべて異なる。
7個はかなり多いので、もう少し小さい数の場合から考えた方がよさそうです。そのために
問題を一般化した形で書きます。
例題8^ k以下の自然数n個をうまく選んで次の条件をみたすようにせよ。
n個の中から何個かを取りだして作った和はすべて異なる。
自然数 n が与えられたとき、これが可能であるような最小の k を求めよ。
条件をみたすようなn個の集合をAと書くことにします。
n=1 のとき、 k=1 で、 A={1}
n=2 のとき、 k=2 で、 A={1,2}
n=3 のとき、 k=4 で、 A={1,2,4} ・・・・・ここまでは問題ないでしょう。
n=4 のとき、 A={1,2,4,8} が条件を満たすのは確かですが、A={3,5,6,7}も
条件を満たすので、多分...k=7 → (確定)
n=5 のとき、 k=13 で、 A={6,9,11,12,13}は条件を満たす。最小性は不明。
n=6、7 ぐらいで最小であるかどうかは別にして、条件を満たすAを作って下さい。
A={1,2,4,8,16,・・・}が条件を満たすのは明らかなので、n=6、7の場合で、32、
64以下ですが、n=7の場合で、44まで下がるとすれば、n=6の場合でも、32よりかなり
小さい数かなと思います。
FNさんからの続報です。(平成23年1月23日付け)
例題8’について、「23」を「25」に変えても鳩の巣原理を使ったきれいな証明がありました。
「26」でもできますが、少し汚くなるので、「25」にしておきます。
例題8’A 25以下の自然数から7個の数を任意に選ぶ。この7個の数からいくつかの相異
なる数の組を2組選んでその和を等しくすることができる。
FNさんからの続報です。(平成23年1月25日付け)
例題8’Aをやや強めた結果を証明する。少しだけだが強い結果である。
この7個の数から4個以下の相異なる数の組を2組選んでその和を等しくすることができる。
強い結果のほうが証明しやすいのは不思議であるが、もともと相当弱い結果なので、少々
強めても楽に成り立ち鳩ノ巣原理ではこちらの方が示しやすいようである。
(証明) 7個の数の中から、4個以下の相異なる数を選んで組を作るとき、その作り方は、
7C1+7C2+7C3+7C4=7+21+35+35=98通りある。(これが鳩)
この中で、和が最大となるのは、 25+24+23+22=94
最小となるのは、 1
従って、和の取りうる値は、 1、2、・・・、94 で、94通り。(これが鳩の巣)
以下は例題8の(解)と同じ。 (証終)
25を26に変えると、最大が 26+25+24+23=98 となり、鳩と鳩の巣が同数とな
る。だから、ただちに結論を出せないが、1から98まですべての値をとることになり、和が
98になるものがあることから、26、25、24、23 を含まなければならない。
そうすると、 26+23=25+24。
26まで証明できたが、43で成り立つらしいから、まだまだ弱い結果である。もう少し細か
い議論をすれば、27や28とかはできるかもしれないが、43までいけるとは思えない。別の
考え方が必要でしょう。
攻略法さんが、例題8^について調べられた。(平成23年1月23日付け)
n=1 のとき、 A={1} よって、 k=1
n=2 のとき、 A={1,2} よって、 k=2
n=3 のとき、 A={1,2,4} または A={2,3,4} よって、 k=4
n=4 のとき、 A={1,2,4,8} または A={3,5,6,7} よって、 k=7
n=5 のとき、 A={3,6,11,12,13} または A={6,9,11,12,13}
または A={1,2,4,8,16} よって、 k=13
n=6 のとき、 A={1,2,4,8,16,32} または A={11,17,20,22,23,24}
よって、 k=24
n=7 のとき、
A={1,2,4,8,16,32,64} 、・・・、A={20,31,37,40,42,43,44}
よって、 k=44
FNさんからのコメントです。(平成23年1月23日付け)
1、2、4、7、13、24、44、・・・ を、オンライン整数列大辞典で検索しました。
Fibonacci数列の親戚のTribonacci数列というそうです。n=1からn=7まであってい
ます。これは偶然でしょうか、それとも必然でしょうか。
※Tribonacci 数列
0,0,1,1,2,4,7,13,24,44,81,149,274,・・・・
のように、前の3項の和として新しい項が定義される数列である。
すなわち、数列{an}がTribonacci数列とは、漸化式
a0=0、a1=0、a2=1、 an+3=an+an+1+an+2 (n=0,1,2,3,・・・)
で定義される数列を言う。
FNさんからの続報です。(平成23年1月24日付け)
攻略法さんの n≦7 の範囲での結果によると、k が Tribonacci数列(ただし、初期値を
t1=1、t2=2、t3=4 としたもの)になっていますが、それだけではなくて、それを実現する
Aも Tribonacci 数列から得られるものになっています。
例えば、n=7 のときの 20, 31, 37, 40, 42, 43, 44
において、最後の数から他の
数を引くと、 1, 2, 4, 7, 13, 24 となり、 tribonacci
数列です。
すべて、この形になっています。ただし、2つあるときはその一方がそうです。
即ち、 tn,
tn−t1, tn−t2,・・・,
tn−tn-1 の形です。
こうなると、偶然であるよりは必然である方がありそうなものですが、これが条件を満たす
ことはとても言えそうな気はしません。さらに条件を満たす中で最小であることも言う必要が
あります。
Aを、 a1,
a2, ・・・, an とすると、条件は、ct
が 0、1、−1 のいずれかとして、
Σct・at=0 が、すべての ct
が0のとき以外成り立たない
ことになります。あるいは、両辺に、Σat を加えて、ct+1 を改めて
ct
とおいて、
Σct・at=Σat (ただし、ct=0、1、2) がすべての
ct が 1 のとき以外成り立たない
と言ってもいいです。
3つの項の和が次の項になるという Tribonacci の性質が、なぜこの問題に絡む可能性
があるのか全くわかりません。
例題8^ k以下の自然数n個をうまく選んで次の条件をみたすようにせよ。
n個の中から何個かを取りだして作った和はすべて異なる
自然数 n が与えられたとき、これが可能であるような最小の k を求めよ。
(→ 参考:「異なる部分和の構成」)
について、攻略法さんが考察された。(平成23年1月25日付け)
2進法で、連続する自然数を重複することなく表現できるので、A={1,2,4,8,・・・}は
題意を満たす。
Fibonacci数列やTribonacci数列のような前 p 項の和で生成される数列を使って、その
右端A(n)を小さくできる。
n=7までは確認して、n=8を検証中。9以上は未確認...。
前2項の和( 1 2 … ) 第2項までは2のべき乗のFibonacci数列
| n=2 |
|
n=3 |
|
n=4 |
1 2
└ 1 ┘差 |
|
2 3 4
└ 1 ┘差
└ 2 ─┘ |
|
2 3 4 5
└ 1 ┘差
└ 2 ─┘
└ 3 ──┘ |
2+3=5、2+5=3+4 で題意を満たさない。
したがって、表現できるのは、n=3までとなる。
前3項の和( 1 2 4 7 13 24 44 …) 第3項までは2のべき乗のTribonacci数列
| n=4 |
|
n=5 |
3 5 6 7
└ 1 ┘差
└ 2 ─┘
└ 4 ──┘ |
|
6 9 11 12 13
└ 1 ┘差
└ 2 ─┘
└ 4 ───┘
└ 7 ─────┘ |
n=6 → 11 17 20 22 23 24
n=7 → 20 31 37 40 42 43 44
n=8 → 40 60 71 77 80 82 83 84
FNさんからのコメントです。(平成23年1月25日付け)
上記の計算から、n=7まではTribonacciでいけたけど、n=8になると無理ということで
すね。Tetranacciとかが役に立ったりするのかもしれません。Tribonacciでいければ面白
いけどなと思いましたが、やはりそんなに甘い話はなさそうですね。
攻略法さんの考察の続きです。
前4項の和(1 2 4 7 14 27 52 100 … ) 同様
n=5 → 6 9 11 12 13
n=6 → 11 18 21 23 24 25
n=7 → 21 34 41 44 46 47 48
n=8 → 44 69 82 89 92 94 95 96
n=9 → 89 137 162 175 182 185 187 188 189
前4項の和( 1 2 4 8 15 29 56 108 208 … ) 同様
n=5 → 6 10 12 13 14
n=6 → 12 19 23 25 26 27
n=7 → 23 37 44 48 50 51 52
n=8 → 44 71 85 92 96 98 99 100
n=9 → 92 144 171 185 192 196 198 199 200
n=10 → 185 285 337 364 378 385 389 391 392 393
前5項の和( 1 2 4 8 16 31 61 120 236 464 … ) 同様
n=11 → 356 584 700 759 789 804 812 816 818 819 820
攻略法さんの考察の続きです。(平成23年1月27日付け)
一日越しの結果になりました。
n=8 → 40 60 71 77 80 82 83 84
39 59 70 77 78 79 81 84
20 40 71 77 80 82 83 84
n=7 のとき、「20 31 37 40 42 43 44」で、
n=8 のとき、「40 60 71 77 80 82 83 84」ですから、場合の数による方
法だと、上限が44、84から大雑把で447、848回の検証になります。n=7 でもかなり厳し
いものになります。
隣接 p 項の和の数列を使って、A(n)=2n-1 を小さくする方法で当たりをつけるのがよい
と思います。n≦8 では、最小になっています。
FNさんからのコメントです。(平成23年1月27日付け)
有難うございました。とても難しそうです。n=5 のとき、k=13 ぐらいは証明できないか
と思ったのですが、なかなかできません。とりあえず、しばらく寝かせるしかなさそうです。
この問題について、らすかるさんからの情報です。(平成23年1月28日付け)
オンライン整数列大辞典のこちらに、Conway-Guy sequenceと言われる漸化式
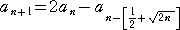
があるようで、証明もされているようです。具体例は、こちらにあるそうです。
らすかるさんによれば、続きは、次のような感じになるとのことです。
n=16 のとき
{8498,12821,15021,16141,16711,16996,17144,17221,17261,17281,17292,17298,
17301,17303,17304,17305}
n=17 のとき
{16996,25494,29817,32017,33137,33707,33992,34140,34217,34257,34277,34288,
34294,34297,34299,34300,34301}
n=18 のとき
{33707,50703,59201,63524,65724,66844,67414,67699,67847,67924,67964,67984,
67995,68001,68004,68006,68007,68008}
n=19 のとき
{66844,100551,117547,126045,130368,132568,133688,134258,134543,134691,
134768,134808,134828,134839,134845,134848,134850,134851,134852}
n=20 のとき
{132568,199412,233119,250115,258613,262936,265136,266256,266826,267111,
267259,267336,267376,267396,267407,267413,267416,267418,267419,267420}
FNさんからのコメントです。(平成23年1月28日付け)
やはり解けていましたか。きれいな問題設定だから、解けていて不思議はないですね。一
般の場合の解答は多分理解できないでしょうが、せめてn=5ぐらいだけでも証明を理解で
きないか、検索して調べてみます。有難うございました。
(追記) 平成23年2月1日付け
例題8に関連して、鳩ノ巣原理とは関係ないが、次のような入試問題に興味を持った。
慶應義塾大学 理工学部(1991) (穴埋め式なので、記述式に改題)
1から2nまでの2n個の整数がある。ただし、nは3以上の整数とする。次の2つの
性質(A)、(B)をもつ4つの整数 a、b、c、d をこの2n個の整数から選ぶ選び方は
何通りあるかを求めたい。次の問いに答えよ。
(A) 1≦a<b<c<d≦2n (B) a+d=b+c
(1) このような選び方が可能であるような a、b の値を固定したとき、2つの整数
c、d の選び方は何通りあるか。
(2) a の値だけを固定したとき、3つの整数 b、c、d の選び方は何通りあるか。
(3) (1)(2)を用いて、求める選び方は何通りあるか。
(答え) (1) 2n−2b−a (通り)
(2) a=2k−1 (kは整数で、1≦k≦n−1) のとき、 (n−k)2 (通り)
a=2k (kは整数で、1≦k≦n−2) のとき、(n−k−1)(n−k) (通り)
(3) n(n−1)(4n−5)/6 (通り)
(解)(1) a、b
を固定するとき、 0≦a<b<c<d≦2n 、 d=b+c−a
c=b+1 のとき、 d=2b−a+1
c=b+2 のとき、 d=2b−a+2
・・・・・・・・・・・・・・・・・・
d=2n となるまで続く。
よって、c、d
の取り得る場合の数は、2n−(2b−a+1)+1=2n−2b+a (通り)
(2) (1)より、 2b−a+1≦2n なので、 2b≦a+2n−1
a=2k(kは整数で、k≧1)のとき、 2b≦a+2n−1=2k+2n−1
b≧2k+1 なので、 2k+1≦b≦k+n−1 より、bの取り得る値は、
(k+n−1)−(2k+1)+1=n−k−1 (通り)
よって、b、c、d
の取り得る場合の数は、
(2n+2k)(n−k−1)−2{(2k+1)+(k+n−1)}(n−k−1)/2
=(n−k−1)(2n+2k−3k−n)
=(n−k−1)(n−k) (通り)
a=2k−1(kは整数で、k≧1)のとき、 2b≦a+2n−1=2k+2n−2
b≧2k なので、 2k≦b≦k+n−1 より、bの取り得る値は、
(k+n−1)−2k+1=n−k (通り)
よって、b、c、d
の取り得る場合の数は、
(2n+2k−1)(n−k)−2{2k+(k+n−1)}(n−k)/2
=(n−k)(2n+2k−3k−n)
=(n−k)2 (通り)
(3) a=2k(kは整数で、k≧1)のとき、 2k+1≦b≦k+n−1 なので、
k=1、2、・・・、n−1
このときの取り得る場合の数は、
Σ(n−k−1)(n−k)
=n(n−1)・(n−1)−(2n−1)・n(n−1)/2+n(n−1)(2n−1)/6
=n(n−1)(6n−6−6n+3+2n−1)/6
=n(n−1)(n−2)/3
a=2k−1(kは整数で、k≧1)のとき、 2k≦b≦k+n−1 なので、
k=1、2、・・・、n−1
このときの取り得る場合の数は、
Σ(n−k)2
=n2・(n−1)−2n・n(n−1)/2+n(n−1)(2n−1)/6
=n(n−1)(6n−6n+2n−1)/6
=n(n−1)(2n−1)/6
よって、求める場合の数は、
n(n−1)(n−2)/3+n(n−1)(2n−1)/6
=n(n−1)(4n−5)/6 (終)
例題9 どんな自然数 N に対しても、フィボナッチ数列は、 0 以外の mod N 周期 p を
持つ。
(解) 解答は、こちらを参照のこと。
例題10 平面上の点( x , y )で、x , y がともに整数であるとき、格子点といわれる。
いま、平面上の相異なる5個の格子点から2個の格子点を選んでできる線分の
中点を考える。このときできる中点のうち少なくとも一つは格子点になるものが
ある。
(解) 格子点のタイプは、
(偶数,偶数)、(偶数,奇数)、(奇数,偶数)、(奇数,奇数)
の4通りある。(これが、鳩ノ巣)
いま、格子点が5個ある(これが、鳩)ので、鳩ノ巣原理により、少なくとも2つ同じ
タイプの格子点が存在する。それらを結ぶ線分の中点が格子点となる。(終)
例題11 1 から 100 までの100個の整数がある。この中から、 55個の整数をどのよ
うに選んでも必ず、その 55 個の中に、2つの相異なる数で、差が、9 となるもの
が存在する。
(解) 任意に選んだ55個の整数を、 1≦a1<a2<・・・<a54<a55≦100 とする。
これらの全てに9を加えて、10≦a1+9<a2+9<・・・<a54+9<a55+9≦109
このとき、 a1、a1+9、・・・、a55、a55+9 と110個の整数がある(これが、鳩)。
ところが、これらは、1 から 109 までの109個の整数である(これが、鳩ノ巣)。
したがって、鳩ノ巣原理により、am=an+9 となる2数 am、an が存在する。
この2数の差が9となる。(終)
FNさんが、この問題を一般化された。(平成23年1月15日付け)
例題11’ 1から n までの n 個の整数がある。この中から k 個の整数をどのように選ん
でも必ず、その k 個の中に、2つの相異なる数で、差が、m となるものが存在す
る。自然数 n、m が与えられたとき、この命題が成り立つような自然数 k の最小
値を求めよ。
(解) 任意に選んだ k 個の整数を、 1≦a1<a2<・・・<ak≦n とする。
これらの全てに m を加えて、m+1≦a1+m<a2+m<・・・<ak+m≦n+m
このとき、 a1、a1+m、・・・、ak、ak+m と 2k 個の整数がある(これが、鳩)。
条件を満たすために、これらは、1 から n+m までの n+m個の整数(これが、鳩
ノ巣)で、 n+m+1=2k
したがって、求める最小値は、 k=(n+m+1)/2 (終)
FNさんからのコメントです。(平成23年1月17日付け)
出題したときに、「大体できているのもありますが」と書いたのはこれのつもりで、考えてた
答えは、[(n+m+1)/2]です。ただ、このときに成り立つのは間違いないですが、それより
小さいときに成り立たないことを示そうとしてできないことに気づきました。
n=100、m=9 のときは、たまたまこれが最小値であったのですが、一般には最小値
ではありません。
例えば、n=100
を、101から108までの数に変えて、mは9のままのとき、kは55のま
まです。まず、例題11の n=100 を n=105
とかに変えたものを証明して、それから一
般化を考えた方がいいと思います。
HN「ケンスー」さんが、この問題の解答を寄せられた。(平成23年1月17日付け)
n=am+b (a∈N、0≦b≦m−1) と表されるとき、k
の最小値は、
([a/2]+1)b+[(a+1)/2](m−b)+1
と表される。ただし、[x]はガウス記号で、x
を超えない最大の整数を表す。
例 n=100、m=9 のとき、 a=11 、 b=1
このとき、 ([a/2]+1)b+[(a+1)/2](m−b)+1=(5+1)・1+6・(9−1)+1
=6+48+1=55
よって、 k=55 である。
例 n=105、m=9 のとき、 a=11 、 b=6
このとき、 ([a/2]+1)b+[(a+1)/2](m−b)+1=(5+1)・6+6・(9−6)+1
=36+18+1=55
よって、 k=55 である。
(コメント) n=100 から多少増えても、k=55のままなんですね!不思議です。
攻略法さんが、私のコメントに対し、反例となる豆をまいて鳩を集められました。
(平成23年1月20日付け)
n が大きいと、nCk が天文学的数値になるということで、小さい値での調査とのことです。
<結果> 反例となる k 個の数(その1つ)
+1 +2 +3 +4 … +(m-1) +m
0m: 1 2 3 4 … m-1 m
2m: 2m+1 2m+2 2m+3 2m+4 … 2m+(m-1) 2m+m
4m: 4m+1 4m+2 4m+3 4m+4 … 4m+(m-1) 4m+m
6m: 6m+1 6m+2 6m+3 6m+4 … 6m+(m-1) 6m+m
:
:
最後は
(2p)m: (2p)m+1 (2p)m+2 … n pは0以上の整数
または
(2p)m: (2p)m+1 (2p)m+2 (2p)m+3 (2p)m+4 … (2p)m+(m-1) (2p)m+m
(2p+1)m: (2p+1)m+1 (2p+1)m+2 … n
Excel VBA サンプル
Sub Test11()
Let N = 20 '自然数n
Let M = 3 '1≦m<n
Debug.Print "n="; N; "m="; M
Let Q = Int(N / M) 'nをmで割ったときの商をq、余りをrとする。n=q*m+r(p∈N,0≦r<m)
Let R = N - Q * M
Debug.Print "k="; (Int(Q / 2) + 1) * R + Int((Q + 1) / 2) * (M - R) + 1
Dim A(50)
For k = 2 To N '2≦k≦n
Debug.Print "k="; k
For i = 1 To k 'k個の数A1,A2,…,Ak(nCk通り)を列挙する
Let A(i) = i
Next i
Do
For i = 1 To k - 1 'AiとAjが題意を満たすか
For j = i + 1 To k
If A(j) - A(i) = M Then Exit For 'Aj-Ai=m(Ai<Aj)なら
Next j
If j <= k Then Exit For '1つでも見つかればよい
Next i
If i > k - 1 Then '見つからなければ、反例となる
For j = 1 To k 'k個の数を表示する
Debug.Print A(j);
Next j
Debug.Print
Exit Do '1つのみ!!! ※ここをコメントアウトするとすべて表示する
End If
Loop While NextComb(A, N, k) = 1 '次へ
Debug.Print
Next k
End Sub
Function NextComb(ByRef A(), ByVal N, ByVal R) '辞書式順序で次の組合せを返す
Let NextComb = 0 '完了
For i = R To 1 Step -1
If A(i) < N - R + i Then 'i〜N-R+iで更新する
Let A(i) = A(i) + 1
For j = i + 1 To R 'A(i)<A(i+1)< … <A(R) 最初の並び
Let A(j) = A(j - 1) + 1
Next j
Let NextComb = 1 '未了
Exit Function
End If
Next i
End Function
ケンスーさんの解答に対して、FNさんからのコメントです。(平成23年1月17日付け)
n、m
に対して、k
が確定すれば十分です。ただし、その数以上であれば成り立つことと、
その数未満であれば成り立たないことの証明をしてください。私が得た式と見かけは異なり
ますがどうやら同じ式のようです。
例題11’について、FNさんの考察です。(平成23年1月24日付け)
n を2mで割った商がqで余りがrであるとき、
k=qm+min(m,r)+1 である。
○ k≧qm+min(m,r)+1 のとき成り立つこと
n=2mq+r (0≦r<2m)である。1からnまでのn個の整数を、次のようにグループに
分ける。
1〜2m、2m+1〜4m、4m+1〜6m、・・・、2m(q−1)+1〜2mq、2mq+1〜2mq+r
(ただし、r=0 のとき、最後のグループはない)
各グループは、連続した2m個(ただし、最後のグループは、r個)からなる。選ばれたk個の
整数がどのグループに属するかを考える。
どのグループもm個以下(最後のグループは、min(m,r)以下)とすると、
k≦qm+min(m,r)
となって仮定に反するから、どれかのグループに、m+1個入っている。
mで割った余りは、m通りしかないから、このうちに余りの等しいものがある。
その差は、mの倍数であるが、2m以上である可能性はないから、mである。
○ k≦qm+min(m,r) のとき成り立たないこと
1〜m、2m+1〜3m、4m+1〜5m、・・・、
2m(q−1)+1〜2m(q−1)、2mq+1〜2mq+min(m,r)
が条件を満たさないのは明らかであり、その部分集合も条件を満たさない。
○ ケンスーさんの結果と一致すること
n=2mq+r で、r<m のときは、 a=2q 、b=r で、
[a/2]=q 、 [(a+1)/2]=q
だから、 ([a/2]+1)b+[(a+1)/2](m−b)+1=(q+1)r+q(m−r)+1
=mq+r+1=mq+min(m,r)+1
r≧m のときは、n=2mq+r=(2q+1)m+(m−r) で、a=2q+1、b=m−r より、
[a/2]=q 、 [(a+1)/2]=q+1
だから、 ([a/2]+1)b+[(a+1)/2](m−b)+1=(q+1)(m−r)+(q+1)r+1
=(q+1)m+1
=mq+m+1
=mq+min(m,r)+1
FNさんが上記で述べられた新しい問題です。(平成23年1月18日付け)
例題11A 1から105までの105個の整数がある。この中から55個の整数をどのよう
に選んでもその55個の中にその差が9となる2つの数が必ず存在する。
例題11と同じ証明ではできません。もう少し細かい議論が必要です。
(解) 1から105までの整数を、次の6つのグループに分ける。
1〜18 、19〜36 、 37〜54 、 55〜72 、 73〜90 、 91〜105
選んだ55個が上のグループに何個入るかを考える。
すべてのグループに9個以下しか入らないとすると、6×9=54個以下であるから少なく
とも1つのグループに10個以上入ることになる。
連続した18個(またはそれ以下)の数の中に、10個の数が入っていることになる。
9で割った余りは9通りしかないので、9で割った余りが等しい2つの数がある。
その差は9の倍数であるが、18以上にはなりえないから9である。 (終)
後半は鳩ノ巣原理そのものですが、前半もその一種なので鳩ノ巣原理を2回使ったという
感じです。55が最善であること、即ち、54であれば成り立たないことは、
1〜9 、19〜27 、 37〜45 、 55〜63 、 73〜81 、 91〜99
の54個が反例になることからわかります。また、105を99から108までの数に変えてもそ
のまま成り立ちます。この証明と同様にすれば、例題11’もできます。
例題12 1 から 4 までの自然数からいくつか選んで作った7個の集合 A1、A2、・・・、A7
がすべて異なるとき、Am⊂An となる Am 、 An が存在する。
(解) 集合 { 1 , 2 , 3 , 4 } の部分集合は全部で、24=16個ある。
それらを列挙すると、、
φ、{ 1 }、{ 2 }、{ 3 }、{ 4 }、{ 1 , 2 }、{
1 , 3 }、{ 1 , 4 }、{ 2 , 3 }、
{ 2 , 4 }、{ 3 , 4 }、{ 1 , 2 , 3 }、{ 1
, 2 , 4 }、{ 1 , 3 , 4 }、
{ 2 , 3 , 4 }、{ 1 , 2 , 3 , 4 }
これらを、どの2つも包含関係を持つように分類すると、
B1 : φ⊂{ 1 }⊂{ 1 , 2 }⊂{ 1 , 2 , 3 }
B2 : { 2 }⊂{ 2 , 3 }
B3 : { 3 }⊂{ 1 , 3 }⊂{ 1 , 3 , 4 }
B4 : { 2 , 4 }⊂{ 2 , 3 , 4 }
B5 : { 4 }⊂{ 1 , 4 }⊂{ 1 , 2 , 4 }
B6 : { 3 , 4 }⊂{ 1 , 2 , 3 , 4 }
の6個(これが、鳩ノ巣)に分けられる。(分類の組合せは他にもある!)
これに対して、7個の集合 A1、A2、・・・、A7 がある(これが、鳩)ので、ある Bk に
少なくとも2つ Am 、 An が含まれ、Am⊂An が成り立つ。(終)
FNさんが、この問題を一般化された。(平成23年1月15日付け)
例題12’ 1から n までの自然数からいくつか選んで作った k 個の集合 A1、A2、・・・、Ak
がすべて異なるとき、Am⊂An となる Am 、 An が存在する。
自然数 n が与えられたとき、この命題が成り立つような自然数
k の最小値を
求めよ。
これについて、一般の n だと雲を掴むような話のような...雰囲気なので、n=5
として
実験してみた。
集合 { 1 , 2 , 3 , 4, 5 } の部分集合は全部で、25=32個ある。
それらを列挙すると、、
φ、{ 1 }、{ 2 }、{ 3 }、{ 4 }、{ 5 }、{ 1 , 2 }、{
1 , 3 }、{ 1 , 4 }、{ 1 , 5 }、
{ 2 , 3 }、{ 2 , 4 }、{ 2 , 5 }、{ 3 , 4 }、{ 3
, 5 }、{ 4 , 5 }、{ 1 , 2 , 3 }、
{ 1 , 2 , 4 }、{ 1 , 2 , 5 }、{ 1 , 3 , 4 }、{
1 , 3 , 5 }、{ 1 , 4 , 5 }、
{ 2 , 3 , 4 }、{ 2 , 3 , 5 }、{ 2 , 4 , 5 }、{
3 , 4 , 5 }、{ 1 , 2 , 3 , 4 }、
{ 1 , 2 , 3 , 5 }、{ 1 , 2 , 4 , 5 }、{ 1 , 3 ,
4 , 5 }、{ 2 , 3 , 4 , 5 }、
{ 1 , 2 , 3 , 4, 5 }
これらを、どの2つも包含関係を持つように分類すると、
B1 : φ⊂{ 1 }⊂{ 1 , 2 }⊂{ 1 , 2 , 3 }⊂{ 1 , 2 ,
3 , 4 }
B2 : { 2 }⊂{ 2 , 3 }⊂{ 2 , 3 , 4 }⊂{ 2 , 3 , 4
, 5 }
B3 : { 3 }⊂{ 3 , 4 }⊂{ 3 , 4 , 5 }
B4 : { 4 }⊂{ 4 , 5 }⊂{ 2 , 4 , 5 }
B5 : { 5 }⊂{ 2 , 5 }⊂{ 1 , 2 , 5 }
B6 : { 1 , 3 }⊂{ 1 , 3 , 4 }⊂{ 1 , 3 , 4 , 5 }
B7 : { 1 , 4 }⊂{ 1 , 4 , 5 }
B8 : { 1 , 5 }⊂{ 1 , 3 , 5 }⊂{ 1 , 2 , 3 , 5 }⊂{
1 , 2 , 3 , 4, 5 }
B9 : { 2 , 4 }⊂{ 1 , 2 , 4 }⊂{ 1 , 2 , 4 , 5 }
B10 : { 3 , 5 }⊂{ 2 , 3 , 5 }
の10個(これが、鳩ノ巣)に分けられる。(分類の組合せは他にもある!)
したがって、鳩ノ巣原理を用いて、ある Bk に少なくとも2つ Am 、 An が含まれ、Am⊂An
が成り立つようにするためには、最低11個の集合 A1、A2、・・・、A11 (これが、鳩)があれ
ばよい。
よって、 n=5 のとき、 k=11 である。
n=4 のとき、 k=7 であるわけだが、これらに規則性はあるのだろうか?
FNさんからのコメントです。(平成23年1月17日付け)
「n=4のときの鳩の巣は6個、n=5のときの鳩の巣は10個」において、
「6」は、4C2=6 で、「10」は、5C2=5C3=10
です。一般に、n に対して、nCr のうち最大のもの、即ち、
r=[n/2] のときの
nCr が鳩の巣の個数になると予想されます。
要素の個数が r 個である部分集合同士の間に包含関係はないので、鳩の巣の個数は
nCr 以上です。あとは、実際に、 nCr 個の鳩の巣があることを示せば十分です。これをど
うやって証明するかですが、2部グラフに関するホールの結婚定理というのを使えばできそ
うです。もっと簡単にできるかどうかわかりません。
この問題について、HN「at」さんが、解答を寄せられた。(平成23年1月17日付け)
シュペルナー族の最大サイズは、 nC[n/2]
です。したがって、
互いに異なる k 個の部分集合
A1、A2、・・・、Ak
をどのように選び出しても必ず
As⊂At となる
As、At が存在するような k の最小値は、
nC[n/2]+1
ですね。
FNさんからのコメントです。(平成23年1月17日付け)
グラフ理論を持ちださないで証明できるのは十分ありうることだと思っていました。ただ、私
は、Sperner's
theorem はもちろん、その証明で使われている LYM inequality
も知りません。
ホールの結婚定理は知っていますが、ホールの結婚定理を使った証明と LYM
inequality
を使った証明とどちらがわかりやすいかはわかりません。
さらに、FNさんからの続報です。(平成23年1月18日付け)
Sperner's theorem というのは、まさに、(2)に対する答えそのものでした。鳩ノ巣原理を使
った証明にはなりませんが、ホールの結婚定理を使って鳩ノ巣原理に持ち込むより簡単な
証明になるようです。
Sperner's
theorem n 個の要素を持つ集合Uの部分集合の族
A1、A2、・・・、Ak
がどの2つを取っても包含関係がないとき、 k≦nCm である。
ただし、m=[n/2] とする。
例題12’は、「ある2つについて包含関係がある」と言っているので、 k≧nCm+1 となり
ます。
証明は、最大鎖(maximal
chain)の数を、2通りで数えるというものです。
鎖(chain)とは、Uの部分集合の列
B1⊂B2⊂B3⊂・・・⊂Br
をいう。ただし、⊂は真部分集
合の意味で使う。最大鎖とは、これ以上延ばせない鎖をいう。
最大鎖は、B0=φ
で、B1は1個の要素を持ち、B2は2個の要素を持ち、・・・、Bn=U であ
るようなものである。
最大鎖は、n!個ある。
実際に、1個の要素(例えば、a)を持つ部分集合の選び方は、n
通り
a を含み、2個の要素を持つ部分集合の選び方は、n−1
通り
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
以上から、 n(n−1)・・・2・1=n!(個)である。
A⊂Uで、Aの要素の数が r であれば、Aを含む最大鎖の数は、r!(n−r)!である。
実際に、要素の個数が r の部分集合の選び方は、nCr 通りで、その1通りに対して、その
部分集合を含む最大鎖の数を N とすると、 nCr×N=n! が成り立つ。
よって、 N=n!÷nCr=r!(n−r)! となる。
AとBの間に包含関係がないなら、Aを含む最大鎖とBを含む最大鎖は必ず異なる。
以上のことから次の補題が成り立つ。
補 題 Sperner's theoremと同じ仮定のもとで、A1、A2、・・・、Ak のうちで要素の
個数が r であるものの個数を s(r)
とすると、
Σs(r)/nCr≦1 (ただし、Σは、r=1 から n
までの和)
(証明) Amの要素の個数が r
だとすると、Amを含む最大鎖は、r!(n−r)!個ある。この
ようなAmが
s(r)個あるから、その和は、s(r)・r!(n−r)!である。これを、r=1から
n まですべて加えたものが最大鎖すべての個数
n!以下だから、
Σs(r)・r!(n−r)!≦n!
両辺をn!で割って、 Σs(r)/nCr≦1 となる。 (証終)
(Sperner's theoremの証明) m=[n/2] とすると、 nCm≧nCr だから、
補題より、Σs(r)/nCm≦Σs(r)/nCr≦1
分母を払って、Σs(r)≦nCm Σs(r)=k だから、 k≦nCm (証終)
さらに、FNさんからの続報です。(平成23年1月19日付け)
例題12’は、Sperner の定理を証明することで、一応終わりですが、鳩ノ巣原理とは関係
がなくなってしまいます。もちろん、それでいいのですが、鳩ノ巣を作ること自体も面白そうで
す。
Sperner の定理の証明で、chain を鎖と書いたのですが、chain のままの方がよさそうなの
でそうします。鳩ノ巣を作るのは、次を示すことになります。
U={1,2,・・・,n} の部分集合の全体を共通要素を持たない nCm 個の chain の
和で表すことができる。ただし、m=[n/2]
この形では数学的帰納法による証明は無理ですが、より強くして、symmetric chain に
変えれば証明できます。
(帰納法による証明では、弱い結果は証明できないのに強い結果は証明できるということが
ときどきあります。帰納法の仮定がある程度強くないとうまくいかないということです。)
ここで、 chain : A1⊂A2⊂・・・⊂At において、
n(A1)+n(At)=n で、 n(As)+1=n(As+1)
が成り立つとき、symmetric chain という。ただし、n(X)は、集合Xの要素の個数。
例 n=4 のときの鳩ノ巣を、symmetric chain で作れば、
B1 : φ⊂{1}⊂{1,2}⊂{1,2,3}⊂{1,2,3,4}
B2 : {2}⊂{2,3}⊂{2,3,4}
B3 : {3}⊂{1,3}⊂{1,3,4}
B4 : {4}⊂{1,4}⊂{1,2,4}
B5 : {2,4}
B6 : {3,4}
定 理
U={1,2,・・・,n} の部分集合の全体を共通要素を持たない symmetric
chain の
和で表すことができる。
(証明) n に関する数学的帰納法による。
n=1 のときは、 φ⊂{1} で成り立つ。
n=m のとき、成り立つと仮定する。すなわち、U={1,2,・・・,m}
の部分集合全体が共
通要素を持たない symmetric chain B1、B2、・・・、Bkの和で表されるものとする。
このとき、V={0,1,2,・・・,m} について考える。
Bs が、 C1⊂C2⊂・・・⊂Ct だとして、Vにおける2つの chain B’s、B”s を次の様に
定める。
B’s : C1⊂C2⊂・・・⊂Ct⊂Ct∪{0}
B”s : C1∪{0}⊂C2∪{0}⊂・・・⊂Ct-1∪{0}
(ただし、B”sは、Bsの長さが2以上のときのみ)
B’s、B”s は、symmetric chain であり、これらの全体(s=1,2,・・・,k)は共通要素を持
たずすべてのVの部分集合を含む。
よって、n=m+1 のときも成り立ち、数学的帰納法により、定理は成り立つ。 (証終)
例 n=4 のときの symmetric chain から、n=5 のときの symmetric chain は、上の証
明に従って次のように作られる。
B1 : φ⊂{1}⊂{1,2}⊂{1,2,3}⊂{1,2,3,4}
→ B’1 : φ⊂{1}⊂{1,2}⊂{1,2,3}⊂{0,1,2,3,4}
→ B”1 : {0}⊂{0,1}⊂{0,1,2}⊂{0,1,2,3}
B2 : {2}⊂{2,3}⊂{2,3,4}
→ B’2 : {2}⊂{2,3}⊂{0,2,3,4}
→ B”2 : {0,2}⊂{0,2,3}
B3 : {3}⊂{1,3}⊂{1,3,4}
→ B’3 : {3}⊂{1,3}⊂{0,1,3,4}
→ B”3 : {0,3}⊂{0,1,3}
B4 : {4}⊂{1,4}⊂{1,2,4}
→ B’4 : {4}⊂{1,4}⊂{0,1,2,4}
→ B”4 : {0,4}⊂{0,1,4}
B5 : {2,4}
→ B’5 : {0,2,4}
B6 : {3,4}
→ B’6 : {0,3,4} (B”5 、B”6 はない。)
symmetric chain は、要素が、m=[n/2]個の部分集合を必ず含むので、 k≧nCm
また、Sperner's theorem より、k≦nCm なので、 k=nCm が成り立つ。
(コメント) n=4のときの鳩の巣は、4C2=6(個)、
n=5のときの鳩の巣は、5C2=10(個)
の合点がいきました。FNさんに感謝します。
攻略法さんが、反例となる豆をまいて鳩を集められました。(平成23年1月20日付け)
n が大きいと、nCk が天文学的数値になるということで、小さい値での調査とのことです。
2n個の部分集合 Sm (0≦m≦2n−1)とする。(mのビットパターンでSmは展開する)
k=nC[n/2] で命題を満たさない A1、A2、・・・、Ak の例は、
n が偶数なら、「要素の個数が[n/2]の Sm (個数は、nC[n/2] 個)」の1通り
n が奇数なら、「要素の個数が[n/2]の Sm 」と
「要素の個数が[n/2]+1の Sm (個数は、nC[n/2]+1個)」の2通り
例えば、n=2 の場合、部分集合は、22=4個
すなわち、 S0=φ 、S1={1} 、 S2={2} 、 S3={1,2}
このとき、求める組は、S1={1}、S2={2} の1通り
n=3 の場合、部分集合は、23=8個
すなわち、 S0=φ 、S1={1} 、 S2={2} 、 S3={1,2} 、
S4={3} 、S5={1,3} 、 S6={2,3} 、 S7={1,2,3}
このとき、求める組は、
S1={1}、S2={2}、S4={3}
および
S3={1,2}、S5={1,3}、S6={2,3} の2通り
n=4 の場合、部分集合は、24=16個
すなわち、
S0=φ 、S1={1} 、 S2={2} 、 S3={1,2} 、
S4={3} 、S5={1,3} 、 S6={2,3} 、 S7={1,2,3}、
S8={4} 、S9={1,4} 、 S10={2,4} 、 S11={1,2,4} 、
S12={3,4} 、S13={1,3,4} 、 S14={2,3,4} 、 S15={1,2,3,4}
このとき、求める組は、
S3={1,2}、S5={1,3}、S6={2,3}、
S9={1,4}、S10={2,4}、S12={3,4} の1通り
例題13 1 から 4 までの自然数からいくつか選んで作った9個の集合 A1、A2、・・・、A9
がすべて異なるとき、Am∩An=φ となる Am 、 An が存在する。
(解) 集合 { 1 , 2 , 3 , 4 } の部分集合は全部で、24=16個ある。
それらを列挙すると、、
φ、{ 1 }、{ 2 }、{ 3 }、{ 4 }、{ 1 , 2 }、{
1 , 3 }、{ 1 , 4 }、{ 2 , 3 }、
{ 2 , 4 }、{ 3 , 4 }、{ 1 , 2 , 3 }、{ 1
, 2 , 4 }、{ 1 , 3 , 4 }、
{ 2 , 3 , 4 }、{ 1 , 2 , 3 , 4 }
これらを、どの2つも共通部分がないように分類すると、
B1 : φ と { 1 , 2 , 3 , 4 }
B2 : { 1 } と { 2 , 3 , 4 }
B3 : { 2 } と { 1 , 3 , 4 }
B4 : { 3 } と { 1 , 2 , 4 }
B5 : { 4 } と { 1 , 2 , 3 }
B6 : { 1 , 2 } と { 3 , 4 }
B7 : { 1 , 3 } と { 2 , 4 }
B8 : { 1 , 4 } と { 2 , 3 }
の8個(これが、鳩ノ巣)に分けられる。
これに対して、9個の集合 A1、A2、・・・、A9 がある(これが、鳩)ので、ある Bk に
少なくとも2つ Am 、 An が含まれ、Am∩An=φ が成り立つ。(終)
FNさんが、この問題を一般化された。(平成23年1月15日付け)
例題13’ 1から n までの自然数からいくつか選んで作った k 個の集合 A1、A2、・・・、Ak
がすべて異なるとき、Am∩An=φ となる Am 、 An が存在する。
自然数 n が与えられたとき、この命題が成り立つような自然数
k の最小値を
求めよ。
これについて、一般の n だと雲を掴むような話のような...雰囲気なので、例題12’と
同様に、n=5 として実験してみた。
集合 { 1 , 2 , 3 , 4, 5 } の部分集合は全部で、25=32個ある。
それらを列挙すると、、
φ、{ 1 }、{ 2 }、{ 3 }、{ 4 }、{ 5 }、{ 1 , 2 }、{
1 , 3 }、{ 1 , 4 }、{ 1 , 5 }、
{ 2 , 3 }、{ 2 , 4 }、{ 2 , 5 }、{ 3 , 4 }、{ 3
, 5 }、{ 4 , 5 }、{ 1 , 2 , 3 }、
{ 1 , 2 , 4 }、{ 1 , 2 , 5 }、{ 1 , 3 , 4 }、{
1 , 3 , 5 }、{ 1 , 4 , 5 }、
{ 2 , 3 , 4 }、{ 2 , 3 , 5 }、{ 2 , 4 , 5 }、{
3 , 4 , 5 }、{ 1 , 2 , 3 , 4 }、
{ 1 , 2 , 3 , 5 }、{ 1 , 2 , 4 , 5 }、{ 1 , 3 ,
4 , 5 }、{ 2 , 3 , 4 , 5 }、
{ 1 , 2 , 3 , 4, 5 }
これらを、どの2つも共通部分がないように分類すると、
B1 : φ と { 1 , 2 , 3 , 4, 5 }
B2 : { 1 } と { 2 , 3 , 4 , 5 }
B3 : { 2 } と { 1 , 3 , 4 , 5 }
B4 : { 3 } と { 1 , 2 , 4 , 5 }
B5 : { 4 } と { 1 , 2 , 3 , 5 }
B6 : { 5 } と { 1 , 2 , 3 , 4 }
B7 : { 1 , 2 } と { 3 , 4 , 5 }
B8 : { 1 , 3 } と { 2 , 4 , 5 }
B9 : { 1 , 4 } と { 2 , 3 , 5 }
B10 : { 1 , 5 } と { 2 , 3 , 4 }
B11 : { 2 , 3 } と { 1 , 4 , 5 }
B12 : { 2 , 4 } と { 1 , 3 , 5 }
B13 : { 2 , 5 } と { 1 , 3 , 4 }
B14 : { 3 , 4 } と { 1 , 2 , 5 }
B15 : { 3 , 5 } と { 1 , 2 , 4 }
B16 : { 4 , 5 } と { 1 , 2 , 3 }
の16個(これが、鳩ノ巣)に分けられる。
したがって、鳩ノ巣原理を用いて、ある Bk に少なくとも2つ Am 、 An が含まれ、
Am∩An=φ が成り立つようにするためには、最低17個の集合 A1、A2、・・・、A17 (これ
が、鳩)があればよい。
よって、 n=5 のとき、 k=17 である。
n=4 のとき、 k=9 であるわけだが、次のような規則性があるような...予感。
任意に与えられた自然数 n に対して、命題が成り立つような自然数 k の最小値は、
k=2n-1+1
である。
FNさんからのコメントです。(平成23年1月17日付け)
これが一番簡単でしょう。2n-1個の鳩の巣があることを示すのは、例題12’のように難し
くないと思います。
FNさんからの補足です。(平成23年1月20日付け)
例題12’の解答の対偶的表現が、Sperner の定理ですが、例題13’の解答の対偶的表
現は次のようになります。
n 個の要素を持つ集合Uの部分集合の族 A1、A2、・・・、Ak がどの2つを取っても
共通部分が空集合でないとき、 k≦2n-1 である。
これは、Sperner の定理と違ってほとんど明らかです。
(証明) Aとその補集合A’は共通部分が空集合だから、どちらか一方しか部分集合の族
には入れない。従って、部分集合の個数は、2n の半分以下である。 (証終)
攻略法さんが、反例となる豆をまいて鳩を集められました。(平成23年1月20日付け)
n が大きいと、nCk が天文学的数値になるということで、小さい値での調査とのことです。
k=2n-1 で命題を満たさない A1、A2、・・・、Ak の例は、n によって個数は違うが、その
2例は、「 Sm が奇数列」または「 Sm が最後からk個」となる。
(ただし、mのビットパターンでSmは展開する)
n=2 の場合 S0=φ 、S1={1} 、 S2={2} 、 S3={1,2}
求める組は、 S1={1}、S3={1,2} および S2={2}、S3={1,2} の2通り
n=3 の場合 S0=φ 、S1={1} 、 S2={2} 、 S3={1,2} 、
S4={3} 、S5={1,3} 、 S6={2,3} 、 S7={1,2,3}
求める組は、 S1={1}、S3={1,2}、S5={1,3}、S7={1,2,3}
および、
S4={3}、S5={1,3}、S6={2,3}、S7={1,2,3}
その他、 S2、S3、S6、S7 および S3、S5、S6、S7
同様に、n=4 の場合
S1、S3、S5、S7、S9、S11、S13、S15 を、(1,3,5,7,9,11,13,15) と略記して、求める組は
(1,3,5,7,9,11,13,15) および (8,9,10,11,12,13,14,15)
その他、 (2,3,6,7,10,11,14,15)、(3,5,6,7,11,13,14,15)、(3,5,7,9,11,13,14,15)、
(3,6,7,10,11,13,14,15)、(3,7,9,10,11,13,14,15)、(4,5,6,7,12,13,14,15)、
(5,6,7,11,12,13,14,15)、(5,7,9,11,12,13,14,15)、(5,7,9,11,12,13,14,15)、
(6,7,10,11,12,13,14,15)、(7,9,10,11,12,13,14,15)
(コメント) 攻略法さん、具体的な例をたくさん計算していただいて感謝します。
例題14 1 から 4 までの自然数から2つを選んで作った4個の集合 A1、A2、A3、A4 が
すべて異なるとき、Am∩An=φ となる Am 、 An が存在する。
(解) 1 から 4 までの自然数から2つを選んで作った集合を列挙すると、、
{ 1 , 2 }、{ 1 , 3 }、{ 1 , 4 }、{ 2 , 3
}、{ 2 , 4 }、{ 3 , 4 }
の6個ある。これらを、どの2つも共通部分がないように分類すると、
B1 : { 1 , 2 } と { 3 , 4 }
B2 : { 1 , 3 } と { 2 , 4 }
B3 : { 1 , 4 } と { 2 , 3 }
の3個(これが、鳩ノ巣)に分けられる。
これに対して、4個の集合 A1、A2、A3、A4 がある(これが、鳩)ので、ある Bk に
少なくとも2つ Am 、 An が含まれ、Am∩An=φ が成り立つ。(終)
FNさんが、この問題の一般化を考えられた。(平成23年1月20日付け)
例題14の自然な一般化は、1から4までの4を2nに、2つをn個に、4個を2nCn/2+1個
に変えることで、これなら鳩ノ巣原理を使った証明がそのままできます。
ただし、2nCn/2=2n-1Cn-1 である。
もっと一般にすることを考えます。ただしそうなると鳩ノ巣原理は使えそうな気はしません。
鳩ノ巣原理が使えないとすると、対偶的表現の方が自然かなと思います。
例題14’ n 個の要素を持つ集合Uがある。k個からなるUの部分集合の族
A1、A2、・・・、Ak (すべて異なる)で、次の条件を満たすものが存在するとき、
k の最大値を求めよ。
(1) 任意の t について、At の要素の個数は、m
(2) 任意の s、t (s≠t)について、 As∩At≠φ
この問題は、「自然数 n、m が与えられたとき、k の最大値を求めよ」ということです。
2m>n であれば、(2)は常に成り立つので、m個の要素をもつ部分集合全体が条件を
満たし、nCm が答えになります。だから、2m≦n としておきます。
因みに、2m=n のときは、上に書いた自然な一般化の場合です。
m=1 のときは、当然、k=1 です。m=2、m=3 の場合はどうなるでしょうか?
FNさんの問いかけに対して、HN「at」さんが答えられた。(平成23年1月21日付け)
これは、Erdos-Ko-Rado Theorem で、k の最大値は、 n-1Cm-1 です。
FNさんからのコメントです。(平成23年1月21日付け)
やはり、綺麗な解答が既に得られているのですね。Erdos-Ko-Radoの論文が1961年だ
そうで、実際には、その二十年以上前に証明されていたそうですが、それにしても、かなり
新しい結果です。
Spernerの定理が1928年らしいので、これもかなり新しい結果です。もっとも、集合という
ようなものが研究対象となったこと自体が20世紀に入る前後なのかもしれませんが...。
上のWikipediaの証明を読んでみましたが理解できませんでした。Erdos-Ko-Radoの原論
文はもっと一般的な形の定理でこれも理解できません。他にもいろいろな証明があるようで
すが、できるだけ簡単な証明を知りたいです。
at さんが、「Erdos-Ko-Rado theorem の証明」を与えられた。(平成23年1月22日付け)
(証明) n個の整数 1、2、・・・、n の任意の順列 π=(a1、a2、・・・、an)を考える。
ある円周上の1点に赤い印をつけておき、この赤い印を出発点として、a1、a2、・・・、an
をこの順に円周上に反時計回りに書き込む。この円上で、隣り合うm個の数を m-ブロック
と呼ぶことにする。(m-ブロックは、全部で n 種類あることになる。)
あるひとつの m-ブロックに含まれるm個の数が、 A1、A2、・・・、Ak のどれかと一致する
とき、このm-ブロックを「良いm-ブロック」と呼ぶことにする。
さらに、任意の順列πに対して、良いm-ブロックの総数を N(π) で表すことにする。
このとき、任意の順列πに対して、N(π)≦m が成り立つ。
実際に、もし、N(π)>m とすると、共通点を持たないような2つの良いm-ブロック
が存
在することになる。しかし、これは、 As∩At≠φ という仮定に反する。
( 例: n=4 、m=2 とする。 U={1,2,3,4}の部分集合
A1={1,2}、A2={2,3}、A3={3,4}
順列 π=(3、1、2、4)に対して、良い2-ブロックとして、(1,2)、(4,3)の2つ
順列 π=(3、1、4、2)に対して、良い2-ブロックとして、(2,3)の1つ
この例からも、 N(π)≦m が納得される。 )
πがすべての順列を動くとき、良いm-ブロックが合計何回現れるのかをカウントする。
ある At に一致するような良いm-ブロックは、それが円周上のどの位置に出現するのか
を考えれば、n 通りの方法がある。さらに、このm-ブロックには、m個の数があるので、こ
のm個の数の順列を考えることにより、m!通りの方法がある。
さらに、このm-ブロックに含まれない数が n−m 個あるので、これらの数の順列を考え
ることにより、(n−m)!通りの方法がある。
以上より、πがすべての順列を動くとき、ある At に一致するような良いm-ブロックは、
n・m!・(n−m)!(回)
だけ出現する。
よって、πがすべての順列を動くとき、良いm-ブロックの出現総数は、
ΣN(π)=k・n・m!・(n−m)!(回) (Σは全ての順列
π にわたる)
となる。
ここで、 ΣN(π)≦m・n! なので、 k・n・m!・(n−m)!≦m・n!
したがって、 k≦n-1Cm-1 である。 (証終)
FNさんからのコメントです。(平成23年1月22日付け)
有難うございます。あちこち見てもわからなかったのが何とか理解できたと思います。日
本語と英語の違いもあり、今までにあちこち見てある程度状況に入れてたこともありますが
at さんの説明が良かったので理解できました。「N(π)≦m」に当たる部分が理解できず、
そこで思考停止を起こしていました。わかった後で見れば、N(π)≦m は明らかと言ってい
いぐらいでした。
例題15 タンスの中に3種類の靴下が1足ずつ入っている。このとき、手探りで、1足を
揃えるにはタンスから何本とればいいか?
(解) 4本とれば必ず1足はできる。
Kelly Burkhard さんからのコメントです。(平成30年8月11日付け)
同じ鳩ノ巣原理を使う問題でもバリエーションがあるのだなと思いました。何が違うのかは
まだ分かりやすく表現できていませんが...。例題15は純粋な鳩ノ巣原理だと感じました。
鳩ノ巣原理では「巣穴」の設定が重要で、別の巣穴に同じ「鳩」が入らないように、「巣穴」
に入れない「鳩」がいないように巣穴を設定しなければならないということに気づきました。
次の問題は鳩ノ巣原理の匂いが感じられないかもしれないが、立派な鳩ノ巣原理の問題
です。
例題16 3m×3mの土地に木を10本植える。このとき、どの2本も1.5m以上離して
植えることは可能だろうか。
(解) 9本だったら可能だが、10本では絶対不可能である。
実際に、3m×3mの土地を1m×1mの土地9区画(これが、鳩ノ巣)に分けるとき、
10本の木(これが、鳩)が植えられるとすると、必ず少なくとも2本は、ある一つの区
画内にある。その距離は、最大で =1.414・・・<1.5 なので条件に反する。
=1.414・・・<1.5 なので条件に反する。
例題17 1から20までの自然数の中から、互いに他で割り切れないように、10個の数を
選べ。また、11個では、そのような選び方は不可能であることを示せ。
(解) 1は全ての数の約数なので、選べない。2を選ぶと、選ばれる候補は、
3、5、7、9、11、13、15、17、19 の奇数 9個
この中で、3と9、3と15、5と15は条件に反するので、10個の数を選ぶことは不可能。
3を選ぶと、3の倍数の 6、9、12、15、18 は選べないので、
4、5、7、8、10、11、13、14、16、17、19、20 の12個から9個を選ぶわけであるが、
4、8、16、20 5、10、20 7、14
は一緒に選べないので、9個を選ぶことは不可能。
5を選ぶと、5の倍数 10、15、20 は選べないので、
6、7、8、9、11、12、13、14、16、17、18、19 の12個から9個を選ぶわけであるが、
6、12、18 7、14 8、16 9、18
は一緒に選べないので、9個を選ぶことは不可能。
6を選ぶと、6の倍数 12、18 は選べないので、
7、8、9、10、11、13、14、15、16、17、19、20 の12個から9個を選ぶわけである
が、6の代わりに12、7の代わりに14、8の代わりに16、9の代わりに18、10の代わりに
20を選ぶことにすれば、11、12、13、14、15、16、17、18、19、20 の10個の数が
条件を満たす。
実際に、この10個の数が条件を満たすことを検証してみよう。
この10個の中に互いに他で割り切れるような組 a、b(11≦a<b≦20)が存在したとする
と、bがaで割り切れるので、b=ka (kは自然数) と書ける。
このとき、k≧2 で、a≧11 より、 b≧22 となり、b≦20 であることに矛盾。
よって、この10個の中には互いに他で割り切れるような組 a、b は存在しない。
それでは、11個では、そのような選び方は不可能であることをどう示せばいいのでしょう。
それを示すために、鳩ノ巣原理が有効に活躍します。
1から20までの自然数の中から、互いに他で割り切れないような11個の数(これが、鳩)
が任意に選ばれたものとする。この数のうち、1〜10までの数を、2倍、2倍、・・・を繰り返
すことにより、11〜20の数(これが、鳩ノ巣)にすることができる。このとき、鳩ノ巣原理に
より、11〜20のある数Nについて、
N=x・2n=y・2m (ただし、x<y で、さらに、m、nは整数で、n>m)
となるものが存在する。このとき、y=x・2n−m と書くことができ、yがxで割り切れることを
示している。これは、矛盾である。
よって、互いに他で割り切れないような11個を選ぶことは、不可能である。 (終)
(コメント) 不可能性の証明は難しいと思いましたが、意外にあっさりで肩すかしを食らった
ような気分ですね!
上記の問題を一般化すると、
1から2n (n≧1)までの自然数の中から、互いに他で割り切れないように、n個の
数を選ぶことは可能であるが、11個では、そのような選び方は不可能である。
前半は、n、n+1、・・・、2n を選べばよい。後半は、上記と同様に示される。
DD++さんから、「オーレの定理」に関する話題をいただきました。
(平成29年7月11日付け)
例題18(鳩ノ巣原理について、面白いものを1つ。)
10個の島があり、それらの間にいくつかの橋がかかっています。簡単のため、同じ2島間
に複数の橋がかかっていることはないとしましょう。
(それを許しても、まとめて1本と数えればいいだけで大差ありませんが...。)
この10島について、任意の2島の組を選んだときに、
「その2島間に橋がかかっている」
「その2島にかかっている橋の本数の和が10以上である」
のいずれか少なくとも一方が成り立つならば、全10島をちょうど一度ずつ通って元の島に
戻ってくる巡回路が存在することが証明できます。
(証明) 背理法を用います。10島から任意の2島の組を選んだときに、
「その2島間に橋がかかっている」
「その2島にかかっている橋の本数の和が10以上である」
のいずれかが成り立っているにも関わらず、全10島を一度ずつ通って元の島に戻ってくる
巡回路が存在しなかったと仮定します。
間に橋がかかっていない2島を選び、橋を1つ建設します。これで巡回路ができればそこ
でストップ、できなければ再び間に橋がかかっていない2島を選び、橋を1つ建設、それを繰
り返して初めて巡回路が存在する状況になった状況について考えます。
最後に橋をかけた2つの島をAおよびJと名付けます。このAJ間の橋によって初めて巡回
路ができたので、今ある巡回路は全てこの橋を通ります。その巡回路のうちの1つを選び、
Aから出発して最後にJに着いてAに戻るまで通る順に島の名前をA、B、C、・・・、Jとします。
さて、AとJはもともと橋がかかっていなかった島の組なので、AJ以外に少なくとも10本、
AまたはJからかかっている橋が存在します。ABとIJは当然橋がかかっているのでこれらも
除外すれば残り少なくとも8本。それがかかっている場所の候補14箇所を
「ACとBJ」、「ADとCJ」、「AEとDJ」、「AFとEJ」、「AGとFJ」、「AHとGJ」、「AIとHJ」
と、7組にグループ分けすると、鳩ノ巣原理より、少なくともどれか1つは実際に橋がかかって
いる2箇所の組になります。
例えば、それが「AEとDJ」だったとしましょう。すると、これら2本の橋を利用して後半を逆
回りするABCDJIHGFEAという巡回路が存在します。
他の組でも同様に、その2本を利用して後半を逆回りする巡回路が存在しますが、いずれ
の場合でも、その巡回路の存在は、今ある巡回路は全てAJ間の橋を通ることに矛盾します。
したがって仮定は誤りであり、条件を満たす10島には、必ず全10島を一度ずつ通って元
の島に戻ってくる巡回路が存在することが示されました。
#もちろんN(≧3)個の島で橋の本数の和をN以上とすれば一般に成り立ちます。
(オーレの定理)
例題19 相異なる7個の整数をどのように選んでも、その差または和が10の倍数となる
2数が存在する。
(解) 相異なる7個の整数を10で割った余りで分類すると、
0、1、2、3、4、5、6、7、8、9
の何れかになる。そこで、10で割った余りが k または 10−k である集合をAkとす
ると、相異なる7個の整数(これが、鳩)は、
A0、A1、A2、A3、A4、A5
の何れかに属する。(これが、鳩ノ巣)
鳩ノ巣原理により、相異なる7個の整数のうちの2数を含むAkが存在する。
その2数を10で割った余りが、ともに k または、ともに 10−k のとき、その2数の
差をとると、10の倍数になる。
その2数を10で割った余りが、一つは k で他方が 10−k のとき、その2数の和をと
ると、10の倍数になる。 (終)
例題20 1から10までの自然数を並べた数列は、少なくとも4個の数からなる単調増加
列または単調減少列を含むことを示せ。
(例) 乱数表を使って、1から10までの10個の自然数を並べてみた。
9 、1 、2 、4 、8 、5 、7 、6 、3 、10
この自然数列に対して、 「1 、2 、4 、8」が条件を満たす。どんな自然数列に対しても
このような数列が存在するところが面白い。
さて、どうやって示すのだろう。もちろん、鳩ノ巣原理を使う訳なのだが...。
この例題20を一般化すれば、次の例題20’が得られる。
例題20’ 1からn2+1までの自然数を並べた数列は、少なくともn+1個の数からなる単
調増加列または単調減少列を含むことを示せ。
DD++さんからのコメントです。(平成29年7月18日付け)
証明してみましたが、鳩ノ巣原理が登場しませんでした。あれぇー?鳩ノ巣原理を使うと、
もっとスパッといくのでしょうか。
(証明) まず、
「異なる実数を並べた数列に含まれる単調増加列または単調減少列が全て n 個以下の
数からなるとき、数列の実数は、n2個以下である」
を数学的帰納法で示します。
(i) n=1 のとき、
2個以上の数からなる単調増加列や単調減少列が存在しないことは、異なる2数が存在し
ないことを意味するので、項数は1以下であり、命題は成立します。
(ii) n=k のとき、命題が成立すると仮定して、n=k+1 のときを考えます。
この数列には、k+2個以上の数からなる単調減少列が存在しないことから、もし、k+1個の
数からなる単調減少列があれば、その先頭の数は、それより前にあるどの数よりも大きく
なければいけません。
そこで、この数列のうち、「その数はそれより前にあるどの数より大きい」を満たす数に赤
い印をつけます。
すると、もし、k+1個の数からなる単調減少列があれば、その先頭の数には赤い印がつい
ていることになります。
同様に、「その数はそれより後ろにあるどの数より大きい」を満たす数に青い印をつけると、
もし、k+1個の数からなる単調増加列があれば、その末尾の数には青い印がついていること
になります。
このとき、k+1個の数からなる単調増加列も単調減少列も印のついた数が必ず含まれるの
で、印が何もついていない数のみからなる単調増加列や単調減少列は全てk個以下の数か
らなります。
よって、帰納法の仮定より、印のない数はk^2個以下です。
また、赤い印をつけた数は単調増加列になっているので、赤い印のある数はk+1個以下。
同様に、青い印をつけた数は単調減少列になっているので、青い印のある数はk+1個以下。
そして、数列全体で最大の数は赤と青の両方の印があるので、数列全体で、
k^2+(k+1)+(k+1)-1=(k+1)^2個以下の数しかないことがわかります。
よって、n=kのとき命題が成立すると仮定すると、n=k+1のときも命題が成立します。
以上、(i)、(ii)より、
「異なる実数を並べた数列に含まれる単調増加列または単調減少列が全てn個以下の数
からなるとき、実数はn2個以下である」
が、任意の自然数nについて成り立つことが示されました。
よって、その対偶である
「n2+1個以上の異なる実数を並べた数列は、n+1個以上の数からなる単調増加列または単
調減少列を含む」
も成り立つので、最初の命題
「1からn2+1までの自然数を並べた数列は、少なくともn+1個の数からなる単調増加列また
は単調減少列を含む」
は示されました。 (証終)
DD++さんからのコメントです。(平成29年7月30日付け)
もしかしてこういうことなのかなあ、というのを見つけたので...。
私は前後から1回ずつ剥ぎ取っていった帰納法で示したわけですが、前からだけ(あるいは
後ろからだけ)n回剥ぎ取る方針でいくと、鳩ノ巣原理を証明中に登場させようと思えばでき
なくはないようです。
まず、「その数はそれより前にあるどの数より大きい」に属する数の集合を A1 とします。
A1 に属する数が n+1 個以上あれば、それらは単調増加列になるので条件を満たします。
以下では、A1 に属する個数が n 個以下であった場合を考えます。
次に、「その数は A1 に属しておらず、それより前にある A1 に属さないどの数より大きい」
に属する数の集合を A2 とします。
すると、A2 に属するどの数も、自身より前にそれより大きな A1 に属する数があることに
なります。A2 に属する数が n+1 個以上あれば、それらは単調増加列になるので条件を満
たします。
以下では、A2 に属する個数も n 個以下であった場合を考えます。
さらに、「その数は A1、A2 に属しておらず、それより前にある A1、A2 に属さないどの数
より大きい」に属する数の集合を A3 とします。
すると、A3 に属するどの数も、自身より前にそれより大きな A2 に属する数があることに
なります。A3 に属する数が n+1 個以上あれば、それらは単調増加列になるので条件を満
たします。
以下では、A3 に属する個数も n 個以下であった場合を考えます。
以下、An ができるまで繰り返します。
A1 から An まで全て n 個以下の場合を考えているので、いずれかの集合に属した数は多
くとも n^2 個。つまり、少なくとも 1 個はどの集合にも属していない数があります。(※)
この数は、自身より前にそれより大きな An に属する数があり、この An に属する数は自
身より前にそれより大きな A(n-1) に属する数があり、以下繰り返して、A1 までたどり着き
ますが、このとき辿った n+1 個の数は、前から順に見れば単調減少列です。
よって、「1 から n^2+1 までの自然数を並べた数列は、少なくとも n+1 個の数からなる単
調増加列または単調減少列を含む」は示されました。
……という証明中の(※)のところ、わざわざ背理法を使うと、こうなります。
もし、この時点で全ての数がいずれかの集合に属していたと仮定すると、集合は n 個で数
は n^2+1 個あるので、鳩ノ巣原理よりいずれかの集合に n+1 個以上含まれることになり、
全ての集合が n 個以下の数しか含まないことに矛盾。
よって、少なくとも 1 個はどの集合にも属していない数があります。
ただ、直接証明に何の困難もないところでわざわざ間接証明を持ち出して、しかも直接証
明より長くなるので、鳩ノ巣原理を使うと綺麗に証明できる命題であるというよりは、鳩ノ巣
原理の話題のために無理して鳩ノ巣原理を使ってみただけの証明という印象が拭えません
ね。
(コメント) DD++さんに触発されて、何とか例題20の鳩ノ巣原理的解法をでっち上げてみ
ました。(平成29年8月4日付け)
(解) 1から10までの自然数を並べた数列を、a1、a2、・・・、a10 とする。(これが、鳩)
akに対して、座標が(xk,yk)の格子点を考える。
ただし、xk は、akで終わる単調減少列の長さの最大値で、同様に、yk は、akから始まる
単調増加列の長さの最大値とする。
いま、どの自然数に対しても、その座標(xk,yk)が、1≦xk≦3 、1≦yk≦3 とする。
(これが、鳩ノ巣)
このとき、鳩ノ巣原理により、同じ座標を持つ2つの自然数 am、an (m<n) が存在する。
すなわち、 am、an から定まる座標を、(xm,ym)、(xn,yn) とすると、
xm=xn かつ ym=yn だが、 am<an なので、これは起こりえない。
すなわち、「3個以下の数からからなる単調増加列および単調減少列を含む」とすると、
鳩ノ巣原理から矛盾が導き出せることがわかった。
よって、少なくとも4個の数からなる単調増加列または単調減少列を含む。 (終)
(コメント) 例えば、
9 、1 、2 、4 、8 、5 、7 、6 、3 、10
について、
a1 ・・・ (x1,y1)=(1,1)
a2 ・・・ (x2,y2)=(2,4)
a3 ・・・ (x3,y3)=(1,3)
a4 ・・・ (x4,y4)=(1,2)
a5 ・・・ (x5,y5)=(1,1)
a6 ・・・ (x6,y6)=(2,2)
a7 ・・・ (x7,y7)=(1,1)
a8 ・・・ (x8,y8)=(2,1)
a9 ・・・ (x9,y9)=(3,2)
a10 ・・・ (x10,y10)=(1,1)
から、1から始まる長さ4の単調増加列 1 、2 、4 、8 が存在することが分かる。
(追記) 当HP読者のHN「河童」さんからメールで、例題20の別証をいただきました。
(令和5年2月11日付け)
少しでも高校生の役に立ちたいと、塾講師やオンライン家庭教師などを行っております。
例題20 1から10までの自然数を並べた数列は、少なくとも4個の数からなる単調増加
列または単調減少列を含むことを示せ。
について、次のような証明はいかがでしょうか。
(証明) 乱数表を使って、1から10までの10個の自然数を並べた、
9 、1 、2 、4 、8 、5 、7 、6 、3 、10
で説明します。例えば、8を末項に持つ数列 9,1,2,4,8 を考えますと、これは、
{1,2,4,8}という増加列を含み、{9,8}という減少列を含みます。これを項数でもって
(4,2)と表すことにします。
8の次の5で同様に考えると、{1,2,4,5}{9,8,5}を含みますから(4,3)と表せます。
8から5に移る際に、5が8より小さいことから、減少列の項がひとつ増えます。
増加列、減少列のいずれかは変化して、他方は変化しないです。
しかし、8から5、7へと移るに従い、増加列、減少列のいずれか一方は必ず変化します。
増加列、減少列ともに項数が3以下のものは、(1,1)、(1,2)……(3,3)の合計9個あ
り、それに対して、元の数列の項数は10項ですから、増加列または減少列が4以上のもの
が必ず1つは含まれるはずです。 (証終)
(コメント) 河童さん、証明をいただきありがとうございます。内容的には、私の証明と趣旨
は同じかな?と思います。ただ、項が飛んでいる部分、すなわち、
{1,2,4,8}という増加列を含み、{9,8}という減少列を含みます。
としている点が気にかかります。
DD++ さんからのコメントです。(令和5年2月14日付け)
河童さんの証明だと、(m,n) という数字の組が「隣接するところでは必ず異なる」ことしか
言っておらず、不完全に思います。
2回変化したり、4回変化して元の数の組に戻る可能性を否定する根拠も必要なのでは。
Dengan kesaktian Indukmu さんからのコメントです。(令和5年2月15日付け)
鳩ノ巣原理を使うアイデアの初出は以下の論文のようですね。
A. Seidenberg, A Simple Proof of a Theorem of Erdos and Szekeres, Journal of the London
Mathematical Society, Volume s1-34, Issue 3, July 1959, Page 352, https://doi.org/10.1112
/jlms/s1-34.3.352
よおすけさんからのコメントです。(平成29年7月19日付け)
 が有理数でないことを、鳩ノ巣原理を使って証明できますか。
が有理数でないことを、鳩ノ巣原理を使って証明できますか。
DD++さんからのコメントです。(平成29年7月19日付け)
やろうと思えば出来なくはないですね。無理数の証明で直接証明的になるのは珍しいです
が、果たしてこの方法をやるメリットがあるかといえば、「ない」と思います。さっさと無限降下
法に持ち込んだ方が簡潔ですし...。
(証明) m[0]+m[1] =0 を満たす整数 m[0] と m[1] について考えます。
=0 を満たす整数 m[0] と m[1] について考えます。
このとき、m[0]^2 = 2*m[1]^2 ≧ m[1]^2 ≧ 0 より、|m[0]| ≧ |m[1]| です。また、
m[0]^2 = 2*m[1]^2 より、m[0]^2 は偶数、よって m[0] は偶数なので、m[2] = m[0]/2 は整数
で、2*m[2]+m[1] =0 から m[1]+m[2]
=0 から m[1]+m[2] =0
=0
同様に、m[1]^2 = 2*m[2]^2 ≧ m[2]^2 ≧ 0 より、|m[1]| ≧ |m[2]| です。また、
m[1]^2 = 2*m[2]^2 より、m[1]^2 は偶数、よって m[2] は偶数なので、m[3] = m[1]/2 は整数
で、2*m[3]+m[2] =0 から m[2]+m[3]
=0 から m[2]+m[3] =0
=0
以下、同様に繰り返して、m[|m[0]|]+m[|m[0]|+1] =0 となるところまで繰り返します。
=0 となるところまで繰り返します。
m[0], m[1], m[2], m[3], ……, m[|m[0]|], m[|m[0]|+1] という数列を作ると、これらは絶対値が
単調減少する整数列なので、その絶対値は 0, 1, 2, ……, |m[0]| の |m[0]|+1 通りしかあり得
ず、鳩ノ巣原理よりこれらの |m[0]|+2 個の中に同じ絶対値を取るものが存在し、しかもそれ
らは隣接項です。
それらを m[k] と m[k+1] とすると、|m[k]| = |m[k+1]| かつ m[k]+m[k+1] =0 なので、連立
=0 なので、連立
方程式を解いて、m[k] = m[k+1] = 0
すると、m[k-1] = 2*m[k+1] = 0 などのようにして、この数列は全て 0 であることが示されま
す。
よって、m[0]+m[1] =0 を満たす整数は、m[0] = m[1] = 0 に限られる、つまり 1 と
=0 を満たす整数は、m[0] = m[1] = 0 に限られる、つまり 1 と 
は有理数体上一次独立なので  は無理数です。 (証終)
は無理数です。 (証終)
例題21 1から10までの自然数を円形に並べる。このとき、連続して並ぶ3数の和で17
以上のものが存在する。
都合よく、「3、5、9」などと連続して並んでいれば、和が17で存在!となるが、上記の問
題の核心は、「1から10までの自然数がランダムに円形に並んでいる」とき、そのような組
は存在するか、ということである。
この問題を解決するには、「鳩ノ巣原理」が有効である。
(解) 連続して並ぶ3数の組は全部で、10組(これが鳩ノ巣)あり、その総和は、
(1+2+・・・+10)×3=165 (これが鳩)
よって、少なくとも1組の和は17以上である。 (終)
(コメント) 上記では「和が17以上」であったが、実は、「和が18以上」とも出来る。
実際に、1以外の2から10までの9つの自然数の総和は、54(これが鳩)で、3数ずつ3
組(これが鳩ノ巣)に分けると、和は平均して、54÷3=18 なので、少なくとも1組の和は
18以上である。
したがって、任意の並びで、連続する3数の和が18以上となるものが存在する。
ハンニバル・フォーチュンさんからのコメントです。(平成30年7月15日付け)
、「少なくとも1組の和は19以上である。」への反例として、具体的には、
5 1 9 7 2 6 8 4 3 10
がありますね!「少なくとも1組の和は18以上である」が最良の評価のようです。
ハンニバル・フォーチュンさんからのコメントです。(平成30年8月30日付け)
OEIS の「A066385」に於いて一般化した話題があります。
"Smallest maximum of sum of 3 consecutive terms in any arrangement of [1..n] in a circle."
だそうです。例題21は n=10 のときのお話でした。
また、17 ≦ n ≦ 38 のときに、 a(n)=3n + 5 - a(n-1) の関係があるようです。
まことに不思議な感じがいたします。
(追記) 令和3年11月17日付け
例題22 n個の自然数 a1、a2、・・・、an がある。このとき、連続する和
ak+ak+1+・・・+am (kからmまでは連続する自然数)
で、nで割り切れるものが必ず存在する。
(解) S1=a1、S2=a1+a2、S3=a1+a2+a3、・・・、Sn=a1+a2+・・・+an とおく。
S1、S2、S3、・・・、Sn の中にnで割り切れるものが少なくとも一つあれば、結論は言える。
よって、S1、S2、S3、・・・、Sn の何れもnで割り切れないものとする。(これが、鳩)
nで割った余りは、1、2、・・・、n−1の n−1個ある。(これが、鳩ノ巣)
鳩ノ巣原理により、S1、S2、S3、・・・、Sn の中に、nで割った余りが同じものが必ず存在
する。
したがって、自然数 k、m(k≦m)に対して、
Sk-1−Sm=ak+ak+1+・・・+am≡0 (mod n)
となるものが必ず存在する。すなわち、
ak+ak+1+・・・+am (kからmまでは連続する自然数)
で、nで割り切れるものが必ず存在する。 (終)
以下、工事中!

