
| ��쌤������� | �@�@�@�@�@�@�@ |
| �@�@�@�w���w�̖��R�[�i�[�x�@�ɒ���I |
�@���̃y�[�W�ł́A�������炨���b�ɂȂ��Ă���L���H�Ƒ�w�̑�쌤��������Â���
�w���w�̖��R�[�i�[�x�̖��ɒ��킵�����Ǝv���B
�i�NjL�j�@���搶����������āA��L�̃T�C�g�������N����Ă���悤�ł��B
�@�@�@Kelly Burkhard������A�܂��l�b�g���ɂ͌�������Ɗ֘A�y�[�W��������Ƃ�����
�@�@�@���������܂����B�������A�c�O�Ȃ�����搶�̏����ꂽ���̂��c���Ă���킯�ł�
�@�@�@�Ȃ��Ƃ̂��Ƃł��BKelly Burkhard����Ɋ��ӂ��܂��B2018.7.14�i���@�Q�l�j
| �ځ@�@�@���@�@�@�i���s���j | ||||||
| ���ԍ� | �o �� �� �� | ���ԍ� | �o �� �� �� | |||
| �P�O�V | �E�E�E�E�E | �������� | �T�U | �E�E�E�E�E | ���������̏ؖ� | |
| �S | �E�E�E�E�E | �����_�i�́j | �V�X | �E�E�E�E�E | �����_�i�����j | |
| �P�P�W | �E�E�E�E�E | �����_�i�������j | �P�O�X | �E�E�E�E�E | ���ʊ� | |
| �Q�O�O | �E�E�E�E�E | �����_�i�s��������j | �R | �E�E�E�E�E | ���������̏ؖ� | |
| �Q�U�O | �E�E�E�E�E | ����i�Q�����j | �Q�U�Q | �E�E�E�E�E | ���������� | |
| �Q�U�R | �E�E�E�E�E | �m���_ | �P�T | �E�E�E�E�E | ���̑��ݔ͈��@ | |
| �P�U�P | �E�E�E�E�E | ����g�����@ | �Q�U�X | �E�E�E�E�E | ��Ԑ}�`�@ | |
| �Q�V�S | �E�E�E�E�E | �����t���ő�ŏ��@ | �P�R | �E�E�E�E�E | �ɒl�̘a�@ | |
| �Q�U�W | �E�E�E�E�E | �s��̂����@�@ | �Q�X�R | �E�E�E�E�E | �������̌v�Z | |
| �P�O�R | �E�E�E�E�E | ���w�p�Y�� | �R�P�U | �E�E�E�E�E | �s�����̏ؖ� | |
| �R�Q�U | �E�E�E�E�E | ���̋Ɍ� | �R�R�X | �E�E�E�E�E | �R���������̉� | |
���P�O�V�@�@���̎���������������B
�@x4 + y4
+ z4 + w4 - 2( x2y2 +
x2z2 + x2w2
+y2z2 + y2w2 +
z2w2 ) + 8xyzw
�@�@�@[�ޑ�]�@x6 - y6
+ z6 -3x4y2 + 3x2y4 +
2x3z3 + 6xy2z3�@��������������B
�@��쌤�����̂g�o�ł́A���͂�����̂̓r���o�߂��Ȃ��̂ŁA���Z���ɖ߂����C���Ŏ��̂�
���ɉ����Ă݂��B
�@���P�O�V�A�ޑ�Ƃ��ɁA��@�̍���ɂ���̂́A������u�������|���v�̎�@�ł���B
�i���j�@�^����x4 + y4
+ z4 + w4 - 2( x2y2 +
x2z2 + x2w2
+y2z2 + y2w2 +
z2w2 ) + 8xyzw
�@�@�@�@�@�@���i x2 - y2 �j2 + 2x2y2 + �i z2 - w2�j2+ 2z2w2
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@- 2( x2y2 +
x2z2 + x2w2 + y2z2 + y2w2 +
z2w2 ) + 8xyzw
�@�@�@�@�@�@���i x + y �j2�i x - y �j2- 2( x2z2 + x2w2 + y2z2 + y2w2 - 4xyzw ) + �i z + w �j2�i z - w �j2
�@�@�@�@�����ŁA�ȒP�Ȍv�Z����A
�@�@�@�@�@�@�i x + y �j2�i z - w �j2+ �i x - y �j2�i z + w �j2�� 2( x2z2 + x2w2 + y2z2 + y2w2- 4xyzw )
�@�@�@�Ȃ̂ŁA�������|���ɂ��A
�@�@�@�@�^����(�i x + y �j2- �i z + w �j2)(�i x - y �j2- �i z - w �j2)
�@�@�@���������āA
�@�@�@�@�^����( x + y + z + w )( x + y - z - w )( x - y + z - w )( x -
y - z + w )
�@�@�@�ƈ������������B�i�I�j
�@�ޑ�����l�ɂł���B
�i���j�@�^����( x2 - y2)3 + z6 + 2x3z3 + 6xy2z3
�@�@�@�@�@�@�@��z6 + ( 2x3 + 6xy2)z3 + �i x + y�j3�i x - y�j3
�@�@�@�@�����ŁA�ȒP�Ȍv�Z����A
�@�@�@�@�@�@�i x + y�j3 + �i x - y�j3 �� 2x3 + 6xy2
�@�@�@�Ȃ̂ŁA�������|���ɂ��A
�@�@�^����( z3+ �i x + y�j3)( z3+ �i x - y�j3)
�@�@�@�@�@��( z + x + y )( z2- z( x + y ) + ( x + y )2 )( z + x - y )( z2 - z( x - y ) + ( x - y )2)
�@�@�@�@�@��( x + y + z )( x2 + y2 + z2+ 2xy - yz - zx )( x - y + z )( x2 + y2 + z2- 2xy + yz - zx )
�@�@�@�ƈ������������B�i�I�j
���T�U�@�@���R�ΐ��̒� e �͖������ł���B
�@���̖��ɂ��ẮA���ɓ��g�o�ʼnf�ڍς݂ł���B�i���@���������Q�Ɓj
�@���P�O�V�Ɋ֘A���āA������� �S�������[���B
��� �S�@�R�̐��@![]() �@�͗L�����̏�ꎟ�Ɨ��ł��邱�Ƃ������B
�@�͗L�����̏�ꎟ�Ɨ��ł��邱�Ƃ������B
�i���j�@ ���܁A�L���� ���A���A�� ��p���āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�Ƃ���B
�@�@�@�@���ӂɏ\���傫�����R���������邱�Ƃɂ��A���߂���A ���A���A�� �͐����Ƃ��Ă悢�B
�@�@�@���A���A�� �̂����A���Ȃ��Ƃ���� �O �łȂ��Ɖ��肷��B
�@�@�@���̂Ƃ��A![]() ���������ł��邱�Ƃ���A���A���A�� �̂ǂ�� �O �Ƃ͂Ȃ�Ȃ��B
���������ł��邱�Ƃ���A���A���A�� �̂ǂ�� �O �Ƃ͂Ȃ�Ȃ��B
�@�@�@�@����āA���A���A�� �̍ő���ŗ��ӂ�����Z���邱�Ƃɂ��A���A���A���@�݂͌��ɑf��
�@�@�@���Ă悢�B
�@�@�@�@�����ŁA�㎮�̗��ӂɁA![]() �@��������B
�@��������B
�@�@�@�W�J���āA��������ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��3�{�Q��3�{�S��3�|�U���������O
�@�@�@�ƂȂ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��3���|�Q��3�|�S��3�{�U������
�@�@�@�ɂ����āA�E�ӂ́A����������A���ӂ� ��3 �A���Ȃ킿�A�� �͋����ƂȂ�B
�@�@�@�@�����Q���@�i���͐����j���A�㎮�ɑ�����āA��������A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��3���|�S��3�|�Q��3�{�U������
�@�@�@����āA���l�ȗ��R����A�� �������ƂȂ�B
�@�@�@�@�����Q���@�i���͐����j���㎮�ɑ�����āA��������A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��3���|�S��3�|�Q��3�{�U������
�@�@�@����āA���l�ȗ��R����A�� �������ƂȂ�B
�@�@�@�@�ȏォ��A���A���A���@�͂Ƃ��ɋ����ƂȂ�A���A���A���@���݂��ɑf�Ƃ������Ƃɖ�������B
�@�@�@���������āA�� �� �� �� �� �� �O �ƂȂ�A![]() �@�͗L�����̏�ꎟ�Ɨ��ƂȂ�B
�@�͗L�����̏�ꎟ�Ɨ��ƂȂ�B
�@���P�O�V�̂悤�ȒP�Ɉ������������̖�肾�����疳�������Ŗ��C�Ȃ����A���̖���
�悤�ȁA���p��̂�������������ƁA��R�P���𑝂��Ă��邩��s�v�c���B
���V�X�@�Q1092�|�P �� �P�O�X�R2 �Ŋ����鎖�������B
�@�@
�@�@ [�ޑ�]�@�Q3510 �|�P �� �R�T�P�P2 �Ŋ����鎖�������B
�@��쌤�����̉́A�ƂĂ��������B���̃y�[�W�ł́A�����Ɍv�Z�𐄂��i�߂āA���ʂ�
�������Ǝv���B�i�����A�N����肽����Ȃ��v�Z���낤�B�j
�@�����P�O�X�R�@�Ƃ����B�@���|�P���P�O�X�Q���Q2�~�R�~�V�~�P�R�@�Ƒf�������������̂ŁA�́A
�@�@�P�A�@�@�Q�A�@�@�R�A�@�@�S�A�@�@�U�A�@�@�V�A�@�P�Q�A�@�P�R�A�@�P�S�A�@�Q�P�A�@�Q�U�A�@�Q�W�A�@�R�X�A�@�S�Q�A
�@�T�Q�A�@�V�W�A�@�W�S�A�@�X�P�A�P�T�U�A�P�W�Q�A�Q�V�R�A�R�U�S�A�T�S�U�A�P�O�X�Q
�� �Q�S����B�����ɂ��āA��2 ��@�Ƃ����A�Q�� �̒l�����߂Ă݂�ƁA
�Q1���Q
�Q2���S
�Q3���W
�Q4���P�U
�Q6���U�S
�Q7���P�Q�W
�Q12�߂S���|�Q�V�U
�Q13�߂V���{�T�S�P
�Q14�߂P�T���|�P�P
�Q21�߁|�Q�U�V���|�R�P�T
�Q26�߂P�X�P���|�Q�S�R
�Q28�߁|�R�R�O���{�P�Q�P
�Q39�߁|�P�R�X���|�R�O�R
�Q42�߁|�Q�P���|�Q�R�W
�Q52�߂P�R�R���{�Q�V
�Q78�߂P�T�V���|�R
�Q84�߂Q�P�P���|�P�X�Q
�Q91�߁|�R�R�X���|�T�R�O
�Q156�߂P�T�P���{�X
�Q182�߁|�P
�@�㎮�̗��ӂ��U�悵�āA (�Q182)6��(�|�P)6�@���Ȃ킿�A�Q1092�߂P
�@�ޑ�����l�ɂ���Ă݂悤�B
�@�����R�T�P�P�@�Ƃ����B�@���|�P���R�T�P�O���Q�~�R3�~�T�~�P�R�@�Ƒf�������������̂ŁA�́A
�@�@�P�A�@�@�Q�A�@�@�R�A�@�@�T�A�@�@�U�A�@�@�X�A�@�P�O�A�@�P�R�A�@�P�T�A�@�P�W�A�@�Q�U�A�@�Q�V�A�@�R�O�A�@�R�X�A
�@�S�T�A�@�T�S�A�@�U�T�A�@�V�W�A�@�X�O�A�P�P�V�A�P�R�O�A�P�R�T�A�P�X�T�A�Q�R�S�A�Q�V�O�A�R�T�P�A�R�X�O�A�T�W�T�A
�V�O�Q�A�P�P�V�O�A�P�V�T�T�A�R�T�P�O
�� �R�Q����B�����ɂ��āA��2 ��@�Ƃ����A�Q�� �̒l�����߂Ă݂�ƁA
�Q1���Q
�Q2���S
�Q3���W
�Q5���R�Q
�Q6���U�S
�Q9���T�P�Q
�Q10���P�O�Q�S
�Q13�߂Q���{�P�P�V�O
�Q15�߂X���{�P�P�U�X
�Q18�߂V�T���|�P�P�W�P
�Q26�߂P�T�T�X���|�R�X�O
�Q27�߁|�R�X�R���|�V�W�O
�Q30�߂R�U�T���{�V�W�Q
�Q39�߂X�P�P���{�P�R�O
�Q45�߂Q�P�R�O���{�P�Q�X�W
�Q54�߁|�P�P�V�Q���{�X�X�V
�Q65�߁|�P�U�U�P���|�P�T�S�U
�Q78�߂P�U�Q�W���|�U�T�T
�Q90�߂P�R�T���|�S�V�U
�Q117�߂P�P�Q�P���|�W�W�U
�Q130�߁|�P�O�O���|�W�V�T
�Q135�߂R�O�R���{�W�W
�Q195�߂R�Q�Q���{�P�O�P�T
�Q234�߂P�O�R�V���{�Q�O�S�R
�Q270�߂U�U�T���{�V�Q�Q
�Q351�߂P�U�P�U���|�P�X�R�R
�Q390�߂X�O�V���{�P�T�O�Q
�Q585�߂Q�W�R���{�V�T�U
�Q702�߁|�R�Q�R���{�V�W�T
�Q1170�߁|�Q�W�R���|�V�T�V
�Q1755�߂P
�@�㎮�̗��ӂ��Q�悵�āA ( �Q1755)2�߂P�@���Ȃ킿�A�Q3510�߂P
�@�@��L�̌v�Z�́A�������d���Ў�Ɍv�Z�������̂ł���B
�����P�O�X�R�@�̏ꍇ�́A����قNjC�̉����Ȃ�悤�Ȍv�Z�ł͂Ȃ��A��r�I�y�ɋ��߂邱�Ƃ�
�ł����B �Q91�߁|�R�R�X���|�T�U�R�@�܂Ōv�Z���āA�W���̑傫���ɕs���ɂȂ����i��쌤����
�̌��ʂ�m���Ă����̂ŁA����قǂł��Ȃ��������D�D�D�j���A�N�₩�ɁA �Q182�߁|�P�@����
����āA�ƂĂ����������B�[���X�̒��ŁA��C�ɓW�]���Ђ炯���悤�ȋC���ł������B
�@����ɑ��āA�����R�T�P�P�@�̏ꍇ�́A��ς������B�v�Z���ẮA�v�Z�~�X����������A��
�x���v�Z���J��Ԃ����B���̖T��ŁA�u��������`���ł���A�E�E�E�v�ƌv�Z�p���������A��
�鏗���̕��́A��ςȌv�Z�Ɂu���Ȃ��������Ƃɂ��܂��I�I�v�ƌ����āA�����ɋ����Ă��܂�
���B�@�����P�O�X�R�@�̏ꍇ�̂悤�ɁA�r���ŁA���������̌��I�Ȏ������҂������A
�Q1755�߂P�@
�ɓ��B����܂ŁA�����Ē�����̓��ł������B�ƂĂ��A��ꂽ�B�P�V�T�T���R3�~�T�~�P�R�@�Ȃ�
�ŁA�����P�O�X�R�@�̂Ƃ��̂悤�ȏ�肢��@�́A���܂���҂ł��Ȃ��Ǝv���B
���P�P�W �́A�t�B�{�i�b�`����̎������Ɋւ�����ł���B
�@�t�B�{�i�b�`���� �o�����p �Ƃ́A�A�Q����
�@�@�@�@�@�@�@��1 �� �P�A��2 �� �P�A ��n + 2 �� ��n + 1 �{ ��n
�ɂ���܂鐔��ł���B�i�ڂ����́A���������Q�Ɓj
�@�ŏ��̂������̍������A
�P�A�P�A�Q�A�R�A�T�A�W�A�P�R�A�Q�P�A�R�S�A�T�T�A�W�X�A�P�S�S�A�Q�R�R�A�R�V�V�A�U�P�O�A�X�W�V�A�P�T�X�V�A�E�E�E
�ƂȂ�B�����̊e�����A�Ⴆ�A������ �Q �ōl����A����́A
�P�A�P�A�O�A�P�A�P�A�O�A�P�A�P�A�O�A�P�A�P�A�O�A�P�A�P�A�O�A�P�A�P�A�E�E�E
�܂��A������ �R �ōl����A����́A
�P�A�P�A�Q�A�O�A�Q�A�Q�A�P�A�O�A�P�A�P�A�Q�A�O�A�Q�A�Q�A�P�A�O�A�P�A�E�E�E
�ƂȂ�A���������̗�i�Ԏ��̕����j���J��Ԃ������B���̂悤�Ȍ��ۂ��A�t�B�{�i�b�`����
���������Ƃ����B
�@���P�P�W�ɂ��A���̂悤�ɒ�`�����B
�@���R�� N �� �� �ɑ��A�� ���t�B�{�i�b�`���� �o�����p �� mod N �����ł���Ƃ́A
�@�@�@�@�C�ӂ̎��R�� �� �ɑ��āA ��n + p �� �����@(mod N)
�����藧�Ƃ��������B
�@���̂悤�� �� �̂����A�ŏ��̐��̐����A�ʏ� mod N ���� �ƌĂԂ��Ƃ́A�O�p���ɂ���
������̏ꍇ�Ɠ����ł���B
�@��L�ɂ�������ɂ��Amod �Q �����́A�R �ŁAmod �R �����́A�W �ƂȂ�B
���̂Ƃ��A���̒藝�����藧�B
�藝�@
�ǂ�Ȏ��R�� N �ɑ��Ă��A�t�B�{�i�b�`����́A �O �ȊO�� mod N ���� ���@�����B
�@���P�P�W�ɂ��A���̒藝�̏ؖ��́A�u�t�B�{�i�b�`����̒�`�̂�����ɂ�肷������
��B�v�Ƃ���Ă��邪�A����قǎ����Ȃ��ƂƂ͎v���Ȃ��̂ŁA�����ŁA�ؖ����Ă��������B
�@�t�B�{�i�b�`���� �o�����p�ɂ����āA���� �� �����@(������ �m)�@�i�������A�O�� �������m�|�P�j�Ƃ���B
���̂Ƃ��A�����i ���� �C ����+1 �j�ɂ����āA�O�� �������m�|�P�A�O�� ����+1���m�|�P �Ȃ̂ŁA�N����
����ꍇ�̐��́A�S���� �m2 ����B
�@�Ƃ���ŁA�� �̒l�͈̔͂Ƃ��āA�O �� �� �� �m2 �i�������A��0 ���O �Ƃ���B�j�ōl������̂Ƃ�
��A�����i ���� �C ����+1 �j�͑S���� �m2�{�P �ł���B
�@���������āA���m�������ɂ��A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i ���� �C ����+1 �j���i ���� �C ����+1 �j
�ƂȂ� ���A�� �i�������j �����݂���B���Ȃ킿�A�@���� �� �����@�A����+1 �� ����+1 �����藧�B
�@�����ŁA�����O�@�Ȃ�A���R�� �� �Ƃ��āA������ �Ƃ����悢�B
�@�����A�����P �Ȃ�A������ �m �ɂ����āA
�@����-1 �� ����-1 ������+1�| ���� �� ����+1�| ���� �� ����+1�| ���� �� ����+1�| ���� �� ����-1 �� ����-1
�@���Ȃ킿�A�@����-1 �� ����-1�@�ƂȂ�B
�ȉ����l�ɂ��āA����-2 �� ����-2 �A�E�E�E�A��0 �� ����-k ���������B
�@�����ŁA�������|���@�Ƃ����A�� �͎��R���ŁA ���� �� ��0 �� �O�@�ƂȂ�B
��L�̌v�Z����A����ɁA�@����+1 �� ��1�@�ł���̂ŁA
�@�@�@����+2 �� ����+2 ������+1�{ ���� �� ����+1�{ ���� �� ��1�{ ��0 �� ��1�{ ��0 �� ��2 �� ��2
�@���Ȃ킿�A�@����+2 �� ��2�@�ƂȂ�B �i�������A��0���O �Ƃ���B�j
�ȉ����l�ɂ��āA����+3 �� ��3 �A�E�E�E�A����+��-1 �� ����-1 �A��2�� �� ���� �� ��0�A�E�E�E�@���������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����ɂ́A���w�I�A�[�@�ɂ�莦�����B�j
�ȏォ��A���鎩�R�� �� �����݂��āA�C�ӂ̎��R�� �� �ɑ��āA��n + p �� �����@(mod N) ��
���藧���Ƃ������ꂽ�B
�i�Q�l�����F�a�c�G�j�@���@���̐��E�@�����_�ւ̓��@�i��g���X�j�j
�i�⑫�j�@�E�E�E�E�E�@�umod �m �����v�ɂ��āA�������ȏꍇ�ɂ́A�z�߂̒��������߂��
�@�@�@�@�@�@�@�@�@�@�������݂���B
�����@�@�@�T�ȊO�̊�f�� �o �ɑ��āA
�@�@�@�@�@�o�߂P�A�X�@�i�������@�P�O�j�@�̂Ƃ��Amod �o �����́A�o�|�P
�@�@�@�@�@�o�߂R�A�V�@�i�������@�P�O�j�@�̂Ƃ��Amod �o �����́A�Q�o�{�Q
�@�@�@�ŗ^������B�@
�@�ؖ��́A�u���@���v�@���@�@�����㐔�w�@�i�X�k�o�Łj�v�ɏڂ����ڂ��Ă���B��������
�����B
�i���@����Ƃ́A�����́A���k��w�ōs��ꂽ�㐔�w�̃V���|�W�E���ł���������Ƃ�����B���̐�y��
�F�l�Ƃ����W�ł��邪�A���w�ɑ��鑢�w�̐[���Ɋ��Q�������Ƃ��o���Ă���B�j
�@�����ł́A��L�̌��������p���Ȃ���A�P���m���U�O�@�̊e�m�̒l�ɑ��āAmod
�m ������
���߂悤�Ǝv���B�������������ǎ҂̕��́A�m���U�P �ɂ��Ă��v�Z���Ă݂ĉ������B
| �m | �P | �Q | �R | �S | �T | �U | �V | �W | �X | �P�O | �P�P | �P�Q | �P�R | �P�S | �P�T |
| ���� | �P | �R | �W | �U | �Q�O | �Q�S | �P�U | �P�Q | �Q�S | �U�O | �P�O | �Q�S | �Q�W | �S�W | �S�O |
| �m | �P�U | �P�V | �P�W | �P�X | �Q�O | �Q�P | �Q�Q | �Q�R | �Q�S | �Q�T | �Q�U | �Q�V | �Q�W | �Q�X | �R�O |
| ���� | �Q�S | �R�U | �Q�S | �P�W | �U�O | �P�U | �R�O | �S�W | �Q�S | 100 | �W�S | �V�Q | �S�W | �P�S | 120 |
| �m | �R�P | �R�Q | �R�R | �R�S | �R�T | �R�U | �R�V | �R�W | �R�X | �S�O | �S�P | �S�Q | �S�R | �S�S | �S�T |
| ���� | �R�O | �S�W | �S�O | �R�U | �W�O | �Q�S | �V�U | �P�W | �T�U | �U�O | �S�O | �S�W | �W�W | �R�O | 120 |
| �m | �S�U | �S�V | �S�W | �S�X | �T�O | �T�P | �T�Q | �T�R | �T�S | �T�T | �T�U | �T�V | �T�W | �T�X | �U�O |
| ���� | �S�W | �R�Q | �Q�S | �S�W | 300 | �V�Q | �W�S | 108 | �V�Q | �Q�O | �S�W | �V�Q | �S�Q | �T�W | 120 |
�@��L�̕\�̍쐬�ɂ́A�\�v�Z�\�t�g �d�������� ��p�����B�t�B�{�i�b�`�����̂��͕̂K�v�ł�
���A�]����A�t�B�{�i�b�`����̑Q�����ɑ�����āA�����]����v�Z����Ɗy�ł���B
�@�܂��A��L�̏ؖ������������悤�ɁA�u�P�A�P�v�ƁA�u�P�v���A������Ƃ���܂ł��z�߂ł�
�邱�Ƃɒ��ӂ���B
�@��L�̕\�ŁA�����ʂ肾�ƁA�m���Q�X �̂Ƃ��A������ �Q�W �ƂȂ�͂��ł��邪�A���ۂ́A�P�S
�ł���B�������A�Q�W �������Ȃ̂����A�ŏ��̐��̐��Ƃ������Ƃ���l����ƁA������a����
�o����B���l�ɁA�m���S�V �̂Ƃ����A�����Ǝ�Y�����������B�����ʂ肾�ƁA������ �X�U �Ƃ�
��͂��ł��邪�A���ۂ́A�R�Q �ł���B�ǂ����āA���̂悤�Ȍ��ۂ��N�������̂ł��낤���B��
��������K�v�����肻�����B
�@�܂��A�f03�m�˃T�[�N���T������ɂ����āA�ɓ�����i���ڍ��Z�j���A���̂悤�Ȍ���
���ؖ�����Ă���B
�����@�@�� ���Q�ȏ�̎��R���Ƃ���B���̂Ƃ��A
�@�@�@mod �Q�� �����́A�R�E�Q��-1�@�ł���Amod �T�� �����́A�S�E�T���@�ł���B
�@��L�̕\�Ŋm�F����ƁAmod �S(���Q2) �����́A�U(���R�E�Q2-1)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ mod �W(���Q3) �����́A�P�Q(���R�E�Q3-1)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ mod �P�U(���Q4) �����́A�Q�S(���R�E�Q4-1)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ mod �R�Q(���Q5) �����́A�S�W(���R�E�Q5-1)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ mod �Q�T(���T2) �����́A�P�O�O(���S�E�T2)
�ŁA�m���ɐ��藧���Ă���B
���P�O�X�@ ���s�l�ӌ` ABCD ������B
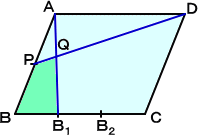 |
�@�@�@AB �̒��_�� P, BC �̎O�����_�� B = B0�A B1�A �@ B2 �AB3 = C, AB1 �� DP �̌�_�� Q �Ƃ��鎞�A�l �@ �p�` BB1QP �̖ʐς́AABCD �̖ʐς̂ǂꂾ�� �@ ���H������߂�B |
�i���j�@ �_�o���A�a�b�ɕ��s���������A�����`�a1�Ƃ̌�_���q�Ƃ���B
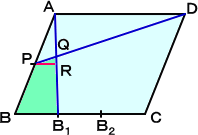 |
�@�@�@���̂Ƃ��A���_�A���̒藝���A�Q�o�q���a�a1 �@�@�ŁA���`�p�c�䁢�q�p�o�@����A�`�p�F�p�q���U �F �P �@�@�@����āA�`�p�F�p�a1���R �F �S�@�ƂȂ�B �@�@���������āA�l�p�`�a�a1�p�o�̖ʐς́A �@���s�l�ӌ`�`�a�b�c�̖ʐς́A |
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�i�R�����g�j�@��쌤�����ł͒��w���x�̖��Ƃ��ďЉ��Ă��邪�A�����܂蒆�w�I
�@�@�@�@�@�@�łȂ��Ƃ̗��R����A�����u�E�E�E�E�E�B�v�ł���B�����A���͏�L�ł����Ă���͂���
�@�@�@�@�@�@���A������Ƃ����s���D�D�D�B�ł��A�ɗp�����@���猾���A�\�����w�I����
�@�@�@�@�@�@�v���̂����D�D�D�H
���Q�O�O�@�@�s�������
�@ �@�@�@�@�@ i)�@y2= x4 �{ x3 �{ x2 �{ x �{ 1 �̎��R������ (x �C y) = ( 3 �C 11)
�@�@�@�@�@�@�@ii)�@y2 = x4
�{ 2x3 �{ 2x2 �{ 2x �{ 5 �̎��R������ (x �C y) = ( 2 �C 7)
�@�@�@�@�@�@�@�@��������ꂪ�S�āB
�@��쌤�����̂g�o�ł̉�@���a�V�������̂ŁA������Ɖ�@���Ȃ����Ă݂��B
�i���j�@�@�j�@�e�i���j��x2 �{�i�P/�Q�j���@�A�f�i���j��x2 �{�i�P/�Q�j���{�P/�Q�@�Ƃ����B
�@�@�@���̂Ƃ��A�@��2�|�i�e�i���j�j2���i�R/�S�jx2 �{���{�P���i�R/�S�j�i���{�Q/�R�j2�{�Q/�R���O
�@�@�@�@�@�@�@�@�@�@�i�f�i���j�j2�|��2���i�P/�S�jx2 �|�i�P/�Q�j���|�i�R/�S�j���i�P/�S�j�i���|�P�j2�|�P
�@�@�@�����ŁA�����R�@�̂Ƃ��A
�@�@�@�@�@�@�@�@�e�i���j���O�@�A�f�i���j���O�@�A��2�|�i�e�i���j�j2���O�@�A�i�f�i���j�j2�|��2���O
�@�@�@�Ȃ̂ŁA�@�����R�@�̂Ƃ��A
�@�@�@�@�@�@�@�i�e�i���j�j2����2���i�f�i���j�j2�@�@���Ȃ킿�A�@�e�i���j�������f�i���j
�@�@�@�����藧�B
�@�@�@���̂Ƃ��A���R�� �� �i�����R�j�ɑ��āA�K���A�e�i���j�A�f�i���j
�̂ǂ��炩�����R���ŁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�f�i���j�|�e�i���j���P/�Q���P
�@�@�@�Ȃ̂ŁA�� �����R���ɂȂ邱�Ƃ͂Ȃ��B
�@�@�@�@����āA�����P�A�Q�A�R �̏ꍇ�ɂ��Ă̂ݒ��ׂ�悢�B
�@�@�@�@�����P�@�̂Ƃ��A�@��2���T�@�i�s�K�j
�@�@�@�@�����Q�@�̂Ƃ��A�@��2���R�P�@�i�s�K�j
�@�@�@�@�����R�@�̂Ƃ��A�@��2���P�Q�P�@���A�@�����P�P
�@�@�@�@���������āA���߂鎩�R�����́A�@�����R�@�A�����P�P�@�̂݁B
�@�@�@�@�A�j�@�@�e�i���j��x2 �{���@�A�f�i���j��x2 �{���{�P�@�Ƃ����B
�@�@�@���̂Ƃ��A�@��2�|�i�e�i���j�j2��x2 �{�Q���{�T���i���{�P�j2�{�S���O
�@�@�@�@�@�@�@�@�@�@�i�f�i���j�j2�|��2��x2 �|�S
�@�@�@�����ŁA�����Q�@�̂Ƃ��A
�@�@�@�@�@�@�@�@�e�i���j���O�@�A�f�i���j���O�@�A��2�|�i�e�i���j�j2���O�@�A�i�f�i���j�j2�|��2���O
�@�@�@�Ȃ̂ŁA�@�����Q�@�̂Ƃ��A
�@�@�@�@�@�@�@�i�e�i���j�j2����2���i�f�i���j�j2�@�@���Ȃ킿�A�@�e�i���j�������f�i���j
�@�@�@�����藧�B
�@�@�@���̂Ƃ��A���R�� �� �i�����Q�j�ɑ��āA�K���A�e�i���j�A�f�i���j
�͂Ƃ��Ɏ��R���ŁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�f�i���j�|�e�i���j���P
�@�@�@�Ȃ̂ŁA�� �����R���ɂȂ邱�Ƃ͂Ȃ��B
�@�@�@�@����āA�����P�A�Q �̏ꍇ�ɂ��Ă̂ݒ��ׂ�悢�B
�@�@�@�@�����P�@�̂Ƃ��A�@��2���P�Q�@�i�s�K�j
�@�@�@�@�����Q�@�̂Ƃ��A�@��2���S�X�@���A�@�����V
�@�@�@�@���������āA���߂鎩�R�����́A�@�����Q�@�A�����V�@�̂݁B
�i�R�����g�j�@���^�̓��ŋ��ݍ��ނƂ������z���f���炵���ł��ˁI
���R�@�@![]() �́A�������ł��鎖���ؖ�����B
�́A�������ł��鎖���ؖ�����B
�@�����P�V�N�R���P�Q���ɓ��g�o�̌f���ɁA���̖��Ɋւ��鏑�����݂��������B��쌤
�����̂g�o�ł̉�@��������ƕ�����ɂ��������̂ŁA��������ꂽ ������ �l�̋^�������
���ׂ��A�������������[���čl���Ă݂��B
�i���j�@![]() ���L�����ł���Ƃ��āA
���L�����ł���Ƃ��āA ![]() �� ��/�� �@�i���A�� �͎��R���ŁA�� �́A�ŏ��̂��́j
�� ��/�� �@�i���A�� �͎��R���ŁA�� �́A�ŏ��̂��́j
�@�@�@�Ƃ���B������A �Q��2 = ��2 �邪�A m ����ł���Ƃ���Ɩ�������̂ŁA
�@�@�@�����Q�� �Ȃ鎩�R�� k ������B������A ��2 = �Q��2 �ƂȂ�A �� �������i �����Q���j ��
�@�@�@�Ȃ�A ![]() �� ��/�� �ł��邪�A����́A �� �̍ŏ����ɔ����邩�疵���B
�� ��/�� �ł��邪�A����́A �� �̍ŏ����ɔ����邩�疵���B
�@�@�@�@����� ![]() �͖������ł���B
�͖������ł���B
�i�ʉ��j�@![]() �� ��/�� �@�i���A�� �͎��R���ŁA�� �́A�ŏ��̂��́j�Ƃ���B���̂Ƃ��A
�� ��/�� �@�i���A�� �͎��R���ŁA�� �́A�ŏ��̂��́j�Ƃ���B���̂Ƃ��A
�@�@�@�@�P��![]() ���Q�@�Ȃ̂ŁA�@�O�����������Q���@�����藧�B
���Q�@�Ȃ̂ŁA�@�O�����������Q���@�����藧�B
�@�@�@�@�@�Ƃ���ŁA�@(![]() �{�P)(
�{�P)(![]() �|1) �� 1�@�Ȃ̂ŁA
�|1) �� 1�@�Ȃ̂ŁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() �� �i��Q�|�P�j- 1 - �P
�� �i��Q�|�P�j- 1 - �P
�@�@�@�@���̂Ƃ��A![]() �� ��/�� ���㎮�ɑ������ƁA
�� ��/�� ���㎮�ɑ������ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]() �� (�Q���|��)/(���|��)
�� (�Q���|��)/(���|��)
�@�@�@�@�O�����|�������@�Ȃ̂ŁA����� �� �̍ŏ����ɔ����邩�疵���ł���B
�@�@�@�@�@����� ![]() �͖������ł���B
�͖������ł���B
�i�X�Ȃ�ʉ��j�@�P��![]() ���Q�@�Ȃ̂ŁA�O�� | �P �|
���Q�@�Ȃ̂ŁA�O�� | �P �| ![]() �b ���P �����藧���Ƃɒ��ӂ���B
�b ���P �����藧���Ƃɒ��ӂ���B
�@�@�@�@�@�@�@�@���̂Ƃ��A�� ���\���傫���Ƃ�A�i �P �| ![]() �j�� �͌���Ȃ� �O �ɋ߂Â��B
�j�� �͌���Ȃ� �O �ɋ߂Â��B
�@�@�@�@�@�@�@�@���܁A �i �P �| ![]() �j�� �� �Q ���W�J���āA
�j�� �� �Q ���W�J���āA ![]() �̋����p�Ɗ�p�̍��ɕ�����
�̋����p�Ɗ�p�̍��ɕ�����
�@�@�@�@�@�@�@�@�ƁA�@�i �P �| ![]() �j���@�� ��n �{ ��n
�j���@�� ��n �{ ��n ![]() �ƂȂ鐮���@��n �A ��n �����݂���B
�ƂȂ鐮���@��n �A ��n �����݂���B
�@�@�@�@�@�@�@�@�\���@����A�@��n���P �A ��n���|�P�@�ł���B
�@�@�@�@�@�@�@�@�@![]() ���L�����ł���Ƃ��āA
���L�����ł���Ƃ��āA ![]() �� ��/�� �@�i���A�� �͎��R���j�ƒu���ƁA
�� ��/�� �@�i���A�� �͎��R���j�ƒu���ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@| �P �| ![]() |n �@= | ��n�E�� �{ ��n�E�� |/��
|n �@= | ��n�E�� �{ ��n�E�� |/��
�@�@�@�@�@�@�@�@��n�E�� �{ ��n�E�� �͐����ŁA�O �Ƃ͈قȂ邩��A | ��n�E�� �{ ��n�E�� |���P
�@�@�@�@�@�@�@�@�@����āA| �P �| ![]() |n ���P/���@�ƂȂ�A����́A�i �P �|
|n ���P/���@�ƂȂ�A����́A�i �P �| ![]() �j�� ������Ȃ� �O
�j�� ������Ȃ� �O
�@�@�@�@�@�@�@�@�ɋ߂Â����Ƃɖ�������B
�@�@�@ �@�@�@�@�@����� ![]() �͖������ł���B
�͖������ł���B
�i�R�����g�j�@![]() ���������ł��邱�Ƃ̏ؖ��́A���������Q�ƁB ������ �l�A���̂悤�ȉ�@�ł�
���������ł��邱�Ƃ̏ؖ��́A���������Q�ƁB ������ �l�A���̂悤�ȉ�@�ł�
�@�@�@�@�@�@�������ł��傤���H
���Q�U�O�@�@���� �o�����p�i�����O�A�P�A�Q�A�E�E�E�j��
�@�@�@�@�@�@�@�@�@�@��0���R�@�A�@�����{1����0��1��2�E�E�E�����{�Q
�@�@�@�@�@�@�Œ�߂�Ƃ��A���̈�ʍ������߂�B
�@�@�@[�ޑ�]�@�@��0���P�R�@�A�@�����{1���S(��0��1��2�E�E�E����)2�{�U(��0��1��2�E�E�E����)�{�R
�@���̖��́A���Z�����x���̖��Ȃ̂ŁA���ڂ��������Ă݂邱�Ƃɂ����B
�i���j�@�Q�������A�@�����{1����0��1��2�E�E�E�����{�Q���i�����|�Q�j�����{�Q�@�����藧�B
�@�@�@����āA�@��1���i��0�|�Q�j��0�{�Q���T���Q2�{�P
�@�@�@�@�@�@�@�@�@��2���i��1�|�Q�j��1�{�Q���P�V���Q4�{�P
�@�@�@�@�@�@�@�@�@��3���i��2�|�Q�j��2�{�Q���Q�T�V���Q8�{�P
�@�@�@�@�@�@�@�@�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�@�@���A
�@�@�@�@�@�@�@�@�@�������Q2���{�P
�@�@�@�Ɨސ������B���̗ސ������������Ƃ𐔊w�I�A�[�@�ɂ�莦���B
�@�@�@�@�����O�@�̂Ƃ��A�@���Ӂ���0���R�@�@�E�Ӂ��Q20�{�P���R�@�ŁA���Ӂ��E��
�@�@�@�@�@����āA�����O�@�̂Ƃ����藧�B
�@�@�@�@�������i�����O�j�̂Ƃ����藧�Ɖ��肷��B���Ȃ킿�A�@�������Q2���{�P
�@�@�@�@�@���̂Ƃ��A�@�����{1���i�����|�Q�j�����{�Q��(�Q2���|�P)(�Q2���{�P)�{�Q���Q2���{1�{�P
�@�@�@�@�ƂȂ�A�������{�P�@�̂Ƃ������藧�B
�@�@�@�@�ȏォ��A�@�������Q2���{�P�@�i�����O�A�P�A�Q�A�E�E�E�j�@�����藧�B
�i�R�����g�j�@�m�ޑ�n�����l�ɂł���̂��낤���A���̕���͍��̂Ƃ��떢�����ł���B���
�@�@�@�@�@�@��������l���邱�Ƃɂ��悤�B
(�NjL�j�@�ޑ肪�悤�₭�����܂����I������Ɩ{��̉ɐ���ς������Ėӓ_�ɓ����Ă�
�@�@�@�@�܂����B
�i�ޑ�̉��j�@�@��������0��1��2�E�E�E�����@�Ƃ����ƁA�@��0���P�R�@�ŁA�^����ꂽ�Q�����́A
�@�@�@�@�@�@�@�@�@�@�@�@�����{1/���� ���S����2�{�U�����{�R
�@�@�@�@�@�@�@�@�ƂȂ�B������āA
�@�@�@�@�@�@�@�@�@�@�@�@�����{1 ���S����3�{�U����2�{�R����
�@�@�@�@�@�@�@�@����āA
�@�@�@�@�@�@�@�@�@�@�@�@�Q�����{1�{�P���W����3�{�P�Q����2�{�U�����{�P��(�Q�����{�P)3
�@�@�@�@�@�@�@�@�R���Ƃ��ė��ӂ̑ΐ����Ƃ�ƁA
�@�@�@�@�@�@�@�@�@�@�@�@������3(�Q�����{1�{�P)���R������3(�Q�����{�P)
�@�@�@�@�@�@�@�@������A���� �o������3(�Q�����{�P)�p �́A���� ������3(�Q��0�{�P)��������3�Q�V���R�@�ŁA
�@�@�@�@�@�@�@�@���� �R �̓��䐔��Ȃ̂ŁA
�@�@�@�@�@�@�@�@�@�@�@�@������3(�Q�����{�P)���R�E�R�����R���{1
�@�@�@�@�@�@�@�@�ƂȂ�B
�@�@�@�@�@�@�@�@����āA�@������(�R3���{1�|�P)/�Q�@
�@�@�@�@�@�@�@�@���̂Ƃ��A�@����������/�����|1��(�R3���{1�|�P)/(�R3���|�P)
�@�@�@�@�@�@�@�@�����ŁA�R�������@�Ƃ���ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�R3���{1�|�P���R3���|�P��(�R��)3�|�P��(�R���|�P)((�R��)2�{�R���{�P)
�@�@�@�@�@�@�@�@�@�@�@�@�@�R3���|�P���R���|�P
�@�@�@�@�@�@�@�@����āA�@�@������(�R��)2�{�R���{�P�@�ƂȂ�̂ŁA���ɒu��������ƁA
�@�@�@�@�@�@�@�@�@�@�@�@�@�������R2�E3���{�R3���{�P
�@�@�@�@�@�@�@�@�ƂȂ�B
�i�R�����g�j�@�u�������ɋC�����Ɠ�Ȃ������܂����B��L�̖{��ł͐��w�I�A�[�@�ŋ���
�@�@�@�@�@�@�܂������A���̂悤�ȉ�@��K�p����Β��ړI�ɋ��܂�܂��ˁI
�i�{��̕ʉ��j�@��������0��1��2�E�E�E�����@�Ƃ����ƁA�@��0���R�@�ŁA�^����ꂽ�Q�����́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�����{1/���� �������{�Q
�@�@�@�@�@�@�@�@�@�ƂȂ�B������āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�����{1 ������2�{�Q����
�@�@�@�@�@�@�@�@�@����āA
�@�@�@�@�@�@�@�@�@�@�@�@�@�����{1�{�P��(�����{�P)2
�@�@�@�@�@�@�@�@�@�Q���Ƃ��ė��ӂ̑ΐ����Ƃ�ƁA
�@�@�@�@�@�@�@�@�@�@�@�@������2(�����{1�{�P)���Q������2(�����{�P)
�@�@�@�@�@�@�@�@�@����āA
�@�@�@�@�@�@�@�@�@�@�@�@������2(�����{�P)���Q���{1�@�@���A�@�������Q2���{1�|�P
�@�@�@�@�@�@�@�@�@���̂Ƃ��A����������/�����|1��(�Q2���{1�|�P)/(�Q2���|�P)���Q2���{�P
�i�R�����g�j�@���̉�@�����āA�ޑ肪�{���ɗޑ�ɂȂ��Ă��邱�Ƃɔ[�����܂����B
���Q�U�Q�@�@��1�A��2�A�E�E�E�A���� �𑊈قȂ�����Ƃ���B���̎��A����������
�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�́An - 1 �̑��قȂ�������������Ƃ������B
�i���j�@��ʐ����������ƂȂ��A�@![]() �@�@�ł���Ƃ��Ă悢�B
�@�@�ł���Ƃ��Ă悢�B
�@�@�^����ꂽ�����������̕�����āA
�@�@�@�@![]()
�@�Ƃ����ƁA�@�e�i���j �́A�A�����ł���B�@���̂Ƃ��A
�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@�@�@�@�@�@![]()
�@�ɂ����āA���炩�ɁA�@![]() �@�@�����藧�B
�@�@�����藧�B
�@�@����āA�������@�e�i���j �� �O�@�́A ��1 �� ��2 �̊ԂɎ����������B
�@���l�ɂ��āA
�@�@�@![]() �@�A
�@�A![]() �@�A�@�E�E�E�@�A
�@�A�@�E�E�E�@�A![]()
�@���A�������@�e�i���j �� �O�@�́A ���� �� �����{1 �i�����Q�A�R�A�E�E�E�A���|�P�j �̊ԂɎ����������B
�@�@�ȏォ��A�������@�e�i���j �� �O�@�́A ���|�P �̑��قȂ�������������A�����́A����
�@�������̕���� �O �ɂ��Ȃ��B
�@�@���������āA�^����ꂽ�����������́An - 1 �̑��قȂ�����������B
�i�R�����g�j�@���Z���x�̗e�Ֆ��Ƃ̂��Ƃł����A�A�����̒m�����g���̂ŁA���w�h�h�h
�i���Z
�@�@�@�@�@�@�R�N�j�����ł��傤���H
���Q�U�R�@�@A1�A A2�A�E�E�E�A An ��Ɨ��Ȋm�����ۂƂ���Ƃ��A���̗]����
�@�@�@�@�@�@ A1c�A A2c�A�E�E�E�A Anc ���Ɨ��ɂȂ邱�Ƃ������B
�i���j�@A1c�A A2c�A�E�E�E�A Anc �̂����̔C�ӂ̗L���� �a1�A �a2�A�E�E�E�A �a�������o���āA
�@�@�@�@�@�@�@�o�i�a1�� �a2���E�E�E�� �a���j���o�i�a1�j�o�i�a2�j�E�E�E�o�i�a���j
�@�@�@�����藧���Ƃ������悢�B�������A�a����An��c�@�Ƃ���B
�@�@�@�@�����Q�@�̂Ƃ��A�@�o�i�a1�� �a2�j���o�iAn1c�� An2c�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���P�|�o�iAn1�� An2�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���P�|�o�iAn1�j�|�o�iAn2�j�{�o�iAn1�� An2�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���P�|�o�iAn1�j�|�o�iAn2�j�{�o�iAn1�j�o�iAn2�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@��(�P�|�o�iAn1�j)(�P�|�o�iAn2�j)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���o�iAn1c�j�o�iAn2c�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���o�i�a1�j�o�i�a2�j
�@�@�@�@�@�@����āA�����Q�@�̂Ƃ��A���藧�B
�@�@�@�@�������i�����Q�j�̂Ƃ��A���藧�Ɖ��肷��B���Ȃ킿�A
�@�@�@�@�@�@�a1�A �a2�A�E�E�E�A�a�� �͓Ɨ��Ƃ���B
�@�@���̂Ƃ��A
�@�@�@�@�@�o�i�a1�� �a2���E�E�E�� �a���{1�j
�@�@�@���o�i�i�a1�� �a2���E�E�E�� �a���j�|�o�i�i�a1�� �a2���E�E�E�� �a���j�� �a���{1c�j
�@�@�@���o�i�a1�j�o�i�a2�j�E�E�E�o�i�a���j�|�o�i�a1�j�o�i�a2�j�E�E�E�o�i�a���j�o�i�a���{1c�j
�@�@�@���o�i�a1�j�o�i�a2�j�E�E�E�o�i�a���j�i�P�|�o�i�a���{1c�j�j
�@�@�@���o�i�a1�j�o�i�a2�j�E�E�E�o�i�a���j�o�i�a���{1�j
�@�@����āA�a1�A �a2�A�E�E�E�A�a���A�a���{1 ���Ɨ��ƂȂ�B
�@�@�ȏォ��AA1�A A2�A�E�E�E�A An ���Ɨ��Ȃ�AA1c�A A2c�A�E�E�E�A Anc ���Ɨ��ɂȂ�B
���P�T�@�@���A�� �����萔�Ƃ��A ��(��)����4�{�����{���@�ƒu���B������ ��(��)���O �̎���
�@�@�@�@�@�@����������ł���Ɖ��肷��B���̂Ƃ��A ���A�� �̊Ԃɐ�������W����
�@�@�@�@�@�@���߁A ��(��)���O �̑S�Ẳ��� �� �i���邢�� ���@�j�ŕ\���A���A��
�����̏���
�@�@�@�@�@�@�����Ȃ��瓮���Ƃ��A���̎�肤��͈͂f���ʏ�ɐ}������B
�@�ڂ����́A�ǎ҂̌v�Z�Ɉς˂�Ƃ���̂ŁA�v�Z���Ă݂��B
�i���j�@��(��)����4�{�����{���@���A���̓����́A�@���f(��)���S��3�{���@�ŁA
�@�@�@�@���f(��)���O�@�͂�����̎����� �� �����B�@�������A
�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�ł���B�@���̂Ƃ��A
�@�@�@�@�@�@�@�@�@
�@�@�@�ɂ��A�@��(��) �́A������ �ŋɏ����ŏ��ł���B
�@�@�@��ӂɂ��A������ ��(��)���O �́A����������������̂ŁA ��(��)���O�@�����藧�B
�@�@�@���̂Ƃ��A�@
�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�ɂ����āA
�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@����āA
�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@���Ȃ킿�A�@�Q�V��4���Q�T�U��3�@�����藧�B
�@�@�@�Ƃ���ŁA�@��(��)����4�{�����{�R��4���i���|���j2�i��2�{�Q�����{�R��2�j�@�ƈ������������̂ŁA
�@�@�@������ ��(��)���O �̉��́A�@�������i�d���j�A�i�|�P�}![]() ���j���@�ƂȂ�B
���j���@�ƂȂ�B
�@�@�@���������āA���̑��ݔ͈͂f���ʏ�ɐ}������A���}�̂悤�ɂȂ�B
�@�@�@�@�@�@�@
���P�U�P�@�@�P�A�Q�A�R�A�E�E�E�P�X�A�Q�O �Ɛ����̏����ꂽ�i�e 1 ���A�v 20 ���j�̃J�[�h
�@�@�@�@�@�@�@����A�ǂ̂Q�̃J�[�h���݂��ɘA�����������ɂȂ�Ȃ��悤�� �W ���̃J
�@�@�@�@�@�@�@�[�h�̑I�т����͉��ʂ肠�邩�H
�@�@�@[�ޑ�]�@�@�P�A�Q�A�R�A�E�E�E�Q�X�A�R�O �̂R�O���̃J�[�h����A�ǂ̂Q�̃J�[�h������
�@�@�@�@�@�@�@�̍��� �R �ȏ�ɂȂ�悤�� �W ���̃J�[�h�̑I�т����͉��ʂ肠�邩�H
�@��쌤���������ł́A�Q�ʂ�̉��p�ӂ���Ă���B�{�肾����������A���Z����
���̉Ƃ��ẮA�ʉ��̕������ʂ��ȁH�Ǝv�������A�ޑ�̂��Ƃ��l����Ƃ�͂�{��
�̕����̂Ă������I
�i���j�@�� �P�Q����ׂ�B�@�@������������������������
�@�@�@�����������߂ɂ́A�����̌��Ԃ܂��͗��[�i�~�@�P�R�j����W�I��Ŗ��߂�
�@�@�@�悢�B
�@�@�@�@�@�@�@�@�@�@�@�~���~���~���~���~���~���~���~���~���~���~���~���~
�@�@�@����āA���߂�ꍇ�̐��́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@13�b8���P�Q�W�V�i�ʂ�j
�@�@�@�i���j�@���Ƃ��A�@�~�������~���������~���~���~���~���~���~ �Ƃ����ꍇ�ɑ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �P �@�@�@�@ �T�@�@�@�@�@ 10�@ �P2�@ 14�@ 16
�@18 �@20
�@�@�@�@�@�@�ẮA�W�̐����Ƃ��āA�@�P�A�T�A�P�O�A�P�Q�A�P�S�A�P�U�A�P�W�A�Q�O�@���I���B
�i�ޑ�̉��j�@�܂��A�W�́�����ׁA���̌��ԂɁ~���Q���}������B
�@�@�@�@�@�@�@�@���~�~���~�~���~�~���~�~���~�~���~�~���~�~��
�@�@�@�@�@�@�c��̂W���A�����m�̌��Ԃ܂��͗��[�̌v�X�ӏ�����d���������ĂW�ӏ���I
�@�@�@�@�@�@��ŕ��ׂ�B
�@�@�@�@�@�@�@���̏ꍇ�̐��́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@9�g8��16�b8���P�Q�W�V�O�i�ʂ�j
�@��L�̖��ɑ��āA�炷���邳�狻������ʉ��Ղ����B�i�����P�V�N�T���Q�T���j
�@�I�ꂽ�W�̐��������ɕ��ׂ�Ƃ��A���Ԗڂ̐��ƂP�Ԗڂ̐��́A�Q(���|�P)�ȏ�̍���
����B����āA�@�Q(���|�P)�|(���|�P)�����|�P �����]�T������̂ŁA���Ԗڂ̐�����A���|�P
��
�����čl���Ă��悢�B���̂Ƃ��A���߂�ꍇ�̐��́A�P�`�P�R�̂P�R�̐�����W�̐���I
�ԏꍇ�̐��ɓ������B
�@����āA�@13�b8���P�Q�W�V�i�ʂ�j
�@�ޑ�̕������l�ɉ������Ƃ��ł���B
�@�I�ꂽ�W�̐��������ɕ��ׂ�Ƃ��A�� �Ԗڂ̐��� �P �Ԗڂ̐��́A�R(���|�P)�ȏ�̍�
������B����āA�@�R(���|�P)�|(���|�P)���Q�i���|�P�j �����]�T������̂ŁA��
�Ԗڂ̐�����A
�Q�i���|�P�j �������čl���Ă��悢�B���̂Ƃ��A���߂�ꍇ�̐��́A�P�`�P�U
�̂P�U�̐�����
�W�̐���I�ԏꍇ�̐��ɓ������B
�@����āA�@16�b8���P�Q�W�V�O�i�ʂ�j
�i�R�����g�j�@��쌤�����̉ł́A�~��u���ĕی���������Ƃ������z�ł������A�炷��
�@�@�@�@�@�@�邳��̔��z�͑S���t�ŁA�]���Ȃ��͎̂�菜���Ƃ����l���ł����B�炷���邳��
�@�@�@�@�@�@�̑f���炵���A�C�f�A�Ɋ��Q�������ł��I
���Q�U�X�@�@��ʂƑ��ʂ������ȎO�p��������B������߂̕��ʂŐ��ď㔼��
�@�@�@�@�@�@�@����菜�����Ƃ���A��ʂ̒��_ A1 , A2 , A3 �ɑ��鍂���� h1 ,
h2 ,
�@�@�@�@�@�@�@h3 �ƂȂ����B���̗��̂̑̐ς��ʐ� S �� h1 , h2, h3 �ŕ\���B
�@��쌤�����ɂ��A���Z���x�̗��̖̊��Ƃ������ƂȂ̂ōl���Ă݂��B�@
| �i���j | |
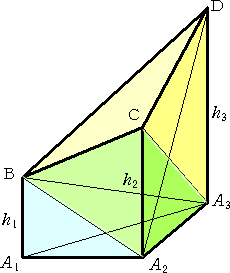 |
�@�@�@�^����ꂽ�O�p�����A���}�̂悤�ɂR�̎O�p�� �@�@�ɕ������čl����B �@�@�@���̂Ƃ��A���߂闧�̂̑̐ς́A�R�̎O�p�� �@�@�@�@�@�a-�`1�`2�`3�@�A�a-�`2�`3�b�@�A�a-�`3�b�c �@�@�̑̐ς̘a�ƂȂ�B �@�@�@�Ƃ���ŁA���� �a�`1 �ƕ��ʂ`2�`3�b �͕��s�Ȃ̂ŁA �@�@�@�@�@�@�a-�`2�`3�b �̑̐ρ��b-�`1�`2�`3 �̑̐� �@�@�����藧�B�@�܂��A���� �b�`2 �Ɛ����c�`3 �͕��s �@�@�Ȃ̂ŁA�@�@�@�@���`3�b�c�����`2�`3�c |
����āA�@�a-�`3�b�c �̑̐ρ��a-�`2�`3�c �̑̐ρ@�����藧�B
�����ŁA���� �a�`1 �ƕ��ʂ`2�`3�c �͕��s�Ȃ̂ŁA�a-�`2�`3�c �̑̐ρ��c-�`1�`2�`3 �̑̐�
���Ȃ킿�A�@�a-�`3�b�c �̑̐ρ��c-�`1�`2�`3 �̑̐ρ@�����藧�B
�@�ȏォ��A���߂闧�̂̑̐ς́A�R�̎O�p��
�@�@�@�@�@�a-�`1�`2�`3�@�A�b-�`1�`2�`3 �@�A�c-�`1�`2�`3
�̘a�ƂȂ�B
�@����āA�@�r�E��1/�R�{�r�E��2/�R�{�r�E��3/�R �� �r�E�i��1�{��2�{��3�j/�R�@�ł���B�@
�i�R�����g�j�@��`�̖ʐς̌����Ƃ̗ސ�����A�����͏\���\�z�ł����B
�@�܂��A��L�̌��ʂ���̐ς͒�ʂ̎O�p�`�̕ӂ̒����ɂ�炸�ʐς݂̂��֗^���邱��
�ɋ��������B���̐����𗘗p����ƁA���̂��Ƃ�������ł��낤�B
�@���������̕ӂ��㉺�Ɉړ������Ă��̐ς͕ς��Ȃ��̂ŁA���������̕ӂ̒���������
�� ��1�{��2�{��3 �ƂȂ�悤�ɁA��L�̗��̐}�`�ɂ����Q�̗��̐}�`���d�˂�ƁA��ʂƒ�
�ʂ����s�ȎO�p�������A�������A���̂R�Ƃ��̐ς͓������B
�i�NjL�j�@��쌤��������A��L�̖��̈�ʉ���^�����T�C�g�u�m�������k�����v�����Љ��
�@�@�@�@�������B�i�����Q�R�N�P�Q���R�P���t���j
�@�@�P���� �e�i���C���j�������{�����{���@�ɑ��āA�e�i�`1�j����1�A�e�i�`2�j����2�A�e�i�`3�j����3 �ŁA
�@���`1�`2�`3 �̏d�S���f�Ƃ���ƁA�@�e�i�f�j���i��1�{��2�{��3�j/�R�@�����藧�B
�@���̂Ƃ��A��L�œ���ꂽ���ʂ́A�@�̐ρ��i��ʐρj�~�e�i�d�S�j�@�Ə������Ƃ��ł���B
���Q�V�S�@�@���� �� �C �� ���A ��2 �{ ���� �{ �Q��2 �� �P �Ȃ���������Ȃ��瓮�����A
�@�@�@�@�@�@�@�Q��2 �| ��2 �̍ő�l�E�ŏ��l�����߂�B
�@�@�@[�ޑ�]�@���� �� �C �� ���A �U��2 �{ �P�Q���� �| �T��2 �� �P �Ȃ���������Ȃ���
�@�@�@�@�@�@�@�������A ��2 �| �Q���� �{ �Q��2 �̍ő�l�E�ŏ��l����т��̎��� x, y �̒l
�@�@�@�@�@�@�@�����߂�B
�@��쌤�����ɂ��A���Z���x�̏����t���ő�ŏ����Ƃ������ƂȂ̂ōl���Ă݂��B
�i���j�@�Q��2 �| ��2 �� ���@�Ƃ����B�@����2 �{ ������ �{ �Q����2 �� ���@��p���āA
�@�@�@�@�@�@�@�i���|�Q�j��2 �{ ������ �{ �i�Q���{�P�j��2 �� �O
�@�@�@�@�� �� �Q�@�̂Ƃ��A�������� �� �A�� �͑��݂���̂ŁA�� �� �Q�@�͋N���蓾��B
�@�@�@�@�� �� �Q�@�̂Ƃ��A�㎮�� �� �̂Q���������ƌ��āA�������������Ƃ���A
�@�@�@�@�@���ʎ��@�c �� ��2��2 �| �S(���|�Q)(�Q���{�P)��2���i��2 �| �S(���|�Q)(�Q���{�P)�j��2 �� �O
�@�@�@�@��2 �� �O�@�Ȃ̂ŁA�@�@��2 �| �S(���|�Q)(�Q���{�P) �� �O
�@�@�@�@���Ȃ킿�A�@�@�V��2 �| �P�Q�� �| �W �� �O
�@�@�@�@���̕s�����̉��ƁA�� �� �Q�@���܂߂āA�萔 �� �̎�蓾��l�͈̔͂́A
| �@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ |
�@�� | �@�� | �@�� | �@ |
�@�@�@�@�����ŁA�@���ʎ��@�c �� �O�@�����萔 �� �� ��0 �ɑ��āA
�@�@�@�@�@�@�@�Q��2 �| ��2�� ��0�@�A�@��2 �{ ���� �{ �Q��2 �� �P
�@�@�@�@�������� �� �A �� �����݂��邱�Ƃ��m�F���Ă������B
�@�@�@�@�@�Q�����������A�d���́A�@�� �� �|��0��/(�Q(��0�|�Q)) �� �����@�Ə�����̂ŁA
�@�@�@�@��2 �{ ���� �{ �Q��2 �� �P�@�ɑ�����āA�@�i��2 �{ �� �{ �Q�j��2 �� �P
�@�@�@�@�ǂ�� �� �ɑ��Ă��A�@��2 �{ �� �{ �Q �� �O�@�Ȃ̂ŁA������ �� �����݂���B
�@�@�@�@�ȏォ��A���ʎ��@�c �� �O�@�����萔 �� �� ��0 �ɑ��āA�m���Ɏ����� �� �A��
�@�@�@�@ �����݂���B
| �@�@�@�@�]���āA�ő�l�́A | �@ |
�@�@�ŏ��l�� | �@ |
�i�R�����g�j�@�O���t�`��\�t�g��p���āA�����Ă݂��B�Ԃ������ő�̏ꍇ�Ő�������
�@�@�@�@�@�@���̏ꍇ�ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�i�ޑ�̉��j�@�@��2 �| �Q���� �{ �Q��2�����@�Ƃ����B�@�U����2 �{ �P�Q������ �| �T����2 �� ���@��p���āA
�@�@�@�@�@�@�@�i�U���|�P�j��2 �{ �i�P�Q���{�Q�j ���� �| �i�T���{�Q�j��2 �� �O
�@�@�@�@�� �� �P/�U�@�̂Ƃ��A�������� �� �A�� �͑��݂���̂ŁA�� ��
�P/�U�@�͋N���蓾��B
�@�@�@�@�� �� �P/�U�@�̂Ƃ��A�㎮�� �� �̂Q���������ƌ��āA�������������Ƃ���A
�@�@�@�㎮�� �� �̂Q���������ƌ��āA�������������Ƃ���A
�@�@�@�@�@���ʎ��@�c/�S �� �i�i�U���{�P�j2 �{ (�U���|�P)(�T���{�Q)�j��2 �� �O
�@�@�@�@��2 �� �O�@�Ȃ̂ŁA�@�@�i�U���{�P�j2 �{ (�U���|�P)(�T���{�Q) �� �O
�@�@�@�@���Ȃ킿�A�@�@�U�U��2 �{ �P�X�� �| �P �� �O�@�@���A�@�@(�Q�Q�� �| �P)(�R�� �{ �P) �� �O
�@�@�@�@�����ŁA�@�����i�� �| ���j2�{��2 �� �O�@�Ȃ̂ŁA�@�R�� �{ �P �� �O
�@�@�@�@����āA�s�����̉��ƁA�� �� �P/�U�@���܂߂āA�萔 �� �̎�蓾��l�͈̔͂́A
�@�@�@�@�@�� ���@�P/�Q�Q�@�@�@�ƂȂ�B
�@�@�@�@�]���āA�ő�l�́A�Ȃ��ŁA�ŏ��l�́A�@�P/�Q�Q�@�@�ł���B
�@�@�@�@���̂Ƃ��A�@�� �� (7/4)���@�Ȃ̂ŁA�U��2 �{ �P�Q���� �| �T��2 �� �P�@�ƘA�����āA
�@�@�@�@�@�@�@�@�@![]() �@�@�A
�@�@�A![]()
�@�@�@�@��B�������A���������ł���B
�i�R�����g�j�@�O���t�`��\�t�g��p���āA�����Ă݂��B�Ԃ�������ʂ̏ꍇ�Ő�������
�@�@�@�@�@�@���̏ꍇ�ł���B
�@�@�@�@�@�@�@�@�@�@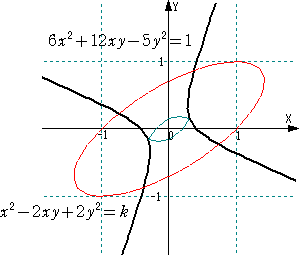
���P�R�@�@f (x) = x3 - 3x2 - 3x �ƒu���B���̊��͋ɑ�l�A�ɏ��l�����ꂼ��1��
�@�@�@�@�@�@��邪�A�����̘a�Ɛς����߂�B�i���Z�Q�N���x�̗e�Ֆ��j
�i���j�@ �O�����̃O���t�́A�ϋȓ_�ɂ��ē_�Ώ̂Ȃ̂ŁA�ϋȓ_�́A�ɑ�_�Ƌɏ��_
�@�@�@�@�̒��_�ł���B
�@�@�@�@�@�@�@�e�h(�w) ���U�w�|�U���O�@ ���A�w���P
�@�@�@�@�@����āA�e(�P)���i�ɒl�̘a�j/�Q�@�Ȃ̂ŁA
�@�@�@�@�@�@�@�@�@�@�@�@�i�ɒl�̘a�j���Q �e(�P)���Q�i�P�|�R�|�R�j���|�P�O
�@�@�@�@�ł���B�i�I�j
���Q�U�W�i����j�@�@�` �� �R�������s��ŁA�Ίp���������ׂ� 0�A���̑��̐�����
�@�@�@�@�@�@�@�@�@�@�@���ׂ� 1/�Q �Ȃ���̂Ƃ���B���̂Ƃ��A�s��̂���̋Ɍ�
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ ![]()
�@�@�@�@�@�@�@�@�@�@�@�����߂�B
�@����ł͈�ʂ� �� �������s��i�����R�j�ł��邪�A�����R �Ƃ��Ă����̎�|�ɂ͔�����
���Ǝv���B
�@���̖��̖ʔ����́A�ɂ�������Ă���Ƃ���A���̂悤�Ȕw�i������_�ł���B
�@�R�l���������o�������B����͊e���C�ӂ̋��z���o�����A�Q��ڈȍ~�́A���̃��[
���ɏ]���ďo�����̂Ƃ���B
�@�@���[���F�@�O�̉�Ɏ����ȊO�̂Q�l���o�������z�̕��ϊz���o��
���̑���𑱂��Ă����ƁA�R�l���o�����z�͂Ƃ��ɁA������z�ɋ߂Â��Ă����B
�i�R�����g�j�@����̋��z�ɂǂ�قǂ���������Ă��Ō�͓����悤�ȋ��z�ɂȂ��Ă���
�@�@�@�@�@�@�Ƃ����_���ʔ����ł��ˁI
�@�����ł́A��쌤�����̉Ƃ͈قȂ邪�ł��W���I�Ǝv�����^�������Ǝv���B
�i���j�@�������i�`�|�ɂd�j���O�@�@���A�@�S��3�|�R�Ɂ|�P���O
�@�@����������āA�@�Ɂ��P�A�|1/2 �i�d���j�@�ƂȂ�B
�@���̂Ƃ��A�ŗL�l �Ɂ��P �ɑ�����ŗL�x�N�g���Ƃ��āA�@�i�P�C�P�C�P�j�@���Ƃ邱�Ƃ��ł���B
�܂��A�ŗL�l �Ɂ��|1/2 �ɑ�����ŗL�x�N�g���Ƃ��āA�@�i�P�C�|�P�C�O�j�A�i�P�C�P�C�Q�j�@���Ƃ�
���Ƃ��ł���B�@�����R�̃x�N�g���݂͌��ɐ����ł���B
�@����āA�e�x�N�g���̐��K�����s���A�R���̐����s��
�@�@�@�@�@�@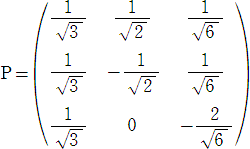
�������B���̂Ƃ��A
�@�@�@�@�@�@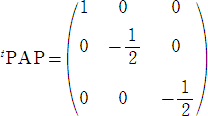
�ƂȂ�̂ŁA
�@�@�@�@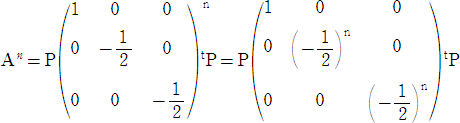
�@����āA
�@�@�@�@�@�@�@�@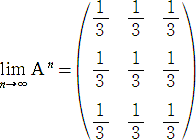 �@�@�@�@�i�I�j
�@�@�@�@�i�I�j
�i�Q�l�j�@ �� ��ڂɂR�l �`�A�a�A�b ���o�����z���A���ꂼ�� �����A�����A���� �Ƃ����B
�@�@�@�@��L���A�����A�����A���� �́A�i��1�{��1�{��1�j/�R�@�Ɏ������邱�Ƃ�������B
�@�����ŁA�������A�����A�����A���� �̎��������肷��A���̂悤�ȉ����蓾�邾�낤�B
�@�i���j�@�@�@�������A�@�@�����{1��(1/2)�����{(1/2)����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �����{1��(1/2)�����{(1/2)����
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@ �����{1��(1/2)�����{(1/2)����
�@����āA�@�����{1�|�����{1��(�|1/2)�i�����|�����j�@�@���A�@�@�����|������(�|1/2)���|1�i��1�|��1�j
�@�@�@�@�@�@�@�����{1�|�����{1��(�|1/2)�i�����|�����j�@�@���A�@�@�����|������(�|1/2)���|1�i��1�|��1�j
�@���̂��Ƃ���A�����A�����A���� �͓���̒l�Ɏ�������B
����ɁA�����{�����{���� �� ��1�{��1�{��1 �Ȃ̂ŁA�@�����A�����A���� �́A�i��1�{��1�{��1�j/�R�@�Ɏ���
����B����āA
�@�@�@�@�@�@�@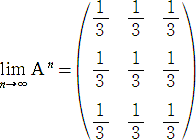 �@�@�@�@�@�i�I�j
�@�@�@�@�@�i�I�j
�i�R�����g�j�@�����A���Q�U�W�ɑ��ẮA��L�̂悤�ȕʉ����v�������������ɒf�O�����B
�@�@�@�@�@�@�����|�����@���O�Ɏ������Ă��A�����A���� ����������Ƃ͌���Ȃ�����ł���B
�@�@�@�@�@�@�i����j�@���������{�Q/���@�A���� �����{�P/��
���Q�X�R�@�@�P�{![]() �́A a �{ b
�́A a �{ b![]() �@�i ���A�� �F �L�����j�̌`�̐��̕����̘a�ɂȂ�
�@�i ���A�� �F �L�����j�̌`�̐��̕����̘a�ɂȂ�
�@�@�@�@�@�@�@�Ȃ����Ƃ������B
�@���̖��͍��Z�Q�N�����x�̊i�D�̉��K���Ƃ�����B�����ł͍��Z���炵������
�������Ǝv���B
�i���j�@ �P�{![]() ���i���{��
���i���{��![]() �j2�{�E�E�E�{�i���{��
�j2�{�E�E�E�{�i���{��![]() �j2�@�Ə�������̂Ɖ��肷��B
�j2�@�Ə�������̂Ɖ��肷��B
�@�@�@���̂Ƃ��A�@�E�Ӂ���2�{�E�E�E�{��2�{�Q��2�{�E�E�E�{�Q��2�{�Q�i�����{�E�E�E�{�����j![]()
�@�@�Ȃ̂ŁA���ӂƔ�r���āA
�@�@�@�@�@��2�{�E�E�E�{��2�{�Q��2�{�E�E�E�{�Q��2���P�@�A�@�Q�i�����{�E�E�E�{�����j���P
�@�@����āA�@��2�{�E�E�E�{��2�{�Q��2�{�E�E�E�{�Q��2���Q�i�����{�E�E�E�{�����j�@����A
�@�@�@�@�@�@�@�@�i���|���j2�{�E�E�E�{�i���|���j2�{��2�{�E�E�E�{��2���O
�@�@���A���A�E�E�E�A���A���@�͗L�����Ȃ̂ŁA���̕����͂O�ȏ�B
�@�@���������āA�@�@���|�����E�E�E�����|���������E�E�E�������O�@�@���Ȃ킿�A
�@�@�@�@�@�@�@�@�@�@���������E�E�E�����������O�@
�@���̂Ƃ��A�@�@�P�{![]() ���O�@�ƂȂ�A��������B
���O�@�ƂȂ�A��������B
�@����āA�P�{![]() �́A���{��
�́A���{��![]() �@�̌`�̐��̕����̘a�ɂȂ�Ȃ��B�@�i�؏I�j
�@�̌`�̐��̕����̘a�ɂȂ�Ȃ��B�@�i�؏I�j
�@�����ŁA��쌤�����̉�⑫���Ă��������B
�@���̎������p������B
�@�L���W���̐������� f (x) = �O�@���A�� �{ ![]() �@�����Ɏ��ĂA�� �|
�@�����Ɏ��ĂA�� �| ![]() �@���܂���
�@���܂���
�ł���B�������A���A�� �͗L������![]() �@�͖������Ƃ���B
�@�͖������Ƃ���B
�@���̎����܂��āA���̂悤�ȉɂȂ�Ǝv���B
�i���j�@�P�{![]() ���i���{��
���i���{��![]() �j2�{�E�E�E�{�i���{��
�j2�{�E�E�E�{�i���{��![]() �j2�@�Ə�������̂Ɖ��肷��B
�j2�@�Ə�������̂Ɖ��肷��B
�@�@�@���̂��Ƃ���A�L���W���̐��������@�@�P�{�����i���{�����j2�{�E�E�E�{�i���{�����j2�@�́A
�@�@����![]() �@�����Ɏ����Ƃ�������̂ŁA��L��������A�@�����|
�@�����Ɏ����Ƃ�������̂ŁA��L��������A�@�����|![]() �@�����ƂȂ�B
�@�����ƂȂ�B
�@�@�@����āA�@�@�P�|![]() ���i���|��
���i���|��![]() �j2�{�E�E�E�{�i���|��
�j2�{�E�E�E�{�i���|��![]() �j2
�j2
�@�@�����藧�B�@���̂Ƃ��A�@���ӂ̕����͕��A������ɁA�E�ӂ̕����͂O�ȏ�B
�@�@�@����͖����ł���B
�@�@����āA�P�{![]() �́A���{��
�́A���{��![]() �@�̌`�̐��̕����̘a�ɂȂ�Ȃ��B�@�i�؏I�j
�@�̌`�̐��̕����̘a�ɂȂ�Ȃ��B�@�i�؏I�j
���P�O�R�@�@���̗l�ȃQ�[�����l����B�F
�@�@�@�@�@�@�@�g�����v�̂P����U�܂ł̎D���S�����v�Q�S������B�����𐔎�������
�@�@�@�@�@�@��悤�ɕ\�ɂ��āA�e�[�u���̏�ɕ��ׂ�B
�@�@�@�@�@�@�@���E���̂Q�l�̋��Z�҂����ԂɂP���������ꂩ�̃J�[�h�����B
�@�@�@�@�@�@���̂Ƃ��A����܂łɎ��ꂽ���҂̃J�[�h�̐��̘a�x�R�P�ɂ����l��
�@�@�@�@�@�@�u�����v�A�R�P�����l���u�����v�Ƃ���B���̃Q�[���̕K���@�͂ǂ��Ȃ��
�@�@�@�@�@�@���낤���H
�@���̃Q�[���́A�P����n�߂ĘA�����鐔�����U�ȉ������݂ɂȂ��Ă����āA�Ō��
�R�P���������l�������Ƃ����Q�[���A�����A�`�u�P�A�Q�A�R�v�A�a�u�S�A�T�v�A�`�u�U�A�V�A�W�A�X�A10�v�A�a
�u11�A12�A13�A14�v�A�`�u15�A16�A17�v�A�a�u18�A19�A20�A21�v�A�`�u22�A23�A24�v�A�a�u25�A26�A27�v�A
�`�u28�A29�A30�A31�E�E�E�Ŏ��̏����I�v�Ƃ������̂Ɏ��Ă���B
�@���̏ꍇ�͐��K���ł���A���́u�R�A�P�O�A�P�V�A�Q�S�v�i���c��̐����V�̔{���ɂ��đ�
��Ɏ��n���I�j�Ƃ������܂Ō����悢�B
�@�������A��L�̖��ł͎g���鐔���̌��ɐ���������A�͂邩�ɓ���Q�[���ƂȂ�
����B
�@��쌤�����̉ɂ�����ʂ�A�{�������p�^�[���ł���u�R�v��������ꍇ�A���K�s
�ɂȂ�Ƃ����_�ɋ������ꂽ�B
�@�@�R�{�S�{�R�{�S�{�R�{�S�{�R�{�S�{�H
�@�H�ŁA�u�R�v����肽���Ƃ��낾���A���ɂS���S�Ă��g�����Ă��܂��Ă���̂Ŏ�ꂸ�A
�u�����v���m�肵�Ă��܂��B
�@�������A��쌤�����ɂ��A���̃Q�[���͂�͂����K�����������B
�@�u�ŏ��ɉ������ΕK���ƂȂ邩�A�S�Ē��ׂĂ݂ĉ������B�v�Ƃ������ƂȂ̂ŁA��v�Z��
�������ׂĂ݂��B
���@��肪�u�P�v��������ꍇ
�@�@����ɑ��āA��肪�R�ȏ��������ꍇ�A���̐��̎�Ԃ̂Ƃ��A���v�P�O�ɂ��邱��
�@���ł���̂ŁA����͐��K���p�^�[���ł���B
�@�@���́A��肪�u�P�܂��͂Q�v��������ꍇ�ł���B
�@��肪�u�P�v��������ꍇ�A���́u�U�v�����A���K���p�^�[���ł���B
�@�@�P�{�P�{�U�{�Q�{�U�{�P�{�U�{�P�{�U�{�H
��肪�������u�U�v�����Ȃ��ꍇ
�@�@�P�{�P�{�P�{�T�{�Q�{�T�{�Q�{�T�{�Q�{�U�{�H�@�Ō��̏���
�@�@�P�{�P�{�Q�{�S�{�Q�{�T�{�Q�{�T�{�Q�{�T�{�H�@�Ō��̏���
�@�@�P�{�P�{�R�{�R�{�Q�{�U�{�P�{�U�{�P�{�U�{�H�@�Ō��̏���
�@�@�P�{�P�{�S�{�Q�{�Q�{�T�{�Q�{�T�{�Q�{�T�{�H�@�Ō��̏���
�@�@�P�{�P�{�T�{�P�{�Q�{�T�{�Q�{�U�{�P�{�U�{�H�@�Ō��̏���
�@��肪�u�Q�v��������ꍇ�A���́u�U�v�����悢�B���̂Ƃ��A���K���p�^�[���ɂ���
���߂Ɍ��́u�P�v����邵���Ȃ��B���̎����𑱂���B
�@�@�P�{�Q�{�U�{�P�{�U�{�P�{�U�{�P�{�U�{�H
�@����ƁA���́A�H�ŁA�u�P�v�����Ώ����ɂȂ�̂����A�u�P�v�͊��ɂS���g�����Ă���
�̂Ŏ�ꂸ�A���̕������m�肷��B
���@��肪�u�Q�v��������ꍇ
�@�@��肪�u�P�v��������ꍇ�Ɠ��l�ɍl����B�@��肪�R�ȏ��������ꍇ�A���̐���
�@��Ԃ̂Ƃ��A���v�P�O�ɂ��邱�Ƃ��ł���̂ŁA����͐��K���p�^�[���ł���B
�@�@���́A��肪�u�P�܂��͂Q�v��������ꍇ�ł���B
�@��肪�u�P�v��������ꍇ
�@���̏ꍇ�́A���̂悤�Ȑ��K���p�^�[�����l������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i���͌��K���p�^�[���ɂȂ�悤�Ɏ����̂Ɖ���j
�@�@�Q�{�P�{�T�{�Q�{�T�{�Q�{�T�{�Q�{�T�{�H�@�@�i�u�Q�v���g�����Ă��܂��A�������m��j
�@��肪�u�Q�v��������ꍇ
�@���́u�Q�v�����A���K���p�^�[���ł���B
���ۂɁA�@�Q�{�Q�{�Q�{�S�{�T�{�Q�{�T�{�P�{�P�{�R�{�S
���@��肪�u�R�v��������ꍇ
�@��肪�u�R�v������Ă��܂��ƁA���K�s�ł���B
�@�@�R�{�R�{�S�{�S�{�R�{�S�{�R�{�S�{�H
�@�܂��A��ŏq�ׂ��悤�ɁA��肪�u�S�v������Ă��܂��ƁA���K�s�ł���B
�@�@�R�{�S�{�R�{�S�{�R�{�S�{�R�{�S�{�H
���@��肪�u�S�v��������ꍇ
�@��肪�u�U�v������Ă��܂��ƁA���K�s�ł���B���ɐ�肪������낤�Ƃ��A���͑���
�āu�V�v�ɂȂ鐔���Ƃ�邩��ł���B
�@�܂��A��肪�u�R�v������Ă��A���K�s�ł���B
�@�@�S�{�R�{�R�{�S�{�R�{�S�{�R�{�S�{�H
���@��肪�u�T�v��������ꍇ
�@�@�T�{�T�{�Q�{�T�{�Q�{�T�{�Q�{�S�{�P
�@�̂悤�Ȏ菇�ŁA���K���I
���@��肪�u�U�v��������ꍇ
�@��肪�u�S�v������Ă��܂��ƁA���K�s�ł���B���ɐ�肪������낤�Ƃ��A���͑���
�āu�V�v�ɂȂ鐔���Ƃ�邩��ł���B
�@�ȏォ��A���K���ƂȂ邽�߂ɂ́A����u�P�܂��͂Q�܂��͂T�v�����悢�B
�i�R�����g�j�@���̖��ɂ��āA���g�o�����������b�ɂȂ��Ă���A�g�m�u�炷����v�����
�@�@�@�@�@�@�������Ă����������B��L�̉́A�����A�b�v���[�h�������̂��C�����Ă�
�@�@�@�@�@�@��B�Ƃ��āA�܂��s���S�ȕ��������邩������Ȃ����A�ǎ҂̕��ɂ́A����
�@�@�@�@�@�@���̕��͋C���`���ΐ����ƌ����邾�낤�B���ōl����Ɣ��ɕ��G�ŁA�u�v
�@�@�@�@�@�@�����ȏ�ɉ��̐[�����ł����B�v�ƁA�炷���邳��͊��z���q�ׂ��Ă���B��
�@�@�@�@�@�@�������I�o��҂̑�삳����A���Z���̍��A�ɂɂ܂����Ă���݂Ԃ��ɍl����
�@�@�@�@�@�@�ꂽ�����ŁA�������C���K�v�Ȗ��̂悤�ł��B�����̍��Z���ɂ͖������ȁH
���R�P�U�@�@���� { (�P�{�P/��)�� } �͒P�������A { (�P�{�P/��)���{1 } �͒P�������ł�
�@�@�@�@�@�@�@�邱�Ƃ�ΐ���l�C�s�A�̐��ȑO�̍��Z�P�N���x�̐��w�ŏؖ�����B
�@�u���Z�P�N���x�̐��w�Łv�Ƃ����Ƃ���Ɉ����ꂽ�B��쌤�����̏ؖ����Q�l�ɂ��Ȃ���
�����ؖ������Ă݂��B�i���Q�l�F���d���ς̒���j
�i�ؖ��j�@�P�{�P/�� �� 1 �̏d�݂����ꂼ�� �� �� �P �Ƃ��ĉ��d���ς��Ƃ�ƁA
�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@���̂Ƃ��A���敽�ς́A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@����āA
�@�@�@�@�@�@�@�@�@�@![]() �@�@�i�����͕s�����I�j
�@�@�i�����͕s�����I�j
�@�@�@�@���Ȃ킿�A
�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�@���̂��Ƃ́A���� { (�P�{�P/��)�� } ���P�������ł��邱�Ƃ������B
�@�@�@���l�ɂ��āA�㔼�������������B
�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@���������߂ɁA
�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�̗��ӂ̋t�����Ƃ���
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�������悢�B
�@�@�@�@�����ŁA��/�i���{�P�j �� 1 �̏d�݂����ꂼ�� ���{�P �� �P �Ƃ��ĉ��d���ς��Ƃ�A����
�@�@�@���ςƂ̊W���l����Ώ�L�̕s�����͒����Ɏ������B�@�i�؏I�j
�i�R�����g�j�@���� { (�P�{�P/��)�� } ���P�������ł��邱�Ƃ͏��Г��ł͉��L�̂悤�Ɏ������
�@�@�@�@�@�@���ʏ�ł���B
�@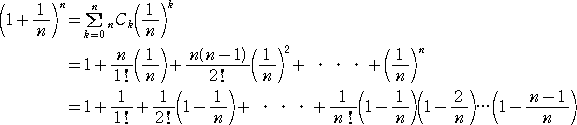
�@![]()
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@��L�Q���̊e�����r���邱�Ƃɂ��A
�@�@�@�@�@�@�@�@�@![]()
�ł��邱�Ƃ�������B
�i�R�����g�j�@�������ςƑ��敽�ς̊W��p���ĊȖ��ɏؖ������Ƃ͋����ł��I
�@�@�������A��L�̏ؖ��͏����I�ł��邪�A�r�͂������Ď������@�����݂���B
�@��
�@�@�@�@�@![]()
���A�����O�@�ɂ����đ������ł��邱�Ƃ��A�����@��p���Ď����B
�@�ΐ������@�ɂ��A�@������ �e�i���j�����i������ �i���{�P�j�|������ ��
�j ����A
�@�@�@�e�f�i���j/�e�i���j�������� �i���{�P�j�|������ �� �{ ���i�P/�i���{�P�j�|�P/���j
�@�@�@�@�@�@�@�@�@�@�@�������� �i���{�P�j�|������ �� �| �P/�i���{�P�j
�@�@�����ŁA�@�f�i���j�������� �i���{�P�j�|������ �� �| �P/�i���{�P�j�@�Ƃ����āA����ɔ�������ƁA
�@�@�@�f�f�i���j���P/�i���{�P�j�|�P/�� �{ �P/�i���{�P�j2���|�P/���i���{�P�j2���O
�@���A�� �f�i���j �͒P���Ɍ�������B
�@�@�� ���@���@�̂Ƃ��A�@�f�i���j���������i�P�{�P/���j�| �P/�i���{�P�j
���@�O
�@�Ȃ̂ŁA�@�����O�@�̂Ƃ��A�@�f�i���j���O�@�ł���B
�@�@����āA�@�e�f�i���j/�e�i���j���O�@�A�@�e�i���j���O�@���A�@�e�f�i���j���O
�@����āA�� �e�i���j �͒P���ɑ�������B
�i�R�����g�j�@�������g�����A���������ؖ������������Ă����ł��ˁI
| ���R�Q�U�@�@�� | �i �� �� �O �j �ɑ��āA���̋Ɍ��l�����߂�B | |
| �@ | ||
| �@�j | ||
| �@ | ||
| �A�j | ||
�@��쌤�����ł͂܂��������Ƃ������Ƃł��邪�A���Z���x�̖��Ƃ��������ɗU�f
����Ē��킵�Ă݂��B
�i���j�@�@�j�@���ϒl�̒藝���A
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�e�i���{�P�j�|�e�i���j���e�f�i���j�@�i�@��
�� �� �� ���{�P�@�j
�@�@�@�@�@�@�@�ƂȂ� �� �����݂���B�����ŁA�@������ �e�i���j�����i�������i���{�P�j�|������
�� �j�@�Ȃ̂ŁA
�@�@�@�@�@�@�@�@�@�@�@�@�e�f�i���j���e�i���j�o�������i���{�P�j�|������
�� �|�P/�i���{�P�j�p
�@�@�@�@�@�@�@�����������i���{�P�j�|������ �� �|�P/�i���{�P�j�@�ɂ����āA
�@�@�@�@�@�@�@�@�@�@���f���|�Q/�i���{�P�j2���O�@�Ȃ̂ŁA�� �͒P���Ɍ�������B
�@�@�@�@�@�@�@����āA�@�� �� �� �� ���{�P�@���A
�@�@�@�@�@�@�@�������i���{�Q�j�|�������i���{�P�j �|�P/�i���{�Q�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���������i���{�P�j�|������ �� �|�P/�i���{�P�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���������i���{�P�j�|������ �� �|�P/�i���{�P�j
�@�@�@�@�@�@�@�� �� ���@�̂Ƃ��A�@�� �� �O�@�Ȃ̂ŁA�@�����O�@�ƂȂ�A�@�e�f�i���j���O
�@�@�@�@�@�@�@����āA�@�e�i���j�͒P���ɑ�������̂ŁA
�@�@�@�@�@�@�@�e�i���j�o�������i���{�Q�j�|�������i���{�P�j �|�P/�i���{�Q�j�p
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���e�i���j�o�������i���{�P�j�|������ �� �|�P/�i���{�P�j�p
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@���e�i���{�P�j�o�������i���{�P�j�|������
�� �|�P/�i���{�P�j�p
�@�@�@�@���Ȃ킿�A
�@�@�@�@�@�@�@��2�E�e�i���j�o�������i���{�Q�j�|�������i���{�P�j �|�P/�i���{�Q�j�p
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@����2�E�i�e�i���{�P�j�|�e�i���j�j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@����2�E�e�i���{�P�j�o�������i���{�P�j�|������ �� �|�P/�i���{�P�j�p
�@�@�@�@�@�@�@�����ŁA�@�� �� ���@�̂Ƃ��A�@�e�i���j �� ���@�A�e�i���{�P�j
�� ���@�ł���B
�@�@�@�@�@�@�@�܂��A�@���s�^���̒藝���A�@�� �� ���@�̂Ƃ��A
�@�@�@�@�@�@�@�@�@������ ��2�o�������i���{�P�j�|������ �� �|�P/�i���{�P�j�p
�@�@�@�@�@�@�@�� ������ �o�������i���{�P�j�|������ �� �|�P/�i���{�P�j�p/�i�P/��2�j
�@�@�@�@�@�@�@�� ������ �o�P/�i���{�P�j�|�P/�� �{�P/�i���{�P�j2�p/�i�|�Q/��3�j
�@�@�@�@�@�@�@�� ������ ��2/�o�Q�i���{�P�j2�p�� �P/�Q
�@�@�@���l�ɂ��āA
�@�@�@�@�@�@�@�@�@������ ��2�o�������i���{�Q�j�|�������i���{�P�j �|�P/�i���{�Q�j�p
�@�@�@�@�@�@�@�� ������ �o�������i���{�Q�j�|�������i���{�P�j �|�P/�i���{�Q�j�p/�i�P/��2�j
�@�@�@�@�@�@�@�� ������ �o�P/�i���{�Q�j�|�P/�i���{�P�j �{�P/�i���{�Q�j2�p/�i�|�Q/��3�j
�@�@�@�@�@�@�@�� ������ ��3/�o�Q�i���{�P�j�i���{�Q�j2�p�� �P/�Q
�@�@�@�@�@�@�@���������āA�������̌����ɂ��A�@�� �� ���@�̂Ƃ��A
�@�@�@�@�@�@�@�@�@�@�@�@��2�E�i�e�i���{�P�j�|�e�i���j�j �� ��/�Q
�A�j�@���s�^���̒藝���A�@�� �� ���@�̂Ƃ��A
�@������ ���i���|�e�i���j�j�� �������i���|�e�i���j�j/�i�P/���j�� �������i�|�e�f�i���j�j/�i�|�P/��2�j�� ������ ��2�E�e�f�i���j
�@�����ŁA�@�j�ɂ�����v�Z���ʂ�p���āA�@�� �� ���@�̂Ƃ��A�@�e�i���j
�� ���@�ŁA
�@�@�@�@�@�@������ ��2�o�������i���{�P�j�|������ �� �|�P/�i���{�P�j�p�� �P/�Q
�ł���B�@���������āA�@�� �� ���@�̂Ƃ��A�@������ ���i���|�e�i���j�j����/�Q�@�ł���B
�i�R�����g�j�@���Z���x�̖��Ƃ������Ƃł��邪�A������ƕW���I�ȍ��Z���ɂ͌��������ȁH
�@�@�@�@��L�̌��ʂ���A�@�� �� ���@�̂Ƃ��A�@���i���|�e�i���j�j�@�͗L���m��l�Ɏ�������̂ŁA
�@�@�@�P/���@�Ɓ@���|�e�i���j �͓��ʂ̖������ł���B��������A�e�i���j��
�� �Ɏ������鑬���́A
�@�@�@�P/���@�� �O �Ɏ������鑬���ɂقړ������Ƃ������Ƃł���B �����P/���@�̃O���t���A����
�@�@�@�`���Ă��炦�Ε�����悤�ɁA���̎������鑬���͔��ɒx���A�ہA�x������D�D�D�I
�@�@�@����ɑ��āA
�@�@�@�@�@�@�@�@�@�@�@�@![]()
�@�@�@�����R�ΐ��̒� �� �Ɏ������鑬���ُ͈�ɑ����A�ہA��������D�D�D���炢�I�I
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i���@�Q�l�F�u���R�ΐ��̒� �� ���������ł��邱���v�j
���R�R�X�@�@�� �Ɋւ���R�������� x3 + x2 - 4x + 1 = 0 �̂R�������߂�B
�@��쌤�����̂g�o�ł́A�R���������̂R���� ���A���A�� �Ƃ��āA
�@�� = 2������(2��/13) + 2�������i16��/13�j = 0.273891..........
�@�� = 2�������i4��/13�j + 2�������i32��/13�j = 1.3772...............
�@�� = 2�������i8��/13�j + 2�������i64��/13�j = -2.65109............
�Ɠ����^�����Ă���B
�@���g�o�����������b�ɂȂ��Ă���g�m�u�炷����v����́A���̂悤�ɍl�@����Ă���B
�@�� = e2��i/13�@�A �� = e-2��i/13�@�Ƃ����ƁA
�@�@�� = ��+��+��8+��8 = ��+��+��5+��5
�@�@�� = ��2+��2+��16+��16 = ��2+��2+��3+��3
�@�@�� = ��4+��4+��32+��32 = ��4+��4+��6+��6
�@���̂Ƃ��A�@��2 = (��+��+��5+��5)2 = ��+2��+4
�@�@�@�@�@�@�@�@��2 = (��2+��2+��3+��3)2 = ��+2��+4
�@�@�@�@�@�@�@�@��2 = (��4+��4+��6+��6)2 = ��+2��+4
�Ȃ̂ŁA�@��+��+�� = ��+��+��5+��5+��2+��2+��3+��3+��4+��4+��6+��6
�@�@�@�@�@�@�@�@�@�@�@�@= ��+��2+��3+��4+��5+��6+��6+��5+��4+��3+��2+��
�@�@�@�@�@�@�@�@�@�@�@�@= ��+��2+��3+��4+��5+��6+��7+��8+��9+��10+��11+��12 = -1
�@�@�@�@�@�@��2+��2+��2 = 3(��+��+��+4) = 9
�@�@�@�@�@�@����+����+���� = {(��+��+��)2 - (��2+��2+��2)}/2 = (1 - 9)/2�@= -4
�@�@�@�@�@�@��3+��3+��3 = ��(��+2��+4) + ��(��+2��+4) + ��(��+2��+4)
�@�@�@�@�@�@�@�@�@�@�@�@�@�@= 3(����+����+����)+4(��+��+��) = -16
�@�@�@�@�@�@������ = {(��+��+��)3 - 3(��+��+��)(��2+��2+��2) + 2(��3+��3+��3)}/6
�@�@�@�@�@�@�@�@�@�@= {(-1) - 3�E(-1)�E9 + 2�E(-16)}/6 = -1
�@����āA ��+��+�� = -1�A ����+����+���� = -4�A ������ = -1 �Ȃ̂ŁA���A���A�� �́A
��3 + ��2 - 4�� + 1 = 0 �̂R���B
�@�Ȃ��A f (��) = ��2 + �� - 3�A g (��) = (�� - 1)/�� �ƒu���ƁA�����̊��͉�����������̂R��
���A���A�� �� �� �� �� �� �� �� �� �̏��Ɉڂ�����������܂��B
�@g (��) �����g�� �R������ƍP���ʑ��ɂȂ鎖�A (i�De�D g (g (g (��))) = ��)�A f (��) = g (��)
�����̕������Ɠ��l�ɂȂ鎖�ȂǁA�ʔ����ł��ˁB�iLast Update 2009/10/13�j
�i���@�Q�l�F�u�������_�v�A�u���̏����v�j
�i�NjL�j�@��쌤�������A���̏���ɂ��āA�i�D�o�D�r�������� �����������Љ�������܂�
�@�@�@�@���B�i�����Q�R�N�P�Q���R�P���t���j
�@�u�e(��) ��L���W���������ŁA�L�����͈̔͂Ŋ���Ƃ���B�e(��) �̔C�ӂ̂Q��
���A��
�ɑ��A�K���ȗL���W���������ŁA�� = g(��) �Ȃ镨�����݂���Ƃ��A�e(��)
�� Galois ����
���ƌĂԎ��ɂ���B�ȉ��̑����� �e(��) �́AT���L�����ŁAQ�����̂Ƃ��A
�@�@�@�@�@�e(��) = ��3 - T��2 + (T - 3)�� + 1 = 0
�́AGalois �������ƂȂ�B�v�Ƃ������Ƃ������Ă���Ƃ̂��ƁB2-nd edition
�ɂ́A��荂����
�����R�����Ă��邻���ł��B