
いろいろな平均があるが、このページでは相加平均の一般化である加重平均について
考え、その応用を見てみたいと思う。
実数 A、B、C に対して、
(ただし、p、q、r は非負の実数で少なくとも一つは 0 でない)
を、A、B、C の加重平均といい、p、q、r をそれぞれA、B、C の重みという。
n 個の実数に対しても同様に加重平均は定義される。
例 実数 A、B、C の相加平均(算術平均)は、
であるが、これは上記の加重平均で、p=q=r=1 の場合である。
例 6人のテスト(5点満点)の結果、得点が 2、4、5、4、4、5 であるとき、
得点合計=2+4+5+4+4+5=24 を出して、24÷6=4 と人数で割って得られ
る平均が相加平均である。
これに対して、
得点2のものが1人、4のものが3人、5のものが2人なので、得点合計を
2×1+4×3+5×2=2+12+10=24 と出してから、24÷6=4 と人数で割って
得られる平均が加重平均である。
この例からも分かるように、加重平均は普段からお馴染みのものだろう。
加重平均については次の定理が基本的である。
定理 実数 A、B、C の加重平均を、WM(A,B,C)と書くとすると、
Min(A,B,C)≦WM(A,B,C)≦Max(A,B,C)
が成り立つ。
平均という意味を考えれば当然だろうし、証明は易しい。
(証明) Min(A,B,C)≦A 、 Min(A,B,C)≦B 、 Min(A,B,C)≦C より、
pMin(A,B,C)≦pA 、 qMin(A,B,C)≦qB 、 rMin(A,B,C)≦rC
3式を辺々加えて、 (p+q+r)Min(A,B,C)≦pA+qB+rC
p+q+r>0 なので、 Min(A,B,C)≦WM(A,B,C) が成り立つ。
同様にして、 WM(A,B,C)≦Max(A,B,C) が成り立つ。 (証終)
例題 実数 A、B と正の数 p、q に対して、次の不等式が成り立つことを示せ。
(解) 実数 A/p 、 B/q の重みをそれぞれ p、q とすると、定理から明らかに成り立つ。
(終)
この事実を用いて、比例式で重要な「加比の理」が説明される。
すなわち、A/p = B/q のとき、 Min(A/p , B/q)=Max(A/p , B/q) なので、
が成り立つ。
例 Y/X=2 ならば、 (Y+2)/(X+1)=2である。
このような考え方は数学のいろいろな場面で登場することだろう。
応用問題 正の数 x 、 y 、 z に対して、等式 (x+y+z)2=x+2y+3z が成り立つとき、
1<x+y+z<3 であることを示せ。
(解) x+y+z=(x+2y+3z)/(x+y+z) は、1 と 2 と 3 の加重平均だから、
1<x+y+z<3 が成り立つことは明らか。 (終)
(コメント) この問題で加重平均を使わないとしたら、どんな解答になるのだろう?
2変数の場合について考えてみよう。
応用問題 正の数 x 、 y に対して、等式 (x+y)2=x+2y が成り立つとき、
1<x+y<2 であることを示せ。
(解) x+y=(x+2y)/(x+y) は、1 と 2 の加重平均だから、
1<x+y<2 が成り立つことは明らか。 (終)
下図のように、放物線 (x+y)2=x+2y に対して、直線 x+y=k が交わるとき、
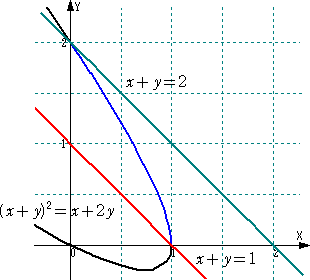
x>0 、y>0 に注意して、 1<k<2 であることが明瞭に理解される。
(コメント) 放物線 (x+y)2=x+2y のグラフを描くことがかなり大変そう!加重平均の
有難味がヒシヒシと伝わってくる。
読者のために練習問題を一つ置いておこう。
練習問題 平面上の4点
P(x1,y1)、Q(x2,y2)、R(x3,y3)、S(x4,y4) (ただし、 x1<x2<x3<x4)
に対して、線分 PQ、QR、RS の傾きを、それぞれ m1、m2、m3 とおく。
このとき、
Min(m1、m2、m3)≦線分 PS の傾き≦Max(m1、m2、m3)
であることを示せ。
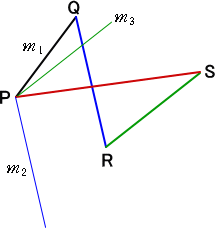
(図形的に考えて、上記の成り立つことは明らかだろう。問題はどのように示すかである。)
(解)
なので、例題で示した公式を用いて、
が成り立つ。 (終)
この加重平均の考え方は当然、相加平均と相乗平均の関係にも適用される。
広島工業大学の大川研究室のHPの「数学の問題コーナー」で、次のような問題が提起
されている。
問題316 数列 { (1+1/n)n } は単調増加、 { (1+1/n)n+1 } は単調減少であ
ることを対数やネイピアの数以前の高校1年程度の数学で証明せよ。
この証明に加重平均の考え方が有効に用いられる。
大川研究室の証明を参考にしながら...。
(証明) 1+1/n と 1 の重みをそれぞれ n と 1 として加重平均をとると、
このとき、相乗平均は、
よって、
すなわち、
このことは、数列 { (1+1/n)n } が単調増加であることを示す。
同様にして、後半部分も示される。
を示すために、
の両辺の逆数をとって
を示せばよい。
そこで、n/(n+1) と 1 の重みをそれぞれ n+1 と 1 として加重平均をとり、相乗
平均との関係を考えれば上記の不等式は直ちに示される。 (証終)
(コメント) 数列 { (1+1/n)n } が単調増加であることは書籍等では下記のように示されの
が通常である。
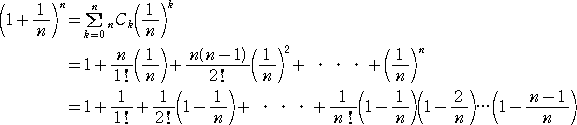
上記2式の各項を比較することにより、
であることが分かる。
また、関数
が、x>0 において増加関数であることを、微分法を用いて示す方法もある。
対数微分法により、 log F(x)=x(log (x+1)−log x ) から、
F’(x)/F(x)=log (x+1)−log x + x(1/(x+1)−1/x)
=log (x+1)−log x − 1/(x+1)
ここで、 G(x)=log (x+1)−log x − 1/(x+1) とおいて、さらに微分すると、
G’(x)=1/(x+1)−1/x + 1/(x+1)2=−1/x(x+1)2<0
より、関数 G(x) は単調に減少する。
x → ∞ のとき、 G(x)=log(1+1/x)− 1/(x+1) → 0
なので、 x>0 のとき、 G(x)>0 である。
よって、 F’(x)/F(x)>0 、 F(x)>0 より、 F’(x)>0
よって、関数 F(x) は単調に増加する。
(コメント) 微分を使った、こういう証明も味があっていいですね!
これらの証明を見て分かるように、加重平均を用いた方が証明がスッキリしていて分か
りやすいと思う。この証明を授けていただいた大川研究室に感謝したい。