フィボナッチ数を極める　　　　　　　　　　　　　　　　　

　フィボナッチ数は、およそ８００年前に刊行された、「算盤の書」（１２０２年）の中の有名な
「兎の問題」から生まれた。

　この書は、通称 Fibonacci （filius　Bonacci：ボナッチの子　を縮めたもの）といわれるイタリアの
数学者、ピサのレオナルドによるものである。

　兎の問題　　１つがいの兎は、１年の間に何つがいの兎になるか？

　　但し、１ヶ月経つと１つがいの兎は１つがいの兎を産み、産まれた兎は、２ヶ月目には
　子供を産むものとする。

　この兎の問題を図式化すると次のようになる。（→参考類題：受験の神様）

０ヶ月 　 1ヶ月 　 2ヶ月　 3ヶ月 ・・・	兎のつがいの増え方は、次の規則に従っている。 　　　ｎ ヶ月後の兎のつがいの数を Ｆ(ｎ) とすると、 Ｆ(ｎ)＝｛（ｎ−２）ヶ月後のつがい数｝＋｛（ｎ−１）ヶ月後のつがい数｝ 　　　　　２ヶ月後に子供を産む数 　　　＝Ｆ(ｎ−２)＋Ｆ(ｎ−１)

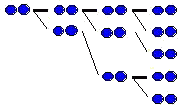　月末の個数だけに注目して、次の数列を得る。

　２，３，５，８，１３，２１，３４，５５，８９，１４４，２３３，３７７，・・・

従って、兎の問題の答は、３７７つがいとなる。


フィボナッチ数の定義

　ａ₁＝１、ａ₂＝1、ａ_ｎ＝ａ_ｎ-1＋ａ_ｎ-2　（ｎ＝３，４，・・・）で定まる数列をフィボナッチ数列

　１ ，１ ，２ ，３ ，５ ，８ ，１３ ，２１ ，３４ ，５５ ，８９ ，１４４ ，２３３ ，３７７ ，・・・

といい、数列の各項を、フィボナッチ数という。

　このページでは、フィボナッチ数の持つ面白い性質と応用を紹介していきたいと思う。

（次のホームページ(１２さんすう３４数学５Ｇｏ！)のフィボナッチ数の項では、フィボナッチ数の性質を、楽しく、具
体的に紹介しているので、大いに参考になります。）

（性質１）　ａ₁＋ａ₂＋・・・＋ａ_ｎ＝ａ_ｎ＋2−１

　　　　ａ₁＝ａ₃−ａ₂，ａ₂＝ａ₄−ａ₃，・・・，ａ_ｎ＝ａ_ｎ+2−ａ_ｎ+1　の各式を辺々加えればよい。

同様にして、次の性質２，３ も簡単に示すことができる。

（性質２）　ａ₁＋ａ₃＋・・・＋ａ_2ｎ-1＝ａ_2n

（性質３）　ａ₂＋ａ₄＋・・・＋ａ_2ｎ＝ａ_2ｎ＋1−１

　性質２ の式から性質３ の式を辺々引くことにより、次の大切な性質を得る。

（性質４）　ａ₁−ａ₂＋ａ₃−ａ₄＋・・・＋（−１）^ｎ+1ａ_ｎ＝（−１）^ｎ+1ａ_ｎ-1＋１

（性質５）　ａ_ｎ＋ｍ＝ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1

　　証明は、ｍ に関する数学的帰納法により、簡単に示すことができる。

実際に、ｍ＝１ のとき、右辺＝ａ_ｎ-1ａ₁＋ａ_ｎａ₂＝ａ_ｎ-1＋ａ_ｎ＝ａ_ｎ+1＝左辺

　ｍ＝２ のとき、右辺＝ａ_ｎ-1ａ₂＋ａ_ｎａ₃＝ａ_ｎ-1＋２ａ_ｎ＝ａ_ｎ-1＋ａ_ｎ＋ａ_ｎ＝ａ_ｎ+2＝左辺

　ｍ＝ｋ、ｋ＋１（ｋ≧１） のとき、成り立つと仮定する。

　　即ち、ａ_ｎ＋ｋ＝ａ_ｎ-1ａ_ｋ＋ａ_ｎａ_ｋ+1　、　ａ_ｎ＋ｋ+1＝ａ_ｎ-1ａ_ｋ+1＋ａ_ｎａ_ｋ+2

　このとき、

ａ_ｎ-1ａ_ｋ+2＋ａ_ｎａ_ｋ+3

＝ａ_ｎ-1(ａ_ｋ+1＋ａ_k)＋ａ_ｎ（ａ_ｋ+2＋ａ_k+1）

＝(ａ_ｎ-1ａ_ｋ＋ａ_ｎａ_ｋ+1)＋(ａ_ｎ-1ａ_ｋ+1＋ａ_ｎａ_ｋ+2)

＝ａ_ｎ＋ｋ＋ａ_ｎ＋ｋ+1

＝ａ_ｎ＋ｋ+2

　よって、ｍ＝ｋ＋２ のときも成り立つので、全ての自然数に対して、与式は成り立つ。


（追記）　平成３０年１０月２１日付けでＨＮ「ｎｙａ」さんより、（性質５）の別証明をいただいた。

（別証）　まず次の等式を証明する。

　　ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1＝ａ_ｎ+1ａ_ｍ＋ａ_ｎａ_ｍ-1　・・・(*)

　実際に、

左辺＝ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ−ａ_ｎａ_ｍ＋ａ_ｎａ_ｍ+1＝（ａ_ｎ-1＋ａ_ｎ）ａ_ｍ＋ａ_ｎ（ａ_ｍ+1−ａ_ｍ）

　　＝右辺　より明らか。

　さて、ｍ＝２ｋ　または　ｍ＝２ｋ＋１　となるような整数ｋが存在する。(*)式をｋ回繰り返し
用いると、

　ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1

＝ａ_ｎ+1ａ_ｍ＋ａ_ｎａ_ｍ-1　　（１回目）

＝ａ_ｎ+3ａ_ｍ＋ａ_ｎａ_ｍ-3　　（２回目）

　・・・・・・・・・・・・・・・・・・・・・

＝ａ_ｎ+2ｋ−1ａ_ｍ＋ａ_ｎａ_ｍ-2ｋ+1　　（ｋ回目）

＝ａ_ｎａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ　　（項を入れ替える）

　ｍ＝２ｋ　のとき、さらに(*)式をｋ−１回繰り返し用いて、

ａ_ｎａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ

＝ａ_ｎ+2ａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ-2　　（１回目）

＝ａ_ｎ+4ａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ-4　　（２回目）

　 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

＝ａ_ｎ+2k-2ａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ-2k+2　　（ｋ−１回目）

＝ａ_ｎ+ｍ-2ａ₁＋ａ_ｎ+ｍ−1ａ₂

＝ａ_ｎ+ｍ-2＋ａ_ｎ+ｍ−1

＝ａ_ｎ+ｍ

　ｍ＝２ｋ＋１　のとき、さらに(*)式をｋ回繰り返し用いて、

ａ_ｎａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ

＝ａ_ｎ+2ａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ-2　　（１回目）

＝ａ_ｎ+4ａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ-4　　（２回目）

　 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

＝ａ_ｎ+2kａ_ｍ-2ｋ+1＋ａ_ｎ+2ｋ−1ａ_ｍ-2k　　（ｋ回目）

＝ａ_ｎ+ｍ-1ａ₂＋ａ_ｎ+ｍ−2ａ₁

＝ａ_ｎ+ｍ-1＋ａ_ｎ+ｍ−2

＝ａ_ｎ+ｍ

　したがって、所要の等式を得る。


（コメント）　ｎｙａ さん、別証明、ありがとうございました。


　性質５で、ｎ＝ｍ のときを考えることにより、次の性質６，７ を得る。

（性質６）　ａ_2ｎは、ａ_ｎで割り切れる

（性質７）　ａ_2ｎ＝ａ_ｎ+1²−ａ_ｎ-1²

次の性質は、ビネ（Ｂｉｎｅｔ）の公式（１８４３）として有名である。

　（結果そのものは、その１世紀以上前にオイラー、ダニエル・ベルヌーイ、ド・モアブルなどには知られていた
　　らしい！）

（性質８）　ａ₁＝１、ａ₂＝１、ａ_ｎ＝ａ_ｎ−1＋ａ_ｎ−2　（ｎ＝３，４，・・・）で定まる数列の
　　　　　一般項は、

　　　

但し、

とする。

（証明）　α、βを用いて、ａ_ｎ+2−αａ_ｎ+1＝β(ａ_ｎ+1−αａ_ｎ)

　　ａ_ｎ+2−βａ_ｎ+1＝α(ａ_ｎ+1−βａ_ｎ)　と変形されるので、

　　ａ_ｎ+1−αａ_ｎ＝(ａ₂−αａ₁)β^ｎ-1＝(１−α)β^ｎ-1＝β^ｎ

　　ａ_ｎ+1−βａ_ｎ＝(ａ₂−βａ₁)α^ｎ-1＝(１−β)α^ｎ-1＝α^ｎ

　この連立方程式を解いて、ビネの公式を得る。　（証終）


　始めに「フィボナッチ数列ありき」でこのビネの公式を見ると、「ａ_ｎ が自然数」であることは
疑うよしもない。しかし、始めに、このビネの公式で定まる数列が与えられるとき、各項は自
然数になると聞いて、「ホント？」と思う人は少なからず存在するだろう。
　　　　　　　　　　　　　　　　　（→　参考 ： 「０２５　平成２１年度後期　横浜国立大学　工学部」）

　証明はいくつか考えられる。

（証明その１）・・・数学的帰納法によるもの

　ｎ＝１　のとき、　ａ₁＝（α−β）/＝/＝１　で自然数。

　　　よって、ｎ＝１ のとき成り立つ。

　ｎ≦ｋ（ｋ≧１）で成り立つと仮定する。すなわち、ｋ 以下の自然数 ｍ に対して、

　　ａ_ｍ＝（α^ｍ−β^ｍ）/　は自然数

　ｎ＝ｋ＋１　のとき、　α^ｋ+1−β^ｋ+1＝（α^ｋ−β^ｋ）（α＋β）−αβ（α^ｋ-1−β^ｋ-1）　より、

　（α^ｋ+1−β^ｋ+1）/＝（α＋β）・（α^ｋ−β^ｋ）/−αβ・（α^ｋ-1−β^ｋ-1）/

　　ここで、　α＋β＝１　、　αβ＝−１　と帰納法の仮定より、

　　ａ_ｋ+1＝（α^ｋ+1−β^ｋ+1）/　は自然数

　よって、ｎ＝ｋ＋１　のときも成り立つ。

　以上から、数学的帰納法により、

　すべての自然数 ｎ に対して、　ａ_ｎ＝（α^ｎ−β^ｎ）/　は自然数である。　（証終）

（証明その２）

　α＋β＝１　、　αβ＝−１　より、α、βは、２次方程式　ｘ²−ｘ−１＝０　の解である。

このとき、　ｘ²＝ｘ＋１　より、　ｘ^ｎ＝Ｍｘ＋Ｎ　（Ｍ、Ｎ は自然数）とおける。

　よって、　α^ｎ＝Ｍα＋Ｎ　、　β^ｎ＝Ｍβ＋Ｎ　より、

　ａ_ｎ＝Ｍ（α−β）/＝Ｍ/＝Ｍ　となり、ａ_ｎ は自然数である。　（証終）


（コメント）　当ＨＰがいつもお世話になっているＳ（Ｈ）さんによれば、数学的帰納法によるも
　　　　　　の以外に、漸化式を変形したり、母関数を使って証明することが可能であるとの
　　　　　　ことである。


　フィボナッチ数は、その定義から明らかなように、単調に増加する数である。果たして、
フィボナッチ数は、どのような速さで増加するのであろうか？この問いに対して、次の定
理がその答となる。

定理

に最も近い整数は、フィボナッチ数 ａｎである。

　証明は、性質 ８ のビネの公式より明らかである。

　この定理はまた、フィボナッチ数を求める新しい方法を我々に示唆している。


対数でフィボナッチ数を求める

　対数表では、有効桁数があまりに小さいので、ここでは、関数電卓（CASIO fx-7200G)を
用いて、求めてみよう。

例えば、ｎ＝１４ のとき、

の常用対数を求めると、２．５７６３４１３９８ となるので、

その真数は、３７７．００００４１５である。よって、この数に一番近い整数は、３７７となる。
（この数は、先の兎の問題の答の数と一致する。）

　関数電卓もわずか１０桁程度の有効数字にしか対応できないので、おのずと限界がある。
ｎ の値が大きくなると、先頭の数桁程度しかその信頼度はない。

　表計算ソフト　Microsoft Excel を用いると、フィボナッチ数は、容易に求められる。

（セルA1に１、セルA2に１、セルA3に=A1+A2を、それぞれ入力し、セルA3の右下隅にカー
ソルをあわせ、下方にドラッグすればよい。）

　ただ、この方法にも限界があって、ｎ＝５４のときの ８６，２６７，５７１，２７２ が、正しく
求められる最大のフィボナッチ数である。いろいろ工夫すれば、この記録はもっとのばせる
と思う。

　関数電卓（CASIO fx-7200G)で求められる最大のフィボナッチ数はいくつであろうか？
計算の結果、それは、ｎ＝４０ のときで、その値は、１０２，３３４，１５５ であった。

　性質５や性質７などを用いると、人力でもっと大きい ｎ に対するフィボナッチ数が求めら
れると思う。

（性質９）　２つのフィボナッチ数の最大公約数は、フィボナッチ数である

　実際に、ａ₁₈＝２５８４ と ａ₁₂＝１４４ の最大公約数は、ａ₆＝８である。

　この性質９を、さらに詳しく言及したのが次の定理である。

定理　　（ａ_ｍ，ａ_ｎ）＝ａ_{（ｍ，ｎ）}　　但し、（Ｘ，Ｙ）は、Ｘ と Ｙ の最大公約数を表す。

　この定理を証明するために、次の性質が用いられる。

（性質１０）　隣り合うフィボナッチ数は、互いに素である

　証明は容易である。

（ａ_ｎ，ａ_ｎ+1）＝ｄ＞１とすると、 ａ_ｎ+1−ａ_ｎ＝ａ_ｎ-1 は ｄ で割り切れる。
このことから、帰納的に、ａ₁＝１ が ｄ で割り切れることになり、矛盾。

（別証）　漸化式の形から明らかに、（ａ_ｎ+2，ａ_ｎ+1）＝（ａ_ｎ+1，ａ_ｎ）
　　　　したがって、（ａ_ｎ+1，ａ_ｎ）＝（ａ_ｎ，ａ_ｎ-1）＝・・・＝（ａ₂，ａ₁）＝１
　　　　よって、題意は示された。

　定理を一般的に証明することは難しいので、専門書に委ねる。ここでは、先ほどの例を
用いて、証明をなぞってみたい。

　ユークリッドの互除法により、１８＝１×１２＋６、１２＝２×６　だから、１８と１２の最大公
約数は、６である。

　このとき、（ａ₁₈，ａ₁₂）

＝（ａ_1×12+6，ａ₁₂）

＝（ａ_1×12-1ａ₆＋ａ_1×12ａ₆₊₁，ａ₁₂）　（←性質５より）

＝（ａ₁₁ａ₆＋ａ₁₂ａ₇，ａ₁₂）

＝（ａ₁₁ａ₆，ａ₁₂）　（←性質Ｂより）

＝（ａ₆，ａ₁₂）　（←性質１０と性質Ｄより）

＝（ａ₆，ａ₆₊₆）

＝（ａ₆，ａ₅ａ₆＋ａ₆ａ₇）　（←性質５より）

＝（ａ₆，（ａ₅＋ａ₇）ａ₆）

＝（１，ａ₅＋ａ₇）ａ₆　（←性質Ｃより）

＝ａ₆


上記の計算では、最大公約数に関する次の性質A、B、C、Ｄが用いられた。

（性質A）　（ａ，ｂ）は（ａｃ，ｂ）の約数

　証明は、明らかであろう。

（性質Ｂ）　ｃ が ｂ で割り切れるとき、（ａ＋ｃ，ｂ）＝（ａ，ｂ）

（証明）　　ｃ＝ｂｃ’、ａ＝ｂｑ＋ｒ より、ａ＋ｃ＝ｂ（ｑ＋ｃ’）＋ｒ となるので、ユークリッドの互除
　　　　　法の原理から明らかである。

（性質Ｃ）　（ａｃ，ｂｃ）＝（ａ，ｂ）ｃ

　証明は、明らかであろう。

（性質Ｄ）　（ｂ，ｃ）＝１ のとき、（ａｃ，ｂ）＝（ａ，ｂ）

（証明）　　性質Aより、（ａｃ，ｂ）は（ａｃ，ａｂ）の約数である。

　　性質Ｃより、（ａｃ，ａｂ）＝（ｃ，ｂ）ａ＝ａ なので、（ａｃ，ｂ）はａの約数となる。

　　（ａｃ，ｂ）はｂの約数でもあるので、（ａｃ，ｂ）は（ａ，ｂ）の約数である。

　　　性質Aより、（ａ，ｂ）は（ａｃ，ｂ）の約数なので、（ａｃ，ｂ）＝（ａ，ｂ）となる。　　（証終）


　上の定理から、次の事実が成り立つ。これも、フィボナッチ数の面白い特性であろう。

系　　ｍ が ｎ で割り切れるとき、ａ_ｍ は ａ_ｎで割り切れる
　　この逆もまた成り立つ

　証明は、定理から明らかであろう。

例　　５４は１８で割り切れる。このとき、

　ａ₁₈＝２５８４
　ａ₅₄＝８６２６７５７１２７２ ＝３３３８５２８３×２５８４＝３３３８５２８３×ａ₁₈

　確かに、ａ₅₄はａ₁₈で割り切れる。

　この系により、性質６は、明らかに成り立つ。

（参考文献：ヴォロビェフ　著　筒井孝胤　訳　フィボナッチ数（東京図書））


（追記）フィボナッチ数列は、いろいろな問題に現れる。例えば、次のような問題である。

　　ｎ段の階段がある。１段ずつでも２段ずつでも、また１段ずつと２段ずつをとりまぜ
て登ってもよいとして、何通りの登り方があるか。

　階段が１段のとき、登り方は、１通り

　階段が２段のとき、登り方は、１段ずつと一気に２段の２通り

　階段が３段のとき、登り方は、１段ずつ・１段と２段・２段と１段の３通り

　階段が４段のとき、登り方は、１段ずつ・１段ずつで最後に２段・1段と２段と１段・最初に

　　２段で残り１段ずつ・２段が2回の５通り

　・・・・・・・・・・・

　このように実験してみると、登り方の数列は、１，２，３，５，・・・ となり、なんとなくフィボ
ナッチ数が見えてくる。

　実際に、ｎ段の階段のときの登り方の総数を、ｂ_ｎ （＝ａ_ｎ+1）とすると、漸化式

　　ｂ₁　＝１、ｂ₂　＝２、　ｂ_ｎ＝ｂ_ｎ−1＋ｂ_ｎ−2　（ｎ＝３，４，・・・）

が成り立つ。漸化式の作り方は、

　最初に１段登ったとき、残りのｎ−１段の登り方　ｂ_ｎ−1 通り
　最初に２段登ったとき、残りのｎ−２段の登り方　ｂ_ｎ−2 通り

から和の法則を用いて明らかでしょう。

　建物の中の階段は、９、１１、１３段などが多い。
　　　　　　　　　　　　　　　　　　　　　　　（因みに、我が家の階段は、１３段です．．．f(^_^)　）
階段を誰かと一緒に登る時の話題の一つとしていかがでしょうか？

（追記）　令和３年８月７日付け

　上記の階段の登り方で、フィボナッチ数が現れることを見た。最近たまたまパズルを考察
していたら、やはり、フィボナッチ数が現れたのだが、よくよく考えてみたら、階段の場合の
文言の言い換えに過ぎないことに気づき、がっかりした覚えがある。

　１×ｎ （ｎは自然数） のマス目がある。このマス目を、１×１、１×２の長方形で埋め
尽くす方法は何通りあるか。

　埋め尽くす方法の数を Ｆ_ｎ と置く。

例　明らかに、　Ｆ₁＝１　である。

　Ｆ₂＝２　である。実際に、１×１の長方形を２個　または、１×２の長方形１個の２通りある。

　Ｆ₃＝３　である。

　　実際に、１×１の長方形を３個　または、１×１の長方形１個と１×２の長方形１個の順列
　も考えて、合計３通りある。

　Ｆ₄＝５　である。

　　実際に、１×１の長方形を「１」、１×２の長方形を「２」で表すことにすると、その場合は、
　　　１１１１、２１１、１２１、１１２、２２　の５通りある。

　一般に、１×（ｎ＋２）のマス目に対して、

　　最初に、１×１の長方形を埋める場合（残りは、１×（ｎ＋１）のマス目）

　　最初に、１×２の長方形を埋める場合（残りは、１×ｎのマス目）

　の何れかがあり得るので、漸化式　Ｆ_ｎ+2＝Ｆ_ｎ+1＋Ｆ_ｎ　が成り立つ。

　　これは、フィボナッチ数の漸化式そのものである。

　従って、後は機械的に、

　　Ｆ₅＝８　、Ｆ₆＝１３　、Ｆ₇＝２１　、Ｆ₈＝３４　、Ｆ₉＝５５　、Ｆ₁₀＝８９　、・・・

が得られる。

　読者のために、パズル問題を１題残しておこう。

問題　　１×１０のマス目がある。

をいくつか用いて埋め尽くす。埋め尽くし方は全部で何通りあるか？


（解）　Ｆ₁₀＝８９（通り）　である。　　（終）


（追記）　次の性質が成り立つ。

（性質１１）　ａ₁²＋ａ₂²＋・・・＋ａ_ｎ²＝ａ_ｎａ_ｎ+1　　　（Ｓｕｍ　ｏｆ　ｓｑｕａｒｅｓ）

　証明は、ｎ に関する数学的帰納法により、簡単に示すことができる。

実際に、ｎ ＝ １ のとき、右辺＝ａ₁ａ₂＝ａ₁²＝左辺　（←　ａ₁＝ａ₂ ）

　ｎ＝ｋ (ｋ≧１）のとき、成り立つと仮定する。即ち、ａ₁²＋ａ₂²＋・・・＋ａ_ｋ²＝ａ_ｋａ_ｋ+1

　このとき、

ａ₁²＋ａ₂²＋・・・＋ａ_ｋ²＋ａ_ｋ+1²

＝ａ_ｋａ_ｋ+1＋ａ_ｋ+1²＝ａ_ｋ+1（ａ_ｋ＋ａ_ｋ+1）＝ａ_ｋ+1ａ_ｋ+2

　よって、ｎ＝ｋ＋１ のときも成り立つので、全ての自然数に対して、与式は成り立つ。


　さて、フィボナッチ数列

　１ ，１ ，２ ，３ ，５ ，８ ，１３ ，２１ ，３４ ，５５ ，８９ ，１４４ ，２３３ ，３７７ ，・・・

について、当ＨＰの掲示板「出会いの泉」に、平成２１年５月１７日付けで、ＨＮ「ｔｅｔｓｕｙａ」
さんが次のような書き込みを残された。

　フィボナッチ数列の1つおきの項

　１ ，１ ，２ ，３ ，５ ，８ ，１３ ，２１ ，３４ ，５５ ，８９ ，１４４ ，２３３ ，３７７ ，・・・

について、例えば、（ １ ，３ ，８ ）や（ ２１ ，５５ ，１４４ ） などについて、

　　相異なる２数を掛けて、１ を足す

という操作をすると平方数になる。

　実際に、　１×３＋１＝４＝２²　、　３×８＋１＝２５＝５²　、　１×８＋１＝９＝３²

　　２１×５５＋１＝１１５６＝３４²　、　５５×１４４＋１＝７９２１＝８９²

　　２１×１４４＋１＝３０２５＝５５²

しかも、すべてフィボナッチ数列に現われる数の平方になっている。

（コメント）　とても美しく面白い性質ですね。ｔｅｔｓｕｙａ様に感謝します。

　ｔｅｔｓｕｙａ様の書き込みによれば、一般に、｢相異なる２数を掛けて、１ を足す」という操作

を施して平方数になる ｎ 個の数の組は、Ｄｉｏｐｈａｎｔｉｎｅ　ｎ-ｔｕｐｌｅ　と言われるという。

　上記の計算から、（ １ ，３ ，８ ）や（ ２１ ，５５ ，１４４ ） などは、Ｄｉｏｐｈａｎｔｉｎｅ　３-ｔｕｐｌｅ
である。

　Ａｎｄｒｅｊ　Ｄｕｊｅｌｌａ　：「Ｔｈｅ　ｐｒｏｂｌｅｍ　ｏｆ　Ｄｉｏｐｈａｎｔｕｓ　ａｎｄ　Ｄａｖｅｎｐｏｒｔ」　によれば、

ギリシャの数学者　Ｄｉｏｐｈａｎｔｕｓ　ｏｆ　Ａｌｅｘａｎｄｒｉａ　は、Ｄｉｏｐｈａｎｔｉｎｅ　４-ｔｕｐｌｅ　として

　（ １/１６　、３３/１６　、１７/４　、１０５/１６ ）

を得ていたという。 フェルマーは、４つの数がすべて自然数という条件で、

　（ １ ，３ ，８ ，１２０ ）

というＤｉｏｐｈａｎｔｉｎｅ　４-ｔｕｐｌｅ　を見出した。

　ところで、Ｂａｋｅｒ　と　Ｄａｖｅｎｐｏｒｔの結果（１９６９）によれば、

　（ １ ，３ ，８ ，ｄ ）が、Ｄｉｏｐｈａｎｔｉｎｅ　４-ｔｕｐｌｅ　である自然数 ｄ の値は、ｄ＝１２０

しかないようだ。　さらに、Ｅｕｌｅｒ は、

　　ａ　、　ｂ　、　ａ＋ｂ＋２ｒ　、　４ｒ（ｒ＋ａ）（ｒ＋ｂ）　　　ただし、　ａｂ＋１＝ｒ²

という解を与えている。 （ １ ，３ ，８ ，１２０ ）は、 ａ＝１、ｂ＝３、ｒ＝２　の場合である。

　上記の計算で、フィボナッチ数から得られる Ｄｉｏｐｈａｎｔｉｎｅ　３-ｔｕｐｌｅ　において、｢相異な
る２数を掛けて、１ を足す」という操作を施すと、フィボナッチ数の平方になるという現象に
遭遇したが、このことを整理すると、次の（性質１２）が得られる。


（性質１２）　ａ_ｎ+1²−ａ_ｎａ_ｎ+2＝(−１)^ｎ

　証明は、ｎ に関する数学的帰納法により、簡単に示すことができる。

実際に、ｎ ＝ １ のとき、左辺＝ａ₂²−ａ₁ａ₃＝１−２＝−１＝左辺

　ｎ＝ｋ (ｋ≧１）のとき、成り立つと仮定する。即ち、ａ_ｋ+1²−ａ_ｋａ_ｋ+2＝(−１)^ｋ

　このとき、

ａ_ｋ+2²−ａ_ｋ+1ａ_ｋ+3

＝ａ_ｋ+2²−ａ_ｋ+1(ａ_ｋ+1＋ａ_ｋ+2)

＝(ａ_ｋ+2−ａ_ｋ+1)ａ_ｋ+2−ａ_ｋ+1²＝ａ_ｋａ_ｋ+2−ａ_ｋ+1²＝−(−１)^ｋ＝(−１)^ｋ+1

　よって、ｎ＝ｋ＋１ のときも成り立つので、全ての自然数に対して、与式は成り立つ。


（追記）　令和３年８月１６日付け

　（性質１２）　ａ_ｎ+1²−ａ_ｎａ_ｎ+2＝(−１)^ｎ　は、非常に有名な恒等式で、カッシーニの公式
と言われる。

　この公式を用いると、　（性質１０）　隣り合うフィボナッチ数は、互いに素である　の別
証が得られる。

（別証）　ａ_ｎ、ａ_ｎ+1 に１以外の公約数ｄがあるとすると、

　ａ_ｎ+1²−ａ_ｎａ_ｎ+2＝(−１)^ｎ　から、(−１)^ｎがｄで割り切れることになるが、これは矛盾。

　よって、隣り合うフィボナッチ数は、互いに素である。　　（別証終）


　カッシーニの公式絡みで、次の文献に興味を引かれた。

（参考）　城野真民・北山秀隆　著　「フィボナッチ数を背景とする教材の考察」（和歌山大学）


　（性質１２）の証明では、数学的帰納法を用いたが、もちろん直接的に示す方法もある。

　（性質８）で示したビネの公式を用いればよい。

　ａ₁＝１、ａ₂＝１、ａ_ｎ＝ａ_ｎ-1＋ａ_ｎ-2　（ｎ＝３，４，・・・）で定まる数列の一般項は　　　　　　　

但し、

で与えられるので、

　

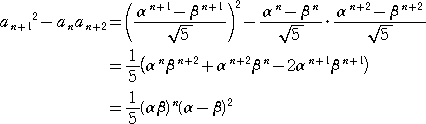
　ここで、　α＋β＝１　、αβ＝−１　なので、　（α−β）²＝（α＋β）²−４αβ＝５

　よって、　ａ_ｎ+1²−ａ_ｎａ_ｎ+2＝（1/5）(−１)^ｎ・５＝(−１)^ｎ　が成り立つ。


　さらに、次のような証明法があることを、ｚｋ４３さんより、ご教示いただいた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２１年５月１９日付け）
　漸化式　ａ_ｎ+2＝ａ_ｎ+1＋ａ_ｎ　より、

　　ａ_ｎａ_ｎ+1＝ａ_ｎ（ａ_ｎ+2−ａ_ｎ）＝ａ_ｎａ_ｎ+2−ａ_ｎ²

　同様に、漸化式　ａ_ｎ+1＝ａ_ｎ＋ａ_ｎ-1　より、

　　ａ_ｎａ_ｎ+1＝（ａ_ｎ+1−ａ_ｎ-1）ａ_ｎ+1＝ａ_ｎ+1²−ａ_ｎ-1ａ_ｎ+1

よって、　ａ_ｎａ_ｎ+2−ａ_ｎ²＝ａ_ｎ+1²−ａ_ｎ-1ａ_ｎ+1　より、　ａ_ｎ+1²−ａ_ｎａ_ｎ+2＝−（ａ_ｎ²−ａ_ｎ-1ａ_ｎ+1）

したがって、　ａ_ｎ+1²−ａ_ｎａ_ｎ+2＝（−１）^ｎ-1（ａ₂²−ａ₁ａ₃）＝（−１）^ｎ-1（１²−１・２）＝（−１）^ｎ

（コメント）　う〜む、なるほど！上手い証明ですね。

　ｚｋ４３さんは、さらに、行列で考えた方が、構造が分かりやすい感じがするとのこと。

すなわち、
　　　　　　　　　、　　

とおくと、　Ａ_ｎ＝ＢＡ_ｎ-1　が成り立つので、　Ａ_ｎ＝Ｂ^ｎ-1Ａ₁

　よって、　ｄｅｔ（Ａ_ｎ）＝ｄｅｔ（Ｂ）^ｎ-1・ｄｅｔ（Ａ₁）＝（−１）^ｎ-1（１・２−１²）＝（−１）^ｎ-1　より、

　　　ａ_ｎａ_ｎ+2−ａ_ｎ+1²＝（−１）^ｎ-1

　すなわち、　ａ_ｎ+1²−ａ_ｎａ_ｎ+2＝（−１）^ｎ　が成り立つ。


（コメント）　計算がスッキリしました．．．_ネ！　ｚｋ４３さんに感謝します。


（追記）　平成２１年３月２７日付け

　数列 ｛ ａ_ｎ ｝ がフィボナッチ数列であるとき、（性質１２）が成り立つわけであるが、逆に、
（性質１２）がなりたつような数列 ｛ ａ_ｎ ｝ はフィボナッチ数列であることを問う入試問題が
あることを、当ＨＰがいつもお世話になっているＳ（Ｈ）さんより伺った。


横浜国立大学　後期工学部（２００１）

　数列 ｛ ａ_ｎ ｝ は、　ａ₁＝１ 、ａ₂＝１ 、ａ_ｎａ_ｎ+2−ａ_ｎ+1²＝（−１）^ｎ+1　（ｎ＝１、２、３、・・・）
により定まる。次の問いに答えよ。

　（１）　ａ_ｎ+2＝ａ_ｎ+1＋ａ_ｎ　（ｎ＝１，２，３，・・・）　が成り立つことを証明せよ。
　（２）　ｍ を自然数とするとき、ａ_6ｍ は８の倍数であることを示せ。

（解）　（１）　ａ₁ａ₃−ａ₂²＝（−１）²　より、ａ₃−１＝１　なので、ａ₃＝２

　ｎ＝１　のとき、　左辺＝ａ₃＝２　、右辺＝ａ₂＋ａ₁＝２　なので、

　ａ_ｎ+2＝ａ_ｎ+1＋ａ_ｎ　は、ｎ＝１ のとき成り立つ。

　ｎ≦ｋ （ｋ≧１） のとき成り立つと仮定する。即ち、

　ａ₃＝ａ₂＋ａ₁　、ａ₄＝ａ₃＋ａ₂　、・・・　、ａ_ｋ+2＝ａ_ｋ+1＋ａ_ｋ

　ａ₁＝１ 、ａ₂＝１ より、　ａ₃＞０ 、ａ₄＞０ 、・・・ 、ａ_ｋ+2＞０　である。

　ここで、与えられた漸化式より、

　ａ_ｋａ_ｋ+2−ａ_ｋ+1²＝（−１）^ｋ+1

　ａ_ｋ+1ａ_ｋ+3−ａ_ｋ+2²＝（−１）^ｋ+2＝−（−１）^ｋ+1

２式を辺々加えて、　ａ_ｋａ_ｋ+2−ａ_ｋ+1²＋ａ_ｋ+1ａ_ｋ+3−ａ_ｋ+2²＝０

　このとき、　（ａ_ｋ−ａ_ｋ+2）ａ_ｋ+2−ａ_ｋ+1²＋ａ_ｋ+1ａ_ｋ+3＝０　において、

　　ａ_ｋ−ａ_ｋ+2＝−ａ_ｋ+1　より、　−ａ_ｋ+1ａ_ｋ+2−ａ_ｋ+1²＋ａ_ｋ+1ａ_ｋ+3＝０

　よって、　ａ_ｋ+1（−ａ_ｋ+2−ａ_ｋ+1＋ａ_ｋ+3）＝０　において、ａ_ｋ+1＞０　より、

　　−ａ_ｋ+2−ａ_ｋ+1＋ａ_ｋ+3＝０　すなわち、　ａ_ｋ+3＝ａ_ｋ+2＋ａ_ｋ+1　が成り立つ。

　よって、ｎ＝ｋ＋１　のときも成り立つので、全ての自然数に対して、与式は成り立つ。

（２）　ａ₆＝ａ₅＋ａ₄＝２ａ₄＋ａ₃＝２（ａ₃＋ａ₂）＋ａ₃＝３ａ₃＋２ａ₂＝３・２＋２・１＝８　で、

（ａ_6ｍ，ａ₆）＝ａ_{（6ｍ，6）}＝ａ₆＝８　より、自然数 ｍ に対して、　ａ_6ｍ は８の倍数である。（終）


（コメント）　（１）がこの問題の眼目で、（２）はサービス問題ですね！


　ＦＮさんからのコメントです。（平成２３年１１月１９日付け）

　上記の(2)の解答で、(性質９)の下の定理を使っています。

(2)は、「ａ_ｍｎはａ_ｎの倍数である。･･･(*)」が、ｎ＝６で成り立つことの証明を要求するもので、

(*)よりかなり強い定理を引用するのは(入試問題の解答としては)駄目でしょう。

　具体的に調べるのがいいと思います。

　ａ_ｍを８で割った余りをｂ_ｍとすると、ｍ＝１、２、・・・、１２　のときのｂ_ｍは次のようになる。

ｍ

１

２

３

４

５

６

７

８

９

１０

１１

１２

ｂｍ

１

１

２

３

５

０

５

５

２

７

１

０

　ｍ＝１３以降は、これを繰り返すから、ｍが６の倍数のとき、ｂ_ｍ＝０

　よって、ａ_6ｍは８の倍数である。

　表から逆も言えてるので、「ａ_ｎが８の倍数　⇔　ｎが６の倍数」が成り立ちます。

　同様にして、次のような関係も成り立ちます。

　　「ａ_ｎが２の倍数　⇔　ｎが３の倍数」

　　「ａ_ｎが３の倍数　⇔　ｎが４の倍数」

　　「ａ_ｎが５の倍数　⇔　ｎが５の倍数」

　大学入試に出題するのに、どのあたりが適当かということでしょう。


（コメント）　ＦＮさん、ありがとうござます。


　ＦＮさんからの続報です。（平成２３年１１月２３日付け）

　上記を、次の形に一般化した場合の証明は難しいだろうと思っていたのですが、それほど
でもありませんでした。

　ａ_ｎ が ａ_ｍ の倍数　⇔　ｎ が ｍ の倍数

ａ_ｎ が ａ_ｍ の倍数　⇔　ｎ が ｍ の倍数

　合同式を使って書けば、　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ｎ≡0　(ｍｏｄ　ｍ)　です。これを

証明するのにキーになるのは、次の性質です。

　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ａ_ｎ+ｍ≡0　(ｍｏｄ　ａ_ｍ)

例　フィボナッチ数列：１ ，１ ，２ ，３ ，５ ，８ ，１３ ，２１ ，３４ ，５５ ，８９ ，１４４，・・・　に
　　おいて、

　ａ₆＝８≡0　(ｍｏｄ　ａ₃＝２)　であるのに対して、ａ₉＝３４≡0　(ｍｏｄ　ａ₃＝２)

　ａ₈＝２１≡0　(ｍｏｄ　ａ₄＝３)　であるのに対して、ａ₁₂＝１４４≡0　(ｍｏｄ　ａ₄＝３)

（証明）　(性質５)より、ａ_ｎ＋ｍ＝ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1　であるから、

　　ａ_ｎ＋ｍ＝ａ_ｎａ_ｍ+1　（ｍｏｄ　ａ_ｍ）　・・・　(*)

よって、　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇒　ａ_ｎ＋ｍ≡0　(ｍｏｄ　ａ_ｍ)

　(性質１０)より、ａ_ｍ と ａ_ｍ+1 は互いに素であるから、ａ_ｍ+1 は、ｍｏｄ　ａ_ｍ で逆元を持つ。

　即ち、ａ_ｍ+1・ｋ≡1 (ｍｏｄ　ａ_ｍ)　となる ｋ が存在する。
　　　　(ａ_ｍ+1・ｋ+ａ_ｍ・ｌ=1 を満たす整数 ｋ、ｌ が存在するということ)

　(*)の両辺に ｋ をかけて、　ａ_ｎ＋ｍ・ｋ≡ａ_ｎ　（ｍｏｄ　ａ_ｍ）

　よって、　ａ_ｎ＋ｍ≡0　(ｍｏｄ　ａ_ｍ)　⇒　ａ_ｎ≡0　（ｍｏｄ　ａ_ｍ）

　したがって、　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ａ_ｎ+ｍ≡0　(ｍｏｄ　ａ_ｍ)　　（証終）


　これを使って、　「 ａ_ｎ が ａ_ｍ の倍数　⇔　ｎ が ｍ の倍数」、即ち、

　　　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ｎ≡0　(ｍｏｄ　ｍ)

を証明します。

（証明）　ｎ を ｍ で割ったときの商を ｑ、余りを ｒ とする。 ｎ=ｍｑ+ｒ　(0≦ｒ＜ｍ)

　　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ａ_ｎ-ｍ≡0　(ｍｏｄ　ａ_ｍ)　を繰り返し使って、

　　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ａ_ｎ-ｍ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ａ_ｎ-2ｍ≡0　(ｍｏｄ　ａ_ｍ)

　　････　⇔　ａ_ｎ-ｑｍ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ａ_ｒ≡0　(ｍｏｄ　ａ_ｍ)

　　0≦r＜m　より、　ａ_ｒ＜ａ_ｍ　なので、

　　　ａ_ｒ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ａ_ｒ＝0　⇔　ｒ=0　⇔　ｎ≡0　(ｍｏｄ　ｍ)

　以上より、　ａ_ｎ≡0　(ｍｏｄ　ａ_ｍ)　⇔　ｎ≡0　(ｍｏｄ　ｍ)　　（証終）

　これは、(性質９)の下にある定理の系ですが、系から定理も容易に出ます。

これを書き直せば、　ａ_ｄ が ａ_ｎ の約数　⇔　ｄ が ｎ の約数

　これから、　ａ_ｄ が、ａ_ｍ、ａ_ｎ の公約数　⇔　ｄ が ｍ、ｎ の公約数

　　　　　　　　ａ_ｄ が、ａ_ｍ、ａ_ｎ の最大公約数　⇔　ｄ が ｍ、ｎ の最大公約数

これが定理です。


（性質１３）　（ａ₁ａ₂）³＋（ａ₂ａ₃）³＋・・・＋（ａ_ｎａ_ｎ+1）³＝(ａ_ｎａ_ｎ+1ａ_ｎ+2)²/４

　この性質は、大塚秀幸先生（元文教大付属高）が見出されたものである。

　フィボナッチ数の定義　ａ_ｎ＝ａ_ｎ-1＋ａ_ｎ-2　（ｎ＝２，３，・・・）　を用いて容易に示すこと
が出来る。ただし、 ａ₀＝０　、ａ₁＝1　とする。

（証明）　任意の ｋ に対して、

　　(ａ_ｋａ_ｋ+1ａ_ｋ+2)²−(ａ_ｋ-1ａ_ｋａ_ｋ+1)²

　＝(ａ_ｋａ_ｋ+1)²（ａ_ｋ+2²−ａ_ｋ-1²）

　＝(ａ_ｋａ_ｋ+1)²（ａ_ｋ+2＋ａ_ｋ-1）（ａ_ｋ+2−ａ_ｋ-1）

　＝(ａ_ｋａ_ｋ+1)²（ａ_ｋ+1＋ａ_ｋ＋ａ_ｋ-1）（ａ_ｋ+1＋ａ_ｋ−ａ_ｋ-1）

　＝(ａ_ｋａ_ｋ+1)²（ａ_ｋ+1＋ａ_ｋ+1）（ａ_ｋ＋ａ_ｋ-1＋ａ_ｋ−ａ_ｋ-1）

　＝(ａ_ｋａ_ｋ+1)²（２ａ_ｋ+1）（２ａ_ｋ）

　＝４(ａ_ｋａ_ｋ+1)³

　すなわち、　４(ａ_ｋａ_ｋ+1)³＝(ａ_ｋａ_ｋ+1ａ_ｋ+2)²−(ａ_ｋ-1ａ_ｋａ_ｋ+1)²

　上式に、ｋ＝１、２、・・・、ｎ を代入して、辺々加えると、

　　　４｛（ａ₁ａ₂）³＋（ａ₂ａ₃）³＋・・・＋（ａ_ｎａ_ｎ+1）³｝＝(ａ_ｎａ_ｎ+1ａ_ｎ+2)²−(ａ₀ａ₁ａ₂)²

　ここで、　ａ₀＝０　、ａ₁＝1　から、　ａ₂＝1　なので、　ａ₀ａ₁ａ₂＝０

　よって、　４｛（ａ₁ａ₂）³＋（ａ₂ａ₃）³＋・・・＋（ａ_ｎａ_ｎ+1）³｝＝(ａ_ｎａ_ｎ+1ａ_ｎ+2)²　より、

　　　　　（ａ₁ａ₂）³＋（ａ₂ａ₃）³＋・・・＋（ａ_ｎａ_ｎ+1）³＝(ａ_ｎａ_ｎ+1ａ_ｎ+2)²/４　　（証終）

（コメント）　この（性質１３）を用いると、

　　　　ａ₀＝０　、ａ₁＝1　から、

　　　ａ₂＝1　、ａ₃＝２　、ａ₄＝３　、ａ₅＝５　、ａ₆＝８　、ａ₇＝1３　、・・・

　なので、　

　　　　（ａ₁ａ₂）³＋（ａ₂ａ₃）³＋（ａ₃ａ₄）³＋（ａ₄ａ₅）³＋（ａ₅ａ₆）³＝(ａ₅ａ₆ａ₇)²/４

　すなわち、　１³＋２³＋６³＋１５³＋４０³＝２６０²　　となる。

　何か、パズルに使えそうですね！


　当ＨＰがいつもお世話になっているＨＮ「攻略法」さんから新しい性質をご教示いただいた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年８月９日付け）

（性質１４）　ａ_ｎ-1ａ_ｎ+2＝ａ_ｎ+1²−ａ_ｎ²

（証明）　ａ_ｎ+1²−ａ_ｎ²＝（ａ_ｎ+1−ａ_ｎ）（ａ_ｎ+1＋ａ_ｎ）＝ａ_ｎ-1ａ_ｎ+2　　（証終）

（性質１５）　ａ_2ｎ+1＝ａ_ｎ+1²＋ａ_ｎ²

（証明）　数学的帰納法による。

　ｎ＝１　のとき、　ａ₃＝ａ₁＋ａ₂＝１＋１＝２　、　ａ₂²＋ａ₁²＝１＋１＝２

　　よって、　ａ₃＝ａ₂²＋ａ₁²　なので、ｎ＝１のとき、命題は成り立つ。

　ｎ＝２　のとき、　ａ₅＝ａ₃＋ａ₄＝２＋３＝５　、　ａ₃²＋ａ₂²＝４＋１＝５

　　よって、　ａ₅＝ａ₃²＋ａ₂²　なので、ｎ＝２のとき、命題は成り立つ。

　ｎ＝ｋ、ｋ＋１（ｋ≧１）のとき、命題が成り立つと仮定する。

　　すなわち、　ａ_2ｋ+1＝ａ_ｋ+1²＋ａ_ｋ²　、ａ_2ｋ+3＝ａ_ｋ+2²＋ａ_ｋ+1²

　このとき、

ａ_ｋ+3²＋ａ_ｋ+2²

＝ａ_ｋ+3²＋ａ_2ｋ+3−ａ_ｋ+1²

＝ａ_2ｋ+3＋（ａ_ｋ+3−ａ_ｋ+1）（ａ_ｋ+3＋ａ_ｋ+1）

＝ａ_2ｋ+3＋ａ_ｋ+2（ａ_ｋ+3＋ａ_ｋ+1）

＝ａ_2ｋ+3＋ａ_ｋ+2ａ_ｋ+3＋ａ_ｋ+2ａ_ｋ+1

ここで、（性質５）　ａ_ｎ＋ｍ＝ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1　より、

　ａ_ｋ+2ａ_ｋ+3＋ａ_ｋ+2ａ_ｋ+1＝ａ_ｋ+1ａ_ｋ+2＋ａ_ｋ+2ａ_ｋ+3＝ａ_2ｋ+4

なので、　ａ_ｋ+3²＋ａ_ｋ+2²＝ａ_2ｋ+3＋ａ_2ｋ+4＝ａ_2ｋ+5

　これより、命題は、ｎ＝ｋ＋２のときも成り立つ。

したがって、すべての自然数 ｎ に対して、命題は成り立つ。　　（証終）


　ＦＮさんからのコメントです。（平成２３年１１月１９日付け）

　(性質１５)　ａ_2ｎ+1＝ａ_ｎ+1²＋ａ_ｎ²　は、

(性質５) 　ａ_ｎ＋ｍ＝ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1　のｎをｎ＋１に、ｍをｎにした式です。

(性質７)　ａ_2ｎ＝ａ_ｎ+1²−ａ_ｎ-1² と並ぶ式です。

（コメント）　確かに並べると、関連性が浮き彫りになりますね！ＦＮさんに感謝します。


　ところで、フィボナッチ数列 ａ₁＝１、ａ₂＝1、ａ_ｎ+2＝ａ_ｎ＋ａ_ｎ+1　（ｎ＝１，２，・・・）で、

　　ａ＝ａ_ｎ-1ａ_ｎ+2　、ｂ＝２ａ_ｎ+1ａ_ｎ　、ｃ＝ａ_2ｎ+1　とおけば、　ａ²＋ｂ²＝ｃ²　が成り立つ。

（→　参考：「ピタゴラス数の発見」）

（証明）　 （性質１４）　ａ_ｎ-1ａ_ｎ+2＝ａ_ｎ+1²−ａ_ｎ²

　　　（性質１５）　ａ_2ｎ+1＝ａ_ｎ+1²＋ａ_ｎ²

より、　ａ＝ａ_ｎ-1ａ_ｎ+2＝ａ_ｎ+1²−ａ_ｎ²　、　ａ_2ｎ+1＝ａ_ｎ+1²＋ａ_ｎ²　なので、

　ａ_ｎ+1＝ｓ　、ａ_ｎ＝ｔ　とすると、ａ＝ｓ²−ｔ²　、　ｂ＝２ｓｔ　、　ｃ＝ｓ²＋ｔ²　なので、

　ａ²＋ｂ²＝ｃ²　が成り立つ。　　（証終）


　攻略法さんから新しい性質をご教示いただいた。（平成２３年８月１６日付け）

（性質１６）　ａ_ｎ+2＋ａ_ｎ-2＝３ａ_ｎ

（証明）　ａ_ｎ+2＋ａ_ｎ-2＝（ａ_ｎ+1＋ａ_ｎ）＋（ａ_ｎ−ａ_ｎ-1）＝ａ_ｎ+1−ａ_ｎ-1＋２ａ_ｎ＝３ａ_ｎ　　（証終）

（性質１７）　ａ_ｎ+1ａ_ｎ−ａ_ｎａ_ｎ-1＝ａ_ｎ²

（証明）　ａ_ｎ+1ａ_ｎ−ａ_ｎａ_ｎ-1＝ａ_ｎ（ａ_ｎ+1−ａ_ｎ-1）＝ａ_ｎ²　　（証終）

（性質１８）　ａ_ｎ+1³＋ａ_ｎ³−ａ_ｎ-1³＝ａ_3ｎ

（証明）

ａ_3ｎ＝ａ_ｎ+2ｎ

　　＝ａ_ｎ-1ａ_2ｎ＋ａ_ｎａ_2ｎ+1　　（←　（性質５）　ａ_ｎ＋ｍ＝ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1）

　　＝ａ_ｎ-1（ａ_ｎ+1²−ａ_ｎ-1²）＋ａ_ｎ（ａ_ｎ+1²＋ａ_ｎ²）
　　　（←　（性質７）　ａ_2ｎ＝ａ_ｎ+1²−ａ_ｎ-1²　、（性質１５）　ａ_2ｎ+1＝ａ_ｎ+1²＋ａ_ｎ²）

　　＝ａ_ｎ+1²（ａ_ｎ＋ａ_ｎ-1）＋ａ_ｎ³−ａ_ｎ-1³

　　＝ａ_ｎ+1³＋ａ_ｎ³−ａ_ｎ-1³　　（証終）

（性質１９）　ａ₁ａ₂＋ａ₂ａ₃＋・・・＋ａ_2ｎ-1ａ_2ｎ＝ａ_2ｎ²

（証明）　ｎ＝１　のとき、　左辺＝ａ₁ａ₂＝１・１＝１　、右辺＝ａ₂²＝１²＝１　なので、

　　左辺＝右辺　となり、ｎ＝１　のとき成り立つ。

ｎ＝ｋ（ｋ≧１）のとき成り立つと仮定する。すなわち、ａ₁ａ₂＋ａ₂ａ₃＋・・・＋ａ_2ｋ-1ａ_2ｋ＝ａ_2ｋ²

　ｎ＝ｋ＋１　のとき、帰納法の仮定より、

　ａ₁ａ₂＋ａ₂ａ₃＋・・・＋ａ_2ｋ+1ａ_2ｋ+2

＝ａ_2ｋ²＋ａ_2ｋａ_2ｋ+1＋ａ_2ｋ+1ａ_2ｋ+2

＝ａ_2ｋ（ａ_2ｋ＋ａ_2ｋ+1）＋ａ_2ｋ+1ａ_2ｋ+2

＝ａ_2ｋａ_2ｋ+2＋ａ_2ｋ+1ａ_2ｋ+2

＝（ａ_2ｋ＋ａ_2ｋ+1）ａ_2ｋ+2

＝ａ_2ｋ+2²

　よって、ｎ＝ｋ＋１　のときも成り立つ。

　したがって、すべての自然数 ｎ に対して成り立つ。　　（証終）


（性質２０）　ａ₁ａ₂＋ａ₂ａ₃＋・・・＋ａ_2ｎａ_2ｎ+1＝ａ_2ｎ+1²−１

（証明）　ｎ＝１　のとき、左辺＝ａ₁ａ₂＋ａ₂ａ₃＝１・１＋１・２＝３、右辺＝ａ₃²−１＝２²−１＝３

　なので、左辺＝右辺　となり、ｎ＝１　のとき成り立つ。

　ｎ＝ｋ（ｋ≧１）のとき成り立つと仮定する。すなわち、

　　ａ₁ａ₂＋ａ₂ａ₃＋・・・＋ａ_2ｋａ_2ｋ+1＝ａ_2ｋ+1²−１

　ｎ＝ｋ＋１　のとき、帰納法の仮定より、

ａ₁ａ₂＋ａ₂ａ₃＋・・・＋ａ_2ｋ+2ａ_2ｋ+3

＝ａ_2ｋ+1²−１＋ａ_2ｋ+1ａ_2ｋ+2＋ａ_2ｋ+2ａ_2ｋ+3

＝ａ_2ｋ+1（ａ_2ｋ+1＋ａ_2ｋ+2）＋ａ_2ｋ+2ａ_2ｋ+3−１

＝ａ_2ｋ+1ａ_2ｋ+3＋ａ_2ｋ+2ａ_2ｋ+3−１

＝（ａ_2ｋ+1＋ａ_2ｋ+2）ａ_2ｋ+3−１

＝ａ_2ｋ+3²−１

　よって、ｎ＝ｋ＋１　のときも成り立つ。

　したがって、すべての自然数 ｎ に対して成り立つ。　　（証終）


　攻略法さんから新しい性質をご教示いただいた。（平成２３年８月２１日付け）

　性質５などを用いると、人力でもっと大きいｎに対するフィボナッチ数が求められる。

　ここで、（性質１５）　ａ_2ｎ+1＝ａ_ｎ+1²＋ａ_ｎ²　←式1　とする。

（性質２１）　ａ_2ｎ＝ａ_ｎ（２ａ_ｎ-1＋ａ_ｎ）＝ａ_ｎ（２ａ_ｎ+1−ａ_ｎ）

（証明）　（性質５）　ａ_ｎ＋ｍ＝ａ_ｎ-1ａ_ｍ＋ａ_ｎａ_ｍ+1

　より、　ａ_2ｎ＝ａ_ｎ-1ａ_ｎ＋ａ_ｎａ_ｎ+1＝ａ_ｎ（ａ_ｎ-1＋ａ_ｎ+1）＝ａ_ｎ（２ａ_ｎ-1＋ａ_ｎ）　なので、

　ａ_2ｎ+2＝ａ_ｎ+1（２ａ_ｎ＋ａ_ｎ+1）　←式2

同様にして、

　ａ_2ｎ＝ａ_ｎ-1ａ_ｎ＋ａ_ｎａ_ｎ+1＝ａ_ｎ（ａ_ｎ-1＋ａ_ｎ+1）＝ａ_ｎ（２ａ_ｎ+1−ａ_ｎ）　←式3　　（証終）


　例　たとえば、ａ₄₀ は次のようにして求められる。

　　40を2で割って、商20、余り0となる。
　　式3より、ａ₄₀＝ａ₂₀（２ａ₂₁−ａ₂₀）　　実際の値 102334155
　　式1より、ａ₄₁＝ａ₂₁²＋ａ₂₀²　　　　　 実際の値 165580141

　　先の商20を2で割って、商10、余り0
　　式3より、ａ₂₀＝ａ₁₀（２ａ₁₁−ａ₁₀）　　実際の値 6765
　　式1より、ａ₂₁＝ａ₁₁²＋ａ₁₀²　　　　　 実際の値 10946

　　先の商10を2で割って、商5、余り0
　　式3より、ａ₁₀＝ａ₅（２ａ₆−ａ₅）　　　　実際の値 55
　　式1より、ａ₁₁＝ａ₆²＋ａ₅²　　　　　　　実際の値 89

　　先の商5を2で割って、商2、余り1
　　式1より、ａ₅＝ａ₃²＋ａ₂²　　　　　　 　実際の値 5
　　式2より、ａ₆＝ａ₃（２ａ₂＋ａ₃）　　 　　実際の値 8

　　先の商2を2で割って、商1、余り0
　　式3より、ａ₂＝ａ₁（２ａ₂−ａ₁）　　 　　実際の値 1
　　式1より、ａ₃＝ａ₂²＋ａ₁²　　　　　 　　実際の値 2

　　先の商1を2で割って、商0、余り1
　　式1より、ａ₁＝ａ₁²＋ａ₀²　　　　　 　　実際の値 1
　　式2より、ａ₂＝ａ₁（２ａ₀＋ａ₁）　　　 　実際の値 1

のように計算手順を組み立てると、

　　商を　「漸化式のn」　、余りを　「式の選択」

に対応させて、手順を遡ると、　ａ₀＝０　、ａ₁＝1　から算出できる。


＜計算手順＞　ａ_ｍ を求める場合、ｍ を２進法展開する。

　ａ₀＝０　、ａ₁＝1　として、最上位から順に

　　　ビットが「1」なら、式1と式2　　　ビットが「0」なら、式3と式1

を計算していく。


　当ＨＰ読者のＫ．Ｓ．さんより、フィボナッチ数列の新たな視点をご教示頂いた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１０月９日付け）

（性質２２）　フィボナッチ数列：

　１ ，１ ，２ ，３ ，５ ，８ ，１３ ，２１ ，３４ ，５５ ，８９ ，１４４ ，２３３ ，３７７ ，・・・

において、

　３番目ごとに、２の倍数
　４番目ごとに、３の倍数
　５番目ごとに、５の倍数
　８番目ごとに、７の倍数
１０番目ごとに、１１の倍数

が現れる。


　ＦＮさんからのコメントです。（平成２３年１１月１５日付け）

　（性質２２）について、ちょっとわかりにくい表現ですが、「3番目、6番目、9番目、･･･　は、2
の倍数である」等々の意味でしょう。次の性質の系になります。

　ａ_ｍｎ は、ａ_ｍ の倍数である。(または、ａ_ｍｎ は、ａ_ｍ および ａ_ｎ の倍数である)

　これは、(性質６)の一般化です。証明は、(性質５)を使って数学的帰納法でできます。これ
はまた、(性質９)の下の定理の系の前半部分でもあります。


　当ＨＰ読者のＫ．Ｓ．さんより、フィボナッチ数列の新たな視点をご教示頂いた。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１１月１１日付け）

（性質２３）　全ての自然数は、異なるいくつかのフィボナッチ数の和として表すことが
　　　　　　できる。

　一見すると「本当？」と思いたくなるような事実に対しても、数学的帰納法は強力な武器と
なる。

（証明）　ｎ＝１　のときは、明らか。

　ｎ＝２　のとき、　２＝１＋１　なので、　ｎ＝２　のときも成り立つ。

　ｎ＝３　のとき、　３＝２＋１　なので、　ｎ＝３　のときも成り立つ。

　ｎ＝４　のとき、　４＝３＋１＝２＋１＋１　なので、　ｎ＝４　のときも成り立つ。

　今、任意の自然数を Ｎ とし、Ｎ未満の自然数については、異なるいくつかのフィボナッチ

数の和として表すことができるものと仮定する。ここで、Ｎを超えない最大のフィボナッチ数

を ａ_ｎ とおく。このとき、　Ｎ＜ａ_ｎ+1　が成り立つ。

　ａ_ｎ+1＝ａ_ｎ＋ａ_ｎ-1 なので、　０≦Ｎ−ａ_ｎ＜ａ_ｎ-1

　ａ_ｎ-1＜ａ_ｎ≦Ｎ　より、帰納法の仮定から、Ｎ−ａ_ｎ は異なるいくつかのフィボナッチ数の和

として表せる。すなわち、Ｎは、異なるいくつかのフィボナッチ数の和として表せる。

　以上から、

　　全ての自然数は、異なるいくつかのフィボナッチ数の和として表すことができる。（証終）


　攻略法さんが（性質２３）に注目され、1から100までのうち個数が最多と最少のものを調査
されました。（平成２３年１１月１４日付け）

　「連続するフィボナッチ数の和」も多々あるとのことです。

（フィボナッチ数）
　　１ ，１ ，２ ，３ ，５ ，８ ，１３ ，２１ ，３４ ，５５ ，８９ ，１４４，２３３ ，３７７ ，・・・

1=1		1+1=2←※ 2=2		1+2=3←※ 3=3		1+1+2=4←※ 1+3=4
1+1+3=5 2+3=5←※ 5=5		1+2+3=6←※ 1+5=6		1+1+2+3=7←※ 2+5=7		1+2+5=8 3+5=8←※ 8=8
1+1+2+5=9 1+8=9		1+1+3+5=10 2+3+5=10←※ 2+8=10		1+2+3+5=11←※ 3+8=11		1+1+2+3+5=12←※ 1+3+8=12
1+1+3+8=13 5+8=13←※ 13=13		1+2+3+8=14 1+13=14		1+1+2+3+8=15 2+13=15		1+2+5+8=16 3+5+8=16←※ 3+13=16

1+1+2+5+8=17 1+3+13=17		1+1+3+5+8=18 2+3+5+8=18←※ 5+13=18		1+2+3+5+8=19←※ 1+5+13=19
1+1+2+3+5+8=20←※ 2+5+13=20		1+2+5+13=21 8+13=21←※ 21=21		1+1+2+5+13=22 1+21=22
1+1+3+5+13=23 2+21=23		1+2+3+5+13=24 3+21=24		1+1+2+3+5+13=25 1+3+21=25
1+1+3+8+13=26 5+8+13=26←※ 5+21=26		1+2+3+8+13=27 1+5+21=27		1+1+2+3+8+13=28 2+5+21=28
1+2+5+8+13=29 3+5+8+13=29←※ 8+21=29		1+1+2+5+8+13=30 1+8+21=30		1+1+3+5+8+13=31 2+3+5+8+13=31←※ 2+8+21=31
1+2+3+5+8+13=32 1+2+3+5+8+13=32←※ 3+8+21=32		1+1+2+3+5+8+13=33 1+1+2+3+5+8+13=33←※ 1+3+8+21=33		1+1+3+8+21=34 13+21=34←※ 34=34
1+2+3+8+21=35 1+34=35		1+1+2+3+8+21=36 2+34=36		1+2+5+8+21=37 3+34=37
1+1+2+5+8+21=38 1+3+34=38		1+1+3+5+8+21=39 5+34=39		1+2+3+5+8+21=40 1+5+34=40
1+1+2+3+5+8+21=41 2+5+34=41		1+2+5+13+21=42 8+13+21=42←※ 8+34=42		1+1+2+5+13+21=43 1+8+34=43
1+1+3+5+13+21=44 2+8+34=44		1+2+3+5+13+21=45 3+8+34=45		1+1+2+3+5+13+21=46 1+3+8+34=46
1+1+3+8+13+21=47 5+8+13+21=47←※ 13+34=47		1+2+3+8+13+21=48 1+13+34=48		1+1+2+3+8+13+21=49 2+13+34=49
1+2+5+8+13+21=50 3+5+8+13+21=50←※ 3+13+34=50		1+1+2+5+8+13+21=51 1+3+13+34=51		1+1+3+5+8+13+21=52 2+3+5+8+13+21=52←※ 5+13+34=52
1+2+3+5+8+13+21=53 1+2+3+5+8+13+21=53←※ 1+5+13+34=53		1+1+2+3+5+8+13+21=54 1+1+2+3+5+8+13+21=54←※ 2+5+13+34=54		1+2+5+13+34=55 21+34=55←※ 55=55
1+1+2+5+13+34=56 1+55=56		1+1+3+5+13+34=57 2+55=57		1+2+3+5+13+34=58 3+55=58
1+1+2+3+5+13+34=59 1+3+55=59		1+1+3+8+13+34=60 5+55=60		1+2+3+8+13+34=61 1+5+55=61
1+1+2+3+8+13+34=62 2+5+55=62		1+2+5+8+13+34=63 8+55=63		1+1+2+5+8+13+34=64 1+8+55=64
1+1+3+5+8+13+34=65 2+8+55=65		1+2+3+5+8+13+34=66 3+8+55=66		1+1+2+3+5+8+13+34=67 1+3+8+55=67
1+1+3+8+21+34=68 13+21+34=68←※ 13+55=68		1+2+3+8+21+34=69 1+13+55=69		1+1+2+3+8+21+34=70 2+13+55=70
1+2+5+8+21+34=71 3+13+55=71		1+1+2+5+8+21+34=72 1+3+13+55=72		1+1+3+5+8+21+34=73 5+13+55=73
1+2+3+5+8+21+34=74 1+5+13+55=74		1+1+2+3+5+8+21+34=75 2+5+13+55=75		1+2+5+13+21+34=76 8+13+21+34=76←※ 21+55=76
1+1+2+5+13+21+34=77 1+21+55=77		1+1+3+5+13+21+34=78 2+21+55=78		1+2+3+5+13+21+34=79 3+21+55=79
1+1+2+3+5+13+21+34=80 1+3+21+55=80		1+1+3+8+13+21+34=81 5+8+13+21+34=81←※ 5+21+55=81		1+2+3+8+13+21+34=82 1+5+21+55=82
1+1+2+3+8+13+21+34=83 2+5+21+55=83		1+2+5+8+13+21+34=84 3+5+8+13+21+34=84←※ 8+21+55=84		1+1+2+5+8+13+21+34=85 1+8+21+55=85
1+1+3+5+8+13+21+34=86 2+3+5+8+13+21+34=86←※ 2+8+21+55=86		1+2+3+5+8+13+21+34=87←※ 3+8+21+55=87		1+1+2+3+5+8+13+21+34=88←※ 1+3+8+21+55=88
1+1+3+8+21+55=89 34+55=89←※ 89=89		1+2+3+8+21+55=90 1+89=90		1+1+2+3+8+21+55=91 2+89=91
1+2+5+8+21+55=92 3+89=92		1+1+2+5+8+21+55=93 1+3+89=93		1+1+3+5+8+21+55=94 5+89=94
1+2+3+5+8+21+55=95 1+5+89=95		1+1+2+3+5+8+21+55=96 2+5+89=96		1+2+5+13+21+55=97 8+89=97
1+1+2+5+13+21+55=98 1+8+89=98		1+1+3+5+13+21+55=99 2+8+89=99		1+2+3+5+13+21+55=100 3+8+89=100

　攻略法さんからの続報です。（平成２３年１１月１６日付け）

　個数が最少のものについての考察です。

（考察１）
・1個目　　Nを超えない最大のフィボナッチ数（n番目）を、ａ_ｎ とする。すなわち、ａ_ｎ ≦N

　　N=ａ_ｎ+(N-ａ_ｎ)

・2個目　　これを繰り返して、

　　N-ａ_ｎ を超えない最大のフィボナッチ数を ａ_ｍ とする。すなわち、ａ_ｍ≦N-ａ_ｎ 、ｍ＜ｎ

　　N=ａ_ｎ+ａ_ｍ+(N-(ａ_ｎ+ａ_ｍ))

・3個目

　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

　残りの数 (N-(ａ_ｎ+ａ_ｍ+…)) がフィボナッチ数になるまで繰り返すことで、最少の個数を求
めることができる。

　また、ｍ は、ｎ-1ではなく、ｍ≦ｎ-2 となる。すなわち、隣り合うフィボナッチ数を使わない
ことがわかる。したがって、その個数が最多になる場合は、

　N=1+2+5+ … +ａ_ｎ-2+ａ_ｎ　または、　N=1+3+8+ … +ａ_ｎ-2+ａ_ｎ

　ｎ/2個と考えられる。ｎ がある程度以上のとき、これより少なくなる。
（参考　1から100までの検証）

（考察２）　「碁石並べ」より、●を 1、○を 0 として、2進法 ｎ 桁で、ビット列が、1が2つ以上
　　　　　並んではいけない（0は2つ以上並んでもかまわない）とする。

　各桁の重みは、ｎ+1 番目のフィボナッチ数 ａ_ｎ+1 で、

　　　　　…、144、89、55、34、21、13、8、5、3、2、1

とする。

6桁の場合、ａ₆=Σ_{k=0〜[(6+1)/2]}{_6-ｋ+1Ｃ_ｋ}=₇Ｃ₀+₆Ｃ₁+₅Ｃ₂+₄Ｃ₃=1+6+10+4=21(通り)

000000 = 0
000001 = 1
000010 = 2
000100 = 3
000101 = 3 + 1 = 4
001000 = 5
001001 = 5 + 1 = 6
001010 = 5 + 2 = 7
010000 = 8
010001 = 8 + 1 = 9
010010 = 8 + 2 = 10
010100 = 8 + 3 = 11
010101 = 8 + 3 + 1 = 12
100000 = 13
100001 = 13 + 1 = 14
100010 = 13 + 2 = 15
100100 = 13 + 3 = 16
100101 = 13 + 3 + 1 = 17
101000 = 13 + 5 = 18
101001 = 13 + 5 + 1 = 19
101010 = 13 + 5 + 2 = 20

　攻略法さんからの続報です。（平成２３年１１月１７日付け）

　1が重複しないようにするには、

・2進法 ｎ が偶数なら、２倍（2ｎ）と２倍して＋１した数（2n+1）を２つ生成する
・2進法 ｎ が奇数なら、２倍の数（2ｎ）を1つ生成する

とする。重複することなく自然数が生成されて、その数の個数はフィボナッチ数となる。

1(1)　※括弧内は対応する自然数
│
10(2)
├─────────────────────────────┐
100(3)　　　　　　　　　　　　　　　　　　　　　　　　　　　101(4)
├─────────────────┐　　　　　　　　　　　│
1000(5)　　　　　　　　　　　　　　　1001(6)　　　　　　　　1010(7)
├───────────┐　　　　　│　　　　　　　　　　　├───────────┐
10000(8)　　　　　　　　10001(9)　　10010(10)　　　　　　　　10100(11)　　　　　　　10101(12)
├─────┐　　　　　│　　　　　├─────┐　　　　　├─────┐　　　　　│
100000(13)　100001(14)　100010(15)　100100(16)　100101(17)　101000(18)　101001(19)　101010(20)


同様に、ｎ=1 から、次の規則で数を順次生成していくこともできる。

・ｎ が偶数なら、２倍（2n）と＋１した数（ｎ+1）を２つ生成する
・ｎ が奇数なら、２倍の数（2n）を１つ生成する

重複することなく自然数が生成されて、その数の個数はフィボナッチ数となる。

1
│
2
├───────────────┐
4　　　　　　　　　　　　　　　　3
├─────────┐　　　　　│
8　　　　　　　　　　5　　　　　6
├─────┐　　　│　　　　　├─────┐
16　　　　　9　　　　10　　　　 12　　　　　7
├───┐　│　　　├───┐　├───┐　│
32　　　17　18　　　20　　　11　24　　　13　14
├─┐　│　├─┐　├─┐　│　├─┐　│　├─┐
64　33　34　36　19　40　21　22　48　25　26　28　15


　ＦＮさんからのコメントです。（平成２３年１１月１５日付け）

　（性質２３）について、「フィボナッチ数とはフィボナッチ数列にあらわれる数」だから、「１」
はフィボナッチ数で、すべての自然数が「１」の何個かの和で表されるのは当たり前である。
だから、「異なる」を書いておくべきでしょう。
（→　ＦＮさんのご指摘ごもっともなので、文言を修正させていただきました。）

　また、「いくつかの」ではあまり面白くないので、「いくつかの」がどの程度に押さえられるか
を考えるのが面白そうに思います。

　ｎ がある程度以上のとき、「いくつかの」は、「[ｌｏｇ₂ ｎ ]-1個以下の」ぐらいにできそうな気
がします。攻略法さんが調べられている範囲(ｎ≦100)では、ｎ≦4、ｎ=6、7、12 を除いて成
り立っています。ただし、ｌｏｇ₂ ｎ は、2を底とする対数、[ｘ]は、ｘ を越えない最大の整数。


（性質２４）　ａ_ｎ+1＝_ｎＣ₀＋_ｎ-1Ｃ₁＋_ｎ-2Ｃ₂＋・・・＋_ｎ-ｒＣ_ｒ　（ただし、ｒ≦ｎ/２）

　パスカルの三角形で、左側の１を揃えて書くと、斜めの和がフィボナッチ数列となる。

　　

　当ＨＰ読者で岩手県在住のＫ．Ｙ．さんから、（性質２４）を直接、数学的帰納法で証明され
たとのことで、その証明をメールにていただきました。（平成２９年５月１日付け）

　２項係数 _nＣ_k　(０≦ｎ、０≦ｋ≦ｎ) とフィボナッチ数列 ｛F_n｝　(０≦ｎ) は、漸化式を用いて、
それぞれ次のように定義される。

　_nＣ_k＝_n-1Ｃ_k＋_n-1Ｃ_k-1　ただし、_nＣ₀＝_nＣ_n＝１

　F_n＝F_n-1＋F_n-2　ただし、F₀＝F₁＝１

　このとき、フィボナッチ数列の一般項 F_n は、２項係数_nＣ_k を用いて次のように表される。

(*)　　F_n＝Σ _{k=0〜[n/2] n-k}Ｃ_n-2k　　（ただし、[x] はx を越えない最大の整数）

　この F_n と（性質２４）における ａ_ｎ との関係は、　F_n＝ａ_ｎ+1 である。

例　F_n＝Σ _{k=0〜[n/2] n-k}Ｃ_n-2k

　　　＝_nＣ_n＋_n-1Ｃ_n-2＋_n-2Ｃ_n-4＋・・・＋_n-ｒＣ_n-2ｒ　ただし、ｒ≦ｎ/２

　　　＝_nＣ₀＋_n-1Ｃ₁＋_n-2Ｃ₂＋・・・＋_n-ｒＣ_ｒ


　式(*)が正しいことを数学的帰納法を用いて証明する。

（証明）　ｎ＝０　のとき、　左辺＝F₀＝１　で、右辺＝₀Ｃ₀＝１　より、　左辺＝右辺

　ｎ＝１　のとき、左辺＝F₁＝１　で、右辺＝₁Ｃ₁＝１　より、　左辺＝右辺

　以上から、命題は、ｎ＝０、１のときに成り立つ。

　ｒ≧ｎ≧０　のき、命題が成り立つと仮定する。すなわち、　F_n＝Σ _{k=0〜[n/2] n-k}Ｃ_n-2k

（イ）　ｒ が奇数のとき、　ｒ＝２ｍ＋１　（ｍは自然数）　と表される。

　　このとき、　_ｒＣ_ｒ＝_ｒ+1Ｃ_ｒ+1＝１、_ｍＣ₀＝_ｍ+1Ｃ₀＝１、ｒ＋１＝２（ｍ＋１）　に注意すると、

　F_r+1＝F_r＋F_r-1

　　　 ＝Σ _{k=0〜m ｒ-k}Ｃ_ｒ-2k＋Σ _{k=0〜m ｒ-1-k}Ｃ_r-1-2k

　　　 ＝_ｒＣ_ｒ＋_ｒ-1Ｃ_ｒ-2＋・・・＋_ｒ-mＣ_ｒ-2m＋_ｒ-1Ｃ_ｒ-1＋_ｒ-2Ｃ_ｒ-3＋・・・＋_ｒ-1-mＣ_ｒ-1-2m

　　　 ＝_ｒＣ_ｒ＋（_ｒ-1Ｃ_ｒ-2＋_ｒ-1Ｃ_ｒ-1）＋・・・＋（_ｒ-mＣ_ｒ-2m＋_ｒ-ｍＣ_ｒ-2ｍ+1)＋_mＣ₀

　　　 ＝_ｒＣ_ｒ＋_ｒＣ_ｒ-1＋・・・＋_ｒ-ｍ+1Ｃ_ｒ-2ｍ+1＋_m+1Ｃ₀

　　　 ＝_ｒ+1Ｃ_ｒ+1＋_ｒ+1-1Ｃ_ｒ+1-2＋・・・＋_ｒ+1-ｍＣ_ｒ+1-2ｍ＋_ｒ+1-(m+1)Ｃ_r+1-2(m+1)

　　　 ＝Σ _{k=0〜m+1 ｒ+1-k}Ｃ_ｒ+1-2k

　となり、命題は、ｎ＝ｒ＋１（ｒ が奇数）のときも成り立つ。

（ロ）　ｒ が偶数のとき、　ｒ＝２ｍ　（ｍは自然数）　と表される。

　このとき、　ｒ−１＝２（ｍ−１）＋１　に注意すると、

　F_r+1

＝F_r＋F_r-1

＝Σ _{k=0〜m ｒ-k}Ｃ_ｒ-2k＋Σ _{k=0〜m-1 ｒ-1-k}Ｃ_r-1-2k

＝_ｒＣ_ｒ＋_ｒ-1Ｃ_ｒ-2＋・・・＋_ｒ-mＣ_ｒ-2m＋_ｒ-1Ｃ_ｒ-1＋_ｒ-2Ｃ_ｒ-3＋・・・＋_ｒ-mＣ_ｒ+1-2m

＝_ｒＣ_ｒ＋（_ｒ-1Ｃ_ｒ-2＋_ｒ-1Ｃ_ｒ-1）＋・・・＋（_ｒ-mＣ_ｒ-2m＋_ｒ-ｍＣ_ｒ-2ｍ+1)

＝_ｒＣ_ｒ＋_ｒＣ_ｒ-1＋・・・＋_r-ｍ+1Ｃ_r-2m+1

＝_ｒ+1Ｃ_ｒ+1＋_ｒ+1-1Ｃ_ｒ+1-2＋・・・＋_r-ｍ+1Ｃ_r-2m+1

＝_ｒ+1Ｃ_ｒ+1＋_ｒ+1-1Ｃ_ｒ+1-2＋・・・＋_r+1-ｍＣ_r+1-2m

＝Σ _{k=0〜m ｒ+1-k}Ｃ_ｒ+1-2k

　となり、命題は、ｎ＝ｒ＋１（ｒ が偶数）のときも成り立つ。

　以上から、命題(*)は、すべての整数ｎ（ｎ≧０）について成り立つ。　　（証終）


（コメント）　久々にフィボナッチ数列に触れる機会をいただいたＫ．Ｙ．さんに感謝します。


　攻略法さんが（性質２４）について考察されました。（平成２３年１１月１４日付け）

　（性質２４）の組合せ論的解釈を得るために、次の問題を考える。

問題　碁石は○と●の２種類ある。10個の碁石を、●が隣り合わないように一列に並べる
　　　並べ方は何通りあるか。

（解）　碁石が１個のときは、　○　または　●　の２通り

　碁石が２個のときは、　○○　、　●○　、　○●　の３通り

　碁石が３個のときは、　○○○　、●○○　、○●○　、○○●　、●○●　の５通り

　碁石が４個のときは、　○○○○　、●○○○　、○●○○　、○○●○　、○○○●　、
　　　　　　　　　　　　　　　●○●○　、●○○●　、○●○●　の８通り

　碁石が５個のときは、　○○○○○　、●○○○○　、○●○○○　、○○●○○　、
　　　　　　　　　　　　　　　○○○●○　、○○○○●　、●○●○○　、●○○●○　、
　　　　　　　　　　　　　　　●○○○●　、○●○●○　、○●○○●　、○○●○●　、
　　　　　　　　　　　　　　　●○●○●　の１３通り

　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

　ｎ個の碁石を、●が隣り合わないように並べる並べ方の総数を、ａ_ｎ+2 通りであるとする。

　ｎ≧３ のとき、 ａ₁、 ａ₂、・・・、ａ_ｎ-2、ａ_ｎ-1 が定まったとする。

　1つ目の石が○の場合、残りの ｎ-１個の並べ方は、ａ_ｎ+1 通りである。

　1つ目の石が●の場合、２つ目は、○でなければならず、残りの ｎ-２個の並べ方は、ａ_ｎ
通りである。

　ゆえに、　ａ_ｎ+2＝ａ_ｎ+1＋ａ_ｎ　が成り立つ。　　（終）

　このことから、

（性質２４）　ａ_ｎ+1＝_ｎＣ₀＋_ｎ-1Ｃ₁＋_ｎ-2Ｃ₂＋・・・＋_ｎ-ｒＣ_ｒ　（ただし、ｒ≦ｎ/２）

において、左辺は、碁石が ｎ−１個ある場合に、●が隣り合わないように並べる並べ方の
総数である。上記の証明から、数列｛ａ_ｎ｝は、フィボナッチ数列となる。

　右辺の _ｎ-ｋＣ_ｋ （ｋ＝０、１、２、・・・、ｒ）は、ｎ−１個の碁石のうち、●が ｋ 個あるときに、

　○の ｎ−１−ｋ＋１＝ｎ−ｋ 個の隙間に ｋ 個の●を挿入する場合の数に等しい。

○の隙間の数 ｎ−ｋ が、●の個数 ｋ 以上であることは自明だろう。

　この組合せ論的解釈を攻略法さんが詳細に調べられました。

（組合せ論的解釈）　●の個数で考える。●と○で計n個並べるとする。

●が0個のとき、　n個すべてが○の1通り

●が1個のとき、　(n-1)個の○、1個の●の並べ方なので、　_ｎＣ₁=n (通り)

●が2個のとき、2個ある●の間に○が1個以上

　例　n=6　の場合

　　●○●○○○　、●○○●○○　、●○○○●○　、●○○○○●　、○●○●○○
　　○●○○●○　、○●○○○●　、○○●○●○　、○○●○○●　、○○○●○●

　これは、○○…○の間および両端を合わせて((n-3)+2)箇所から、2個の●を選び1個ずつ
入れることなので、　_ｎ-3+2Ｃ₂=_ｎ-1Ｃ₂ (通り)

●がk個のとき、すべての●と●の間に○が1個以上。これは、○○…○の間および両端を
合わせて、((n-(k+1))+2)箇所からk個の●を選び1個ずつ入れることなので、_ｎ-ｋ+1Ｃ_ｋ (通り)

　ここで、ｋの範囲は、すべての●と●の間(k-1)箇所に○が1個は必要なので、○の個数を
mとすると、k-1≦m　で、k+m=n より、0≦k≦n-k+1 となる。

　以上から、●が0個のとき、 _ｎ+1Ｃ₀ と表して合計すると、ａ_ｎ+2＝Σ_{0≦k≦n-k+1}（_ｎ-ｋ+1Ｃ_ｋ）


　実際に計算してみると、

　ａ₁=1、 ａ₂=1、　ａ₃=Σ_k=0〜1（_2-ｋＣ_ｋ）=₂Ｃ₀+₁Ｃ₁=1+1=2、

　ａ₄=Σ_k=0〜1（_3-ｋＣ_ｋ）=₃Ｃ₀+₂Ｃ₁=1+2=3、　ａ₅=Σ_k=0〜2（_4-ｋＣ_ｋ）=₄Ｃ₀+₃Ｃ₁+₂Ｃ₂=1+3+1=5、

　ａ₆=Σ_k=0〜2（_5-ｋＣ_ｋ）=₅Ｃ₀+₄Ｃ₁+₃Ｃ₂=1+4+3=8、

　ａ₇=Σ_k=0〜3（_6-ｋＣ_ｋ）=₆Ｃ₀+₅Ｃ₁+₄Ｃ₂+₃Ｃ₃==1+5+6+1=13、

　　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

　また、●と○のn個の列は、(n+1)段の階段の上り方で、各段を踏むか踏まないかの状態
（足跡、○は踏む）を具体的に示している。（→　参考：「階段」）

（コメント）　攻略法さん、組合せ論的解釈に感動しました！証明はどうするのだろうと思案
　　　　　　していました。感謝いたします。なお、一部文言等を修正させていただきました。
　　　　　　ご了承ください。同趣旨のことをＫ．Ｓ．さんからもメールで頂きました。Ｋ．Ｓ．さん
　　　　　　に感謝いたします。


　Ｋ．Ｓ．さんからの続報です。（平成２３年１１月１１日付け）

　Ｎ試合で連敗しないような試合のあり方は、階段で踏まなかったところが負けた意味となり、
連続して踏まないことはないので、同じ数になる。

　また、１×２のタイルを、２×Ｎに敷き詰める方法の数について、

　Ｎ＝１　のとき、明らかに、１通り

　Ｎ＝２　のとき、横２列　または　縦２列　の２通り

　Ｎ＝３　のとき、最初に、縦１列のとき、その右隣は、横２列　または　縦２列　の２通り

　　　　　　　　　　最初に、横２列のとき、その右隣は、縦１列のみ

　　　　　以上から、場合の数は、３通り

　Ｎ＝４　のとき、最初に、縦１列のとき、その右隣は、２×３　なので、敷き詰め方は、３通り

　　　　　　　　　　最初に、横２列のとき、その右隣は、２×２　なので、敷き詰め方は、２通り

　　　　　以上から、場合の数は、３＋２＝５通り

　　・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・

　したがって、敷き詰め方の場合の数は、フィボナッチ数となる。

　また、次の性質も成り立つ。

（性質２５）

　これは、ビネの公式から明らかだろう。

（コメント）　フィボナッチ数列の種々の視座を与えていただいて、Ｋ．Ｓ．さんに感謝します。


　攻略法さんが、いろいろな問題に現れるフィボナッチ数列について考察されました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（平成２３年１１月１８日付け）

例１　黄金比φとして、1，φ，φ²，φ³，φ⁴， … という等比数列を考えたとき、1+φ=φ² を
　　利用すると

φ = φ φ2 = φ + 1 φ3 = 2φ + 1 φ4 = 3φ + 2 φ5 = 5φ + 3 φ6 = 8φ + 5 φ7 = 13φ + 8　　　 　：

１次式の係数や定数項にフィボナッチ数が現れる。

（追記）　令和３年６月２８日付け

　攻略法さんの上記の式を変形すると、フィボナッチ数は黄金比の累乗で表せる。これは、
ビネ（Ｂｉｎｅｔ）の公式（１８４３）からも推察されることだろう。

　１＝φ⁰＋0/φ²

　２＝φ¹＋１/φ²　・・・　φ¹＋１/φ²＝（φ³＋１）/φ²＝２（φ＋１）/φ²＝２

　３＝φ²＋１/φ²　・・・　φ²＋１/φ²＝（φ⁴＋１）/φ²＝３（φ＋１）/φ²＝３

　５＝φ³＋２/φ²

　８＝φ⁴＋３/φ²

　１３＝φ⁵＋５/φ²

　２１＝φ⁶＋８/φ²

　・・・・・・・・・・・・・・

　リュカ数についても同様の表現が可能である。

　１＝φ−１/φ　・・・　φ−１/φ＝（φ²−１）/φ＝φ/φ＝１

　３＝φ²＋１/φ²　・・・　φ²＋１/φ²＝（φ⁴＋１）/φ²＝３（φ＋１）/φ²＝３

　４＝φ³−１/φ³　・・・　φ³−１/φ³＝（２φ＋１）−１/（２φ＋１）＝４（２φ＋１）/（２φ＋１）＝４

　７＝φ⁴＋１/φ⁴

　１１＝φ⁵−１/φ⁵

　１８＝φ⁶＋１/φ⁶

　・・・・・・・・・・・・・・


例２　２倍取りゲーム　（→　参考：「ニムゲームの話題」）

　1つの山にいくつかの石がある。次のルールで、２人が交互に石を取っていき、最後の石
を取った方が勝ちというゲームをする。

・先手は第1手では1個以上何個取ってもよい。ただし、山全部の石を取ってはいけない。

・先手の第1手以外では、1個以上直前の相手の取った石の個数の２倍以下の石を取って
よい。

　たとえば、最初に20個の石があったなら、先手の第1手では1個から19個まで取れる。仮
に3個取ったとすると、後手は1個から6個まで取れる。

　このゲームの必勝法を考えよ。

（解）　最初の石の数がフィボナッチ数でない限り先手必勝となる。

　石が20個の場合、20=13+5+2のように、より大きなフィボナッチ数（隣接するフィボナッチ

数ではない）を用いて石の個数を分解し、そのうち最小のフィボナッチ数の個数の石を取

ればよい。実際に、

(a)　この条件でのフィボナッチ数への分解は一意である。

(b)　分解した数の比は２倍よりも大きい。なぜならば、ｎ≧m+2 なら、ａ_ｎ＞２・ａ_ｍ

　 ルールから最小のフィボナッチ数を取った次の手では、その次のフィボナッチ数を取れ

ない。よって、和の中のフィボナッチ数の個数を減らせない。　　（終）


例　石の個数が３個のとき、先手の第１手は、１個または２個取れる。

　　先手の取った石が１個のとき、残りは２個。後手は、１×２＝２個以下の石が取れるの
　　で、２個全部取って、後手の勝利！

　　先手の取った石が２個のとき、残りは１個。後手は、２×２＝４個以下の石が取れるの
　　で、１個全部取って、後手の勝利！

例　石の個数が４個のとき、先手の第１手は、１個または２個または３個取れる。
　　先手の取った石が１個のとき、残りは３個。後手は、１×２＝２個以下の石しか取れな
　　いので、残りは、１個または２個。何れにしても次の先手が残り全部の石を取れるので、
　　先手の勝利！

　　先手の取った石が２個のとき、残りは２個。後手は、２×２＝４個以下の石が取れるの
　　で、残り全部取って、後手の勝利！

　　先手の取った石が３個のとき、残りは１個。後手は、３×２＝６個以下の石が取れるの
　　で、残り全部取って、後手の勝利！

　　以上から、先手必勝のためには、先手が第１手で、１個取ればよい。

　　この戦略は次の事実に基づいている。
　　　４＝３＋１　と、より大きなフィボナッチ数に分解するとき最小のフィボナッチ数は１

例　石の個数が６個のとき、６＝５＋１　なので、先手が第１手で石を１個取れば必勝であ
　る。実際に、残りは５個で、後手が取れる石の個数は２個以下。

　　後手の取る石が１個のとき、残りは４個で、
　　　　　　４＝３＋１　より、先手が１個取って、先手の勝利。

　　後手の取る石が２個のとき、残りは３個で、
　　　　　　先手が３個全部取って、先手の勝利。

例　石の個数が７個のとき、７＝５＋２　なので、先手が第１手で石を２個取れば必勝であ
　る。実際に、残りは５個で、後手が取れる石の個数は４個以下。

　　後手の取る石が１個のとき、残りは４個で、
　　　　　　４＝３＋１　より、先手が１個取って、先手の勝利。

　　後手の取る石が２個のとき、残りは３個で、先手が３個全部取って、先手の勝利。

　　後手の取る石が３個のとき、残りは２個で、先手が２個全部取って、先手の勝利。

　　後手の取る石が４個のとき、残りは１個で、先手が１個全部取って、先手の勝利。


（追記）　令和２年１２月１２日付け

　上記で、

（性質２３）　全ての自然数は、異なるいくつかのフィボナッチ数の和として表すことが
　　　　　　できる。

の話題が取り上げられたが、もっと強い事実があることをDD++さんよりご教示いただいた。

ゼッケンドルフの定理

　　任意の正の整数は「連続しない」フィボナッチ数の和で一意に表すことができる

　フィボナッチ数は、

　１ ，１ ，２ ，３ ，５ ，８ ，１３ ，２１ ，３４ ，５５ ，８９ ，１４４ ，２３３ ，３７７ ，・・・

という数であるが、「連続しない」ということを考慮すると、次のように一意に表現できる。

1=1		2=2		3=3		1+3=4
5=5		1+5=6		2+5=7		8=8
1+8=9		2+8=10		3+8=11		1+3+8=12
13=13		1+13=14		2+13=15		3+13=16	・・・・・・

　攻略法さんからの続報です。（平成２３年１１月１８日付け）

例３　ｘ^ｎ を ｘ²-ｘ-1 で割ったとき、商や余りの係数にフィボナッチ数が現れる。

例　ｘ¹⁰÷(ｘ²-ｘ-1)　の商は、ｘ⁸+ｘ⁷+2ｘ⁶+3ｘ⁵+5ｘ⁴+8ｘ³+13ｘ²+21ｘ+34、余りは、55ｘ+34

（証明）　ｘ^ｎ=(ｘ²-ｘ-1)(ａ₁ｘ^n-2+ａ₂ｘ^n-3+ … +ａ_n-k-1ｘ^k+ … +ａ_n-3ｘ²+ａ_n-2ｘ+ａ_n-1) + ａ_nｘ+ａ_n-1

　　　　両辺の係数を比較して、

　　ｘ^ｎ の係数から、　ａ₁=1

　　ｘ^n-1 の係数から、　ａ₂-ａ₁=0　 なので、　ａ₂=1

　　ｘ^n-2 の係数から、　ａ₃-ａ₂-ａ₁=0　 なので、　ａ₃=ａ₂+ａ₁=2

　　：

　　ｘ の係数　ａ_ｎ-ａ_ｎ-1-ａ_ｎ-2=0　 なので、　ａ_ｎ=ａ_ｎ-1+ａ_ｎ-2

　　定数項　ａ_ｎ-1-ａ_ｎ-1=0　　（証終）

　ここで、例１は、ｘ=φ として、余りに着目したもの。

例４　数理マジック「17番目の不思議」　・・・　任意の3桁の数の各桁の和を計算する。

　724
+ 111　← 最初は111との和
-----
+ 835
-----　+ 111
+ 946　← 2回目以降は、1つ上の数（ここでは、111）との和
-----　+ 835
+ 771　← 5+6=11、8+9=17のように10を超える場合は、1位の数のみ。桁上りはしない。
-----　+ 946
+ 617
-----　+ 771
+ 388
-----　+ 617
+ 995
-----　+ 388
+ 273
-----　+ 995
+ 168
-----　+ 273
+ 331
-----　+ 168
+ 499
-----　+ 331
+ 720
-----　+ 499
+ 119
-----　+ 720
+ 839
-----　+ 119
+ 948
-----　+ 839
+ 777　← 17番目の数

（証明）　最初の２つの数を、ａ、ｂ=111 とする。

ａ+ｂ、ａ+2ｂ、2ａ+3ｂ、3ａ+5ｂ、5ａ+8ｂ、8ａ+13ｂ=8ａ+3ｂ、13ａ+11ｂ=3ａ+ｂ、
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 … 、4ａ+3ｂ、3ａ+7ｂ、7ａ、7ｂ

　ａ_ｎ （ｍｏｄ　10）に着目して、　1、1、2、3、5、8、…、4、3、7、0、7　　（証終）


（追記）　当ＨＰがいつもお世話になっているＨＮ「空舟」さんより、平成２５年４月１６日付けで
　　　　「フィボナッチ数をｐで割った余りについて」と題して投稿頂いた。

　[行列によって示されること]

　A=(0,1 ; 1,1) によって[";"は改行を表す]、A²=(1,1 ; 1,2)、A³=(1,2 ; 2,3)、A⁴=(2,3 ; 3,5) ・・が
得られる。

　ｐを素数とする時、A^m≡(1,0 ; 0,1)　(mod ｐ) となるｍを見つけることは、フィボナッチ数列
をｐで割った余りの周期がｍとなることを意味する。

　(a,b ; b,c) (a,b,c∈Z/pZ) の形の"剰余類"は、ｐ³個ある。そのうち、行列式≡0 となるもの
を除いた"既約剰余類"は、ｐ³−ｐ個ある。

　既約剰余類は乗法群をなすので、群論のラグランジュの定理により、A^p3-p≡(1,0 ; 0,1) が
得られた。すなわち、フィボナッチ数をｐで割った余りは周期 ｐ³−ｐ を持つ。

　以上の議論は簡単だが、結果の精度は悪い。（ａⁿを15で割った余りが周期φ(p)=8を持つ
という主張と似ている。）実際、整数論的な考察をすると、さらに強い結果が得られる。
（剰余体Z/pZにおける(x²-x-1)の根の様子によって分類される）

　その結果は大変興味深いと思うので紹介したい：

ｐ=2 では、周期は3である。
ｐ=5 では、周期は20である。（実際 F[n]≡2n*3ⁿ (mod 5) が成り立つ）
ｐ＝5N±1型素数のときは、F[n]をｐで割った余りは周期 ｐ-1 を持つ。
ｐ＝5N±2型素数のときは、F[n]をｐで割った余りは周期 2(ｐ+1)を持つ。
（ただしこれらが最短周期かどうかは分からない。）

　F[0]=0であるから、その周期に対してF[n]がｐで割り切れることが従うが、ｐを4で割った余
りによりもう一歩踏み込める。

　複号は、ｐ＝5N±1型の時マイナス、ｐ＝5N±2型のときプラスとする。

ｐ＝4N±1型のときは、 F[(ｐ±1)/2]がｐで割り切れる。
ｐ＝4N±3型のときは、 F[(ｐ±1)]はｐで割り切れるがF[(ｐ±1)/2]はｐで割り切れない。

　素数のべきについては次が成り立つ。

　ｐを素数、q≧1とすると、

　F[n]がｐ^q で割り切れる　⇒　F[ｎｐ]は ｐ^q+1 で割り切れる

（p=q=2を除けば、逆もたぶん成り立つと思います。）


（追記）　平成２５年１２月１４日付け

　「フィボナッチでの新たな驚き」と題して、当ＨＰがいつもお世話になっているＨＮ「ＧＡＩ」さん
からの投稿です。

　フィボナッチ数列には、いろいろな性質があることは、上記でも数多く紹介されているとは
思いますが、次のことを計算していて気づいたことがありました。

　ａ₀＝１、ａ₁＝1、ａ_ｎ+2＝ａ_ｎ+1＋ａ_ｎ　（ｎ＝０，１，・・・）で定まるフィボナッチ数列の母関数とし
て(　→　参考：「不思議な分数」）

　

　　　　＝ａ₀＋ａ₁Ｘ＋ａ₂Ｘ²＋・・・＋ａ_ｎＸⁿ＋ａ_ｎ＋1Ｘ^n＋1＋ａ_ｎ＋2Ｘ^n＋2＋・・・

が決められるが、この関数から、

　F(0/1)=1(=1^2)　、F(1/2)=4(=2^2)　、F(3/5)=25(=5^2)　、F(8/13)=169(=13^2)

　F(21/34)=1156(=34^2)　、F(55/89)=7921(=89^2)　、F(144/233)=54289(=233^2)

　　　･･･････････

と一般に、F(ａ_ｎ-1/ａ_ｎ)＝ａ_ｎ²　が成立していく。（右辺の値→整数列大辞典「A081068」）

また、ａ₁＝１、ａ₂＝1、ａ_ｎ+2＝ａ_ｎ+1＋ａ_ｎ　（ｎ＝１，２，・・・）で定まるフィボナッチ数列の母関数
として、
　　　　　G(Ｘ)＝Ｘ/(1−Ｘ−Ｘ²)＝ａ₁Ｘ＋ａ₂Ｘ²＋・・・＋ａ_ｎＸⁿ＋・・・

が決められるが、この関数から、

　G(1/2)=2(=1・2)　、G(3/5)=15(=3・5)　、G(8/13)=104(=8・13)　、G(21/34)=714(=21・34)

　G(55/89)=4895(=55・89)　、G(144/233)=33552(=144・233)　、G(377/610)=229970(=377・610)

　　　･･････････

と一般に、G(ａ_ｎ-1/ａ_ｎ)＝ａ_ｎ-1・ａ_ｎ　が成立していく。（右辺の値→整数列大辞典「A081018」）

　こんな法則が潜んでいることにびっくりしました。


（コメント）　母関数って、不思議ですね！大変美しい性質だと思います。ＧＡＩ さんに感謝し
　　　　　　ます。


　カルピスさんからのコメントです。（平成２５年１２月１５日付け）

　私も、数日前に知ったことですが、フィボナッチ数列は、隣同士が、どんどん黄金比に近
づいていくことを初めて知って感動しました。（参考　→　（性質２５））


（追記）　平成２６年８月２４日付け

　当ＨＰ読者のＨＮ「Ｆｉｂｏ」さんから、フィボナッチ数の性質についてコメントを頂いた。

　フィボナッチ数列は、一般に、「前々項+前項=自項」となる数列ですので、

　(1)前々項と前項　　(2)前々項と自項　　(3)前項と自項

の三つのうちどれか一つの組み合わせが判れば、三数のうちの残りの数値を求める事がで
きます。

(例)　(1)　Fn-2+Fn-1=Fn　　(2)　Fn-Fn-2=Fn-1 　　(3)　Fn-Fn-1=Fn-2

(A)　FnとFn+3を使って、Fn+1を導く事ができます。　→　 (Fn+3/2 - Fn/2)  =Fn+1
(B)　同じく、FnとFn+3を使って、Fn+2を導く事ができます。　→　(Fn+3   + Fn)/2  =Fn+2

(実例に用いる表)
項数　 1　 ２　 3　  4　  5　 6　  7　  8　  9   10　 11　  12
fib数　1　  1　 2　　3　　5　 8　 13   21 　34　 55　 89   144
Fn    -5   -4   -3   -2   -1  Fn  +1   +2   +3   +4    +5   +6

(A)　Fnが第1項の時　(  3/2=1.5  - 1/2 =0.5 ) = 1=Fn+1
　　　Fnが第2項の時　(  5/2=2.5  - 1/2 =0.5 ) = 2=Fn+1
　　　　Fnが第3項の時　(  8/2=4    -  2/2=1   ) = 3=Fn+1
　　　Fnが第4項の時　( 13/2=6.5  -  3/2=1.5 ) = 5=Fn+1
　　　Fnが第5項の時　( 21/2=10.5 -  5/2=2.5 ) = 8=Fn+1　　（以下略）

　ここで、お気付きになられたと思いますが、上記のカッコ内の「-」符号を「+」に替えた場合、
Fn+2が求まる事がお解かりになられると思います。

　(B)の式も順を追って検証して頂ければ納得して頂けると思います。


（コメント）　Ｆｉｂｏさん、投稿ありがとうございます。堪能させていただきました。


（追記）　平成２７年３月１日付け

　平成２７年度入試　東京大学　前期理系　で次のような問題が出題された。数学的帰納法
の適当な練習となろう。

問題　数列｛ｐ_ｎ｝を次のように定める。

　　　　　ｐ₁＝１、ｐ₂＝２、ｐ_ｎ+2＝（ｐ_ｎ+1²＋１）/ｐ_ｎ　　（ｎ＝１，２，３，・・・）

（１）　（ｐ_ｎ+1²＋ｐ_ｎ²＋１）/（ｐ_ｎ+1ｐ_ｎ）がｎによらないことを示せ。

（２）　すべてのｎ＝２，３，４，・・・に対し、ｐ_ｎ+1＋ｐ_ｎ-1をｐ_ｎのみを使って表せ。

（３）　数列｛ｑ_ｎ｝を次のように定める。

　　　　　ｑ₁＝１、ｑ₂＝１、ｑ_ｎ+2＝ｑ_ｎ+1＋ｑ_ｎ　　（ｎ＝１，２，３，・・・）

　　　すべてのｎ＝１，２，３，・・・に対し、ｐ_ｎ＝ｑ_2ｎ-1を示せ。

（解）（１）　（ｐ_ｎ+2²＋ｐ_ｎ+1²＋１）/（ｐ_ｎ+2ｐ_ｎ+1）

　＝（｛（ｐ_ｎ+1²＋１）/ｐ_ｎ｝²＋ｐ_ｎ+1²＋１）/（｛（ｐ_ｎ+1²＋１）/ｐ_ｎ｝ｐ_ｎ+1）

　＝（（ｐ_ｎ+1²＋１）²＋（ｐ_ｎ+1²＋１）ｐ_ｎ²）/｛（ｐ_ｎ+1²＋１）ｐ_ｎｐ_ｎ+1｝

　＝（ｐ_ｎ+1²＋ｐ_ｎ²＋１）/（ｐ_ｎｐ_ｎ+1）

　よって、（ｐ_ｎ+1²＋ｐ_ｎ²＋１）/（ｐ_ｎ+1ｐ_ｎ）はｎによらず一定である。

（２）　（１）より、　（ｐ_ｎ+1²＋ｐ_ｎ²＋１）/（ｐ_ｎ+1ｐ_ｎ）＝（ｐ₂²＋ｐ₁²＋１）/（ｐ₂ｐ₁）＝６/２＝３

　　よって、　ｐ_ｎ+1²＋ｐ_ｎ²＋１＝３ｐ_ｎ+1ｐ_ｎ

　　また、　ｐ_ｎ+1²＋１＝ｐ_ｎ+2ｐ_ｎ　なので、　ｐ_ｎ²＋ｐ_ｎ+2ｐ_ｎ＝３ｐ_ｎ+1ｐ_ｎ

　　ｐ_ｎ≠０　なので、　ｐ_ｎ＋ｐ_ｎ+2＝３ｐ_ｎ+1　より、　ｐ_ｎ-1＋ｐ_ｎ+1＝３ｐ_ｎ

（３）　自然数ｎについての数学的帰納法により、命題「ｐ_ｎ＝ｑ_2ｎ-1」が成り立つことを示す。

ｎ＝１のとき、左辺＝ｐ₁＝１、右辺＝ｑ₁＝１　より、左辺＝右辺で、ｎ＝１のとき成り立つ。

ｎ＝２のとき、左辺＝ｐ₂＝２、右辺＝ｑ₃＝ｑ₁＋ｑ₂＝２　より、左辺＝右辺で、ｎ＝２のとき

成り立つ。

ｎ＝ｋ、ｋ＋１（ｋ≧１）のとき成り立つと仮定する。すなわち、　ｐ_ｋ＝ｑ_2ｋ-1、ｐ_ｋ+1＝ｑ_2ｋ+1

このとき、

ｑ_2ｋ+3＝ｑ_2ｋ+2＋ｑ_2ｋ+1

　　　＝ｑ_2ｋ+1＋ｑ_2ｋ＋ｑ_2ｋ+1＝２ｑ_2ｋ+1＋ｑ_2ｋ＝２ｑ_2ｋ+1＋ｑ_2ｋ+1−ｑ_2ｋ-1＝３ｑ_2ｋ+1−ｑ_2ｋ-1

において、（２）より、３ｐ_ｋ+1＝ｐ_ｋ＋ｐ_ｋ+2　なので、　３ｑ_2ｋ+1＝ｑ_2ｋ-1＋ｐ_ｋ+2　すなわち、

ｐ_ｋ+2＝３ｑ_2ｋ+1−ｑ_2ｋ-1　より、　ｐ_ｋ+2＝ｑ_2ｋ+3

　よって、命題は、ｎ＝ｋ＋２のときも成り立つ。

　したがって、すべての自然数ｎに対して、命題は成り立つ。　　（終）


（コメント）　標準的な数学的帰納法の問題でした。合格のためには落とせない問題ですね。


　とるえんさんからのコメントです。（平成２８年６月１３日付け）

　ｎ番目のフィボナッチ数を F(ｎ) と表すことにします。

　F(ｎ²)がF(ｎ)²で割り切れるようなF(n)は無数に存在するのでしょうか？

　自分で見つけられたのは、ｎ＝１、２、５のときだけでした。もっとも、プログラムの関係で
ｎ＝２２までしか調べられていないのですが・・・。どなたかご教示ください。


（コメント）　F(ｎ²) がF(ｎ)で割り切れることは明らかなので、さらに、その商F(ｎ²) /F(ｎ)が
　　　　　　F(ｎ) で割り切れることが無限にあるかということ。


　Seiichi　Manyamaさんからのコメントです。（平成２８年６月１４日付け）

　F(ｎ^k) が F(ｎ)^k で割り切れるような例を(Ruby)によるプログラムで見つけました。ちなみに
調べる範囲を狭めているので実行時間は１分くらいでしょう。

（実行結果）　ｋ＝２、３、４、５、６、７、８、９、１０　について、ｎ＝１、２、５　のみ

　そこで、すこし強引ですが、次の予想をしてみました。

（予想）　ｋ を２以上の整数とする。F(ｎ^k) が F(ｎ)^k で割り切れるとき、ｎ＝１、２、５ に限る。

　ｎ＝１、２ は自明ですね。


　Seiichi　Manyamaさんからのコメントです。（平成２８年６月１５日付け）

　「A128935」のコメントを読むと、F(５ⁿ) / F(５)ⁿ = m * 1000 + 1 と書けるらしい。


（コメント）　F(５ⁿ) / ５ⁿ＝F(５ⁿ) / F(５)ⁿ≡１　（ｍｏｄ　１０００）　ということですね。


　ａｔ さんからのコメントです。（平成２８年６月１９日付け）

　数学サイト「数学の部屋」の「フィボナッチ数列の性質」によれば、F(m) が F(n)² で割り切
れるような m の最小値は、m=n*F(n)であるようです。

　そうすると、n＞6　のときには、 n*F(n)＞n² ですから、F(n²) が F(n)² で割り切れるような
n は、n=1、2、5 のみ ということになりますね。


　Seiichi　Manyamaさんからのコメントです。（平成２８年６月１９日付け）

　k = 2 のときについて、F(n^k) が F(n)^k で割り切れるような n は、n=1、2、5 のみということ
みたいですね。素晴らしいです！


　とるえんさんからのコメントです。（平成２８年６月２１日付け）

　皆様ご回答ありがとうございます。

　興味深い性質ですが、このことの証明は易しくないようですね・・・。フィボナッチ数の神秘を
また一つ垣間見た気分です。


　空舟さんからのコメントです。（平成２８年６月２５日付け）

　いくつかの性質を既知とすると見通し良いと思います

[結論]　F[ｎ]が２または５以外の奇素数で割り切れる時、F[ｎ^k]はF[ｎ]^kで割り切れ得ない。

（そうでないｎが、ｎ=1、2、5に限ることを示すのは難しくないと思います。）

　断らない変数は（文脈に応じて正の）整数とする。

[場合1]　F[ｎ]が２で割り切れる場合

　　Xが２で割り切れる回数を v(X) とおく。

[補題1-1]　F[ｎ]が２で割り切れる時、ｎ=3j　とおける。

[補題1-2]　j が奇数のとき、v(F[3j])=1

　　　　　　　j が偶数のとき、v(F[3j])=2+v(j)　が成り立つ。

[議論]

・j が奇数のとき、v(F[ｎ]^k)=k　、v(F[ｎ^k])=1

・j が偶数のとき、v(F[ｎ]^k)=k*{2+v(j)}　、v(F[ｎ^k])=2+v(3^k-1*j^k) = 2 + k*v(j)

　[ｎ^k=3J による J=3^k-1*j^k を j として補題1-2に適用]

　比較により、k≧2 のとき、F[ｎ^k]はF[ｎ]^kで割り切れ得ないことが言える。


[場合2]　F[ｎ]が奇素数pで割り切れる場合

　　Xがpで割り切れる回数をv(X)とおく。

[補題2-1]　F[ｎ]がpで割り切れる時、F[ｎ]がpで割り切れる最小の正の整数ｎをｍとおくと、
　　　　　　n=mj とおける。

[補題2-2]　このｍによって、v(F[mj])=v(F[m])+v(j)　が成り立つ。

[補題2-3]　p=5N±1型素数のとき、ｍはp-1の約数
　　　　　　　p=5N±2型素数のとき、ｍはp+1の約数

　従って、p≠5ならば、mとpは互いに素である。これを　v(m^k-1)=0　として後で使う。

[議論]

v(F[ｎ]^k)=k*{v(F[m])+v(j)}

v(F[ｎ^k])=v(F[m])+v(m^k-1*j^k) = v(F[m]) + k*v(j)

　比較により、k≧2 のとき、F[ｎ^k]はF[ｎ]^kで割り切れ得ないことが言える。


　因みに、この設定でのv(F[m])は大抵の素数pに対して1となりますが、1にならないようなp
が存在するかどうかは未解決のようです。
（→　参考）（→　補題の周辺）（→　素数ベキによる整除に関する定理）
　x,yの範囲を非整数x={(1+√5)/2}^m, y={(1-√5)/2}^mに形式的に拡張した形。


　ＧＡＩ さんからのコメントです。（平成２９年５月３日付け）

　一連のフィボナッチ数列に関する話題の中に、逆数や積のことが入ってなかったので、そ
れに関することで、次のことが成り立つことを読んだのでメモしておきます。

　フィボナッチ数列 ａ[1]＝１、ａ[2]＝1、ａ[ｎ+2]＝ａ[ｎ]＋ａ[ｎ+1]　（ｎ＝１，２，・・・）であるとき、

（イ）　Σ_n=1〜∞ 1/a[n]＝Σ_n=0〜∞ (-1)ⁿ/(φ²ⁿ⁺¹-(-1)ⁿ)＝3.3598856662･･･

（ロ）　Σ_n=0〜∞ 1/a[2ⁿ]＝4-φ＝2.38196601125･･･

（ハ）　Π_k=1〜n a[k]〜C*φ^(n(n+1)/2)/5^(n/2)

　ただし、φ＝(１＋)/２＝1.6180339887･･･ （黄金比）
　　　 　　 C＝Π_n=1〜∞ (1-(-1)ⁿ/φ²ⁿ)＝1.2267420107･･･ なる定数とする。

　フィボナッチ数列には黄金比が深く関わっていることが見てとれます。


（追記）　「フィボナッチ数のべき乗数」と題して、ＧＡＩ さんからご投稿いただきました。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（令和２年１２月１３日付け）

　フィボナッチ数 {F(n)}：0,1,1,2,3,5,8,13,21,35,･･･　に関して、必ず示される漸化式が

　　F(n+2)=F(n+1)+F(n)

　そこで、このフィボナッチ数のm乗数:F(n)^mについて調べると、

F(n+3)^2=2*F(n+2)^2+2*F(n+1)^2-F(n)^2

F(n+4)^3=3*F(n+3)^3+6*F(n+2)^3-3*F(n+1)^3-F(n)^3

F(n+5)^4=5*F(n+4)^4+15*F(n+3)^4-15*F(n+2)^4-5*F(n+1)^4+F(n)^4

　　･･･････････････

が成立しています。

　m=5、6、･･･　に挑戦してほしい。


（コメント）　少し気になったので計算してみました。

F(n+3)^2=（F(n+2)＋F(n+1)）^2=F(n+2)^2+2*F(n+2)F(n+1)+F(n+1)^2

=F(n+2)^2+2*(F(n+1)+F(n))F(n+1)+(F(n+2)-F(n))^2

=F(n+2)^2+2*F(n+1)^2+2*F(n) F(n+1)+F(n+2)^2-2*F(n+2)F(n)+F(n)^2

=2*F(n+2)^2+2*F(n+1)^2+2*F(n) (F(n+1)-F(n+2))+F(n)^2

=2*F(n+2)^2+2*F(n+1)^2-2*F(n)^2+F(n)^2

=2*F(n+2)^2+2*F(n+1)^2-F(n)^2

　他も同様かな？でも大変そう．．．。


　ａｔ さんからのコメントです。（令和４年７月３１日付け）

　m=5、6、･･･　に挑戦してほしい。

　(F(n+6))^5、(F(n+7))^6 は、次のようになります。

(F(n+6))^5=8*(F(n+5))^5+40*(F(n+4))^5-60*(F(n+3))^5-40*(F(n+2))^5+8*(F(n+1))^5+(F(n))^5

(F(n+7))^6=13*(F(n+6))^6+104*(F(n+5))^6-260*(F(n+4))^6
　　　　　　　　　　　　　　　　　　　　　-260*(F(n+3))^6+104*(F(n+2))^6+13*(F(n+1))^6-(F(n))^6

　一般には、次のようになります。

　mを正整数、s、t を実数(ただし、t^2+4*s≠0、t≠0)とするとき、漸化式

　　a(n+2)=s*a(n)+t*a(n+1)

を満たす数列 {a(n)} に対して、等式

(a(n+m+1))^m
=Σ[k=1〜m+1](a(n+m+1-k))^m*((-1)^(k+1))*((-s)^(k*(k-1)/2))*(Π[j=1〜k]A(m+2-j)/A(j))

が成り立ちます。ここで、{A(n)}は以下で定まる数列です。

　A(0)=0　、A(1)=1　、A(n+2)=s*A(n)+t*A(n+1) (n≧0)

(証明)　α=(t+√(t^2+4*s))/2、β=(t-√(t^2+4*s))/2 とします。

　a(n)=v*α^n+w*β^n (v,wは定数) と表せます。G(z)=Σ[n≧0](a(n))^m*z^n とおくと、

G(z)
=Σ[n≧0](v*α^n+w*β^n)^m*z^n
=Σ[n≧0]z^n*(Σ[j≧0]comb(m,j)*(v*α^n)^j*(w*β^n)^(m-j))
=Σ[n≧0]z^n*(Σ[j≧0]comb(m,j)*(v^j*w^(m-j))*((α/β)^j*β^m)^n)
=Σ[n≧0]Σ[j≧0]comb(m,j)*(v^j*w^(m-j))*(z*(α/β)^j*β^m)^n
=Σ[j≧0]comb(m,j)*(v^j*w^(m-j))*(Σ[n≧0](z*(α/β)^j*β^m)^n)
=Σ[j≧0]comb(m,j)*(v^j*w^(m-j))*(1/(1-z*(α/β)^j*β^m)).

よって、　G(z/(β^m))=Σ[j≧0]comb(m,j)*(v^j*w^(m-j))*(1/(1-z*(α/β)^j)).

両辺に、Π[j=0〜m](1-z*(α/β)^j) をかけると、

　G(z/(β^m))*Π[j=0〜m](1-z*(α/β)^j)=(zについてのm次以下の多項式)

となります。両辺の z^(n+m+1) の係数を比較して、

　[z^(n+m+1)](G(z/(β^m))*Π[j=0〜m](1-z*(α/β)^j))=0

　[z^(n+m+1)](G(z/(β^m))*Π[j=0〜m](1-z*(α/β)^j))
=Σ[k=0〜m+1]([z^(n+m+1-k)]G(z/(β^m)))*([z^k]Π[j=0〜m](1-z*(α/β)^j)))

ここで、[z^(n+m+1-k)]G(z/(β^m))=(a(n+m+1-k))^m*(1/β)^(m*(n+m+1-k))

また、[z^k]Π[j=0〜m](1-z*(α/β)^j) は少々厄介ですが、

[z^k]Π[j=0〜m](1-z*(α/β)^j)
=((-1)^k)*((α/β)^(k*(k-1)/2))*Π[j=1〜k](1-(α/β)^(m+2-j))/(1-(α/β)^j)

となります。

(一般に、

[z^k](Π[j=0〜m](1-z*γ^j))=((-1)^k)*(γ^(k*(k-1)/2))*Π[j=1〜k](1-γ^(m+2-j))/(1-γ^j))

となります。このことは後に証明します。)

よって、

[z^(n+m+1)](G(z/(β^m))*Π[j=0〜m](1-z*(α/β)^j))
=Σ[k=0〜m+1](a(n+m+1-k))^m*(1/β)^(m*(n+m+1-k))*((-1)^k)*((α/β)^(k*(k-1)/2))
　　　　　　　　　　　　　　　　　　　　　　　　　　　*Π[j=1〜k](1-(α/β)^(m+2-j))/(1-(α/β)^j)
=Σ[k=0〜m+1](a(n+m+1-k))^m*((-1)^k)*((α*β)^(k*(k-1)/2))
　　　　　　　　　　　　*(Π[j=1〜k](β^(m+2-j)-α^(m+2-j))/(β^j-α^j))*(1/β)^(m*(n+m+1))
=Σ[k=0〜m+1](a(n+m+1-k))^m*((-1)^k)*((-s)^(k*(k-1)/2))
　　　　　　　　　　　　　　　　　　　　　　　　　　*(Π[j=1〜k]A(m+2-j)/A(j))*(1/β)^(m*(n+m+1))

　これが 0 に等しいので、

(a(n+m+1))^m
= Σ[k=1〜m+1](a(n+m+1-k))^m*((-1)^(k+1))*((-s)^(k*(k-1)/2))*(Π[j=1〜k]A(m+2-j)/A(j)).


[z^k](Π[j=0〜m](1-z*γ^j))=((-1)^k)*(γ^(k*(k-1)/2))*Π[j=1〜k](1-γ^(m+2-j))/(1-γ^j)

であることの証明：

　G(γ,z)=Π[j=0〜m](1-z*γ^j)　とおき、G(γ,z)を展開したときの z^k の係数を U(γ,k) とし
ます。

　そうすると、G(γ,z)=Σ[k=0〜m+1]U(γ,k)*z^k

　等式 (1-z*γ^(m+1))*G(γ,z)=(1-z)*G(γ,z*γ) が成り立ちます。

　この等式の両辺のz^kの係数を比較して、

　　U(γ,k)-U(γ,k-1)*γ^(m+1)=U(γ,k)*γ^k-U(γ,k-1)*γ^(k-1)

よって、

U(γ,k)=((γ^(m+1)-γ^(k-1))/(1-γ^k))*U(γ,k-1)
　　　　=((γ^(m+1)-γ^(k-1))*(γ^(m+1)-γ^(k-2))/((1-γ^k)*(1-γ^(k-1))))*U(γ,k-2)
　　　　=…
　　　　=(Π[j=1〜k](γ^(m+1)-γ^(k-j))/(1-γ^j))*U(γ,0)
　　　　=Π[j=1〜k](γ^(m+1)-γ^(k-j))/(1-γ^j)
　　　　=((-1)^k)*(γ^(k*(k-1)/2))*Π[j=1〜k](1-γ^(m+2-j))/(1-γ^j)


　ＧＡＩ さんからのコメントです。（令和４年８月１日付け）

　２年前の投稿だったので忘れていました。ちなみに10乗までの式を置いておきます。

F(n+8)^7=21*(F(n+7))^7+273*(F(n+6))^7-1092*(F(n+5))^7-1820*(F(n+4))^7
　　　　　　　　　　　　　　　　　　　　 +1092*(F(n+3))^7+273*(F(n+2))^7-21*(F(n+1))^7-(F(n))^7

F(n+9)^8=34*(F(n+8))^8+714*(F(n+7))^8-4641*(F(n+6))^8-12376*(F(n+5))^8
　　　　　　　　　+12376*(F(n+4))^8+4641*(F(n+3))^8-714*(F(n+2))^8-34*F(n+1))^8+(F(n))^8

F(n+10)^9=55*(F(n+9))^9+1870*(F(n+8))^9-19635*(F(n+7))^9-85085*(F(n+6))^9+136136*(F(n+5))^9
　　　　　　　　　　　　　+85085*(F(n+4))^9-19635*(F(n+3))^9-1870*(F(n+2))^9+55*(F(n+1))^9+(F(n))^9

F(n+11)^10=89*(F(n+10))^10+4895*(F(n+9))^10-83215*(F(n+8))^10-582505*(F(n+7))^10
　　　　　　　　　　　　　　+1514513*(F(n+6))^10+1514513*(F(n+5))^10-582505*(F(n+4))^10
　　　　　　　　　　　　　　　-83215*(F(n+3))^10+4895*(F(n+2))^10 +89*(F(n+1))^10-(F(n))^10

　なお、10乗の式を構成するには、プログラム的に

gp > A(n)=matrix(n,n,i,j,binomial(i-1,n-j));
gp > charpoly(A(11),x)
%150 =x^11 - 89*x^10 - 4895*x^9 + 83215*x^8 + 582505*x^7 - 1514513*x^6
　　　　　　　　　　　　　　　- 1514513*x^5 + 582505*x^4 + 83215*x^3 - 4895*x^2 - 89*x + 1

　なお、

gp > A(11)
%151 =
[0  0  0   0   0   0   0   0   0  0 1]
[0  0  0   0   0   0   0   0   0  1 1]
[0  0  0   0   0   0   0   0   1  2 1]
[0  0  0   0   0   0   0   1   3  3 1]
[0  0  0   0   0   0   1   4   6  4 1]
[0  0  0   0   0   1   5  10  10  5 1]
[0  0  0   0   1   6  15  20  15  6 1]
[0  0  0   1   7  21  35  35  21  7 1]
[0  0  1   8  28  56  70  56  28  8 1]
[0  1  9  36  84 126 126  84  36  9 1]
[1 10 45 120 210 252 210 120  45 10 1]

の行列を意味する。(パスカルの三角形を右詰めで作る。)　この行列の特性方程式を導くの
がcharpolyコマンドです。

　この式から、%150=0　と置いて、一気に

x^11=89*x^10 + 4895*x^9 - 83215*x^8 - 582505*x^7 + 1514513*x^6
　　　　　　　　　　　　　　　+ 1514513*x^5 - 582505*x^4 - 83215*x^3 + 4895*x^2 + 89*x - 1

の表示が入手でき、これを元に組み立てられる。


　ＧＡＩ さんからのコメントです。（令和４年８月５日付け）

　x^n を x^2-x-1 で割った商と余りにはフィボナッチ数が密接に関わってくる。

x^2 = (x^2 - x - 1)*(1) + (x + 1)
x^3 = (x^2 - x - 1)*(x + 1) + (2*x + 1)
x^4 = (x^2 - x - 1)*(x^2 + x + 2) + (3*x + 2)
x^5 = (x^2 - x - 1)*(x^3 + x^2 + 2*x + 3) + (5*x + 3)
x^6 = (x^2 - x - 1)*(x^4 + x^3 + 2*x^2 + 3*x + 5) + (8*x + 5)
x^7 = (x^2 - x - 1)*(x^5 + x^4 + 2*x^3 + 3*x^2 + 5*x + 8) + (13*x + 8)
x^8 = (x^2 - x - 1)*(x^6 + x^5 + 2*x^4 + 3*x^3 + 5*x^2 + 8*x + 13) + (21*x + 13)
x^9 = (x^2 - x - 1)*(x^7 + x^6 + 2*x^5 + 3*x^4 + 5*x^3 + 8*x^2 + 13*x + 21) + (34*x + 21)
x^10 = (x^2 - x - 1)*(x^8 + x^7 + 2*x^6 + 3*x^5 + 5*x^4 + 8*x^3
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　+ 13*x^2 + 21*x + 34) + (55*x + 34)
x^11 = (x^2 - x - 1)*(x^9 + x^8 + 2*x^7 + 3*x^6 + 5*x^5 + 8*x^4
　　　　　　　　　　　　　　　　　　　　　　　　　　　 + 13*x^3 + 21*x^2 + 34*x + 55) + (89*x + 55)
x^12 = (x^2 - x - 1)*(x^10 + x^9 + 2*x^8 + 3*x^7 + 5*x^6 + 8*x^5
　　　　　　　　　　　　　　　　　　　　 + 13*x^4 + 21*x^3 + 34*x^2 + 55*x + 89) + (144*x + 89)
x^13 = (x^2 - x - 1)*(x^11 + x^10 + 2*x^9 + 3*x^8 + 5*x^7 + 8*x^6
　　　　　　　　　　　　　 + 13*x^5 + 21*x^4 + 34*x^3 + 55*x^2 + 89*x + 144) + (233*x + 144)
x^14 = (x^2 - x - 1)*(x^12 + x^11 + 2*x^10 + 3*x^9 + 5*x^8 + 8*x^7
　　　　　　 + 13*x^6 + 21*x^5 + 34*x^4 + 55*x^3 + 89*x^2 + 144*x + 233) + (377*x + 233)
x^15 = (x^2 - x - 1)*(x^13 + x^12 + 2*x^11 + 3*x^10 + 5*x^9 + 8*x^8 + 13*x^7
　　　　　　 + 21*x^6 + 34*x^5 + 55*x^4 + 89*x^3 + 144*x^2 + 233*x + 377) + (610*x + 377)
　　　　･･････････････････



　　以下、工事中！



（付記）　当ページは、ＮＩＣＥＲ（教育情報ナショナルセンター（国立教育政策研究所））に、
　　　　　平成１６年１０月２２日付けで登録されました。当ＨＰは、ＮＩＣＥＲの趣旨に賛同し、
　　　　　参画しております。

（追記）　国の事業仕分けにより、「教育情報ナショナルセンター」は平成２３年４月以降運
　　　　用終了とされ、公益財団法人学習ソフトウェア情報研究センターに移管された模
　　　　様です。検索機能が追加され、使い勝手は向上したかもしれません。
　　　　　その中に、「フィボナッチ数を極める」が登録されているのを確認しました。登録番
　　　　号は「７１９」です。（平成２３年５月２９日付け）