・　不思議な分数　　　 　　　　　　　　　　　　　　　Ｓ．Ｈ氏

　不思議な分数がある。それは、
　　　　　　　　　　　　　　　　　　　　　
という分数である。

　これを、小数点以下１００桁まで小数展開すると、次のようになる。

　0．0112 3595 5056 1797 7528 0898 8764 0449 4382 0224 7191 0112
　　 3595 5056 1797 7528 0898 8764 0449 4382 0224 7191 0112 3595
　　 5056 ・・・・

（この計算には、Ｅｘｃｅｌ　のＶＢＡを活用した。普通の電卓では、ここまで出力することはできないでしょう！）

　この小数展開の最初の部分を眺めていると、　１，１，２，３，５，・・・　となっていて、何と
なく、フィボナッチ数列の匂いがすることに気がつく。

　そこで、小数展開を次のように分解すると、フィボナッチ数列が、ものの見事に続いてい
る。何て、美しい現象だろう！何て不思議な分数なんだろう！と、思わず感動してしまった。

　0．0112 3595 5056 1797 7528 0898 8764 0449 4382 0224 7191 0112
　　　　1
　　 　　 1
　　　　　　2
　　　　　　　 3
　　　　　　　　 5
　　　　　　　　　 8
　　　　　　　　　 1 3
　　　　　　　　　 　 2 1
　　　　　　 　　　　　 3 4
　　　　　　　 　　 　　　 5 5
　　　　　　　　 　　　　　　 8 9
　　　　 　　　　　　　　　　 1 4 4
　　　　　 　　　　　 　　　　　 2 3 3
　　　　 　　　　　 　　　　　　　　3 7 7
　　 　　　　 　　　　　　　　 　　　　6 1 0
　　　　　　　　 　　　　　 　　 　 　　　9 8 7
　　　　　　　 　　　 　 　　　　　　　 　1 5 9 7
　　　　　　 　　　　 　　　　　 　 　　　　 2 5 8 4
　　　　 　　　　　　　　 　　　　　　　 　　　 4 1 8 1
　　　　　　　　　　　　　　　 　 　　　　 　　　　6 7 6 5
　　　　　　　　　　 　 　　　　 　　 　　　　　　 1 0 9 4 6
　　　　　　　　　　　　　　 　 　　　　　　 　　　 　1 7 7 1 1
　　　　　　　　　　　　　　　　　　　　　　　　　　　　 ・・・・・・・・・・・・・・・・・・・

　最初の方は、確かにフィボナッチ数列になっているが、これが、そのまま続くのかどうか、
実は、私自身検証していない。どうやって証明するのだろう？ご存知の方、メール下さい。

（参考文献：佐藤修一　著　　自然にひそむ数学　（講談社））

（追記）　上記の件に関して、猫目石さんから情報をいただいた。（２００３年８月１２日付け）

　　　　その情報によると、分数 １/８９ の小数展開には、フィボナッチ数列が完全に関わっ
　　　ているとのことである。

　　　　猫目石さんから、べき級数(母関数)を使った証明を教わったので、それを紹介したい
　　　と思う。
　　　（猫目石さんによると、いくつかある証明の中で、一番スマートな証明らしい。）

　　　フィボナッチ数列｛ａｎ｝は、漸化式 ａ₀＝１、ａ₁＝１、ａ_ｎ＋2＝ａ_ｎ＋ａ_ｎ＋1 （ｎ＝０，１，・・・）
　　により定義される数列である。すなわち、

　　　　１、１、２、３、５、８、１３、２１、３４、５５、８９、１４４、２３３、３７７、６１０、９８７、・・・

　　（参考：フィボナッチ数を極める）

　　　そこで、関数 Ｆ(Ｘ) を、フィボナッチ数列の項を用いて、べき級数

　　　　　Ｆ(Ｘ)＝ａ₀＋ａ₁Ｘ＋ａ₂Ｘ²＋・・・＋ａ_ｎＸⁿ＋・・・

　　　により、定義する。その収束半径は、ビネの公式を用いて、

　　　　　　
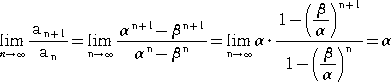
　　　　　　　　　　　　　　　　　　　　ただし、
　　　　　　　　　　　　　　　　　　　　　　　　　　
　　　により（ダランベールの定理）、

　　　　　　　　　　　
　　　となる。
　　　　いま、次の３式を考える。

　　 　　　　Ｆ(Ｘ)＝ａ₀＋ａ₁Ｘ＋ａ₂Ｘ²＋・・・＋ａ_ｎＸⁿ＋ａ_ｎ＋1Ｘ^n＋1＋ａ_ｎ＋2Ｘ^n＋2＋・・・

　 　　　　ＸＦ(Ｘ)＝　　　ａ₀Ｘ＋ａ₁Ｘ²＋ａ₂Ｘ³＋・・・・・・＋ａ_ｎＸ^n＋1＋ａ_ｎ＋1Ｘ^n＋2＋・・・

　　　　　Ｘ²Ｆ(Ｘ)＝　　　　　　 ａ₀Ｘ²＋ａ₁Ｘ³＋ａ₂Ｘ⁴＋・・・・・・・・・・・＋ａ_ｎＸ^n＋2＋・・・

　　　ａ_ｎ＋2＝ａ_ｎ＋ａ_ｎ＋1 （ｎ＝０，１，・・・）という関係から、

　　　　　　　　　　　　Ｆ(Ｘ)−ａ₀−ａ₁Ｘ＝（ＸＦ(Ｘ)−ａ₀Ｘ）＋Ｘ²Ｆ(Ｘ)

　　　が成り立つ。

　　　　ａ₀＝１、ａ₁＝１ を代入して、Ｆ(Ｘ)−１＝ＸＦ(Ｘ)＋Ｘ²Ｆ(Ｘ)　より、

　　　　　　　　　　　　（１−Ｘ−Ｘ²）Ｆ(Ｘ)＝１
　　　すなわち、
　　　　　　　　　　　　
　　　が成り立つ。

　　　　ここで、Ｘ＝１/１０ （Ｘ＜１/α）を、Ｆ(Ｘ) に代入して、

　　　　　　　　Ｆ(１/１０)＝１/（１−１/１０−１/１００）＝１００/８９

　　　となるので、

　　　１/８９＝Ｆ(１/１０)/１００
　　　　　　 ＝ａ₀(1/10)²＋ａ₁(1/10)³＋ａ₂(1/10)⁴＋・・・＋ａ_ｎ(1/10)^n＋2＋・・・

　　　以上から、各桁の数字にフィボナッッチ数が関わっていることが示された。

　猫目石さんによれば、同様に、

１/９８９９＝０．０００１０１０２０３０５０８１３２１３４５５９０４６３６８３２００３２３２６４９７６２６０２２８３０５８８・・・・・

１/９９８９９９＝０．０００００１００１００２００３００５００８０１３０２１０３４０５５０８９１４４２３３３７７６１０９８８・・・・・

もフィボナッチ数で構成されるそうだ。

　貴重な情報を頂戴して、猫目石さんに、感謝いたします。


（追々記）　２００４年９月号の数学セミナーに、札幌市の萱場　修さんが、「１/８９の不思議」
　　　　　と題して投稿されている。１０年以上前からずっと不思議な数の関係にとらわれてい
　　　　　られたとかで、その疑問が解けて楽しくなったとのことである。

　　　　　　基本的な解答の方法は、猫目石さんのものとほとんど同じであるが、萱場さんは、
　　　　　数列の和 Ｓ_ｎ を、
　　　　　　　　　　　　　　　　Ｓ_ｎ ＝ａ₀Ｘ²＋ａ₁Ｘ³＋・・・＋ａ_ｎＸ^n＋1　　（Ｘ＝１/１０）

　　　　　として、（１−Ｘ−Ｘ²）Ｓ_ｎ を巧妙に計算し、上記の Ｆ(Ｘ) と同様の式を導き、

　　　　　　　　　　　　　　　　Ｓ_ｎ → １/８９ 　　（ｎ → ∞）

　　　　　を得ている。

　　　　　　萱場さんによれば、

　　　　　　　　　１/９８９９　は、Ｘ＝１/１００　のとき

　　　　　　　　　１/９９８９９９　は、Ｘ＝１/１００　のとき

　　　　　に、それぞれ与えられるそうだ。


　ＨＮ「ＧＡＩ」さんからのコメントです。（平成２４年１２月２５日付け）

　私の備忘録の解析分野に「フィボナッチ数を極める」の項目があり、いろいろな性質が成
立することを知ることができます。ただそこに記載されてない部分で近頃ある本を読んでい
て、このフィボナッチ数列について衝撃的な印象を受けた記事に出会ったので紹介します。

　まず、フィボナッチ数列できまる数列：a₁=1，a₂=1，a₃=2，a₄=3，a₅=5，a₆=8，a₇=13，.....　と
続くものとする。このとき、

　a₁/10²+a₂/10³+a₃/10⁴+a₄/10⁵+a₅/10⁶+a₆/10⁷+a₇/10⁸+....+a_n/10ⁿ⁺¹+.....

というように、ｎ番目のフィボナッチ数a_nを小数以下n+1桁目になるように加工して加えていく
と、その和が、0.001123595505617977528089887640449438202247191.....　となりますが、一
方　1/89=0.001123595505617977528089887640449438202247191.....　と一致することに驚き
ました。


（コメント）　なぜそうなるかは、猫目石さんによる証明で納得されると思います。