ピタゴラス数の発見　　　　　　　　　　　　　　　　

　Ｂ．Ｃ．１８００年頃（ピタゴラス（Ｂ．Ｃ．５８０年？〜Ｂ．Ｃ．４９７年）より１３００年ほど前）バビロ
ニアの粘土板の中に、

　　「１つの平方数が、２つの平方数の和となる」

ような、３つの数の例が数多く見い出されている。かなり昔から、そのような性質を持つ数
に関心を持たれていたようである。

　Ｐ＞Ｑ で Ｐ、Ｑは互いに素、かつ、Ｐ、Ｑのどちらかは偶数であるようなＰ、Ｑを用いて、
そのような３つの数は、
　　　　　　　　　　　　　　　Ｐ²−Ｑ²　、　２ＰＱ　、　Ｐ²＋Ｑ²

と書けることも、古代バビロニアの人々は知っていたものと推測されている。

（厳密な証明は、ユークリッド原論（Ｂ．Ｃ．３５０年頃）にある。和田秀男　著　数の世界（岩
波書店）に、その証明がのっている。）


　ピタゴラス自身は、ｍを３以上の奇数として、そのような数は、

　　ｍ　、（ｍ²−１）/２　、（ｍ²＋１）/２

であることを示している。（→　参考：「ピタゴラス数発見の道標」）

　実際に、　ｍ²＋｛（ｍ²−１）/２｝²＝｛（ｍ²＋１）/２｝²　が成り立つ。

　ここで、「ｍ　、（ｍ²−１）/２　、（ｍ²＋１）/２」を「２ｍ・１　、ｍ²−１²　、ｍ²＋１²」と考え

　ｍ＝Ｐ　、１＝Ｑ　とおいてあげると、　「　２ＰＱ　、　Ｐ²−Ｑ²　、Ｐ²＋Ｑ²　」　が導かれる。


　これに対して、１〜２世紀頃の数学者ディオファントスは、ユークリッド原論とは違う考え方
で、この問題をとらえている。私の知らなかった考え方なので、紹介したい。

　条件を満たす３つの数を求めることは、単位円周上の有理点を求めることに等しい。

点（−１，０）を通る傾きｍの直線の方程式は、Ｙ＝ｍ(Ｘ＋１) と書ける。この直線と単位円

との交点を求めると、
　　　　　　　　　　　　　　

である。このとき、この点が有理点ということと ｍ が有理数ということは同値である。

　そこで、互いに素な自然数Ｐ、Ｑを用いて、

　　　　　　　　　　　

と表し、上の座標に代入することにより、求める３つの数として、


　　　　　Ｐ²−Ｑ²　、　２ＰＱ　、　Ｐ²＋Ｑ²

を得ることが出来る。

（参考文献：志賀浩二　著　おお、ピタゴラス（教育出版高校通信））


（追記）　平成１８年８月１３日付け

　ピタゴラス数を機械的に計算する公式としては、上記の公式が有名である。最近、その方
法以外にもいろいろな手があることを知った。

（方法その１）　１ から始まる連続した奇数列の和は、奇数列の項数の平方に等しい。

　上記の性質を用いると、

　１＋３＋５＋７＝４²　、１＋３＋５＋７＋９＝５²　　より、　　４²＋３²＝５²　が得られる。

１＋３＋５＋７＋９＋１１＋１３＋１５＋１７＋１９＋２１＋２３＝１２²　と、

１＋３＋５＋７＋９＋１１＋１３＋１５＋１７＋１９＋２１＋２３＋２５＝１３²　　より、

　　　１２²＋５²＝１３²　が得られる。

簡便にピタゴラス数を得るとしたら、この方法の方が楽かもしれない。

（方法その２）　　　（２ｎ）²＋（ｎ²−１）²＝（ｎ²＋１）²

　上記の性質を用いると、

ｎ＝２　のとき、　　４²＋３²＝５²　 が得られる。

ｎ＝４　のとき、　　８²＋１５²＝１７²　 が得られる。

ｎ＝５　のとき、　　５²＋１２²＝１３²　 が得られる。

ダブりでピタゴラス数を得ることもあるが、公式は単純である。

（　→　参考：ピタゴラス数のある性質）

（追記）　平成２０年１０月４日付け

　ピタゴラス数は、方程式　ｘ²＋ｙ²＝ｚ²　を満たす正の整数解であるが、これと同じタイプで、
次のような方程式の正の整数解を求めることも興味深い。

　　　　　　ｘ²＋２ｙ²＝ｚ²

　この方程式を満たす解として、（ ｘ ， ｙ ， ｚ ）＝（ １ ， ２ ， ３ ）　は直ぐに見つかるだろう。

この ワン・ツー・スリー（フランス語で言えば、アン・ドゥ・トロワ・・・思わず、キャンディーズの唄

を思い出してしまった！）という美しい響きにその一般解を知りたいという気持ちがざわめく。

　結論から言えば、

　　ｘ²＋２ｙ²＝ｚ²　を満たす互いに素な正の整数 ｘ ， ｙ ， ｚ は、

　　　　　ｘ＝±（ａ²−２ｂ²）　、　ｙ＝２ａｂ　、　ｚ＝ａ²＋２ｂ²

　　　　　　　　　ただし、ａ、ｂ は互いに素な正の整数で、特に、ａ は奇数

で与えられる。

　（ ｘ ， ｙ ， ｚ ）＝（ １ ， ２ ， ３ ）　は、ａ＝ｂ＝１　の場合である。

　結果を知ってしまえば、

（ａ²−２ｂ²）²＋２（２ａｂ）²＝ａ⁴−４ａ²ｂ²＋４ｂ⁴＋８ａ²ｂ²＝ａ⁴＋８ａ²ｂ²＋４ｂ⁴＝（ａ²＋２ｂ²）²

という計算で納得できる。しかし、どのような推論をすると、この公式が得られるのか、大い
に興味・関心が湧くところである。

（解）　ｘ ， ｙ ， ｚ は、互いに素な正の整数で、ｘ²＋２ｙ²＝ｚ²　を満たすので、

　　　ｘ と ｙ ， ｙ と ｚ ， ｚ と ｘ も互いに素である。　さらに、 ｘ および ｚ は奇数である。

　　　　実際に、２つの数が素数である公約数 ｐ　（ｐ＞１）　を持つとすると、残りの数の平

　　　方数は、ｐ の倍数となり、すなわち、残りの数も ｐ の倍数となり、３つの数が互いに

　　　素であることに矛盾する。また、ｘ が偶数と仮定すると、ｘ²＋２ｙ²＝ｚ²　より、ｚ は偶

　　　数となり、ｘ と ｚ が互いに素であることに矛盾する。 ｚ が偶数と仮定しても同様にし

　　　て矛盾を得る。

　　次に、ｘ²＋２ｙ²＝ｚ²　より、　２ｙ²＝ｚ²−ｘ²＝（ｚ＋ｘ）（ｚ−ｘ）　で、 ｘ と ｚ がともに奇数

　　であることから、 ｚ＋ｘ 、 ｚ−ｘ はともに偶数であるが、（ｚ＋ｘ）/２ 、 （ｚ−ｘ）/２ の少な

　　くとも一方は奇数である。

　　　　実際に、両方とも偶数とすると、　ｚ＋ｘ＝４ｍ 、 ｚ−ｘ＝４ｎ （ｍ、ｎ は整数）　と書け

　　ることになるが、この連立方程式を解くと、　ｘ＝２（ｍ−ｎ）　、ｚ＝２（ｍ＋ｎ）　となり、こ

　　れは、ｘ と ｚ がともに奇数であることに矛盾する。

　　　以上から、

　　　　（ｚ＋ｘ）/２ と ｚ−ｘ　が互いに素、または、 （ｚ−ｘ）/２ と ｚ＋ｘ　が互いに素

　　の何れかとなる。

　　（１）　（ｚ＋ｘ）/２ と ｚ−ｘ　が互いに素の場合

　　　　　　　ｚ＋ｘ＝２ｍ²　、　ｚ−ｘ＝ｎ²

　　　　と書ける。

　　　　　このとき、　ｘ＝（２ｍ²−ｎ²）/２　、　ｚ＝（２ｍ²＋ｎ²）/２　、　ｙ＝ｍｎ

　　（２）　（ｚ−ｘ）/２ と ｚ＋ｘ　が互いに素の場合

　　　　　　　ｚ＋ｘ＝ｎ²　、　ｚ−ｘ＝２ｍ²

　　　　と書ける。

　　　　　このとき、　ｘ＝−（２ｍ²−ｎ²）/２　、　ｚ＝（２ｍ²＋ｎ²）/２　、　ｙ＝ｍｎ

　　ただし、上記で、ｍ、ｎ は互いに素な正の整数で、ｍ は奇数、ｎ は偶数となる。

　　したがって、求める解は、

　　　　　ｘ＝±（２ｍ²−ｎ²）/２　、　ｙ＝ｍｎ　、　ｚ＝（２ｍ²＋ｎ²）/２

　　ここで、　ｍ＝ａ　、　ｎ＝２ｂ　（ａ、ｂ は互いに素な正の整数）　とおくと、

　　　　　ｘ＝±（ａ²−２ｂ²）　、　ｙ＝２ａｂ　、　ｚ＝a²＋２ｂ²

　が得られる。　（終）

（コメント）　この公式を知ると、　ｘ²＋２ｙ²＝ｚ²　の解は、

　　　　　　（ ｘ ， ｙ ， ｚ ）＝（ １ ， ２ ， ３ ）　以外に、

　　　　　（ ｘ ， ｙ ， ｚ ）＝（ ７ ， ４ ， ９ ）、（ ７ ， ６ ， １１ ）、（ １７ ， ６ ， １９ ）、・・・・・

　　　　とたくさん作れて楽しいですね！

　ｘ²＋２ｙ²＝ｚ²　の解は、上記の公式から無数に存在するが、

　　ｘ⁴＋２ｙ⁴＝ｚ²　は、自明な解 （ ｘ ， ｙ ， ｚ ）＝（ ０ ， ０ ， ０ ） しか持たない

という事実も興味深い。

　証明は、背理法を用いる。（ちょっとだけ、無限降下法を意識してるかも．．．！）

（証明）　ｘ⁴＋２ｙ⁴＝ｚ²　が正の整数解 （ ｘ ， ｙ ， ｚ ）＝（ ｓ ， ｔ ， ｕ ）　を持つと仮定する。

　ここで、ｘ ， ｙ ， ｚ は、互いに素であるとしてよい。さらに、これらの解のうち、ｚ＝ｕ　が最

小であるものとする。

　このとき、（ ｓ² ， ｔ² ， ｕ ）は、方程式　ｘ²＋２ｙ²＝ｚ²　の解となるので、上記の結果から、

　　　ｓ²＝±（ａ²−２ｂ²） ， ｔ²＝２ａｂ ， ｕ＝a²＋２ｂ²

　　　　　　　　ただし、　ａ、ｂ は互いに素な正の整数で、特に、ａ は奇数

と書ける。

　ｔ²＝２ａｂ において、ｔ² すなわち ｔ は偶数となるので、　ａｂ＝ｔ²/２　は偶数で、ｂ も偶数と

なる。　よって、　（ｔ/２）²＝ａ×（ｂ/２）　において、ａ、ｂ は互いに素なので、ａ、ｂ/２ も互い

に素で、ｔ/２ は整数より、　ａ＝ｍ²　、　ｂ/２＝ｎ²　と書けることになる。ただし、ｍ、ｎ は互

いに素な正の整数である。

　このとき、　ｓ² すなわち、ｓ は奇数であるので、ｓ² は４で割ると１余り、ｍ⁴−８ｎ⁴ も４で

割ると１余ることから、　ｓ²＝ｍ⁴−８ｎ⁴　でなければならない。

　よって、　ｓ²＋２（２ｎ²）²＝（ｍ²）²　となり、（ ｘ ， ｙ ， ｚ ）＝（ ｓ ， ２ｎ² ， ｍ² ）　は、

方程式　ｘ²＋２ｙ²＝ｚ²　の解となる。しかも、ｓ 、２ｎ² 、ｍ² は互いに素である。

　よって、同様にして、

　　　ｓ＝±（ｃ²−２ｄ²） ， ２ｎ²＝２ｃｄ ， ｍ²＝ｃ²＋２ｄ²

　　　　　　　　ただし、　ｃ、ｄ は互いに素な正の整数で、特に、ｃ は奇数

と書ける。

　このとき、ｃ、ｄ は互いに素で、ｎ²＝ｃｄ　より、ｃ＝ｅ²　、ｄ＝ｆ²　（ｅ、ｆ は互いに素な整数）

と書ける。

　よって、　ｍ²＝ｃ²＋２ｄ²　に代入して、　ｅ⁴＋２ｆ⁴＝ｍ²　となり、

（ ｘ ， ｙ ， ｚ ）＝（ ｅ ， ｆ ， ｍ ）　は、方程式 ｘ⁴＋２ｙ⁴＝ｚ²　の解となる。

　ところで、ｕ＝a²＋２ｂ²　、ａ＝ｍ²　より、ｕ＞ｍ　が成り立つので、これは、ｕ の最小性に

反する。

　以上から、方程式 ｘ⁴＋２ｙ⁴＝ｚ²　は、自明な解 （ ｘ ， ｙ ， ｚ ）＝（ ０ ， ０ ， ０ ） しか持た

ない。　（証終）


（参考文献：ゲルファント　著　銀林　浩　訳　　方程式の整数解　（東京図書））


（追記）　平成２３年８月７日付け

　当ＨＰがいつもお世話になっているＨＮ「攻略法」さんに、上記の話題に関連して、いろい
ろ補足していただいた。

（方法その１）　１ から始まる連続した奇数列の和は、奇数列の項数の平方に等しい。

　上記の性質を用いると、

　　　１＋３＋５＋・・・＋（２ｎ−３）＋（２ｎ−１）＝ｎ²　より、

　　　（ｎ−１）²＋（２ｎ−１）＝ｎ²

　これより、恒等式 ｎ²−（ｎ−１）²＝２ｎ−１　（連続する２数の平方の差は奇数となる）から、
奇数のうち平方数になるものをとればよい。

例　９＝３²＝２・５−１＝５²−（５−１）²＝５²−４²

（方法その２）　　　（２ｎ）²＋（ｎ²−１）²＝（ｎ²＋１）²

　上記の性質を用いると、ａ²＋ｂ²＝ｃ²　を満たす自然数の組 (ａ ，ｂ ，ｃ) の求め方が分か
る。

　◇　プラトンの方法　・・・　ａ が偶数なら、　ｂ＝（ａ/２）²−１　、ｃ＝（ａ/２）²＋１

　　　　ａ＝２ｎ　より、　ｎ＝ａ/２　なので、上記の性質より明らかだろう。

　これに対して、上記の性質より、

　　　　（２ｎ）²＋（ｎ²−１）²＝（ｎ²＋１）²　の両辺を４で割って、

　　　　　ｎ²＋｛（ｎ²−１）/２｝²＝｛（ｎ²＋１）/２｝²

　ここで、ｎ＝ａ が奇数とするとき、　ａ＝２ｍ＋１　（ｍは整数）　とおけることから、

　　　（ｎ²−１）/２＝（４ｍ²＋４ｍ＋１−１）/２＝２ｍ（ｍ＋１）　は整数

　　　（ｎ²＋１）/２＝（４ｍ²＋４ｍ＋１＋１）/２＝２ｍ²＋２ｍ＋１　は整数

　以上をまとめると、

　◇　ピタゴラスの方法　・・・　ａ が奇数なら、　ｂ＝（ａ²−１）/２　、ｃ＝（ａ²＋１）/２

例　ａ＝３　のとき、　ｂ＝（３²−１）/２＝４　、ｃ＝（３²＋１）/２＝５

　方程式　ｘ²＋２ｙ²＝ｚ²　を満たす解について

　　ａ²＋ｋ・ｂ²＝ｃ²　として、行列 Ｐ_ｋ を考える。

　　　　

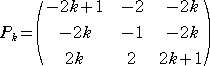
　題意を満たす ( ａ ｂ ｃ ) で、( −ａ ｂ ｃ )Ｐ_ｋ　、( −ａ −ｂ ｃ )Ｐ_ｋ　、( ａ −ｂ ｃ )Ｐ_ｋ　を計算
する。

例 ( １　２　３ ) は、題意を満たす。他の解は、次のようにして求められる。

　　　　( −ａ　ｂ　ｃ )Ｐ_ｋ＝( −１　２　３ )Ｐ_ｋ＝( ７　６　１１ )

　　　　( −ａ　−ｂ　ｃ )Ｐ_ｋ ( −１　−２　３ )Ｐ_ｋ＝ ( ２３　１０　２７ )

　　　　( ａ　−ｂ　ｃ )Ｐ_ｋ＝ ( １　−２　３ )Ｐ_ｋ＝ ( １７　６　１９ )


　　　（追記）　平成２３年１２月９日付け

　　　　　上記で、特に、「ｋ＝１」とした場合、行列 Ｐ₁ のことを「ピタゴラス行列」というそうだ。

　　　　互いに素なピタゴラス数の１つの組 ( ａ ｂ ｃ ) が平面 ｚ＝ｃ における第一象限にある

　　　　とすれば、( −ａ ｂ ｃ ) は第２象限、( −ａ −ｂ ｃ ) は第３象限、( ａ −ｂ ｃ ) は第４象

　　　　限にあるとみなされ、これらと行列 Ｐ₁ との積により、次々と互いに素なピタゴラス数

　　　　が量産される。

　　　　　この「ピタゴラス行列」の発見者は、Ｆ．Ｊ．Ｍ．Ｂａｒｎｉｎｇ（1963）やＲｏｂｅｒｔｓ（1977）と

　　　　言われるが、その他独立に発見した人も何人かいたという。

　　　　　このピタゴラス行列 Ｐ₁ は特異な性質を有する。すなわち、

　　　　　　　　　 Ｐ₁^-1 ＝ Ｐ₁ 　、　ｄｅｔ Ｐ₁ ＝ −１

　　　　　このような性質をもつ行列として、２次の正方行列

　　　　　　　　　

　　　　がある。この行列Ｑは、行列 Ｐ₁ の構成に本質的に寄与するらしい。


　　　　（参考文献）　小林吹代　著　　ピタゴラス数を生み出す行列のはなし　（ベレ出版）
　　　　　　　　　　　　「Pythagorean Triple」


（方法その３）　恒等式　(ａ²＋ｂ²)²＝(ａ²−ｂ²)²＋(２ａｂ)²

　上記の性質を用いると、プラトンの方法は、ｂ＝１としたものとなる。

（→　参考：「フィボナッチ数を極める」）

例　１０１＝１０²＋１²　より、　１０１2＝９９²＋２０²

（方法その４）　恒等式　４（ｎ＋１）＋ｎ²＝（ｎ＋２）²

　上記の性質を用いると、ｎ＋１ が平方数のときを考えればよい。

例　ｎ＝３　のとき、　４²＋３²＝５²

　　ｎ＝１５　のとき、　８²＋１５²＝１７²

（方法その５）　ｐ＝４ｋ＋１型の素数のとき、ｐ²は、２つの自然数の平方和で表される。

例　５²＝３²＋４²　、１３²＝５²＋１２²　、１７²＝８²＋１５²


（方法その６）　ブラマグプタの恒等式　(ａ²＋ｂ²)(ｃ²＋ｄ²)＝（ａｃ＋ｂｄ）²＋（ａｄ−ｂｃ）²

例　ピタゴラス数　(３，４，５)、(５，１２，１３)　のとき、

　　（ａ，ｂ）＝（３，４）、（ｃ，ｄ）＝（５，１２）　として、

　　　(３²＋４²)(５²＋１２²)＝（３・５＋４・１２）²＋（３・１２−４・５）²　より、　６５²＝６３²＋１６²