・ 受験の神様 S.H氏
「受験の神様」というと私ぐらいの年代だと旺文社の佐藤 忠先生を真っ先に思い浮かべ
てしまうが、最近冒頭のタイトルのテレビ番組(日本テレビ系 土曜21時〜)が注目を集め
ている。番組の雰囲気は「女王の教室」に似ているかな?
そうは言っても実は今日(8月11日)初めて見た。今日は算数の問題が何題か出題され
て、楽しい1時間だった。成海璃子さんが演じる「菅原道子」が、多分小学生の理解を超え
ているようなことをボソボソと冷静に宣って去っていく颯爽とした雰囲気に思わず引き込ま
れてしまった。
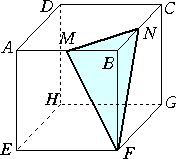 一辺の長さが4cmの立方体ABCD−EFGHにおいて、
一辺の長さが4cmの立方体ABCD−EFGHにおいて、
辺AB、BCの中点をそれぞれM、Nとおく。
このとき、△MFNの面積を求めよ。
計算力があれば腕力にまかせて解くことも可能だろうが、
成海璃子さんの次の解答には感心してしまった。
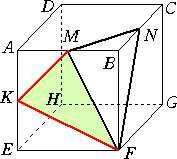
右図において、辺AEの中点をKとすると、
△KFMと△MFNは合同で面積は等しい。
よって、求める面積は、
16−(2+4+4)=6(cm2) |
 |
また、次の問題も公式慣れしている方には難問に思えるだろう。
5g、7g の重りを使って量ることが出来ない重さで最大のものを求めよ。
次のように考えるのがとても新鮮だ。
自然数を、5個毎に区切り下図のように並べる。ある数を量ることが出来れば、その数か
ら下の行は全て量ることができる。(5gをいくつか追加すればよい!)
| |
| 1 |
2 |
3 |
4 |
5 |
| 6 |
7 |
8 |
9 |
10 |
| 11 |
12 |
13 |
14 |
15 |
| 16 |
17 |
18 |
19 |
20 |
| 21 |
22 |
23 |
24 |
25 |
| 26 |
27 |
28 |
29 |
30 |
|
量ることが出来る数を赤色で示す。 |
上表から、求める最大値は、 23 である。
次は、電話連絡の問題。
ある学校の連絡網は次のようになっている。
まず、先生がA君に電話をかける。電話を受けた生徒は、それぞれ2人の生徒に電話を
かける。電話をかけるのにかかる時間は全て1分とする。8分後には、何人の生徒に連絡
が回っているだろうか?
これも絵を描いて考えると分かりやすいだろう。
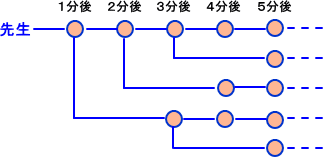
上図から、 n 分後に連絡を受けた生徒の数を F(n) とすると、次の規則に従っている。
F(n)=((n−2)分前に連絡を受けた生徒の数)+((n−1)分前に連絡を受けた生徒の数)
=F(n−2)+F(n−1)
これは、正しくフィボナッチ数列の漸化式だ。よって、次の数列を得る。
1,1,2,3,5,8,13,21,34,55,89,144,233,377,・・・
よって、8分後までに連絡を受けた生徒の数は、
1+1+2+3+5+8+13+21=54
より、54人となる。
(コメント) 番組中、成海さんは「フィボナッチ数の幾何学的構造」という本を読まれていた。
どちらかというと、その本の方にも興味を持った。果たしてその本は市販されてい
るのだろうか?

 一辺の長さが4cmの立方体ABCD−EFGHにおいて、
一辺の長さが4cmの立方体ABCD−EFGHにおいて、

