自然対数の底　 　　　　　　　　　　　　　 　　　　　　　　

自然対数の底 ｅ（Ｎａｐｉｅｒ の数）は、

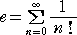により定義される。

高校では、

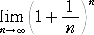で定義されることが多いが、前者の級数は非常に速く収束する

ので、ｅ の値を計算するのに便利である。２項定理を用いて、容易に

　

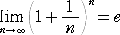
であることが示される。実際に、２項定理を用いて展開して整理すると、

（１＋１/ｎ）^ｎ＝１/０！＋１/１！＋（１－１/ｎ）/２！＋（１－１/ｎ）（１－２/ｎ）/３！＋・・・

　　＋（１－１/ｎ）（１－２/ｎ）・・・（１－（ｎ－１）/ｎ）/ｎ！

ここで、ｎ → ∞ とすると、　ｌｉｍ_ｎ→∞ （１＋１/ｎ）^ｎ＝Σ_ｎ=0^∞ （１/ｎ！）　が成り立つ。


　ところで、自然対数の底ｅは「Ｎａｐｉｅｒ（ネイピア）の数」と呼ばれるが、発見したのはオイラ
ーで、ネイピアではない。「ｅ」はＥｕｌｅｒの「ｅ」なのである。

　ｅ^πが超越数であることは、１８７３年にシャルル・エルミートにより示されている。

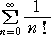が収束する速さは、次のような不等式を用いて評価される。

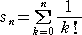とおくとき、

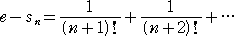
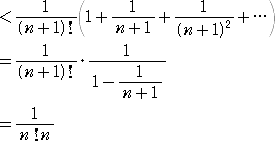
よって、

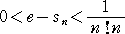・・・・・　(*)　　が成り立つ。

　ｅ ＝２．７１８２８１８２８４５９０４５２３５３・・・・・　に対して、

　ｓ₁₀＝２．７１８２８１・・・・・

　

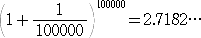
であることを考えれば、収束の速さは明らかである。

　ｓ_ｎ の収束が非常に速いので、電卓を用いて計算してみようという気になる方もおられよう。

たとえば、ｓ₁₀ の計算は、広島工業大学の大川研究室によれば、

　　［・・・{｛（１/１０＋１）/９＋１｝/８＋１}・・・］/１＋１

と考え、前から順番にキーを叩けば、紙にメモすることなく計算できるとのことだ。
　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　（→参考：「面白い電卓の使い方」）

　また、評価式 (*) を用いると、ｅ が無理数であることが容易に示される。

　今、ｅ が有理数と仮定すると、

　

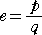
と書ける。ただし、ｐ 、 ｑ は、互いに素な正の整数である。

　このとき、 (*) より、

　

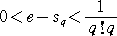
なので、

　

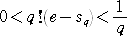
　ここで、　ｑ！ｅ　および　ｑ！ｓ_ｑ　はともに整数なので、　ｑ≧１　より、０ と １ の間に整数

が存在することになり、これは矛盾である。よって、 ｅ は無理数である。


（参考文献 ： Ｗａｌｔｅｒ Ｒｕｄｉｎ　著　Principleｓ ｏｆ Mathematical Analysis　（McGRAWHILL））


（追記）　平成２８年６月４日付け

　ｅ の近似分数として、１９/７、１９３/７１、２７２１/１００１などが知られている。

　実際に、　１９/７＝２．７１４２８・・・

　１９３/７１＝２．７１８３０９・・・

　２７２１/１００１＝２．７１８２８１７１８・・・

　また、ｅ については、次のモローの不等式

　e/（２ｎ＋２）＜e－（１＋１/ｎ）^ｎ＜e/（２ｎ＋１）　　ただし、ｎは正の整数

が知られている。次のように式変形されることも多い。

　｛２ｎ/（２ｎ＋１）｝ｅ＜（１＋１/ｎ）^ｎ＜｛（２ｎ＋１）/（２ｎ＋２）｝ｅ


　高校生でも十分解きうる問題として、数学検定（１級レベルかな？）や大学入試などで、こ
の不等式を題材とする問題が出題されている。

　古くは、次の学習院大学　理学部（１９８９）の問題が有名だろう。

学習院大学　理学部（１９８９）

　次の不等式が成り立つことを証明せよ。ただし、ｅは自然対数の底である。

（１）　ｘ＞０　のとき、　（１/ｘ）ｌｏｇ（１＋ｘ）＞１＋ｌｏｇ（２/（ｘ＋２））

（２）　ｎが正の整数のとき、　ｅ－（１＋１/ｎ）^ｎ＜ｅ/（２ｎ＋１）


（解）（１）　ｘ＞０　なので、　ｌｏｇ（１＋ｘ）＞ｘ（１＋ｌｏｇ（２/（ｘ＋２）））　を示せばよい。

　Ｆ（ｘ）＝ｌｏｇ（１＋ｘ）－ｘ（１＋ｌｏｇ（２/（ｘ＋２）））　とおくと、

　Ｆ’（ｘ）＝１/（ｘ＋１）－（１＋ｌｏｇ（２/（ｘ＋２）））＋ｘ/（ｘ＋２）

　Ｆ”（ｘ）＝－１/（ｘ＋１）²＋１/（ｘ＋２）＋２/（ｘ＋２）²＝ｘ（ｘ²＋５ｘ＋５）/（ｘ＋１）²（ｘ＋２）²

よって、Ｆ”（ｘ）＞０　より、Ｆ’（ｘ）は単調増加で、　Ｆ’（０）＝１－１＋０＝０　より、

　ｘ＞０　のとき、　Ｆ’（ｘ）＞０　で、Ｆ（ｘ）は単調増加

　Ｆ（０）＝０－０＝０　なので、　ｘ＞０　のとき、　Ｆ（ｘ）＞０

したがって、　ｌｏｇ（１＋ｘ）＞ｘ（１＋ｌｏｇ（２/（ｘ＋２）））　より、

　（１/ｘ）ｌｏｇ（１＋ｘ）＞１＋ｌｏｇ（２/（ｘ＋２））

が成り立つ。

（２）　（１）で、ｘ＝１/ｎ（＞０）　とおくと、　ｎｌｏｇ（１＋１/ｎ）＞１＋ｌｏｇ（２ｎ/（２ｎ＋１））

すなわち、　ｌｏｇ（１＋１/ｎ）^ｎ＞ｌｏｇｅ（２ｎ/（２ｎ＋１））　より、

　（１＋１/ｎ）^ｎ＞ｅ（１－１/（２ｎ＋１））　より、　ｅ－（１＋１/ｎ）^ｎ＜ｅ/（２ｎ＋１）　　（終）


　学習院大学の問題で、モローの不等式の右辺は示されたので、左辺を示すのも同様に出
来る。

　e/（２ｎ＋２）＜e－（１＋１/ｎ）^ｎ　より、　（１＋１/ｎ）^ｎ＜ｅ（２ｎ＋１）/（２ｎ＋２）　の両辺の対

数をとって、ｎｌｏｇ（１＋１/ｎ）＜１＋ｌｏｇ（２ｎ＋１）/（２ｎ＋２）　となるので、ｎ＝１/ｘ　とおいて

　（１/ｘ）ｌｏｇ（１＋ｘ）＜１＋ｌｏｇ（（ｘ＋２）/（２ｘ＋２））　（ｘ＞０）

そこで、　Ｇ（ｘ）＝ｌｏｇ（１＋ｘ）－ｘ（１＋ｌｏｇ（（ｘ＋２）/（２ｘ＋２）））　とおくと、

　Ｇ’（ｘ）＝１/（ｘ＋１）－（１＋ｌｏｇ（（ｘ＋２）/（２ｘ＋２）））－ｘ（１/（ｘ＋２）－１/（ｘ＋１））

　＝－ｌｏｇ（（ｘ＋２）/（２ｘ＋２）））－ｘ/（ｘ＋２）

　Ｇ”（ｘ）＝－１/（ｘ＋２）＋１/（ｘ＋１）－２/（ｘ＋２）²＝－ｘ/（（ｘ＋１）（ｘ＋２）²）＜０

　よって、Ｇ’（ｘ）は単調減少で、Ｇ’（０）＝０　より、　ｘ＞０　のとき、　Ｇ’（ｘ）＜０

　このとき、Ｇ（ｘ）は単調減少で、Ｇ（０）＝０　より、　ｘ＞０　のとき、　Ｇ（ｘ）＜０

　したがって、　（１/ｘ）ｌｏｇ（１＋ｘ）＜１＋ｌｏｇ（（ｘ＋２）/（２ｘ＋２））　が成り立ち、

　ｘ＝１/ｎ（＞０）　とおくと、　ｎｌｏｇ（１＋１/ｎ）＜１＋ｌｏｇ（２ｎ＋１）/（２ｎ＋２）

すなわち、　（１＋１/ｎ）^ｎ＜ｅ（２ｎ＋１）/（２ｎ＋２）　より、

　e/（２ｎ＋２）＜e－（１＋１/ｎ）^ｎ

が成り立つ。


　高知県土佐高校の藤岡優太先生が数研通信Ｎｏ．８５で、モローの不等式をスッキリ証明
されている。それを参考にしながら、モローの不等式の図形的意味を考えてみよう。

　モローの不等式　e/（２ｎ＋２）＜e－（１＋１/ｎ）^ｎ＜e/（２ｎ＋１）　から示される不等式

　｛２ｎ/（２ｎ＋１）｝ｅ＜（１＋１/ｎ）^ｎ＜｛（２ｎ＋１）/（２ｎ＋２）｝ｅ

の両辺の対数をとって式変形すると、

　ｌｏｇ（ｎ（ｎ＋１））－ｌｏｇ（ｎ＋１/２）＜（ｎ＋１）ｌｏｇ（ｎ＋１）－ｎｌｏｇｎ－１＜ｌｏｇ（ｎ＋１/２）

となる。ここで、

　∫_ｎ^ｎ+1 ｌｏｇ ｘ ｄｘ＝（ｎ＋１）ｌｏｇ（ｎ＋１）－ｎｌｏｇｎ－１

より、Ｓ＝（ｎ＋１）ｌｏｇ（ｎ＋１）－ｎｌｏｇｎ－１は、ｙ＝ｌｏｇ ｘ とｘ＝ｎ、ｘ＝ｎ＋１、ｘ軸で囲まれた
面積となっている。

　さらに、点（ｎ，ｌｏｇｎ）と点（ｎ＋１，ｌｏｇ（ｎ＋１））を結ぶ線分とｘ＝ｎ、ｘ＝ｎ＋１、ｘ軸で囲まれ
た台形の面積Ｔは、

　Ｔ＝（ｌｏｇｎ＋ｌｏｇ（ｎ＋１））/２＝（１/２）ｌｏｇｎ（ｎ＋１）

で与えられる。

　さらに、ｙ＝ｌｏｇ（ｎ＋１/２）とｘ＝ｎ、ｘ＝ｎ＋１、ｘ軸で囲まれた長方形の面積Ｕは、

　Ｕ＝ｌｏｇ（ｎ＋１/２）

で与えられる。

　このとき、モローの不等式の図形的意味が明らかとなる。すなわち、

　２Ｔ－Ｕ＜Ｓ＜Ｕ

が成り立つ。


（コメント）　ＳとＵの関係は微妙な雰囲気なのですが、モローの不等式から、確実に、Ｓ＜Ｕ
　　　　　　と言えるわけですね。直感的には、ｙ＝ｌｏｇ ｘ が上に凸の曲線で勾配がだんだん
　　　　　　緩やかになっていることを考えれば、Ｓ＜Ｕであることは予想されますが．．．。


（追記）　令和６年１１月２３日付け

　Dengan kesaktian Indukmu さんから、「ネイピア数の近似」と題して、ご投稿いただきました。

　「棋士デビュー70年の加藤一二三九段(84)が詰め将棋出題65年間継続でギネス記録、って
全数字綺麗に出てるなぁ」という大発見がShiromaruさんによってX(旧ツイッター)で報告され話
題となりました。（→　URL）

　このツイートをうけてサイエンスライター兼 vtuber の彩恵りり氏(@Science_Release)氏が紹
介したネイピア数の、0から9までをかぶらずにヒトモジづつ使った近似方法がとてつもなかっ
たので皆様にご紹介します。

＝引用始め＝　　（引用は、こちら より。）

e≈(1+0.2^(9^(7×6)))^(5^(3^(84)))

　ネイピア数と小数点以下

　8368澗4289溝8906穣8425秭9438垓1759京0916兆4450億0188万7164桁

まで一致する近似値(Daniel Bamberger (2024) による)

＝引用終わり＝

　Daniel Bambergerによるオリジナルは、こちらで確認できますが、こちらはよりディープか
つ趣味的なデータベースになっています。

※ 0.2=1/5　だから、言い換えると、N=5^(3^84)に対して、e≒(1+1/N)^N　ですね。
　との解説が @hironino さんによりツイッター上で披露されました。


　ＧＡＩ さんからのコメントです。（令和６年１１月２３日付け）

　1～９にこだわってみました。

(15768/3942)×(12345/9876)=13485/2697　・・・　５

(18534/9267)×(17469/5823)=34182/5697　・・・　６

(17469/5823)×(31689/4527)×(65934/1782)=748251/963=615384/792　・・・　７７７

　なお昔、掲示板に投稿されていた記事をメモしていたノートを見直していたら、多分2017年
ごろ、DD++ さんが「e≈(1+.2^(3^84))^(5^(9^(6*7)))」を投稿されていたと思います。

　また、これを、(1+9^(-4^(6*7)))^(3^(2^85))　、(1+2^(-76))^(4^38+.5)　等にもでき、円周率π
も、
　π≈2^5^.4-.6-(.3^9/7)^.8^.1
　(((2^7+8)/(90-1))^5.4+.6)*.3 (りらひい氏発見）
　(8-(1+.6/(.2*.5+9))/(.3+7))*.4 (らすかる氏発見）

などの常連さんの驚くべき技が紹介されていました。


　DD++ さんからのコメントです。（令和６年１１月２３日付け）

　「小町算で無理数近似」の記事ですかね。


　ＧＡＩ さんからのコメントです。（令和６年１１月２４日付け）

　「小町算で無理数近似」を読み返していたら、ネイピア数と小数点以下8368澗4289溝8906穣
8425秭9438垓1759京0916兆4450億0188万7164桁まで一致する近似値の精度がどうやって導
けたのかの謎が、

マクローリン展開が

1/e*(1+x)^(1/x)=1-1/2*x+11/24*x^2-7/16*x^3+2447/5760*x^4-959/2304*x^5+O(x^6)

これから、　e-(1+x)^1/x≒1/2*e*x

　これに、x=.2^(3^84)=(1/5)^(3^84) なる微小な値を取ることで、両辺のlog[10]をとると右辺が

gp > log(exp(1)/2)/log(10)-3^84*log(5)/log(10)
%139 = -8368428989068425943817590916445001887164.5053429251

正にeとの誤差が　1/10^(8368428989068425943817590916445001887164)　つまり、

　8368澗4289溝8906穣8425秭9438垓1759京0916兆4450億0188万7164桁まで一致

ということを示す、という計算なのですね。



　　以下、工事中！
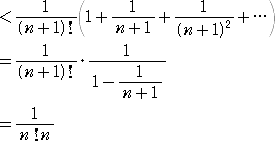