
相異なる n 個のものを円形に並べる場合の数が(n−1)!通りになることは、高校の数
学Aで学ぶ。 n 個のもののうちに、同じものがいくつか含まれる場合の円順列については
簡単に求める公式はないとされている。
例1 赤球2個、青球2個を円形に並べる場合の数を求めよ。
この場合は、実際に図を書いて考えた方がはやいかな?答は下図の2通りしかない。
円順列の数え上げ 
相異なる n 個のものを円形に並べる場合の数が(n−1)!通りになることは、高校の数
学Aで学ぶ。 n 個のもののうちに、同じものがいくつか含まれる場合の円順列については
簡単に求める公式はないとされている。
例1 赤球2個、青球2個を円形に並べる場合の数を求めよ。
この場合は、実際に図を書いて考えた方がはやいかな?答は下図の2通りしかない。
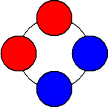 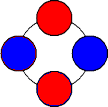 |
しかし、次の例の場合には図を書いて考えようとは思わないだろう!
例2 赤球4個、青球4個を円形に並べる場合の数を求めよ。
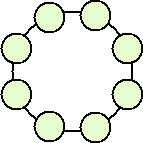
赤球4個、青球4個を一列に並べる場合の数は、
![]()
である。これを円形に並べると、一般には、8通りずつ同じものができるが、赤球2個、青球
2個ずつ左右同順に並ぶ場合はこの限りでない。
赤球2個、青球2個を一列に並べる場合の数は、
![]()
であるが、これを円形に並べるときにできる場合は次の2通りしかない。
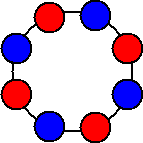 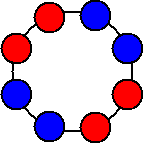 |
したがって、求める場合の数は、
![]()
(補足) 例2のように例1も計算で解こうと思ったら、次のように解けるだろう。
![]()
上記の問題では赤球、青球の数が固定されていたが、次のように問題を拡張したらどう
だろうか?
問題 赤球、青球、黄球
![]()
の何れか4個を円形に並べる場合の数を求めよ。
(解) 4個全てが同色の場合は、 3×1=3 (通り)
3個が同色で1個が異なる場合は、 3C1×2C1×1=6 (通り)
2個ずつ同色の場合は、 3C2×2=6 (通り) (← 例1の結果利用)
2個が同色で他の2球がそれぞれ異なる場合
まず、色の場合の数は、3C1=3 (通り)で、そのうちの1通り、たとえば、赤球2個、
青球1個、黄球1個の場合は、次の3通りができる。
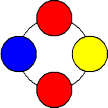 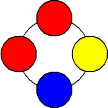 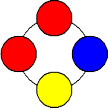 |
よって、この場合の数は、 3C1×3=9 (通り)
以上から、求める場合の数は、3+6+6+9=24 (通り) (終)
このような円順列の数え上げ問題に対して、バーンサイドの定理が知られている。
バーンサイドの定理
集合 S の置換群 G によって誘起される同値関係による S の同値類の個数は、
![]()
によって与えられる。
ここで、|G|は、G に含まれる要素の個数、φ(σ) は、置換 σ で不変な
S の要
素の個数を表すものとする。
この定理を証明する前に、上記の問題に、この定理を適用して解いてみよう。
(別解) 集合 S は、下図のように番号の割り振られた場所に
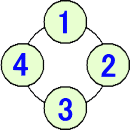
赤球、青球、黄球の何れか4個を並べる場合すべてを要素とする。
したがって、その要素の個数は、 34=81 (個) ある。
求める場合の数は、このうち回転により重なるものを同じものと見なして、異なる並べ方の
総数に等しい。
集合 G は、上記の円形の図形を時計回りに 0°の回転、90°の回転、180°の回転、
270°の回転させる置換により構成される。
その置換を、それぞれ σ0 、σ1 、σ2 、σ3 と表すと、
G={ σ0 、σ1 、σ2 、σ3 } で、 |G|= 4
である。 集合 G は、置換の合成 ・ に関して群となる。単位元は、σ0 である。
x 、 y ∈ S に対して、 ある置換 σ により、 σ(x)=y であるとき、x 〜 y
と定義する。このとき、〜は、置換群 G によって誘起される同値関係となる。
よって、求める場合の数は、 同値関係 〜 による集合 S の同値類の個数に等しい。
ここで、 φ(σ0)= σ0 により不変な S の要素の個数 =81
φ(σ1)= σ1 により不変な S の要素の個数 =3
φ(σ2)= σ2 により不変な S の要素の個数 =3×3=9
φ(σ3)= σ3 により不変な S の要素の個数 =3
したがって、バーンサイドの定理より、 (81+3+9+3)/4=24 (個) (終)
今まで経験のない新鮮な方法で、その解法の美しさに感動しました!その感動を与えてく
れたバーンサイドの定理をますます深く勉強しようと思った。そのために、置換群の基礎知
識をまずまとめることにしよう。
群Gに含まれる元の個数(位数という)が有限個のとき、特に、有限群と言われる。群の
位数のことを記号で |G| と表すことは上記で用いた通りである。
例 3次方程式 x3=1 の解の集合を G とする。1 の3乗根を ω で表すと、
G={ 1 , ω , ω2 }
で、明らかに、Gは、乗法について群となる。その位数|G|は 3 である。
Gはまた、{恒等変換、原点中心の120°回転、原点中心の240°回転}とも捉えること
ができる。
Gは、下図のように番号が割り振られた集合 S={ 1 , 2 , 3 } の置換群となる。
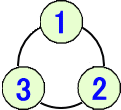
当HPがいつもお世話になっているHN「攻略法」さんが、冒頭の問題 例1、例2に取り組
まれました。(平成23年10月27日付け)
例1 赤球2個、青球2個を円形に並べる場合の数を求めよ。
実際に計算してみた。赤球、青球をそれぞれ 1、2 とする。
すべての解は、4!/(2!2!)=6(通り)である。
| 1: 1 1 2 2 σ0: 1 1 2 2 =3* 不変 σ1: 1 2 2 1 =6 σ2: 2 2 1 1 =12 σ3: 2 1 1 2 =9 No. 1 ← 異なる解 1 1 2 2 |
2: 1 2 1 2 σ0: 1 2 1 2 =5* 不変 σ1: 2 1 2 1 =10 σ2: 1 2 1 2 =5 不変 σ3: 2 1 2 1 =10 No. 2 1 2 1 2 |
3: 1 2 2 1 σ0: 1 2 2 1 =6* 不変 σ1: 2 2 1 1 =12 σ2: 2 1 1 2 =9 σ3: 1 1 2 2 =3* |
||
| 4: 2 1 1 2 σ0: 2 1 1 2 =9* 不変 σ1: 1 1 2 2 =3* σ2: 1 2 2 1 =6 σ3: 2 2 1 1 =12 |
5: 2 1 2 1 σ0: 2 1 2 1 =10* 不変 σ1: 1 2 1 2 =5* σ2: 2 1 2 1 =10 不変 σ3: 1 2 1 2 =5 |
6: 2 2 1 1 σ0: 2 2 1 1 =12* 不変 σ1: 2 1 1 2 =9* σ2: 1 1 2 2 =3* σ3: 1 2 2 1 =6 |
よって、φ(σm)=6、0、2、0 より、(6+2)/4=2通り
並びのパターンの抽出について
上記の計算過程で、並びのパターンはすべて出現される。具体的には、2進法4桁の数に
対応付けられる。では、どれが異なる解のパターンなのか。
たとえば、1122は、並びを2進法4桁の数と考えると、1122は0011として、
0・23+0・22+1・22+1・20=3
と符号化する。回転させた他も同様に算出すると、この並びが最小値を示す。ここで、この
並びを「採用する」とする。(同様に考えて、最大値でもよい)
例2 赤球4個、青球4個を円形に並べる場合の数を求めよ。
すべての解は、8!/(4!4!)=70通り
| 1: 1 1 1 1 2 2 2 2 σ0: 1 1 1 1 2 2 2 2 =15* 不変 σ1: 1 1 1 2 2 2 2 1 =30 σ2: 1 1 2 2 2 2 1 1 =60 σ3: 1 2 2 2 2 1 1 1 =120 σ4: 2 2 2 2 1 1 1 1 =240 σ5: 2 2 2 1 1 1 1 2 =225 σ6: 2 2 1 1 1 1 2 2 =195 σ7: 2 1 1 1 1 2 2 2 =135 No. 1 ← 異なる解 1 1 1 1 2 2 2 2 |
2: 1 1 1 2 1 2 2 2 σ0: 1 1 1 2 1 2 2 2 =23* 不変 σ1: 1 1 2 1 2 2 2 1 =46 σ2: 1 2 1 2 2 2 1 1 =92 σ3: 2 1 2 2 2 1 1 1 =184 σ4: 1 2 2 2 1 1 1 2 =113 σ5: 2 2 2 1 1 1 2 1 =226 σ6: 2 2 1 1 1 2 1 2 =197 σ7: 2 1 1 1 2 1 2 2 =139 No. 2 1 1 1 2 1 2 2 2 |
3: 1 1 1 2 2 1 2 2 σ0: 1 1 1 2 2 1 2 2 =27* 不変 σ1: 1 1 2 2 1 2 2 1 =54 σ2: 1 2 2 1 2 2 1 1 =108 σ3: 2 2 1 2 2 1 1 1 =216 σ4: 2 1 2 2 1 1 1 2 =177 σ5: 1 2 2 1 1 1 2 2 =99 σ6: 2 2 1 1 1 2 2 1 =198 σ7: 2 1 1 1 2 2 1 2 =141 No. 3 1 1 1 2 2 1 2 2 |
||
| 4: 1 1 1 2 2 2 1 2 σ0: 1 1 1 2 2 2 1 2 =29* 不変 σ1: 1 1 2 2 2 1 2 1 =58 σ2: 1 2 2 2 1 2 1 1 =116 σ3: 2 2 2 1 2 1 1 1 =232 σ4: 2 2 1 2 1 1 1 2 =209 σ5: 2 1 2 1 1 1 2 2 =163 σ6: 1 2 1 1 1 2 2 2 =71 σ7: 2 1 1 1 2 2 2 1 =142 No. 4 1 1 1 2 2 2 1 2 |
5: 1 1 1 2 2 2 2 1 σ0: 1 1 1 2 2 2 2 1 =30* 不変 σ1: 1 1 2 2 2 2 1 1 =60 σ2: 1 2 2 2 2 1 1 1 =120 σ3: 2 2 2 2 1 1 1 1 =240 σ4: 2 2 2 1 1 1 1 2 =225 σ5: 2 2 1 1 1 1 2 2 =195 σ6: 2 1 1 1 1 2 2 2 =135 σ7: 1 1 1 1 2 2 2 2 =15* |
6: 1 1 2 1 1 2 2 2 σ0: 1 1 2 1 1 2 2 2 =39* 不変 σ1: 1 2 1 1 2 2 2 1 =78 σ2: 2 1 1 2 2 2 1 1 =156 σ3: 1 1 2 2 2 1 1 2 =57 σ4: 1 2 2 2 1 1 2 1 =114 σ5: 2 2 2 1 1 2 1 1 =228 σ6: 2 2 1 1 2 1 1 2 =201 σ7: 2 1 1 2 1 1 2 2 =147 No. 5 1 1 2 1 1 2 2 2 |
||
| 7: 1 1 2 1 2 1 2 2 σ0: 1 1 2 1 2 1 2 2 =43* 不変 σ1: 1 2 1 2 1 2 2 1 =86 σ2: 2 1 2 1 2 2 1 1 =172 σ3: 1 2 1 2 2 1 1 2 =89 σ4: 2 1 2 2 1 1 2 1 =178 σ5: 1 2 2 1 1 2 1 2 =101 σ6: 2 2 1 1 2 1 2 1 =202 σ7: 2 1 1 2 1 2 1 2 =149 No. 6 1 1 2 1 2 1 2 2 |
8: 1 1 2 1 2 2 1 2 σ0: 1 1 2 1 2 2 1 2 =45* 不変 σ1: 1 2 1 2 2 1 2 1 =90 σ2: 2 1 2 2 1 2 1 1 =180 σ3: 1 2 2 1 2 1 1 2 =105 σ4: 2 2 1 2 1 1 2 1 =210 σ5: 2 1 2 1 1 2 1 2 =165 σ6: 1 2 1 1 2 1 2 2 =75 σ7: 2 1 1 2 1 2 2 1 =150 No. 7 1 1 2 1 2 2 1 2 |
9: 1 1 2 1 2 2 2 1 σ0: 1 1 2 1 2 2 2 1 =46* 不変 σ1: 1 2 1 2 2 2 1 1 =92 σ2: 2 1 2 2 2 1 1 1 =184 σ3: 1 2 2 2 1 1 1 2 =113 σ4: 2 2 2 1 1 1 2 1 =226 σ5: 2 2 1 1 1 2 1 2 =197 σ6: 2 1 1 1 2 1 2 2 =139 σ7: 1 1 1 2 1 2 2 2 =23* |
||
| 10: 1 1 2 2 1 1 2 2 σ0: 1 1 2 2 1 1 2 2 =51* 不変 σ1: 1 2 2 1 1 2 2 1 =102 σ2: 2 2 1 1 2 2 1 1 =204 σ3: 2 1 1 2 2 1 1 2 =153 σ4: 1 1 2 2 1 1 2 2 =51 不変 σ5: 1 2 2 1 1 2 2 1 =102 σ6: 2 2 1 1 2 2 1 1 =204 σ7: 2 1 1 2 2 1 1 2 =153 No. 8 1 1 2 2 1 1 2 2 |
11: 1 1 2 2 1 2 1 2 σ0: 1 1 2 2 1 2 1 2 =53* 不変 σ1: 1 2 2 1 2 1 2 1 =106 σ2: 2 2 1 2 1 2 1 1 =212 σ3: 2 1 2 1 2 1 1 2 =169 σ4: 1 2 1 2 1 1 2 2 =83 σ5: 2 1 2 1 1 2 2 1 =166 σ6: 1 2 1 1 2 2 1 2 =77 σ7: 2 1 1 2 2 1 2 1 =154 No. 9 1 1 2 2 1 2 1 2 |
12: 1 1 2 2 1 2 2 1 σ0: 1 1 2 2 1 2 2 1 =54* 不変 σ1: 1 2 2 1 2 2 1 1 =108 σ2: 2 2 1 2 2 1 1 1 =216 σ3: 2 1 2 2 1 1 1 2 =177 σ4: 1 2 2 1 1 1 2 2 =99 σ5: 2 2 1 1 1 2 2 1 =198 σ6: 2 1 1 1 2 2 1 2 =141 σ7: 1 1 1 2 2 1 2 2 =27* |
||
| 13: 1 1 2 2 2 1 1 2 σ0: 1 1 2 2 2 1 1 2 =57* 不変 σ1: 1 2 2 2 1 1 2 1 =114 σ2: 2 2 2 1 1 2 1 1 =228 σ3: 2 2 1 1 2 1 1 2 =201 σ4: 2 1 1 2 1 1 2 2 =147 σ5: 1 1 2 1 1 2 2 2 =39* σ6: 1 2 1 1 2 2 2 1 =78 σ7: 2 1 1 2 2 2 1 1 =156 |
14: 1 1 2 2 2 1 2 1 σ0: 1 1 2 2 2 1 2 1 =58* 不変 σ1: 1 2 2 2 1 2 1 1 =116 σ2: 2 2 2 1 2 1 1 1 =232 σ3: 2 2 1 2 1 1 1 2 =209 σ4: 2 1 2 1 1 1 2 2 =163 σ5: 1 2 1 1 1 2 2 2 =71 σ6: 2 1 1 1 2 2 2 1 =142 σ7: 1 1 1 2 2 2 1 2 =29* |
15: 1 1 2 2 2 2 1 1 σ0: 1 1 2 2 2 2 1 1 =60* 不変 σ1: 1 2 2 2 2 1 1 1 =120 σ2: 2 2 2 2 1 1 1 1 =240 σ3: 2 2 2 1 1 1 1 2 =225 σ4: 2 2 1 1 1 1 2 2 =195 σ5: 2 1 1 1 1 2 2 2 =135 σ6: 1 1 1 1 2 2 2 2 =15* σ7: 1 1 1 2 2 2 2 1 =30 |
||
| 16: 1 2 1 1 1 2 2 2 σ0: 1 2 1 1 1 2 2 2 =71* 不変 σ1: 2 1 1 1 2 2 2 1 =142 σ2: 1 1 1 2 2 2 1 2 =29* σ3: 1 1 2 2 2 1 2 1 =58 σ4: 1 2 2 2 1 2 1 1 =116 σ5: 2 2 2 1 2 1 1 1 =232 σ6: 2 2 1 2 1 1 1 2 =209 σ7: 2 1 2 1 1 1 2 2 =163 |
17: 1 2 1 1 2 1 2 2 σ0: 1 2 1 1 2 1 2 2 =75* 不変 σ1: 2 1 1 2 1 2 2 1 =150 σ2: 1 1 2 1 2 2 1 2 =45* σ3: 1 2 1 2 2 1 2 1 =90 σ4: 2 1 2 2 1 2 1 1 =180 σ5: 1 2 2 1 2 1 1 2 =105 σ6: 2 2 1 2 1 1 2 1 =210 σ7: 2 1 2 1 1 2 1 2 =165 |
18: 1 2 1 1 2 2 1 2 σ0: 1 2 1 1 2 2 1 2 =77* 不変 σ1: 2 1 1 2 2 1 2 1 =154 σ2: 1 1 2 2 1 2 1 2 =53* σ3: 1 2 2 1 2 1 2 1 =106 σ4: 2 2 1 2 1 2 1 1 =212 σ5: 2 1 2 1 2 1 1 2 =169 σ6: 1 2 1 2 1 1 2 2 =83 σ7: 2 1 2 1 1 2 2 1 =166 |
||
| 19: 1 2 1 1 2 2 2 1 σ0: 1 2 1 1 2 2 2 1 =78* 不変 σ1: 2 1 1 2 2 2 1 1 =156 σ2: 1 1 2 2 2 1 1 2 =57* σ3: 1 2 2 2 1 1 2 1 =114 σ4: 2 2 2 1 1 2 1 1 =228 σ5: 2 2 1 1 2 1 1 2 =201 σ6: 2 1 1 2 1 1 2 2 =147 σ7: 1 1 2 1 1 2 2 2 =39* |
20: 1 2 1 2 1 1 2 2 σ0: 1 2 1 2 1 1 2 2 =83* 不変 σ1: 2 1 2 1 1 2 2 1 =166 σ2: 1 2 1 1 2 2 1 2 =77* σ3: 2 1 1 2 2 1 2 1 =154 σ4: 1 1 2 2 1 2 1 2 =53* σ5: 1 2 2 1 2 1 2 1 =106 σ6: 2 2 1 2 1 2 1 1 =212 σ7: 2 1 2 1 2 1 1 2 =169 |
21: 1 2 1 2 1 2 1 2 σ0: 1 2 1 2 1 2 1 2 =85* 不変 σ1: 2 1 2 1 2 1 2 1 =170 σ2: 1 2 1 2 1 2 1 2 =85 不変 σ3: 2 1 2 1 2 1 2 1 =170 σ4: 1 2 1 2 1 2 1 2 =85 不変 σ5: 2 1 2 1 2 1 2 1 =170 σ6: 1 2 1 2 1 2 1 2 =85 不変 σ7: 2 1 2 1 2 1 2 1 =170 No. 10 1 2 1 2 1 2 1 2 |
||
| 22: 1 2 1 2 1 2 2 1 σ0: 1 2 1 2 1 2 2 1 =86* 不変 σ1: 2 1 2 1 2 2 1 1 =172 σ2: 1 2 1 2 2 1 1 2 =89 σ3: 2 1 2 2 1 1 2 1 =178 σ4: 1 2 2 1 1 2 1 2 =101 σ5: 2 2 1 1 2 1 2 1 =202 σ6: 2 1 1 2 1 2 1 2 =149 σ7: 1 1 2 1 2 1 2 2 =43* |
23: 1 2 1 2 2 1 1 2 σ0: 1 2 1 2 2 1 1 2 =89* 不変 σ1: 2 1 2 2 1 1 2 1 =178 σ2: 1 2 2 1 1 2 1 2 =101 σ3: 2 2 1 1 2 1 2 1 =202 σ4: 2 1 1 2 1 2 1 2 =149 σ5: 1 1 2 1 2 1 2 2 =43* σ6: 1 2 1 2 1 2 2 1 =86 σ7: 2 1 2 1 2 2 1 1 =172 |
24: 1 2 1 2 2 1 2 1 σ0: 1 2 1 2 2 1 2 1 =90* 不変 σ1: 2 1 2 2 1 2 1 1 =180 σ2: 1 2 2 1 2 1 1 2 =105 σ3: 2 2 1 2 1 1 2 1 =210 σ4: 2 1 2 1 1 2 1 2 =165 σ5: 1 2 1 1 2 1 2 2 =75* σ6: 2 1 1 2 1 2 2 1 =150 σ7: 1 1 2 1 2 2 1 2 =45* |
||
| 25: 1 2 1 2 2 2 1 1 σ0: 1 2 1 2 2 2 1 1 =92* 不変 σ1: 2 1 2 2 2 1 1 1 =184 σ2: 1 2 2 2 1 1 1 2 =113 σ3: 2 2 2 1 1 1 2 1 =226 σ4: 2 2 1 1 1 2 1 2 =197 σ5: 2 1 1 1 2 1 2 2 =139 σ6: 1 1 1 2 1 2 2 2 =23* σ7: 1 1 2 1 2 2 2 1 =46 |
26: 1 2 2 1 1 1 2 2 σ0: 1 2 2 1 1 1 2 2 =99* 不変 σ1: 2 2 1 1 1 2 2 1 =198 σ2: 2 1 1 1 2 2 1 2 =141 σ3: 1 1 1 2 2 1 2 2 =27* σ4: 1 1 2 2 1 2 2 1 =54 σ5: 1 2 2 1 2 2 1 1 =108 σ6: 2 2 1 2 2 1 1 1 =216 σ7: 2 1 2 2 1 1 1 2 =177 |
27: 1 2 2 1 1 2 1 2 σ0: 1 2 2 1 1 2 1 2 =101* 不変 σ1: 2 2 1 1 2 1 2 1 =202 σ2: 2 1 1 2 1 2 1 2 =149 σ3: 1 1 2 1 2 1 2 2 =43* σ4: 1 2 1 2 1 2 2 1 =86 σ5: 2 1 2 1 2 2 1 1 =172 σ6: 1 2 1 2 2 1 1 2 =89 σ7: 2 1 2 2 1 1 2 1 =178 |
||
| 28: 1 2 2 1 1 2 2 1 σ0: 1 2 2 1 1 2 2 1 =102* 不変 σ1: 2 2 1 1 2 2 1 1 =204 σ2: 2 1 1 2 2 1 1 2 =153 σ3: 1 1 2 2 1 1 2 2 =51* σ4: 1 2 2 1 1 2 2 1 =102 不変 σ5: 2 2 1 1 2 2 1 1 =204 σ6: 2 1 1 2 2 1 1 2 =153 σ7: 1 1 2 2 1 1 2 2 =51 |
29: 1 2 2 1 2 1 1 2 σ0: 1 2 2 1 2 1 1 2 =105* 不変 σ1: 2 2 1 2 1 1 2 1 =210 σ2: 2 1 2 1 1 2 1 2 =165 σ3: 1 2 1 1 2 1 2 2 =75* σ4: 2 1 1 2 1 2 2 1 =150 σ5: 1 1 2 1 2 2 1 2 =45* σ6: 1 2 1 2 2 1 2 1 =90 σ7: 2 1 2 2 1 2 1 1 =180 |
30: 1 2 2 1 2 1 2 1 σ0: 1 2 2 1 2 1 2 1 =106* 不変 σ1: 2 2 1 2 1 2 1 1 =212 σ2: 2 1 2 1 2 1 1 2 =169 σ3: 1 2 1 2 1 1 2 2 =83* σ4: 2 1 2 1 1 2 2 1 =166 σ5: 1 2 1 1 2 2 1 2 =77* σ6: 2 1 1 2 2 1 2 1 =154 σ7: 1 1 2 2 1 2 1 2 =53* |
||
| 31: 1 2 2 1 2 2 1 1 σ0: 1 2 2 1 2 2 1 1 =108* 不変 σ1: 2 2 1 2 2 1 1 1 =216 σ2: 2 1 2 2 1 1 1 2 =177 σ3: 1 2 2 1 1 1 2 2 =99* σ4: 2 2 1 1 1 2 2 1 =198 σ5: 2 1 1 1 2 2 1 2 =141 σ6: 1 1 1 2 2 1 2 2 =27* σ7: 1 1 2 2 1 2 2 1 =54 |
32: 1 2 2 2 1 1 1 2 σ0: 1 2 2 2 1 1 1 2 =113* 不変 σ1: 2 2 2 1 1 1 2 1 =226 σ2: 2 2 1 1 1 2 1 2 =197 σ3: 2 1 1 1 2 1 2 2 =139 σ4: 1 1 1 2 1 2 2 2 =23* σ5: 1 1 2 1 2 2 2 1 =46 σ6: 1 2 1 2 2 2 1 1 =92 σ7: 2 1 2 2 2 1 1 1 =184 |
33: 1 2 2 2 1 1 2 1 σ0: 1 2 2 2 1 1 2 1 =114* 不変 σ1: 2 2 2 1 1 2 1 1 =228 σ2: 2 2 1 1 2 1 1 2 =201 σ3: 2 1 1 2 1 1 2 2 =147 σ4: 1 1 2 1 1 2 2 2 =39* σ5: 1 2 1 1 2 2 2 1 =78 σ6: 2 1 1 2 2 2 1 1 =156 σ7: 1 1 2 2 2 1 1 2 =57 |
||
| 34: 1 2 2 2 1 2 1 1 σ0: 1 2 2 2 1 2 1 1 =116* 不変 σ1: 2 2 2 1 2 1 1 1 =232 σ2: 2 2 1 2 1 1 1 2 =209 σ3: 2 1 2 1 1 1 2 2 =163 σ4: 1 2 1 1 1 2 2 2 =71* σ5: 2 1 1 1 2 2 2 1 =142 σ6: 1 1 1 2 2 2 1 2 =29* σ7: 1 1 2 2 2 1 2 1 =58 |
35: 1 2 2 2 2 1 1 1 σ0: 1 2 2 2 2 1 1 1 =120* 不変 σ1: 2 2 2 2 1 1 1 1 =240 σ2: 2 2 2 1 1 1 1 2 =225 σ3: 2 2 1 1 1 1 2 2 =195 σ4: 2 1 1 1 1 2 2 2 =135 σ5: 1 1 1 1 2 2 2 2 =15* σ6: 1 1 1 2 2 2 2 1 =30 σ7: 1 1 2 2 2 2 1 1 =60 |
36: 2 1 1 1 1 2 2 2 σ0: 2 1 1 1 1 2 2 2 =135* 不変 σ1: 1 1 1 1 2 2 2 2 =15* σ2: 1 1 1 2 2 2 2 1 =30 σ3: 1 1 2 2 2 2 1 1 =60 σ4: 1 2 2 2 2 1 1 1 =120 σ5: 2 2 2 2 1 1 1 1 =240 σ6: 2 2 2 1 1 1 1 2 =225 σ7: 2 2 1 1 1 1 2 2 =195 |
||
| 37: 2 1 1 1 2 1 2 2 σ0: 2 1 1 1 2 1 2 2 =139* 不変 σ1: 1 1 1 2 1 2 2 2 =23* σ2: 1 1 2 1 2 2 2 1 =46 σ3: 1 2 1 2 2 2 1 1 =92 σ4: 2 1 2 2 2 1 1 1 =184 σ5: 1 2 2 2 1 1 1 2 =113 σ6: 2 2 2 1 1 1 2 1 =226 σ7: 2 2 1 1 1 2 1 2 =197 |
38: 2 1 1 1 2 2 1 2 σ0: 2 1 1 1 2 2 1 2 =141* 不変 σ1: 1 1 1 2 2 1 2 2 =27* σ2: 1 1 2 2 1 2 2 1 =54 σ3: 1 2 2 1 2 2 1 1 =108 σ4: 2 2 1 2 2 1 1 1 =216 σ5: 2 1 2 2 1 1 1 2 =177 σ6: 1 2 2 1 1 1 2 2 =99 σ7: 2 2 1 1 1 2 2 1 =198 |
39: 2 1 1 1 2 2 2 1 σ0: 2 1 1 1 2 2 2 1 =142* 不変 σ1: 1 1 1 2 2 2 1 2 =29* σ2: 1 1 2 2 2 1 2 1 =58 σ3: 1 2 2 2 1 2 1 1 =116 σ4: 2 2 2 1 2 1 1 1 =232 σ5: 2 2 1 2 1 1 1 2 =209 σ6: 2 1 2 1 1 1 2 2 =163 σ7: 1 2 1 1 1 2 2 2 =71 |
||
| 40: 2 1 1 2 1 1 2 2 σ0: 2 1 1 2 1 1 2 2 =147* 不変 σ1: 1 1 2 1 1 2 2 2 =39* σ2: 1 2 1 1 2 2 2 1 =78 σ3: 2 1 1 2 2 2 1 1 =156 σ4: 1 1 2 2 2 1 1 2 =57 σ5: 1 2 2 2 1 1 2 1 =114 σ6: 2 2 2 1 1 2 1 1 =228 σ7: 2 2 1 1 2 1 1 2 =201 |
41: 2 1 1 2 1 2 1 2 σ0: 2 1 1 2 1 2 1 2 =149* 不変 σ1: 1 1 2 1 2 1 2 2 =43* σ2: 1 2 1 2 1 2 2 1 =86 σ3: 2 1 2 1 2 2 1 1 =172 σ4: 1 2 1 2 2 1 1 2 =89 σ5: 2 1 2 2 1 1 2 1 =178 σ6: 1 2 2 1 1 2 1 2 =101 σ7: 2 2 1 1 2 1 2 1 =202 |
42: 2 1 1 2 1 2 2 1 σ0: 2 1 1 2 1 2 2 1 =150* 不変 σ1: 1 1 2 1 2 2 1 2 =45* σ2: 1 2 1 2 2 1 2 1 =90 σ3: 2 1 2 2 1 2 1 1 =180 σ4: 1 2 2 1 2 1 1 2 =105 σ5: 2 2 1 2 1 1 2 1 =210 σ6: 2 1 2 1 1 2 1 2 =165 σ7: 1 2 1 1 2 1 2 2 =75 |
||
| 43: 2 1 1 2 2 1 1 2 σ0: 2 1 1 2 2 1 1 2 =153* 不変 σ1: 1 1 2 2 1 1 2 2 =51* σ2: 1 2 2 1 1 2 2 1 =102 σ3: 2 2 1 1 2 2 1 1 =204 σ4: 2 1 1 2 2 1 1 2 =153 不変 σ5: 1 1 2 2 1 1 2 2 =51 σ6: 1 2 2 1 1 2 2 1 =102 σ7: 2 2 1 1 2 2 1 1 =204 |
44: 2 1 1 2 2 1 2 1 σ0: 2 1 1 2 2 1 2 1 =154* 不変 σ1: 1 1 2 2 1 2 1 2 =53* σ2: 1 2 2 1 2 1 2 1 =106 σ3: 2 2 1 2 1 2 1 1 =212 σ4: 2 1 2 1 2 1 1 2 =169 σ5: 1 2 1 2 1 1 2 2 =83 σ6: 2 1 2 1 1 2 2 1 =166 σ7: 1 2 1 1 2 2 1 2 =77 |
45: 2 1 1 2 2 2 1 1 σ0: 2 1 1 2 2 2 1 1 =156* 不変 σ1: 1 1 2 2 2 1 1 2 =57* σ2: 1 2 2 2 1 1 2 1 =114 σ3: 2 2 2 1 1 2 1 1 =228 σ4: 2 2 1 1 2 1 1 2 =201 σ5: 2 1 1 2 1 1 2 2 =147 σ6: 1 1 2 1 1 2 2 2 =39* σ7: 1 2 1 1 2 2 2 1 =78 |
||
| 46: 2 1 2 1 1 1 2 2 σ0: 2 1 2 1 1 1 2 2 =163* 不変 σ1: 1 2 1 1 1 2 2 2 =71* σ2: 2 1 1 1 2 2 2 1 =142 σ3: 1 1 1 2 2 2 1 2 =29* σ4: 1 1 2 2 2 1 2 1 =58 σ5: 1 2 2 2 1 2 1 1 =116 σ6: 2 2 2 1 2 1 1 1 =232 σ7: 2 2 1 2 1 1 1 2 =209 |
47: 2 1 2 1 1 2 1 2 σ0: 2 1 2 1 1 2 1 2 =165* 不変 σ1: 1 2 1 1 2 1 2 2 =75* σ2: 2 1 1 2 1 2 2 1 =150 σ3: 1 1 2 1 2 2 1 2 =45* σ4: 1 2 1 2 2 1 2 1 =90 σ5: 2 1 2 2 1 2 1 1 =180 σ6: 1 2 2 1 2 1 1 2 =105 σ7: 2 2 1 2 1 1 2 1 =210 |
48: 2 1 2 1 1 2 2 1 σ0: 2 1 2 1 1 2 2 1 =166* 不変 σ1: 1 2 1 1 2 2 1 2 =77* σ2: 2 1 1 2 2 1 2 1 =154 σ3: 1 1 2 2 1 2 1 2 =53* σ4: 1 2 2 1 2 1 2 1 =106 σ5: 2 2 1 2 1 2 1 1 =212 σ6: 2 1 2 1 2 1 1 2 =169 σ7: 1 2 1 2 1 1 2 2 =83 |
||
| 49: 2 1 2 1 2 1 1 2 σ0: 2 1 2 1 2 1 1 2 =169* 不変 σ1: 1 2 1 2 1 1 2 2 =83* σ2: 2 1 2 1 1 2 2 1 =166 σ3: 1 2 1 1 2 2 1 2 =77* σ4: 2 1 1 2 2 1 2 1 =154 σ5: 1 1 2 2 1 2 1 2 =53* σ6: 1 2 2 1 2 1 2 1 =106 σ7: 2 2 1 2 1 2 1 1 =212 |
50: 2 1 2 1 2 1 2 1 σ0: 2 1 2 1 2 1 2 1 =170* 不変 σ1: 1 2 1 2 1 2 1 2 =85* σ2: 2 1 2 1 2 1 2 1 =170 不変 σ3: 1 2 1 2 1 2 1 2 =85 σ4: 2 1 2 1 2 1 2 1 =170 不変 σ5: 1 2 1 2 1 2 1 2 =85 σ6: 2 1 2 1 2 1 2 1 =170 不変 σ7: 1 2 1 2 1 2 1 2 =85 |
51: 2 1 2 1 2 2 1 1 σ0: 2 1 2 1 2 2 1 1 =172* 不変 σ1: 1 2 1 2 2 1 1 2 =89* σ2: 2 1 2 2 1 1 2 1 =178 σ3: 1 2 2 1 1 2 1 2 =101 σ4: 2 2 1 1 2 1 2 1 =202 σ5: 2 1 1 2 1 2 1 2 =149 σ6: 1 1 2 1 2 1 2 2 =43* σ7: 1 2 1 2 1 2 2 1 =86 |
||
| 52: 2 1 2 2 1 1 1 2 σ0: 2 1 2 2 1 1 1 2 =177* 不変 σ1: 1 2 2 1 1 1 2 2 =99* σ2: 2 2 1 1 1 2 2 1 =198 σ3: 2 1 1 1 2 2 1 2 =141 σ4: 1 1 1 2 2 1 2 2 =27* σ5: 1 1 2 2 1 2 2 1 =54 σ6: 1 2 2 1 2 2 1 1 =108 σ7: 2 2 1 2 2 1 1 1 =216 |
53: 2 1 2 2 1 1 2 1 σ0: 2 1 2 2 1 1 2 1 =178* 不変 σ1: 1 2 2 1 1 2 1 2 =101* σ2: 2 2 1 1 2 1 2 1 =202 σ3: 2 1 1 2 1 2 1 2 =149 σ4: 1 1 2 1 2 1 2 2 =43* σ5: 1 2 1 2 1 2 2 1 =86 σ6: 2 1 2 1 2 2 1 1 =172 σ7: 1 2 1 2 2 1 1 2 =89 |
54: 2 1 2 2 1 2 1 1 σ0: 2 1 2 2 1 2 1 1 =180* 不変 σ1: 1 2 2 1 2 1 1 2 =105* σ2: 2 2 1 2 1 1 2 1 =210 σ3: 2 1 2 1 1 2 1 2 =165 σ4: 1 2 1 1 2 1 2 2 =75* σ5: 2 1 1 2 1 2 2 1 =150 σ6: 1 1 2 1 2 2 1 2 =45* σ7: 1 2 1 2 2 1 2 1 =90 |
||
| 55: 2 1 2 2 2 1 1 1 σ0: 2 1 2 2 2 1 1 1 =184* 不変 σ1: 1 2 2 2 1 1 1 2 =113* σ2: 2 2 2 1 1 1 2 1 =226 σ3: 2 2 1 1 1 2 1 2 =197 σ4: 2 1 1 1 2 1 2 2 =139 σ5: 1 1 1 2 1 2 2 2 =23* σ6: 1 1 2 1 2 2 2 1 =46 σ7: 1 2 1 2 2 2 1 1 =92 |
56: 2 2 1 1 1 1 2 2 σ0: 2 2 1 1 1 1 2 2 =195* 不変 σ1: 2 1 1 1 1 2 2 2 =135* σ2: 1 1 1 1 2 2 2 2 =15* σ3: 1 1 1 2 2 2 2 1 =30 σ4: 1 1 2 2 2 2 1 1 =60 σ5: 1 2 2 2 2 1 1 1 =120 σ6: 2 2 2 2 1 1 1 1 =240 σ7: 2 2 2 1 1 1 1 2 =225 |
57: 2 2 1 1 1 2 1 2 σ0: 2 2 1 1 1 2 1 2 =197* 不変 σ1: 2 1 1 1 2 1 2 2 =139* σ2: 1 1 1 2 1 2 2 2 =23* σ3: 1 1 2 1 2 2 2 1 =46 σ4: 1 2 1 2 2 2 1 1 =92 σ5: 2 1 2 2 2 1 1 1 =184 σ6: 1 2 2 2 1 1 1 2 =113 σ7: 2 2 2 1 1 1 2 1 =226 |
||
| 58: 2 2 1 1 1 2 2 1 σ0: 2 2 1 1 1 2 2 1 =198* 不変 σ1: 2 1 1 1 2 2 1 2 =141* σ2: 1 1 1 2 2 1 2 2 =27* σ3: 1 1 2 2 1 2 2 1 =54 σ4: 1 2 2 1 2 2 1 1 =108 σ5: 2 2 1 2 2 1 1 1 =216 σ6: 2 1 2 2 1 1 1 2 =177 σ7: 1 2 2 1 1 1 2 2 =99 |
59: 2 2 1 1 2 1 1 2 σ0: 2 2 1 1 2 1 1 2 =201* 不変 σ1: 2 1 1 2 1 1 2 2 =147* σ2: 1 1 2 1 1 2 2 2 =39* σ3: 1 2 1 1 2 2 2 1 =78 σ4: 2 1 1 2 2 2 1 1 =156 σ5: 1 1 2 2 2 1 1 2 =57 σ6: 1 2 2 2 1 1 2 1 =114 σ7: 2 2 2 1 1 2 1 1 =228 |
60: 2 2 1 1 2 1 2 1 σ0: 2 2 1 1 2 1 2 1 =202* 不変 σ1: 2 1 1 2 1 2 1 2 =149* σ2: 1 1 2 1 2 1 2 2 =43* σ3: 1 2 1 2 1 2 2 1 =86 σ4: 2 1 2 1 2 2 1 1 =172 σ5: 1 2 1 2 2 1 1 2 =89 σ6: 2 1 2 2 1 1 2 1 =178 σ7: 1 2 2 1 1 2 1 2 =101 |
||
| 61: 2 2 1 1 2 2 1 1 σ0: 2 2 1 1 2 2 1 1 =204* 不変 σ1: 2 1 1 2 2 1 1 2 =153* σ2: 1 1 2 2 1 1 2 2 =51* σ3: 1 2 2 1 1 2 2 1 =102 σ4: 2 2 1 1 2 2 1 1 =204 不変 σ5: 2 1 1 2 2 1 1 2 =153 σ6: 1 1 2 2 1 1 2 2 =51 σ7: 1 2 2 1 1 2 2 1 =102 |
62: 2 2 1 2 1 1 1 2 σ0: 2 2 1 2 1 1 1 2 =209* 不変 σ1: 2 1 2 1 1 1 2 2 =163* σ2: 1 2 1 1 1 2 2 2 =71* σ3: 2 1 1 1 2 2 2 1 =142 σ4: 1 1 1 2 2 2 1 2 =29* σ5: 1 1 2 2 2 1 2 1 =58 σ6: 1 2 2 2 1 2 1 1 =116 σ7: 2 2 2 1 2 1 1 1 =232 |
63: 2 2 1 2 1 1 2 1 σ0: 2 2 1 2 1 1 2 1 =210* 不変 σ1: 2 1 2 1 1 2 1 2 =165* σ2: 1 2 1 1 2 1 2 2 =75* σ3: 2 1 1 2 1 2 2 1 =150 σ4: 1 1 2 1 2 2 1 2 =45* σ5: 1 2 1 2 2 1 2 1 =90 σ6: 2 1 2 2 1 2 1 1 =180 σ7: 1 2 2 1 2 1 1 2 =105 |
||
| 64: 2 2 1 2 1 2 1 1 σ0: 2 2 1 2 1 2 1 1 =212* 不変 σ1: 2 1 2 1 2 1 1 2 =169* σ2: 1 2 1 2 1 1 2 2 =83* σ3: 2 1 2 1 1 2 2 1 =166 σ4: 1 2 1 1 2 2 1 2 =77* σ5: 2 1 1 2 2 1 2 1 =154 σ6: 1 1 2 2 1 2 1 2 =53* σ7: 1 2 2 1 2 1 2 1 =106 |
65: 2 2 1 2 2 1 1 1 σ0: 2 2 1 2 2 1 1 1 =216* 不変 σ1: 2 1 2 2 1 1 1 2 =177* σ2: 1 2 2 1 1 1 2 2 =99* σ3: 2 2 1 1 1 2 2 1 =198 σ4: 2 1 1 1 2 2 1 2 =141 σ5: 1 1 1 2 2 1 2 2 =27* σ6: 1 1 2 2 1 2 2 1 =54 σ7: 1 2 2 1 2 2 1 1 =108 |
66: 2 2 2 1 1 1 1 2 σ0: 2 2 2 1 1 1 1 2 =225* 不変 σ1: 2 2 1 1 1 1 2 2 =195* σ2: 2 1 1 1 1 2 2 2 =135* σ3: 1 1 1 1 2 2 2 2 =15* σ4: 1 1 1 2 2 2 2 1 =30 σ5: 1 1 2 2 2 2 1 1 =60 σ6: 1 2 2 2 2 1 1 1 =120 σ7: 2 2 2 2 1 1 1 1 =240 |
||
| 67: 2 2 2 1 1 1 2 1 σ0: 2 2 2 1 1 1 2 1 =226* 不変 σ1: 2 2 1 1 1 2 1 2 =197* σ2: 2 1 1 1 2 1 2 2 =139* σ3: 1 1 1 2 1 2 2 2 =23* σ4: 1 1 2 1 2 2 2 1 =46 σ5: 1 2 1 2 2 2 1 1 =92 σ6: 2 1 2 2 2 1 1 1 =184 σ7: 1 2 2 2 1 1 1 2 =113 |
68: 2 2 2 1 1 2 1 1 σ0: 2 2 2 1 1 2 1 1 =228* 不変 σ1: 2 2 1 1 2 1 1 2 =201* σ2: 2 1 1 2 1 1 2 2 =147* σ3: 1 1 2 1 1 2 2 2 =39* σ4: 1 2 1 1 2 2 2 1 =78 σ5: 2 1 1 2 2 2 1 1 =156 σ6: 1 1 2 2 2 1 1 2 =57 σ7: 1 2 2 2 1 1 2 1 =114 |
69: 2 2 2 1 2 1 1 1 σ0: 2 2 2 1 2 1 1 1 =232* 不変 σ1: 2 2 1 2 1 1 1 2 =209* σ2: 2 1 2 1 1 1 2 2 =163* σ3: 1 2 1 1 1 2 2 2 =71* σ4: 2 1 1 1 2 2 2 1 =142 σ5: 1 1 1 2 2 2 1 2 =29* σ6: 1 1 2 2 2 1 2 1 =58 σ7: 1 2 2 2 1 2 1 1 =116 |
||
| 70: 2 2 2 2 1 1 1 1 σ0: 2 2 2 2 1 1 1 1 =240* 不変 σ1: 2 2 2 1 1 1 1 2 =225* σ2: 2 2 1 1 1 1 2 2 =195* σ3: 2 1 1 1 1 2 2 2 =135* σ4: 1 1 1 1 2 2 2 2 =15* σ5: 1 1 1 2 2 2 2 1 =30 σ6: 1 1 2 2 2 2 1 1 =60 σ7: 1 2 2 2 2 1 1 1 =120 |
よって、φ(σm)=70、0、2、0、6、0、2、0 より、10通り
問題 赤球、青球、黄球の何れか4個を円形に並べる場合の数を求めよ。
すべての解は、34=81通り
| 1: 1 1 1 1 σ0: 1 1 1 1 =0* 不変 σ1: 1 1 1 1 =0 不変 σ2: 1 1 1 1 =0 不変 σ3: 1 1 1 1 =0 不変 No. 1 1 1 1 1 |
2: 1 1 1 2 σ0: 1 1 1 2 =1* 不変 σ1: 1 1 2 1 =3 σ2: 1 2 1 1 =9 σ3: 2 1 1 1 =27 No. 2 1 1 1 2 |
3: 1 1 1 3 σ0: 1 1 1 3 =2* 不変 σ1: 1 1 3 1 =6 σ2: 1 3 1 1 =18 σ3: 3 1 1 1 =54 No. 3 1 1 1 3 |
||
| 4: 1 1 2 1 σ0: 1 1 2 1 =3* 不変 σ1: 1 2 1 1 =9 σ2: 2 1 1 1 =27 σ3: 1 1 1 2 =1* |
5: 1 1 2 2 σ0: 1 1 2 2 =4* 不変 σ1: 1 2 2 1 =12 σ2: 2 2 1 1 =36 σ3: 2 1 1 2 =28 No. 4 1 1 2 2 |
5: 1 1 2 3 σ0: 1 1 2 3 =5* 不変 σ1: 1 2 3 1 =15 σ2: 2 3 1 1 =45 σ3: 3 1 1 2 =55 No. 5 1 1 2 3 |
||
| 7: 1 1 3 1 σ0: 1 1 3 1 =6* 不変 σ1: 1 3 1 1 =18 σ2: 3 1 1 1 =54 σ3: 1 1 1 3 =2* |
8: 1 1 3 2 σ0: 1 1 3 2 =7* 不変 σ1: 1 3 2 1 =21 σ2: 3 2 1 1 =63 σ3: 2 1 1 3 =29 No. 6 1 1 3 2 |
9: 1 1 3 3 σ0: 1 1 3 3 =8* 不変 σ1: 1 3 3 1 =24 σ2: 3 3 1 1 =72 σ3: 3 1 1 3 =56 No. 7 1 1 3 3 |
||
| 10: 1 2 1 1 σ0: 1 2 1 1 =9* 不変 σ1: 2 1 1 1 =27 σ2: 1 1 1 2 =1* σ3: 1 1 2 1 =3 |
11: 1 2 1 2 σ0: 1 2 1 2 =10* 不変 σ1: 2 1 2 1 =30 σ2: 1 2 1 2 =10 不変 σ3: 2 1 2 1 =30 No. 8 1 2 1 2 |
12: 1 2 1 3 σ0: 1 2 1 3 =11* 不変 σ1: 2 1 3 1 =33 σ2: 1 3 1 2 =19 σ3: 3 1 2 1 =57 No. 9 1 2 1 3 |
||
| 13: 1 2 2 1 σ0: 1 2 2 1 =12* 不変 σ1: 2 2 1 1 =36 σ2: 2 1 1 2 =28 σ3: 1 1 2 2 =4* |
14: 1 2 2 2 σ0: 1 2 2 2 =13* 不変 σ1: 2 2 2 1 =39 σ2: 2 2 1 2 =37 σ3: 2 1 2 2 =31 No. 10 1 2 2 2 |
15: 1 2 2 3 σ0: 1 2 2 3 =14* 不変 σ1: 2 2 3 1 =42 σ2: 2 3 1 2 =46 σ3: 3 1 2 2 =58 No. 11 1 2 2 3 |
||
| 16: 1 2 3 1 σ0: 1 2 3 1 =15* 不変 σ1: 2 3 1 1 =45 σ2: 3 1 1 2 =55 σ3: 1 1 2 3 =5* |
17: 1 2 3 2 σ0: 1 2 3 2 =16* 不変 σ1: 2 3 2 1 =48 σ2: 3 2 1 2 =64 σ3: 2 1 2 3 =32 No. 12 1 2 3 2 |
18: 1 2 3 3 σ0: 1 2 3 3 =17* 不変 σ1: 2 3 3 1 =51 σ2: 3 3 1 2 =73 σ3: 3 1 2 3 =59 No. 13 1 2 3 3 |
||
| 19: 1 3 1 1 σ0: 1 3 1 1 =18* 不変 σ1: 3 1 1 1 =54 σ2: 1 1 1 3 =2* σ3: 1 1 3 1 =6 |
20: 1 3 1 2 σ0: 1 3 1 2 =19* 不変 σ1: 3 1 2 1 =57 σ2: 1 2 1 3 =11* σ3: 2 1 3 1 =33 |
21: 1 3 1 3 σ0: 1 3 1 3 =20* 不変 σ1: 3 1 3 1 =60 σ2: 1 3 1 3 =20 不変 σ3: 3 1 3 1 =60 No. 14 1 3 1 3 |
||
| 22: 1 3 2 1 σ0: 1 3 2 1 =21* 不変 σ1: 3 2 1 1 =63 σ2: 2 1 1 3 =29 σ3: 1 1 3 2 =7* |
23: 1 3 2 2 σ0: 1 3 2 2 =22* 不変 σ1: 3 2 2 1 =66 σ2: 2 2 1 3 =38 σ3: 2 1 3 2 =34 No. 15 1 3 2 2 |
24: 1 3 2 3 σ0: 1 3 2 3 =23* 不変 σ1: 3 2 3 1 =69 σ2: 2 3 1 3 =47 σ3: 3 1 3 2 =61 No. 16 1 3 2 3 |
||
| 25: 1 3 3 1 σ0: 1 3 3 1 =24* 不変 σ1: 3 3 1 1 =72 σ2: 3 1 1 3 =56 σ3: 1 1 3 3 =8* |
26: 1 3 3 2 σ0: 1 3 3 2 =25* 不変 σ1: 3 3 2 1 =75 σ2: 3 2 1 3 =65 σ3: 2 1 3 3 =35 No. 17 1 3 3 2 |
27: 1 3 3 3 σ0: 1 3 3 3 =26* 不変 σ1: 3 3 3 1 =78 σ2: 3 3 1 3 =74 σ3: 3 1 3 3 =62 No. 18 1 3 3 3 |
||
| 28: 2 1 1 1 σ0: 2 1 1 1 =27* 不変 σ1: 1 1 1 2 =1* σ2: 1 1 2 1 =3 σ3: 1 2 1 1 =9 |
29: 2 1 1 2 σ0: 2 1 1 2 =28* 不変 σ1: 1 1 2 2 =4* σ2: 1 2 2 1 =12 σ3: 2 2 1 1 =36 |
30: 2 1 1 3 σ0: 2 1 1 3 =29* 不変 σ1: 1 1 3 2 =7* σ2: 1 3 2 1 =21 σ3: 3 2 1 1 =63 |
||
| 31: 2 1 2 1 σ0: 2 1 2 1 =30* 不変 σ1: 1 2 1 2 =10* σ2: 2 1 2 1 =30 不変 σ3: 1 2 1 2 =10 |
32: 2 1 2 2 σ0: 2 1 2 2 =31* 不変 σ1: 1 2 2 2 =13* σ2: 2 2 2 1 =39 σ3: 2 2 1 2 =37 |
33: 2 1 2 3 σ0: 2 1 2 3 =32* 不変 σ1: 1 2 3 2 =16* σ2: 2 3 2 1 =48 σ3: 3 2 1 2 =64 |
||
| 34: 2 1 3 1 σ0: 2 1 3 1 =33* 不変 σ1: 1 3 1 2 =19* σ2: 3 1 2 1 =57 σ3: 1 2 1 3 =11* |
35: 2 1 3 2 σ0: 2 1 3 2 =34* 不変 σ1: 1 3 2 2 =22* σ2: 3 2 2 1 =66 σ3: 2 2 1 3 =38 |
36: 2 1 3 3 σ0: 2 1 3 3 =35* 不変 σ1: 1 3 3 2 =25* σ2: 3 3 2 1 =75 σ3: 3 2 1 3 =65 |
||
| 37: 2 2 1 1 σ0: 2 2 1 1 =36* 不変 σ1: 2 1 1 2 =28* σ2: 1 1 2 2 =4* σ3: 1 2 2 1 =12 |
38: 2 2 1 2 σ0: 2 2 1 2 =37* 不変 σ1: 2 1 2 2 =31* σ2: 1 2 2 2 =13* σ3: 2 2 2 1 =39 |
39: 2 2 1 3 σ0: 2 2 1 3 =38* 不変 σ1: 2 1 3 2 =34* σ2: 1 3 2 2 =22* σ3: 3 2 2 1 =66 |
||
| 40 : 2 2 2 1 σ0: 2 2 2 1 =39* 不変 σ1: 2 2 1 2 =37* σ2: 2 1 2 2 =31* σ3: 1 2 2 2 =13* |
41: 2 2 2 2 σ0: 2 2 2 2 =40* 不変 σ1: 2 2 2 2 =40 不変 σ2: 2 2 2 2 =40 不変 σ3: 2 2 2 2 =40 不変 No. 19 2 2 2 2 |
42: 2 2 2 3 σ0: 2 2 2 3 =41* 不変 σ1: 2 2 3 2 =43 σ2: 2 3 2 2 =49 σ3: 3 2 2 2 =67 No. 20 2 2 2 3 |
||
| 43: 2 2 3 1 σ0: 2 2 3 1 =42* 不変 σ1: 2 3 1 2 =46 σ2: 3 1 2 2 =58 σ3: 1 2 2 3 =14* |
44: 2 2 3 2 σ0: 2 2 3 2 =43* 不変 σ1: 2 3 2 2 =49 σ2: 3 2 2 2 =67 σ3: 2 2 2 3 =41* |
45: 2 2 3 3 σ0: 2 2 3 3 =44* 不変 σ1: 2 3 3 2 =52 σ2: 3 3 2 2 =76 σ3: 3 2 2 3 =68 No. 21 2 2 3 3 |
||
| 46: 2 3 1 1 σ0: 2 3 1 1 =45* 不変 σ1: 3 1 1 2 =55 σ2: 1 1 2 3 =5* σ3: 1 2 3 1 =15 |
47: 2 3 1 2 σ0: 2 3 1 2 =46* 不変 σ1: 3 1 2 2 =58 σ2: 1 2 2 3 =14* σ3: 2 2 3 1 =42 |
48: 2 3 1 3 σ0: 2 3 1 3 =47* 不変 σ1: 3 1 3 2 =61 σ2: 1 3 2 3 =23* σ3: 3 2 3 1 =69 |
||
| 49: 2 3 2 1 σ0: 2 3 2 1 =48* 不変 σ1: 3 2 1 2 =64 σ2: 2 1 2 3 =32* σ3: 1 2 3 2 =16* |
50: 2 3 2 2 σ0: 2 3 2 2 =49* 不変 σ1: 3 2 2 2 =67 σ2: 2 2 2 3 =41* σ3: 2 2 3 2 =43 |
51: 2 3 2 3 σ0: 2 3 2 3 =50* 不変 σ1: 3 2 3 2 =70 σ2: 2 3 2 3 =50 不変 σ3: 3 2 3 2 =70 No. 22 2 3 2 3 |
||
| 52: 2 3 3 1 σ0: 2 3 3 1 =51* 不変 σ1: 3 3 1 2 =73 σ2: 3 1 2 3 =59 σ3: 1 2 3 3 =17* |
53: 2 3 3 2 σ0: 2 3 3 2 =52* 不変 σ1: 3 3 2 2 =76 σ2: 3 2 2 3 =68 σ3: 2 2 3 3 =44* |
54: 2 3 3 3 σ0: 2 3 3 3 =53* 不変 σ1: 3 3 3 2 =79 σ2: 3 3 2 3 =77 σ3: 3 2 3 3 =71 No. 23 2 3 3 3 |
||
| 55: 3 1 1 1 σ0: 3 1 1 1 =54* 不変 σ1: 1 1 1 3 =2* σ2: 1 1 3 1 =6 σ3: 1 3 1 1 =18 |
56: 3 1 1 2 σ0: 3 1 1 2 =55* 不変 σ1: 1 1 2 3 =5* σ2: 1 2 3 1 =15 σ3: 2 3 1 1 =45 |
57: 3 1 1 3 σ0: 3 1 1 3 =56* 不変 σ1: 1 1 3 3 =8* σ2: 1 3 3 1 =24 σ3: 3 3 1 1 =72 |
||
| 58: 3 1 2 1 σ0: 3 1 2 1 =57* 不変 σ1: 1 2 1 3 =11* σ2: 2 1 3 1 =33 σ3: 1 3 1 2 =19 |
59: 3 1 2 2 σ0: 3 1 2 2 =58* 不変 σ1: 1 2 2 3 =14* σ2: 2 2 3 1 =42 σ3: 2 3 1 2 =46 |
60: 3 1 2 3 σ0: 3 1 2 3 =59* 不変 σ1: 1 2 3 3 =17* σ2: 2 3 3 1 =51 σ3: 3 3 1 2 =73 |
||
| 61: 3 1 3 1 σ0: 3 1 3 1 =60* 不変 σ1: 1 3 1 3 =20* σ2: 3 1 3 1 =60 不変 σ3: 1 3 1 3 =20 |
62: 3 1 3 2 σ0: 3 1 3 2 =61* 不変 σ1: 1 3 2 3 =23* σ2: 3 2 3 1 =69 σ3: 2 3 1 3 =47 |
63: 3 1 3 3 σ0: 3 1 3 3 =62* 不変 σ1: 1 3 3 3 =26* σ2: 3 3 3 1 =78 σ3: 3 3 1 3 =74 |
||
| 64: 3 2 1 1 σ0: 3 2 1 1 =63* 不変 σ1: 2 1 1 3 =29* σ2: 1 1 3 2 =7* σ3: 1 3 2 1 =21 |
65: 3 2 1 2 σ0: 3 2 1 2 =64* 不変 σ1: 2 1 2 3 =32* σ2: 1 2 3 2 =16* σ3: 2 3 2 1 =48 |
66: 3 2 1 3 σ0: 3 2 1 3 =65* 不変 σ1: 2 1 3 3 =35* σ2: 1 3 3 2 =25* σ3: 3 3 2 1 =75 |
||
| 67: 3 2 2 1 σ0: 3 2 2 1 =66* 不変 σ1: 2 2 1 3 =38* σ2: 2 1 3 2 =34* σ3: 1 3 2 2 =22* |
68: 3 2 2 2 σ0: 3 2 2 2 =67* 不変 σ1: 2 2 2 3 =41* σ2: 2 2 3 2 =43 σ3: 2 3 2 2 =49 |
69: 3 2 2 3 σ0: 3 2 2 3 =68* 不変 σ1: 2 2 3 3 =44* σ2: 2 3 3 2 =52 σ3: 3 3 2 2 =76 |
||
| 70: 3 2 3 1 σ0: 3 2 3 1 =69* 不変 σ1: 2 3 1 3 =47* σ2: 3 1 3 2 =61 σ3: 1 3 2 3 =23* |
71: 3 2 3 2 σ0: 3 2 3 2 =70* 不変 σ1: 2 3 2 3 =50* σ2: 3 2 3 2 =70 不変 σ3: 2 3 2 3 =50 |
72: 3 2 3 3 σ0: 3 2 3 3 =71* 不変 σ1: 2 3 3 3 =53* σ2: 3 3 3 2 =79 σ3: 3 3 2 3 =77 |
||
| 73: 3 3 1 1 σ0: 3 3 1 1 =72* 不変 σ1: 3 1 1 3 =56* σ2: 1 1 3 3 =8* σ3: 1 3 3 1 =24 |
74: 3 3 1 2 σ0: 3 3 1 2 =73* 不変 σ1: 3 1 2 3 =59* σ2: 1 2 3 3 =17* σ3: 2 3 3 1 =51 |
75: 3 3 1 3 σ0: 3 3 1 3 =74* 不変 σ1: 3 1 3 3 =62* σ2: 1 3 3 3 =26* σ3: 3 3 3 1 =78 |
||
| 76: 3 3 2 1 σ0: 3 3 2 1 =75* 不変 σ1: 3 2 1 3 =65* σ2: 2 1 3 3 =35* σ3: 1 3 3 2 =25* |
77: 3 3 2 2 σ0: 3 3 2 2 =76* 不変 σ1: 3 2 2 3 =68* σ2: 2 2 3 3 =44* σ3: 2 3 3 2 =52 |
78: 3 3 2 3 σ0: 3 3 2 3 =77* 不変 σ1: 3 2 3 3 =71* σ2: 2 3 3 3 =53* σ3: 3 3 3 2 =79 |
||
| 79: 3 3 3 1 σ0: 3 3 3 1 =78* 不変 σ1: 3 3 1 3 =74* σ2: 3 1 3 3 =62* σ3: 1 3 3 3 =26* |
80: 3 3 3 2 σ0: 3 3 3 2 =79* 不変 σ1: 3 3 2 3 =77* σ2: 3 2 3 3 =71* σ3: 2 3 3 3 =53* |
81: 3 3 3 3 σ0: 3 3 3 3 =80* 不変 σ1: 3 3 3 3 =80 不変 σ2: 3 3 3 3 =80 不変 σ3: 3 3 3 3 =80 不変 No. 24 3 3 3 3 |
よって、φ(σm)=81、3、9、3 より、24通り (以上)
攻略法さんからのコメントです。(平成23年10月28日付け)
「p、q、・・・、r個が計p+q+・・・+r=S個」のSが素数の場合、場合の数は、
(1列に並べる場合の数)÷S、すなわち、{S!/(p!q!・・・r!)}/S 通り
となる。例えば、
(1) 赤球2個、青球1個を円形に並べる場合の数を求めよ。
(112の円順列の総数を求めよ。)
(解) {3!/(2!1!)}/3=1(通り) 実際に、「赤赤青」のみ (終)
(2) 赤球2個、青球3個を円形に並べる場合の数を求めよ。
(11222の円順列の総数を求めよ。)
(解) {5!/(2!3!)}/5=2(通り) 実際に、「赤赤青青青」と「赤青赤青青」 (終)
(3) 赤球1個、青球2個、緑球2個を円形に並べる場合の数を求めよ。
(12233の円順列の総数を求めよ。)
(解) {5!/(1!2!2!)}/5=6(通り)
実際に、「赤青青緑緑」、「赤青緑青緑」、「赤青緑緑青」、「赤緑青青緑」、
「赤緑青緑青」、「赤緑緑青青」 (終)
(4) 赤球3個、青球2個、緑球2個を円形に並べる場合の数を求めよ。
(1112233の円順列の総数を求めよ。)
(解) {7!/(3!2!2!)}/7=30(通り)
実際に、
「赤赤赤青青緑緑」、「赤赤赤青緑青緑」、「赤赤赤青緑緑青」、「赤赤赤緑青青緑」、
「赤赤赤緑青緑青」、「赤赤赤緑緑青青」、「赤赤青赤青緑緑」、「赤赤青赤緑青緑」、
「赤赤青赤緑緑青」、「赤赤青青赤緑緑」、「赤赤青青緑赤緑」、「赤赤青緑赤青緑」、
「赤赤青緑赤緑青」、「赤赤青緑青赤緑」、「赤赤青緑緑赤青」、「赤赤緑赤青青緑」、
「赤赤緑赤青緑青」、「赤赤緑赤緑青青」、「赤赤緑青赤青緑」、「赤赤緑青赤緑青」、
「赤赤緑青青赤緑」、「赤赤緑青緑赤青」、「赤赤緑緑赤青青」、「赤赤緑緑青赤青」、
「赤青赤青赤緑緑」、「赤青赤青緑赤緑」、「赤青赤緑赤青緑」、「赤青赤緑赤緑青」、
「赤青赤緑青赤緑」、「赤青青赤緑赤緑」 (終)
gcd(p,q,・・・,r)=1 の場合、場合の数は、
(1列に並べる場合の数)÷S、すなわち、{S!/(p!q!・・・r!)}/S 通り
前出の(1)、(2)、(3)、(4)はこれにも該当する。
(5) 赤球4個、青球5個を円形に並べる場合の数を求めよ。
(111122222の円順列の総数を求めよ。)
(解) {9!/(4!5!)}/9=14(通り)
実際に、
「赤赤赤赤青青青青青」、「赤赤赤青赤青青青青」、「赤赤赤青青赤青青青」、
「赤赤赤青青青赤青青」、「赤赤赤青青青青赤青」、「赤赤青赤赤青青青青」、
「赤赤青赤青赤青青青」、「赤赤青赤青青赤青青」、「赤赤青赤青青青赤青」、
「赤赤青青赤赤青青青」、「赤赤青青赤青赤青青」、「赤赤青青赤青青赤青」、
「赤赤青青青赤青赤青」、「赤青赤青赤青赤青青」
(6) 赤球2個、青球3個、緑球3個を円形に並べる場合の数を求めよ。
(111122222の円順列の総数を求めよ。)
(解) {8!/(2!3!3!)}/8=70(通り)
実際に、
「赤赤青青青緑緑緑」、「赤赤青青緑青緑緑」、「赤赤青青緑緑青緑」、「赤赤青青緑緑緑青」、
「赤赤青緑青青緑緑」、「赤赤青緑青緑青緑」、「赤赤青緑青緑緑青」、「赤赤青緑緑青青緑」、
「赤赤青緑緑青緑青」、「赤赤青緑緑緑青青」、「赤赤緑青青青緑緑」、「赤赤緑青青緑青緑」、
「赤赤緑青青緑緑青」、「赤赤緑青緑青青緑」、「赤赤緑青緑青緑青」、「赤赤緑青緑緑青青」、
「赤赤緑緑青青青緑」、「赤赤緑緑青青緑青」、「赤赤緑緑青緑青青」、「赤赤緑緑緑青青青」、
「赤青赤青青緑緑緑」、「赤青赤青緑青緑緑」、「赤青赤青緑緑青緑」、「赤青赤青緑緑緑青」、
「赤青赤緑青青緑緑」、「赤青赤緑青緑青緑」、「赤青赤緑青緑緑青」、「赤青赤緑緑青青緑」、
「赤青赤緑緑青緑青」、「赤青赤緑緑緑青青」、「赤青青赤青緑緑緑」、「赤青青赤緑青緑緑」、
「赤青青赤緑緑青緑」、「赤青青赤緑緑緑青」、「赤青青青赤緑緑緑」、「赤青青青緑赤緑緑」、
「赤青青青緑緑赤緑」、「赤青青緑赤青緑緑」、「赤青青緑赤緑青緑」、「赤青青緑赤緑緑青」、
「赤青青緑青赤緑緑」、「赤青青緑青緑赤緑」、「赤青青緑緑赤青緑」、「赤青青緑緑赤緑青」、
「赤青青緑緑青赤緑」、「赤青緑赤青緑青緑」、「赤青緑赤青緑緑青」、「赤青緑赤緑青青緑」、
「赤青緑赤緑青緑青」、「赤青緑赤緑緑青青」、「赤青緑青赤青緑緑」、「赤青緑青赤緑青緑」、
「赤青緑青赤緑緑青」、「赤青緑青青赤緑緑」、「赤青緑青青緑赤緑」、「赤青緑青緑赤緑青」、
「赤青緑青緑青赤緑」、「赤青緑緑赤緑青青」、「赤青緑緑青赤緑青」、「赤青緑緑青青赤緑」、
「赤緑赤緑青青青緑」、「赤緑赤緑青青緑青」、「赤緑赤緑青緑青青」、「赤緑赤緑緑青青青」、
「赤緑青赤緑青青緑」、「赤緑青赤緑青緑青」、「赤緑青赤緑緑青青」、「赤緑青青赤緑青緑」、
「赤緑青青赤緑緑青」、「赤緑青青青赤緑緑」
攻略法さんからの続報です。(平成23年10月29日付け)
例1 赤球2個、青球2個を円形に並べる場合の数を求めよ。
数学的解法を試みると、
「周期がm」とは、「m個分を回転させると元の並びと同じになること」を言うとする。
周期が1の並びは、x│x│x│x だが、2種類を扱うので、0通り。
周期が2の並びは、赤青│赤青 の 2!/(1!1!)=2通り。
周期が1との重複を除くと、2-0=2通り
周期が4の並びは、赤赤青青 の 4!/(2!2!)=6通り。
周期が2との重複を除くと、6-2=4通り
よって、「周期」の部分は円順列なので、2/2 + 4/4 = 1 + 1 = 2 通り (終)
CF定理では、
周期が1、2、4の値より、 (6+2)/4=2通り (終)
「周期がm」は、「(4/m)等分する」なので、球の個数 gcd(2,2)=2 の約数、すなわち、1、2
より、4/1=4、4/2=2を考えればよい。
例1と同様にして、
例2 赤球4個、青球4個を円形に並べる場合の数を求めよ。
数学的解法を試みる。周期は、gcd(4,4)=4より、8/1=8、8/2=4、8/4=2を考える。
周期が2の並びは、赤青│赤青│赤青│赤青 の 2!/(1!1!)=2通り。
周期が4の並びは、赤赤青青│赤赤青青 の 4!/(2!2!)=6通り。
周期が2との重複を除くと、6-2=4通り
周期が8の並びは、赤赤赤赤青青青青 の 8!/(4!4!)=70通り。
周期が4との重複を除くと、70-6=64通り
よって、「周期」の部分は円順列なので、2/2 + 4/4 +64/8 = 1 + 1 + 8 = 10 通り (終)
CF定理では、
周期が1、2、4、8の値より、 (70+2*2+6)/8=10通り (終)
当HP読者のHN「プレリュード」さんから、同じものを含む円順列についての話題を頂いた。
(平成24年5月31日付け)
高校にて円順列について勉強している際、以下のような問題が出されました。
問 袋の中に白と黒の碁石が無数に入っている。その中から4つ石を取り出して円形
に並べると、その並べ方は何通りあるか。
答は、
| 白 白 白 白 白 黒 白 白 黒 白 黒 白 黒 黒 黒 黒 黒 黒 白 白 黒 白 黒 黒 |
の6通り。この問題では石が4つということで数え上げてもたいした手間はかかりませんでし
たが、5個になったらどうなるだろうと興味が出ました。その結果、8通りとなりました。では、
6個にしたら10通りになるのではないかと思い考えてみたところ、14通りになってしまいま
した(自信がありません)。公式化できるのかと思いネットで調べたところ、同じものを含む
円順列に該当するのではないかという結論に達し、さらにこちらのサイトにたどり着きました。
ちなみに、私が見つけた公式は、
(Σk=1〜n 2(n,k))/n (ただし、(n,k)は最大公約数)
という式で、計算してみたところ、石4個の場合や石5個の場合で成り立つようなので、これ
で分かったと一度は納得しました。
はじめ、この問題を自宅で考えているとき碁石の代わりにオセロを用いていたのですが、
その際に面白いことに気付きました。オセロですと裏が違う色になっているので、ひっくり返
すと同じ順列になる組み合わせがあります。これは数珠順列の問題になるのではないかと
思い、その個数を求める公式を調べてみましたが、バーンサイドの定理などを用いて導いた
n個のときの円順列の個数に関する公式
(Σk|d φ(k) (n/k)!/(n1/k)!(n2/k)!)/n
というのにたどり着きました。この式の意味もあまり理解できなかったのですが、これに碁石
の問題を適用して計算を試みたところ、白3個、黒2個などの時の組み合わせが計算できる
のかなと思いました。
ここからが質問です。
最初の例題のように、石n個と決まっていた場合の全ての組み合わせの個数を一気に求
める公式はありますでしょうか?白4黒0、白3黒1、白2黒2、白1黒3、黒4白0の場合を
それぞれ計算するのは骨が折れるように思えます。
数え上げてみたところ、石4個では4通り、石5個ではやはり4通りとなり、計6個では9通
りができました。特に、計6個の時は、
| 黒 黒 白 黒 黒 白 黒 白 白 黒 白 白 |
という組み合わせがあって、これは回転や対角線で折り返しても重ならない関係にあって、
丁度ひっくり返した形になっています。このような組み合わせを数学的に区別できるのでしょ
うか?
空舟さんからのコメントです。(平成24年5月31日付け)
「らいおんの家」というwebサイトに群論入門のpdfファイルが公開されており、「群論入門そ
の3」のバーンサイドの定理の所に、腕輪問題と言って、今回と似た問題が扱われています。
参考にされてはと思います。(説明が面白くておすすめです)
プレリュードさんからのコメントです。(平成24年6月1日付け)
空舟さん、ご紹介いただきありがとうございました。私の疑問は群論という分野であること
は理解できました。
腕輪問題が非常に気になります。こちらを詳細に見る事によって疑問が解ける気がしまし
た。紹介いただいたサイトのpdfファイルでは裏返しを考慮しない例となっていました。また、
回転だけを考えているようですが、石5個ではいいかもしれませんが、石6個の時は成り立
たないように思えます。単純に、(26+2+2+2+2+2)/6 では自然数になりません。他の置換群
を考える必要がありそうなのですが、それをn角形に一般化するのは容易ではないでしょう
か?
S(H)さんからのコメントです。(平成24年6月1日付け)
「円順列の数え上げ」(当頁)に、バーンサイドの定理の応用と在り、「群論入門3」等も在
り。私は、D--f-->R なるRD の全体に、Dに作用する群とRに作用する群で、RD を類別する
等、長期に亘り、随分悩んだことを想起しました。「Advanced Combinatorics」の249p に
Burnside-Frobenius の定理とあり、美し過ぎる定理で人を沈黙させる力が在ります。この目
次を視て、250p 以降に記されている事柄を忖度願います。
空舟さんからのコメントです。(平成24年6月1日付け)
この「私的数学塾」にも既にこの話題があるのに気づかず、他のウェブページを紹介して
しまって失礼しました。
頂点が6個の場合に詳細に見てみましたので参考にして下さい。同一視したい頂点の置
換の仕方の集合をGとします。
<回転だけ考慮する場合はGは次の6つの置換の集合です>
(123456)→(123456)、(123456)→(234561)、(123456)→(345612)、(123456)→(456123)
(123456)→(561234)、(123456)→(612345)
<裏返しも考慮する場合は次の6個の置換が加わります>
(123456)→(165432)、(123456)→(216543)、(123456)→(321654)、(123456)→(432165)
(123456)→(543216)、(123456)→(654321)
Gの各元をγとして、γによって不変な塗り方の個数をφ(γ)とすると、Σφ(γ)/
|G| で
色の塗り方の個数が求まる、というのがバーンサイドの定理です。
そこで、γによって不変な色の塗り方の個数φ(γ)を知る必要があります。
・γ=(123456)→(123456)の時は、任意の塗り方がγによって不変です。φ(γ)=26
・γ=(123456)→(234561)の時は、全部黒or全部白だけがγで不変です。φ(γ)=2
・γ=(123456)→(345612)によって不変な塗り方は次の4通りです:
白白白白白白、黒黒黒黒黒黒、黒白黒白黒白、白黒白黒白黒白
....
・一般に、γによって不変な色の塗り方は、2(部分巡回の個数) であることが理解されます。
例えば、頂点1、4を軸とする裏返し:(123456)→(165432)では、(1)(4)(26)(35)の4つの部分
巡回からなっていますので、この置換によって不変な色の塗り方は、24=16通りとなります。
(4つの部分巡回する頂点集合に、それぞれ2通りの色を与え得るから。)
・全部のγとφ(γ)を一覧にすると、以下の通りです。
(123456)→(123456):26 、(123456)→(234561):2 、(123456)→(345612):22
(123456)→(456123):23 、(123456)→(561234):22 、(123456)→(612345):2
(123456)→(165432):24 、(123456)→(216543):23 、(123456)→(321654):24
(123456)→(432165):23 、(123456)→(543216):24 、(123456)→(654321):23
(頂点をつなぐ軸での裏返しでは、24、辺の中点をつなぐ軸での裏返しは23となっています。
ちなみに、頂点の数が奇数の時にはこの場合分けは必要なくなります。)
よって、回転だけを考慮した場合の塗り方の個数は、
(26+2+22+23+22+2)/6=14通り
裏返しも考慮した場合は、
(26+2+22+23+22+2+24+23+24+23+24+23)/12=13通り
という風に計算されます。
回転だけを考慮する場合は、まさにプレリュードさんの式そのものです。裏返しも考慮する
場合は上記のようにちょっと項が増えることになります。
プレリュードさんからのコメントです。(平成24年6月1日付け)
S(H)さん、ご紹介ありがとうございました。サイトやファイルを読ませていただきました。残
念ながら、高校生の身では、Amazonの専門書を買う余力もなく、また英語で数学を理解す
るというのもハードルが高いです。迷惑ではございませんので、何かアドバイスをいただけ
れば嬉しいです。
空舟さん、詳細なご説明ありがとうございました。私は、「私的数学塾」が検索でヒットして、
こちらのサイトにたどりつきました。
6個の並び替えは私もオセロを使って試行錯誤しまして、14通りというのを見つけました。
26=64通り並べ方があり、その中で回転と裏返しで同じものを場合分けした結果やっとた
どり着いた結論です。その過程が空船様に説明していただいた操作に該当するものと理解
できました。
裏返しを入れる場合は、重複数珠順列の個数の公式
r が偶数のとき、 1/(2r)(Σk=1〜r {n(r,k)+(r/2)nr/2+1+(r/2)nr/2)
で13通りと計算できました。
そして、先日の質問では大きな勘違いをしていることに気づきました。オセロをひっくり返し
たら重なるから数珠順列になるかと思ったら、全く違いますね。こんな事を考えた人がいな
いのか、こういったケースは検索しても一向に出てきませんでした。
オセロの場合は、全部黒と全部白などが同じものとみなされるので、頂点が6個の時の円
順列の14通りの半分の7通りとなるのかと始め思ったのですが、
1白白白白白白(2黒黒黒黒黒黒) 、3黒白白白白白(4白黒黒黒黒黒)
5黒黒白白白白(6白白黒黒黒黒) 、7黒白黒白白白(8白黒白黒黒黒)
9黒白白黒白白(10白黒黒白黒黒) 、11黒黒黒白白白(白白白黒黒黒)回転で重なる
12黒白黒白黒白(白黒白黒白黒)回転で重なる 、13黒黒白白黒白 、14白白黒黒白黒
の9通りとなりました。このうち、11と12はひっくり返すのではなく、回転でも同じものになるの
で、14通りの中でも、もとから裏返しが同じものとみなされています。私が面白いと思ったの
は13と14で、この二つは黒と白が入れ替わっているだけなのに裏返しても重ならず違う組み
合わせとして数えられています。
石が7個の場合、重複数珠順列の数は公式で求める事ができそうだとわかりましたが、オ
セロのひっくり返して上の13、14のような関係が現れるかをやってみようと思ったのですが
27=128通りもあるので躊躇しています。やはり、n個の時には何通りというのを一つの式で
表すのは無理でしょうか?
空舟さんからのコメントです。(平成24年6月2日付け)
どうやら前回「裏返し」の意味を、私が勝手に誤解していたようでした。私の説明の「裏返
し」は、「ひっくり返し」ではなく「鏡的反転」のつもりでした。改めて、以下「ひっくり返し」を含
めて考察します。
・まず、n=6で「ひっくり返し」を入れた場合、ご指摘のうち
13黒黒白白黒白 と 14白白黒黒白黒
は同一視されるので、9通りではなく8通りということになります。
偶数 n=6 でひっくり返しをバーンサイドの定理で計算するには、ひっくり返し置換で不変に
なる並びを数えれば良いと思います。
γ=(123456)→裏(******) という置換で不変である並べ方は、部分巡回の長さが全部偶
数のときに限り可能で、2(部分巡回) 通りです。(やはり各部分巡回に2通りずつの色を与えうるから)
・(123456)→裏(123456):不可能 ・(123456)→裏(234561):φ(γ)=2
・(123456)→裏(345612):不可能 ・(123456)→裏(456123):φ(γ)=23
・(123456)→裏(561234):不可能 ・(123456)→裏(612345):φ(γ)=2
<一般に回転の長さkとnの最大公約数(n,k)が、n/(偶数)の時のみ可能です>
・(123456)→裏(165432):不可能 ・(123456)→裏(216543):φ(γ)=23
・(123456)→裏(321654):不可能 ・(123456)→裏(432165):φ(γ)=23
・(123456)→裏(543216):不可能 ・(123456)→裏(654321):φ(γ)=23
<一般に辺の中点をつなぐ軸での鏡的反転の時のみ可能です>
以前のφ(γ)に新たにこれらを項に加えることによって、
{(26+2+22+23+22+2)+(24+23+24+23+24+23)+(0+2+0+23+0+2)+(0+23+0+23+0+23)}/24=8
を得ます。
・n=7個の場合では、よく考えれば、黒石と白石の個数が違うので、「ひっくり返したものが回
転で重なったり鏡的反転で重なったりする」のは不可能です。
従って、7個のような奇数個の場合では、「14通りの半分の7通りとなるのかと始め思ったの
ですが...」というような推論が正しく成り立ちます。
一般のnについて、同様の考察をすれば以下のようになります。
回転置換での(Σφ(γ))/n: A=Σk=1〜n 2(n,k)/n
鏡的反転置換の(Σφ(γ))/n: B={2n/2+1+2n/2}/2 (nが偶数の時)
B=2n/2+1/2 (nが奇数の時)
回転+ひっくり返しの(Σφ(γ))/n: C=Σk=1〜n 2(n,k) /n
[ただし、n/(n,k)が偶数の時のみの和をとる。nが奇数なら0]
鏡的反転+ひっくり返しの(Σφ(γ))/n: D={2n/2}/2 (nが偶数の時)
D=0 (nが奇数の時)
・回転のみを同一視する並びは、W=A
・回転・鏡的反転を同一視する並びは、X=(A+B)/2
・回転・ひっくり返しを同一視する並びは、Y=(A+C)/2
・回転・鏡的反転・ひっくり返しを同一視する並びは、Z=(A+B+C+D)/2
という風になります。
n=6では、(A,B,C,D)=(14,12,2,4)、(W,X,Y,Z)=(14,13,8,8)
n=7では、(A,B,C,D)=(20,16,0,0)、(W,X,Y,Z)=(20,18,10,9)
n=8では、(A,B,C,D)=(36,24,4,8)、(W,X,Y,Z)=(36,30,20,18)
・・・・・・・・・
南海さんからのコメントです。(平成24年6月2日付け)
この問題は、GRAPES の友田先生 の古い論文が一番まとまっていてわかりよいと思いま
す。
攻略法さんからのコメントです。(平成24年6月3日付け)
参考サイトの紹介です。
2色の円順列 → A000031 2色のじゅず順列 → A000029
2色のオセロ円順列 → A000013 2色のオセロじゅず順列 → A000011
枚挙すると、並びは、時計の文字盤のように、12時の位置から時計まわりに順に並べた
ものを、2進法N桁(0:白、1:黒)とみなし、それを10進法て表記しました。実際の並びを得る
には、2進法N桁に変換してください。
例 4: 5 ( 10 17 20 34 40 ) なら、
○○○●○● ( ○○●○●○、○●○○○●、○●○●○○、●○○○●○、●○●○○○ )
として、
| ○ ○ ○ ○ ● ● ● ○ ○ ○ ● ● ○ ● ○ ○ ○ ○ ○ ○ ● ● ○ ○ ○ ○ ● ○ ○ ● ● ○ ○ ● ○ ○ |
となる。括弧内は同一視するものである。
N=6 の場合
|
円順列 1: 0 () 2: 1 ( 2 4 8 16 32 ) 3: 3 ( 6 12 24 33 48 ) 4: 5 ( 10 17 20 34 40 ) 5: 7 ( 14 28 35 49 56 ) 6: 9 ( 18 36 ) 7: 11 ( 22 25 37 44 50 ) 8: 13 ( 19 26 38 41 52 ) 9: 15 ( 30 39 51 57 60 ) 10: 21 ( 42 ) 11 : 23 ( 29 43 46 53 58 ) 12 : 27 ( 45 54 ) 13 : 31 ( 47 55 59 61 62 ) 14 : 63 () 以上 14 通り |
じゅず順列 1: 0 () 2: 1 ( 2 4 8 16 32 ) 3: 3 ( 6 12 24 33 48 ) 4: 5 ( 10 17 20 34 40 ) 5: 7 ( 14 28 35 49 56 ) 6: 9 ( 18 36 ) 7: 11 ( 13 19 22 25 26 37 38 41 44 50 52 ) 8: 15 ( 30 39 51 57 60 ) 9: 21 ( 42 ) 10: 23 ( 29 43 46 53 58 ) 11: 27 ( 45 54 ) 12: 31 ( 47 55 59 61 62 ) 13: 63 () 以上 13 通り |
オセロ円順列 1: 0 ( 63 ) 2: 1 ( 2 4 8 16 31 32 47 55 59 61 62 ) 3: 3 ( 6 12 15 24 30 33 39 48 51 57 60 ) 4: 5 ( 10 17 20 23 29 34 40 43 46 53 58 ) 5: 7 ( 14 28 35 49 56 ) 6: 9 ( 18 27 36 45 54 ) 7: 11 ( 13 19 22 25 26 37 38 41 44 50 52 ) 8: 21 ( 42 ) 以上 8 通り |
||
|
オセロじゅず順列 1: 0 ( 63 ) 2: 1 ( 2 4 8 16 31 32 47 55 59 61 62 ) 3: 3 ( 6 12 15 24 30 33 39 48 51 57 60 ) 4: 5 ( 10 17 20 23 29 34 40 43 46 53 58 ) 5: 7 ( 14 28 35 49 56 ) 6: 9 ( 18 27 36 45 54 ) 7: 11 ( 13 19 22 25 26 37 38 41 44 50 52 ) 8: 21 ( 42 ) 以上 8 通り |
||||
N=7 の場合
|
円順列 1: 0 () 2: 1 ( 2 4 8 16 32 64 ) 3: 3 ( 6 12 24 48 65 96 ) 4: 5 ( 10 20 33 40 66 80 ) 5: 7 ( 14 28 56 67 97 112 ) 6: 9 ( 17 18 34 36 68 72 ) 7: 11 ( 22 44 49 69 88 98 ) 8: 13 ( 26 35 52 70 81 104 ) 9: 15 ( 30 60 71 99 113 120 ) 10: 19 ( 25 38 50 73 76 100 ) 11: 21 ( 37 41 42 74 82 84 ) 12: 23 ( 46 57 75 92 101 114 ) 13: 27 ( 51 54 77 89 102 108 ) 14: 29 ( 39 58 78 83 105 116 ) 15: 31 ( 62 79 103 115 121 124 ) 16: 43 ( 45 53 85 86 90 106 ) 17: 47 ( 61 87 94 107 117 122 ) 18: 55 ( 59 91 93 109 110 118 ) 19: 63 ( 95 111 119 123 125 126 ) 20: 127 () 以上 20 通り |
じゅず順列 1: 0 () 2: 1 ( 2 4 8 16 32 64 ) 3: 3 ( 6 12 24 48 65 96 ) 4: 5 ( 10 20 33 40 66 80 ) 5: 7 ( 14 28 56 67 97 112 ) 6: 9 ( 17 18 34 36 68 72 ) 7: 11 ( 13 22 26 35 44 49 52 69 70 81 88 98 104 ) 8: 15 ( 30 60 71 99 113 120 ) 9: 19 ( 25 38 50 73 76 100 ) 10: 21 ( 37 41 42 74 82 84 ) 11: 23 ( 29 39 46 57 58 75 78 83 92 101 105 114 116 ) 12: 27 ( 51 54 77 89 102 108 ) 13: 31 ( 62 79 103 115 121 124 ) 14: 43 ( 45 53 85 86 90 106 ) 15: 47 ( 61 87 94 107 117 122 ) 16: 55 ( 59 91 93 109 110 118 ) 17: 63 ( 95 111 119 123 125 126 ) 18: 127 () 以上 18 通り |
オセロ円順列 1: 0 ( 127 ) 2: 1 ( 2 4 8 16 32 63 64 95 111 119 123 125 126 ) 3: 3 ( 6 12 24 31 48 62 65 79 96 103 115 121 124 ) 4: 5 ( 10 20 33 40 47 61 66 80 87 94 107 117 122 ) 5: 7 ( 14 15 28 30 56 60 67 71 97 99 112 113 120 ) 6: 9 ( 17 18 34 36 55 59 68 72 91 93 109 110 118 ) 7: 11 ( 22 29 39 44 49 58 69 78 83 88 98 105 116 ) 8: 13 ( 23 26 35 46 52 57 70 75 81 92 101 104 114 ) 9: 19 ( 25 27 38 50 51 54 73 76 77 89 100 102 108 ) 10: 21 ( 37 41 42 43 45 53 74 82 84 85 86 90 106 ) 以上 10 通り |
||
|
オセロじゅず順列 1: 0 ( 127 ) 2: 1 ( 2 4 8 16 32 63 64 95 111 119 123 125 126 ) 3: 3 ( 6 12 24 31 48 62 65 79 96 103 115 121 124 ) 4: 5 ( 10 20 33 40 47 61 66 80 87 94 107 117 122 ) 5: 7 ( 14 15 28 30 56 60 67 71 97 99 112 113 120 ) 6: 9 ( 17 18 34 36 55 59 68 72 91 93 109 110 118 ) 7: 11 ( 13 22 23 26 29 35 39 44 46 49 52 57 58 69 70 75 78 81 83 88 92 98 101 104 105 114 116 ) 8: 19 ( 25 27 38 50 51 54 73 76 77 89 100 102 108 ) 9: 21 ( 37 41 42 43 45 53 74 82 84 85 86 90 106 ) 以上 9 通り |
||||
N=8 の場合
|
円順列 1: 0 () 2: 1 ( 2 4 8 16 32 64 128 ) 3: 3 ( 6 12 24 48 96 129 192 ) 4: 5 ( 10 20 40 65 80 130 160 ) 5: 7 ( 14 28 56 112 131 193 224 ) 6: 9 ( 18 33 36 66 72 132 144 ) 7: 11 ( 22 44 88 97 133 176 194 ) 8: 13 ( 26 52 67 104 134 161 208 ) 9: 15 ( 30 60 120 135 195 225 240 ) 10: 17 ( 34 68 136 ) 11: 19 ( 38 49 76 98 137 152 196 ) 12: 21 ( 42 69 81 84 138 162 168 ) 13: 23 ( 46 92 113 139 184 197 226 ) 14: 25 ( 35 50 70 100 140 145 200 ) 15: 27 ( 54 99 108 141 177 198 216 ) 16: 29 ( 58 71 116 142 163 209 232 ) 17: 31 ( 62 124 143 199 227 241 248 ) 18: 37 ( 41 73 74 82 146 148 164 ) 19: 39 ( 57 78 114 147 156 201 228 ) 20: 43 ( 86 89 101 149 172 178 202 ) 21: 45 ( 75 90 105 150 165 180 210 ) 22: 47 ( 94 121 151 188 203 229 242 ) 23: 51 ( 102 153 204 ) 24: 53 ( 77 83 106 154 166 169 212 ) 25: 55 ( 110 115 155 185 205 220 230 ) 26: 59 ( 103 118 157 179 206 217 236 ) 27: 61 ( 79 122 158 167 211 233 244 ) 28: 63 ( 126 159 207 231 243 249 252 ) 29: 85 ( 170 ) 30: 87 ( 93 117 171 174 186 213 234 ) 31: 91 ( 107 109 173 181 182 214 218 ) 32: 95 ( 125 175 190 215 235 245 250 ) 33: 111 ( 123 183 189 219 222 237 246 ) 34: 119 ( 187 221 238 ) 35: 127 ( 191 223 239 247 251 253 254 ) 36: 255 () 以上 36 通り |
じゅず順列 1: 0 () 2: 1 ( 2 4 8 16 32 64 128 ) 3: 3 ( 6 12 24 48 96 129 192 ) 4: 5 ( 10 20 40 65 80 130 160 ) 5: 7 ( 14 28 56 112 131 193 224 ) 6: 9 ( 18 33 36 66 72 132 144 ) 7: 11 ( 13 22 26 44 52 67 88 97 104 133 134 161 176 194 208 ) 8: 15 ( 30 60 120 135 195 225 240 ) 9: 17 ( 34 68 136 ) 10: 19 ( 25 35 38 49 50 70 76 98 100 137 140 145 152 196 200 ) 11: 21 ( 42 69 81 84 138 162 168 ) 12: 23 ( 29 46 58 71 92 113 116 139 142 163 184 197 209 226 232 ) 13: 27 ( 54 99 108 141 177 198 216 ) 14: 31 ( 62 124 143 199 227 241 248 ) 15: 37 ( 41 73 74 82 146 148 164 ) 16: 39 ( 57 78 114 147 156 201 228 ) 17: 43 ( 53 77 83 86 89 101 106 149 154 166 169 172 178 202 212 ) 18: 45 ( 75 90 105 150 165 180 210 ) 19: 47 ( 61 79 94 121 122 151 158 167 188 203 211 229 233 242 244 ) 20: 51 ( 102 153 204 ) 21: 55 ( 59 103 110 115 118 155 157 179 185 205 206 217 220 230 236 ) 22: 63 ( 126 159 207 231 243 249 252 ) 23: 85 ( 170 ) 24: 87 ( 93 117 171 174 186 213 234 ) 25: 91 ( 107 109 173 181 182 214 218 ) 26: 95 ( 125 175 190 215 235 245 250 ) 27: 111 ( 123 183 189 219 222 237 246 ) 28: 119 ( 187 221 238 ) 29: 127 ( 191 223 239 247 251 253 254 ) 30: 255 () 以上 30 通り |
オセロ円順列 1: 0 ( 255 ) 2: 1 ( 2 4 8 16 32 64 127 128 191 223 239 247 251 253 254 ) 3: 3 ( 6 12 24 48 63 96 126 129 159 192 207 231 243 249 252 ) 4: 5 ( 10 20 40 65 80 95 125 130 160 175 190 215 235 245 250 ) 5: 7 ( 14 28 31 56 62 112 124 131 143 193 199 224 227 241 248 ) 6: 9 ( 18 33 36 66 72 111 123 132 144 183 189 219 222 237 246 ) 7: 11 ( 22 44 61 79 88 97 122 133 158 167 176 194 211 233 244 ) 8: 13 ( 26 47 52 67 94 104 121 134 151 161 188 203 208 229 242 ) 9: 15 ( 30 60 120 135 195 225 240 ) 10: 17 ( 34 68 119 136 187 221 238 ) 11: 19 ( 38 49 59 76 98 103 118 137 152 157 179 196 206 217 236 ) 12: 21 ( 42 69 81 84 87 93 117 138 162 168 171 174 186 213 234 ) 13: 23 ( 29 46 58 71 92 113 116 139 142 163 184 197 209 226 232 ) 14: 25 ( 35 50 55 70 100 110 115 140 145 155 185 200 205 220 230 ) 15: 27 ( 39 54 57 78 99 108 114 141 147 156 177 198 201 216 228 ) 16: 37 ( 41 73 74 82 91 107 109 146 148 164 173 181 182 214 218 ) 17: 43 ( 53 77 83 86 89 101 106 149 154 166 169 172 178 202 212 ) 18: 45 ( 75 90 105 150 165 180 210 ) 19: 51 ( 102 153 204 ) 20: 85 ( 170 ) 以上 20 通り |
||
|
オセロじゅず順列 1: 0 ( 255 ) 2: 1 ( 2 4 8 16 32 64 127 128 191 223 239 247 251 253 254 ) 3: 3 ( 6 12 24 48 63 96 126 129 159 192 207 231 243 249 252 ) 4: 5 ( 10 20 40 65 80 95 125 130 160 175 190 215 235 245 250 ) 5: 7 ( 14 28 31 56 62 112 124 131 143 193 199 224 227 241 248 ) 6: 9 ( 18 33 36 66 72 111 123 132 144 183 189 219 222 237 246 ) 7: 11 ( 13 22 26 44 47 52 61 67 79 88 94 97 104 121 122 133 134 151 158 161 167 176 188 194 203 208 211 229 233 242 244 ) 8: 15 ( 30 60 120 135 195 225 240 ) 9: 17 ( 34 68 119 136 187 221 238 ) 10: 19 ( 25 35 38 49 50 55 59 70 76 98 100 103 110 115 118 137 140 145 152 155 157 179 185 196 200 205 206 217 220 230 236 ) 11: 21 ( 42 69 81 84 87 93 117 138 162 168 171 174 186 213 234 ) 12: 23 ( 29 46 58 71 92 113 116 139 142 163 184 197 209 226 232 ) 13: 27 ( 39 54 57 78 99 108 114 141 147 156 177 198 201 216 228 ) 14: 37 ( 41 73 74 82 91 107 109 146 148 164 173 181 182 214 218 ) 15: 43 ( 53 77 83 86 89 101 106 149 154 166 169 172 178 202 212 ) 16: 45 ( 75 90 105 150 165 180 210 ) 17: 51 ( 102 153 204 ) 18: 85 ( 170 ) 以上 18 通り |
||||
プレリュードさんからのコメントです。(平成24年6月3日付け)
ほとんど空舟様のご説明で考え方を含めて理解できました。どうもありがとうございました。
n個のときの一般式まで教えていただきありがとうございました。本当に分かりやすくて、今
まで悩んでたのはなんだったんだろうかという位、明るく前が開けました。実は昨日7個の場
合などを必死に数えていたのですが、途中で挫折しておりました。
ただ、 まずn=6で「ひっくり返し」を入れた場合、ご指摘のうち、
13黒黒白白黒白 と 14白白黒黒白黒
は同一視されるので9通りではなく8通り、ということになります。
がどうも納得できていなくて、「13黒黒白白黒白」をひっくり返しても「14白白黒黒白黒」とは同
じにならないのではないかということです。
このように一列で書いてしまうとひっくり返しで同じになりますが、実物は一致しないのです。
ちょうど鏡で映したようになっています。ちなみに13をひっくり返すと、
| 黒 白 白 白 黒 → 白 黒 となり、黒 白 とはなりません。 黒 白 黒 白 白 黒 白 黒 黒 |
右回り、左回りの違いですが、これが数珠になっているとすると、別の物と考えるべきでは
ないでしょうか?
南海さん、友田先生の論文をご紹介いただきありがとうございました。こちらのPDFファイル
は検索にて探し当てておりました。メビウス関数、オイラー関数など難解な用語があり、解読
に苦労しましたが、結局のところ私の悩んでいた組み合わせの個数を導くのには最後の公
式が役立ちそうなことまでは理解できました。
ただ、この公式ですと、例えばn=6の時、黒4白2の場合といった個別の個数が計算できる
ものの、その他の黒白の組み合わせ全て考えて計算しなければいけないので、nが大きくな
ったらしんどいのかなあと思いました。
攻略法さん、参考サイトを教えていただきありがとうございました。英語は少し不慣れだった
のですが、参考になる文献が書かれているのがわかりました。ただ、その文献を手に入れる
術が無くて・・・。
2色のオセロじゅず順列という用語があるのですね。正に私が悩んでいる問題そのものな
ので、私のような高校生が考えるようなことは、どこかで誰かが思いついているんでちょっと
残念な気もしました(思い上がりはよくないですね)。
空舟様へのレスにも書かせていただきましたが、じゅず順列であれば鏡に映して重ならな
い組み合わせを考慮しなければいけないと思うのですが、オセロじゅず順列ではそれは同じ
ものとみなされるのが普通でしょうか?
空舟さんからのコメントです。(平成24年6月4日付け)
私は「ひっくり返し」の意味を、「オセロの位置を固定したまま全部のオセロをめくる」という
意味でとらえておりました。「下から見る」ということでしたら、「ひっくり返し」+「鏡的反転」と
いうことになります。ということは、「回転」「下から見る」だけを同一視する場合は、以前の投
稿の記号を使うと、(A+D)/2 で計算できて、実際、n=6のときに、9 を与えます。
攻略法さんからのコメントです。(平成24年6月4日付け)
「2色のオセロじゅず順列」という用語は、私の造語です。正式な呼称は知りません。また、
じゅず順列であれば鏡に映して重ならない組み合わせを考慮しなければいけないと思うの
ですが、オセロじゅず順列ではそれは同じものとみなされるのが普通でしょうか?
については、「ひっくり返す」などの用語の定義(意味)によると思います。
(→ 参考サイト:「A053656」)
|
N=6 の場合 1: 0 ( 63 ) 2: 1 ( 2 4 8 16 31 32 47 55 59 61 62 ) 3: 3 ( 6 12 15 24 30 33 39 48 51 57 60 ) 4: 5 ( 10 17 20 23 29 34 40 43 46 53 58 ) 5: 7 ( 14 28 35 49 56 ) 6: 9 ( 18 27 36 45 54 ) 7: 11 ( 22 25 37 44 50 ) 8: 13 ( 19 26 38 41 52 ) 9: 21 ( 42 ) 以上 9 通り |
N=7 の場合 1: 0 ( 127 ) 2: 1 ( 2 4 8 16 32 63 64 95 111 119 123 125 126 ) 3: 3 ( 6 12 24 31 48 62 65 79 96 103 115 121 124 ) 4: 5 ( 10 20 33 40 47 61 66 80 87 94 107 117 122 ) 5: 7 ( 14 15 28 30 56 60 67 71 97 99 112 113 120 ) 6: 9 ( 17 18 34 36 55 59 68 72 91 93 109 110 118 ) 7: 11 ( 22 23 44 46 49 57 69 75 88 92 98 101 114 ) 8: 13 ( 26 29 35 39 52 58 70 78 81 83 104 105 116 ) 9: 19 ( 25 27 38 50 51 54 73 76 77 89 100 102 108 ) 10: 21 ( 37 41 42 43 45 53 74 82 84 85 86 90 106 ) 以上 10 通り |
|
|
N=8 の場合 1: 0 ( 255 ) 2: 1 ( 2 4 8 16 32 64 127 128 191 223 239 247 251 253 254 ) 3: 3 ( 6 12 24 48 63 96 126 129 159 192 207 231 243 249 252 ) 4: 5 ( 10 20 40 65 80 95 125 130 160 175 190 215 235 245 250 ) 5: 7 ( 14 28 31 56 62 112 124 131 143 193 199 224 227 241 248 ) 6: 9 ( 18 33 36 66 72 111 123 132 144 183 189 219 222 237 246 ) 7: 11 ( 22 44 47 88 94 97 121 133 151 176 188 194 203 229 242 ) 8: 13 ( 26 52 61 67 79 104 122 134 158 161 167 208 211 233 244 ) 9: 15 ( 30 60 120 135 195 225 240 ) 10: 17 ( 34 68 119 136 187 221 238 ) 11: 19 ( 38 49 55 76 98 110 115 137 152 155 185 196 205 220 230 ) 12: 21 ( 42 69 81 84 87 93 117 138 162 168 171 174 186 213 234 ) 13: 23 ( 46 92 113 139 184 197 226 ) 14: 25 ( 35 50 59 70 100 103 118 140 145 157 179 200 206 217 236 ) 15: 27 ( 39 54 57 78 99 108 114 141 147 156 177 198 201 216 228 ) 16: 29 ( 58 71 116 142 163 209 232 ) 17: 37 ( 41 73 74 82 91 107 109 146 148 164 173 181 182 214 218 ) 18: 43 ( 86 89 101 149 172 178 202 ) 19: 45 ( 75 90 105 150 165 180 210 ) 20: 51 ( 102 153 204 ) 21: 53 ( 77 83 106 154 166 169 212 ) 22: 85 ( 170 ) 以上 22 通り |
||
プレリュードさんからのコメントです。(平成24年6月5日付け)
空舟さん、私の説明不足で申し訳ありませんでした。正に、この計算式 (A+D)/2
で私の
求めているものが分かりました。昨日から、n=7 の時の並びを必死にやってみたところ、計
算とぴったり合いました!流石に、n=8 を自力でやる気はもう起きないのでこれで納得です。
ちなみに「下から見る」ときだけ一致する数は簡単には出ないですよね?教えていただい
た{(A+B+C+D)/4}-{(A+D)/2}で求められることはわかりました。
空舟様、攻略法様、多数の方々からあたたかいアドバイスをいただき本当に感謝していま
す。私のような小娘に対しても丁寧に教えていただきましたこと、なんとお礼を言っていいか
言葉もありません。オセロを使って並べ替えたり、難しい式を解いたりするのは本当に楽しか
ったです。将来数学の道に進むかはちょっとわかりませんが、理系には行きたいと思ってい
るので、またなにかありましたらその時はまたよろしくお願いします!
以下、工事中