正三角形の個数 
目で見えるものを数えることは、少しの忍耐を許容すれば易しい。目で見えないものを数
えるには、目で見える場合から規則性を発見して、その性質を利用して数える場合が多い。
このページでは、いくつかの例を通して、そのような場合の対処の仕方を整理しておこうと
思う。
例 下図のように、1辺 n の正方形の縦、横が n 等分され、平行線が引かれている。
この図の中に正方形は大小合わせていくつあるか?

n=4 の場合について、その数え方の実際を見てみよう。
面積 12 のもの ・・・・・ 16個 これは、 42 個と考えてもよい。
面積 22 のもの ・・・・・ 9個 これは、 32 個と考えてもよい。
面積 32 のもの ・・・・・ 4個 これは、 22 個と考えてもよい。
面積 42 のもの ・・・・・ 1個 これは、 12 個と考えてもよい。
よって、求める正方形の個数は、 16+9+4+1=30 (個)
このことから、一般の n について、求める正方形の個数は、
n2 + (n-1)2 + (n-2)2 + ・・・ + 22 + 12 = n(n+1)(2n+1)/6 (個)
であると言える。
例 下図のように、1辺 n の正三角形の各辺が n 等分され、平行線が引かれている。
この図の中に正三角形は大小合わせていくつあるか?
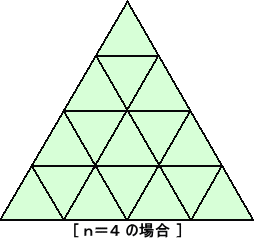
n=4 の場合について、その数え方の実際を見てみよう。
ここで、1辺 1 の正三角形の面積を、S とおく。
面積 S のもの ・・・・・ 16個
面積 4S のもの ・・・・・ 7個
面積 9S のもの ・・・・・ 3個
面積 16S のもの ・・・・・ 1個
よって、求める正三角形の個数は、 16+7+3+1=27 (個)
この例の場合、正方形の場合と違って、その一般化は少し難しそうであるが、元の正三角
形と同じ向きのものと逆向きのものに区分けして考えると、何かしらの規則性が見えてくる。
面積 S のもの ・・・・・ 16個( → 10+6 = (1+2+3+4)+6 )
面積 4S のもの ・・・・・ 7個( → 6+1 = (1+2+3)+1 )
面積 9S のもの ・・・・・ 3個( → 3+0 = (1+2)+0 )
面積 16S のもの ・・・・・ 1個( → 1+0 = (1)+0 )
元の正三角形と同じ向きの正三角形の個数には明白な規則性がある。それに対して、逆
向きの正三角形にはどのような規則性があるのだろうか?
n=4 の場合について、正三角形の向きが逆向きという性格上、その面積は、4S以下で
あることは明らかである。上記の計算でも、面積 9S 、16S の場合は、その個数は
0 個
となっている。
n=4 の場合、元の正三角形と逆向きの正三角形の個数は、
面積 S のもの ・・・・・ 6個( → 1+2+3=6 )
面積 4S のもの ・・・・・ 1個
よって、逆向きの正三角形の個数は、 6+1=7 (個)
さらに、n=5 の場合
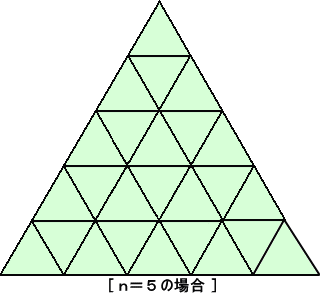
元の正三角形と逆向きの正三角形の個数は、
面積 S のもの ・・・・・ 10個( → 1+2+3+4=10 )
面積 4S のもの ・・・・・ 3個( → 1+2=3 )
よって、逆向きの正三角形の個数は、 10+3=13 (個)
同様にして、n=6 の場合、元の正三角形と逆向きの正三角形の個数は、
面積 S のもの ・・・・・ 15個( → 1+2+3+4+5=15 )
面積 4S のもの ・・・・・ 6個( → 1+2+3=6 )
面積 9S のもの ・・・・・ 1個
よって、逆向きの正三角形の個数は、 15+6+1=22 (個)
このことから、一般の n (n≧2)について、元の正三角形と逆向きの正三角形の個数は、
A(n)=1+2+・・・+n=n(n+1)/2 とおくと、
n が偶数(n=2m mは自然数)のとき、
A(1)+A(3)+A(5)+・・・+A(2m-1)
| = |
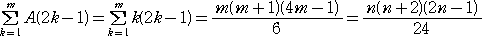 |
n が奇数(n=2m+1 mは自然数)のとき、
A(2)+A(4)+A(6)+・・・+A(2m)
| = |
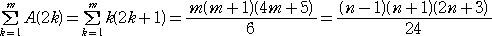 |
であると言える。以上から、一般の n (n≧2)について、求める正三角形の個数は、
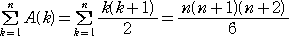
であることに注意して、
n が偶数のとき、 n(n+1)(n+2)/6+n(n+2)(2n-1)/24
=n(n+2)(2n+1)/8=(2n3+5n2+2n)/8
n が奇数のとき、 n(n+1)(n+2)/6+(n-1)(n+1)(2n+3)/24
=(n+1)(2n2+3n-1)/8=(2n3+5n2+2n-1)/8
したがって、1辺 n の正三角形において、正三角形は大小合わせて、
 個
個
あると言える。
(追記) 令和3年3月2日付け
早稲田大学教育学部(2021)で、上記と全く同じ問題が出題された。
第4問 (1) 1辺の長さが1の正三角形を5段積んだとき、上向きと下向きとを合わせた正
三角形の個数を求めよ。
(2) 1辺の長さが1の正三角形をn段(ただし、nは自然数)積んだとき、上向きの正三角形
の総数を求めよ。
(3) 1辺の長さが1の正三角形をn段(ただし、nは自然数)積んだとき、下向きの正三角形
の総数を求めよ。
解答が次のようになることは、上記の計算から直ぐ分かるだろう。
(1) 上向き:35個 、下向き:13個 より、 48個
(2) n(n+1)(n+2)/6
(3) nが偶数のとき、 n(n+2)(2n-1)/24
nが奇数のとき、 (n-1)(n+1)(2n+3)/24
(コメント) この「正三角形の個数」のページは、平成17年4月30日付けでアップしたもの
で、およそ16年かけて、早稲田大学の入試問題に登場したようだ。嬉しい限りで
す。
例 下図のように、1辺 n の正三角形の各辺が n 等分され、平行線が引かれている。
この平行線の交点、および平行線と各辺との交点ならびに頂点からなる図を考える。
この図の中に正三角形は大小合わせていくつあるか?
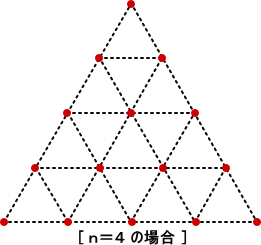
この例は、一見すると前の例と同じではないかと思う方がいられるかもしれない。
正直に告白すると、実は、私も当初誤解していた。この例では、点のみが考察の対象で線
分は無関係である。要は、3点を結んで正三角形が何個作れるかという問題である。
この問題は、当HPがいつもお世話になっている未菜実さんより、掲示板「出会いの泉」に
提起されたものである。(平成17年4月27日付け)
この問題に対して、やはり当HPがいつもお世話になっているHN「らすかる」さんが明解に
解決された。(平成17年4月28日付け)
ここでは、らすかるさんの研究の成果を備忘録として記録に留めることにする。
n=4 の場合について、その数え方の実際を見てみよう。
ここで、1辺 1 の正三角形の面積を、S とおく。面積に注目して、
面積 S のもの ・・・・・ 16個
面積 4S のもの ・・・・・ 7個
面積 9S のもの ・・・・・ 3個
面積 16S のもの ・・・・・ 1個
であるが、ここで注意しなければならないことは、
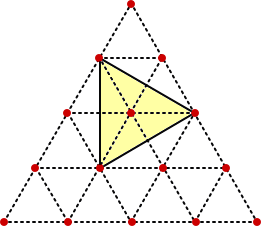
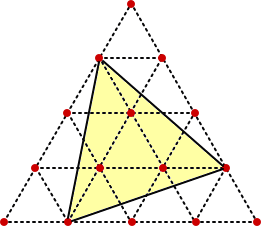
のように、
面積 3S のもの ・・・・・ 6個
面積 7S のもの ・・・・・ 2個
も考慮しなければいけないというところである。
したがって、求める正三角形の個数は、 16+7+3+1+6+2=35 (個)
はたして、この計算にどのような規則性が隠されているのであろうか?
この問題に対して、らすかるさんは、素晴らしいアイデアを考案された。すなわち、
元の正三角形と向きの異なる正三角形は必ず元の正三角形と同じ向きの正三角形
に内接しているという事実に着目し、元の正三角形と同じ向きの正三角形において、
内接する正三角形(自分自身は当然内接していると考える)を数えきる
という手法である。
この手法によれば、次のようにして、正三角形の個数が求められる。
n=4のとき、最小の正三角形の1辺を1として1辺が4の正三角形に内接する正三角形は、
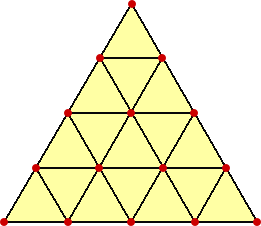

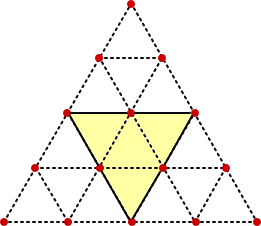
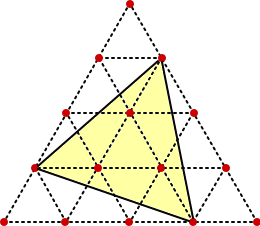
自分自身と面積7の正三角形2個と面積4の正三角形1個 の計4個
(→ この数字は、正三角形の一辺の長さと一致することに注目!すなわち、その個数は
内接する正三角形の頂点の場合の数に一致する。)
1辺が4の正三角形は1個なので、この場合正三角形の個数は、4×1=4(個)
同様にして、1辺が3の正三角形に内接する正三角形は、自分自身と面積3の正三角形
2個の計3個で、1辺が3の正三角形で元の正三角形と同じ向きの正三角形は3個なので、
この場合正三角形の個数は、3×3=9(個)
1辺が2の正三角形に内接する正三角形は、自分自身と面積1の正三角形1個の計2個
で、1辺が2の正三角形で元の正三角形と同じ向きの正三角形は6個なので、この場合正
三角形の個数は、2×6=12(個)
1辺が1の正三角形に内接する正三角形は、自分自身の1個で、1辺が1の正三角形で
元の正三角形と同じ向きの正三角形は10個なので、この場合正三角形の個数は、
1×10=10(個) より、正三角形の総数は、4×1+3×3+2×6+1×10=35(個)
このことを一般化すると、
n×1+(n-1)×(1+2)+・・・+1×(1+2+・・・+n)
=Σ(n+1-k)×k(k+1)/2
=(1/2)((n+1)Σk(k+1)-Σk2(k+1))
=n(n+1)(n+2)(n+3)/24=n+3P4/4!=n+3C4
以上から、求める正三角形の個数は、
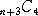 (個)
(個)
であると言える。
(コメント) 線分による正三角形より、点による正三角形の個数の方が公式として美しいの
は感動的でした!この感動を与えてくれたらすかるさん、そして問題の出題者の
未菜実さんに感謝いたします。
(追記) 平成24年1月7日付け
当HP読者のK.S.さんより、平成24年1月5日付けのメールで次のことをご教示頂
いた。ご教示頂いた K.S.さんに感謝いたします。
上記で、正三角形状の格子点の場合の正三角形の個数が求められたが、正方形状
の格子点について、同様に正方形の個数を求める。次の結果が得られた。
n×nの正方形の辺に間隔1で点を配置したものを考え、その点から4個選んで
正方形を作るとき、その個数は、 n+3C4+n+2C4
例 n=2 のとき、正方形の個数は、6個である。
このとき、 n+3C4+n+2C4=5C4+4C4=5+1=6 で、上記の結果に一致する。
FNさんからのコメントです。(平成24年1月7日付け)
「正三角形の個数」で考えられている問題の答えが、「n+3C4」と2項係数1つで書けるとい
う、非常にきれいな答えなので、組合せ論的な証明(説明)ができないか考えてみました。
「n+3C4」の「4」というのは、組合せ論的な解釈をするには難しいので、これを、「3」、「2」と
落としていくことを考えます。そのために次の式を使います。
(*) n+1Ck+1=kCk+k+1Ck+・・・・+nCk (n≧k)
この等式(*)は、
n+1個のもの 1、2、・・・、n、n+1 から k+1 個を選ぶのに、
1を含むものは、nCk個
1を含まないで、2を含むものは、 n-1Ck個
・・・・・・・・・・・・・・・・・・
と考えれば出ます。「2項係数の性質」の性質11の n=k のときの式で文字を変えたもの
です。(→ 参考:性質11の組合せ論的証明)
求める数を、S(n)と書く。S(n) = n+3C4 を示したいわけで、これが成り立つとして、S(n)、
S(n-1)を、(*)を使って書くと、
S(n) = n+3C4 = 3C3+4C3+・・・・+n+1C3+n+2C3
S(n-1) = n+2C4 = 3C3+4C3+・・・・+n+1C3
このとき、 S(n) - S(n-1) = n+2C3 となる。
逆に、これが示せれば、 S(n) = n+3C4 はすぐ出る。
S(n)-S(n-1) の意味を考えると、これは、最下行に頂点があるような正三角形の個数で
あると考えてよい。
S(n) - S(n-1) = n+2C3 に対して、(*)を使うと、
S(n) - S(n-1) = n+2C3 =2C2+3C2+・・・・+nC2+n+1C2
n+1C2 は最下行に、2頂点があるような正三角形の個数である。
従って、2C2+3C2+・・・・+nC2 が最下行にちょうど1頂点がある正三角形の個数であるこ
とが言えれば、S(n) - S(n-1) = n+2C3 が言えて、S(n) = n+3C4 がでる。
2C2+3C2+・・・・+nC2 の各項に再び(*)を使う。と言っても単に、1+2+・・・+(k-1)=k(k-1)/2
だけのことだが。
1+(1+2)+(1+2+3)+・・・・+(1+2+・・・・+(n-1))=1・(n-1)+2・(n-2)+・・・・+(n-1)・1
これが最下行にちょうど1頂点がある正三角形の個数であると言えればよい。だらだらと
書けば説明できそうだけどすっきりしません。何かうまい説明はできないでしょうか。
正方形の問題についてですが、一般化して長方形の中にある正方形の個数を求めるとし
た方が考えやすいのではないかと思います。やりかたによるので一概には言えませんが、
上のように、S(n)を求めるのに、S(n)-S(n-1)を求めてというような方法を取るなら、正方形
は不適切です。それはともかくとして、長方形の場合に同じ様なきれいな式になるか興味が
あります。
n×m (n≦m) の長方形の中にある正方形の個数 T(n,m) を求めよ。
らすかるさんからのコメントです。(平成24年1月8日付け)
ちょっとこじつけ感がありますが、とりあえず組合せ論的な考え方で解釈出来ました。基本
的には「外接正三角形」の考え方を使います。
まず、説明しやすいように、頂点などを定義します。
辺の長さが n の正三角形ABC(底辺左がB、右がC)において、辺ACのn等分点をAの隣
から順に、A1、A2、・・・、An-1 とします。
n+3C4=nH4 ですから、A、A1、A2、・・・、An-1 から4点重複を許して選びます。選んだ点を
Aに近い方から順に、P、Q、R、S とします。当然、P=Q=R=S=A ということもあり得ます。
Pを通り辺ABに平行な直線とQを通り辺BCに平行な直線の交点をDとします。(つまり、P
から左下に進みQから左に進んでぶつかったところです。) P=Q=A ならば、D=A です。
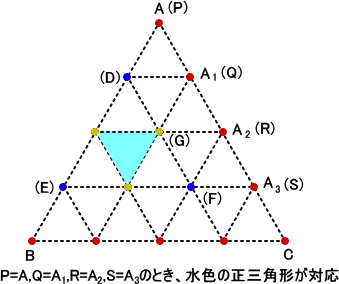 そして、Dを1つの頂点として、辺の長さ
そして、Dを1つの頂点として、辺の長さ
がRCである、元の正三角形と向きが同
じ正三角形DEFを「外接正三角形」とし
て、その中に内接する正三角形を、辺
DF上に存在する頂点Gの位置が、
GF=SCとなるようにとれば、P、Q、R、S
とすべての正三角形が一対一に対応し
ます。
n=4 の場合、上記で得られた正三角形は、それぞれ次の(P,Q,R,S)に対応している。
| (P,Q,R,S)=(A,A,A1,A3) |
(P,Q,R,S)=(A,A,A,A3) |
(P,Q,R,S)=(A,A,A,A) |

|

|

|
| |
|
|
| (P,Q,R,S)=(A,A,A,A2) |
(P,Q,R,S)=(A,A,A,A1) |
|
 |
 |
|
上記の「そしてDを~」以降は、以下のようにした方がわかりやすいかも知れません。
そして、R、S、Cを、R=D となるように平行移動します。移動先の点は S→S’、 C→C’ と
します。DC’を1辺として、元の正三角形と向きが同じ正三角形を考え、その中に一つの頂
点がS’となる内接正三角形を考えれば、P、Q、R、Sとすべての正三角形が一対一に対応
します。
FNさんからのコメントです。(平成24年1月8日付け)
十分理解できているとは言えませんが、こじつけなどというものでは全くない、すばらしい
解釈だと思います。
まず、n+3C4 の「n+3」の解釈がしようがないと思ったのですが、確かに、nH4 とすればで
きますね。ここまではできたとしても、そのあとの対応を考えるのはとてもではないが無理
です。もともとの解答を考えられたらすかるさんでないとできないでしょう。
逆向きの対応は次のようでいいでしょうか。(らすかるさんからの修正済み)
正三角形DEFに対して、それが外接するABCと同じ向きの正三角形をGHIとする。(GHIは
ABCの順序と同じ、DEFがABCと同じ向きのときはGHI=DEF)
GHとACの交点・・・P 、GからBCに平行に引いた線とACの交点・・・Q、
GからICに平行に引いた線とACの交点・・・R、
DEFの頂点のうちGI上にある点(ただしGHI=DEFのときはG)
からICに平行に引いた線とACの交点・・・S
FNさんからのコメントです。(平成24年1月8日付け)
らすかるさんの外接正三角形の方法は非常に強力ですね。正方形(長方形)の問題も簡単
に解決してしまいます。正方形でやります。
正方形についても、もとの正方形と同じ向きの外接正方形が決まる。もとの正方形と同じ
向きの正方形(1辺の長さk)に内接する正方形は、自分自身を含めてk個。正方形(1辺の長
さk)は、(n-k+1)2個ある。従って、Σk=1~n k・(n-k+1)2 が求めるものである。
n-k+1をあらためてkとすると、
Σk=1~n (n-k+1)・k2=(n+1)Σk2-Σk3
=(1/6)n(n+1)2(2n+1)-(1/4)n2(n+1)2
=(1/24)n(n+1)2(8n+4-6n)=(1/12)n(n+1)2(n+2)
これは、(1/12)n(n+1)2(n+2)=(1/24)n(n+1)(n+2)(2n+2)
=(1/24)n(n+1)(n+2)(n+3+n-1)
=(1/24)n(n+1)(n+2)(n+3)+(1/24)(n-1)n(n+1)(n+2)
より、 n+3C4+n+2C4 に等しい。
長方形もほぼ同様でできるでしょう。組合せ論的な解釈もあるかもしれません。
攻略法さんからのコメントです。(平成24年1月8日付け)
線分による正方形の場合は、Σk2=n(n+1)(2n+1)/6=n+2C3+n+1C3 となりますね。
らすかるさんからのコメントです。(平成24年1月8日付け)
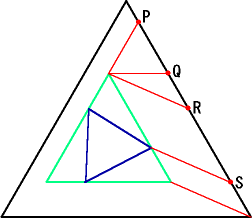 一目でわかるように図を作ってみました。
一目でわかるように図を作ってみました。
一般に、正三角形ABCの内部(辺を含む)に存
在する正三角形は、辺AC(Aは含み、Cは除く)か
ら重複を許して選んだ4点と一対一に対応すると
いうことになりますね。
らいさんからのコメントです。(平成24年1月8日付け)
らすかるさんの図の考え方を真似て、正方形バージョンについても組み合わせ論的証明
ができました。
FNさんの結果によれば、n+3C4+n+2C4=nH4+n-1H4 です。
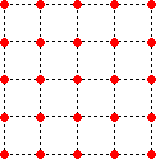 |
正方形の右の辺に任意の4点(重なってもよい)をとる。上から
順に、P、Q、R、S とする。らすかるさんの図と同じように正方形
で作図する。ただし、正三角形ではQから下の辺に平行に引い
ていたのを、正方形の左上-右下の対角線に平行に引くことに
する。つまり、
|
Pから上の辺に平行に引く。Qから対角線(左上-右下)に平行に引く。
Rからその交点に引いた線分と平行に右下から同じ長さをとる。
その線分を同じようにSからも引く。
この作図で内部の正方形の一部は一対一対応になります。 |
内部の正方形のうち、ここで対応していないのは、
左上の頂点同士が重なっていない、かつ、右下の頂点が対角線よりも下側にあるもの
です。この正方形については、今度は、左の辺に、下から4点P、Q、R、S をとり、先ほどと
上下左右逆の作図をすることによって、一対一対応を作ることができます。このとき、4点
は左上の頂点に重ならないことに注意します。
この2パターンの作図によって、正方形の内部の正方形は網羅されています。
4点P、Q、R、S が正方形の辺を n 等分した点の上にあるとすれば、前者の作図に対応
する内部の正方形の個数は、nH4 で、後者の個数は、左上の点を除くので、n-1H4
すなわち、総数は、nH4+n-1H4 となります。
(コメント)
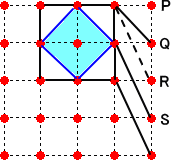 左図のような対応を考えるということかな?
左図のような対応を考えるということかな?
らすかるさんからのコメントです。(平成24年1月9日付け)
上記で、「正方形の右の辺に任意の4点(重なってもよい)をとる。」ということは、「nH4」で
はなく「n+1H4」となり、「今度は、左の辺に、下から4点P、Q、R、S をとり、先ほどと上下左
右逆の作図をすることによって、一対一対応を作ることができます。このとき、4点は左上
の頂点に重ならないことに注意します。」は、「n-1H4」ではなく「nH4」になるのではないでし
ょうか。
# 例えば、「正方形の右の辺に任意の4点(重なってもよい)をとる。」において、4点とも「右
下の頂点」だった場合、正方形が出来ないと思います。
(コメント) 正方形の右下の頂点をらすかるさんの場合と同様に除外すればいいのかな?
らいさんからのコメントです。(平成24年1月9日付け)
確かに右下の頂点は除外する必要がありました。ただ、そうすると、内部の正方形との対
応の過不足がそのほかの場所にもあることになりますが...。もう少し考え直します。
GAI さんからのコメントです。(平成24年1月9日付け)
正三角形の個数を重複組合わせで算出する説明で、外接三角形を利用するらすかるさ
んのアイデアでの具体例を示していただけませんか。n=3での図でお願いします。
三角形ABCで、辺ACを3等分した点をAに近い方から、A0(=A)、A1、A2 とした時、3点A0、
A1、A2 から重複を許して4つ選ぶ方法は、 3H4=6C4=15(通り) となる。
| (A0,A0,A0,A0) |
(A0,A0,A0,A1) |
(A0,A0,A0,A2) |
(A0,A0,A1,A1) |
| |
|
|
|
| (A0,A0,A1,A2) |
(A0,A0,A2,A2) |
(A0,A1,A1,A1) |
(A0,A1,A1,A2) |
| |
|
|
|
| (A0,A1,A2,A2) |
(A0,A2,A2,A2) |
(A1,A1,A1,A1) |
(A1,A1,A1,A2) |
| |
|
|
|
| (A1,A1,A2,A2) |
(A1,A2,A2,A2) |
(A2,A2,A2,A2) |
|
この選び方がどの正三角形に対応しているのか、教えてください。
・A=A0 1
・・A1
2 3
・・・A2 ---→ 4 5 6
B・・・・C 7 8 9 10 |
<例>
(A0,A0,A0,A0)→対応する正三角形(1,7,10) |
らすかるさんからのコメントです。(平成24年1月9日付け)
 左図を見ながら読んで頂ければわかりやすいかと
左図を見ながら読んで頂ければわかりやすいかと
思います。
最初の二つで外接正三角形の頂点の位置が決ま
ります。
(A0,A0) → 1 、(A0,A1) → 2 、(A0,A2) → 4
(A1,A1) → 3 、(A1,A2) → 5 、(A2,A2) → 6
1点目から左下方向(ベクトルABの方向)、
2点目から左方向(ベクトルCBの方向)へ進んだ
交点です。
次の一つで、外接正三角形の大きさが決まります。3点目とCとの距離が外接正三角形
の辺の長さです。
A0 → 辺の長さ 3 、A1 → 辺の長さ 2 、A2 → 辺の長さ 1
最後の一つで、外接正三角形のどこに内接するかが決まります。
(3点目,4点目,C) が
(外接正三角形の上頂点,内接正三角形の1頂点,,外接正三角形の右下頂点)
の位置関係に対応します。 よって、
(A0,A0,A0,A0) → (1,7,10) 、(A0,A0,A0,A1) → (3,4,9) 、(A0,A0,A0,A2) → (6,2,8)
(A0,A0,A1,A1) → (1,4,6) 、(A0,A0,A1,A2) → (3,2,5) 、(A0,A0,A2,A2) → (1,2,3)
(A0,A1,A1,A1) → (2,7,9) 、(A0,A1,A1,A2) → (5,4,8) 、(A0,A1,A2,A2) → (2,4,5)
(A0,A2,A2,A2) → (4,7,8) 、(A1,A1,A1,A1) → (3,8,10) 、(A1,A1,A1,A2) → (6,5,9)
(A1,A1,A2,A2) → (3,5,6) 、(A1,A2,A2,A2) → (5,8,9) 、(A2,A2,A2,A2) → (6,9,10)
という対応になります。
らいさんが証明を改良されました。(平成24年1月9日付け)
 |
正方形の右の辺上の n+1個の点のうち右下の頂点を除いた
n個の点から重複を許して4つの点をとり、上から順に、P、Q、
R、S とする。らすかるさんの図と同じように正方形で作図する。
ただし、正三角形ではQから下の辺に平行に引いていたのを、
正方形の左上-右下の対角線に平行に引くことにする。つまり、
|
Pから上の辺に平行に引く。Qから対角線(左上-右下)に平行に引く。
Rからその交点に引いた線分と平行に右下から同じ長さをとる。
その線分を同じようにSからも引く。
この作図を行うと、一部の内部の正方形と一対一に対応する。 |
外接正方形の右下の頂点が対角線(左上-右下)の下に来てしまうときは、この作図では
作れない。そこで、今度は左の辺上に、左下から4つの点P、Q、R、S をとり、上下左右逆
の作図をする。このとき、先ほどと同じように左上の頂点は除外する。
この2つのパターンの作図で、数えすぎた正方形が存在する。それは、外接正方形の中
心が対角線に重なっているものである。
これらを数えるために、右の辺に上から3点T、U、V (重なってもよい)をとる。
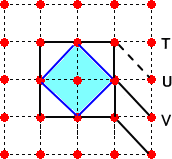 |
Tから上の辺に平行な直線を引く。Uから対角線(左上-右下)
に平行な直線を引く。引いた2直線の交点とUを結んだ線分
を、Uが右下の頂点に重なるように平行移動する。平行移動
する前の線分の左の端点が右上の頂点、平行移動した後の
線分の左の端点が右下の頂点になるように外接正方形を作
|
る。Vから対角線と平行に直線を引き、最初に外接正方形とぶつかった点を内接正方形の
頂点とする。 |
以上の作図によって、選んだ3点と数えたい正方形が一対一対応する。ただし、3点が元
の正方形の右下の頂点に重なると正方形に対応しないので、この頂点は選ぶ範囲から除
外する。
前者の2パターンの作図でできる正方形の総数は、 2・nH4
多く数えすぎた、後者の作図でできる正方形の総数は、 nH3
従って、求める場合の数は、 2・nH4-nH3=nH4+nH4-nH3
=nH4+n+3C4-n+2C3
=nH4+(n+2)(n+1)n(n-1)/24
=nH4+n-1H4 (らすかるさんより修正済み)
ところで、正三角形の個数の別な解答をベクトルで考えてみようと思ったのですが、うまく
いきませんでした。以下が考えたことで、どこが違うのか教えていただけたら幸いです。
原点をOとし、なす角が60度の2つの単位ベクトル e1と e2をとる。
便宜的に、OP=ae1+be2 となる点Pを(a,b)と表し、特にa、bが整数のとき、これを格子点
と呼ぶことにする。
すると、問題は、
a+b≦n、0≦a、0≦b を満たす格子点(a,b)から3点選ぶとき、3点が正三角形を
なすような点の選び方の総数を求めよ
という問題に帰着される。このe1-e2平面上での原点中心に60°回転する操作を f とすれ
ば、
f:(1,0)→(0,1) 、 f:(0,1)→(-1,1)
とすることができる。
△ABCが正三角形であるような点A(p,q)、B(r,s)、C(t,u)をとる。
(ただし、p、q、r、s、t、uは非負整数で、p+q≦n、r+s≦n、t+u≦n とする。)
ACはABを60度回転させたものだから、AC=(-s+q,r-p+s-q)
よって、OC=(p-s+q,r-p+s)
したがって、 t=p-s+q 、u=r-p+s
ここで、t、uは非負整数、かつ、t+u≦n だったので、 -r≦s-p≦q 、t+u=q+r≦n
s-pは、-n~nまでの値をとりえるから、s-p<0 のときは、r の値が制限され、s-p>0
のときは、qの値が制限される。 |s-p|=k とおくと、q+r≦n をみたす(q,r)の組の数は、
x+y≦n-k (x、yは非負整数)を満たす(x,y)の組の数と同じで、その値は、
2H0+2H1+・・・+2Hn-k = 1H1+2H1+・・・+n-k+1H1 = n-k+1H2
s-pが、-n~nを動くので、(q,r)の組の総数は、
2Σk=0~n n-k+1H2 - n+1H2 = 2・n+1H3 - n+1H2
さらに、3点ABCが1点に集まってしまう場合の数が、(n+1)(n+2)/2=n+1H2 なので、
△ABCが正三角形になる場合の数は、 2・n+1H3 - n+1H2 - n+1H2 = 2・nH3
・・・・・・・・・・・・・・・・・・・・・・ 答えがだいぶずれています。どこで間違えているでしょうか?
(q,r)一組に対し、ほかの文字の値も一意的に決まっていると思うのですが...。
らすかるさんからのコメントです。(平成24年1月9日付け)
上記で、「(q,r)一組に対し、ほかの文字の値も一意的に決まっていると思う」という、この
考え方に誤りがあるのでは?
例えば、n=5 として、A(1,1)、B(3,2)、C(0,4) と A(2,1)、B(3,2)、C(1,3) は、両方と
も正三角形ですが、(q,r)=(1,3) で一緒です。
らいさんからのコメントです。(平成24年1月9日付け)
なるほど、一意的ではないのですね。問題点を明らかにして下さって、ありがとうございま
す。もう少し考えてみます。
(p,q,r,s) を決めれば一意的になるので、
s-p≧0 のとき、s-p=n-k 、(s,p)=(n-i,k-i) (0≦i≦k)
とおき、それぞれのi、kに対して、 0≦r≦i 、n-k≦q≦n-k+i 、かつ、 r+q≦n を満た
す(r,q)の組の数を出し、総和を出すというやり方を試みました。
しかし、式はどんどん複雑になり、正解からは遠ざかる一方のように思います。途中までは
わりと簡明で、ベクトルの解法で解けるかと思ったのですが、やはり無理なのでしょうか...。
ここからひたすら計算でゴリ押しすれば解けるのかもしれませんが、気が進みません。
このやり方でうまく解を導くことはできるでしょうか?
FNさんからのコメントです。(平成24年1月10日付け)
私が丸2日以上ネットにつなげない間(ADSLからフレッツ光に切り替え)にいろいろ書きこ
まれているようです。正方形の場合の組合せ論的証明もできたようですね。理解するまでに
かなり時間がかかりそうです。
n+3C4+n+2C4=nH4+n-1H4 というよりは、2・n+3C4-n+2C3=2・nH4-nH3 という感じなのでしょ
うか。三角形に比べたら、正方形は2倍ぐらいはある。でも、2倍よりは少し少ない、といった
ところでしょうか。正三角形の場合と正方形の場合とで論理的なつながりは多分ないのでしょ
うね。
らいさんからのコメントです。(平成24年1月10日付け)
nH4+n-1H4 という見方もできる考え方はあります。というのも、ついさっき、もう少し簡明に
見える証明ができることに気付いたからです。その証明ですが、昨日の証明の途中、上下
左右、逆の作図をするところで全く同じ作図ではなく、少し変えることで、あとで数えすぎた
分を引くことがなくなります。
逆向きの作図の際に、すでに数えてある「中心が対角線に乗っている正方形」を数えない
ためには、点Q、Rが一致していなければよい。よって、Q、Rが重ならない4点の選び方の総
数を出せばよい。
これは、4点(P、Q、R、S)を選ぶ場合の数から、3点(P、Q(=R)、S)を選ぶ場合の数を引い
たものなので、 nH4-nH3 = n-1H4 ここを計算しないで、最初の作図の分に足すと、
2・nH4-nH3 計算してから足すと、 nH4+n-1H4 という結果になります。
また、Q、Rが重ならない4点の選び方の総数は、別の方法でも求められます。
左下から数えて、k番目(1≦k≦n-1)の点にQがあるとすると、
Pの選び方の総数は、k(=kH1) R、Sの選び方の総数は、n-kH2
よって、求める場合の数は、Σk=1~n-1 kH1・n-kH2 で、計算すれば、n-1H4に一致します。
これを、少し一般化します。n個の点 A1、A2、・・・、An から重複を許して、m個の点 P1、
P2、・・・、Pm を選ぶとき、PiとPi+1 (1≦i≦n-1) が重ならないように選ぶ場合の数は、
nHm - nHm-1 = n-1Hm
また、PiがAk (1≦k≦n-1)に重なる時を考えると、それぞれのkに対するほかの点の選び
方は、
kHi-1・n-kHm-i
よって、総数は、 Σk=1~n-1 kHi-1・n-kHm-i
したがって、 Σk=1~n-1 kHi-1・n-kHm-i= n-1Hm が成り立つ。
面白い式だと思ったのですが、少し文字の多さが否めないですね...。これに対応する
二項係数の性質は(違う形、文字などで)既出でしょうか?
FN さんからのコメントです。(平成24年1月12日付け)
「2項係数の性質」のページで定理として書いてあるものと同じであるように思います。
定理 nCm・kC0+n-1Cm-1・k+1C1+・・・+n-mC0・k+mCm=n+k+1Cm
これを、(A) とします。らいさんの式を2項係数で書くと次のようになります。
Σk=1~n-1 k+i-2Ci-1・n+m-k-i-1Cm-i=n+m-2Cm
これを、nCr=nCn-r を使って書きなおすと、
Σk=1~n-1 k+i-2Ck-1・n+m-k-i-1Cn-k-1=n+m-2Cn-2
これをΣを使わないで書いて、積の順序を入れ替えると、次の(B)になります。
(B) n+m-i-2Cn-2・i-1C0+n+m-i-3Cn-3・iC1+・・・+m-iC0・n+i-3Cn-2=n+m-2Cn-2
(A)と(B)は似たような文字が使われていて、使い方が全然違うので、わかりにくいです
が、次の対応で同じになるように思います。
(A) k m n
(B) i-1 n-2 n+m-i-2
らすかるさんからのコメントです。(平成24年1月10日付け)
n点 A1、A2、・・・、An からm点 P1、P2、・・・、Pm (便宜上、A1、P1 の方向を“上”とします)
を Pi≠Pi+1 という条件で選ぶ場合の数は、
n-1点 A1、A2、・・・、An-1 から、m点 P1、P2、・・・、Pi、Qi+1、・・・、Qm を重複して選び、
Qi+1、・・・、Qm の一つ“下”を、Pi+1、・・・、Pm とすればよい
ので、ただちに、n-1Hm 通りとわかりますね。
らいさんからのコメントです。(平成24年1月11日付け)
そんな考え方がありましたか。とても簡明で素晴らしいと思いました。
攻略法さんが、種々の解法を整理されました。(平成24年1月11日付け)
数列の計算による
●正方形の個数
(1) 線分による正方形の場合、すなわち、傾いていない正方形の個数
長方形領域 0≦y≦M、0≦x≦N の格子点として、左下の頂点が(x,y)となる傾いていな
い正方形について、重複しないように数え上げる。
このとき、線分による正方形の個数をA、点による正方形の個数をBとする。
右下の頂点を(X,Y)とすると、求める個数は、
(x,y)と(X,Y)を結ぶ線分を1辺とする反時計まわりの正方形の個数である。
右下の頂点(X,Y)の候補は、 x<X≦M、Y=y の範囲で、(M-x)個となる。
具体的に、M=7、N=5の場合で、(x,y)=(1,1)なら、
○○○○○○○○
○○○○○○○○
○○○○○○○○
○○○○○○○○
○★●●●●●● ←ここ
○○○○○○○○
となる。一般に、0≦x≦M、0≦y≦Nの範囲で、直線 y=x で場合分けして、
min(M-x,N-y) 個
となる。
(2)点による正方形の場合、すなわち、斜めに傾いた正方形を含む個数
斜めに傾いた正方形の個数について、(1)と同様に、この格子点を頂点する傾いた正方形
を考えることができるが、次のことに気付く。
先の(1)で求めた値は、各格子点で(格子点を左下頂点とする)傾いていない正方形の個
数である。
例えば、値が「3」なら、「1辺が、1、2、3 の傾いていない正方形がある」ということである。
これに内接する正方形(傾いていないもの、斜めに傾いたもの)の個数を考える。
1辺が p>0 の正方形には、p 個の内接する正方形が存在するので、その個数は、
1+2+3+ … +p個
となる。よって、1頂点に対しての議論なので、これを累積すればよい。数学モデルに帰着し
て解いてみよう。
問 題 正の整数M、Nは、M≧N>0とする。点(x,y)は、領域 0≦y≦N、0≦x≦M
内の格
子点とする。点(x,y)の値として、p(x,y)=min(M-x,N-y)
を考える。
(1) 領域内の A=Σp を求めよ。
(2) s(p)=Σk=1~p k とするとき、領域内のB=Σs を求めよ。
(解)(1) M=7、N=5の場合、
Y
↑
5
00000000
11111110
22222210
33333210
44443210
─55543210 →
X
│ 7
となる。数の並びは、(この数の並びはお馴染みである)
┌─┬──┐
│2k│ k2 │
└─┴──┘
であるので、A=2Σk+Σk2
一般に、A=(M-N)Σk+Σk2=(M-N)N(N+1)/2+N(N+1)(2N+1)/6=N(N+1)(3M-N+1)/6
(2) 例えば、点(1,1)では値4なので、s(4)=Σk=1~4 k=4(4+1)/2=10 となる。
また、値4は、左側に2個、右側に3個ある。よって、Bの値4の部分は、(2+3)・10=50 と
なる。同様に、値1、2、3、5 について求めれば、Bを得る。
一般に、数pは、(M-N) + 2(N-p)+1= M+N+1-2p 個ある。Bの値pの部分は、
s(p)=Σk=1~p k=(p2+p)/2なので、
(M+N+1-2p)s(p)=(M+N+1-2p)(p2+p)/2=((M+N-1)p2+(M+N+1)p-2p3)/2
以上より、
Σp=1~N {((M+N-1)p2+(M+N+1)p-2p3)/2}
=(1/2){ (M+N-1)N(N+1)(2N+1)/6 +(M+N+1)N(N+1)/2 -2(N(N+1)/2)2 }
=(1/12)N(N+1){ 2MN+4M+2-N-N2 } (終)
題意を求めるアルゴリズムを、センター試験で採用されているBASIC言語で記述すると、
110
LET M=7
120 LET N=5
130 LET A=0
140 LET B=0
150 FOR y=0 TO
N
160 FOR x=0 TO M
170 LET p=MIN(M-x,N-y)
180 LET
A=A+p
190 LET B=B+p*(p+1)/2
200 NEXT x
210 NEXT y
220 PRINT
"線分による正方形="; A; "個"
230 PRINT "点による正方形="; B; "個"
235 PRINT
N*(N+1)*(3*M-N+1)/6; N*(N+1)*(2*M*N+4*M+2-N-N^2)/12
240
END
●正三角形の個数
(2) 領域の条件として、N=M、y≦x(または、y≧x)を追加する。同様に、各格子点で右下頂
点(.△)を基準にする同じ向きの相似三角形を考える。
N=5の場合、
Y
↑
5 ・・・・・0
・・・・10
・・・210
・・3210
・43210
─543210 →
X
│ 5
となる。(図としては、右に傾けて右詰めしたもの)
△ ⊿
△△ → ⊿⊿
△△△
⊿⊿⊿
(1) 逆向きの三角形(▽)が存在するので、その個数を考慮する。
点(x,y)のもう1つの値として、q(x,y)=min(N-x,y) を考える。すなわち、点(x,y)の値と
して、q(x,y)=min(N-x,y) を考える。
(1)’ 領域内のA’=Σq を求めよ。
N=5の場合、
Y ↑
5
・・・・・0
・・・・10
・・・210
・・2210
・11110
─000000 →
X
│ 5
となる。数列の並びを、
⊿
⊿□
として、2Σi=1~[(N-1)/2] { Σk=1~i k } + Σk=1~[N/2] k2 ※[x]はガウス記号
これをAに加味する。よって、そのアルゴリズムは、
110
LET N=3
120 LET A=0
130 LET B=0
140 FOR y=0 TO N
150 FOR x=0 TO
N
160 LET p=N-x
170 LET q=MIN(N-x,y)
180 IF y<=x
THEN LET A=A+(p+q)
190 IF y<=x THEN LET B=B+p*(p+1)/2
200 NEXT
x
210 NEXT y
220 PRINT "線分による三角形="; A; "個"
230 PRINT "点による三角形="; B;
"個"
240 END
攻略法さんがアルゴリズムを改良されました。(平成24年1月13日付け)
時間性能では、こちらが好まれるでしょう。
110 LET N=3
120 LET A=0
130 LET B=0
140 FOR y=0 TO N
150 FOR x=y TO N
160 LET p=N-x
170 LET q=MIN(N-x,y)
180 LET A=A+(p+q)
190 LET B=B+p*(p+1)/2
200 NEXT x
210 NEXT y
220 PRINT "線分による三角形="; A; "個"
230 PRINT "点による三角形="; B; "個"
240 END
GAI さんからのコメントです。(平成24年1月11日付け)
攻略法さんのプログラムを基に表を作成してみました。
M×N(M≧N)の長方形内において、
<線分を含む正方形の数>
M\N 1 2 3 4 5 6 7 8 9 10
1 1
2 2 5
3 3 8
14
4 4 11 20
30
5 5 14 26 40 55
6 6 17 32
50 70 91
7 7 20 38
60 85 112 140
8 8 23 44 70 100 133 168 204
9 9 26 50
80 115 154 196 240 285
10 10 29 56 90 130 175 224 276 330 385
<点を含む正方形の数>
M\N 1 2 3 4 5 6 7 8 9 10
1 1
2 2 6
3 3 10 20
4 4 14 30
50
5 5 18 40 70 105
6 6 22 50
90 140 196
7 7 26 60 110 175 252 336
8 8 30 70 130 210 308 420 540
9 9 34 80 150 245 364 504 660 825
10 10 38 90 170 280 420 588 780 990 1210
攻略法さんが作図による解法をまとめられました。(平成24年1月12日付け)
頂点を先に決めて、外接三角形や内接三角形を決めます。
●正三角形の場合
1辺を n の正三角形とする。底辺を広げた1辺を n+2 の正三角形を考えると、底辺の格
子点の個数は、n+3 個である。
この格子点から順に4点A、B、C、Dを選ぶ。場合の数は、n+3C4通り。
A、C、Dで外接三角形を決める。
(決め方) 3直線で囲まれる三角形
点Aを通る傾き60°の直線(元の三角形の左側の辺に平行)
点Dを通る傾き120°の直線(元の三角形の右側の辺に平行)
点Cを通る傾き60°の直線と点Dの直線との交点C'から水平な直線
Bで内接三角形を決める。
(決め方)
点Bを通る傾き60°の直線と外接三角形の底辺(水平な直線)との交点B’を頂点とする
よって、n+3個の点から4点を選ぶと、求める三角形が一意に決まる。
n=3の場合
| 外接三角形 |
内接三角形 |
△
△▲
△▲▲.C'
△△△△
△△△△△
A B C D |
△
△ .
△ ▼ .
△ B' .
△△△△△
A B
C D |
(別解) 1辺をnの正三角形とする。この三角形の底辺の格子点の個数は、n個
この格子点から重複を許して順に4点A、B、C、Dを選ぶ場合の数は、nH4通り。
A、C、Dで外接三角形を決める。
(決め方) 3直線で囲まれる三角形
点Aを通る傾き60°の直線
点Dを通る傾き120°の直線
点Cを通る傾き60°の直線と点Dの直線との交点C'から水平な直線
Bで内接三角形を決める。
(決め方)
点Bを通る傾き60°の直線と外接三角形の底辺(水平な直線)との交点B’を
頂点とする
よって、n個の点から4点を選ぶと、求める三角形が一意に決まる。
n=3の場合
| 外接三角形 |
内接三角形 |
△
△▲
△▲▲
A B C
D |
△
△ .
△ ▼
.
A
B C
D |
●正方形の場合
1辺nの正方形を、対角線で1辺をnと1辺を(n-1)との二等辺三角形に分割する。この二
等辺三角形に対して、上の議論を行う。よって、 nH4+n-1H4
らすかるさんからのコメントです。(平成24年1月12日付け)
●正三角形の場合について、提示された方法ですと、
・n=3 の例で、Cがもう一つ右にあるとき、外接正三角形が元の正三角形の内部に収まら
ないのではないでしょうか。
・どのようにA~Dを選んでも、元の正三角形と同じ向きの正三角形は出来ないのではない
でしょうか。
4点を選んだ後で、Cだけ一つ左にずらせばうまくいきそうですが...。
別解の方は、
・底辺の格子点の個数は、n個でなく、n+1個です。
・ABが左端でCDが右端の場合と、Aが左端でBCDが右端の場合では結果が同じになってし
まうと思います。
攻略法さんからのコメントです。(平成24年1月12日付け)
●正三角形の場合について、正三角形の1辺を、n とする。底辺を広げた1辺 n+2 の正三
角形を考えると、底辺の格子点の個数は、n+3個である。この格子点から順に4点A、B、C、
Dを選ぶ場合の数は、n+3C4通り。A、C、Dで外接三角形を決める。
(決め方) 3直線で囲まれる三角形
点Aを通る傾き60°の直線(元の三角形の左側の辺に平行)
点Dを通る傾き120°の直線(元の三角形の右側の辺に平行)
点Cを通る傾き60°の直線と点Dの直線との交点C'から水平な直線
Bで内接三角形を決める。
(決め方)
点Bを通る傾き60°の直線と外接三角形の底辺(水平な直線)との交点B’を頂点(接点)
とする。
ただし、C、Dが隣り合うときは、A、B、Dで外接三角形を決めて、それ自身を求める
三角形とする。
攻略法さんからの続報です。(平成24年1月14日付け)
正三角形の頂点(格子点)の番号
0 n=0
1 2 n=1
3 4 5 n=2
6 7 8 9 n=3
10 11 12 13 14 n=4
15 16 17
18 19
20 n=5
とする。
・数 0、1、2、3、・・・、n、n+1、n+2 として、n+3個から4つを選んでできる数の組(A,B,C,D)
・外接正三角形PQRとそれに内接する正三角形との接点Sの組(P,Q,R,S)の対応につい
て、たとえば、n=4の場合のA、B、C、Dは、0 1 2 3 4 5 6 となる。
n+3C4=35個の対応は、
数の組(A,B,C,D) 頂点の組(P,Q,R,S)
1:
0 1 2 3 6 10 11
2: 0 1 2 4 3 10 12 11
3:
0 1 2 5 1 6 8 7
4: 0 1 2 6 0 3 5 4
5:
0 1 3 4 3 6 7
6: 0 1 3 5 1 10 13 11
7:
0 1 3 6 0 6 9 7
8: 0 1 4 5 1 3 4
9:
0 1 4 6 0 10 14 11
10: 0 1 5 6 0 1 2
11:
0 2 3 4 3 10 12
12: 0 2 3 5 1 10 13 12
13:
0 2 3 6 0 6 9 8
14: 0 2 4 5 1 6 8
15:
0 2 4 6 0 10 14 12
16: 0 2 5 6 0 3 5
17:
0 3 4 5 1 10 13
18: 0 3 4 6 0 10 14 13
19:
0 3 5 6 0 6 9
20: 0 4 5 6 0 10 14
21:
1 2 3 4 7 11 12
22: 1 2 3 5 4 11 13 12
23:
1 2 3 6 2 7 9 8
24: 1 2 4 5 4 7 8
25:
1 2 4 6 2 11 14 12
26: 1 2 5 6 2 4 5
27:
1 3 4 5 4 11 13
28: 1 3 4 6 2 11 14 13
29:
1 3 5 6 2 7 9
30: 1 4 5 6 2 11 14
31:
2 3 4 5 8 12 13
32: 2 3 4 6 5 12 14 13
33:
2 3 5 6 5 8 9
34: 2 4 5 6 5 12 14
35:
3 4 5 6 9 13 14
となる。
別解について、1辺 n の正三角形とする。底辺で、この三角形と同じ向きの三角形の個
数は、n個。これらの三角形から重複を許して順に4つの三角形A、B、C、Dを選ぶ場合の数
は、nH4通り。
A、C、Dで外接三角形を決める。
(決め方) 3直線で囲まれる三角形
Aの左頂点を通る傾き60°の直線
Dの右頂点を通る傾き120°の直線
Cの右頂点を通る傾き60°の直線と点Dの直線との交点C'から水平な直線
Bで内接三角形を決める。
(決め方)
Bの右頂点を通る傾き60°の直線と外接三角形の底辺(水平な直線)との交点B'を頂点
(接点)とする。
FNさんからのコメントです。(平成24年1月12日付け)
n×m (n≦m) の長方形の中にある正方形の個数 T(n,m) を求めよ。
攻略法さんも解かれていますが、私もやってみました。特に新しい内容はありません。結
果の書き方だけです。
正方形の場合と同様にして、 Σk=1~n (n-k+1)(m-k+1)k となる。
m-n=m0 とおくと、 m=n+m0 で、上の式は、
Σk=1~n (n-k+1)(n+m0-k+1)k=Σk=1~n (n-k+1)2・k+m0・Σk=1~n (n-k+1)k
となる。第1式は、m=n のときの式だから、前に書いたように、nH4+n-1H4 である。
第2式のΣ部分は、(n+1)・Σk=1~n k-Σk=1~n k2=(n+1)・n(n+1)/2-n(n+1)(2n+1)/6
=n(n+1)/6・(3n+3-2n-1)
=(n+2)(n+1)n/6=n+2C3=nH3
従って、求める値は、次式で与えられる。
nH4+n-1H4+nH3・(m-n)
この結果からすると、正方形の場合が本質的で、長方形の場合は正方形の場合に少し
つけ足せばよいということのようです。もとの長方形に平行な辺を持つ正方形に限定した
場合については、同様にして、もう少し楽な計算で次の結果が得られます。
nH3+n-1H3+nH2・(m-n)
かなり似た結果であるのが面白いです。なお、正方形の場合、即ち、最後の項がない場
合は既に攻略法さんが書かれてます。
FNさんからのコメントです。(平成24年1月12日付け)
正方形の中に正方形が何個あるかという問題の、外の正方形を長方形に変えても、あま
り問題は変わりませんでした。中の正方形を他の形に変えることを考えます。
自然数nに対して、(n+1)2個の格子点(x,y) (x、y は整数で、0≦x、y≦n)を考える。
(A) この中から、3個の点を選んでできる次のような図形は何個あるか。
(A1) 直角をはさむ2辺がx軸,y軸に平行な直角三角形
(A2) 直角三角形
(A3) 直角2等辺三角形
(A4) 2等辺三角形
(A5) 鋭角三角形
(A6) 三角形
(B) この中から、4個の点を選んでできる次のような図形は何個あるか。
(B1) 正方形
(B2) 長方形
(B3) 平行四辺形
(B4) 凸四角形
(B5) 四角形
(A1)は、高校生向けの標準問題です。(B1)は、解決済みです。他は、どの程度難しいかは
わかりません。問題として面白いかどうかもわかりません。どれでもいいからやってみてくだ
さい。
攻略法さんから参考サイトの紹介です。(平成24年1月14日付け)
(A6) 三角形 → 参考サイト:「A045996」
(B5) 四角形 → 参考サイト:「A175383」
FNさんからのコメントです。(平成24年1月14日付け)
2重のΣに最大公約数を使ったとても複雑な式ですね。問題として成立しないようです。
FNさんからのコメントです。(平成24年1月14日付け)
正確な値を求めるのは難しいのが多いのではないかと思います。(頑張ればできるかもし
れないのは、(B3)(A3)(A6)あたりかな?)
正確な値が無理なら大体の挙動でもわからないでしょうか。これらの答えが、n の多項式
になる保証はないですが、そうなるような気がします。そうなるとして、n の何次式であるか、
それがわかれば、最高次の係数は何か。即ち、最高次の項(主要項)を求められないでしょ
うか。
n の多項式であることを前提としない形で書けば求める数値を X(n) としたとき、X(n)/nk
が、n→∞ のとき、0でない有限の極限値になるようなkと、そのときの極限値を求めよとい
うことです。もちろんこのようなkと極限値の存在は保証されてません。(kは自然数)
例えば、(A6) なら、(n+1)2個から3点を選べば、大抵の場合は三角形になるから、ほぼ
(n+1)2C3 で、主要項は、多分、(1/6)n6でしょう。(A5)は鋭角三角形と鈍角三角形がどの程
度の割合でできるかを考えれば得られます。(直角三角形は無視してよい)
実験結果によると、鋭角三角形:鈍角三角形は、1:3ぐらいだそうです。これはこれで面
白そうな問題です。
(n+1)2個の格子点(x,y) (x,yは整数で、0≦x、y≦n)から任意に3点をとったとき、この3
点を結んで鋭角三角形ができる確率を、P(n)とする。n→∞のときのP(n)の極限を求めよ。
Excel VBAで、Nを107から1012ぐらいで試行回数を106か107ぐらいで調べてみました。鋭
角三角形になる確率は、0.2743から0.2749の間ぐらいでした。エクセルの精度がどの程
度かによるので、Nをあまり大きくしても意味はないかと思います。試行回数を大きくすると
時間がかかります。鋭角三角形になる確率が、1/4であれば、とか思ったのですが、その
可能性はなさそうです。
FNさんからのコメントです。(平成24年1月16日付け)
(A3) 直角2等辺三角形ももっと複雑ですが、なんとかなりそうな気がします。他は無理な
ようです。(A1)(A3)(B1)(B3)以外は、n の多項式にならないのでしょう。
攻略法さんが、(A2) 直角三角形についての参考サイト:「A077435」を紹介されました。
(平成24年1月17日付け)
さらに、自然数nに対して、(n+1)2個の格子点(x,y) (x、y は整数で、0≦x、y≦n)を考え、
この中から、3個の点を選んでできる次のような図形は何個あるか。
(A1) 直角をはさむ2辺がx軸,y軸に平行な直角三角形
(A2) 直角三角形
(A3) 直角2等辺三角形
(A4) 2等辺三角形
(A5) 鋭角三角形
(A6) 三角形
という問題についても考察されました。(平成24年1月17日付け)
格子点の選び方は、(2+1)2C3=84 通りなので、列挙して調べてみました。
数字の順を、
(0)直角をはさむ2辺が軸に平行な直角三角形
(1)直角三角形
(2)直角二等辺三角形
(3)正三角形
(4)二等辺三角形
(5)鈍角三角形
(6)三角形 ─┐格子点の選び方
(*)不成立 ─┘
とする。
三角形= 36 44 28 0 36 24 76 8
個
鋭角三角形= 8 個
(詳細) 頂点番号
6 7 8
3 4 5
0 1 2 として、
| 組(A,B,C) |
|
組(A,B,C) |
(0,1,2)= ×
(0,1,3)= b=c ∠A=直角 軸に平行
(0,1,4)= c=a ∠B=直角 軸に平行
(0,1,5)= ∠B=鈍角
(0,1,6)= ∠A=直角 軸に平行
(0,1,7)= ∠B=直角 軸に平行
(0,1,8)= ∠B=鈍角
(0,2,3)= ∠A=直角 軸に平行
(0,2,4)= a=b ∠C=直角
(0,2,5)= ∠B=直角 軸に平行
(0,2,6)= b=c ∠A=直角 軸に平行
(0,2,7)= a=b
(0,2,8)= c=a ∠B=直角 軸に平行
(0,3,4)= 時計まわり c=a ∠B=直角 軸に平行
(0,3,5)= 時計まわり ∠B=直角 軸に平行
(0,3,6)= ×
(0,3,7)= 時計まわり ∠B=鈍角
(0,3,8)= 時計まわり ∠B=鈍角
(0,4,5)= 時計まわり ∠B=鈍角
(0,4,6)= c=a ∠B=直角
(0,4,7)= ∠B=鈍角
(0,4,8)= ×
(0,5,6)= c=a
(0,5,7)= b=c
(0,5,8)= ∠B=鈍角
(0,6,7)= 時計まわり ∠B=直角 軸に平行
(0,6,8)= 時計まわり c=a ∠B=直角 軸に平行
(0,7,8)= 時計まわり ∠B=鈍角
(1,2,3)= ∠A=鈍角
(1,2,4)= b=c ∠A=直角 軸に平行
(1,2,5)= c=a ∠B=直角 軸に平行
(1,2,6)= ∠A=鈍角
(1,2,7)= ∠A=直角 軸に平行
(1,2,8)= ∠B=直角 軸に平行
(1,3,4)= 時計まわり a=b ∠C=直角 軸に平行
(1,3,5)= 時計まわり b=c ∠A=直角
(1,3,6)= 時計まわり ∠B=鈍角
(1,3,7)= 時計まわり c=a ∠B=直角
(1,3,8)= 時計まわり a=b
(1,4,5)= 時計まわり c=a ∠B=直角 軸に平行
(1,4,6)= ∠B=鈍角
(1,4,7)= ×
(1,4,8)= 時計まわり ∠B=鈍角 |
|
(1,5,6)= a=b
(1,5,7)= c=a ∠B=直角
(1,5,8)= ∠B=鈍角
(1,6,7)= 時計まわり ∠C=直角 軸に平行
(1,6,8)= 時計まわり b=c
(1,7,8)= 時計まわり ∠B=直角 軸に平行
(2,3,4)= 時計まわり ∠C=鈍角
(2,3,5)= 時計まわり ∠C=直角 軸に平行
(2,3,6)= 時計まわり ∠B=鈍角
(2,3,7)= 時計まわり b=c
(2,3,8)= 時計まわり c=a
(2,4,5)= 時計まわり a=b ∠C=直角 軸に平行
(2,4,6)= ×
(2,4,7)= 時計まわり ∠B=鈍角
(2,4,8)= 時計まわり c=a ∠B=直角
(2,5,6)= ∠B=鈍角
(2,5,7)= ∠B=鈍角
(2,5,8)= ×
(2,6,7)= 時計まわり ∠C=鈍角
(2,6,8)= 時計まわり a=b ∠C=直角 軸に平行
(2,7,8)= 時計まわり ∠C=直角 軸に平行
(3,4,5)= ×
(3,4,6)= b=c ∠A=直角 軸に平行
(3,4,7)= c=a ∠B=直角 軸に平行
(3,4,8)= ∠B=鈍角
(3,5,6)= ∠A=直角 軸に平行
(3,5,7)= a=b ∠C=直角
(3,5,8)= ∠B=直角 軸に平行
(3,6,7)= 時計まわり c=a ∠B=直角 軸に平行
(3,6,8)= 時計まわり ∠B=直角 軸に平行
(3,7,8)= 時計まわり ∠B=鈍角
(4,5,6)= ∠A=鈍角
(4,5,7)= b=c ∠A=直角 軸に平行
(4,5,8)= c=a ∠B=直角 軸に平行
(4,6,7)= 時計まわり a=b ∠C=直角 軸に平行
(4,6,8)= 時計まわり b=c ∠A=直角
(4,7,8)= 時計まわり c=a ∠B=直角 軸に平行
(5,6,7)= 時計まわり ∠C=鈍角
(5,6,8)= 時計まわり ∠C=直角 軸に平行
(5,7,8)= 時計まわり a=b ∠C=直角 軸に平行
(6,7,8)= × |
(コメント) 力作ですね!攻略法さんに感謝します。
FNさんからのコメントです。(平成24年1月17日付け)
確かに、n が小さければできそうですね。大学入試なら、n=3 あたりが妥当かなと思いま
す。(A1)~(A6)全部では多すぎるし、難しすぎるから、適当に選ばないといけませんが、一
応全部にしておきます。底辺がx軸に平行な2等辺三角形とかいろいろ作れますが、前のま
まにします。
16個の格子点(x,y) (x,yは整数で、0≦x、y≦3)を考える。この中から、3個の点を選んで
できる、次のような図形は何個あるか。
(1)直角をはさむ2辺がx軸、y軸に平行な直角三角形
(2)直角三角形
(3)直角2等辺三角形
(4)2等辺三角形
(5)鋭角三角形
(6)三角形
一応全部やりましたが自信は全然ありません。
攻略法さんが、次の問題に取り組まれました。(平成24年1月17日付け)
16個の格子点(x,y)
(x,yは整数で、0≦x、y≦3)を考える。この中から、3個の点を選んで
できる、次のような図形は何個あるか。
(1) 直角をはさむ2辺がx軸、y軸に平行な直角三角形
(2) 直角三角形
(3) 直角2等辺三角形
(4) 2等辺三角形
(5) 鋭角三角形
(6) 三角形
まず、(6) 三角形 について、
4×4個の点から3点を選ぶ組合せは、4・4C3=560(通り)
三角形が成立しないのは、3点が一直線上に並ぶときである。その場合の数は、縦・横・
斜めの10本、斜めの4本、計2種類の直線から選べばよい。
10・4C3+4・3C3=10×4+4×1=44 より、 560-44=516(通り)
4C3 3C3
\││││/ \ /
─・・・・─ \・・・・/
─・・・・─ ・・・・
─・・・・─ ・・・・
─・・・・─ /・・・・\
/││││\ / \
次に、(1) 直角をはさむ2辺がx軸、y軸に平行な直角三角形について、対称性を利用して、
数え上げる。
★●●●
○・・・
○・・・
○・・・ |
★を直角の頂点として、これをはなさむ2辺として、3つの●から1つ、3つの
○から1つを選べば軸に平行となる。したがって、(3*3)*4=36通り
直角二等辺三角形は、(3)*4=12通り |
●★●●
・○・・
・○・・
・○・・ |
(3*3)*8=72通り
直角二等辺三角形は、(3)*8=24通り |
・○・・
●★●●
・○・・
・○・・ |
(3*3)*4=36通り
直角二等辺三角形は、(5)*4=20通り |
よって、 36+72+36=144通りで、直角二等辺三角形は、12+24+20=56通り
次に、(2) 直角三角形について、傾いたものを探す。
★・◎・ ★・・・ ★・・・ ★・・・
・◎・・ ・◎・・ ・・・○ ・・・・
・・・・ ◎・・・ ・・○・ ・・○・
・・・・ ・・・・ ・・・・ ・○・・ |
(4)*4=16通り
直角二等辺三角形は、
(2)*4=8通り |
・★・◎ ・★・・ ・★・・ ・★・・
・・◎・ ・・◎・ ◎・◎・ ・・・・
・・・・ ・◎・・ ・・・・ ・・・○
・・・・ ・・・・ ・・・・ ・・○・ |
(4)*8=32通り
直角二等辺三角形は、
(3)*8=24通り
|
・・◎・ ・・・・
・★・・ ・★・・
・・◎・ ◎・◎・
・・・・ ・・・・ |
(2)*4=8通り
直角二等辺三角形は、
(2)*4=8通り |
よって、先の軸に平行なものを加味して、16+32+8+144=200通りで、直角二等辺三角形は、
(8+24+8)+56=96通り
次に、(4) 2等辺三角形について、
★・・・ ★・・・ ★・・・
・・○・ ・・・○ ・・・・
・○・・ ・・・・ ・・・○
・・・・ ・○・・ ・・○・ |
(3)*4=12通り |
・★・・ ・★・・ ・★・・ ・★・○
・・・・ ・・・・ ・・・○ ・・・・
○・○・ ・・・・ ・・○・ ・・○・
・・・・ ○・○・ ・・・・ ・・・・ |
(4)*8=32通り |
・・・・ ・・・・
・★・・ ・★・・
・・・・ ・・・○
○・○・ ・・○・ |
(2)*4=8通り |
よって、直角二等辺三角形を加味して、(12+32+8)+96=148通り
FNさんからのコメントです。(平成24年1月18日付け)
私がやったものと結果が同じでないところがあるので、見直します。鋭角三角形も一応や
ったのですが、ちょっと少なすぎる気がするのでもう一度やってみます。
攻略法さんが、問題(B)に関連して、参考サイトを紹介されました。
(平成24年1月18日付け)
参考サイト:四角形→「A175383」、台形(平行四辺形も含む)→「A189415」、
平行四辺形(正方形、長方形も含む)→「A189416」、
ひし形(正方形も含む)→「A189418」、凸四角形→「A189413」
さらに、自然数nに対して、(n+1)2個の格子点(x,y)
(x、y は整数で、0≦x、y≦n)を考え、
この中から、3個の点を選んでできる図形の個数を数えられました。
n=2 の場合、格子点の選び方は、 126 通り
(Bo)凸系 (B1)正方形= 6
(B2)長方形(正方形を除く)= 4
(B3')ひし形(正方形を除く)= 0
(B3)平行四辺形(正方形、長方形を除く)= 12
(B4)台形(正方形、長方形、平行四辺形を除く)= 28
(B5)それ以外= 20
(B6)凹四角形= 8
(B7)四角形(凸系+凹)= 78
(B*)不成立= 48
※格子点の選び方=四角形+不成立
頂点番号
6 7 8
3 4 5
0 1 2
(0,1,2,3)= ×
(0,1,2,4)= ×
(0,1,2,5)= ×
(0,1,2,6)= ×
(0,1,2,7)= ×
(0,1,2,8)= ×
(0,1,3,4)= 正方形
(0,1,3,5)= 台形
(0,1,3,6)= ×
(0,1,3,7)= 台形
(0,1,3,8)=
(0,1,4,5)= 平行四辺形
(0,1,4,6)= 台形
(0,1,4,7)= ×
(0,1,4,8)= ×
(0,1,5,6)=
(0,1,5,7)=
(0,1,5,8)= 台形
(0,1,6,7)= 長方形
(0,1,6,8)= 台形
(0,1,7,8)= 平行四辺形
(0,2,3,4)= 台形
(0,2,3,5)= 長方形
(0,2,3,6)= ×
(0,2,3,7)=
(0,2,3,8)= 台形
(0,2,4,5)= 台形
(0,2,4,6)= ×
(0,2,4,7)= 凹四角形
(0,2,4,8)= ×
(0,2,5,6)= 台形
(0,2,5,7)=
(0,2,5,8)= ×
(0,2,6,7)= 台形
(0,2,6,8)= 正方形
(0,2,7,8)= 台形
(0,3,4,5)= ×
(0,3,4,6)= ×
(0,3,4,7)= 平行四辺形
(0,3,4,8)= ×
(0,3,5,6)= ×
(0,3,5,7)=
(0,3,5,8)= 平行四辺形
(0,3,6,7)= ×
(0,3,6,8)= ×
(0,3,7,8)= 台形
(0,4,5,6)= 凹四角形
(0,4,5,7)= 凹四角形
(0,4,5,8)= ×
(0,4,6,7)= 台形
(0,4,6,8)= ×
(0,4,7,8)= ×
(0,5,6,7)=
(0,5,6,8)= 台形
(0,5,7,8)=
(0,6,7,8)= ×
(1,2,3,4)= 平行四辺形
(1,2,3,5)= 台形
(1,2,3,6)= 台形
(1,2,3,7)=
(1,2,3,8)=
(1,2,4,5)= 正方形
(1,2,4,6)= × |
|
(1,2,4,7)= ×
(1,2,4,8)= 台形
(1,2,5,6)=
(1,2,5,7)= 台形
(1,2,5,8)= ×
(1,2,6,7)= 平行四辺形
(1,2,6,8)= 台形
(1,2,7,8)= 長方形
(1,3,4,5)= ×
(1,3,4,6)= 平行四辺形
(1,3,4,7)= ×
(1,3,4,8)= 凹四角形
(1,3,5,6)=
(1,3,5,7)= 正方形
(1,3,5,8)=
(1,3,6,7)= 台形
(1,3,6,8)=
(1,3,7,8)=
(1,4,5,6)= 凹四角形
(1,4,5,7)= ×
(1,4,5,8)= 平行四辺形
(1,4,6,7)= ×
(1,4,6,8)= 凹四角形
(1,4,7,8)= ×
(1,5,6,7)=
(1,5,6,8)=
(1,5,7,8)= 台形
(1,6,7,8)= ×
(2,3,4,5)= ×
(2,3,4,6)= ×
(2,3,4,7)= 凹四角形
(2,3,4,8)= 凹四角形
(2,3,5,6)= 平行四辺形
(2,3,5,7)=
(2,3,5,8)= ×
(2,3,6,7)=
(2,3,6,8)= 台形
(2,3,7,8)=
(2,4,5,6)= ×
(2,4,5,7)= 平行四辺形
(2,4,5,8)= ×
(2,4,6,7)= ×
(2,4,6,8)= ×
(2,4,7,8)= 台形
(2,5,6,7)= 台形
(2,5,6,8)= ×
(2,5,7,8)= ×
(2,6,7,8)= ×
(3,4,5,6)= ×
(3,4,5,7)= ×
(3,4,5,8)= ×
(3,4,6,7)= 正方形
(3,4,6,8)= 台形
(3,4,7,8)= 平行四辺形
(3,5,6,7)= 台形
(3,5,6,8)= 長方形
(3,5,7,8)= 台形
(3,6,7,8)= ×
(4,5,6,7)= 平行四辺形
(4,5,6,8)= 台形
(4,5,7,8)= 正方形
(4,6,7,8)= ×
(5,6,7,8)= × |
FNさんからの続報です。(平成24年1月19日付け)
16個の格子点(x,y)
(x,yは整数で、0≦x、y≦3)を考える。この中から、3個の点を選んで
できる、次のような図形は何個あるか。
(1)直角をはさむ2辺がx軸、y軸に平行な直角三角形
(2)直角三角形
(3)直角2等辺三角形
(4)2等辺三角形
(5)鋭角三角形
(6)三角形
(1) 2辺がx軸、y軸に平行な長方形は、縦4本から2本、横4本から2本を選べば良いから、
4C2・4C2=36
1つの長方形から、この形の直角三角形が4個できるから、 36×4=144個
(2) (1)以外の直角三角形を数える。直角をはさむ2辺の長さは、
( ,
, )、(
)、( ,2
,2 )、(
)、( ,
, )
)
しかない。それぞれの外接長方形は、1-2型、2-3型、2-3型で、それぞれの個数は、
12個、4個、4個
それぞれの型の1個の長方形に内接するそれぞれの直角三角形は、2個、4個、4個
従って、 12×2+4×4+4×4=56 に、(1)の144を加えて、200個
(3) (2)のうちでは、 ( ,
, )、(
)、( ,
, )型が該当するから、 12×2+4×4=40
)型が該当するから、 12×2+4×4=40
(1)のうちでは外接長方形は、1-1型、2-2型、3-3型のどれかで、それぞれ 9個、4個、1個
で、計14個 これらから4個ずつできるから、 14×4=56 で、40+56=96個
(4) (3)以外の2等辺三角形を数える。底辺がx軸に平行なものは、底辺の長さは2である。
数えると、 (2×2+2)×2=12 で、y軸に平行なものも同じだから、両方で、 12×2=24
底辺が、y=x に平行なものを数えると、 7×2=14 で、底辺が、y=-x に平行なものも同じ
で、合せて、 14×2=28
(3)を加えて、 96+24+28=148個(平成24年1月19日付け 修正済み)
(5) 1辺がx軸に平行なものを数える。その辺の長さは、2か3 で、
3のとき、他の2辺の2乗は、(5,8)か(10,13)で、(5,8)は、8個、(10,13)は、4個
2のとき、他の2辺の2乗は、(5,5)か(10,10)で、(5,5)は、8個、(10,10)は、4個
以上で24個
1辺がy軸に平行なものも同じく、24個
3辺ともにx軸、y軸に平行でないものを数える。外接長方形が、1-k型であることはない。
2-2型のとき、3辺の2乗が、(2,5,5) しかない。 4×4=16個
2-3型のときはない。
3-3型のとき、1つの頂点は外接正方形の隅の点である。1つの隅の点を定めたとき4個で
きるから、 4×4=16個
よって、 24×2+16×2=80個
(6) 16個の点から3点を選ぶのは、16C3=560通り。このうち、3点が1直線上になる場合を数
える。x軸、y軸に平行な直線は、全部で8本。1本について、4C3=4通りあるから、4×8=32
斜めの直線で、3点以上を含むものは、3点が4本、4点が2本だから、
3C3×4+4C3×2=12 で、560-32-12=516個
(4)は攻略法さんの結果とあいませんが、攻略法さんの二等辺三角形の2行目の最後の図
は正しくないので除いて、☆が(2,2)で、○が(1,4)、(4,1)にあるもの(唯一の鈍角二等辺三
角形)を加えて、148-8+4=144 であいます。(5)鋭角三角形は不安があったので、鈍角三角
形を数えてみました。直角、鋭角、鈍角三角形を合わせて、516になったつもりだったのです
が、見直してみてやはり正しかったです。
(7) 鈍角三角形 1辺がx軸に平行なもの 長さが1のものは全部で12本あり、1本を固定した
とき第3の頂点の選び方は6通りだから、12×6=72 長さが2のもの 同様にして8*3=24
長さが3のもの 2+4+4+2=12 で、72+24+12=108
y軸に平行なものも同じで、合わせて108*2=216
どの辺も座標軸に平行でないもの 1頂点は隅の点である。
1点だけが隅の点のとき4個あるから、4×4=16個となり、216+4+16=236個(修正済み)
(2) 直角三角形 200個 (5) 鋭角三角形 80個 (7) 鈍角三角形 236個を足すと、
200+80+236=516個(修正済み)
攻略法さんからの続報(修正)です。(平成24年1月19日付け)
2等辺三角形について、直角二等辺三角形でないもの
★・・・ ★・・・ ★・・・ ★・・・ ★・・・
・・・○ ・・○・ ・・○・ ・・・○ ・・・・
○・・・ ○・・・ ・○・・ ・・・・ ・○・・
・・・・ ・・・・ ・・・・ ・○・・ ・・・○ |
※鈍角の二等辺三角形
(5)*4=20通り |
・★・・ ・★・・ ・★・・ ・★・・
・・・○ ・・・○ ・・・・ ○・・・
・○・・ ・・○・ ○・○・ ・・○・
・・・・ ・・・・ ・・・・ ・・・・ |
(4)*8=32通り |
・・・・
・★・・
・・・・
・・・・ |
(0)*4=0通り |
よって、直角二等辺三角形を加味して、(20+32+0)+96=148通り
「(2)直角三角形200個 (5)鋭角三角形80個 (7)鈍角三角形220個を足すと、
200+80+220=500 で、16個足りません。
(5)か(7)の少なくとも一方が間違っています。私にはわかりません。捜してください。」
について、鋭角三角形は、
★・・・ ★・・・ ★・・・ ★・・・ ★・・・ ★・・・ ★・・・ ★・・・
・・・◎ ・・◎・ ・・◎・ ・・○・ ・・・○ ・・・・ ・・・・ ・・・◎
◎・・・ ◎・・・ ・◎・・ ・・・・ ・・・・ ・・○・ ・・・○ ・・・・
・・・・ ・・・・ ・・・・ ○・・・ ○・・・ ○・・・ ○・・・ ・◎・・ |
(8)*4=32通り
2等辺三角形は、(4)*4=16通り
・★・・ ・★・・ ・★・・ ・★・・ ・★・・ ・★・・
・・・◎ ・・・◎ ・・・・ ・・・・ ・・・・ ◎・・・
・◎・・ ・・◎・ ◎・◎・ ○・・○ ・・・○ ・・◎・
・・・・ ・・・・ ・・・・ ・・・・ ・○・・ ・・・・ |
(6)*8=48通り |
2等辺三角形は、(4)*8=32通り
・・・・
・★・・
・・・・
・・・・ |
(0)*4=0通り |
よって、 32+48+0=80通り
二等辺三角形は、直角と鈍角のものを加味して、(16+32)+(96)+(1*4)=148通り
したがって、鈍角三角形は、236通り
GAI さんが、三角形の形状別総数を求める参考サイトを紹介されました。
(平成24年1月19日付け)
「オンライン整数列大辞典」で、n×n個の格子点(x,y) (x、y は整数で、0≦x、y≦n-1) を
考える。この中から3個の点を選んでできる次のような図形は何個あるか。
(1)三角形の総数--------------→ 「A045996」
(2)直角三角形----------------→ 「A077435」
(3)直角2等辺三角形-----------→ 「A187452」
(4)2等辺三角形---------------→ 「A186434」
(5)鋭角三角形----------------→ 「A190019」
(6)鈍角三角形----------------→ 「A190020」
の結果が載っていました。
FNさんからのコメントです。(平成24年1月20日付け)
オンライン整数列大辞典には本当に何でも載っているんですね。せっかくだから、n≦10
の範囲を表にしてみました。
n 1
2 3 4
5 6 7
8 9 10
鋭角三角形 0 8 80
404 1392 3880 9208 19536 38096 69288
鈍角三角形 0 24 236 1148 3932
10760 25392 53576 103824 188104
直角三角形 4 44 200
596 1444 2960 5520 9496 15332 23596
直角2等辺三角形 4 28 96 244 516
968 1664 2680 4100 6020
2等辺三角形 4 36 148
444 1064 2200 4024 6976 11284 17396
三角形
4 76 516 2148 6768 17600 40120 82608 157252
280988
n=3 で四苦八苦だったから、n=4や5はとても大変でしょう。でも、できるのも多少はあるか
もしれません。
以下、工事中!










 そして、Dを1つの頂点として、辺の長さ
そして、Dを1つの頂点として、辺の長さ 一目でわかるように図を作ってみました。
一目でわかるように図を作ってみました。
 左図のような対応を考えるということかな?
左図のような対応を考えるということかな?