
�@�Q���W���Ɋւ�����Łu����������`�v�Ƃ������������������������̂Ƃ��āA���̖�
����w�̖�肪�L���Ɏc��B�����琔�\�N�ȏ�O�̂��̂����A�Ƃ��ǂ����ɂ��Ȃ����B
�i������ƌ����߂����ȁD�D�D��(^_^;)�@�j
������w�������
�Q���W���̐����@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@�Q���W���Ɋւ�����Łu����������`�v�Ƃ������������������������̂Ƃ��āA���̖�
����w�̖�肪�L���Ɏc��B�����琔�\�N�ȏ�O�̂��̂����A�Ƃ��ǂ����ɂ��Ȃ����B
�i������ƌ����߂����ȁD�D�D��(^_^;)�@�j
������w�������
| �@ |
�@�������R�� �� �A�� �����߂�B |
�i���j�@���Ӂ�60�b10�E40�b40�{60�b11�E40�b39�{�E�E�E�{60�b50�E40�b0 �Ȃ̂ŁA������
�@�@�i�P�{���j100���i�P�{���j60�i�P�{���j40
��W�J�����Ƃ��́A��50 �̍��̌W�������߂邱�Ƃɓ������B
�@����āA�@���Ӂ�100�b50�@�ƂȂ�A�@�����P�O�O�@�A�@�����T�O�@�ł���B�@�@�i�I�j
�@�����Ă��܂��ΈՂ������������邪�A�̂悤�Ȕ��z���u���Ɏv�������Z���͓�
�{�ɉ��l����̂��낤�B�����ɍ�������ƁA�Q���W���̐��������˂���ĉ��Ƃ�����
�����������悤�ȋC������B
�@��L�̉́A���̂悤�ɍl����A�������R�Ȕ��z�Ƃ������Ƃ���������邾�낤�B
�@�ԋ��U�O�A�����S�O�̍��v�P�O�O�̋�����T�O�̋������o���ꍇ�̐��́A
�@60�b10�E40�b40�{60�b11�E40�b39�{�E�E�E�{60�b50�E40�b0
�ł���B
�@�܂��A�ŒZ�o�H���Ƃ��Ď��̂悤�ɍl���Ă��悢�B
�@�_�`����_�a�Ɏ���ŒZ�o�H�́A�_�o1�A�o2�A�E�E�E�A�o41 �̉��ꂩ��K���ʂ�B
�@
�@�����Q�S�N�x�����s���{�̐V�w�K�w���v�̂ŁA�Q���藝���ƂĂ���a���̂��鈵����
�邱�ƂɂȂ�B���������Q���藝�́A����ȑO�ɂ��s���Ȉ������Ă���A���ނ̂�
�܂��I�����ɊÂĂ���B
�@�������A�Q���藝����h�������X�̂Q���W���̐����́A�L�x�Ȑ��w�I�b�����A��
�w�I�ɂ͕K���}�X�^�[���ׂ��d�v�����Ƃ����ʒu�Â��͗h�邬�Ȃ����̂ƍl����B
�@���̃y�[�W�ł́A���ȏ�����W�Ō����Q���W���̐����݂̂Ȃ炸�A����Ƃ�����
�������܂Ƃ߂Ă��������Ǝv���B
�@���ɁA���g�o�ł́A���̃y�[�W�łQ���W���Ɋւ���b������グ�Ă���B
�@����Q���W���̊W�@�@�p�X�J���̎O�p�`�@�@�������̓W�J
�@�����̃y�[�W���\���ӎ����A�V�����q�C�ɏo�悤�Ǝv���B
�@���ꂩ��l����Q���W���̐����̔w�i�ɂ���藝���Q���藝�����܂��m�F���Ă������B
�Q���藝�i�a���������������@�s�����������j�@�@�@�@�@�@
�@![]()
�@�����ŁA���b�� �́A�Q���W���Ƃ����A�قȂ� �� �̂��̂���A�قȂ� �� �̂��̂��Ƃ�g
�����̐��ł���B
�@![]()
�@�A���A![]() �@�i�� �̊K��j�Ƃ���B
�@�i�� �̊K��j�Ƃ���B
| �@���b�� �Ƃ����L���ɑ��āA | �Ƃ����L�����p������ꍇ������B |
�i�ؖ��j�@�i���{���j�� ��W�J�����Ƃ��̊e���́A�����@�A����-1���@�A����-2��2�@�A�E�E�E�@�A�����@�ł���B
�@����-������ �̌W���́A�� �̈����@���{���@�̂��ꂼ�ꂩ��A�� �� ���|�� �A�� �� �� �Ƃ�
�g�����̐� ���b�� �ɓ������B�@�@�i�؏I�j
�@��L�̏ؖ��́A���ȏ��ɂ悭������̂����A���̂悤�ȏؖ����\���낤�B
�i�ʏj�@�W�� �r���o�P�C�Q�C�E�E�E�C���p�ƏW�� �`�A�a�i�A���A�`���a���ӁA���i�`�j�����A���i�a�j�����j��
�@�@���āA�ʑ��@�e �F �r�@���@�`���a�@�̌��𐔂���B
�@�r �̊e�v�f�ɂ��āA���{�� �ʂ�̒l�̎���������̂ŁA�ʑ��̌��́A�i���{���j�� ��
����B
�@�܂��A�r �̗v�f���A���|�� �� �� �i�����O�A�P�A�Q�A�E�E�E�A���j�ɕ�����B���̕������̑���
�́A���b�� �ʂ�B
�@���̂P�ʂ�ɑ��āA���|�� �̗v�f�ɂ́A�`�̗v�f���Ή����A�� �̗v�f�ɂ́A�a�̗v
�f���Ή�����ƍl����ƁA�ʑ��̌��́A����-������ �ʂ�B
�@���������āA
�@![]() �@�@�i�؏I�j
�@�@�i�؏I�j
�@���̂Q���藝���玟�̓W�J�����i�m�����������̂Q���藝�j���������B
�@�i�P�{���j�������b0�{���b1���{���b2��2�{���b3��3�{�E�E�E�{���b�������{�E�E�E�{���b������
�@���̓W�J�����i�d�o�j��p����ƁA��X�̂Q���W���̐�����������B
�i�Q�l�����F�A�E���O�����A�C�E���O�����@���@����F���@��
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����I�ɉ������������w�̖��i�U�j�@�@�i�����}���j�j
�Q���W���̐���
�i�P�j�@���b�������b��-���@�i���@�Q�l�F�u�p�X�J���̎O�p�`�v�́i�P�j �j
�i�ؖ��j�@�� �̂��̂��� �� ���o���ꍇ�̐��� �� ���c���ꍇ�̐��͓������B�i�؏I�j
�@���̐����i�P�j�����p������Ƃ��Ď�����������B�i�����R�P�N�R���T���t���j
���K����@�@��k=0715�bk �̐��̖͂������邩�B
�i���j�@��k=0715�bk����k=0715�b15-k����k=81515�bk �Ȃ̂ŁA��k=01515�bk���Q��k=0715�bk
�@�Ƃ���ŁA�@��k=01515�bk���i�P�{�P�j15���Q15 ���A�@��k=0715�bk���Q14
�@����āA���߂鐳�̖̌��́A�P�T�ł���B�@�@�i�I�j
�i�R�����g�j�@���̖��͎��̂悤�Ɉ�ʉ������B
����@�@��k=0n2n+1�bk �̐��̖̌��́A�Q���{�P�ł��邱�Ƃ������B
�i���j�@��k=0��2n+1�bk����k=0��2n+1�b2n+1-k����k=n+12n+12n+1�bk �Ȃ̂ŁA
�@�@��k=02n+12n+1�bk���Q��k=0��2n+1�bk
�@�Ƃ���ŁA�@��k=02n+12n+1�bk���i�P�{�P�j2n+1���Q2n+1 ���A�@��k=0��2n+1�bk���Q2n
�@����āA���߂鐳�̖̌��́A�Q���{�P�ł���B�@�@�i�I�j
�i�Q�j�@���b������-1�b���{��-1�b��-1�@�@�i�P���������|�P�j
�@�i���@�Q�l�F�u�p�X�J���̎O�p�`�v�́i�Q�j �j
�@���̌����́A�u�a�̌����v�Ƃ�������B
�i�ؖ��j�@�� �̂��̂��� �� ���o���ꍇ�̐��́A���̂Q�̏ꍇ�̐��̘a�ł���B
�@����̂��̂��܂܂Ȃ��ꍇ�̐��́A�@��-1�b���@�ʂ�
�@����̂��̂��܂ޏꍇ�̐��́A�@��-1�b��-1�@�ʂ�@�@�i�؏I�j
�i�R�j�@���E���b�������E��-1�b��-1�@�i���@�Q�l�F�u�p�X�J���̎O�p�`�v�́i�T�j �j
�i�ؖ��j�@�� �l���钆���� �� �l��I��ŁA���̒��ň�l�ǒ������߂�ꍇ�̐��ƁA�ǒ���
�@��l�I��ŁA�c��� ���|�P �l����Lj� ���|�P �l��I�ԏꍇ�̐��͓������B�@�@�i�؏I�j
�@�u���E���b�������E��-1�b��-1�v�Ƃ���������L�̑g�����_�I�ؖ����ӎ�����Ε�����₷��
���A���S�҂ɂƂ��Ă͊o�����炢��������Ȃ��B
| �@���w�̐�发�ł́A�g�����̋L���Ƃ��āA���b�� �̑���ɁA | �Ƃ����L�����p����� |
��ꍇ������B���̋L����p����ƁA��L�̐�����
�@![]()
�ƕ\�����B���̌����́A�u���肾���̌����v�Ƃ��Ă�邪�A���̕\������A���̈Ӗ���
���ɓ`����Ă���悤�Ɋ�����B
�i�S�j�@���b0�{���b1�{���b2�{���b3�{�E�E�E�{���b���{�E�E�E�{���b�����Q��
�@�i���@�Q�l�F�u�p�X�J���̎O�p�`�v�́i�R�j �j
�i�ؖ��j�@�W�J�����i�d�o�j�ɂ����āA�����P �Ƃ����悢�B�@�i�؏I�j
�i�ʏj�@�� �̗v�f����Ȃ�W���`�̕����W���̌��𐔂���B
�@�����W���̗v�f�̌��ɒ��ڂ��āA�� �̗v�f����Ȃ镔���W���̌��́A���b�� ��
�Ȃ̂ŁA�����W���̌��́A���b0�{���b1�{���b2�{���b3�{�E�E�E�{���b���{�E�E�E�{���b��
�@�Ƃ���ŁA�� �̗v�f�̂��ꂼ�ꂪ�����W���̗v�f�ɂȂ邩�ǂ����̏ꍇ�̐����l���āA
�����W���̌��́A�Q�� �ŁA���炩�ɁA���҂͓������̂ŁA
�@���b0�{���b1�{���b2�{���b3�{�E�E�E�{���b���{�E�E�E�{���b�����Q���@�@�i�ʏ؏I�j
�i�T�j�@���b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b���{�E�E�E�{�i�|�P�j�����b�����O
�i�ؖ��j�@�W�J�����i�d�o�j�ɂ����āA�����|�P �Ƃ����悢�B�@�i�؏I�j
�@�@�i���@�g�����_�I�ؖ��j
�i�U�j�@���b0�{���b2�{���b4�{�E�E�E���Q��-1
�i�ؖ��j�@�i�S�j�{�i�T�j��薾�炩�B�@�i�؏I�j�@�@�@�i���@�g�����_�I�ؖ��j
�@���R�A�i�S�j�|�i�T�j���A�@���b1�{���b3�{���b5�{�E�E�E���Q��-1�@��������B
�@���g�o�����������b�ɂȂ��Ă���g�m�u�e�m�v���A���̖����g�����A�l�@���ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�Q���Q�R���t���j
�@��L�i�U�j�̂悤�ɁA���b�� �� �� �������̂Ƃ��̓����́A�悭�m���Ă��܂��B�ł́A�� ���R��
�{���A�S�̔{���ł���Ƃ��̘a�͂ǂ��Ȃ�ł��傤���B
����@�@���̘a�����߂�B
(�C) �@���b0�{���b3�{���b6�{�E�E�E
�@�i�O�������� �����R�̔{���ł��� �� ���ׂĂɂ��āA���b�� �̘a�j
(��)�@���b0�{���b4�{���b8�{�E�E�E
�@�i�O�������� �����S�̔{���ł��� �� ���ׂĂɂ��āA���b�� �̘a�j
�@��w�����ɏo�肷��Ȃ�A�� �𐧌�����ł��傤�B�Ⴆ�A�����炢�ɁD�D�D�B
(�C)�f�@�� ���U�̔{���ł���Ƃ��A���b0�{���b3�{���b6�{�E�E�E�{���b�� �̘a�����߂�B
(��)�f �� ���W�̔{���ł���Ƃ��A���b0�{���b4�{���b8�{�E�E�E�{���b�� �̘a�����߂�B
��(�C)�f(��)�f�́A(�C)(��)�ɔ�ׂĖ{���I�ɈՂ����킯�ł͂���܂��A�v�Z�͂��Ȃ�y��
�@�Ȃ�܂��B
�@�e�m����̖₢�����ɁA���� ���i�C�j�i���j��������܂����B�i�����Q�R�N�Q���Q�R���t���j
�i���j�@f(��)��(�P�{��)���@�A������������(�Q��/��)�{���E������(�Q��/��)�@�Ƃ���B
�@���̂Ƃ��A
���b0�{���b3�{���b6�{�E�E�E
���o��[j��1�`3]f(��3j)�p/�R�@�@�i���@��3�{��32�{��33���O�@�j
���o�Q���{�Q������(����/�R)�p/�R�@�@�i���@���p�̌����ƃh�E���A�u���̒藝�@�j
�@���l�ɂ��āA
���b0�{���b4�{���b8�{�E�E�E
���o��[j��1�`4]f(��4j)�p/�S���Q��-2�{�Q(��-2)/2������(����/�S)�@�@�i�I�j
�@�e�m����̃R�����g�ł��B�i�����Q�R�N�Q���Q�R���t���j
�@���� ����̂�肩���̗��K�Ƃ����Ӗ��ł̏o��Ȃ̂ŁA���� ����ȊO�̕��ɓ����Ă�������
���Ƃ�z�肵�Ă��܂����B��������Ȃ��킯�ł͂Ȃ��̂ł����D�D�D�B
�@��L�ŁA�u(�C)�f(��)�f�́A(�C)(��)�ɔ�ׂĖ{���I�ɈՂ����킯�ł͂���܂��A�v�Z�͂�
�Ȃ�y�ɂȂ�܂��B�v�Ə������̂́A���Z���x�����ӎ��������̂ł��B
�@���݂̍��Z�ł͕��f�����ʂ͂��܂���B�������A�h����A�u���̒藝������܂���A
�� �ŏꍇ�������ē����邵������܂���B
�@�����猋�\�ʓ|�ɂȂ�̂ŁA(�C)�f(��)�f���炢�ł������ȂƂ����C�����܂��B
�@�e�m���A(�C)�f(�C)�̉���^�����܂����B�i�����Q�R�N�Q���Q�S���t���j
�i�i�C�j�f�̉��j�@�� ���P�̋����������Ƃ���ƁA�@�P�{�ց{��2���O�@�A��3���P�@�ł���B
�@�@(�P�{��)�������b0�{���b1���{���b2��2�{���b3��3�{���b4��4�{���b5��5�{�E�E�E
�@���̎��ɁA�����P�A�ցA��2�@�������āA
�@�@�Q�������b0�{���b1�{���b2�{���b3�{���b4�{���b5�{�E�E�E
�@�@(�P�{��)�������b0�{���b1�ց{���b2��2�{���b3��3�{���b4��4�{���b5��5�{�E�E�E
�@�@(�P�{��2)�������b0�{���b1��2�{���b2�ց{���b3�{���b4��2�{���b5�ց{�E�E�E
�@�����ŁA���͂U�̔{��������A�@(�P�{��)����(�|��2)������2�����P
�@���l�ɁA�@(�P�{��2)����(�|��)�����������P
�@��̂R����������ƁA���Ӂ��Q���{�Q�@�A�E�Ӂ��R�i���b0�{���b3�{���b6�{�E�E�E�j
�@���������āA�@���b0�{���b3�{���b6�{�E�E�E�{���b�����i�Q���{�Q�j/�R�@�@�i�I�j
�i�i�C�j�̉��j�@(�P�{��)���{(�P�{��2)���@�̌v�Z�ȊO�͏�Ɠ����ł��B
�@�@(�P�{��)���{(�P�{��2)����(�|��2)���{(�|��)����(�|�P)���i�����{��2���j
�@�����ŁA�@�����R�̔{���̂Ƃ��A�@(�|�P)���E�Q�@�A
�@�@ �@�@�@�@�����R�̔{���łȂ��Ƃ��A�@(�|�P)���E(�|�P)��(�|�P)��-1
�@����ɏڂ������ނ���ƁA
�@�����U�Ŋ������]�肪�O�̂Ƃ��A�Q�A
�@�����U�Ŋ������]�肪�R�̂Ƃ��A�|�Q�A
�@�����U�Ŋ������]�肪�P���T�̂Ƃ��A�P
�@�����U�Ŋ������]�肪�Q���S�̂Ƃ��A�|�P
�@�ȏ���A���̂悤�ɂȂ�B
�@���߂O (������ �U)�@�̂Ƃ��A�@�i�Q���{�Q�j/�R
�@���߂R (������ �U)�@�̂Ƃ��A�@�i�Q���|�Q�j/�R
�@���߂P�A�T (������ �U)�@�̂Ƃ��A�@�i�Q���{�P�j/�R
�@���߂Q�A�S (������ �U)�@�̂Ƃ��A�@�i�Q���|�P�j/�R�@�@�i�I�j
�@�U���@�������L�̖��i�C�j��������܂����B�i�����Q�R�N�Q���Q�S���t���j
�@�i���@�Q�l�F�u�I���K�i�ցj�̐^���v�j
�i(�C)�̉��j�@��3��������(�Q��/�R)�{���E������(�Q��/�R)�@�i�� �͋����P��) ���A
�@��3��(�|�P�{i�E![]() )/�Q���ց@�i�P�̋����������j
)/�Q���ց@�i�P�̋����������j
f(��)��(�P�{��)���@���A
���b0�{���b3�{���b6�{�E�E�E
���o(�P�{��)���{(�P�{��2)���{(�P�{��3)���p/�R
���o(�|��2)���{(�|��)���{�Q���p/�R
���o(�|�P)���i��2���{�����j�{�Q���p/�R�@�@�����P
�@���ꂪ���߂�l�ƂȂ�B�@�� ���ꍇ��������A
�����R���@�̏ꍇ�@�@(�|�P)���i��2���{�����j��(�|�P)���i�P�{�P�j���Q(�|�P)��
�����R���{�P�@�̏ꍇ
�@(�|�P)���i��2���{�����j��(�|�P)��+1�i��2�{�ցj��(�|�P)��+1�i�|�P�j��(�|�P)��
�����R���{�Q�@�̏ꍇ
�@(�|�P)���i��2���{�����j��(�|�P)���i�ց{��2�j��(�|�P)���i�|�P�j���|(�|�P)��
�ƂȂ�̂ŁA���P�́A
�����R���@�̏ꍇ�@�@�i�Q���{�Q(�|�P)���j/�R
����ȊO�̏ꍇ�@�@�i�Q���|(�|�P)���j/�R�@�@�i�I�j
�Q�l�T�C�g�F�@�uA024493�v�@�A�i���j�̎Q�l�T�C�g�F�@�uA038503�v
�@�e�m����̃R�����g�ł��B�i�����Q�R�N�Q���Q�S���t���j
�@�S�ʂ�ɕ�������A�Q�ʂ�̂ق���������������܂���B
�@�ł��邾�����Z���w�͈̔͂łƍl���Ă��܂��B(��)���قƂ�Ǔ����ł����A���\�ʓ|������
�̂ŁA(��)�f�̉������Ă����܂��B�P�A�ցA��2�̑���ɁA�P�A�|�P�A���A�|�� �����邾��
�ł����D�D�D�B
�i�i���j�f�̉��j�@(�P�{��)�������b0�{���b1���{���b2��2�{���b3��3�{���b4��4�{���b5��5�{�E�E�E
�@���̎��ɁA�����P�A�|�P�A���A�|�� �������āA
�@�Q�������b0�{���b1�{���b2�{���b3�{���b4�{���b5�{�E�E�E
�@�O�����b0�|���b1�{���b2�|���b3�{���b4�|���b5�{�E�E�E
�@(�P�{��)�������b0�{���b1���|���b2�|���b3���{���b4�{���b5���{�E�E�E
�@(�P�|��)�������b0�|���b1���|���b2�{���b3���{���b4�|���b5���{�E�E�E
�@���̂S���������āA�@�Q���{(�P�{��)���{(�P�|��)�����S�i���b0�{���b4�{���b8�{�E�E�E�j
�����ŁA�@(�P�}��)2���}�Q���@�A(�P�}��)4���|�S�@�A(�P�}��)8���P�U���Q4�@�ŁA
�@�����W�̔{��������A�����W���@�Ƃ����ƁA�@(�P�}��)�����i�Q4�j�����Q��/2
�]���āA�@�Q���{(�P�{��)���{(�P�|��)�����Q���{�Q(��+2)/2 ���A
�@���b0�{���b4�{���b8�{�E�E�E�{���b�����Q��-2�{�Q(��-2)/2�@�@�i�I�j
�@�e�m����́i�i���j�f�̉��j���Q�l�ɂ��āA�i�i���j�̉��j���l���Ă݂܂����B
�i�i���j�̉��j�@ �i�S�j���A�@���b0�{���b1�{���b2�{���b3�{���b4�{�E�E�E�{���b�����Q��
�@�@�@�@�@ �@�@�i�T�j���A�@���b0�|���b1�{���b2�|���b3�{���b4�|�E�E�E�{�i�|�P�j�����b�����O
�@�܂��A���b0�{���b1���|���b2�|���b3���{���b4�{���b5���{�E�E�E��(�P�{��)��
�@�@�@�@���b0�|���b1���|���b2�{���b3���{���b4�|���b5���{�E�E�E��(�P�|��)��
�@�����̂S����ӁX�����āA�@�S�i���b0�{���b4�{���b8�{�E�E�E�j���Q���{(�P�{��)���{(�P�|��)��
�@�����ŁA�h�E���A�u���̒藝���A�@�P�{�� ��![]() �i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�@(�P�{��)�� ���Q��/2�i�������i����/�S�j�{���E�������i����/�S�j�j
���l�ɂ��āA�@(�P�|��)�� ���Q��/2�i�������i����/�S�j�|���E�������i����/�S�j�j�@�Ȃ̂ŁA
�@�S�i���b0�{���b4�{���b8�{�E�E�E�j���Q���{�Q�E�Q��/2�������i����/�S�j�@���A
�@���b0�{���b4�{���b8�{�E�E�E���Q��-2�{�Q(��-2)/2�������i����/�S�j�@�@�i�I�j
�i�V�j�@���b1�{�Q���b2�{�R���b3�{�E�E�E�{�����b���{�E�E�E�{�����b�������E�Q��-1
�i�ؖ��j�@�W�J�����i�d�o�j�̗��ӂ�������āA�����P �Ƃ����悢�B�@�i�؏I�j
�i�ʏj�@�����i�R�j�@���E���b�������E��-1�b��-1�@���A
�@�P�E���b1�����E��-1�b0
�@�Q�E���b2�����E��-1�b1
�@�R�E���b3�����E��-1�b2
�@�@�E�E�E�E�E�E�E�E�E
�@���E���b�������E��-1�b��-1
����āA
���b1�{�Q���b2�{�R���b3�{�E�E�E�{�����b��
�����i��-1�b0�{��-1�b1�{��-1�b2�{�E�E�E�{��-1�b��-1�j�����E�Q��-1�@�@�i�ʏ؏I�j
�i�R�j��p�����A�i�P�j��p�����ʏ��l������B���@�_�I�ɑ���ȁH
�i�ʏQ�j�@�����i�P�j�@���b�������b��-���@���A
�@���b1�����b��-1
�@�Q���b2���Q���b��-2
�@�R���b3���R���b��-3
�@�@�E�E�E�E�E�E�E�E�E
�@�����b���������b0
����āA�@�r�����b1�{�Q���b2�{�R���b3�{�E�E�E�{�i���|�P�j���b��-1�{�����b���@�Ƃ����ƁA
�@�r�������b0�{�i���|�P�j���b1�{�i���|�Q�j���b2�{�E�E�E�{�Q���b��-2�{���b��-1�@�Ȃ̂ŁA
�@�Q�r�������b0�{�����b1�{�����b2�{�E�E�E�{�����b��-2�{�����b��-1�{�����b��
�@�@�����i���b0�{���b1�{���b2�{�E�E�E�{���b��-2�{���b��-1�{���b���j�����E�Q��
����āA�@���b1�{�Q���b2�{�E�E�E�{�i���|�P�j���b��-1�{�����b�������E�Q��-1�@�@�i�ʏQ�I�j
�i���@�g�����_�I�ؖ��j
�i�W�j�@���b1�|�Q���b2�{�R���b3�|�E�E�E�{�i�|�P�j��-1�����b���{�E�E�E�{�i�|�P�j��-1�����b�����O
�i�ؖ��j�@�W�J�����i�d�o�j�̗��ӂ�������āA�����|�P �Ƃ����悢�B�@�i�؏I�j
�i���@�i�W�j�̈�ʉ��j
�i�ʏj�@���E���b�������E��-1�b��-1�@���A
�@�P�E���b1�����E��-1�b0
�@�Q�E���b2�����E��-1�b1
�@�R�E���b3�����E��-1�b2
�@�@�E�E�E�E�E�E�E�E�E
�@���E���b�������E��-1�b��-1
����āA
�@���b1�|�Q���b2�{�R���b3�|�E�E�E�{�i�|�P�j��-1�����b��
�����i��-1�b0�|��-1�b1�{��-1�b2�|�E�E�E�{�i�|�P�j��-1��-1�b��-1�j���O�@�@�i�ʏ؏I�j
�i���@�g�����_�I�ؖ��j
�i�X�j�@���b0�{(1/2)���b1�{(1/3)���b2�{(1/4)���b3�{�E�E�E�{(1/(n+1))���b��
�@�@���i�Q��+1�|�P�j/�i���{�P�j
�i�ؖ��j�@�W�J�����i�d�o�j�̗��ӂ��A�����O ���� �����P �܂Œ�ϕ�����悢�B�@�i�؏I�j
�i�ʏj�@���E���b�������E��-1�b��-1�@���A�@�i���{�P�j�E��+1�b��+1���i���{�P�j�E���b���@�Ȃ̂ŁA
�@�P�E��+1�b1���i���{�P�j�E���b0
�@�Q�E��+1�b2���i���{�P�j�E���b1
�@�R�E��+1�b3���i���{�P�j�E���b2
�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�i���{�P�j�E��+1�b��+1���i���{�P�j�E���b��
����āA
�@���b0�{(1/2)���b1�{(1/3)���b2�{(1/4)���b3�{�E�E�E�{(1/(n+1))���b��
���i��+1�b1�{��+1�b2�{��+1�b3�{�E�E�E�{��+1�b��+1�j/�i���{�P�j���i�Q��+1�|�P�j/�i���{�P�j�@�i�ʏ؏I�j
�i���@�g�����_�I�ؖ��j
�i�P�O�j�@���b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b���@�̒l�́A
�@�@�������@�̂Ƃ��A�@�i�|�P�j����-1�b���@�A�������@�̂Ƃ��A�@�O
�i�ؖ��j�@�����O�A�P�A�Q�A�E�E�E�A���@�ɑ��āA�i�|�P�j�����b���@�́A �����|���i�P�|���j���@��W�J������
�@�@�@�@���� ���� �̌W���ł���B
�@����āA���b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b���@�́A
�@�@�����i�P�|���j���{�����|1�i�P�|���j���{�����|2�i�P�|���j���{�E�E�E�{�����|���i�P�|���j���@��W�J�����Ƃ�
�� ���� �̌W���ł���B
�@�����ŁA
�@�����i�P�|���j���{�����|1�i�P�|���j���{�����|2�i�P�|���j���{�E�E�E�{�����|���i�P�|���j��
�������|���i�P�|���j���i�P�{���{��2�{�E�E�E�{�����j
�������|���i�P�|���j���E�i�P�|����+1�j/�i�P�|���j
���i�P�|���j��-1�E�i�����|���|����+1�j
�Ȃ̂ŁA
�@�������@�̂Ƃ��A�@�i�P�|���j��-1�E�i�����|���|����+1�j���i�P�|���j��-1�E�i�P�|����+1�j ��W�J�����Ƃ�
���� �̍��͂Ȃ��̂ŁA ���� �̌W���́A�@�O
�@�������@�̂Ƃ��A�@�i�P�|���j��-1�E�i�����|���|����+1�j ��W�J�����Ƃ��� ���� �̌W���́A
�@�i�P�|���j��-1 ��W�J�����Ƃ��� ���� �̌W���ɓ������B���Ȃ킿�A�@�i�|�P�j����-1�b���@�ł���B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�؏I�j
�i�R�����g�j�@�������@�̂Ƃ��A�@���b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b�����O�@�ł��邱
�@�@�Ƃ́A�@�i�P�{���j�������b0�{���b1���{���b2��2�{���b3��3�{�E�E�E�{���b�������@�ɂ����āA
�@�����|�P�@�Ƃ����ƁA�@�O�����b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b���@���疾�炩�����A
�@�������@�̂Ƃ��������̂�����B��L�̏ؖ��̔��z�͂ƂĂ��V�N�ł���B
�@�e�m���A�i�P�O�j�̕ʏ��l����ꂽ�B�i�����Q�R�N�R���Q�V���t���j
�@�i�P�O�j�́A������ �̂Ƃ��A���b�����O �ƍl����A���̂悤�ɂ��\���ł���B
�i�P�O�j�@���b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b�����i�|�P�j����-1�b��
�@�ꍇ�̐����Q�ʂ�l���邱�Ƃɂ���ē������ؖ�����Ƃ����Ӗ��ł̑g�����_�I�ؖ��ł�
�Ȃ����A���b������-1�b���{��-1�b��-1 ���g�����ʏł���B
�i�ʏj �����O�@�̂Ƃ��A���b0����-1�b0�@�ɒ��ӂ��āA
�@����
�����b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b��
����-1�b0�|�i��-1�b0�{��-1�b1�j�{�i��-1�b1�{��-1�b2�j
�@�@�|�i��-1�b2�{��-1�b3�j�{�E�E�E�{�i�|�P�j���i��-1�b��-1�{��-1�b���j
���i�|�P�j����-1�b���@�@�i���ׂƏ��������Ă����p�^�[���I�j�@�@�i�ʏ؏I�j
�@�i�P�O�j�Ŋl��������@��p����ƁA���́i�P�P�j�i�P�Q�j���e�Ղ��낤�B
�i�P�P�j�@���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b���@�̒l�́A
�@�@�������@�̂Ƃ��A�@��+��+1�b��+1�|���b��+1�@�A�������@�̂Ƃ��A�@��+��+1�b��+1
�i�ؖ��j�@�����O�A�P�A�Q�A�E�E�E�A���@�ɑ��āA��+���b���@�́A �i�P�{���j��+���@��W�J�����Ƃ��� ������
�@�@�@�@�W���ł���B
�@����āA���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b�� �́A
�@�i�P�{���j���{�i�P�{���j��+1�{�i�P�{���j��+2�{�E�E�E�{�i�P�{���j��+��
��W�J�����Ƃ��� ���� �̌W���ł���B
�@�����ŁA
�@�i�P�{���j���{�i�P�{���j��+1�{�i�P�{���j��+2�{�E�E�E�{�i�P�{���j��+��
���i�P�{���j���o�i�P�{���j��+1�|�P�p/��
���o�i�P�{���j��+��+1/���p�|�o�i�P�{���j��/���p
�Ȃ̂ŁA�������@�̂Ƃ��A�@�i�P�{���j��/�� ��W�J�����Ƃ� ���� �̍��͂Ȃ��̂ŁA ���߂�l�́A
�@�i�P�{���j��+��+1 ��W�J�����Ƃ��� ����+1 �̌W�� ��+��+1�b��+1 �ɓ������B
�@�������@�̂Ƃ��A���߂�l�́A�i�P�{���j��+��+1�|�i�P�{���j�� ��W�J�����Ƃ��� ����+1 �̌W����
�������B���Ȃ킿�A�@��+��+1�b��+1�|���b��+1�@�ł���B�@�@�i�؏I�j
�i���@�g�����_�I�ؖ��j
�i�NjL�j�@�����Q�V�N�P�P���Q�Q���t��
�@�i�P�P�j�̓��ʂȏꍇ�F�@���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b������+��+1�b��+1
�́A���̂悤�Ȑ}�i�����Q�A�����R�j��^���������킩��₷����������Ȃ��B�}�g��w����
���Z���̌����p�l���Ɏh������܂����B
�@�@
�i�NjL�j�@�����Q�U�N�P�O���P�W���t��
�@�����W�N�x�@�w�K�@��w�o�ϊw���̓������ɂ����āA�����i�P�P�j�̍l�������L���ɗp
������B
�@�@�����R�ȏ�̎��R���Ƃ���Ƃ��A�@����=3�`�� ���b3����+1�b4
�i���j�@�� ��=3�`�����b3��3�b3�{4�b3�{5�b3�{�E�E�E�{n�b3 �ɂ����āA���b3 �́A�i�P�{���j����W�J
�@�@�����Ƃ��� ��3 �̌W���ł���B���������āA3�b3�{4�b3�{5�b3�{�E�E�E�{n�b3 �́A
�@�i�P�{���j3�{�i�P�{���j4�{�i�P�{���j5�{�E�E�E�{�i�P�{���jn�@��W�J�����Ƃ��� ��3 �̌W���ł���B
�����ŁA
�@�i�P�{���j3�{�i�P�{���j4�{�i�P�{���j5�{�E�E�E�{�i�P�{���jn
���i�P�{���j3�o�i�P�{���j��-2�|�P�p/�����i�P�{���j��+1/���|�i�P�{���j3/��
�@����āA��3 �̌W���́A��+1�b4 �ƂȂ�B�@�@�i�I�j
�@��L�̏ؖ��͋@�B�I�œ����̎��{���̈Ӗ����������Ȃ��B��͂肻�̂��߂ɂ́A�g
�����_�I�ؖ������߂���B�i�����Q�U�N�P�O���Q�T���t���j
�i�ʉ��j�@���{�P�̐� �o�P�C�Q�C�R�C�E�E�E�C���C���{�P�p ����S�Ƃ�g�����̐����A��+1�b4�ʂ��
�@����B�����ŁA�S�̐��̍ő吔�ɒ��ڂ���B
�@�ő吔�����̂Ƃ��A�c��̂R�̐��̑I�ѕ��́A���b3 �ʂ�
�@�ő吔�����|�P�̂Ƃ��A�c��̂R�̐��̑I�ѕ��́A��-1�b3 �ʂ�
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�ő吔���S�̂Ƃ��A�c��̂R�̐��̑I�ѕ��́A3�b3 �ʂ�
�ȏォ��A�����@3�b3�{4�b3�{5�b3�{�E�E�E�{n�b3����+1�b4 �����藧�B�@�@�i�I�j
�@�܂��A�u�����i�Q�j�@���b������-1�b���{��-1�b��-1�@�@�i�P���������|�P�j�v��p����A���̂悤
�ȉ��\�ł���B
�i�ʉ��j�@���b3����+1�b4�|���b4 �A3�b4���O�@�Ȃ̂ŁA
�@�� ��=3�`�� ���b3��(��+1�b4�|���b4)�{(���b4�|��-1�b4)�{�E�E�E�{(4�b4�|3�b4)����+1�b4�@�@�i�I�j
�i�R�����g�j�@�g�����_�I�ؖ������킢�������Ă����ł����A�Ԃ��S�ď�������Ƃ�����L��
�@�@�@�@�@�@�ʉ����u���ł��ˁI
�@�i�P�P�j�ŁA������ �̂Ƃ��́A���b�������b��-���@���A���̌`�ɂ��ό`�ł���B
�@�@�@�@�@�@���b0�{��+1�b1�{��+2�b2�{�E�E�E�{��+���b������+��+1�b��
�@���̌����́A�u���a�̌����v�Ƃ�������B
��@4�b0�{5�b1�{6�b2�{7�b3��8�b3���T�U
�@�a�̌����i�Q�j ���b������-1�b���{��-1�b��-1 ���J��Ԃ��p���邱�Ƃɂ��A���a�̌���������
���Ƃ��ł���B
�i�ʏj�@���b0�{��+1�b1����+1�b0�{��+1�b1����+2�b1
�@�@��+2�b1�{��+2�b2����+3�b2
�@�@��+3�b2�{��+3�b3����+4�b3
�@�@�@�@�E�E�E�E�E�E�E�E�E
�@�@��+���b��-1�{��+���b������+��+1�b��
�@�ȏォ��A���b0�{��+1�b1�{��+2�b2�{�E�E�E�{��+���b������+��+1�b���@�����藧�B�@�@�i�ʏ؏I�j
�@���̑��a�̌�����p����ƁA�悭�m��ꂽ���̘a���������B�@
| (�`)�@�P�{�Q�{�R�{�E�E�E�{�� �� |
| (�a)�@�P2�{�Q2�{�R2�{�E�E�E�{��2 �� |
�@���ۂɁA�i�`�j�́A
�@�P�{�Q�{�R�{�E�E�E�{��
��1�b1�{2�b1�{3�b1�{�E�E�E�{���b1
��1�b0�{2�b1�{3�b2�{�E�E�E�{���b��-1
����+1�b��-1����+1�b2�����i���{�P�j/�Q
�@���l�ɁA�i�a�j�́A�܂��A�@��2���i��2�|���j�{�����Q�o���i���|�P�j/�Q�p�{�����Q���b2�{���b1�@�Ə�
����̂ŁA
�@�P2�{�Q2�{�R2�{�E�E�E�{��2
���Q�����b2�{�����b1
���Q�i2�b2�{3�b2�{�E�E�E�{���b2�j�{�i1�b1�{2�b1�{�E�E�E�{���b1�j�@�@�i�������A1�b2���O �j
���Q�i2�b0�{3�b1�{�E�E�E�{���b��-2�j�{�i1�b0�{2�b1�{�E�E�E�{���b��-1�j
���Q��+1�b��-2�{��+1�b��-1
���Q��+1�b3�{��+1�b2
���Q�i���{�P�j���i���|�P�j/�U�{�i���{�P�j��/�Q
���i���{�P�j���o�Q�i���|�P�j�{�R�p/�U
�����i���{�P�j�i�Q���{�P�j/�U
�i�R�����g�j�@�a�V�ȋ��ߕ��ł��ˁI
�i�P�Q�j�@2���b0�|2��-1�b1�{2��-2�b2�|�E�E�E�{�i�|�P�j�����b���@�̒l�́A�� �𐮐��Ƃ��āA
�@�@�����R���@�̂Ƃ��A�P�@�A�����R���{�P�@�̂Ƃ��A�O�@�A�����R���{�Q�@�̂Ƃ��A�|�P
�i�ؖ��j�@�����O�A�P�A�Q�A�E�E�E�A���@�ɑ��āA2��-���b�� �́A ��2��-���i�P�|���j2��-���@��W�J�����Ƃ�
�@�@�@�@�� ��2�� �̌W���ł���B
�@����āA2���b0�|2��-1�b1�{2��-2�b2�|�E�E�E�{�i�|�P�j�����b���@�́A
�@�@��2���i�P�|���j2���{��2��-1�i�P�|���j2��-1�{��2��-2�i�P�|���j2��-2�{�E�E�E�{�����i�P�|���j��
��W�J�����Ƃ��� ��2�� �̌W���ł���B�����ŁA
�@��2���i�P�|���j2���{��2��-1�i�P�|���j2��-1�{��2��-2�i�P�|���j2��-2�{�E�E�E�{�����i�P�|���j��
�ɁA����-1�i�P�|���j��-1�{����-2�i�P�|���j��-2�{�E�E�E�{���i�P�|���j�{�P�@�������Ă� ��2�� �̌W���͕�
���Ȃ��B
�@���̂Ƃ��A��2�� �̌W���́A���̓W�J�ɂ�蓾����B
�@�@�o�P�|��2��+1�i�P�|���j2��+1�p/�o�P�|���i�P�|���j�p���o��2��+1�i���|�P�j2��+1�{�P�p/�i��2�|���{�P�j
�@�����ŁA�P/�i��2�|���{�P�j���i�P�{���j/�i�P�{��3�j���i�P�{���j�i�P�|��3�{��6�|�E�E�E�j�@�Ȃ̂ŁA
�@��2�� �̌W���́A
�@�i�P�{���j�i�P�|��3�{��6�|�E�E�E�j
���P�{���{�O�|��3�|��4�{�O�{��6�{��7�{�O�|��9�|��10�{�O�{�E�E�E
���瓾����B���̂��Ƃ���A
�@�Q�����U���@���Ȃ킿�A�@�����R���@�̂Ƃ��A�@��2�� �̌W���́A�@�P
�@�Q�����U���{�Q�@���Ȃ킿�A�@�����R���{�P�@�̂Ƃ��A�@��2�� �̌W���́A�@�O
�@�Q�����U���{�S�@���Ȃ킿�A�@�����R���{�Q�@�̂Ƃ��A�@��2�� �̌W���́A�@�|�P�@�@�i�؏I�j
�i�P�R�j�@2���b���{�Q�E2��-1�b���{�S�E2��-2�b���{�E�E�E�{�Q���E���b�����Q2��
�i�ؖ��j�@�����O�A�P�A�Q�A�E�E�E�A���@�ɑ��āA�Q���E2��-���b���@�́A �Q���i�P�{���j2��-���@��W�J������
�@�@�@�@���� ���� �̌W���ł���B
�@����āA 2���b���{�Q�E2��-1�b���{�S�E2��-2�b���{�E�E�E�{�Q���E���b�� �́A
�@�@�@�i�P�{���j2���{�Q�i�P�{���j2��-1�{�Q2�i�P�{���j2��-2�{�E�E�E�{�Q���i�P�{���j��
��W�J�����Ƃ��� ���� �̌W���ł���B
�@�����ŁA
�i�P�{���j2���{�Q�i�P�{���j2��-1�{�Q2�i�P�{���j2��-2�{�E�E�E�{�Q���i�P�{���j��
���Q���i�P�{���j���{�Q��-1�i�P�{���j��+1�{�E�E�E�{�Q�i�P�{���j2��-1�{�i�P�{���j2��
���Q���i�P�{���j���E�o�i�P�{���j��+1/�Q��+1�|�P�p/�o�i�P�{���j/�Q�|�P�p
���o�i�P�{���j2��+1�|�Q��+1�i�P�{���j���p/�i���|�P�j
���o�Q��+1�i�P�{���j���|�i�P�{���j2��+1�p/�i�P�|���j
�@�㎮�ɂ����āA�@�P/�i�P�|���j���P�{���{��2�{��3�{�E�E�E�@�Ȃ̂ŁA
�@�o�Q��+1�i�P�{���j���|�i�P�{���j2��+1�p�i�P�{���{��2�{��3�{�E�E�E�j
��W�J�����Ƃ��� ���� �̌W���ł���B
�@�Q��+1�i�P�{���j���i�P�{���{��2�{��3�{�E�E�E�j ��W�J�����Ƃ��� ���� �̌W���́A
�@�Q��+1�i���b0�{���b1�{���b2�{���b3�{�E�E�E�{���b���j���Q��+1�E�Q�����Q2��+1
�@�i�P�{���j2��+1�i�P�{���{��2�{��3�{�E�E�E�j ��W�J�����Ƃ��� ���� �̌W���́A
�@2��+1�b0�{2��+1�b1�{2��+1�b2�{�E�E�E�{2��+1�b��
�@�Ƃ���ŁA2��+1�b0�{2��+1�b1�{�E�E�E�{2��+1�b���{2��+1�b��+1�{�E�E�E�{2��+1�b2��+1���Q2��+1
�ɂ����āA2��+1�b��+1��2��+1�b���@�A�E�E�E�A2��+1�b2��+1��2��+1�b0�@�Ȃ̂ŁA
�@�Q�i2��+1�b0�{2��+1�b1�{2��+1�b2�{�E�E�E�{2��+1�b���j���Q2��+1
���A�@2��+1�b0�{2��+1�b1�{2��+1�b2�{�E�E�E�{2��+1�b�����Q2��
�@�ȏォ��A���߂� ���� �̌W���́A�@�Q2��+1�|�Q2�����Q2���@�ƂȂ�̂ŁA
�@2���b���{�Q�E2��-1�b���{�S�E2��-2�b���{�E�E�E�{�Q���E���b�����Q2��
�����藧�B�@�@�i�؏I�j
�i���@�g�����_�I�ؖ��j
�i�P�S�j�@���b02�{���b12�{���b22�{�E�E�E�{���bn2��2���b��
�@�i���@�Q�l�F�u�p�X�J���̎O�p�`�v�́i�S�j �j
�i�ؖ��j �� �̈قȂ�ԋ��ƁA�� �̈قȂ锒��������B���̈قȂ� �Q�� �̂��̂���A��
�@�@�@�@�Ȃ� �� �̂��̂��Ƃ�g�����̐� 2���bn �́A�ԋ��̌��ŏꍇ�������āA�ԋ� �� ��
�@�@�@�@�Ɣ��� ���|�� ���Ƃ�g�����̐��̐� ���b���E���bn-��
�����b��2�@�̘a�ɓ������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�؏I�j
�@�i�P�O�j�`�i�P�R�j�̗�����l����ƁA���̂悤�ȕʏ��l������B
�i�ʏj�@���b���@�́A �i�P�{���j���@��W�J�����Ƃ��� ���� �̌W���ŁA���b�������bn-���@�ł���B
�@����āA�@(�P�{��)�������b0�{���b1���{���b2��2�{�E�E�E�{���b��-1����-1�{���b�������@�ł���A
�@(�P�{��)�������b���{���b��-1���{���b��-2��2�{�E�E�E�{���b1����-1�{���b0����
�@���̂Ƃ��A���b02�{���b12�{���b22�{�E�E�E�{���bn2 �́A
�i���b0�{���b1���{�E�E�E�{���b��-1����-1�{���b�������j�i���b���{���b��-1���{�E�E�E�{���b1����-1�{���b0�����j
���Ȃ킿�A�i�P�{���j���i�P�{���j�����i�P�{���j2�� ��W�J�����Ƃ��� ���� �̌W���ɓ������B
�@���������āA�@2���b���@�ł���B�@�@�i�ʏ؏I�j
�@���̕ʏ̍l�����͂ƂĂ���Ȃ̂ŁA�ǎ҂̕��̂��߂ɗ��K����u���Ă������B
���K����@�@���̓��������藧���Ƃ������B
�@���b���{�R�E���b��-1�{�R�E���b��-2�{���br-3����+3�b��
�i���j�@�i�P�{���j��+3���i�P�{���j���i�P�{���j3 �ɂ����āA
�i�P�{���j��+3 ��W�J�����Ƃ��� ���� �̌W�����A��+3�b��
����A�i�P�{���j�� ��W�J�����Ƃ��� ���� �̌W�����A���b�� �ŁA�i�P�{���j3 ��W�J�����Ƃ��� �P ��
�@�@�@�W�����A�P
���l�ɁA�i�P�{���j�� ��W�J�����Ƃ��� ����-1 �̌W�����A���b��-1 �ŁA�i�P�{���j3 ��W�J�����Ƃ���
�@�@�@ �� �̌W�����A3�b1���R
�i�P�{���j�� ��W�J�����Ƃ��� ����-2 �̌W�����A���b��-2 �ŁA�i�P�{���j3 ��W�J�����Ƃ��� ��2 ��
�W�����A3�b2���R
�i�P�{���j�� ��W�J�����Ƃ��� ����-3 �̌W�����A���b��-3 �ŁA�i�P�{���j3 ��W�J�����Ƃ��� ��3 ��
�W�����A3�b3���P
�Ȃ̂ŁA�i�P�{���j���i�P�{���j3 ��W�J�����Ƃ��� ���� �̌W���́A
�@���b���{�R�E���b��-1�{�R�E���b��-2�{���br-3
���������āA�@���b���{�R�E���b��-1�{�R�E���b��-2�{���br-3����+3�b���@�����藧�B�@�@�i�I�j
���������A���b�� �̒�`����p���āA�n���Ɍv�Z���Ă��ؖ��ł���B
�i�P�T�j�@���b02�|���b12�{���b22�|�E�E�E�{�i�|�P�j�����bn2�@�̒l�́A�� �𐮐��Ƃ��āA
�@�@�����Q���@�̂Ƃ��A�@�i�|�P�j��2���b���@�A�����Q���{�P�@�̂Ƃ��A�@�O
�i�ؖ��j �@���b���@�́A �i�P�{���j���@��W�J�����Ƃ��� ���� �̌W���ŁA���b�������bn-���@�ł���B
�@����āA�@(�P�|��)�������b0�|���b1���{���b2��2�|�E�E�E�{�i�|�P�j�����b�������@�ł���A
�@�@�@�@�@�@(�P�{��)�������b���{���b��-1���{���b��-2��2�{�E�E�E�{���b1����-1�{���b0�����@
�@���̂Ƃ��A���b02�|���b12�{���b22�|�E�E�E�{�i�|�P�j�����bn2 �́A
�@�@�i���b0�|���b1���{�E�E�E�{�i�|�P�j�����b�������j�i���b���{���b��-1���{�E�E�E�{���b0�����j
���Ȃ킿�A�i�P�|���j���i�P�{���j�����i�P�|��2�j�� ��W�J�����Ƃ��� ���� �̌W���ɓ������B
�@�����Q���{�P�@�̂Ƃ��́A���炩�ɁA���� �̌W���� �O
�@�����Q���@�̂Ƃ��A���� �̌W���� �i�|�P�j��2���b�� �ł���B�@�@�i�؏I�j
�i�P�U�j�@���@���f�������h�̂����ݍ���
�@���b0�E���b���{���b1�E���b��-1�{���b2�E���b��-2�{�E�E�E�{���b���E���b0����+���b��
�i�ؖ��j�@���b���@�́A �i�P�{���j���@��W�J�����Ƃ��� ���� �̌W���ŁA
�@(�P�{��)�������b0�{���b1���{���b2��2�{�E�E�E�{���b��-1����-1�{���b������
�@(�P�{��)�������b0�{���b1���{���b2��2�{�E�E�E�{���b��-1����-1�{���b������
���̂Ƃ��A�@���b0�E���b���{���b1�E���b��-1�{���b2�E���b��-2�{�E�E�E�{���b���E���b0�@�́A
�@(�P�{��)��(�P�{��)����(�P�{��)��+���@��W�J�����Ƃ��� ���� �̌W���ɓ������B
���Ȃ킿�A ��+���b�� �ł���B�@�@�i�؏I�j�@�@�@�i���@�g�����_�I�ؖ��j�@�i���@�ʏ��j
�i�P�V�j�@2��+1�b��+1�{2��+1�b��+2�{2��+1�b��+3�{�E�E�E�{2��+1�b2��+1���Q2��
�i�ؖ��j�@�Q���藝���A
�@�i�P�{���j2��+1��2��+1�b0�{2��+1�b1���{2��+1�b2��2�{�E�E�E�{2��+1�b2����2���{2��+1�b2��+1��2��+1
�����ŁA�@�����P�@�Ƃ����ƁA
�@�Q2��+1��2��+1�b0�{2��+1�b1�{2��+1�b2�{�E�E�E�{2��+1�b2���{2��+1�b2��+1
�@�܂��A�i�P�j���A�@2��+1�b0��2��+1�b2��+1�@�A2��+1�b1��2��+1�b2���@�A�E�E�E�@�Ȃ̂ŁA
�Q2��+1��2��+1�b2��+1�{2��+1�b2���{�E�E�E�{2��+1�b��+1�{2��+1�b��+1�{�E�E�E�{2��+1�b2���{2��+1�b2��+1
�@���Q�i2��+1�b��+1�{2��+1�b��+2�{�E�E�E�{2��+1�b2���{2��+1�b2��+1�j
���A�@2��+1�b��+1�{2��+1�b��+2�{�E�E�E�{2��+1�b2���{2��+1�b2��+1���Q2���@�@�i�؏I�j
�i�P�W�j�@���b0�{�R���b1�{�T���b2�{�E�E�E�{�i�Q���{�P�j���b�����i���{�P�j�E�Q��
�i�ؖ��j�@�i�P�j�@���b�������b��-���@���A
�@���b0�����b��
�@�R���b1���R���b��-1
�@�T���b2���T���b��-2
�@�@�E�E�E�E�E�E�E�E�E
�@�i�Q���{�P�j���b�����i�Q���{�P�j���b0
����āA�@�r�����b0�{�R���b1�{�T���b2�{�E�E�E�{�i�Q���{�P�j���b���@�Ƃ����ƁA
�@�r���i�Q���{�P�j���b0�{�i�Q���|�P�j���b1�{�i�Q���|�R�j���b2�{�E�E�E�{�R���b��-1�{���b��
�Ȃ̂ŁA
�Q�r���Q�i���{�P�j�i���b0�{���b1�{���b2�{�E�E�E�{���b��-2�{���b��-1�{���b���j���Q�i���{�P�j�E�Q��
����āA�@���b0�{�R���b1�{�T���b2�{�E�E�E�{�i�Q���{�P�j���b�����i���{�P�j�E�Q���@�@�i�؏I�j
�@�i�U�j�́i�C�j�i���j�̍l���������p����A���̐������e�Ղ��낤�B
�i�P�X�j�@���b0�|���b2�{���b4�|���b6�{�E�E�E���Q��/2�������i����/�S�j
�i�ؖ��j�@(�P�{��)�������b0�{���b1���|���b2�|���b3���{���b4�{���b5���{�E�E�E�@�ɂ����āA
�@���b0�|���b2�{���b4�|���b6�{�E�E�E�@�́A(�P�{��)�� �̎����ɓ������B
�@�h�E���A�u���̒藝���A�@�P�{�� ��![]() �i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�@(�P�{��)�� ���Q��/2�i�������i����/�S�j�{���E�������i����/�S�j�j
����āA�@���b0�|���b2�{���b4�|���b6�{�E�E�E���Q��/2�������i����/�S�j�@�@�i�؏I�j
�i�Q�O�j�@���b1�|���b3�{���b5�|���b7�{�E�E�E���Q��/2�������i����/�S�j
�i�ؖ��j�@(�P�{��)�������b0�{���b1���|���b2�|���b3���{���b4�{���b5���{�E�E�E�@�ɂ����āA
�@���b1�|���b3�{���b5�|���b7�{�E�E�E�@�́A(�P�{��)�� �̋����ɓ������B
�@�h�E���A�u���̒藝���A�@�P�{�� ��![]() �i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�@(�P�{��)�� ���Q��/2�i�������i����/�S�j�{���E�������i����/�S�j�j
����āA�@���b1�|���b3�{���b5�|���b7�{�E�E�E���Q��/2�������i����/�S�j�@�@�i�؏I�j
�i�Q�P�j�@���b1�{���b5�{���b9�{�E�E�E���Q��-2�{�Q(��-2)/2�E�������i����/�S�j
�i�ؖ��j �i�S�j���A�@���b0�{���b1�{���b2�{���b3�{���b4�{�E�E�E�{���b�����Q��
�i�T�j���A�@�|���b0�{���b1�|���b2�{���b3�|���b4�{�E�E�E�|�i�|�P�j�����b�����O
�܂��A�|���b0���{���b1�{���b2���|���b3�|���b4���{���b5�{�E�E�E���|���E(�P�{��)��
�@�@���b0���{���b1�|���b2���|���b3�{���b4���{���b5�|�E�E�E�����E(�P�|��)��
�����̂S����ӁX�����āA
�@�S�i���b1�{���b5�{���b9�{�E�E�E�j���Q���|���E(�P�{��)���{���E(�P�|��)��
�����ŁA�h�E���A�u���̒藝���A�@�P�{�� ��![]() �i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�@(�P�{��)�� ���Q��/2�i�������i����/�S�j�{���E�������i����/�S�j�j
���l�ɂ��āA�@(�P�|��)�� ���Q��/2�i�������i����/�S�j�|���E�������i����/�S�j�j�@�Ȃ̂ŁA
�@�S�i���b1�{���b5�{���b9�{�E�E�E�j���Q���{�Q�E�Q��/2�������i����/�S�j�@���A
�@���b1�{���b5�{���b9�{�E�E�E���Q��-2�{�Q(��-2)/2�������i����/�S�j�@�@�i�؏I�j
�i�Q�Q�j�@���b2�{���b6�{���b10�{�E�E�E���Q��-2�|�Q(��-2)/2�E�������i����/�S�j
�i�ؖ��j �i�S�j���A�@���b0�{���b1�{���b2�{���b3�{���b4�{�E�E�E�{���b�����Q��
�@�i�T�j���A�@���b0�|���b1�{���b2�|���b3�{���b4�|�E�E�E�{�i�|�P�j�����b�����O
�܂��A�|���b0�|���b1���{���b2�{���b3���|���b4�|���b5���{�E�E�E���|(�P�{��)��
�@�|���b0�{���b1���{���b2�|���b3���|���b4�{���b5���{�E�E�E���|(�P�|��)��
�����̂S����ӁX�����āA
�@�S�i���b2�{���b6�{���b10�{�E�E�E�j���Q���|(�P�{��)���|(�P�|��)��
�����ŁA�h�E���A�u���̒藝���A�@�P�{�� ��![]() �i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�@(�P�{��)�� ���Q��/2�i�������i����/�S�j�{���E�������i����/�S�j�j
���l�ɂ��āA�@(�P�|��)�� ���Q��/2�i�������i����/�S�j�|���E�������i����/�S�j�j�@�Ȃ̂ŁA
�@�S�i���b2�{���b6�{���b10�{�E�E�E�j���Q���|�Q�E�Q��/2�E�������i����/�S�j
���A�@���b2�{���b6�{���b10�{�E�E�E���Q��-2�|�Q(��-2)/2�E�������i����/�S�j�@�@�i�؏I�j
�i�Q�R�j�@���b3�{���b7�{���b11�{�E�E�E���Q��-2�|�Q(��-2)/2�E�������i����/�S�j
�i�ؖ��j �i�S�j���A�@���b0�{���b1�{���b2�{���b3�{���b4�{�E�E�E�{���b�����Q��
�@�i�T�j���A�@�|���b0�{���b1�|���b2�{���b3�|���b4�{�E�E�E�|�i�|�P�j�����b�����O
�܂��A�@���b0���|���b1�|���b2���{���b3�{���b4���|���b5�|�E�E�E�����E(�P�{��)��
�@�@�|���b0���|���b1�{���b2���{���b3�|���b4���|���b5�{�E�E�E���|���E(�P�|��)��
�����̂S����ӁX�����āA
�@�@�S�i���b3�{���b7�{���b11�{�E�E�E�j���Q���{���E(�P�{��)���|���E(�P�|��)��
�����ŁA�h�E���A�u���̒藝���A�@�P�{�� ��![]() �i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�i�������i��/�S�j�{���E�������i��/�S�j�j�@�Ȃ̂ŁA
�@�@(�P�{��)�� ���Q��/2�i�������i����/�S�j�{���E�������i����/�S�j�j
���l�ɂ��āA�@(�P�|��)�� ���Q��/2�i�������i����/�S�j�|���E�������i����/�S�j�j�@�Ȃ̂ŁA
�@�@�S�i���b3�{���b7�{���b11�{�E�E�E�j���Q���|�Q�E�Q��/2�������i����/�S�j
���A�@���b3�{���b7�{���b11�{�E�E�E���Q��-2�|�Q(��-2)/2�������i����/�S�j�@�@�i�؏I�j
�@�i�U�j�́i�C�j�̍l���������p����A���̐������e�Ղ��낤�B
�i�Q�S�j�@���b0�{���b3�{���b6�{�E�E�E���o�Q���{�Q�������i����/�R�j�p/�R�@�i�i�U�j�́i�C�j�Čf�j
�i�ؖ��j�@�� ���P�̋����������Ƃ���ƁA�ց�������(�Q��/�R)�{���E������(�Q��/�R)�@�@�i�� �͋����P��)
�ŁA�@�P�{�ց{��2���O�@�A��3���P�@�ł���B���̂Ƃ��A
�@���b0�{���b1�ց{���b2��2�{���b3�{���b4�ց{���b5��2�{�E�E�E��(�P�{��)��
�@���b0�{���b1��2�{���b2�ց{���b3�{���b4��2�{���b5�ց{�E�E�E��(�P�{��2)��
�܂��A �i�S�j���A�@���b0�{���b1�{���b2�{���b3�{���b4�{�E�E�E�{���b�����Q��
�@�����̂R����ӁX�����āA�@�R�i���b0�{���b3�{���b6�{�E�E�E�j���Q���{(�P�{��)���{(�P�{��2)��
�����ŁA
�@�P�{�ց��|��2���|�o������(�S��/�R)�{���E������(�S��/�R)�p��������(��/�R)�{���E������(��/�R)
�@�P�{��2���|�ց��|�o������(�Q��/�R)�{���E������(�Q��/�R)�p��������(��/�R)�|���E������(��/�R)
�Ȃ̂ŁA�@�@�R�i���b0�{���b3�{���b6�{�E�E�E�j���Q���{�Q������(����/�R)
�@���������āA�@���b0�{���b3�{���b6�{�E�E�E���o�Q���{�Q������(����/�R)�p/�R�@�@�i�؏I�j
�i�Q�T�j�@���b1�{���b4�{���b7�{�E�E�E���o�Q���{�Q�������i�i���{�S�j��/�R�j�p/�R
�i�ؖ��j�@�� ���P�̋����������Ƃ���ƁA�ց�������(�Q��/�R)�{���E������(�Q��/�R)�@�@�i�� �͋����P��)
�ŁA�@�P�{�ց{��2���O�@�A��3���P�@�ł���B���̂Ƃ��A
�@���b0��2�{���b1�{���b2�ց{���b3��2�{���b4�{���b5�ց{�E�E�E����2(�P�{��)��
�@���b0�ց{���b1�{���b2��2�{���b3�ց{���b4�{���b5��2�{�E�E�E����(�P�{��2)��
�@�܂��A �i�S�j���A�@���b0�{���b1�{���b2�{���b3�{���b4�{�E�E�E�{���b�����Q��
�@�����̂R����ӁX�����āA
�@�R�i���b1�{���b4�{���b7�{�E�E�E�j���Q���{��2(�P�{��)���{��(�P�{��2)��
�����ŁA
�@�P�{�ց��|��2���|�o������(�S��/�R)�{���E������(�S��/�R)�p��������(��/�R)�{���E������(��/�R)
���A
��2(�P�{��)��
���i������(�S��/�R)�{���E������(�S��/�R)�j�i������(����/�R)�{���E������(����/�R)�j
��������(�i���{�S�j��/�R)�{���E������(�i���{�S�j����/�R)
�P�{��2���|�ց��|�o������(�Q��/�R)�{���E������(�Q��/�R)�p��������(��/�R)�|���E������(��/�R)
���A
��(�P�{��2)��
���i������(�Q��/�R)�{���E������(�Q��/�R)�j�i������(����/�R)�|���E������(����/�R)�j
���i������(�S��/�R)�|���E������(�S��/�R)�j�i������(����/�R)�|���E������(����/�R)�j
��������(�i���{�S�j��/�R)�|���E������(�i���{�S�j����/�R)
�Ȃ̂ŁA�@�R�i���b1�{���b4�{���b7�{�E�E�E�j���Q���{�Q������(�i���{�S�j��/�R)
�@���������āA�@���b1�{���b4�{���b7�{�E�E�E���o�Q���{�Q������(�i���{�S�j��/�R)�p/�R�@�@�i�؏I�j
�i�Q�U�j�@���b2�{���b5�{���b8�{�E�E�E���o�Q���{�Q�������i�i���{�Q�j��/�R�j�p/�R
�i�ؖ��j�@�� ���P�̋����������Ƃ���ƁA�ց�������(�Q��/�R)�{���E������(�Q��/�R)�@�@�i�� �͋����P��)
�ŁA�@�P�{�ց{��2���O�@�A��3���P�@�ł���B���̂Ƃ��A
�@���b0�ց{���b1��2�{���b2�{���b3�ց{���b4��2�{���b5�{�E�E�E����(�P�{��)��
�@���b0��2�{���b1�ց{���b2�{���b3��2�{���b4�ց{���b5�{�E�E�E����2(�P�{��2)��
�@�܂��A �i�S�j���A�@���b0�{���b1�{���b2�{���b3�{���b4�{�E�E�E�{���b�����Q��
�����̂R����ӁX�����āA
�@�R�i���b2�{���b5�{���b8�{�E�E�E�j���Q���{��(�P�{��)���{��2(�P�{��2)��
�����ŁA�@�P�{�ց��|��2���|�o������(�S��/�R)�{���E������(�S��/�R)�p��������(��/�R)�{���E������(��/�R)
���A
��(�P�{��)��
���i������(�Q��/�R)�{���E������(�Q��/�R)�j�i������(����/�R)�{���E������(����/�R)�j
��������(�i���{�Q�j��/�R)�{���E������(�i���{�Q�j����/�R)
�P�{��2���|�ց��|�o������(�Q��/�R)�{���E������(�Q��/�R)�p��������(��/�R)�|���E������(��/�R)
���A
��2(�P�{��2)��
���i������(�S��/�R)�{���E������(�S��/�R)�j�i������(����/�R)�|���E������(����/�R)�j
���i������(�Q��/�R)�|���E������(�Q��/�R)�j�i������(����/�R)�|���E������(����/�R)�j
��������(�i���{�Q�j��/�R)�|���E������(�i���{�Q�j����/�R)
�Ȃ̂ŁA�@�R�i���b2�{���b5�{���b8�{�E�E�E�j���Q���{�Q������(�i���{�Q�j��/�R)
���������āA�@���b2�{���b5�{���b8�{�E�E�E���o�Q���{�Q������(�i���{�Q�j��/�R)�p/�R�@�@�i�؏I�j
�@�e�m���A��L�̐����̑g�����_�I�ȏؖ�����߂Ɏ��g�܂ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�R���Q�T���t���j
�@��L�̐����̒��ŁA�g�����_�I�ȏؖ����\�ȏꍇ�������A������Ȃ��Ȃ��ʔ����B�g
�����_�I�ȕʏؖ���^���邱�Ƃ��l�������B�g�����_�I�ȏؖ��Ƃ́A�ꍇ�̐����Q�ʂ��
�l���邱�Ƃɂ�蓙�������Ƃ��Ӗ�����Ƃ��Ă����B
�@(�T)����(�P�U)�̂����A���ɑg�����_�I�ȏؖ����^�����Ă���(�P�S)�ȊO�ɂ��āA�g����
�_�I�ȏؖ����\�Ȕ͈͂ŗ^���邱�Ƃ�ڕW�Ƃ������B
�@�Q���W�� ���b�� �ɂ����āA������ �̂Ƃ��A���b�����O �Ƃ���B
�@�܂��A�P���� �� �܂ł̎��R���S�̂̏W�����A[��] �ŕ\���B�P���� �� �܂ł̖��O������
��
�l�������L���ŕ\�����̂Ƃ���B
�i�T�j�@���b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b���{�E�E�E�{�i�|�P�j�����b�����O
�i�U�j�@���b0�{���b2�{���b4�{�E�E�E���Q��-1
���܂Ƃ߂�ƁA
�@�@���b0�{���b2�{�E�E�E�����b1�{���b3�{�E�E�E���Q��-1
�i�g�����_�I���߁j
�@[��] �̒����牽�l������Ȃ�ǂ����B���̂����ŁA�ǂ̐l���������ł���̂���P�ӁA
��ł���̂���Q�ӁB��R�ӂ́A �� �l�̂����A���|�P�l�͓���邩����Ȃ�����C�ӂ�
�ł���B���ꂪ�A�Q��-1�ʂ�B�Ō�̂P�l�́A�ǂ̐l��������������œ�������Ȃ���
�����P�ʂ�ɒ�܂�B
�i�V�j�@���b1�{�Q���b2�{�R���b3�{�E�E�E�{�����b���{�E�E�E�{�����b�������E�Q��-1
�i�g�����_�I�ؖ��j
�@[��] �̒����牽�l��(�O�l�ł͂Ȃ�)����Ȃ�ǂ����A���A���̔ǒ���I�ԏꍇ�̐����l
����B���ӂ́A�P�l�A�Q�l�A�R�l�A����@����Ȃ�ǂ����ǒ���I�ԂƂ��Đ��������̂ŁA�E��
�́A�܂��ǒ���I�сA�c�����l�����̔ǂɓ���邩����Ȃ����𐔂������̂ł���B�i�؏I�j
�i�V�j�@���b1�{�Q���b2�{�R���b3�{�E�E�E�{�����b���{�E�E�E�{�����b�������E�Q��-1
�i�W�j�@���b1�|�Q���b2�{�R���b3�|�E�E�E�{���i�|�P�j��-1���b���{�E�E�E�{���i�|�P�j��-1���b�����O
���܂Ƃ߂�ƁA
�@�@���b1�{�R���b3�{�T���b5�{�E�E�E���Q���b2�{�S���b4�{�U���b6�{�E�E�E�����E�Q��-2
�i�g�����_�I���߁j
�@[��] �̒����牽�l��(�O�l�ł͂Ȃ�)����Ȃ�ǂ����A���A���̔ǒ���I�ԁB���̂����ŁA
�ǂ̐l������ł���̂���P�ӁA�����ł���̂���Q�ӁB��R�ӂ́A�܂��A�ǒ���I��
�ŁA�c��� ���|�P�l�̂��� ���|�Q�l�͓���邩����Ȃ�����C�ӂɂł���B���ꂪ�A�Q��-2��
��B�Ō�̂P�l�͔ǂ̐l��������������œ�������Ȃ��������P�ʂ�ɒ�܂�B
����āA���E�Q��-2�ʂ�B
�i�X�j�@���b0�{(1/2)���b1�{(1/3)���b2�{(1/4)���b3�{�E�E�E�{(1/(n+1))���b��
�@�@���i�Q��+1�|�P�j/�i���{�P�j
�i�g�����_�I�ؖ��j
�@���ӂɁA���{�P �������āA
�@�i���{�P�j���b0�{�i���{�P�j���b1/�Q�{�E�E�E�{�i���{�P�j���b��/�i���{�P�j���Q��+1�|�P
�������B[���{�P] �̒����牽�l��(0�l�ł͂Ȃ�)����Ȃ�ǂ����ꍇ�̐��𐔂��āA
�Q��+1�|�P �ŁA���ꂪ�E�ӂł���B�܂��A���ӂ́A�ǒ���I��ŁA������ �O�l�A�P�l�A�Q�l�A���
�̔Lj�������ƍl������ŁA���ۂɂ͔ǒ����N���͖��ɂ��Ȃ�����A�ǒ����Ⴄ������
�Ǖ������Ƃ݂Ȃ����ꍇ�ł���B�@�@�i�؏I�j
�i�P�P�j�@���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b������+��+1�b��+1�|���b��+1
�i�g�����_�I�ؖ��j
�@���b��+1 ���ڍ������`
�@���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b���{���b��+1����+��+1�b��+1
�ŏؖ�����B�ԋʂP�A�Q�A�R�A�E�E�E�A���{�P�Ɣ��ʂ����炋�{�P�����o���ꍇ�̐��́A
��+��+1�b��+1�ʂ�ŁA���ꂪ�E�ӂł���B���ӂ́A���ʂȐԋʂɒ��ڂ��ďꍇ�������s���B
�ԋʂP���܂݂Q�ȏ�͊܂܂Ȃ��Ƃ��A���b��
�ԋʂQ���܂݂R�ȏ�͊܂܂Ȃ��Ƃ��A�ԋʂP�� ���̔��ʂ̌v ���{�P���� ���Ƃ�̂ŁA
��+1�b��
�@�����E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�ԋʂ����܂݂��{�P�͊܂܂Ȃ��Ƃ��A��+��-1�b��
�ԋʂ��{�P���܂ނƂ��A��+���b��
�ԋʂ��܂܂Ȃ��Ƃ��A���b��+1
�����̍��v�����ӂƂȂ�B�@�@�i�؏I�j
�i�P�R�j�@2���b���{�Q�E2��-1�b���{�S�E2��-2�b���{�E�E�E�{�Q���E���b�����Q2��
�@������ʉ����āA���̌`
(�P�R�`)�@���b���{�Q�E��-1�b��-1�{�S�E��-2�b��-2�{�E�E�E�{�Q���E��-���b0
�@�@�@����+1�b0�{��+1�b1�{��+1�b2�{����{��+1�b��
�ɂ������̂������B�i�����Q�R�N�R���Q�X���t���j
�@�����ŁA(�P�R�`)�ɂ����āA�� �� �Q���A�� �� �� �Ƃ���ƁA
���Ӂ�2���b���{�Q�E2��-1�b��-1�{�S�E2��-2�b��-2�{�E�E�E�{�Q���E���b0
�@��2���b���{�Q�E2��-1�b���{�S�E2��-2�b���{�E�E�E�{�Q���E���b��
���A(�P�R)�̍��ӂɓ������Ȃ�A�܂��A
�E�Ӂ�2��+1�b0�{2��+1�b1�{2��+1�b2�{����{2��+1�b��
�@��2��+1�b2��+1�{2��+1�b2���{2��+1�b2��-1�{����{2��+1�b��+1
�ŁA
�i2��+1�b0�{2��+1�b1����{2��+1�b���j�{�i2��+1�b2��+1�{2��+1�b2���{����{2��+1�b��+1�j���Q2��+1
���A�@�E�Ӂ��Q2���@�ƂȂ�A(�P�R)�̉E�ӂɓ������Ȃ�B
�i�P�R�`�̏ؖ��j�@�`���A[���{�P] �̕����W���ŗv�f�̌��� �� �ȉ��ł�����̂Ƃ���B
�@�E�ӂ́A���̂悤�ȕ����W���̌��ł���B
���A[���{�P] �̕����W���Ŏ��̂��̂��l����B
�@�`�m�P�n �F �P ���܂܂Ȃ��ŁA�Q�ȏ�̗v�f�̌��� �� �ł������
�@�`�m�Q�n �F �Q ���܂܂Ȃ��ŁA�R�ȏ�̗v�f�̌��� ���|�P �ł������
�@�`�m�R�n �F �R ���܂܂Ȃ��ŁA�S�ȏ�̗v�f�̌��� ���|�Q �ł������
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�`�m���n �F �� ���܂܂Ȃ��ŁA���{�P�ȏ�̗v�f�̌��� ���|���{�P �ł������
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�`�m���n �F �� ���܂܂Ȃ��ŁA���{�P�ȏ�̗v�f�̌��� �P �ł������
�@�`�m���{�P�n �F ���{�P ���܂܂Ȃ��ŁA���{�Q�ȏ�̗v�f�̌��� �O �ł������
���̂Ƃ��A
�@�`�m�P�n�Ɋ܂܂�镔���W���̌��́A���b��
�@�`�m�Q�n�Ɋ܂܂�镔���W���̌��́A
�@�@�܂��A�Q ���܂܂Ȃ��ŁA�R�ȏ�̗v�f�̌��� ���|�P �ł�����̂́A��-1�b��-1����
�@���A���̂P�ʂ�ɑ��āA�v�f�P��t������ꍇ�ƕt�����Ȃ��ꍇ�̂Q�ʂ肪����̂ŁA
�@�Q�E��-1�b��-1�@�ƂȂ�B
�@�`�m�R�n�Ɋ܂܂�镔���W���̌��́A
�@�@�܂��A�R ���܂܂Ȃ��ŁA�S�ȏ�̗v�f�̌��� ���|�Q �ł�����̂́A��-2�b��-2����
�@���A���̂P�ʂ�ɑ��āA�v�f�P�A�v�f�Q��t������ꍇ�ƕt�����Ȃ��ꍇ���A���ꂼ��
�@�Q2���S�ʂ肪����̂ŁA�@�S�E��-2�b��-2�@�ƂȂ�B
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@���̂��Ƃ���A���ӂ́A�`�m�P�n�A�`�m�Q�n�A�E�E�E�A�`�m���{�P�n�Ɋ܂܂�镔���W���̌��̑��a
�ɓ������B
�@���̂Ƃ��A�W���`���A�`�m�P�n�A�`�m�Q�n�A�E�E�E�A�`�m���{�P�n�̒��a�ɂȂ邱�Ƃ������A�ؖ���
�������邪�A����́A����قǖ��炩�ł͂Ȃ��D�D�D�B����Ȃɖ��������Ȃ��ŁA�������R
�ɂ��̂Ȃ琔�w�I�A�[�@���낤�B���b������-1�b���{��-1�b��-1 �����ŊȒP�ɂł���I
�@(�P�R�`)���A���A���Ő��藧�Ƃ��āA���{�P�A���{�P�̂Ƃ����l����B
�@��+2�b0�{��+2�b1�{��+2�b2�{����{��+2�b��+1
����+1�b0�{�i��+1�b1�{��+1�b0�j�{�i��+1�b2�{��+1�b1�j�{����{�i��+1�b��+1�{��+1�b���j
���Q�i��+1�b0�{��+1�b1�{��+1�b2�{�E�E�E�{��+1�b���j�{��+1�b��+1
���Q�i���b���{�Q�E��-1�b��-1�{�S�E��-2�b��-2�{�E�E�E�{�Q���E��-���b0�j�{��+1�b��+1
����+1�b��+1�{�Q�E���b���{�S�E��-1�b��-1�{�W�E��-2�b��-2�{�E�E�E�{�Q��+1�E��-���b0
�ƂȂ�A���w�I�A�[�@�͐�������B�@�@�i�؏I�j
�i�P�U�j�@���b0�E���b���{���b1�E���b��-1�{���b2�E���b��-2�{�E�E�E�{���b���E���b0����+���b��
�i�g�����_�I�ؖ��j
�@�ԋʂ��A���ʂ����炋�����o���ꍇ�̐��́A��+���b�� �ʂ�ŁA���ꂪ�E�ӂł���B
���ӂ́A�ԋʁE���ʂ̌��ɒ��ڂ��ďꍇ�������s���B
�Ԃ��O�Ŕ������̂Ƃ��A���b0�E���b��
�Ԃ��P�Ŕ������|�P�̂Ƃ��A���b1�E���b��-1
�@�����E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�Ԃ����Ŕ����O�̂Ƃ��A���b���E���b0
�����̍��v�����ӂƂȂ�B�@�@�i�؏I�j
�i�⑫�j�@�����Q�R�N�T���P���t��
�@��L�́i�P�U�j�̑g�����_�I�ؖ��Ƃ��āA���̂悤�Ɏ����Ă��悢�B
�@�܂��A���̕��������B
����@�@���b���{��-1�b��-1�{��-2�b��-2�{�E�E�E�{��-���b0����+1�b��
�i�ؖ��j�@�����i�P�P�j�F���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b������+��+1�b��+1�|���b��+1
��p����B�����ŁA�����i�P�j�F���b�������b��-���@����A
�@���b���{��-1�b��-1�{��-2�b��-2�{�E�E�E�{��-���b0����+1�b��
���������߂ɂ́A�@���b��-���{��-1�b��-���{��-2�b��-���{�E�E�E�{��-���b��-������+1�b��
���Ȃ킿�A�t���ɉ����āA
�@��-���b��-���{��-��+1�b��-���{�E�E�E�{��-���{�i��-1�j�b��-���{��-���{���b��-������+1�b��
�������悢�B����́A�����i�P�P�j����A
�@���Ӂ��i��-���j+��+1�b�i��-���j+1����+1�b��-��+1����+1�b�����E��
�ƂȂ莦���ꂽ�B�@�i�؏I�j
�@�i�g�����_�I�ؖ��j�Ƃ��āA���̂悤�Ɏ����Ă��悢�B
�i�ʏؖ��j�@�c�̓��̖{�����A���|���{�Q�{�A���̓��̖{�����A���{�P�{�̎s�X�H���l����B
�@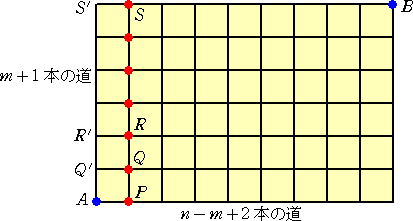
�@�`�@���@�a�@�̍ŒZ�o�H�́A�@��+1�b�� �ʂ�
�Ƃ���ŁA�@�`�@���@�o�@���@�a�@�̍ŒZ�o�H�́A�@���b�� �ʂ�
�@�`�@���@�p�f�@���@�p�@���@�a�@�̍ŒZ�o�H�́A�@��-1�b��-1 �ʂ�
�@�`�@���@�q�f�@���@�q�@���@�a�@�̍ŒZ�o�H�́A�@��-2�b��-2 �ʂ�
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�`�@���@�r�f�@���@�r�@���@�a�@�̍ŒZ�o�H�́A�@��-���b0 �ʂ�
�Ȃ̂ŁA�@���b���{��-1�b��-1�{��-2�b��-2�{�E�E�E�{��-���b0����+1�b���@�@�i�ʏ؏I�j
�@�܂��A���̂悤�ȕʏ��l������B
�i�ʏؖ��j�@�����O�A�P�A�Q�A�E�E�E�A�� �ɂ����āA��-���b��-���@�́A �����i�P�{���j��-���@��W�J�����Ƃ���
�@ ���� �̌W���ł���B�����ŁA
�i�P�{���j���{���i�P�{���j��-1�{��2�i�P�{���j��-2�{�E�E�E�{�����i�P�{���j��-��
���i�P�{���j���o�P�|����+1/�i�P�{���j��+1�p/�o�P�|��/�i�P�{���j�p
���i�P�{���j��+1�o�P�|����+1/�i�P�{���j��+1�p
���i�P�{���j��+1�|����+1�i�P�{���j��-��
�Ȃ̂ŁA���� �̌W���́A��+1�b�� �ɓ������B
�@����āA�@���b���{��-1�b��-1�{��-2�b��-2�{�E�E�E�{��-���b0����+1�b���@�@�i�ʏ؏I�j
�@��L�̕�����ʉ����āA���̒藝��B
�藝�@�@���b���E���b0�{��-1�b��-1�E��+1�b1�{�E�E�E�{��-���b0�E��+���b������+��+1�b��
�i�ؖ��j�@�c�̓��̖{�����A���|���{���{�Q�{�A���̓��̖{�����A���{�P�{�̎s�X�H���l����B
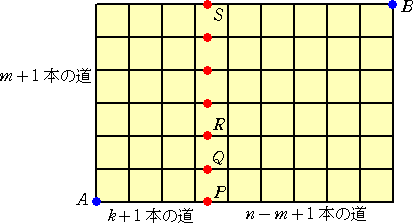
�`�@���@�a�@�̍ŒZ�o�H�́A�@��+��+1�b�� �ʂ�
�Ƃ���ŁA�@�`�@���@�o�@���@�a�@�̍ŒZ�o�H�́A�@���b0�E���b�� �ʂ�
�@�`�@���@�p�@���@�a�@�̍ŒZ�o�H�́A�@��+1�b1�E��-1�b��-1 �ʂ�
�@�`�@���@�q�@���@�a�@�̍ŒZ�o�H�́A�@��+2�b2�E��-2�b��-2 �ʂ�
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�`�@���@�r�@���@�a�@�̍ŒZ�o�H�́A�@��+���b���E��-���b0 �ʂ�
�Ȃ̂ŁA
�@���b���E���b0�{��-1�b��-1�E��+1�b1�{�E�E�E�{��-���b0�E��+���b������+��+1�b���@�@�i�؏I�j
�@���̒藝�̏ؖ��Ɠ��l�ɂ��āA���̐����i�P�U�j�F
�@���b0�E���b���{���b1�E���b��-1�{���b2�E���b��-2�{�E�E�E�{���b���E���b0����+���b��
�̕ʏ��l������B
�i�ʏؖ��j�@�c�̓��̖{�����A���{���|���{�P�{�A���̓��̖{�����A���{�P�{�̎s�X�H���l����B
�@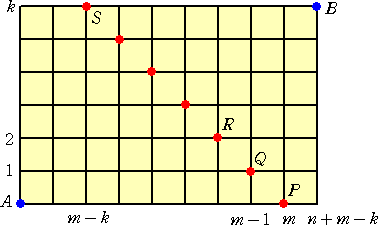
�`�@���@�a�@�̍ŒZ�o�H�́A�@��+���b�� �ʂ�
�Ƃ���ŁA�@�`�@���@�o�@���@�a�@�̍ŒZ�o�H�́A�@���b0�E���b�� �ʂ�
�@�`�@���@�p�@���@�a�@�̍ŒZ�o�H�́A�@���b1�E���b��-1 �ʂ�
�@�`�@���@�q�@���@�a�@�̍ŒZ�o�H�́A�@���b2�E���b��-2 �ʂ�
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@�`�@���@�r�@���@�a�@�̍ŒZ�o�H�́A�@���b���E���b0 �ʂ�
�Ȃ̂ŁA
�@���b0�E���b���{���b1�E���b��-1�{�E�E�E�{���b���E���b0����+���b���@�@�i�ʏ؏I�j
�i�R�����g�j�@�e�m����̐ԋʁE���ʂ̌��ɒ��ڂ����ꍇ�����Ɠ���|�ł����A�ڐ������
�@�@�@�@�@�@�ς����Ƃ������ƂŁD�D�D��(^_^;)�B
�@�c�����̂́A(�P�O)(�P�Q)(�P�T)(�P�V)�i�P�W�j(�P�X)�i�Q�O�j�i�Q�P�j�i�Q�Q�j�i�Q�R�j�i�Q�S�j�i�Q�T�j�i�Q�U�j�ł��B
�@�����ɂ��āA�g�����_�I�ȏؖ��͉\�ł��傤���B
�@���R�� �� �̊K��@���I�́A�@���I�����i���|�P�j�i���|�Q�j�E�E�E�R�E�Q�E�P�@�ŋ��߂���B
����́A�قȂ� ��
�̂��̂̏���̐��ɓ������B���̍l��������ʉ����āA
�@�قȂ� �� �̂��̂���قȂ� �� ���Ƃ鏇��̐�
���o��
�́A
�@���o�������i���|�P�j�i���|�Q�j�E�E�E�i���|���{�P�j
�ŋ��߂���B�����ŁA���� ���A�� �ɑ��āA��L�̃A�i���W�[���l����B
�@�� �̈����@���@�A���|���@�A���|�Q���@�A���|�R���@�A�E�E�E�@�A���|�i���|�P�j���@�̐ς��A��(��) �ƕ\��
���Ƃɂ���B
���Ȃ킿�A�@��(��) �����i���|���j�i���|�Q���j�i���|�R���j�E�E�E�i���|�i���|�P�j���j
��@�����O�@�̂Ƃ��A�@��(��) �����E���E�E�E�E�E���������@�ŁA�� �� �� ��ɓ������B
�@�@�����P�@�̂Ƃ��A�@��(��) �����i���|�P�j�i���|�Q�j�E�E�E�i���|���{�P�j�����o���@�ł���B
�@�@�@�@���ɁA�@��(��) �����I�@�ł���B
�@�܂��A�@�����O�@�̂Ƃ��A�@��(0) ���P�@�ŁA�@�����P�@�̂Ƃ��A�@��(1) �����@�ł���B
�@�@����āA�����O�A�P�@�ɂ��ẮA��(��) �́A���� �Ɠ������o�ł����Ƃ������ƂɂȂ�B
��@�i���{���j(1) �����{��
�@�@�i���{���j(2) ���i���{���j�i���{���|���j���i���{���j2�|�i���{���j������2�{�Q�����{��2�|�����|����
�@�����i���|���j�{�Q�����{���i���|���j����(2)�{�Q��(1)��(1)�{��(2)
���Ȃ킿�A�@�i���{���j(2) ����(2)�{�Q��(1)��(1)�{��(2)�@�ƂȂ�A���ƂȂ������̌���
�@�i���{���j2����2�{�Q�����{��2
�Ɏ��Ă���B���l�ɁA
�@�@�i���{���j(3) ���i���{���j�i���{���|���j�i���{���|�Q���j
�@���i���{���j3�|�R�i���{���j2���{�Q�i���{���j��2
�@����3�{�R��2���{�R����2�{��3�|�R��2���|�U�������|�R��2���{�Q����2�{�Q����2
�@����3�|�R��2���{�Q����2�{�R��2���|�U�������{�R����2�{��3�|�R��2���{�Q����2
�@�����i���|���j�i���|�Q���j�{�R���i���|���j���{�R�����i���|���j�{���i���|���j�i���|�Q���j
�@����(3)�{�R��(2)��(1)�{�R��(1)��(2)�{��(3)
���Ȃ킿�A�@�i���{���j(3) ����(3)�{�R��(2)��(1)�{�R��(1)��(2)�{��(3)�@�����藧�B
�i�R�����g�j�@��(��) �ɂ��āA�Q���藝�Ɠ��l�̎������藧�悤�Ŗʔ����ł��ˁI
�@�㎮�́A�@�i���{���j(3) ���i���{���j(2)�i���{���|�Q���j���i��(2)�{�Q��(1)��(1)�{��(2)�j�i���{���|�Q���j
�@�@�@�@�@�@����(2)�i���{���|�Q���j�{�Q��(1)��(1)�i���{���|�Q���j�{��(2)�i���{���|�Q���j
�@�@�@�@�@�@����(3)�{��(2)���{�Q��(1)��(1)�i���|���j�{�Q��(1)��(1)�i���|���j�{����(2)�{��(3)
�@�@�@�@�@�@����(3)�{�R��(2)��(1)�{�R��(1)��(2)�{��(3)
�Ƃ��Ă����߂���B��L����ʉ����āA
�K��Q���藝
�@�i���{���j�i���j�����b0���i���j�{���b1���i��-1�j��(1)�{���b2���i��-2�j��(2)�{�E�E�E�{���b����(��)
�����藧���Ƃ𐔊w�I�A�[�@�ɂ�莦���Ă������B
�i�ؖ��j�@�����P�@�̂Ƃ��A�@�i���{���j(1) �����{����1�b0���i1�j�{1�b1���i1�j�@��萬�藧�B
�@�������i�����P�j�̂Ƃ��A���藧�Ɖ��肷��B���Ȃ킿�A
�@�@�i���{���j�i���j�����b0���i���j�{���b1���i��-1�j��(1)�{���b2���i��-2�j��(2)�{�E�E�E�{���b����(��)
���̂Ƃ��A
�i���{���j�i��+1�j
�� �i���{���j�i���j�i���{���|�����j
���i���b0���i���j�{���b1���i��-1�j��(1)�{���b2���i��-2�j��(2)�{�E�E�E�{���b����(��)�j�i���{���|�����j
�����b0���i���j�i���{���|�����j�{���b1���i��-1�j��(1)�i���{���|�����j�{���b2���i��-2�j��(2)�i���{���|�����j�{
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�E�E�E�{���b����(��)�i���{���|�����j
����+1�b0���i��+1�j�{���b0���i���j���{���b1���i��-1�j��(1)�i���|�i���|�P�j���{���|���j
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�E�E�E�{���b����(��)�i���{���|�����j
����+1�b0���i��+1�j�{���b0���i���j��(1)�{���b1���i���j��(1)�{���b1���i��-1�j��(2)�{
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�{�E�E�E�{���b����(��)�i���{���|�����j
����+1�b0���i��+1�j�{��+1�b1���i���j��(1)�{��+1�b2���i��-1�j��(2)�{�E�E�E�{��+1�b��+1��(��+1)
�ƂȂ�A�������{�P�@�̂Ƃ������藧�B
�@���������āA���ׂĂ̎��R�� �� �ɂ��āA
�@�@�@�i���{���j�i���j�����b0���i���j�{���b1���i��-1�j��(1)�{���b2���i��-2�j��(2)�{�E�E�E�{���b����(��)
�����藧�B�@�@�i�؏I�j
�@���̊K��Q���藝��p����ƁA
�i�P�U�j�@���b0�E���b���{���b1�E���b��-1�{���b2�E���b��-2�{�E�E�E�{���b���E���b0����+���b��
�͎��̂悤�ɂ��������Ƃ��o����B
�i�ʏj�@���b�������i���|�P�j�E�E�E�i���|�i���|�P�j�j/���I�����i���j/���I�@�i���@�����P�j
�@���l�ɁA�@���b���|�������i���|�P�j�E�E�E�i���|�i���|���|�P�j�j/�i���|���j�I�����i���|���j/�i���|���j�I
�@����āA�@���b���E���b���|�������i���j/���I�E���i���|���j/�i���|���j�I
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����b�����i���j���i���|���j/���I�@�@�i�����O�A�P�A�Q�A�E�E�E�A���j
�@�����ŁA�@���b�����i���j���i���|���j �́A�i���{���j�i���j �̑� ���{�P ���Ȃ̂ŁA���̑��a�́A
�@�@�i���{���j�i���j /���I���i���{���j�i���{���|�P�j�E�E�E�i���{���|���{�P�j/���I�����{���b��
�@�ɓ������B�@�@�i�ʏ؏I�j
�@�K��Q���藝��p���āA���̐������������B
�i�Q�V�j�@���b0�E���b���|��+1�b1�E���b��-1�{�E�E�E�{�i�|�P�j����+���b���E���b0����-��-1�b��
�i�ؖ��j�@�i�|�P�j����+���b�����i�|�P�j���i���{���j�i���{���|�P�j�E�E�E�i���{�P�j/���I
�@�@�@�@�@�@�@�@�@�@�@�@�@���i�|���|�P�j�i�|���|�Q�j�E�E�E�i�|���|���j/���I
�@�@�@�@�@�@�@�@�@�@�@�@�@���i�|���|�P�j�i���j/���I�@�i���@�����P�j
�@���l�ɁA�@���b���|�������i���|�P�j�E�E�E�i���|�i���|���|�P�j�j/�i���|���j�I�����i���|���j/�i���|���j�I
�@����āA�i�|�P�j����+���b���E���b���|�����i�|���|�P�j�i���j/���I�E���i���|���j/�i���|���j�I
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�����b���i�|���|�P�j�i���j���i���|���j/���I�@�@�i�����O�A�P�A�Q�A�E�E�E�A���j
�@�����ŁA���b���i�|���|�P�j�i���j���i���|���j �́A�i���|���|�P�j�i���j �̑� ���{�P ���Ȃ̂ŁA
���̑��a�́A�@�i���|���|�P�j�i���j /���I����-��-1�b���@�@�ɓ������B�@�@�i�؏I�j
�@��L�̂��낢��Ȑ����̏ؖ��ŁA�W�J�����F
�m�����������̂Q���藝
�@�i�P�{���j�������b0�{���b1���{���b2��2�{���b3��3�{�E�E�E�{���b�������{�E�E�E�{���b������
�̗L�p�����m���߂�ꂽ�B���l�̋c�_���A�i�P�{���{��2�j���@�ɂ����Ă��s�������B
�@��̓I�ȏꍇ�ɂ��ẮA�u�p�X�J���̎O�p�`�v�Œ��ׂ��Ă���B�����ł́u���̎O�p
�`�v�Ƃ������̂������B
�@���܁A�i�P�{���{��2�j���@��W�J���āA
�@�@�i�P�{���{��2�j�������a0�{���a1���{���a2��2�{���a3��3�{�E�E�E�{���a2����2��
�ƁA�e���̌W�����߂�B
��@�����O�@�̂Ƃ��A�@�i�P�{���{��2�j0���P�@���A�@0�a0���P
�@�@�����P�@�̂Ƃ��A�@�i�P�{���{��2�j1���P�{���{��2�@���A�@1�a0���P�@�A1�a1���P�@�A1�a2���P
�@�@�����Q�@�̂Ƃ��A�@�i�P�{���{��2�j2���P�{�Q���{�R��2�{�Q��3�{��4�@���A
�@�@�@�@�@�@2�a0���P�@�A2�a1���Q�@�A2�a2���R�@�A2�a3���Q�@�A2�a4���P
�@���a0�@�A���a1�@�A���a2�@�A�E�E�E�@�A���a2���@�ɂ��āA���̐��������藧�B
�i�a�P�j�@���a�������a2��-��
�i�ؖ��j�@�i�P�{���{��2�j�������a0�{���a1���{�E�E�E�{���a�������{�E�E�E�{���a2����2���@�� �� �ɁA�P/�� ���
�@�@�@�@�����āA
�@�i�P�{�P/���{�P/��2�j�������a0�{���a1/���{�E�E�E�{���a��/�����{�E�E�E�{���a2��/��2��
���ӂɁA��2�� ���|���āA
�@�i�P�{���{��2�j�������a0��2���{���a1��2��-1�{�E�E�E�{���a����2��-���{�E�E�E�{���a2��
�����a2���{���a2��-1���{�E�E�E�{���a2��-�������{�E�E�E�{���a1��2��-1�{���a0��2��
����āA���� �̌W�����r���āA�@���a�������a2��-���@�����藧�B�@�@�i�؏I�j
�i�a�Q�j�@��+1�a�������a��-2�{���a��-1�{���a��
�@�i�������A�����O�@�܂��́@�����Q���@�̂Ƃ��A���a�����O�@�Ƃ���B�j
�i�ؖ��j�@��+1�a�� �́A�i�P�{���{��2�j��+1 ��W�J�����Ƃ��� ���� �̌W���ł���B����A
�@�i�P�{���{��2�j��+1���i�P�{���{��2�j���E�i�P�{���{��2�j
���i���a0�{�E�E�E�{���a��-2����-2�{���a��-1����-1�{���a�������{�E�E�E�{���a2����2���j�E�i�P�{���{��2�j
��W�J�����Ƃ��� ���� �̌W���́A�@���a��-2�{���a��-1�{���a��
����āA�@��+1�a�������a��-2�{���a��-1�{���a���@�����藧�B�@�@�i�؏I�j
�i�a�R�j�@���a0�{���a1�{���a2�{�E�E�E�{���a2�����R��
�i�ؖ��j�@�i�P�{���{��2�j�������a0�{���a1���{���a2��2�{�E�E�E�{���a2����2���@�ɂ����āA
�@�@�����P�@�Ƃ����ƁA�@���a0�{���a1�{���a2��2�{�E�E�E�{���a2�����R���@�@�i�؏I�j
�i�a�S�j�@���a0�|���a1�{���a2�|�E�E�E�{���a2�����P
�i�ؖ��j�@�i�P�{���{��2�j�������a0�{���a1���{���a2��2�{�E�E�E�{���a2����2���@�ɂ����āA
�@�@�����|�P�@�Ƃ����ƁA�@���a0�|���a1�{���a2�|�E�E�E�{���a2�����P�@�@�i�؏I�j
�i�a�T�j�@���a02�{���a12�{���a22�{�E�E�E�{���a2��2��2���a2��
�i�ؖ��j�@�i�P�{���{��2�j�������a0�{���a1���{���a2��2�{�E�E�E�{���a2����2���@�ɂ����āA
�@���a�������a2��-���@���A
�@�i�P�{���{��2�j�������a2���{���a2��-1���{���a2��-2��2�{�E�E�E�{���a0��2��
���̂Ƃ��A�@���a02�{���a12�{���a22�{�E�E�E�{���a2��2�@�́A
�@�i�P�{���{��2�j���i�P�{���{��2�j�����i�P�{���{��2�j2��
��W�J�����Ƃ��� ��2�� �̌W���ɓ������B������ɁA����́A�@2���a2��
����āA�@���a02�{���a12�{���a22�{�E�E�E�{���a2��2��2���a2���@�@�i�؏I�j
�@�i�W�j����ʉ����āA���̐�����B
�i�Q�W�j�@�P�����b1�|�Q�����b2�{�R�����b3�|�E�E�E�{�i�|�P�j��-1�������b�����O�@�i�������j
�@�@�@�P�����b1�|�Q�����b2�{�R�����b3�|�E�E�E�{�i�|�P�j��-1�������b�����i�|�P�j��-1���I
�@�@�����P�@�̂Ƃ��́A�@���E���b�������E��-1�b��-1�@�Ƃ����������L���ł��������A�����Q�@�ɂ�
�@���Ă͕ʂȕ��K�v�ł���B
�@�����ŁA���̖����l����B
�@���P�A���Q�A�E�E�E�A���� ���P��ɔԍ����ɒu����Ă���B���� �� �̔��ɁA�قȂ�
�� �̋���C�ӂɓ���Ă����B
�@���̂Ƃ��A���ꂼ��̔��ɏ��Ȃ��Ƃ��P�̋��������Ă���ꍇ�̐������߂�B
�i���j�@�قȂ� �� �̋����A�� �̔��ɓ����ꍇ�̐��́A���� �ʂ肠��B���̒��ɂ́A��
�@�@�ꂩ�̔�����ɂȂ��Ă���ꍇ���܂܂��B���̏ꍇ�̐��́A
�@�@�@���b1�E�i���|�P�j���|���b2�E�i���|�Q�j���{�E�E�E�|�i�|�P�j��-1���b��-1�E�P��
�@�@����āA���ꂼ��̔��ɏ��Ȃ��Ƃ��P�̋��������Ă���ꍇ�̐��́A������ɂ��A
�@�@�@�����|���b1�E�i���|�P�j���{���b2�E�i���|�Q�j���|�E�E�E�{�i�|�P�j��-1���b��-1�E�P���@�@�i�I�j
�@�㎮��p���āA�i�Q�W�j�́A���̂悤�Ɏ������B
�i�i�Q�W�j�̏ؖ��j�@���b�������b��-���@���A�㎮�́A
�@�@�@���b�������|���b��-1�E�i���|�P�j���{���b��-2�E�i���|�Q�j���|�E�E�E�{�i�|�P�j��-1���b1�E�P��
�@�Ƃ�����������B�@�������@�̂Ƃ��A���̏ꍇ�̐��́A���炩�� �O �ł���B
�@�@���Ȃ킿�A
�@�@�@���b�������|���b��-1�E�i���|�P�j���{���b��-2�E�i���|�Q�j���|�E�E�E�{�i�|�P�j��-1���b1�E�P�����O
�@���ӂɁA�i�|�P�j��-1 ���|���āA
�@�@�@�@�@�@�i�|�P�j��-1���b�������{�E�E�E�{���b3�E�R���|���b2�E�Q���{���b1�E�P�����O
�@���Ȃ킿�A�@�P�����b1�|�Q�����b2�{�R�����b3�|�E�E�E�{�i�|�P�j��-1�������b�����O�@�����藧�B
�@�������@�̂Ƃ��A���̏ꍇ�̐��́A���炩�� ���I �ł���B
�@�@���Ȃ킿�A
�@�@�@���b�������|���b��-1�E�i���|�P�j���{���b��-2�E�i���|�Q�j���|�E�E�E�{�i�|�P�j��-1���b1�E�P�������I
�@���ӂɁA�i�|�P�j��-1 ���|���āA
�@�@�@�@�@�@�i�|�P�j��-1���b�������{�E�E�E�{���b3�E�R���|���b2�E�Q���{���b1�E�P�����i�|�P�j��-1���I
�@���Ȃ킿�A
�@�@�P�����b1�|�Q�����b2�{�R�����b3�|�E�E�E�{�i�|�P�j��-1�������b�����i�|�P�j��-1���I
�@�����藧�B�@�@�i�؏I�j
�i�Q�X�j�@�� ��f���Ƃ���B���̂Ƃ��A���̓��������藧�B
�i�C�j�@��-1�b���߁i�|�P�j���@�i�������@���j�@�@�������A�@�O���������|�P
�i���j�@��+1�b���߂O�@�i�������@���j�@�@�������A�@�Q���������|�P
�i�n�j�@�����b���������b���@�i�������@���j�@�@�������A�@���������O
�i�j�j�@2���b���߂Q�@�i�������@���j
�@��L�̐������A�e�m�������ꂽ�B�i�����Q�R�N�T���P�X���t���j
�@�Q���W���� �� ��@�Ƃ��Ă̒l�ɂ��ẮA
�@���b���߂O�@�i�������@���j�@�@�������A�O��������
����{�I�ł��B
���ۂɁA ���b�������i���|�P�j�E�E�E�i���|���{�P�j/���I�@�͐����ŁA���i���|�P�j�E�E�E�i���|���{�P�j��
�@���I�Ŋ����邪�A�� �͑f���Ȃ̂ŁA�i���|�P�j�i���|�Q�j�E�E�E�i���|���{�P�j�� ���I�Ŋ����
��B����āA���b�� �́A�� �Ŋ�����B
�@���ꂩ��A�@�i�P�{���j���߂P�{�����@�i�������@���j�@�����藧�B
�@������g���Ώؖ��ł��܂��B(�n)�ȊO�͎g��Ȃ��ł��ؖ��ł��܂����A(�n)�͍��̂Ƃ���
�g��Ȃ��ؖ��͂킩��܂���B
(�C)�̏ؖ��F�@ �i�P�{���j��-1�߁i�P�{�����j/�i�P�{���j���P�|���{��2�|��3�{����{����-1�@��薾�炩�B
(��)�̏ؖ��F�@ �i�P�{���j��+1�߁i�P�{�����j�i�P�{���j���P�{���{�����{����+1�@��薾�炩�B
(�n)�̏ؖ��F�@ �i�P�{���j�����߁i�P�{�����j���@��薾�炩�B
(�j)�̏ؖ��F�@ (�n)�ŁA�����Q�A�����P�@�Ƃ����悢�B
�@�i�ʏj �i�P�{���j2���߁i�P�{�����j2���P�{�Q�����{��2���@��薾�炩�B
�@�i�P�{���j���߂P�{�����@�i�������@���j�@���g��Ȃ��ؖ����l���Ă݂܂����B
(�C)�̕ʏF�@����́A���I�A���q�́�(�|�P)���E���I�@�i�������@���j�@��薾�炩�B
(��)�̕ʏF�@ ���q�͑f���� �� ���܂ݕ���͊܂܂Ȃ�����B
(�j)�̕ʏF�@�u �i�P�S�j�@���b02�{���b12�{���b22�{�E�E�E�{���bn2��2���b���@�v�ŁA������ �Ƃ���B
�@���b02�{���b12�{���b22�{�E�E�E�{���b��2��2���b���@���A���藧�B
�i�NjL�j�@���g�o�ǎ҂̂g�m�uezofuji_z�v���A�i�Q�X�j�̊g���ɂ��čl�@���ꂽ�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�T�N�W���P�W���t���j
�i�Q�X�j�f�@�� ��f���Ƃ���B���̂Ƃ��A���̓��������藧�B
�i�C�j�f�@����-1�b���߁i�|�P�j���@�i�������@���j�@�@�������A�@�O�����������|�P
�i���j�f�@����+���b���߂O�@�i�������@���j�@�@�������A�@�O���������|�P�A������������
�@���̂悤�ɁA�i�Q�X�j�́u���� �o�[�W�����v�Ɋg������܂��B
���@���ɁA�����O�̂Ƃ��́A�@���b���߂O�@�i�������@���j�@�̊g���ƂȂ��Ă܂��B
���@�܂��A�����P�̂Ƃ����A�@�P�������������͈̔͂ŁA�����₩�ł����g������Ă��܂��B
�i�n�j�f�@�O�����A�������|�P �̂Ƃ��A
�@�@������ �Ȃ�A����+���b����+�������b���E���b���@�i�������@���j
�@�@�������Ȃ�A����+���b����+���߂O�@�i�������@���j�@�@�������A�@�����{���������{�����O
�@�ؖ��́A�i�P�{���j����+h�߁i�P�{��p�ja�E�i�P�{���jh�@�i�������@���j�@���g���悢�ł��B
�i�n�j�f���J��Ԃ��g���Ɓi�A�[�@�ɂ��j�A���̂��Ƃ�������܂��B�@
�@������ �����i�\�����������̈ʂ̐����e�X �����A�����i0�������A���������|1�j�Ƃ��āA
�@�@������e�E��e + ��e-1�E��e-1 + �c + ��1�E�� + ��0�@�i��e��0�j�A
�@�@������e�E��e + ��e-1�E��e-1 + �c + ��1�E�� + ��0�@�i��e����e�j
�ƕ\�킷�Ƃ��A
�E�@���������� �i0���͂���e�j�@�Ȃ�A�@���b�� �� ����= 0�`e�@�����b���� ��0�@�i�������@���j
�E�@0������e�@�ɑ��āA�@�����������@ �Ȃ�A�@���b�� ��0�@�i�������@���j
�@�ŏ��ɏq�ׂ�(�C)�A(��)�̊g���o�[�W����(�C)�f�A(��)�f�́A���̌��ʂ̓��ʂȏꍇ�Ƃ��Ď�
�����Ƃ��ł��܂��B
�i����������������g������A�g�����_�I�Ȓ��ڏؖ����\�Ǝv���܂��B�j
�@����ɁA�e�m����́A�u��g�̐��w�����U�v�ɍڂ��Ă���Q���W���̌����ŁA���̃y�[�W�ɂ�
�����̂Ƃ��āA�R������ꂽ�B�i�����Q�R�N�T���P�X���t���j
�i�R�O�j�@�P2���b1�{�Q2���b2�{�R2���b3�{�E�E�E�{��2���b�������i���{�P�j�E�Q��-2
�i�R�P�j�@���b0�|(1/2)���b1�{(1/3)���b2�|�E�E�E�{�i�|�P�j��(1/(n+1))���b�����P/�i���{�P�j
�i�R�Q�j�@���b12�{�Q�E���b22�{�R�E���b32�{�E�E�E�{���E���bn2�����E2��-1�b��
�@�ؖ����l���Ă݂Ă��������B
�@���̂e�m����̖₢�����ɑ��A���� ���ؖ����ꂽ�B�i�����Q�R�N�T���Q�P���t���j
�i�R�O�j�@�P2���b1�{�Q2���b2�{�R2���b3�{�E�E�E�{��2���b�������i���{�P�j�E�Q��-2
�i�ؖ��j�@�i�P�{���j�������b0�{���b1���{���b2��2�{���b3��3�{�E�E�E�{���b�������@�ɂ����āA
�@���ӂ� �� �Ŕ������āA����ɗ��ӂ� �� ���|���āA
�@�����i�P�{���j��-1�����b1���{�Q���b2��2�{�R���b3��3�{�E�E�E�{�����b������
�@����ɁA���ӂ� �� �Ŕ������āA����ɗ��ӂ� �� ���|���āA
�����i�P�{���j��-1�{���i���|�P�j��2�i�P�{���j��-2�����b1���{�Q2���b2��2�{�R2���b3��3�{�E�E�E�{��2���b������
�@���̓����ɂ����āA�����P �������āA
�@���E�Q��-1�{���i���|�P�j�E�Q��-2�����b1�{�Q2���b2�{�R2���b3�{�E�E�E�{��2���b��
���Ȃ킿�A�@�P2���b1�{�Q2���b2�{�R2���b3�{�E�E�E�{��2���b�������i���{�P�j�E�Q��-2�@�@�i�؏I�j
�i�R�P�j�@���b0�|(1/2)���b1�{(1/3)���b2�|�E�E�E�{�i�|�P�j��(1/(n+1))���b�����P/�i���{�P�j
�i�ؖ��j�@�i�P�|���j�������b0�|���b1���{���b2��2�|���b3��3�{�E�E�E�{�i�|�P�j�����b�������@�̗��ӂ��A
�@�����O ���� ������ �܂Œ�ϕ����A����ɗ��ӂ� �� �ł���āA
�o�P�|�i�P�|���j��+1�p/�o���i���{�P�j�p�����b0�|���b1��/2�{���b2��2/3�|�E�E�E�{�i�|�P�j�����b������/�i��+1�j
�@���̓����ɂ����āA�����P �������āA
�@�P/�i���{�P�j�����b0�|���b1�i1/2�j�{���b2�i1/3�j�|�E�E�E�{�i�|�P�j�����b���i1/�i��+1�j�j
���Ȃ킿�A
�@���b0�|(1/2)���b1�{(1/3)���b2�|�E�E�E�{�i�|�P�j��(1/(n+1))���b�����P/�i���{�P�j�@�@�i�؏I�j
�i�R�Q�j�@���b12�{�Q�E���b22�{�R�E���b32�{�E�E�E�{���E���bn2�����E2��-1�b��
�i�ؖ��j�@�����i�P�{���j��-1�����b1���{�Q���b2��2�{�R���b3��3�{�E�E�E�{�����b�������@�E�E�E�i�C�j
�@�i�P�{���j�������b0�{���b1���{���b2��2�{���b3��3�{�E�E�E�{���b�������@�@�ɂ����āA
���b�������bn-���@���A
�@�i�P�{���j�������b���{���b��-1���{���b��-2��2�{���b��-3��3�{�E�E�E�{���b0�����@�E�E�E�i���j
����āA�i�C�j�Ɓi���j��ӁX�|���āA
�@�����i�P�{���j2��-1
���i���b1���{�Q���b2��2�{�E�E�E�{�����b�������j�i���b���{���b��-1���{���b��-2��2�{�E�E�E�{���b0�����j
�ɂ����āA���ӂ� ���� �̌W�����r���āA
�@���Ӂ����E2��-1�b��-1�����E2��-1�b��
�@�E�Ӂ����b12�{�Q�E���b22�{�R�E���b32�{�E�E�E�{���E���bn2
����āA�@���b12�{�Q�E���b22�{�R�E���b32�{�E�E�E�{���E���bn2�����E2��-1�b���@�@�i�؏I�j
�i�R�����g�j�@���� ����Ɋ��ӂ��܂��B
�@�e�m����̃R�����g�ł��B�i�����Q�R�N�T���Q�P���t���j
�@��͂�Q���藝���g�����ؖ������ʂł���ˁB���͑g�����_�I�ȏؖ����D���Ȃ̂ł���
�ɂ�������Ă��܂��܂��B
�i�R�O�j�@�P2���b1�{�Q2���b2�{�R2���b3�{�E�E�E�{��2���b�������i���{�P�j�E�Q��-2
�i�ؖ��j�@�� �l���牽�l����I�сA���A�ǒ��ƕ��ǒ���I�ԁB�������A�ǒ������ǒ������C
�@���Ă��悢�B���̏ꍇ�̐����Q�ʂ�̕��@�ōl����B
�@�� �l��I�ԏꍇ�̐��́A���b�� �ʂ�B���̒�����A�ǒ��ƕ��ǒ���I�ԏꍇ�̐��́A
��(���|�P) �ʂ�ŁA�ǒ������ǒ������C����ꍇ�́A�� �ʂ�B
�@����āA�@��(���|�P)�{������2�@����A��2�E���b�� �ƂȂ�A���ӂ����߂���B
�@����A�ǒ��ƕ��ǒ���I�сA�c��� ���|�Q�l��K���ɑI�ԏꍇ�̐��́A
�@�@���i���|�P�j��Q��-2�@�ʂ�
�@�ǒ������ǒ���I�сA�c��� ���|�P�l��K���ɑI�ԏꍇ�̐��́A�@����Q��-1�@�ʂ�
���������āA���i���|�P�j��Q��-2�{����Q��-1�����i���{�P�j��Q��-2�@���A���ӂƂȂ�B�@�i�؏I�j
�@��L�̏ؖ��ŁA�ǒ������ǒ������C���Ă��悢�͕̂s���R�ŁA���R�Ȃ͎̂��̎���
���傤�B
�@1�0����b1�{2�1����b2�{3�2����b3�{����{��(��-1)����b�������i���|�P�j��Q��-2
�����ŁA�i�V�j�@���b1�{�Q���b2�{�R���b3�{�E�E�E�{�����b���{�E�E�E�{�����b�������E�Q��-1�@���A
�@���b1�{2�E���b2�{3�E���b3�{�E�E�E�{�����b�����Q���E�Q��-2
��ӁX�����āA�@���i���|�P�j�{������2�@����A�^���̐��藧���Ƃ�������B
�i�R�P�j�@���b0�|(1/2)���b1�{(1/3)���b2�|�E�E�E�{�i�|�P�j��(1/(n+1))���b�����P/�i���{�P�j
�i�ؖ��j�@���ӂɁA���{�P ��������ƁA���ӂ̍��́A���b���(n+1)/(r+1)����+1�b��+1�@�ŁA����
�@���A�@(n+1)�E���b������+1�b��+1�E(r+1)�@�ŁA���{�P�l���炒�{�P�l��I�сA���A
�@�ǒ���I�ԏꍇ�̐��ł��邱�Ƃ��킩��B���̂Ƃ��A
�@���Ӂ~�i���{�P�j����+1�b1�|��+1�b2�{��+1�b3�|�E�E�E�{�i�|�P�j����+1�b��+1
�@�i�T�j�@���b0�|���b1�{���b2�|���b3�{�E�E�E�{�i�|�P�j�����b�����O
�@���A�@��+1�b0�|��+1�b1�{��+1�b2�|��+1�b3�{�E�E�E�|�i�|�P�j����+1�b��+1���O�@�Ȃ̂ŁA
�@��+1�b1�|��+1�b2�{��+1�b3�|�E�E�E�{�i�|�P�j����+1�b��+1����+1�b0���P���E�Ӂ~�i���{�P�j
����āA�@���Ӂ��E�Ӂ@�����藧�B�@�@�i�؏I�j
�i�R�Q�j�@���b12�{�Q�E���b22�{�R�E���b32�{�E�E�E�{���E���bn2�����E2��-1�b��
�i�ؖ��j�@�j�q �� �l�A���q �� �l���킹�� �Q�� �l���� �� �l��I�сA���A�ǒ���I�ԁB
�@�������A�ǒ��͏��q�Ƃ���B���̏ꍇ�̐����A�Q�ʂ�̕��@�Ő�����B
�@���q�� �� �l�̏ꍇ�A���q�̑I�ѕ��́A���b�� �ʂ�ŁA�j�q�̑I�ѕ��́A���b��-�������b���ʂ�B
�@���̂P�ʂ�ɑ��āA�ǒ��̑I�ѕ��́A�� �ʂ�B
����āA�@���b���E���b��-���E�������E���b��2�@�ƂȂ�A���ӂ����߂���B
����A�܂��A�ǒ���I�ԏꍇ�̐����A�� �ʂ�B�c���� �Q���|�P�l���� ���|�P�l��I�Ԃ̂ŁA
�@���E2��-1�b��-1�����E2��-1�b���@�ƂȂ�A�E�ӂƂȂ�B�@�@�i�؏I�j
�i�R�R�j�@�P�E�Q�E���b2�{�Q�E�R�E���b3�{�E�E�E�{�i���|�P�j�E���E���b�����i���|�P�j���E�Q��-2
�i�ؖ��j�@�@�i�P�{���j�������b0�{���b1���{���b2��2�{���b3��3�{�E�E�E�{���b�������@�ɂ����āA
�@���ӂ��Q��������āA
�@���i�P�{���j��-1�����b1�{�Q���b2���{�R���b3��2�{�E�E�E�{�����b������-1
�@�i���|�P�j���i�P�{���j��-2���P�E�Q�E���b2�{�Q�E�R�E���b3���{�E�E�E�{�i���|�P�j�E���E���b������-2
�@�����P�@�Ƃ����ƁA
�@�P�E�Q�E���b2�{�Q�E�R�E���b3�{�E�E�E�{�i���|�P�j�E���E���b�����i���|�P�j���E�Q��-2�@�@�i�؏I�j
�i�R�S�j
�@�@�@�@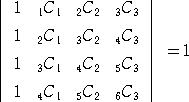
�i�ؖ��j
�@�@�@�@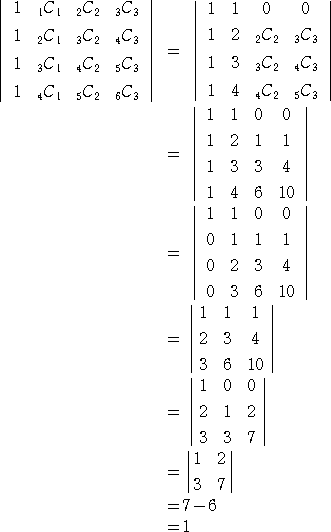
�i�R�����g�j�@�Q���W���̐������g�����Ă��Ȃ����ȁH��L�̂悤�Ɍv�Z����������
�@�@�@�@�@�@������
�@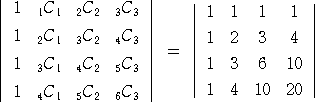
�Ƃ��Čv�Z�����������������D�D�D�B
�@��L�ł́A�g�����̐��𐔂ɒu�������Čv�Z���Ă��܂������A���������䖝���Čv�Z��
����ƋK�����������Ă���B
�@���ꂾ�ƈ�ʂ̏ꍇ�����w�I�A�[�@�ŏؖ��o�������ȁD�D�D����ȕ��͋C�B

�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@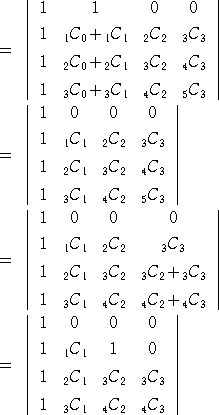
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@
�@���g�o�̓ǎ҂̂g�m�u�炢�v������A
�i�P�S�j�@���b02�{���b12�{���b22�{�E�E�E�{���bn2��2���b��
�̈�ʉ��Ƃ��āA���̐���
�i�R�T�j�@���b0�E���b���{���b1�E���b��+1�{�E�E�E�{���b��-���E���b����2���b��-���@�i�O���������j
�����藧�|�A�����������������B�炢����Ɋ��ӂ��܂��B�i�����Q�R�N�P�P���U���t���j
�i�ؖ��j�@���b���@�́A �i�P�{���j���@��W�J�����Ƃ��� ���� �̌W���ŁA���b�������bn-���@�ł���B
�@����āA�@(�P�{��)�������b0�{���b1���{���b2��2�{�E�E�E�{���b��-1����-1�{���b�������@�ł���A
�@�@(�P�{��)�������b���{���b��-1���{���b��-2��2�{�E�E�E�{���b1����-1�{���b0�����@
�@���̂Ƃ��A�@���b0�E���b���{���b1�E���b��+1�{�E�E�E�{���b��-���E���b��
�@�@�����b0�E���b��-���{���b1�E���b��-��-1�{�E�E�E�{���b��-���E���b0�@�́A
�@�i���b0�{���b1���{�E�E�E�{���b��-1����-1�{���b�������j�i���b���{���b��-1���{�E�E�E�{���b1����-1�{���b0�����j
���Ȃ킿�A�i�P�{���j���i�P�{���j�����i�P�{���j2�� ��W�J�����Ƃ��� ����-m �̌W���ɓ������B
���������āA�@2���b��-���@�ł���B�@�@�i�؏I�j
�@�炢����̑���ł��B�i�����Q�R�N�P�P���V���t���j
�@��L�̐����F��k=0�`n-m nCk�EnCk+m = 2nCn-m�@����A����Ɉ�ʉ���i�߂Ă݂܂����B
�����A��ʉ��ɏd����u�������ߕ����������A�ꍇ�������K�v�ɂȂ�A�����������Ȃ���
���܂����悤�ł��c�B
�@0��m��l��n �̂Ƃ��A�@��k=0�`n-�� n+��C��-��+k�En-��Ck = 2nCn-m�@�E�E�E�iA�j
�@0����������n �̂Ƃ��A�@��k=0�`n-�� n+��Ck�En-��C��-��+k = 2nCn-m�@�E�E�E�iB�j
�����ŁA���iA�j�́A�@��k=��-���`n-�� n+��Ck�En-��C��-l+k = 2nCn-m�@�E�E�E�iC�j
�@���iB�j�́A�@��k=��-���`n-�� n+��C��-��+k�En-��Ck = 2nCn-m�@�E�E�E�iD�j
�Ƃ��ꂼ��ό`���邱�Ƃ��ł��A��������ƁA�iA�j�ƁiD�j�A�iB�j�ƁiC�j�����ꂼ�ꎗ�Ă��邱��
���m�F�ł��܂��B
�@1�ԏ�̎��́A���iB�j�ɂ��āA�u l = 0 �v�Ƃ���Ɠ����܂��B�`����������w�̖���
���iC�j�ɂ��āA�u n = 50 m = 0 l = 10 �v�Ƃ��邱�Ƃʼn����܂��B�������͂��܂�Ȃ�
�ł����A���ӂɏo�Ă���u���v�̒l���E�ӂɉe�����Ȃ����Ƃ��l�I�ɖʔ����Ǝv���܂����B
���܂�����Ɩʔ�����肪��ꂻ���ȋC�����܂��B
�@���Ȃ݂ɁA��قǂ̌����̑g�ݍ��킹�_�I�ȉ��߂́A
�@n+l�̈قȂ�ԋ��ƁAn-l�̈قȂ锒��������B���̈قȂ� 2n�̂��̂���A�قȂ�
n-m�̂��̂��Ƃ�g�����̐� 2nCn-m �́A�ԋ��̌��ŏꍇ�������āA�ԋ�n-m-k��
�Ɣ���k���Ƃ�g�����̐��̐� n+lCn-m-k�En-lCk = n+lCl-m+k�En-lCk�@�̘a�ɓ������B
�ƂȂ�܂��B
�@�e�m����̃R�����g�ł��B�i�����Q�R�N�P�P���V���t���j
(�R�T)�@���b0�E���b���{���b1�E���b��+1�{�E�E�E�{���b��-���E���b����2���b��-���@�i�O���������j
�́A(�P�S)�̈�ʉ��ł���܂����A(�P�U)�̓��ꉻ�ł�����܂��B(35)���������������ƁA
�@�@���b0�E���b��-���{���b1�E���b��-��-1�{�E�E�E�{���b��-���E���b0��2���b��-���@�i�O���������j
����́A
�i�P�U�j�@���b0�E���b���{���b1�E���b��-1�{���b2�E���b��-2�{�E�E�E�{���b���E���b0����+���b��
�ɂ����āA�������ɁA������-���ɕς������̂ł��B
(�P�S)�́A�j���l�A�����l�̌v2���l���炎�l��I�ԑI�ѕ����A2�ʂ�ōl���ē�����B
(�R�T)�́A�j���l�A�����l�̌v2���l���炎-���l��I�ԑI�ѕ����A2�ʂ�ōl���ē�����B
(�P�U)�́A�j���l�A�����l�̌v��+���l���炋�l��I�ԑI�ѕ����A2�ʂ�ōl���ē�����B
�@(�R�T)�̂�-�������ɕς��Ă����藧���܂����A������ �̂Ƃ��A���b��=0 �Ƃ��̖��K�v�ɂ�
��܂��B
�@�炢�������ꂽ��L�̎��iA�j�iB�j���A(�P�U)�̓��ꉻ���Ǝv���܂��B
�@4�ʂ�̏ꍇ�������K�v�ɂȂ����̂́A2���W������`�ł��邱�Ƃ��C�ɂ�������ŁA
�������A�����O �̂Ƃ��́A���b��=0 �Ƃ��Ă����ΕK�v�Ȃ��Ȃ�Ǝv���܂��B
�@4�ʂ�̎��ŁA����(�P�U)�̂�+���������̏ꍇ�ɑ�������Ǝv���܂��B������ƃ`�F�b�N��
���킯�ł͂���܂���Ԉ���Ă邩������܂���B
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���V���t���j
�@�Ȃ�قǁA���������Ă݂���̒ʂ�ł��B�i�P�U�j�̎��͂����ƊȌ��ɏ����Ă�������
�ł��ˁI���������̂͂����ԑO�ŁA�ǂ������o�܂ł��̎��ɂ��ǂ蒅�����̂��o���ĂȂ�
�̂ł����A��̎����������߂���̂ł��ˁD�D�D�B���낢��Ƃ��肪�Ƃ��������܂����B
�@���g�o�̓ǎ҂̂g�m�u�炢�v�������A�����O�ɁA�F�B���������ؖ��ł��Ȃ������������A
�̂̃������甭�@���ꂽ�Ƃ������ƂŁA���̌������������������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�R�N�P�P���P�X���t���j
�i�R�U�j�@��k=0�`n ���b��(��+1-��)��(-1)�� = ���I
�@��=0�`3�@�܂Ŏ����āA�ǂ���獇���Ă���悤�ł��B���w�I�A�[�@�ŏ�肭�������Ǝv����
�̂ł����A��肭�����܂���B���ƈ�����Ǝv�����̂ł����D�D�D�B�ؖ����Ă���������Ɗ�
�����ł��B
�@�e�m���ؖ�����܂����B�i�����Q�R�N�P�P���P�X���t���j
�i�ؖ��j�@1�A2�A����A�� ���� �� �Ƃ鏇����Q�ʂ�ōl����B���ʂɐ����āA���I��
�@0�A1�A2�A�����A�� ����d���������� �� �Ƃ鏇����l����ƁA���̌��́A(��+1)��
�@���̂����ŁA1�A2�A�����A�� ���� �� �Ƃ鏇��łȂ����̂������Ă����B
�@�܂��A1���܂܂Ȃ����̂̌��́A�����A2���܂܂Ȃ����́A����A�� ���܂܂Ȃ����̂�������
�@����A1�A2�A�����A�� �̂����̂ǂꂩ���܂܂Ȃ����̂́A���E������
�@(��+1)�����炎�E�������Ђ��B�������A�������A����͏d�����Đ����Ă���̂ň����߂��B
�@1��2���܂܂Ȃ����̂́A1���܂܂Ȃ����̂Ƃ��Đ����A2���܂܂Ȃ����̂Ƃ��Đ����Ă���B
�@1��2���܂܂Ȃ����̂́A(��-1)���B1��3�����X�������ŁA���̑I�ѕ��́A���b2�ʂ�B
�@�������������𑫂��āA(��+1)��-���E����+���b2(��-1)���@�����A���x�͑����߂��B
�@1��2��3���܂܂Ȃ����̓��X�������āA(��+1)��-���E����+���b2(��-1)��+���b3(��-2)��
�@������ǂ�ǂ�J��Ԃ��Ă����B1�A2�A����A�� ���� �� �Ƃ鏇��͂ǂ�ɂ��Y�����Ȃ���
�@�瑫����邱�Ƃ�������邱�Ƃ��Ȃ��B����ȊO�̂��̂͂��傤��1��������B
�@�@�]���āA���藧�B�@�@�i�؏I�j
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���P�X���t���j
�@�Ȃ�قǁI������ł����B����ȍl�������ł���̂ł��ˁI�Q�l�ɂȂ�܂����B
�@�Ƃ���ŁA��L�̊K��̓����́A���l�̍l��������p����ƁA
�@��k=0�`n-1 ���b��(��-��)��(-1)�� = ���I
�̂悤�ɂ��낢��Ȍ`�̎�����邱�Ƃ��ł���̂ł��ˁB�����A���̎����� ��=0 �ɑΉ�����
���Ȃ��Ƃ����̂��Ⴄ�_�ł��ˁB�܂��A����ȂɋC�ɂȂ�Ⴂ�ł�����܂��D�D�D�B
�@�U���@����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�R���t���j
�@����1 �̂Ƃ��A�@��k=0�`n {���b������(-1)n�}k} = ���I
�@�@�@�@�@�@�@�@�@�@��k=0�`n {���b��-���i��-���j��(-1)k} = ���I�@�Ɠ��l�B
�@���b�������b��-�� ���A�@��k=0�`n {���b���i��-���j��(-1)k} = ���I�@�Ɠ��l�B
�@���� ����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�S���t���j
�@�Ȃ�قǁB���̏ؖ��@�͋����[���ł��ˁB���l�ɍl���āA���̓��������藧���Ƃ��킩
��܂��ˁB
�@�C�ӂ̐��̐��� ���A�� �ɑ��āA�@��k=0�`n (-1)�����b��(��+��-��)�� = ���I
�@���̓��������藧���܂��B�ؖ��͓����l�����łł��܂��B
�@�C�ӂ̐��̐��� ���A�� �ɑ��āA
�@�@��a=0�`n��b=0�`n-a (-1)a+b���b���E��-���b���E2���b�� ���I(��+��-��-��)2n-b = (2��)�I/2��
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@��L�̌���
�@�C�ӂ̐��̐��� ���A�� �ɑ��āA�@��k=0�`n (-1)�����b��(��+��-��)�� = ���I
�́A���������ł����藧���܂��B���Ȃ킿�A
�@�C�ӂ̐��̐��� ���A�� �ɑ��āA�@��k=0�`n (-1)�����b��(���}��-��)�� = ���I
�@�Ƃ���ŁA�� �͎����S�̂ɑ��Đ��藧�������ł��B��=3�A��=�ł���Ă݂܂������A����
�Ƀ������Ă���܂����B�܂��A
�@�C�ӂ̐��̐��� ���A�� �ɑ��āA
�@�@��a=0�`n��b=0�`n-a (-1)a+b���b���E��-���b���E2���b�� ���I(��+��-��-��)2n-b = (2��)�I/2��
�ɂ��Ă��A�����炭�A�������Ƃ�������̂ł͂Ȃ��ł��傤���H
�@�Ƃ���ŁA�@��k=0�`n (-1)�����b��(��-��)�� = ���I�@�̗��ӂ����I�Ŋ���ƁA
�@��k=0�`n (-1)��(��-��)��/�o���I(��-��)�I�p = �P
�@����ɓ��ꉻ����ƁA�@����+k=n (-��)���E����/�o���I���I�p = �P�@�Ƃ�������������B
�@���� ����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@�����ł��ˁB�m���ɁA���͎����S�̂ɑ��Đ��藧�������ł��ˁB�������ď����ƁA���̂�
�Ƃ�������悤�ł��B
�@�C�ӂ̎��� �� �ɑ��āA��k=0�`n (-1)�����b��(��-��)�� = ���I
�@���Ƃ́A���̓������{���ɐ��������Ƃ��ؖ��ł�������ł��ˁB
�@�e�m����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@���܂ł̋c�_���������Ƃ���ƁA�����̂�(��=n+1�An+2�A���)�ɑ��Đ��藧�B
�@���ӂ́A���ɂ��Ă����ȉ��̎�������A�P�����łȂ�����A����葽�����������Ƃ�
�Ȃ��B�]���āA�P�����ł���B���Ȃ킿�A���ׂĂ̂��ɂ��Đ��藧�B�ł��A���ڏ�̎���
�ؖ����Ȃ��Ƃ����܂���ˁB
�@���� ����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@�Ȃ�قǁI���������ؖ��@������܂������B�P���I��0�łȂ��悤�Ȃ����ȉ��̑��������A
����葽���̍��������Ƃ͂��蓾�Ȃ��Ƃ��������𗘗p�����̂ł��ˁB����ȊO�̏ؖ�
������̂ł��傤���H������ł��B
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@�m���ɂ���ŏؖ��͂ł��Ă���悤�ł��ˁB���ڏؖ����邽�߂ɁA�܂�����p�ӂ��܂��B
��@���@���R�� ���A���� ���@(������)�@�ɑ��āA��k=0�`n (-1)�����b������ = 0
�i�ؖ��j�@(1+��)�� = ��k=0�`n ���b�������@�̗��ӂ�������A����ɁA�� ��������ƁA
�@����(1+��)��-1 = ��k=0�`n �����b������
������A����J��Ԃ��A��=-1 ��������Ɠ�����B�@�@�i�؏I�j
�����p���āA�@��k=0�`n (-1)�����b��(��-��)�� = ���I�@���ؖ�����B
�i�ؖ��j�@(��-��)�� ���Q���藝�œW�J���A�� �ɂ��č~�ׂ��̏��ɕ��ׂ�B
�@��=0�A1�A2�A�E�E�E�A��-1�@�ɂ��āA(��-��)�� �̓W�J���ɂ����� ����-�� �̌W���́A���b��(-��)��
�Ȃ̂ŁA(-1)�����b������-�� �̌W���́A��k=0�`n (-1)�����b�������@���Ȃ킿�A0 �ɂȂ�B
�@�萔���́A��k=0�`n (-1)�����b��(-��)���@�ŁA����́A
�@��k=0�`n (-1)�����b��(��+��-��)�� = ���I�@(���͐���)
�ɂ��āA��=-���@�Ƃ������̂ł���B�@����āA(�萔��)=���I�@�Ȃ̂ŁA
�@��k=0�`n (-1)�����b��(��-��)�� = ���I
�������ꂽ�B�@�@�i�؏I�j
�_�����肢���܂��B�i���@�ꕔ�C�������Ă��������܂����B�ؖ��͐��������̂ł��B�j
�@�e�m����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@��k=0�`n (-1)�����b��(��+��-��)�� = ���I�@(���͐���)�@���g���̂ł���A���̉ł�����
���ƂɂȂ��Ă��܂�Ȃ��ł��傤���B�����I�Ɏg���Ă�̂́A��k=0�`n (-1)�����b��(-��)�������I
����������A�����Ƃ������Ƃɂ͂Ȃ�Ȃ��ł��傤���D�D�D�B
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@���A�����ł����ˁI�������肵�܂����B�ł́A�萔�� ��k=0�`n (-1)�����b��(-��)�� �l�Ȏ�
��k=0�`n (-1)�����b��(��-��)���@(��@(-1)�����b��(-��)�� = ���b��-�������E(-1)��+�� �ŁA��-�������ɒu��
������)�ɕό`����A�O�q�̕������p�����ؖ��ɋA���ł���ł��傤�B
�@��قǗp�������ɂ��Ĉ�ʉ����l���Ă݂܂����B��ʉ��̑O�ɁA��قǂ̏ؖ���
�o�Ă����萔����k=0�`n (-1)�����b��(-��)�������I�́A���̉����Ƃ��ďؖ��ł��邱�Ƃ���
����܂����B
�@�Q���藝�@(1+��)�� = ��k=0�`n ���b�������@�̗��ӂ�������A����ɁA�� ��������ƁA
�@����(1+��)��-1 = ��k=0�`n �����b������
������A����J��Ԃ��B���̏ؖ��ł́A�u�������v�Ƃ��܂������A�����ŁA�u�������v�̂Ƃ��A
�@���I���� �{�E�E�E= ��k=0�`n �������b�������@���Ȃ킿�A���I�{�E�E�E = ��k=0�`n �������b������-��
�����ŁA��=-1 �Ƃ���A��k=0�`n (-1)��-�����b������ = ���I�ƂȂ�̂ŁA�������p�����ɁA
�@��k=0�`n (-1)�����b��(-��)�� = ��k=0�`n (-1)��+�����b������ = ��k=0�`n (-1)��-�����b������ = ���I
�Ɠ����܂����B���āA��ʉ��ł����A
���Q�@�@���R�� ���A���� ���@(������)�@�ɑ��āA
�@��k=0�`n �o(-1)�����b������=1�`���i�����{���j�p= 0
�������A��1�A��2�A�E�E�E�A���� �́A�C�ӂ̎���
�@���́A��1=��2=�E�E�E=��m=0�@�̏ꍇ�ł��B
�@�]�k�ł����A���̘b��̔��[�ƂȂ��������@��k=0�`n (-1)�����b��(��+1-��)�� = ���I�́A���R��
�Ƃ��F�l���������̂ł����A���̂Ƃ��ނ́A�����Ȃ�ƂȂ��������A�����������n�搔��
�������J�肩�����Ƃ��Ă��������炵���̂ł��B����ŁA�Ō�ɂ͊K��ɂ��ǂ蒅���Ƃ�������
�����A���̎������o�����悤�Ȃ̂ł����A�܂������搔�̍����ƁA���̂悤�ȑg�ݍ��킹
�Ɋւ��鑽���̓������Ȃ����Ă���Ƃ́c�B��͂�A���w�͉����[���A�ǂ��łȂ����Ă�
�邩�킩��Ȃ����̂ł��ˁB
�@�e�m����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@���̈�ʉ��͂��܂�Ӗ����Ȃ��ł��ˁB����=1�`���i�����{���j�́A���̂������ŁA���� (������)��
���āA��k=0�`n (-1)�����b������ = 0�@���ؖ��ł��Ă�̂ŁA���R���藧���܂��B
������A���ƁA��=�� �̂Ƃ��̎��̏ؖ��������ł��ˁI
�@��k=0�`n (-1)�����b������ = 0
�@��k=0�`n (-1)�����b��(-��)�� = ��k=0�`n (-1)��-�����b������= ���I
�@�Q���W���̐�����(�Q�W)�̂悤�ł����A�����̏ؖ��͕�������g���Ă���悤�ł��B�Q��
�藝�ɔ���������g���ďؖ��ł���̂��ʔ����ł��B
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@�Ȃ�قǁA�m���Ɂc�B�Ƃ������Ƃ́A��k=0�`n (-1)�����b������ = 0�@��������A�Q���W���̌W
�������ꂢ�Ȗ@���ɂ̂��Ƃ�悤�Șa�ŁA�E�ӂ�0�ɂȂ�悤�Ȃ��̂�������ł�����Ă���
���̂ł��ˁB
�@(��-1)�I���b0 - (���I/1�I)���b1 + ((��+1)�I/2�I)���b2 -�E�E�E+ (-1)��((2��-1)�I/���I)���b�� = 0
�Ƃ��c�B�t�ɂ������������̏ؖ����ȒP�ɂł��Ă��܂��̂ł��ˁB
�@�������̂͊��o�������̂ł��ˁB�ł��A�V�����ؖ��@��^�����Č��h�ł��B�l�͉���
��������ƁA�����ɐ摖���Ă��܂��悤�ŁA�����ŏo�������������̓��ꉻ�ł��邱�Ƃ���
���悤�ł��O�O�G
�@���� ����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@�炢����̎咣�F���Q�͐������ł��B����Ɉ�ʂɁA���̓��������藧���Ƃ��m����
���܂��B
�@����0�ȏ�̔C�ӂ̐����A��0�A��1�A��2�A�E�E�E�A���� ��C�ӂ̎����Ƃ���Ƃ��A
�@�@(-1)����k=0�`n (-1)�����b��(-1)��-k�i��0+��1��+��2��2+�E�E�E+���������j = ���I����
���㎮�́A�f�`�h ����̂��w�E�ŏC������Ă��܂��B�i�Ԏ������j�i�ߘa�T�N�T���P�O���t���j
�@�炢����̕��Q�́A���̎��ɂ����āA����=0�@�Ƃ������̂ł��B
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�U���t���j
�@�Ȃ�قǁB����W�J�������A���́A��-1�܂ł̒l���Ƃ肦��̂ŁA����=0 �̂Ƃ��ƈ�v�����
���ł��ˁIFN����̌����悤�ɁA��0+��1��+��2��2+�E�E�E+����-1����-1 �̕����̓��������ɂ�
�ꂼ��0�ɂȂ�̂ŁA��0�A��1�A��2�A�E�E�E�A����-1 �̒l���e�����Ȃ���ł��ˁB��قǎ�����
�@��k=0�`n (-1)�����b������ = 0�@�i�������j
�@��k=0�`n (-1)��-�����b������= ���I
�����ꂼ��萔�{���Ă܂Ƃ߂�ƁA���� ����̎��ɂȂ�Ƃ������Ƃł��ˁB�ƂĂ��[�������܂����B
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�X���t���j
�@����A�@��k=0�`n (-1)�����b������ = 0�@�i�������j�@�A��k=0�`n
(-1)��-�����b������= ���I�@�̏ؖ���
�g�����A�u�Q���W�J���̗��ӂ�������A�� ��������B�����m��J��Ԃ��B�v�Ƃ�����Ƃ�����
�܂����B������A�������ɑ��Ċg���ł��Ȃ����ƍl���܂����B
�@f0(��) = (1+��)���@�Afm+1(��) = ��fm�f(��)�@�Ƃ��Af��(��) �����߂܂��B
fm(��)�@�� ��(��-1)�c(��-��+1)����-��(1+��)�� �̌W���� a[m�Ck] �Ƃ���ƁA
�@�@a[m�C1] = 1�@�Aa[m�Ck] = ���Ea[m-1�Ck] + a[m-1�Ck-1]
�����藧�̂ŁA��������Aa[m�Ck] �����߂���Έ�Ԃ����̂ł����Am�Ak�Œ��ڂ͕\��
�Ȃ��悤�ł��D�D�D�B�������A�Q��������Aa[n+k�Cn] �����߂���Af��+��(��)�@�ƂQ���藝��
�W����A
�@�@�@����=0�`n (-1)��-�����b������+�� = a[n+k�Cn]�E���I
�ƂȂ�܂��B��+��=�� �Ƃ��āA�@����=0�`n
(-1)��-�����b������ =
a[���Cn]�E���I
�Ƃ��Ă��܂��ق����킩��₷���ł��傤���B�Ƃ�����
�@a[n�Cn] = 1�@�Aa[n+1�Cn] = n(n+1)/2�@�Aa[n+2�Cn] = n(n+1)(n+2)(3n+1)/4�I
�@a[n+3�Cn] = {n(n+1)}2(n+2)(n+4)/(4�I�E2)
�Ƃ������Ƃ܂ł͂킩��܂������A�Ȃ��Ȃ���ʍ��ɂ��ǂ蒅���܂���D�D�D�B
a[n+k�Cn] �͋��߂���ł��傤���H
�@�U���@����̃R�����g�ł��B�i�����Q�R�N�P�P���Q�X���t���j
�@�u���̔��Y�^�v�|�u�x�����v�@�ŁA��Q��X�^�[�����O���̕\������܂��B
�@a[n�C��]�E���I=��k=0�`�� (-1)�����b���i��-���j��
�Ƃ��āA�\�߂�B
| ���_�� | �P | �Q | �R | �S | �T | �U | �V | �W | �X | �@ | �a�i���j |
| �P | �P | �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E | �@ | �P | |||||||
| �Q | �P | �P | �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E | �@ | �Q | ||||||
| �R | �P | �R | �P | �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E | �@ | �T | |||||
| �S | �P | �V | �U | �P | �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E | �@ | �P�T | ||||
| �T | �P | 15 | 25 | 10 | �P | �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E | �@ | �T�Q | |||
| �U | �P | 31 | 90 | 65 | 15 | �P | �E�E�E�E�E�E�E�E�E�E�E�E�E�E�E�E | �@ | �Q�O�R | ||
| �V | �P | 63 | 301 | 350 | 140 | 21 | �P | �E�E�E�E�E�E�E�E�E�E | �@ | �W�V�V | |
| �W | �P | 127 | 966 | 1701 | 1050 | 266 | 28 | �P | �E�E�E�E | �@ | �S�P�S�O |
| �X | �P | 255 | 3025 | 7770 | 6951 | 2646 | 462 | 36 | �P | �@ | �Q�P�P�S�V |
�E�[�̎߁@1,1,1,1,1,1,1,1,1,1,1,1,1,1,1,�c�@����Aa[n�Cn] =1
�E�[����2�Ԗڂ̎߁@1,3,6,10,15,21,28,36,45,55,66,78,91,105,120,�c�@����A
a[n+1�Cn]=(1/2)n(n+1)
�E�[����3�Ԗڂ̎߁@1,7,25,65,140,266,462,750,1155,1705,2431,3367,4550,6020,7820,�c
�@a[n+2�Cn]=(1/24)n(n+1)(n+2)(3n+1)
�E�[����4�Ԗڂ̎�
�@1,15,90,350,1050,2646,5880,11880,22275,39325,66066,106470,165620,249900,367200,�c
�@a[n+3�Cn]=(1/48)n2(n+1)2(n+2)(n+3)
�E�[����5�Ԗڂ̎�
�@1,31,301,1701,6951,22827,63987,159027,359502,752752,1479478,2757118,4910178,8408778,13916778,�c
�@a[n+4�Cn]=(1/5760)n(n+1)(n+2)(n+3)(n+4)(15n3+30n2+5n-2)
�E�[����6�Ԗڂ̎�
�@1,63,966,7770,42525,179487,627396,1899612,5135130,12662650,28936908,62022324,125854638,243577530,452329200,�c
�@a[n+5�Cn]=(1/11520)n2(n+1)2(n+2)(n+3)(n+4)(n+5)(3n2+7n-2)
n��2 �̂Ƃ��Aa[n�C2]=2n-1-1�@2���
�@�炢����̃R�����g�ł��B�i�����Q�R�N�P�P���R�O���t���j
�@������ɏ����Ă���܂������B�����Ă��������Ă��肪�Ƃ��������܂��B6�Ԗڂ̈�ʍ��܂�
�o���A�ȑO�ɂ��̃y�|�W���������Ƃ�����ɂ�������炸�A�Ȃ�������o���܂���ł����B
�@��������A��͂��ʂ̏ꍇ�̎��͏��Ȃ��Ƃ��Ȍ��ɂ͏o�Ȃ��悤�ł��ˁB�Q���W���̘a
�̓����Ƃ��āA�g���Ă݂Ă��ꂢ�Ȃ̂���ڂɌ���3�Ԗڂ��炢�܂łł����ˁc
�@�g�m�u���Ђ��v����A��������W�������������������܂����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�S�N�U���Q�R���t���j
�@���̔]�ɋ����Ă��t���Ă��鎮����E�E�E�B
�@�@��i=0�`m��j=0�`n (-1)i+j�Ei+j�bi�Em�bi�En�bj=��[m�Cn]
�@�@�@�i�������A��[m�Cn] ���N���l�b�J�[�̃f���^�j
��@�������������Ă݂��B�@�����P�A�����P�̂Ƃ��A
�@��i=0�`1��j=0�`1 (-1)i+j�Ei+j�bi�E1�bi�E1�bj
�@=0�b0�E1�b0�E1�b0+(-1)�E1�b0�E1�b0�E1�b1+(-1)�E1�b1�E1�b1�E1�b0+2�b1�E1�b1�E1�b1
�@=�P+(-1)+(-1)+2=�P
�@�����P�A�����Q�̂Ƃ��A
�@��i=0�`1��j=0�`2 (-1)i+j�Ei+j�bi�Em�bi�En�bj
�@=0�b0�E1�b0�E2�b0+(-1)�E1�b0�E1�b0�E2�b1+2�b0�E1�b0�E2�b2
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@+(-1)�E1�b1�E1�b1�E2�b0+2�b1�E1�b1�E2�b1+(-1)�E3�b1�E1�b1�E2�b2
�@=�P+(-2)+1+(-1)+4+(-3) = 0
�i�R�����g�j�@��u�A�{�����ȁH�Ɠ����߂���܂������A���藧�������ł��ˁI
�@���� ���l�@����܂����B�i�����Q�S�N�V���P�U���t���j
�@��L�̓����̏ؖ����l���Ă݂܂����B�ؖ��ɂ́AChu-Vandermonde identity �ƁA
�@���b����(-1)���Ek-n-1�bk
�Ƃ����������g���܂����B
(�ؖ�) n��m�̏ꍇ�F
�@����=��i=0�`m��j=0�`n (-1)i+j�Ei+jCi�EmCi�EnCj
=��i=0�`m��j=0�`n (-1)i+j�E(-1)i�E-j-1Ci�EmCm-i�EnCj
=��i=0�`m��j=0�`n (-1)j�E-j-1Ci�EmCm-i�EnCj
=��j=0�`n (-1)j�EnCj��i=0�`m(-j-1Ci�EmCm-i)
=��j=0�`n (-1)j�EnCj�Em-j-1Cm
=��j=0�`n (-1)j�EnCj�E(-1)m�E��C��
=��j=0�`n (-1)j+���EnCj�E��C��
=��[m,n].
n��m�̏ꍇ�F�@���ӂ�ό`���Ă����ƁA����=��i=0�`m (-1)i+n�EmCi�EiCn=0
�@���Ђ�����̃R�����g�ł��B�i�����Q�S�N�V���P�X���t���j
�@�ؖ����Ă��������Ă��肪�Ƃ��������܂��B�킽���ɂ͏ؖ����v�����Ȃ��������߁A����
�������Ɏc���Ă����̂ł����B����ŏ����������肵�܂����B�Q�l�܂łɁA�������̊W����
�������@�������Ă����܂��B
�@�u���Q�[���������̒����W��\�����ɓW�J���������ēW�J���A�����Ƃɐϕ������s
�@�������́v
�@���g�o�����������b�ɂȂ��Ă���g�m�u�j�D�r�D�v������A�V���ȂQ���W���̐�����������
�����������B�i�����Q�T�N�V���P�U���t���j
�@�g���������́A�����[���悤�ł��B
�i�R�V�j�@2n-1�b1�{2n-3�b1�{�E�E�E�{1�b1���Q�En�b2�{�P�En�b1�{�O�En�b0�@�@�i�����Q�j
�i�R�W�j�@2n-2�b2�{2n-4�b2�{�E�E�E�{2�b2���S�En�b3�{�P�En�b2�{�O�En�b1�@�@�i�����Q�j
�i�R�X�j�@2n-1�b3�{2n-3�b3�{�E�E�E�{3�b3���W�En�b4�{�W�En�b3�{�P�En�b2�@�@�i�����R�j
�i�S�O�j�@2n-2�b4�{2n-4�b4�{�E�E�E�{4�b4���P�Un�b5�{�P�Q�En�b4�{�P�En�b3�@�@�i�����R�j
�@�j�D�r�D���炢�������������̏ؖ����l���Ă݂��B
�i�R�V�j�́i�ؖ��j
�@�i���Ӂj���i�Q���|�P�j�{�i�Q���|�R�j�{�E�E�E�{�P�����i�Q���|�P�{�P�j/�Q����2
�@�i�E�Ӂj�����i���|�P�j�{������2�@�@�Ȃ̂ŁA�@�i���Ӂj���i�E�Ӂj�@�@�i�؏I�j
�i�R�W�j�́i�ؖ��j
�i���Ӂj���i���|�P�j�i�Q���|�R�j�{�i���|�Q�j�i�Q���|�T�j�{�E�E�E�{�P
��������1�`��-1 ���i�Q���|�P�j
�����i���|�P�j�i�Q���|�P�j/�R�|���i���|�P�j/�Q
�����i���|�P�j�i�S���|�Q�|�R�j/�U�����i���|�P�j�i�S���|�T�j/�U
�i�E�Ӂj���Q���i���|�P�j�i���|�Q�j/�R�{���i���|�P�j/�Q
�@�����i���|�P�j�i�S���|�W�{�R�j/�U�����i���|�P�j�i�S���|�T�j/�U
�Ȃ̂ŁA�@�i���Ӂj���i�E�Ӂj�@�@�i�؏I�j
�D�D�D�D�D�D�ƈꉞ�v�Z����A�c��́i�R�X�j�A�i�S�O�j���ؖ��o����̂��낤�B
�@�������A�����������ƕʂȎ��_�Ŗ��炩�ɂ��邱�Ƃ͏o����̂��낤���H
�@��M���A(�R�V)���`(�S�O)���ɂ��čl�@����܂����B�i�����Q�T�N�V���Q�U���t���j
�@���������ď����Ă݂܂��B
(**) ��k=1�`n 2��-1�b0���� k=1�`n 2��-2�b0������n�b1
�@�i�R�V�j�@�� k=1�`n 2��-1�b1���Q�En�b2�{�P�En�b1�{�O�En�b0�@�i�����Q�j�ɑ��āA
(�R�V)�f �@��k=1�`n 2��-1�b1����2���Q�En�b2�{n�b1
(�R�V)�h �@�� k=1�`n 2��-2�b1����2�|�����Q�En�b2
�@�i�R�W�j�@�� k=1�`n 2��-2�b2���S�En�b3�{�P�En�b2�{�O�En�b1�@�i�����Q�j�ɑ��āA
(�R�W)�f �@��k=1�`n 2��-1�b2���S�En�b3�{�R�En�b2
(�R�W)�h �@��k=1�`n 2��-2�b2���S�En�b3�{�P�En�b2
�@�i�R�X�j�@�� k=1�`n 2��-1�b3���W�En�b4�{�W�En�b3�{�P�En�b2�@�i�����Q�j�ɑ��āA
(�R�X)�f �@��k=1�`n 2��-1�b3���W�En�b4�{�W�En�b3�{�P�En�b2
(�R�X)�h �@��k=1�`n 2��-2�b3���W�En�b4�{�S�En�b3
�@�i�S�O�j�@�� k=1�`n 2��-2�b4���P�Un�b5�{�P�Q�En�b4�{�P�En�b3�@�i�����Q�j�ɑ��āA
(�S�O)�f �@��k=1�`n 2��-1�b4���P�Un�b5�{�Q�O�En�b4�{�T�En�b3
(�S�O)�h �@��k=1�`n 2��-2�b4���P�Un�b5�{�P�Q�En�b4�{�P�En�b3
�i���Ӂj�@ 0��a��b �̂Ƃ��́A�Q���W�� ���b�����O �ƈ����Ă��܂��B���������킯�ŁA�Ⴆ�A
�@�@�@�@��L��(40)�h���ł́A�����R���炎�܂łƓ����ł��B
�@�����ŁA�Ⴆ�A���̂悤�ȂR���Ԃ̊W�����藧���Ă��܂��B
(�S�O)�f���� (�R�W)�f����(�R�X)�f���̂Q�{�𑫂��āA���b�� �̂��̒l�Ɂ{�P��������
(�S�O)�h���� (�R�W)�h����(�R�X)�h���̂Q�{�𑫂��āA���b�� �̂��̒l�Ɂ{�P��������
(**�C�R�V�C�R�W)�̊ԁA(�R�V�C�R�W�C�R�X)�̊Ԃɂ��Ă����l�ɐ��藧���܂��B
���ہA���̂悤�ɂ��āA���̊W���m�F���邱�Ƃ��ł��܂��B
��k=1�`n 2��-1�b���� Fm(��) �Ƃ����B
2��+1�b���|2��-1�b���� �Q�E2��-1�b��-1�{ 2��-1�b��-2�@�E�E�E (��)
���ɂ��āA�P���炎�|�P�܂ŗ��ӂ̘a���Ƃ邱�ƂŁA
2��-1�b���� �Q�EFm-1(n-1) �{ Fm-2(n-1)
�������Ƃ����āA�P���炎�܂ŗ��ӂ̘a���Ƃ邱�ƂŁA
�@Fm(��) �� �Q��k=1�`n Fm-1(��-1) �{ ��k=1�`n Fm-2(��-1)
�ł��邱�Ƃ����L�̐�����B
���@�Q���{�P���炍�I�ԕ��@�́G
�E�i�Q���|�P���炍�I�ԕ��@�j�~�i�Q����O�I�ԕ��@�j
�E�i�Q���|�P���炍�|�P�I�ԕ��@�j�~�i�Q����P�I�ԕ��@�j
�E�i�Q���|�P���炍�|�Q�I�ԕ��@�j�~�i�Q����Q�I�ԕ��@�j
�̍��v�Ɉ�v���邱�Ƃ���B
���@(�S�O)�f�@ �� k=1�`n 2��-1�b4���P�Un�b5�{�Q�O�En�b4�{�T�En�b3�@�Ƃ������̌W���͍ŋ��ǂ�����
�@�������Ƃ�����悤�ȋC�����܂��ˁI
�@5�{�p�̌��� �ƌ���ׂāAF(x)=16x^5-20x^3+5x �Ƃ��ăO���t���E�E�E
�����֘A�t��������͂���̂ł��傤���E�E
�@�炷���邳��̃R�����g�ł��B�i�����Q�T�N�V���Q�U���t���j
(�R�V)�f(�R�W)�f(�R�X)�f(�S�O)�f�̉E�ӂ̌W���́A
�@cos(2��)=2(cos2��)-1
�@cos(3��)=4(cos3��)-3(cos��)
�@cos(4��)=8(cos4��)-8(cos2��)+1
�@cos(5��)=16(cos5��)-20(cos3��)+5(cos��)
�̉E�ӂ̌W���𐳂ɂ������̂ƈ�v���܂����A(�R�V)�h(�R�W)�h(�R�X)�h(�S�O)�h'�̉E�ӂ̌W����
�@sin(2��)/(sin��)=2cos��
�@sin(3��)/(sin��)=4(cos2��)-1
�@sin(4��)/(sin��)=8(cos3��)-4(cos��)
�@sin(5��)/(sin��)=16(cos4��)-12(cos2��)+1
�̉E�ӂ̌W���𐳂ɂ������̂ƈ�v���܂��ˁB
�i�R�����g�j�@���ƂȂ������[���悤�ȁD�D�D���͋C�I
�@�j�D�r�D����̃R�����g�ł��B�i�����Q�T�N�V���R�P���t���j
�i�S�O�j�@2n-2�b4�{2n-4�b4�{�E�E�E�{4�b4���P�Un�b5�{�P�Q�En�b4�{�P�En�b3�@�@�i�����R�j
�ɂ��āA
��������@�@�Q���|�T�̔��ʂƂT�̐ԋʂ�������E�ֈ��ɕ��ׂ���@���l����B
�@�@�@�@�@�@�@���̂����ŁA�ł��E���ɂ���ԋʂ���Ԗڂɂ�����ו��͉��ʂ肠�邩�B
�̉ɂȂ�܂��B
�@���ӂ̎��̍l�����́A�Q�����Q�g�����ׂčl����Ƃ��A�悸�A��ԉE���̑g�ɐԋ�
�������Ƃ��A�c��S�̓���ꏊ�́A2n-2�b4�ʂ肠��B���ɁA�E����ł��E���ɂ���ԋʂ�
�E�����g�߂ɂ���Ƃ��A�c��S�̓���ꏊ�́A2n-4�b4�ʂ肠��B�ȉ����l�ɂ��āA4�b4
�܂ł̑S�Ęa�����߂�B
�@�E�ӂ̎��̍l�����́A�Q�����A�Q�g�Â��ׂčl����Ƃ��A�T�̐ԋʂ��T�g�ɂP�Â�
����ꍇ�An�b5�ʂ肠��A���̂S�ɂ��Ă͉E���ǂ���ł��悢�̂ŁA�Q4���P�U�ʂ肠���
���B���ɂT�̐ԋʂ��S�g�ɓ���ꍇ�A�K�R�I�ɐԐԂƓ���g����g����A�R�g�̂������
�Ȃ̂ŁA�R�ʂ�A�ł��E���͐Ԕ��ƂȂ�B�Q�g�͉E���ǂ���ł��悢�̂ŁA�S�ʂ�A����āA
�R�~�S���P�Q�ʂ肠��܂��B�Ō�ɂT�̐ԋʂ��R�g�ɓ���ꍇ�An�b3�ʂ肠��܂��B�S�Ă�
�a���E�ӂɂȂ�܂��B���l�̍l�����ŁA
�@�R���̋ʂ̒��A�ԋʂT�Ǝc�蔒�ʂ�������E�ֈ��ɕ��ׂ���@���l����B���̂���
�ŁA�ł��E���ɂ���ԋʂ��R�Ŋ���ƂP�]��Ԗڂ�����ו��͉��ʂ肠�邩�B
�ɂ��ẮA
�@3n-3�b4�{3n-6�b4�{�E�E�E�{6�b4���W�P�En�b5�{�W�P�En�b4�{�P�T�En�b3
�������܂����B
�i�R�����g�j�@�Ȃ�قǁ`�A�l�������悭������܂����B�j�D�r�D����Ɋ��ӂ��܂��B
�i�R�V�j�@2n-1�b1�{2n-3�b1�{�E�E�E�{1�b1���Q�En�b2�{�P�En�b1�{�O�En�b0�@�@�i�����Q�j
�ɂ��ẮA���̂悤�ɍl��������킯�ł��ˁB
�@�Q���|�Q�̔��ʂƂQ�̐ԋʂ�������E�ֈ��ɕ��ׂ���@���l����B���̂����ŁA�ł�
�E���ɂ���ԋʂ������Ԗڂɂ�����ו��͉��ʂ肠�邩�B
�@���ӂ̎��̍l�����́A�Q�����Q�g�����ׂčl����Ƃ��A�悸�A��ԉE���̑g�ɐԋ�
�������Ƃ��A�c��P�̓���ꏊ�́A2n-1�b1�ʂ肠��B���ɁA�E����ł��E���ɂ���ԋʂ�
�E�����g�߂ɂ���Ƃ��A�c��P�̓���ꏊ�́A2n-3�b1�ʂ肠��B�ȉ����l�ɂ��āA1�b1
�܂ł̑S�Ęa�����߂�B
�@�E�ӂ̎��̍l�����́A�Q�����A�Q�g�Â��ׂčl����Ƃ��A�Q�̐ԋʂ��Q�g�ɂP�Â�
����ꍇ�An�b2�ʂ肠��A���̂P�ɂ��Ă͉E���ǂ���ł��悢�̂ŁA�Q�ʂ肠��܂��B��
�ɂQ�̐ԋʂ��P�g�ɓ���ꍇ�A�P�ʂ肠��܂��B�R���ڂ́u�O�En�b0�v�͑��Ƃ̃o�����X���l
���Č`���I�ɓ���Ă����܂��B�S�Ă̘a���E�ӂɂȂ�܂��B
�@���l�ɁA
�i�R�W�j�@2n-2�b2�{2n-4�b2�{�E�E�E�{2�b2���S�En�b3�{�P�En�b2�{�O�En�b1�@�@�i�����Q�j
�ɂ��ẮA
�@�Q���|�R�̔��ʂƂR�̐ԋʂ�������E�ֈ��ɕ��ׂ���@���l����B���̂����ŁA�ł�
�E���ɂ���ԋʂ���Ԗڂɂ�����ו��͉��ʂ肠�邩�B
�i�R�X�j�@2n-1�b3�{2n-3�b3�{�E�E�E�{3�b3���W�En�b4�{�W�En�b3�{�P�En�b2�@�@�i�����R�j
�ɂ��ẮA
�@�Q���|�S�̔��ʂƂS�̐ԋʂ�������E�ֈ��ɕ��ׂ���@���l����B���̂����ŁA�ł�
�E���ɂ���ԋʂ������Ԗڂɂ�����ו��͉��ʂ肠�邩�B
�Ƃ������̉Ƃ��ĂƂ炦������킯�ł��ˁB
�@���l�s����w��w���i�Q�O�P�R�j�̓������Ɏ��̓����̒l�����߂��肪�o�肳�ꂽ�B
�i�S�P�j�@(1/2)2���b1�{(1/4)2���b3�{(1/6)2���b5�{�E�E�E�{(1/(2n))2���b2��-1
�@�@���i�Q2���|�P�j/�i�Q���{�P�j
�@�@�i�ؖ��j�@�W�J�����@2���b0�{2���b1���{2���b2��2�{�E�E�E�{2���b2����2�����i�P�{���j2���@�̗��ӂ��A
�@�����O ���� ������ �܂Œ�ϕ�����ƁA
�@2���b0x�{(1/2)2���b1��2�{(1/3)2���b2��3�{�E�E�E�{(1/(2n+1))2���b2����2��+1���o�i�P�{���j2��+1�|�P�p/(2n+1)
�@�����P �������āA
�@2���b0�{(1/2)2���b1�{(1/3)2���b2�{�E�E�E�{(1/(2n+1))2���b2�����o�Q2��+1�|�P�p/(2n+1)
�@�����|�P �������āA
�@�|2���b0�{(1/2)2���b1�|(1/3)2���b2�{�E�E�E�|(1/(2n+1))2���b2�����|�P/(2n+1)
�@���̂Q����ӁX�����āA���ӂ��Q�Ŋ���ƁA
�@�@�@(1/2)2���b1�{(1/4)2���b3�{�E�E�E�{(1/(2n))2���b2��-1���o�Q2���|�P�p/(2n+1)�@�@�i�؏I�j
�i�NjL�j�@�W���̐V���Ȑ����Ƃ������ƂŁA�j�D�r�D�����胁�[�������B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�T�N�P�O���X���t���j
�@�����^�@�P�C�Q�C�R�C�S�@��Q�C�S�C�U�@�̃^�C�v�͂���̂ł����A����^�@�P�C�Q�C�S�C�W�@�̃^�C
�v�ƌ�����Ǝv���܂��B
�i�S�Q�j�@���b0�{�Q�E���b2�{�S�E���b4�{�W�E���b6�{�E�E�E���o�i�P�{![]() �j���{�i�P�|
�j���{�i�P�|![]() �j���p/�Q
�j���p/�Q
�@�@�i�ؖ��j�@�i�P�{���j�������b0�{���b1���{���b2��2�{�E�E�E�{���b�������@�ɂ����āA
�@�@�@�@�@�@�����}![]() �@�Ƃ����悢�B�@�@�i�؏I�j
�@�Ƃ����悢�B�@�@�i�؏I�j
�@���Ђ����玟�̓����̓��e������܂����B�i�����Q�V�N�Q���W���t���j
�i�S�R�j�@����0�A1�A2�A�c�A���|�P �̂Ƃ��A
�@�@��i=0�`k (2nCi�E2(n-i)�E2n-k-iCk-i/(2n-k-i))���Q2k�E��C��
�@���ӂƉE�ӂɎ��������̂���t�ɂ��ǂ�Ύ������Ƃ��ł���̂ł����A�I���Ȋ����ł��B
�����ƒ��ڐ����ł��Ȃ����Ȃƍl���Ă�������ǁA�����A�C�f�B�A�������т܂���ł����B
�i�R�����g�j�@�����Q�Ƃ��āA�����̈Ӗ����l���Ă݂��B
2nC0�E2n�E 2n-2C2/(2n-2)�{2nC1�E2(n-1)�E 2n-3C1/(2n-3)�{2nC2�E2(n-2)�E2n-4C0/(2n-4)
���Q4�E��C2
�i���Ӂj��2n�E�i2n-3�j/2�{2n�E2(n-1)�E1�{n(2n-1)�E2(n-2)/(2n-4)
�@�@�@�@��2n2-3n+4n2-4n+2n2-n��8n2-8n�@�E�E�E�@�C���ς݁@���Ђ�����Ɋ��ӁI
�i�E�Ӂj���Q4�E��C2��16�En(n-1)/2��8n2-8n
�i�NjL�j�@�u������ėL���ł����H�v�Ƒ肵�āA�g�m�u���v����̓��e�ł��B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�V�N�P�O���R���t���j
�i�S�S�j�@��k=1�`n �in�bk�|�Qk�{�P�j/�����O
�@������������ł����ǂ��c�c�A������ėL���ł����H
�@DD++����̃R�����g�ł��B�i�����Q�V�N�P�O���S���t���j
�@�L���Ƃ����Ӗ��ɂ����܂��ˁB����s���|�C���g�ňӎ��I�ɒm���Ă���l�͂܂����Ȃ���
���傤����ǁA���ł����̓�����������l�͂��Ȃ肢��ł��傤�B���o��3�s����Ώ\���ł�
���D�D�D�B
�@������̃R�����g�ł��B�i�����Q�V�N�P�O���S���t���j
�@�Ȃ�قǁB������܂ł͒m��Ȃ������̂ŁA������������Ă�����̊Ԃɂ͒m��n����
����̂��Ȃ��ƁA������Ƌ^��Ɏv�����e��������ł��B�ł��Ȃ�ƂȂ���ʂ菑�������
�������ł��ˁB�藝�̎��������������āA���̌�ϕ����Č����܂����B�ꉞ�A���w�I
�A�[�@�ł��ؖ����Ă����܂����B
�@DD++����̃R�����g�ł��B�i�����Q�V�N�P�O���S���t���j
�@�܂��o��@�����Ȃɂ��鎮�ɂ͌����܂��ˁB�ꕔ����̖��ɂ͐��ȈЗ͂�
���������ł��傤����ǁB
�i�R�����g�j�@DD++����́u���o��3�s����Ώ\���v�Ƃ������t�Ɏ䂩��čl���Ă݂܂����B
�@�j���[�g���̂Q���藝���A�@
�@�i�P�{���j�������b0�{���b1���{���b2��2�{���b3��3�{�E�E�E�{���b�������{�E�E�E�{���b������
�@����āA�@���b1�{���b2���{���b3��2�{�E�E�E�{���b������-1�{�E�E�E�{���b������-1
�@���o�i�P�{���j���|�P�p/�����o�i�P�{���j���|�P�p/�o�i�P�{���j�|�P�p
�@���P�{�i�P�{���j�{�i�P�{���j2�{�E�E�E�{�i�P�{���j��-1
���̂Ƃ��A���ӂ��O����P�܂Œ�ϕ�����ƁA
�@���b1�{���b2/�Q�{���b3/�R�{�E�E�E�{���b��/���{�E�E�E�{���b��/��
���i�Q�|�P�j�{�i�Q2�|�P�j/�Q�{�i�Q3�|�P�j/�R�{�E�E�E�{�i�Q���|�P�j/��
�ƂȂ�̂ŁA�@��k=1�`n �in�bk�|�Qk�{�P�j/�����O�@�����藧�B
�����������ɏ����A�قڂR�s���炢���ȁH
�@DD++����̃R�����g�ł��B�i�����Q�V�N�P�O���T���t���j
�@�ȉ��ŁA�R�s�̂���ł����B����Ă邱�Ƃ͐�����킸�����ł����A���䐔����o��
���������X���[�Y�ł��B
�@��[k=1..n] (1+x)k-1 = {(1+x)n-1}/x = ��[k=1..n] n�bk xk-1
�@����āA��[k=1..n] { n�bk xk-1 - (1+x)k-1 } = 0
�@���ӂ� 0 ���� 1 �܂Őϕ����āA ��[k=1..n] (n�bk-2k+1)/k = 0
�i�R�����g�j�@�Ȃ�قǁA���䐔����̕����X�b�L�����Ă��܂��ˁB���̕��́A�j���[�g����
�@�@�@�@�@�@�Q���藝����u�P/���v����邽�߂̉����������āA���̂Ƃ��ɏo��������́u���v��
�@�@�@�@�@�@�u�i�P�{���j�|�P�v�ƂƂ炦�邱�ƂɋC�����A��L�̉Ɏ���܂����B
�@�Q���W���̐����Ƃ��āA���̂��i�W�J�Ƃ̊W�͂��Ȃ�L���ŗL�p�炵���B
�i�S�T�j�@�f�� �� �ɑ��āA���A���i�������j�̂��i�W�J��
�@�@�@������0�{��1���{��2��2�{�E�E�E�{���������@�A������0�{��1���{��2��2�{�E�E�E�{��������
�@�@�Ƃ����Ƃ��A�@���b������0�b��0�E��1�b��1�E�E�E��k�b��k�@�i�������@���j�@�����藧�B
�i��j�@�����P�X�A�����V�A�����T�@�Ƃ���B���̂Ƃ��A���A�� ���T�i�W�J���āA
�@�@�����S�{�R�E�T�@�A�����Q�{�P�E�T
�����ŁA�@19�b7���R�E�S�E�P�R�E�P�V�E�P�X���T�O�R�W�W�@�A4�b2���U�@�A3�b1���R�@�Ȃ̂ŁA
�@19�b7�|4�b2�E3�b1���T�O�R�V�O�߂O�@�i�������@�T�j�@���A�@19�b7��4�b2�E3�b1�@�i�������@�T�j
�����藧�B
�i�NjL�j�@�����i�S�T�j�������ɂ́A�������������K�v���B�i�����Q�X�N�T���V���t���j
�@�Q���W�� ���b�������I/{���I(���|��)�I}�@�ɂ��āAa��b �̏ꍇ�́A���b�����O�@�ƒ�߂�B
���P�@�� ��f���Ƃ���B���̂Ƃ��A�P���������|�P �������R�� �� �ɑ��āA���b���� ��
�@�@�@�@�Ŋ�����B
�i�ؖ��j�@{���I(���|��)�I}���b�������I ���A���ӂ� �� �̔{���B�P���������|�P �ŁA
�@�@���I(���|��)�I�́A�f�� �� �ƌ݂��ɑf������A���b�� �͂��Ŋ�����B�@�@�i�؏I�j
�@�܂��A�����W���̑����� f(��) �� g(��) ���A
�@f(��)��a(n)��n�{a(n-1)��n-1�{�E�E�E�{a(1)���{a(0)
�@g(��)��b(n)��n�{b(n-1)��n-1�{�E�E�E�{b(1)���{b(0)
�Ƃ����B(�K�X�Aa(n)��0 �� b(n)��0 �ȂǂƂ��āAf(��) �� g(��) �̎����𑵂���j
���̂Ƃ��A������������ f(��)��g(��)�@(�������@��)�@�ł��邱�Ƃ��A�������藧�Ƃ��ƒ�`����B
�@�@a(0)��b(0)�@�Aa(1)��b(1)�@�A�E�E�E�Aa(n)��b(n)�@(�������@��)
���Q�@���R�� �� �Ƒf�� �� �ɑ��āA�@(���{�P)pn�߂�pn�{�P�@(�������@��)�@�����藧�B
�i�ؖ��j�@�����P�̂Ƃ��A���P���A�P���������|�P �ɑ��āA���b���߂O�@ (�������@��)�@�Ȃ̂ŁA
�@(���{�P)p����p�{���b1��p-1�{���b2��p-2�{�E�E�E�{���b��-1���{�P�߂����{�P�@(�������@��)
�@����āA�����P�̂Ƃ����藧�B
�@�������i�����P�j�̂Ƃ��A���藧�Ɖ��肷��B���Ȃ킿�A�@(���{�P)p���߂�p���{�P�@(�������@��)
�@�������{�P�̂Ƃ��A�A�[�@�̉�����A�@(���{�P)p��+1�߁i��p���{�P�j���߂�p��+1�{�P�@(�������@��)
�@����āA�������{�P�̏ꍇ���A����͐��藧�B
�@���������āA�C�ӂ̎��R�����ɑ��āA����͐��藧�B�@�@�i�؏I�j
���R�@���R�� �� �Ƒf�� �� �ɑ��āAa�Ab ���Aa��b��0 ���݂������R���Ƃ���B���̂Ƃ��A
�@�@�@pn�Ea�bpn�Eb�����b���@(�������@��)
�i�ؖ��j�@���Q���A�@(���{�P)pn�߂�pn�{�P�@(�������@��)�@�����藧�̂ŁA
�@�@(���{�P)pn�E���߁i(���{�P)pn�j���߁i��pn�{�P�j���@(�������@��)
�@�㎮�̗��ӂ�W�J���āApn�Eb���̍����r����ƁApn�Ea�bpn�Eb�����b���@(�������@��) ������
�����Ƃ��킩��B�@�@�i�؏I�j
�@�����ŁAa��b �̏ꍇ���Apn�Ea�bpn�Eb�����b�����O�@�ƂȂ�̂ŁAa��b �̏ꍇ�����R������
���Ƃ��Ă悢�B
�@���Ȃ킿�A���R�� �� �Ƒf�� �� �ɑ��āA�@pn�Ea�bpn�Eb�����b���@(�������@��) �����藧�B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�؏I�j
�@�ȏ�ŁA�����i�S�T�j�������������o�����B�����i�S�T�j�����������āA���̒藝�������B
�藝�@�f�� �� �ɑ��āA���R�� ���A�� �i�������j�� �� �i�@�ŕ\�����Ƃ��l����B���Ȃ킿�A
�@��h��������h+1 �������� �� ���Ƃ�ƁA
�@�@������(��)�E��h�{��(���|�P)�E��h-1�{�c�{��(0)�@�A������(��)�E��h�{��(���|�P)�E��h-1�{�c�{��(0)
�@�Ə�����B
���̂Ƃ��A ���b����a(h)�bb(h)�Ea(h-1)�bb(h-1)�E�E�E�E�Ea(0)�bb(0)�@(�������@��)�@�����藧�B
�i�ؖ��j�@(���{�P)����(���{�P)��(��)�E��h�E(���{�P)��(���|�P)�E��h-1�E�E�E�E�E(���{�P)��(0)�@�ɂ����āA
�@(���{�P)��(��)�E��h �� ��(��)�E��h ���̌W���́A��(��)�E��h�b��(��)�E��h �ŁA���R���A
�@�@ph�Ea(��)�bph�Eb(��)����(��)�b��(��)�@(�������@��)
�@(���{�P)��(��-1)�E��h-1 �� ��(��-1)�E��h-1 ���̌W���́A��(��-1)�E��h-1�b��(��-1)�E��h-1 �ŁA���R���A
�@�@ph-1�Ea(��-1)�bph-1�Eb(��-1)����(��-1)�b��(��-1)�@(�������@��)
�@�@�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�@(���{�P)��(1)�E�� �� ��(1)�E�� ���̌W���́A��(1)�E���b��(1)�E�� �ŁA���R���A
�@�@p�Ea(1)�bp�Eb(1)����(1)�b��(1)�@(�������@��)
����āA(���{�P)����(���{�P)��(��)�E��h�E(���{�P)��(���|�P)�E��h-1�E�E�E�E�E(���{�P)��(0)�@�̂����̍��̌W���́A
�@��(��)�b��(��)�E��(��-1)�b��(��-1)�E�E�E�E�E��(1)�b��(1)�E��(0)�b��(0)�@(�������@��)
�ɓ������B
�@�ȏォ��A�@���b����a(h)�bb(h)�Ea(h-1)�bb(h-1)�E�E�E�E�Ea(0)�bb(0)�@(�������@��)�@�@�i�؏I�j
��@40�b10 ���V�Ŋ������]������߂�B
�@�����i�S�T�j�ɂ��A�@�S�O���T�E�V�{�T�@�A�P�O���P�E�V�{�R�@�Ȃ̂ŁA
�@�@40�b10��5�b1�E5�b3���T�O�߂P�@(�������@�V)�@�@�ł��邱�Ƃ�������B
�@���ۂɁA40�b10���W�S�V�U�U�O�T�Q�W�@�ɂ����āA�P�O3�߁|�P�@�i�������@�V�j�@���A
�@�W�S�V�U�U�O�T�Q�W�߂W�S�V�|�U�U�O�{�T�Q�W���V�P�T�߂P�@�i�������@�V�j
�@����āA40�b10 ���V�Ŋ���Ɨ]��͊m���� �P �ł���B
�i�R�����g�j�@��r�I�傫�� ���A�� �̒l�ɑ��āA���b�� ����v�Z�ŋ��߂邱�Ƃ͑�ςł����A
�@ �@�@�@�@��]�̒l���v�Z���邾���������猋�\�A��v�Z�ł��������Ⴂ�܂��ˁI
�i�NjL�j�@�Ȃ���u�R���r�l�[�V�����̘a�v�Ƒ肵�Ă����e���������܂����B
�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�@�i�����Q�W�N�P�Q���Q�X���t���j
�@���̑O�A�Ƃ�����������Ă��ċ��R�R���r�l�[�V�����Ɋւ���P�����������܂����B
�@�@�� k=t�`n kCt �� n+1Ct+1
�@�ǂ������ꂪ���藧�������Ȃ̂ł��B�ǂ̂悤�ɏؖ�����悢�̂ł��傤���c�c�B���ƁA��
�̂悤�ȂQ���W���̘a�Ɋւ���P�����͑��ɑ��݂���̂ł��傤���B
�@�g�m�u�܂����`�v����̃R�����g�ł��B�i�����Q�W�N�P�Q���Q�X���t���j
�@���̃y�[�W���i�P�P�j�� ������ �̏ꍇ�ŁA
�@�@���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b������+��+1�b��+1
�����Ă�悤�ȁD�D�D�B
�@DD++����̃R�����g�ł��B�i�����Q�W�N�P�Q���Q�X���t���j
�@���̒m���Ă���ؖ���4�����Ă����܂��B���D���Ȃ��̂��ǂ����B
[1]�@����̗��_����
�@t+1 �̐ԋʂ� n-t �̔��ʁi���v n+1 �j�������ɕ��ׂ܂��B���̕��ו��́A�ԋ�
�̈ʒu���l���āAn+1Ct+1 �ʂ�B������ł��E�̐ԋʂ��ǂ��ɂ��邩�ŕ��ނ���ƁA
�@�ł��E�̐Ԃ� t+1 �Ԗڂ̂��̂��AtCt �ʂ�
�@�ł��E�̐Ԃ� t+2 �Ԗڂ̂��̂��At+1Ct �ʂ�
�@�ł��E�̐Ԃ� t+3 �Ԗڂ̂��̂��At+2Ct �ʂ�
�@�@�c�c
�@�ł��E�̐Ԃ� n+1 �Ԗڂ̂��̂��AnCt �ʂ�
�ƂȂ邱�Ƃ��瓙�����������܂��B
[2]�@�K������̗��_����
�@a+1Cb+1��aCb + aCb+1 ���Aa+1Cb+1�|aCb+1��aCb
�܂�A�� k ���� kCt+1 �ŕ\����鐔��̊K������́AkCt �ł��B���������āA���ӂ̘a��
�� t ���ł��� tCt+1�i=0�j �ɉ�����A�� n+1 ���ł��� n+1Ct+1 �ɂȂ�܂��B
[3]�@�p�X�J���̎O�p�`����
�@kCt �� t��k��n �Ƃ��ăp�X�J���̎O�p�`�ŒT���ƁA�߈��ɕ���ł��܂��B���̍��v��
���ӂƂ������ƂɂȂ�܂��B�������� tCt �������āA��+1Ct+1 �𑫂��܂��B�i1��������1�𑫂���
�̂Œl�Ƃ��Ă͕ς���Ă��܂���j
�@�Ƃ���ŁA�p�X�J���̎O�p�`�͉��ɕ���̐��̘a�͂��̓�̊Ԃ̉��ɂ��鐔��
�Ȃ�܂��̂ŁA�����ׂ����̕��ѕ�����A���v���E�ӂ̒l�ɂȂ邱�Ƃ��킩��܂��B
�i���ۂɎ�����Ă݂�Ƃ킩��₷���Ǝv���܂��j
[4]�@�������̌W������
�@�P�����@x + x(1+x) + x(1+x)2 + �c�c + x(1+x)n = (1+x)n+1 - 1 �� xt+1 �̌W�����r����
�����܂��B
�@�Ȃ���̃R�����g�ł��B�i�����Q�W�N�P�Q���R�O���t���j
�@�܂����`����A���肪�Ƃ��������܂�m(_ _)m�B�܂���(11)�̎��ł�����^^;�B
4�ʂ���c�c�I�IDD++����A���肪�Ƃ��������܂�m(_ _)m�B�g�ݍ��킹�_�ł��������ł�
�ˁD�D�D�B
�i�S�U�j�@���R�� �� �ɑ��āA�@���b2�{��+1�b2����2�@�����藧�B
�@�ؖ��͈Ղ����B����͐��Ƀp�X�J���̎O�p�`�̒��ɐ��ގ��ŁA�����̎��ł���B�����A
�����̕����������낤�Ǝv���B
�i�ؖ��j�@���b2�{��+1�b2�����i���|�P�j/�Q�{���i���{�P�j/�Q����2�@�@�i�I�j
�@�c���A�����̊i�q����P��I�ԑI�ѕ��́A��2�ʂ�
�@�Ƃ���ŁA���b2�{��+1�b2���Q���b2�{���b1�����E��-1�b1�{���b1�@�Ȃ̂ŁA
��P�s����P�I�сA���̂P�ʂ�ɑ��đ�Q�s�`�悎�s����P�I��
�܂��́A�@��P�s����P�I�ԁ@�ƍl����A��2�ʂ肪�������B
�i�NjL�j�@�������� ����̂����e�ł��B�i�����R�P�N�S���P�V���t���j
�@�u�W���̐����v�ŁA�ȉ������肽�Ǝv���̂ł����ؖ����ł����ɂ���܂��B
�@B(n�Ck)��n�bk����!/{��!(���|��)!}�@�A0������1�@�Ƃ��Ĉȉ��̂Q�͓������i�H�j
�@��k=0n B(n�Ck)B(n�Cn-k)��k����k=0n B(n�Ck)B(n+k�Cn)��k(�P�|��)n-k
�@�Ⴆ�An=2 �̂Ƃ��A�����Ƃ��@1+4��+��2�An=3 �̂Ƃ��A�����Ƃ��@1+9��+9��2+��3�@�������
�Ĉ�v���܂��B
�@���m�b��q�ł���Α�ς��肪���������܂��B
�@DD++����̃R�����g�ł��B�i�����R�P�N�S���P�W���t���j
�@3�̔��� a�Ab�Ac �i������ a��c�Ab��c�j�ɑ��A�uP = (Y+1)a (Y+X)b ��W�J�����Ƃ�
�� Yc �̌W���͉����v�Ƃ��������l���Ă݂܂��B
[1]�@a������̂܂ܓW�J���܂��B�@P = ��[k=0..a] B(a,k) Y^k (Y+X)^b
�@�����āAb����W�J���܂��B
P = ��[k=0..a] B(a,k) Y^k ��[m=0..b] B(b,m) Y^m X^(b-m)
= ��[k=0..a] ��[m=0..b] B(a,k) B(b,m) X^(b-m) Y^(k+m)
�@���̂����A Y^c �ƂȂ鍀�́Am=c-k �ł���Ƃ��ł��B����� k��c �͈̔͂ł̂ݑ��݂���
���B���Ȃ킿�AY^c �̌W���́A
�@�@��[k=0..c] B(a,k) B(b,c-k) X^(b-c+k)
�ƂȂ�܂��B
[2]�@a��������ό`���Ă���W�J���܂��B
P = {(Y+X)+(1-X)}^a (Y+X)^b
= ��[k=0..a] B(a,k) (Y+X)^k (1-X)^(a-k) (Y+X)^b
= ��[k=0..a] B(a,k) (1-X)^(a-k) (Y+X)^(b+k)
�@�����āA(b+k)���W�J���܂��B
P = ��[k=0..a] B(a,k) (1-X)^(a-k) ��[m=0..(b+k)] B(b+k,m) Y^m X^(b+k-m)
= ��[k=0..a] ��[m=0..(b+k)] B(a,k) B(b+k,m) X^(b+k-m) (1-X)^(a-k) Y^m
�@���̂����AY^c �ƂȂ鍀�� m=c �ł���Ƃ��ł��B���Ȃ킿�AY^c �̌W���́A
�@�@��[k=0..a] B(a,k) B(b+k,c) X^(b-c+k) (1-X)^(a-k)
�ƂȂ�܂��B[1] �� [2] �͓������ɂ��ċc�_�������̂Ȃ̂ŁA�����͓����͂��B
�@����āA
��[k=0..c] B(a,k) B(b,c-k) X^(b-c+k) = ��[k=0..a] B(a,k) B(b+k,c) X^(b-c+k) (1-X)^(a-k)
�ł��B���̓����̓���ȏꍇ�Ƃ��āAa=b=c=n �Ƃ���A
��[k=0..n] B(n,k) B(n,n-k) X^k = ��[k=0..n] B(n,k) B(n+k,n) X^k (1-X)^(n-k)
��������܂��B
�������g�����_�ł̏ؖ�������Ζʔ������ł����A������͎��͎v�����܂���ł����B
�@���Ђ�����̃R�����g�ł��B�i�����R�P�N�S���P�W���t���j
> �uk=0����k=n�܂ŁCB(n,k) B(n+k,n) X^k(1-X)^{n-k} �̑��a�v
=��[k=0�`n]B(n,k)*B(n+k,n)*X^k*(1-X)^(n-k)
=��[k=0�`n]B(n,k)*B(n+k,n)*X^k*{��[i=0�`n-k]B(n-k,i)*(-1)^i*X^i}
=��[k=0�`n]��[i=0�`n-k]B(n,k)*B(n+k,n)*B(n-k,i)*(-1)^i*X^(k+i)
�@�����ŁAh=k+i�Ƃ����ƁA
=��[k=0�`n]��[h=k�`n]B(n,k)*B(n+k,n)*B(n-k,h-k)*(-1)^(h-k)*X^h
�@�a�̎�����ς���ƁA
=��[h=0�`n]��[k=0�`h]B(n,k)*B(n+k,n)*B(n-k,h-k)*(-1)^(h-k)*X^h
=��[h=0�`n]��[k=0�`h]{n!/k!/(n-k)!}*B(n+k,n)*{(n-k)!/(h-k)!/(n-h)!}*(-1)^(h-k)*X^h
=��[h=0�`n]��[k=0�`h]B(n+k,n)*{n!/k!/(h-k)!/(n-h)!}*(-1)^(h-k)*X^h
=��[h=0�`n]��[k=0�`h]B(n+k,n)*{n!/h!/(n-h)!}*{h!/k!/(h-k)!}*(-1)^(h-k)*X^h
=��[h=0�`n]��[k=0�`h]B(n+k,n)*B(n,h)*B(h,k)*(-1)^(h-k)*X^h
=��[h=0�`n]B(n,h)*(-1)^h*X^h*{��[k=0�`h]B(n+k,n)*B(h,k)*(-1)^(-k)}
�@�����ŁA�u�W���̐����v��(27)�̎��𗘗p����ƁA
��[k=0�`h]B(n+k,n)*B(h,k)*(-1)^(-k)
=��[k=0�`h]B(n+k,k)*B(h,h-k)*(-1)^k
=B(h-n-1,h)
=(-1)^h*B(n,h)
�����藧�̂ŁA
=��[h=0�`n]B(n,h)*(-1)^h*X^h*{(-1)^h*B(n,h)}
=��[h=0�`n]B(n,h)*B(n,h)*X^h
�@h��k�Ə���������A
=��[k=0�`n]B(n,k)*B(n,k)*X^k
=��[k=0�`n]B(n,k)*B(n,n-k)*X^k
> �uk=0����k=n�܂ŁCB(n,k) B(n,n-k) X^k �̑��a�v
���Ƃ肠�������ǂ蒅�������ǁA�킽���͂܂��u�W���̐����v(27)�𗝉����Ă��Ȃ�����A
�@�ؖ��ł����Ƃ͌����Ȃ��ȁc�B
�@������������̃R�����g�ł��B�i�����R�P�N�S���Q�O���t���j
�@DD++����A�f�����ɋ����Ă��܂��B���肪�Ƃ��������܂����B�Q�l�ɂ����Ē����܂��B
�@���Ђ�����A(27)�̎����g���Ƃ͎v�������܂���ł����B���肪�Ƃ��������܂����B
�@�f�`�h ����̃R�����g�ł��B�i�����R�P�N�S���Q�O���t���j
�@toru����̋L�������āA
�@��[k=0,n]B(n,k)*B(n+k,n)*X^k*(1-X)^(n-k)=��[k=0,n]B(n,k)^2*X^k
���������邱�Ƃ��Ӗ����邪�A�����ɁA�P^n=(X+1-X)^n=��[k=0,n]B(n,k)*X^k*(1-X)^(n-k)
�ł��邱�ƂƗނ��āA
�@(2x)^n=(X+1+X-1)^n=��[k=0,n]B(n,k)*(X+1)^k*(X-1)^(n-k)
�̂ɁA�@2^n*x^n=��[k=0,n]B(n,k)*(X+1)^k*(X-1)^(n^k)
�]���āA�@x^n=��[k=0,n]B(n,k)*(X+1)^k*(X-1)^(n-k)/2^n
�����ŁA�@L(n)=��[k=0,n]B(n,k)^2*(X+1)^k*(X-1)^(n-k)/2^n�@�Ȃ�����`���Ă��ƁA
L(0)=1
L(1)=X
L(2)=3/2*X^2-1/2
L(3)=5/2*X^3-3/2*X
L(4)=35/8*X^4-15/4*X^2+3/8
L(5)=63/8*X^5-35/4*X^3+15/8*X
�����
�ƂȂ�Alegendre function �ƌĂ������\�����Ă����\���ɗނ��Ă���悤�Ɍ�����B
�@����ɁA����L(n)���u��g�ݍ��킹��ƁAChe(n)=��[k=0,n]L(k)*L(n-k)�@����A
Che(0)=1
Che(1)=2*X
Che(2)=4*X^2-1
Che(3)=8*X^3-4*X
Che(4)=16*X^4-12*X^2+1
Che(5)=32*X^5-32*X^3+6*X
�����
�ƂȂ�Asecond chebychev function �ƌĂ����Ɍq����B
�i�NjL�j�@�ߘa���N�P�P���P�T���t��
�i�S�V�j�@��+1�b1�{�Q��+2�b2�{�R��+3�b3�{�E�E�E�{����+r�b�����i���{�P�j��+r+1�bn+2
�i�ؖ��j�@���En+k�bk�����E�i���{���j�I/�i���I���I�j���i���{���j�I/�i�i���|�P�j�I���I�j
���i���{�P�j�E�i���{���j�I/�i�i���|�P�j�I�i���{�P�j�I�j���i���{�P�j�En+k�bn+1
����āA
���Ӂ��i���{�P�j�En+1�bn+1�{�i���{�P�j�En+2�bn+1�{�i���{�P�j�En+3�bn+1�{�E�E�E�{�i���{�P�j�En+r�bn+1
���i���{�P�j�in+1�bn+1�{n+2�bn+1�{n+3�bn+1�{�E�E�E�{n+r�bn+1�j
�@��L�́i�P�P�j���A�@���bn�{��+1�bn�{��+2�bn�{�E�E�E�{��+���bn����+��+1�b��+1 �Ȃ̂ŁA
�@�@n+1�bn+1�{n+2�bn+1�{n+3�bn+1�{�E�E�E�{n+1+(r-1)�bn+1����+��+1�b��+2
����āA�@��+1�b1�{�Q��+2�b2�{�R��+3�b3�{�E�E�E�{����+r�b�����i���{�P�j��+r+1�bn+2�@�@�i�؏I�j
�i�NjL�j�@�ߘa�Q�N�V���R�P���t��
�@�ŋ߁A���̂悤�Ȓ����₪���邱�Ƃ�m�����B
�i�S�W�j�@��k=0n 2k�bk�E2n-2k�bn-k���S���@�����藧���Ƃ��ؖ�����B
�@���𗝉����邽�߂ɁA�����P�A�Q�A�R�̏ꍇ�ɂ��ď��������Ă݂��B
�@�����P�@�̂Ƃ��A0�b0�E2�b1�{2�b1�E0�b0���S
�@�����Q�@�̂Ƃ��A0�b0�E4�b2�{2�b1�E2�b1�{4�b2�E0�b0���S2���P�U
�@�����R�@�̂Ƃ��A0�b0�E6�b3�{2�b1�E4�b2�{4�b2�E2�b1�{6�b3�E0�b0���S3���U�S
�@���������Ă݂͂����̖̂��̈Ӗ����悭�킩��܂���ˁI
�i���j�@�i�P�|�S���j^�i-1/2�j�̂����̌W���́A�i�Q���j�I/�i���I�j2��2n�bn �Ȃ̂ŁA
�@�@�@�i�P�|�S���j^�i-1/2�j����n=0�� 2n�bn ��k�@�E�E�E�@(*)
�@�����ŁA�@�i�P�|�S���j^�i-1�j���P�{�S���{�S2��2�{�S3��3�{�E�E�E�E
�@(*)�̉E�ӂ̕����̂����̌W���́A�@��k=0n 2k�bk�E2n-2k�bn-k
�@����āA�@��k=0n 2k�bk�E2n-2k�bn-k���S���@�����藧�B�@�@�i�I�j
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�Q�N�W���P���t���j
�@��L�́A�W����4^n������Ă����̂����āA�ł́A3^n�͂ǂ���������邩�F�X��
�킵�Ă�����A���R�A
�@��k=0n 2^k*nCk=3^n
����ɁA
�@��k=0n 3^k*nCk=4^n
�@��k=0n 4^k*nCk=5^n
�@��k=0n 5^k*nCk=6^n
�@����������������
�ƂȂ�ł͂Ȃ����I���܂ł���ȕ\�����������Ƃ��Ȃ������̂Łi����������k=0n nCk=2^n)
�r�b�N�����܂����B
�@���̌��ۂ͓��R�Ȃ�ł����ˁH�Q���W���̐����Ƃ��Ă͂ƂĂ��ʔ����Ǝv���܂��̂ŁA��
�����Ă����Ă��炢�����B
�i�ǐL�j�@�ォ��l������A�@(1+X)^n=��k=0n nCk*X^k�@�Ȃ̂ŁAX=1,2,3,4,����@�Ƃ����A��
�@�@�@�@��͓��R�ł����I
�i�R�����g�j�@�g�����́u�b�v������p���ĕ\�����Ƃ���Ɋ������܂����B
�@���Ђ�����̃R�����g�ł��B�i�ߘa�T�N�W���P�S���t���j
�@�����ߋ��Ɍv�Z�������̂��܂Ƃ߂Ă݂܂����B�����ŁAn�bk �� C[n,k] �Ə������Ƃɂ��܂��B
�i�S�X�j�@C[M+N,M] ����k=0M C[n+k-1,k]*C[M+N-n-k,M-k]
�@����k=0N C[m+k-1,k]*C[M+N-m-k,N-k]
�@����k=0m-1 C[n+k-1,k]*C[M+N-n-k,M-k]�{��k=0n-1 C[m+k-1,k]*C[M+N-m-k,N-k]
�@����k=mM C[n+k-1,k]*C[M+N-n-k,M-k]�{��k=nN C[m+k-1,k]*C[M+N-m-k,N-k]
�@�������A 1��m��M�@�A1��n��N
�i�ؖ��j�́A�u���w������b�v�́u�m���v���Q�ƁB�����̒u�����������Ď������Ă��܂����A
�u�m���v�̃y�[�W�ŁA�����������W���ƍl�����͓����ł��B���̂悤�ɑΉ����܂��B
�l���u�m���v�� m+m'+1�@�AN���u�m���v�� n+n'+1�@�Am���u�m���v�� m+1�@�An���u�m���v�� n+1
�i�T�O�j�@(a�{b)^n/a����k=0n C[n,k]*(a�{k)^(k-1)*(b�|k)^(n-k)�@�@�������A a��0
�i�ؖ��j�́A�u���w������b�v�́u�܂��j�̖��v���Q�ƁB
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�U�N�V���U���t���j
�@�g������ ���b�� �Ő��������\�I�Ȃ��̂Ƃ��āA
�@�@���b0�{���b1�{���b2�{���b3�{�E�E�E�{���b���{�E�E�E�{���b�����Q��
������B���̑��A�F�X�Ɨ���グ�Ă݂܂��̂ŁA���킵�Č��ĉ������B
��nCk ���܂܂��ƁA���͒����ł͂Ȃ��Ȃ��C���t���܂���B
(A) ���������̂Ƃ��A�@���b0�{���b2�{���b4�{�E�E�E�{���b��
(B) ������̂Ƃ��A�@���b0�{���b2�{���b4�{�E�E�E�{���b��-1
(C) ���̕����Œ肷��B�@���b���{��+1�b���{��+2�b���{�E�E�E�{��+���b��
(D) ���A�����ɕω�������B�@���b���{��-1�b��-1�{��-2�b��-2�{�E�E�E�{��-k�b0
(E) ���A���A�������ɕω�������B2���b0�|2��-1�b1�{2��-2�b2�{�E�E�E�{(�|�P�jn���bn
(F) �Q��C���̐ς�g���킷�B
�@���b0�E���b���{���b1�E���b��-1�{���b2�E���b��-2�{�E�E�E�{���b���E���b0
(G) �Q��C���̐ς������݂ɑg���킷�B
�@���b0�E���b���|���b1�En-1�b��-1�{���b2�En-2�b��-2�{�E�E�E�{(�|�P�j�����b���En-k�b0
(H) C�ɌW����t��������B�@�Q���b���{�Q�E�Q��-1�b���{�Q2�E�Q��-2�b���{�E�E�E�{�Q���E���b��
�@�炷���邳��̃R�����g�ł��B�i�ߘa�U�N�V���U���t���j
�@(A)��(B)�́A��L��(6)�A(C)�́A��L��(11)�A(F)�́A��L��(16)�ɑ������܂��ˁB
�@���Ђ�����̃R�����g�ł��B�i�ߘa�U�N�V���U���t���j
�@(E)�́A��L��(12)�A(H)�́A��L��(13)�ɑ������܂��ˁB
(D)�́A��L��(11)�̐������̂Ȃ���
�@�i�P�P�j�ŁA������ �̂Ƃ��́A���b�������b��-���@���A���̌`�ɂ��ό`�ł���B
�@�@�@�@�@�@���b0�{��+1�b1�{��+2�b2�{�E�E�E�{��+���b������+��+1�b��
�@���̌����́A�u���a�̌����v�Ƃ�������B
�ɂ����āAn �� n-k �������� m �� k ��������ƁA
�@���Ӂ�n-k�b0�{n-k+1�b1�{n-k+2�b2�{�E�E�E�{n�b��
���Ȃ킿�A�@���Ӂ����b���{��-1�b��-1�{��-2�b��-2�{�E�E�E�{��-k�b0�@�ƂȂ�̂ŁA�����́An+1Ck
(G)�́A��L��(27)�F
�@���b0�E���b���|��+1�b1�E���b��-1�{�E�E�E�{�i�|�P�j����+���b���E���b0����-��-1�b��
�ɂ����āA���ӂ� (-1)k �������āAn �� n-k �������āAm �� n �����������̂Ȃ̂ŁA
�����́A(-1)k�Ek-1Ck���O
�i�R�����g�j�@�炷���邳��A���Ђ�����A�T�����Ă��������Ă��肪�Ƃ��������܂��B
�@�f�`�h ����̃R�����g�ł��B�i�ߘa�U�N�V���W���t���j
�@�����ɂȂ����̂�����Ă݂܂����B
(�h) aCb�EcC0�{a+1Cb�EcC1�{a+2Cb�EcC2�{����{a+cCb�EcCc�@(�������Aa��b��c��0)
(�i) aC0�EsCa�|aC1�Es-tCa�{����{(-1)kaCk�Es-ktCa�{����{(-1)aaCa�Es-atCa
�@(�������Aa�As�At���O �̐���)
�i�NjL�j�@�ߘa�V�N�T���Q�W���t��
�@���̓��k��w�@�O�����n�i�P�X�X�S�j�̖��́A�Q���W���̐V���ȓ����������Ă���B
����@�@N���Q�ȏ�̐����Ƃ���BA�`�[���Ƃa�`�[�������鎎��������Ԃ��čs���A���N��
�@�@�����`�[����D���Ƃ���B�e�����ɂ����Ĉ��������͂Ȃ����̂Ƃ��A���ꂼ��̏��m��
�@�@�͂P/�Q�Ƃ���B�w��ڂ̎����ŗD���`�[�������܂������̂Ƃ��āA���ɓ�����B
�i�P�j�@P(X��N�{�P) �����߂�B
�i�Q�j�@P(X���m�{���j�@(�����O�A�P�A�E�E�E�A�m�|�P�j�����߂�B
�i�R�j�@��n����j=0n n+j�bj�i�P/�Q�jj�@(�����P�A�Q�A�E�E�E�j�@�����߂�B
�i���j�i�P�j�@P(X��N�{�P)���Q�E�i�P/�Q�jN�{�Q�EN�b1(�P/�Q)N�E�i�P/�Q�j���i�m�{�Q�j/�QN
�i�Q�j�@P(X���m�{���j���Q�EN+j-1�bj(�P/�Q)N+j-1�E�i�P/�Q�j��N+j-1�bj(�P/�Q)N+j-1
�i�R�j�@��j=0N-1 N+j-1�bj(�P/�Q)N+j-1���P�@�Ȃ̂ŁA��j=0N-1 N+j-1�bj(�P/�Q)j���QN-1
�����ŁA�@�m�|�P�����@�Ƃ����ƁA�@��n����j=0n n+j�bj�i�P/�Q�jj���Qn�@�@�i�I�j
�i�R�����g�j�@��L�̌��ʂ���A���̓��������藧���Ƃ�������B
�@n�b0�{n+1�b1�i�P/�Q�j�{n+2�b2�i�P/�Q�j2�{�E�E�E�{2n�bn�i�P/�Q�j�����Qn
�@���̓����́An�b0��n�b���An+1�b1��n+1�b���An+2�b2��n+2�b���A�E�E�E�@�Ƃ��A���ӂ��Q���{����
�i�P�R�j�@2���b���{�Q�E2��-1�b���{�S�E2��-2�b���{�E�E�E�{�Q���E���b�����Q2��
�ƕό`����A���ڎ������Ƃ��\�ł���B�i���@�i�P�R�j���ؖ��j
�i�NjL�j�@�ߘa�V�N�P�Q���P���t��
�@���̓��k��w�@������n�i�Q�O�O�R�j�̖��́A�Q���W���̐V���ȓ����������Ă���B
����@�@ �i�P�j�@���̐������ɑ��āA�e�i���j���i�����|��-���j�� �Ƃ���B�e�f�i�O�j�����߂�B
�i�Q�j�@��k=0n n�bk�i�|�P�jk�i���|�Q���j�@���ȒP�ɂ���B
�i���j�i�P�j�@�����P�@�̂Ƃ��A�@�e�i���j�������|��-���@���A�e�f�i���j�������{��-���@����A�e�f�i�O�j���Q
�@�����Q�@�̂Ƃ��A�@�e�i���j���i�����|��-���j�� ���A�@�e�f�i���j�����i�����|��-���j��-1�E�i�����{��-���j�@����A
�@�e�f�i�O�j���O
�i�Q�j�@�e�i���j���i�����|��-���j�� �ɂ��āA�Q���藝���A
�@�e�i���j����k=0n n�bk�i�����jn-k�i�|��-���jk����k=0n n�bk�i�|�P�jk�i�����jn-2k
����āA�@�e�f�i���j����k=0n n�bk�i�|�P�jk�i���|�Q���j�i�����jn-2k�@����A
�@��k=0n n�bk�i�|�P�jk�i���|�Q���j���e�f�i�O�j
�����藧�B���������āA�i�P�j���A
�@�����P�@�̂Ƃ��A�@��k=0n n�bk�i�|�P�jk�i���|�Q���j���Q
�@�����Q�@�̂Ƃ��A�@��k=0n n�bk�i�|�P�jk�i���|�Q���j���O�@�@�i�I�j
�@���������āA���̌�����B
�i�T�P�j�@��k=0n n�bk�i�|�P�jk�i���|�Q���j���O�@�@�������A �����Q
�@�������A�����P�̂Ƃ��́A��L�̒l�́A�Q�@�ƂȂ�B
�@�@�@�ȉ��H����