目の積 
当HPの掲示板「出会いの泉」に、GAI さんが次のような問題を提起された。
(平成22年5月5日付け)
しばらく、サイコロの目の和が話題になっていたので、「では目の積はどうなるんだろう?」
の疑問が湧いてきました。この場合はどうなるのかな?
すなわち、
n 回サイコロを投げ、出た目の積がPである場合の数を求めよ。
早速、FNさんが挑戦され、次のような解答を得た。(平成22年5月6日付け)
(一部文言等を修正させていただきました。)
目の和の場合は、GAI さんも書いておられるように、
n 個のサイコロを投げるとき、目の和が N となる場合の数は、多項式
(x+x2+x3+x4+x5+x6)n
を展開したときの、xN の係数を調べればよい。目の積の場合は、
(1+x+x2+y+xy+z)n
を展開したときの、xa・yb・zc の係数が、積が、2a・3b・5c となる場合の数になる。
Maxima とかを使って展開するのが妥当かと思いますが、一応やってみます。
(解) サイコロの目の数は、 1、2、3、4、5、6 で、素因数に注目すれば、
2 と 3 と 5
しかない。よって、出る目の積 P は、
P=2a・3b・5c ( a、b、c は、0以上の整数)
と書くことができる。
n 回のうち、5の目は c 回出る。いま、6の目が s 回、4の目が t 回出るとすると、
3の目は、b−s 回、 2の目は、a−s−2t 回、 1の目は、n+s+t−a−b−c
回
出る。したがって、同じものを含む順列の公式から、
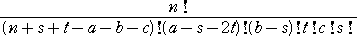
後は、これを、 s=0 〜 min(a,b)、 t=max(0,a+b+c−n−s) 〜 (a−s)/2 に
ついて和をとればよい。 (終)
例 n=20、P=214・37・53 のとき、場合の数は、22,417,812,674,400通り。
例 大小2個のサイコロを投げるとき、目の積が12になるのは何通りあるか。
素朴に数え上げれば、 (2,6)、(3,4)、(4,3)、(6,2) の4通りだが、上記の考え
方で求めてみよう。
出る目の積 P は、 P=22・3 と素因数分解できる。
2 個のサイコロうち、6の目が s 回、4の目が t 回出るとすると、
3の目は、1−s 回、 2の目は、2−s−2t 回、 1の目は、s+t−1
回
出る。ここで、 0≦s≦1 、 1−s≦t≦(2−s)/2 である。
すなわち、 s=0 のとき、 t=1 で、 s=1 のとき、 t=0 と定まる。
| s |
t |
1の目 |
2の目 |
3の目 |
4の目 |
5の目 |
6の目 |
| 0 |
1 |
0 |
0 |
1 |
1 |
0 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
0 |
1 |
したがって、同じものを含む順列の公式から、求める場合の数は、
2!/(1!1!)+2!/(1!1!)=4 (通り)
となる。
例 大中小3個のサイコロを投げるとき、目の積が60になるのは何通りあるか。
素朴に数え上げれば、12通りだが、上記の考え方で求めてみよう。
出る目の積 P は、 P=22・3・5 と素因数分解できる。
3 個のサイコロうち、6の目が s 回、4の目が t 回出るとすると、5の目は
1 回で、
3の目は、1−s 回、 2の目は、2−s−2t 回、 1の目は、s+t−1
回
出る。ここで、 0≦s≦1 、 1−s≦t≦(2−s)/2 である。
すなわち、 s=0 のとき、 t=1 で、 s=1 のとき、 t=0 と定まる。
| s |
t |
1の目 |
2の目 |
3の目 |
4の目 |
5の目 |
6の目 |
| 0 |
1 |
0 |
0 |
1 |
1 |
1 |
0 |
| 1 |
0 |
0 |
1 |
0 |
0 |
1 |
1 |
したがって、同じものを含む順列の公式から、求める場合の数は、
3!/(1!1!1!)+3!/(1!1!1!)=12 (通り)
となる。
(コメント) 上記の公式では、4の目と6の目が出る回数を変数としたところがポイントです
ね!素朴に数え上げるときも、この点に注意すれば機械的に速く求まりそうです。
FNさんに感謝します!
HN「ぽっぽ」さんからの出題です。(平成23年2月13日付け)
サイコロを n
回投げたとき、その積が 6k の倍数になる確率を求めよ。
k=1、2
のときは計算できましたが、何も見えてきませんでした。そもそもk
が任意の整
数のとき、これを一般化することは、できるのでしょうか?
ぽっぽさんの問いかけに、当HPがいつもお世話になっているHN「FN」さんが考察されま
した。(平成23年2月14日付け)
6k
の倍数はかなり難しいですから、もう少し簡単な場合から考えます。
(1) 3k の倍数(5k
の倍数)のとき
これは、n 回のうち、k
回以上3または6が出る場合だから、
ΣnCr(1/3)r・(2/3)n-r ただし、Σは、r=k、k+1、・・・、n
の和
(5k
の倍数のときは、Σ(1/6)r・(5/6)n-r ただし、Σは、r=k、k+1、・・・、n
の和)
この式のΣを、Σを使わないで表すのは無理だと思います。
kが小さいとき(例えば、k=1、2)は余事象を考えれば、Σの項数は、1とか2なので、Σ
なしで書けますが、一般のkでは無理でしょう。
(2) 2k
の倍数のとき
4がs回、2または6がr回出るとすると、 2s+r≧k だから、
ΣnCs(1/6)sΣn-sCr(1/3)r・(1/2)n-s-r
ただし、前のΣは、s=0から[k/2]までの和、後のΣは、r=k−2sからn−sまでの和
(3) 6k
の倍数のとき
同様に考えると、4重のΣになると思います。Σの数を減らすのは多分無理でしょう。余事
象を考えても、一般の k
については状況に変化は起きないでしょう。だから、Σを使った式
では駄目ということならできないと思います。もちろん、k
が小さいときは余事象を考えて、で
きる可能性はあります。
k=1 のときが、平成4年の京都大学の入試問題で次の形で出題されています。
京都大学 前期(1992) (1)(2):文系 (1)(3):理系
さいころを繰り返し n 回振って、出た目の数を掛け合わせた積をXとする。すなわち、
k 回目に出た目の数を
Yk とすると、 X=Y1Y2・・・Yn
(1) Xが3で割り切れる確率
pn を求めよ。
(2) Xが4で割り切れる確率 qn
を求めよ。
(3) Xが6で割り切れる確率 rn
を求めよ。
(解)(1) Xが3で割り切れないとき、Y1、Y2、・・・、Yn の何れもが3で割り切れない。
よって、 1−pn=(2/3)n より、 pn=1−(2/3)n
(2) Xが4で割り切れないとき、
(イ) Y1、Y2、・・・、Yn の何れもが 1、3、5 のどれか
(ロ) Y1、Y2、・・・、Yn のうち、1つだけ 2または6 で、他は 1、3、5 のどれか
よって、 1−pn=(1/2)n+n(1/3)(1/2)n-1=(2n+3)(1/2)n/3 より、
pn=1−(2n+3)(1/2)n/3
(3) Xが6で割り切れないとき、
(イ) Y1、Y2、・・・、Yn の何れもが 1、2、4、5 のどれか
(ロ) Y1、Y2、・・・、Yn の何れもが 1、3、5 のどれか
ただし、(イ)(ロ)の場合の中には、
Y1、Y2、・・・、Yn の何れもが 1、5 の場合が重複している。
よって、 1−pn=(2/3)n+(1/2)n−(1/3)n より、
pn=1−(2/3)n−(1/2)n+(1/3)n (終) (→ (別解))
(コメント) 余事象を考える点がポイントですね!
京大の問題は、上の(1)(2)(3)の k=1、k=2、k=1 の場合です。河合塾の「ハイレベ
ル理系数学50テーマ150題」にはやや難のマークがついています。かなり難しいとされて
いる本です。その本でやや難とされているということは相当難しいということでしょう。
そこまで難しいとは思いませんが、k=1でもかなり難しいと言えます。k=1とk=2では相
当な差がありそうです。k=2の場合を考えましたが、面倒で途中で放棄してしまいました。
ぽっぽさんがどのようにして
k=2
のときを解かれたかを書いていただけますか。
ぽっぽさんからのコメントです。(平成23年2月15日付け)
6を2つ含む時、1つ含む時、含まない時に
場合分けしましたが、相当時間がかかり
ました。
結果は、 [6n+2n−3n−4n+n{(n+5)・2n-2−2・3n-1−2・4n-1}]/6n です。
一般の場合は、P(6k)−P(6k-1) で漸化式にするという方針が一番よさそうな気がし
ます。
FNさんによれば、それは必要ないとのことであるが...。(平成23年2月16日付け)
P(6k)は、4重のΣを使って書くのは難しくありません。そして、その式を簡単にするの
は多分無理です。P(3k)ならΣひとつで書けますが、それをΣを使わないで書くのが無
理なのと同じです。そういう意味で、P(6k)を一般の
k について求めることについては
終わっていると思います。あとは小さい k
に対する値、例えば、P(63)を求めることとか
でしょう。
「それは必要ないと思います」というのは、P(6k)とP(6k-1)の間にはあまり関係がない
からです。P(36)を求めるのに、P(6)の値がほとんど役に立たないのと同じです。
P(3k)とP(3k-1)なら関係はあるでしょうが、漸化式を作るより直接求めてしまうでしょう。
また、ぽっぽさんは、この問題を考えている最中に、
ΣΣ(kCp・nCk・2n-k)=4n (ただし、k=0〜n 、p=0〜k)
という関係を見つけられました。
ぽっぽさんの見いだされた関係を、らすかるさんが、証明されました。
(平成23年2月15日付け)
(証明)
ΣΣ(kCp・nCk・2n-k)
=Σ[k](nCk・2n-kΣ[p]kCp)
=Σ[k](nCk・2n-k・2k)
=Σ[k](nCk・2n)=2n・Σ[k]nCk=2n・2n=4n (証終)
一般の
k は駄目でしょうから、k が小さいところだけを考えてみます。京都大学で出題さ
れたものを含みます。
さいころを n 回投げて、その積が
m の倍数になる確率を求めたい。m が小さいときだけ
を考えるので、余事象の方が求めやすい。
余事象の確率を P(m)
とする。即ち、さいころを n 回投げて、その積がm の倍数になら
ない確率を P(m) とする。n は固定して考えるものとして、n
は表記しないこととする。
m1の倍数でもなくて、m2の倍数でもない確率を、P(m1,m2)
と書く。
P(2)については、n 回全てが奇数の目なので、 P(2)=(1/2)n
P(3)については、n 回全てが 1、2、4、5 の何れかなので、 P(3)=(2/3)n
P(5)については、n 回全てが
1、2、3,4、6 の何れかなので、 P(5)=(5/6)n
ここまでは問題ありません。
P(10)について、 10の倍数=2かつ5の倍数 なので、
10の倍数でない=2の倍数でない または 5の倍数でない
なので、個数定理により、
n(10の倍数でない)
=n(2の倍数でない)+n(5の倍数でない)−n(2の倍数でも5の倍数でもない)
なので、 P(10)=P(2)+P(5)−P(2,5)=(1/2)n+(5/6)n−(1/3)n
同様にして、P(15)=P(3)+P(5)−P(3,5)=(2/3)n+(5/6)n−(1/2)n
P(6)=P(2)+P(3)−P(2,3)=(1/2)n+(2/3)n−(1/3)n
※ 6の目があるから、P(6)はP(10)等と違うかと思いましたが同じでした。
P(9)について、n
回全てが 1、2、4、5 の何れかであるか、または、n回中1回だけ3また
は6がでて、それ以外は
1、2、4、5 の何れかであるときなので、
P(9)=(2/3)n+nC1(1/3)(2/3)n-1=(2/3)n-1(n+2)/3
同様にして、P(25)=(5/6)n+nC1(1/6)(5/6)n-1=(5/6)n-1(n+5)/6
P(4)について、n 回全てが 1、3、5 の何れかであるか、または、n 回中1回だけ2または
6がでて、それ以外は 1、3、5 の何れかであるときなので、
P(4)=(1/2)n+nC1(1/3)(1/2)n-1=(1/2)n-1(n/3+1/2)
※ 4の目があるから、少しだけP(9)等と違いますが、ほとんど同じです。
30=2・3・5 なので、個数定理により
P(30)=P(2)+P(3)+P(5)−P(2,3)−P(2,5)−P(3,5)+P(2,3,5)
=(1/2)n+(2/3)n+(5/6)n−(1/3)n−(1/3)n−(1/2)n+(1/6)n
=(2/3)n+(5/6)n+(1/6)n−2(1/3)n
P(12)=P(4)+P(3)−P(4,3) において、まず、P(4,3)を求める。
P(4,3)=(1/3)n+nC1(1/3)(1/3)n-1=(1/3)n-1(n+1)/3
これを代入して出ます。P(20)、P(18)、P(45)、P(50)、P(75)は似たようなものでしょう。
P(36)=P(4)+P(9)−P(4,9) もできそうです。
上記の結果を用いて、ぽっぽさんの問題(k=2のとき):
サイコロを n 回投げたとき、その積が 62
の倍数になる確率を求めよ。
の解は、 (6n+2n−3n−4n+n(2n-2・(n+5)−2・3n-1−2・4n-1))/6n
となることを、FNさんが検証されました。(平成23年2月16日付け)
P(4)=(1/2)n+(n/3)(1/2)n-1={(2n+3)/3}(1/2)n
P(9)=(2/3)n+(n/3)(2/3)n-1={(n+2)/2}(2/3)n
P(4,9)は、4でも9でも割り切れない場合だから、4は駄目で、ほとんどが1か5で、2、3、
6が1回も出ないか、2、3、6のどれかが1回だけか、2、3が1回ずつだから、
P(4,9)=(1/3)n+(n/2)(1/3)n-1+n(n−1)・(1/6)2(1/3)n-2
=(1/3)n+(3n/2)(1/3)n+n(n−1)/4・(1/3)n
={(n2+5n+4)/4}(1/3)n
これらを用いて、
P(36)=P(4)+P(9)−P(4,9)
={(2n+3)/3}(1/2)n+{(n+2)/2}(2/3)n−{(n2+5n+4)/4}(1/3)n
これに対して、ぽっぽさんの結果を変形すると、
[6n+2n−3n−4n+n{(n+5)・2n-2−2・3n-1−2・4n-1}]/6n
=1+(1/3)n−(1/2)n−(2/3)n+(n2/4)(1/3)n
+(5n/4)(1/3)n−(2n/3)(1/2)n−(n/2)(2/3)n
=1−(1/2)n−(2n/3)(1/2)n−(2/3)n−(n/2)(2/3)n
+(n2/4)(1/3)n+(5n/4)(1/3)n+(1/3)n
=1−{(2n+3)/3}(1/2)n−{(n+2)/2}(2/3)n+{(n2+5n+4)/4}(1/3)n
=1−P(36)
となり、ぽっぽさんの結果と一致する。
問題:「サイコロを n
回投げたとき、その積が 6k の倍数になる確率を求めよ。」に
ついて、HN「at」さんが考察されました。(平成23年2月20日付け)
サイコロを n 回振ったとき、その積が 6k の倍数になる確率を、p(n,k)とする。
k=3、4、5の場合のp(n,k)は次のようになる。
p(n,3)={3n-2(9・2n−2n2−7n−9)−22n-3(n2+3n+8)
+2n-6(n4+14n3+39n2+74n+64)}/6n
p(n,4)={3n-4(81・2n−4n3−24n2−53n−81)−22n-4(n3+3n2+20n+48)/3
+2n-8(n6+27n5+133n4+453n3+1594n2+2400n+2304)/9}/6n
p(n,5)=[3n-5{243・2n−(4n4+36n3+107n2+339n+486)/2}
−22n-7(n4+2n3+35n2+154n+384)/3
+2n-14(n8+44n7+362n6+992n5+12041n4
+31268n3+87820n2+162384n+147456)/9]/6n
サイコロを n 回振ったときに、2、3、4、6の目がそれぞれA回、B回、C回、D回出るもの
とすれば、p(n,k)の指数型母関数は次のようになる。
{e6x−e3xΣ[A+2C+D<k](xA/A!)(xC/C!)(xD/D!)
−e4xΣ[B+D<k](xB/B!)(xD/D!)
+e2xΣ[A+2C+D<kかつB+D<k](xA/A!)(xB/B!)(xC/C!)(xD/D!)}/6n
この母関数から、p(n,k)の式が得られます。たとえば、K=2のときを考えてみると、
Σ[A+2C+D<2](xA/A!)(xC/C!)(xD/D!)=1+2x
Σ[B+D<2](xB/B!)(xD/D!)=1+2x
Σ[A+2C+D<2 かつ B+D<2](xA/A!)(xB/B!)(xC/C!)(xD/D!)=1+3x+x2
となるので、p(n,2)の指数型母関数は、
{e6x−e3x(1+2x)−e4x(1+2x)+e2x(1+3x+x2)}/6n
これを級数展開したときのxnの係数にn!を掛けたものがp(n,2)です。
p(n,2)
=(6n−(3n+2n・3n-1)−(4n+2n・4n-1)+(2n+3n・2n-1+n(n−1)・2n-2)/6n
=[6n+2n−3n−4n+n{(n+5)・2n-2−2・3n-1−2・4n-1}]/6n
これは、ぽっぽさんの結果:
[6n+2n−3n−4n+n{(n+5)・2n-2−2・3n-1−2・4n-1}]/6n
と一致する。
(コメント) at さんに感謝します。
FNさんより、新しい課題の提案です。(平成23年2月19日付け)
さいころを n 回投げて、その和が m の倍数になる確率を求めよ。
まず、m が6の約数であるとき、即ち、m=1、2、3、6 はごく簡単です。次に、m=7は
漸化式を使って確率を求めるタイプの問題の基本問題です。平成6年に京都大学で出題さ
れています。
京都大学 前期文系(1994)
さいころを n 回続けて投げるとき、k 回目に出る目の数を Xk とし、
Yn=X1+X2+・・・+Xn とする。Yn が7で割り切れる確率を pn とする。
(1) pn を pn-1 を用いて表せ。
(2) pn を求めよ。
(解)(1) Yn が7で割り切れるとき、Yn-1 は7で割り切れず、Yn が7で割り切れるように、
Xn=Yn − Yn-1 は一意に定まる。
よって、 pn =(1/6)(1− pn-1 ) である。
(2) p1 =0 で、 pn −1/7=(−1/6)( pn-1−1/7 ) より、
pn −1/7=(−1/6)n-1(−1/7 ) なので、
pn ={1−(−1/6)n-1}/7 (終)
m=1、2、3、6、7以外は、簡単にはできそうにありませんが、その中では、m=5
が一
番ましかなと思います。
(1) さいころを n 回投げて、その和が5の倍数になる確率を求めよ。
5次の正方行列の固有値、固有ベクトルを計算して求めることもできるようですが、そして
その方が理論的にはきれいですが手計算では難しそうです。そこまでしなくても、高校数学
の範囲内で、出来ます。
教科書には、「大小2個のさいころを投げるとき、目の和が5の倍数になる確率を求めよ。」
程度は載っています。具体的に数え上げてみたいと思います。
起こりうる全ての場合の数は、 6×6=36通り
目の和が5の倍数、すなわち、5または10 になる場合の数は、
(1,4)、(2,3)、(3,2)、(4,1)、(4,6)、(5,5)、(6,4)
の7通り。 よって、求める確率は、 7/36 となる。
同様に、「大中小3個のさいころを投げるとき、目の和が5の倍数になる確率を求めよ。」
の解は、
起こりうる全ての場合の数は、 6×6×6=216通り
目の和が5の倍数、すなわち、5または10または15 になる場合の数は、
(1,1,3)型・・・3通り 、(1,2,2)型・・・3通り 、(1,3,6)型・・・6通り
(1,4,5)型・・・6通り 、(2,2,6)型・・・3通り 、(2,3,5)型・・・6通り
(2,4,4)型・・・3通り 、(3,3,4)型・・・3通り 、(3,6,6)型・・・3通り
(4,5,6)型・・・6通り 、(5,5,5)型・・・1通り
の43通り。 よって、求める確率は、 43/216 となる。
同様に、「4個のさいころを投げるとき、目の和が5の倍数になる確率を求めよ。」の解は、
起こりうる全ての場合の数は、 6×6×6×6=1296通り
目の和が5の倍数、すなわち、5または10または15または20 になる場合の数は、
(1,1,1,2)型・・・4通り 、(1,1,2,6)型・・・12通り 、(1,1,3,5)型・・・12通り
(1,1,4,4)型・・・6通り 、(1,2,2,5)型・・・12通り 、(1,2,3,4)型・・・24通り
(1,3,3,3)型・・・4通り 、(2,2,2,4)型・・・4通り 、(2,2,3,3)型・・・6通り
(1,2,6,6)型・・・12通り 、(1,3,5,6)型・・・24通り 、(1,4,4,6)型・・・12通り
(1,4,5,5)型・・・12通り 、(2,2,5,6)型・・・12通り 、(2,3,4,6)型・・・24通り
(2,3,5,5)型・・・12通り 、(2,4,4,5)型・・・12通り 、(3,3,3,6)型・・・4通り
(3,3,4,5)型・・・12通り 、(3,4,4,4)型・・・4通り 、(2,6,6,6)型・・・4通り
(3,5,6,6)型・・・12通り 、(4,4,6,6)型・・・6通り 、(4,5,5,6)型・・・12通り
(5,5,5,5)型・・・1通り
の259通り。 よって、求める確率は、 259/1296 となる。
同様に、「5個のさいころを投げるとき、目の和が5の倍数になる確率を求めよ。」の解は、
起こりうる全ての場合の数は、 6×6×6×6×6=7776通り
目の和が5の倍数、すなわち、5、10、15、20、25、30 になる場合の数は、
(1,1,1,1,1)型・・・1通り 、(1,1,1,1,6)型・・・5通り 、(1,1,1,2,5)型・・・20通り
(1,1,1,3,4)型・・・20通り 、(1,1,2,2,4)型・・・30通り 、(1,1,2,3,3)型・・・30通り
(1,2,2,2,3)型・・・20通り 、(2,2,2,2,2)型・・・1通り 、(1,1,1,6,6)型・・・10通り
(1,1,2,5,6)型・・・60通り 、(1,1,3,4,6)型・・・60通り 、(1,1,3,5,5)型・・・30通り
(1,1,4,4,5)型・・・30通り 、(1,2,2,4,6)型・・・60通り 、(1,2,2,5,5)型・・・30通り
(1,2,3,3,6)型・・・60通り 、(1,2,3,4,5)型・・・120通り 、(1,2,4,4,4)型・・・20通り
(1,3,3,3,5)型・・・20通り 、(1,3,3,4,4)型・・・30通り 、(2,2,2,3,6)型・・・20通り
(2,2,2,4,5)型・・・20通り 、(2,2,3,3,5)型・・・30通り 、(2,2,3,4,4)型・・・30通り
(2,3,3,3,4)型・・・20通り 、(3,3,3,3,3)型・・・1通り 、(1,1,6,6,6)型・・・10通り
(1,2,5,6,6)型・・・60通り 、(1,3,4,6,6)型・・・60通り 、(1,3,5,5,6)型・・・60通り
(1,4,4,5,6)型・・・60通り 、(1,4,5,5,5)型・・・20通り 、(2,2,4,6,6)型・・・30通り
(2,2,5,5,6)型・・・30通り 、(2,3,3,6,6)型・・・30通り 、(2,3,4,5,6)型・・・120通り
(2,3,5,5,5)型・・・20通り 、(2,4,4,4,6)型・・・20通り 、(2,4,4,5,5)型・・・30通り
(3,3,3,5,6)型・・・20通り 、(3,3,4,4,6)型・・・30通り 、(3,3,4,5,5)型・・・30通り
(3,4,4,4,5)型・・・20通り 、(4,4,4,4,4)型・・・1通り 、(1,6,6,6,6)型・・・5通り
(2,5,6,6,6)型・・・20通り 、(3,4,6,6,6)型・・・20通り 、(3,5,5,6,6)型・・・30通り
(4,4,5,6,6)型・・・30通り 、(4,5,5,5,6)型・・・20通り 、(5,5,5,5,5)型・・・1通り
(6,6,6,6,6)型・・・1通り
の1556通り。 よって、求める確率は、 1556/7776=389/1944 となる。
FNさんの問いかけに対して、ぽっぽさんが考察されました。(平成23年2月19日付け)
理屈は分かりませんが、n が5の倍数ならば、 ((6n−1)/5+1)/6n
n が5の倍数でないならば、 (6n−1)/(5・6n)
ですね。正確には、今から考えてみます。
(コメント) 上記の n=2〜5 の計算から、上記の公式が納得されますネ。
FNさんからのコメントです。(平成23年2月19日付け)
ぽっぽさんの式を見て、意外と簡単にできそうだなと思いました。漸化式を作って真面目
に解くことを考えていたのですが、場合の数を数えるだけでできてしまいそうですね。
FNさんからの続報です。(平成23年2月20日付け)
場合の数を数えるという方針で行けば、それほど難しくないようで、大学入試に出せるレ
ベルのようです。それでも、7の倍数の場合よりは難しいし、7の倍数の場合でも一応誘導
がついていたので誘導をつけてみました。
さいころを n 回投げて、k回目(1≦k≦n)に出た目を、Xk、X1+X2+・・・+Xn をYとする。
(1) X1<6 で、Yが5の倍数である場合の数を求めよ。
(2) X1=X2=・・・=Xk-1=6、Xk<6 でYが5の倍数である場合の数を求めよ。
(結果だけでよい。)
(3) Yが5の倍数である確率を求めよ。
普通は、(2)はいらないと思いますが、付けてみました。これだけの誘導があれば大学入
試で出題可能と思います。ただ、場合の数という表現がちょっと気になります。確率にして
しまってもいいのですが、ちょっと違う感じです。
FNさんからの続報です。(平成23年2月21日付け)
1回目、2回目、・・・、n
回目と順に考えていく思考形態に合わせて、次の様な誘導にした
方がいいかもしれません。場合の数という言葉もやめて確率にしました。
さいころを n 回投げて、k回目(1≦k≦n)に出た目を、Xk とし、それらの和 ΣXk
をYとす
る。このとき、次の確率を求めよ。
(1) Xn<6 で、かつ、Yが5の倍数である確率
(2) Xk<6 で、Xk+1=Xk+2=・・・=Xn=6
で、かつ、Yが5の倍数である確率
ただし、1≦k≦n とする。
(3) Yが5の倍数である確率
この場合は、(2)が必要な感じです。(1)は前の(1)よりやさしくなったように思います。(2)は
前の(2)よりちょっと難しいかなという気がします。前の形なら、(1)ができれば、(2)は大概で
きるけど、(1)が易しくなって(2)が少し難しくなったので、(1)ができて(2)ができない人がかな
り出るでしょう。(1)(2)(3)で正解者がだんだん減っていくという意味で、このほうがよさそうで
す。
私自身は前の形で考えます。順序は関係ないから条件をつけるのは後ろからより前からに
したいからで、確率より場合の数で考えたいのははじめから分数が出てくるのはできれば避
けたいからです。
ぽっぽさんからの情報です。(平成23年2月21日付け)
HPサイト「さいころを
n
個投げたときの目の和の確率について」を見つけました。
FNさんからのコメントです。(平成23年2月21日付け)
気がついています。他にもあります。5の倍数や8の倍数についてもあります。
何れも、2005年ごろのものだと思います。
私は、基本的にはこのあたりで議論されているような行列の固有値や固有ベクトルを使う
方法かなと思っていたのですが、m=5のときのぽっぽさんの書かれた式を見て、素朴な方
法でも、m=5、4あたりはできるかもしれないと、今は思っています。とりあえず、しばらくは
行列は考えないで行ける所まで行きたいと考えています。m≧8
となると多分無理でしょう。
FNさんが次の問題
さいころを n 回投げて、k回目(1≦k≦n)に出た目を、Xk とし、それらの和 ΣXk
をYとす
る。このとき、次の確率を求めよ。
(1) Xn<6 で、かつ、Yが5の倍数である確率
(2) Xk<6 で、Xk+1=Xk+2=・・・=Xn=6
で、かつ、Yが5の倍数である確率
ただし、1≦k≦n とする。
(3) Yが5の倍数である確率
の解答を与えられました。(平成23年2月22日付け)
(解)(1) (1/6)n-1 が何であっても、これに
1、2、3、4、5
のうちのどれか1つ
を足せば、5の倍数になる。そしてそのような数は、1つしかない。
従って、Xn<6 で、かつ、Yが5の倍数である確率は、1/6
(2) Xk+1、Xk+2、・・・、Xn がすべて6になる確率は、(1/6)n-k
X1、X2、・・・、Xk-1 は何でもよい。Xkは、(1)と同様に考えて確率は、1/6
従って、求める確率は、 (1/6)n-k+1
(3) (2)の確率を、k=1からk=nまですべて加えると
(1/6)n+(1/6)n-1+・・・+(1/6)={1−(1/6)n}/5=(6n−1)/(5・6n)
Yが5の倍数であるケースで数えられてない可能性があるのは、
「X1、X2、・・・、Xn
がすべて6」
のケースだけで、これが5の倍数になるのは、n
が5の倍数のときである。
5の倍数のときだけ、1/6n を加えればよい。
以上から、
n
が5の倍数ならば、 ((6n−1)/5+1)/6n
n
が5の倍数でないならば、 (6n−1)/(5・6n)
となる。 (終)
(コメント) ぽっぽさんの与えられた公式がこれで合点がいきました。FNさんに感謝します。
また、FNさんによれば、次のような誘導も可能とのことです。解答は短くなるでしょう。難し
いか易しいかは何とも言えません。
さいころを n 回投げて、k回目(1≦k≦n)に出た目を、Xk とし、それらの和 ΣXk
をYとし、
(X1−1)+(X2−1)・6+・・・+(Xn−1)・6n-1
をZとする。
(1) Yを5で割った余りと
Z+n
を5で割った余りは等しいことを示せ。
(2) Yが5で割り切れる確率を求めよ。
FNさんの問いかけに対して、攻略法さんが解決されました。(平成23年2月22日付け)
(解)(1) mod 5 で
Z+n
≡(X1−1)+(X2−1)・6+・・・+(Xn−1)・6n-1+n
≡(X1−1)+(X2−1)・{(61−1)+1}+・・・+(Xn−1)・{(6n-1−1)+1}+n
≡(X1−1)+(X2−1)+・・・+(Xn−1)+n
≡X1+X2+・・・+Xn=Y
よって、Yを5で割った余りと
Z+n を5で割った余りは等しい。
(2) Zは6進法表記なので、範囲は、[0,6n−1]
となる。
(1)より、YとZ+nは同値になるので、求める確率は、
分子は、範囲 [n,n+6n−1]
で、5の倍数の数 [(n+6n−1)/5] -
[(n−1)/5]
分母は、6n ただし、[ ]はガウス記号。
FNさんからのコメントです。(平成23年2月22日付け)
(1) mod
5 を表に出すなら、6≡1 (mod 5)で、6を1に変えてしまってもいいかもしれ
ません。すなわち、mod 5 で
Z+n=(X1−1)+(X2−1)・6+・・・+(Xn−1)・6n-1+n
≡(X1−1)+(X2−1)+・・・+(Xn−1)+n
=X1+X2+・・・+Xn=Y
よって、Yを5で割った余りと
Z+n を5で割った余りは等しい。
(2) (1)より、Yが5で割り切れる ⇔ Z+( n を5で割った余り )
が5で割り切れる
また、Zは、[0,6n−1]の中にあるが、この両端の0と6n−1は5の倍数で、この中にある
5の倍数は(6n−1)/5+1個である。
Z+( n を5で割った余り
)は、この区間を、0、1、2、
3、4ずらすことになる。両端が5の倍数だから、1、2、3、4ずらした場合は1個減る。
従って、 n
が5の倍数のとき、(6n−1)/5+1個、それ以外のとき、(6n−1)/5個
確率は、これを、6nで割ればよい。
ほぼ自明なケース、m=1、2、3、6 も一応やっておきます。
m=1 のときは、明らかに、1
m=2 のときは、n−1回目までの和が何であっても、n回目は、3通りで、3/6=1/2
m=3 のときは、n−1回目までの和が何であっても、n回目は、2通りで、2/6=1/3
m=6 のときは、n−1回目までの和が何であっても、n回目は、1通りで、1/6
m=5 のとき(はじめの誘導のやり方)は、6を排除することで、m=6と同じ状況にしよう
としたということです。即ち、n回目が6であるケースを除けば、n−1回目までの和が何で
あっても、n回目は1通りで、1/6。n回目が6であるケースは別に考えようということです。
最初の誘導では、n回目、n−1回目、・・・
と書くより、1回目、2回目、・・・
と書く方が書きや
すいので、逆にしましたが...。ほぼ自明なケースの考え方を使っていると言えなくもありま
せん。
m=5 ができれば、m=1、2、3、5、6、7 ができたことになるので、次は、m=4です。
(2) さいころを n 回投げて、目の和が4の倍数になる確率を求めよ。
at さんが、次の問題
さいころを n 回投げて、その和が m
の倍数になる確率を求めよ。
を解かれました。(平成23年2月21日付け)
(解) m≧2 として考えます。さいころを
n 回投げて、その和が m の倍数になる確率を
p(n,m)とします。f(x)=(x+x2+x3+x4+x5+x6)n
とおきます。
さいころを n 回投げて、目の和が m
の倍数になるような目の出方は、f(x)を展開した
ときの、xkm
(kは整数) という形で表される項の係数の総和です。
この総和を
S(n,m)とすると、 p(n,m)=S(n,m)/6n
α=cos(2π/m)+i・sin(2π/m) ( i
は、虚数単位)とします。 αm=1 です。
また、m の倍数ではないような任意の正整数 k
に対して、
αk+(α2)k+(α3)k+・・・+(αm)k
=αk+(αk)2+(αk)3+・・・+(αk)m=0
よって、 S(n,m)={f(α)+f(α2)+f(α3)+・・・+f(αm)}/m より、
p(n,m)={f(α)+f(α2)+f(α3)+・・・+f(αm)}/(m・6n) (終)
いくつかの
m
の値に対するp(n,m)を計算してみよう。
p(n,4)=Σf(ij)/(4・6n)=1/4+2(n+2)/2・cos(3nπ/4))/(4・6n)
p(n,5)=Σf((cos(2π/5)+i・sin(2π/5))j)/(5・6n)
=1/5+2{cos(4nπ/5)+cos(2nπ/5)}/(5・6n)
p(n,10)=Σf((cos(2π/10)+i・sin(2π/10))j)/(10・6n)
=1/10+2{(5−2 )n/2cos(9nπ/10)
)n/2cos(9nπ/10)
+(5+2 )n/2cos(7nπ/10)+cos(2nπ/5)}/(10・6n)
)n/2cos(7nπ/10)+cos(2nπ/5)}/(10・6n)
FNさんからのコメントです。(平成23年2月21日付け)
一気にすべて解決ですね。私は行列の固有ベクトルを使って何とか最後の式にはたどり
着いてたのですが、詰めは甘く、きちんと書けばなかなか大変だろうと思っていました。
やっぱり母関数をちゃんと勉強しなければいけないようです。
ということで、この問題で残っているのは、「m=5、4の場合を素朴な方法で解く」だけとい
うことになります。
ぽっぽさんからのコメントです。(平成23年2月21日付け)
すごい複雑になるんですね。ただ、4や5など具体的な数を初等的に解くのは不可能じゃ
なさそうですね。(「算数にチャレンジ」等初等的な解法を追求するサイトによく行くのでどち
らかといえばこっちの方が得意そうです)
FNさんからのコメントです。(平成23年2月22日付け)
at
さんのあざやかな解答で終了していますが、他の人が苦労したあとを見るのも意味があ
ると思います。ぽっぽさんがあげていたページ以外にこの問題を扱っているページを上げて
おきます。他にもあると思いますが...。
http://www.riverplus.net/sci/2005/01/post_216.html
http://www.riverplus.net/sci/2005/02/post_232.html
http://www.riverplus.net/sci/2005/02/post_31.html
FNさんから問題の提起です。(平成23年2月22日付け)
m=4 の場合を誘導形式の問題にしました。m=5 に比べてかなり難しくなります。
さいころを n 回投げて、k回目(1≦k≦n)に出た目を、Xk とし、それらの和 ΣXk
をYとす
る。
(1) X1>2 で、Yが4の倍数である場合の数を求めよ。
(2) X1<3 、X2<3 、・・・、Xk-1<3 、Xk>2 で、Yが4の倍数である場合の数を求め
よ。
(3) すべてのk(1≦k≦n)について、Xk<3 で、Yが4の倍数である場合の数を求めよ。
(4) Yが4の倍数である確率を求めよ。
計算がかなり増えるので、m=5
のときの誘導のはじめの形にしました。(1)(2)(4)は、
m=5
のときの(1)(2)(3)と同じです。計算は多少多いですが...。違いは(3)です。
m=5
のときは、これはすべて6の場合だったので問題ありませんでした。しかし、(3)は
結構面倒です。
一般の場合を、さらに一般化すると次の形になります。
{1,2,・・・,k}から1個を取り出す操作を n 回行ったとき、その和が m
の倍数に
なる確率を求めよ。
k=6の場合がさいころの問題です。(3)は、k=2、m=4のケースです。
k=6、m=4の問題が、k=2、m=4の問題を部分問題として含んでいるということです。
もちろん、k=2、m=4が、k=6、m=4より簡単なのは間違いないですがかなり面倒です。
しかし、こんなやり方より、at
さんのやり方のほうが当然いいです。at
さんのあざやかな解
答を自分のものにする、即ち、別の問題を解くのに使える可能性があるようにするためには、
m=4の場合の解答を自分で書いてみるのがいいと思います。この場合は、atさんのαが
虚数単位 i になりますから、考えやすいです。残務処理( i とかをなくす)もきちんとしたほうが
いいです。
攻略法さんからのコメントです。(平成23年2月22日付け)
HPサイト「http://www.riverplus.net/sci/2005/02/post_31.html」からの引用です。
一般の場合、結果は、固有値の n 乗の和を、k で割ったものになっている。
さいころを n
個投げたときの、目の和が k の倍数になる確率 a(k,n) は、確率の
遷移を x(n) = A *
x(n−1) のように表現したときの、確率行列Aの固有値
λ0、・・・、λk を使って、 a(k,n)
= (1/k)・( λ0n+・・・+λkn
) と書ける。
(引用終)
at
さんの式 : p(n,m)={f(α)+f(α2)+f(α3)+・・・+f(αm)}/(m・6n) は、
(λj)n=f(αj)/6n
としたもののようです。私にとって、一連の簡潔した式の導出は、どちらも難しい問題です。
FNさんからのコメントです。(平成23年2月23日付け)
そういうことになりますね。私はもっぱら固有値、固有ベクトルで考えていました。atさんの
やり方がはるかにいいです。
さて、目の和とは直接関係がない練習問題です。
正方形の頂点上を動く点Pがある。さいころを投げて、出た目によって定められただけ一
定方向に動く。この操作を
n
回行ったとき、点Pがもとの位置にある確率を、次のそれぞれ
の場合で求めよ。
(1) 1か2なら1、3か4なら2、5か6なら3
(2) 1か2なら1、3か4なら2、5か6なら0
(3) 1なら1、2か3なら2、4か5か6なら0
(4) 1なら1、2なら3、3か4か5か6なら0
FNさんからのコメントです。(平成23年2月24日付け)
at さんのやり方でやればできます。ただし、一般には複素数のn乗を計算しなければなり
ませんから、面倒になる可能性があります。上記では、(3)以外は簡単です。
at さんのやり方を使わないとした場合ですが、(1)は簡単な漸化式になります。(2)はがん
ばればなんとかなりそうです。(3)(4)はやや苦しいかなと思います。(4)は、2006年に誘導
付きで京都府立大で出題されているようです。誘導なしでは難しいように思います。
(4)を、at さんのやり方で解いておきます。
(解) f(x)=(4+x+x3)n とおく。これを展開したときの、xk の係数が、n回目までで k だ
け動いた場合の数である。従ってこれらの係数のうちで、k が4の倍数であるものすべ
ての和を求めて、それを、6nで割ればよい。
f(x)を、xの4の倍数乗の形の項の和Sと、それ以外の項の和Tの和とする。
1k+ik+(−1)k+(−i)k を考えると、
(*1) kが4の倍数のときは、4
(*2) kが4の倍数でないときは、0である。 (k=1、2、3だけ確認すればよい)
f(x)に、x=1、i、−1、−i を代入して、それらを加える。
即ち、f(1)+f(i)+f(−1)+f(−i) を考えると、Tの部分については、(*2)より0になる。
Sの部分については、(*1)より、すべての係数の和の4倍になる。
従って、{f(1)+f(i)+f(−1)+f(−i)}/4が、n回目に元の位置に戻る場合の数である。
f(1)=6n 、f(−1)=2n 、f(i)=4n 、f(−i)=4n なので、求める確率は
(6n+2・4n+2n)/(4・6n)=1/4+(2/3)n/2+(1/3)n/4 (終)
攻略法さんが、(3)の解を示されました。(平成23年2月25日付け)
(解) f(x)=(3+x+2x2)n より、
f(1)=6n 、f(−1)=4n 、f(i)=(1+i)n 、f(−i)=(1+i)n である。
このとき、 nC0−nC2+nC4−nC6+・・・={(1+i)n+(1+i)n}/2
数値計算にて、
n=4k、4k+1 の場合 (−4)[n/4] ただし、[ ]はガウス記号
n=4k+2 の場合 0
n=4k+3 の場合 −2・(−4)[n/4]
したがって、求める確率は、
n=4k、4k+1 の場合 {4n+6n+2・(−4)[n/4]}/(4・6n)
n=4k+2 の場合 (4n+6n)/(4・6n)
n=4k+3 の場合 {4n+6n−4・(−4)[n/4]}/(4・6n) (終)
さらに、攻略法さんは、漸化式を利用して(1)の解を示されました。
(平成23年2月26日付け)
(解) 頂点を順に、A、B、C、Dとする。Pは、最初Dにあるとする。Pが頂点A、B、C、Dに
いる「場合の数」は、遷移表で表すと、
| |
| |
次A |
B |
C |
D |
| 今A |
− |
{1,2} |
{3,4} |
{5,6} |
| B |
{5,6} |
− |
{1,2} |
{3,4} |
| C |
{3,4} |
{5,6} |
− |
{1,2} |
| D |
{1,2} |
{3,4} |
{5,6} |
− |
|
※ { }内は出た目を表す。
{1,2}は、1または2の意 |
確率 p は、
| |
| |
次A |
B |
C |
D |
| 今A |
0 |
1/3 |
1/3 |
1/3 |
| B |
1/3 |
0 |
1/3 |
1/3 |
| C |
1/3 |
1/3 |
0 |
1/3 |
| D |
1/3 |
1/3 |
1/3 |
0 |
|
Pが頂点A、B、C、Dにいる確率を、それぞれ an、bn、cn、dn とすると
an=(bn-1+cn-1+dn-1)/3 ・・・ 式1
bn=(an-1+cn-1+dn-1)/3 ・・・ 式2
cn=(an-1+bn-1+dn-1)/3 ・・・ 式3
dn=(an-1+bn-1+cn-1)/3 ・・・ 式4
辺々を加えて、 an+bn+cn+dn=an-1+bn-1+cn-1+dn-1
これから、 an+bn+cn+dn=a0+b0+c0+d0=0+0+0+1=1
式4 dn=(an-1+bn-1+cn-1)/3 より、 dn=(1−dn-1)/3
よって、 dn−1/4=(−1/3)(dn-1−1/4) 、d0−1/4=3/4 から
dn=(3/4)(−1/3)n+1/4 (終)
FNさんからのコメントです。(平成23年2月26日付け)
(1)はサイコロの問題で、m=7の場合に相当します。同じ状態には移れないが、その他
の状態には等確率で移るという場合、即ち、遷移確率行列が主対角線上が0で他がすべて
等しい場合です。この場合は、pnが1−pn-1の定数倍だから簡単な漸化式になります。
また、dn=(1−dn-1)/3 はすぐに出るので、an、bn等は必要ないかも...。
(2)は(1)のようには簡単ではないですが、遷移確率行列の4乗が主対角線上が一定値
で、他も別の一定値になるので、pn+4がpnの1次式になります。従ってできるはずです。
あるいは、an、bn、cn、dnのうちの3つが等しくなると言ってもいいです。今年の広島大
学の理系の5番は、正方形ではなくて三角形でもっと簡単ですが、似たような状況です。
攻略法さんが、次の問題
{1,2,・・・,k}から1個を取り出す操作を n 回行ったとき、その和が m
の倍数に
なる確率を求めよ。
を、Excel
VBAの数値計算で求められました。(平成23年2月23日付け)
at
さんの式を使っています。固有値、固有ベクトルの算出がないので楽です。
K=6,
m=5
1 : 0.999999999999998 / 6
2 : 6.99999999999999 / 36
3 : 43 /
216
4 : 259 / 1296
5 : 389 / 1944
6 : 9331 / 46656
7 : 55987 /
279936
8 : 335923 / 1679616
9 : 2015539 / 10077696
10 : 3023309 /
15116544
Sub
Test()
'-----------------
'問題
'{1,2,3,,…,k}から1個を取り出す操作をn回行ったとき、その和がmの倍数になる確率を求めよ。
Let
m = 4 'mの倍数
Let K = 6 '{1,2,3,4,5,6}から1個を取り出す操作をn回行う
Dim C(20)
'x^kの係数
For j = 1 To K
C(j) = 1
Next
j
'-----------------
'問題
'正方形の頂点上を動く点Pがある。さいころを投げて出た目によって定められた
'だけ一定方向に動く。この操作をn回行ったとき点Pがもとの位置にある確率を
'次のそれぞれの場合で求めよ。
'(1)1か2なら1、3か4なら2、5か6なら3
'(2)1か2なら1、3か4なら2、5か6なら0
'(3)1なら1、2か3なら2、4か5か6なら0
'(4)1なら1、2なら3、3か4か5か6なら0
''Let
m = 4 'mの倍数
''Dim C(20) 'x^kの係数
''K = 3: C(1) = 1: C(2) = 1: C(3) = 1
'x+x^2+x^3
''K = 4: C(1) = 1: C(2) = 1: C(3) = 0: C(4) = 1 'x+x^2+x^4
''K
= 4: C(1) = 1: C(2) = 2: C(3) = 0: C(4) = 3 'x+2x^2+3x^4
''K = 4: C(1) = 1:
C(2) = 0: C(3) = 1: C(4) = 4 'x+x^3+4x^4
'-----------------
CC = 0
'係数の和
For j = 1 To K
CC = CC + C(j)
Next j
Pi =
3.14159265358979
Let th = 2 * Pi / m 'θ
For n = 1 To 10
'n回
Let ReT = 0 'Σ[j=1,m]{f(α^j)}
Let ImT = 0
For j = 1 To m
'α = cosθ + i * sinθのとき、
'ド・モアブルの定理より、α^n = (cosθ + i * sinθ)^n = cos(nθ) +
i * sin(nθ) となる。
Let ReAj = Cos(j * th) 'α^j
Let ImAj = Sin(j * th)
Call FNC(ReAj, ImAj, C, K, n, ReFN, ImFN) 'f(α^j)の算出
Let ReT = ReT + ReFN 'Σf(α^j)の算出
Let ImT = ImT + ImFN
'''Debug.Print j; "("; ReAj; ImAj; ") ("; ReFN
/ K ^ n; ImFN / CC ^ n; ")" 'debug"
Next
j
'''Debug.Print n; ": ("; ReT / m; ImT / m; ")"; CC
^ n 'p(n,m)=Σ[j=1,m]{f(α^j)}/(m*CC^n)
w = GCD(ReT / m, CC ^ n)
Debug.Print n; ":"; ReT / m / w; "/"; CC ^ n / w
'p(n,m)=Σ[j=1,m]{f(α^j)}/(m*CC^n)
Next
n
End Sub
'母関数
f(x)=(C[1]x+C[2]x^2+C[3]x^3+C[4]x^4+C[5]x^5+C[6]x^6+ … +C[k]x^k)^n
Sub
FNC(ByVal ReX, ByVal ImX, ByRef C(), ByVal K, ByVal n, ByRef ReFN, ByRef
ImFN)
'x(C[1]+x(C[2]+x(C[3]+x(C[4]+x( … )))))
Let ReT = C(K) *
ReX
Let ImT = C(K) * ImX
For i = 1 To K - 1
Let w = C(K - i) + ReT '(1+x)
Let u = ImT
Let ReT = ReX * w - ImX * u 'x(1+x)
Let ImT = ReX * u + ImX * w
Next i
'べき乗 z=(x+y*i)^n →
X+Y*i
' z^n=r^n*(COS(n*θ)+i*SIN(n*θ))、r=SQR(x*x+y*y), θ=ARG(x,y)
Let r =
Sqr(ReT * ReT + ImT * ImT)
Let th = ANGLE(ReT, ImT)
Let t = r ^ n
Let
ReFN = t * Cos(n * th) 'X
Let ImFN = t * Sin(n * th) 'Y
End
Sub
Function ANGLE(ByVal x, ByVal y) '偏角θ (-π,π]
Pi =
3.14159265358979
If x > 0 Then '第1象限、第4象限
Let r = Atn(y / x)
Else
If x < 0 Then
If y >= 0 Then '第2象限
Let r = Atn(y / x) + Pi
Else '第3象限
Let r = Atn(y / x) - Pi
End If
Else 'x = 0
If y > 0 Then '∞
Let r = Pi / 2
Else
If y < 0 Then '-∞
Let r = -Pi / 2
Else 'y = 0
Debug.Print "ARG関数は不定です。"
Stop
End If
End If
End If
End If
Let ANGLE = r
End Function
Function GCD(a,
b) '最大公約数
Do Until b = 0
Let t = b
Let b = a Mod b
Let a = t
Loop
Let GCD = a
End Function
京都大学で次のような問題が出題されている。
京都大学 前期理系(2000)
n、k は整数で、n≧2、0≦k≦4 とする。サイコロを n 回投げて出た目の和を5で
割ったときの余りがk に等しくなる確率を pn(k)とする。
(1) pn+1(0)、・・・、pn+1(4)をpn(0)、・・・、pn(4)を用いて表せ。
(2) pn(0)、・・・、pn(4)の最大値をMn、最小値をmnとするとき、次の(イ)(ロ)が
成立することを示せ。
(イ) mn≦1/5≦Mn
(ロ) 任意の
k、l
(0≦k、l≦4)に対し pn+1(k)−pn+1(l)≦(Mn−mn)/6
(3) n→∞ のとき、lim
pn(k) を求めよ。
京都大学は、どうもこの手の問題がお好きらしい。
(追記) 「ものは考えよう」と題して、当HPがいつもお世話になっているHN「GAI」さんからの
投稿です。(平成26年8月24日付け)
3個のサイコロを投げて出た3つの目の積が6の倍数である確率を求めるのをどう考えま
すか?あなたが考える方法を知らせて下さい。また、この確率が0.9(9割)を越えるために
は何個のサイコロを投げればよいか?
DD++さんからのコメントです。(平成26年8月24日付け)
n個のサイコロの出目は独立で、また1つのサイコロについて偶数が出る事象と3の倍数が
出る事象は独立です。
積が6の倍数になるには、少なくとも1つ偶数かつ少なくとも1つ3の倍数であればよく、その
確率は、
(1-(1/2)n)(1-(2/3)n)
サイコロ3つのときには、 7/8 × 19/27 = 133/216
0.9 を超えるには、順に代入して、n≧7
当HPがいつもお世話になっているHN「at」さんから類題を頂きました。
(平成26年8月25日付け)
nを正の整数とします。n個のサイコロを振って、それらの出目の積が立方数となる確率を
P(n) とします。
例 P(1)=1/6 、P(2)=1/12 、P(3)=1/18
P(n)を、nの式で表すとどうなるかを考えてみてください。
(コメント) 出る目の積 P は、 P=2a・3b・5c ( a、b、c は、0以上の整数) と書くこと
ができる。
n 個のうち、5の目は c 個出る。いま、6の目が s 個、4の目が t 個出るとすると、
3の目は、b−s 個、 2の目は、a−s−2t 個、 1の目は、n+s+t−a−b−c 個
出る。ところで、
n=1のとき、立方数は1のみなので、目の数は1。よって、確率は、P(1)=1/6
n=2のとき、 1〜36の中で起こりうる立方数は、1、8なので、
1→(1,1) 8→(2,4)、(4,2)
よって、確率は、P(2)=3/36=1/12
n=3のとき、1〜216の中で起こりうる立方数は、1、8、27、64、125、216なので、
1→(1,1,1)
8→(1,2,4)、(1,4,2)、(2,1,4)、(4,1,2)、(2,4,1)、(4,2,1)、(2,2,2)
27→(3,3,3)
64→(4,4,4)
125→(5,5,5)
216→(6,6,6)
よって、確率は、P(3)=12/216=1/18
GAI さんが考察されました。(平成26年8月26日付け)
例の続きをすごく原始的に調べてみました。
n=4のとき、4つのサイコロの数の組合せが
1;1;1;1 1;1;2;4 1;2;2;2 1;3;3;3 1;4;4;4 1;5;5;5 1;6;6;6 2;2;4;4 2;3;6;6 3;3;4;6
の10パターンで、この順列を考えて、63通り。 よって、確率P(4)=63/6^4=7/144
n=5のとき、同様に、
1;1;1;1;1 1;1;1;2;4 1;1;2;2;2 1;1;3;3;3 1;1;4;4;4 1;1;5;5;5 1;1;6;6;6 1;2;2;4;4
1;2;3;6;6 1;3;3;4;6 2;2;2;2;4 2;2;3;3;6 2;3;3;3;4 2;4;4;4;4 2;4;5;5;5 2;4;6;6;6
3;4;4;6;6 17パターン
これを元に、351通りなので、確率P(5)=351/6^5=13/288
n=6のとき、
1;1;1;1;1;1 1;1;1;1;2;4 1;1;1;2;2;2 1;1;1;3;3;3 1;1;1;4;4;4 1;1;1;5;5;5 1;1;1;6;6;6
1;1;2;2;4;4 1;1;2;3;6;6 1;1;3;3;4;6 1;2;2;2;2;4 1;2;2;3;3;6 1;2;3;3;3;4 1;2;4;4;4;4
1;2;4;5;5;5 1;2;4;6;6;6 1;3;4;4;6;6 2;2;2;2;2;2 2;2;2;3;3;3 2;2;2;4;4;4 2;2;2;5;5;5
2;2;2;6;6;6 2;2;3;4;6;6 2;3;3;4;4;6 3;3;3;3;3;3 3;3;3;4;4;4 3;3;3;5;5;5 3;3;3;6;6;6
4;4;4;4;4;4 4;4;4;5;5;5 4;4;4;6;6;6 5;5;5;5;5;5 5;5;5;6;6;6 6;6;6;6;6;6
の34パターンで、これを元に1926通り。 よって、確率P(6)=1926/6^6=107/2592
n=7のとき、
1;1;1;1;1;1;1 1;1;1;1;1;2;4 1;1;1;1;2;2;2 1;1;1;1;3;3;3 1;1;1;1;4;4;4 1;1;1;1;5;5;5
1;1;1;1;6;6;6 1;1;1;2;2;4;4 1;1;1;2;3;6;6 1;1;1;3;3;4;6 1;1;2;2;2;2;4 1;1;2;2;3;3;6
1;1;2;3;3;3;4 1;1;2;4;4;4;4 1;1;2;4;5;5;5 1;1;2;4;6;6;6 1;1;3;4;4;6;6 1;2;2;2;2;2;2
1;2;2;2;3;3;3 1;2;2;2;4;4;4 1;2;2;2;5;5;5 1;2;2;2;6;6;6 1;2;2;3;4;6;6 1;2;3;3;4;4;6
1;3;3;3;3;3;3 1;3;3;3;4;4;4 1;3;3;3;5;5;5 1;3;3;3;6;6;6 1;4;4;4;4;4;4 1;4;4;4;5;5;5
1;4;4;4;6;6;6 1;5;5;5;5;5;5 1;5;5;5;6;6;6 1;6;6;6;6;6;6 2;2;2;2;2;4;4 2;2;2;2;3;6;6
2;2;2;3;3;4;6 2;2;3;3;3;4;4 2;2;4;4;4;4;4 2;2;4;4;5;5;5 2;2;4;4;6;6;6 2;3;3;3;3;6;6
2;3;4;4;4;6;6 2;3;5;5;5;6;6 2;3;6;6;6;6;6 3;3;3;3;3;4;6 3;3;4;4;4;4;6 3;3;4;5;5;5;6
3;3;4;6;6;6;6 49パターン
これを元に、10809通りなので、確率P(7)=10809/6^7=1201/31104
これ以上になると、自分が書いているプログラムがむちゃ長くなるので諦めました。でも、
これから一般式P(n)を作り出すのが難しかったです。1の目が出るときと、出ないときに分け
て考えるのがコツのような気がします。
GAI さんからのコメントです。(平成26年8月27日付け)
このページの冒頭を読んで、ピンと思ったのでやってみました。
P=1+x+x2+y+xy+z とおく。(← FNさんの、このアイデアが面白い!)
(サイコロの目の素因数 2→x、3→y、5→z に対応させたもの)
すると、
P2=1 + 2 x + 3 x^2 + 2 x^3 + x^4 + 2 y + 4 x y + 4 x^2 y + 2 x^3 y + y^2 + 2 x y^2 + x^2 y^2
+ 2 z + 2 x z + 2 x^2 z + 2 y z + 2 x y z + z^2
P3=1 + 3 x + 6 x^2 + 7 x^3 + 6 x^4 + 3 x^5 + x^6 + 3 y + 9 x y + 15 x^2 y
+ 15 x^3 y
+ 9 x^4 y + 3 x^5 y + 3 y^2 + 9 x y^2 + 12 x^2 y^2 + 9 x^3 y^2 + 3 x^4
y^2 + y^3
+ 3 x y^3 + 3 x^2 y^3 + x^3 y^3 + 3 z + 6 x z + 9 x^2 z + 6 x^3 z + 3 x^4 z + 6 y z
+ 12 x y z + 12 x^2 y z + 6 x^3 y z + 3 y^2 z + 6 x y^2 z + 3 x^2 y^2
z + 3 z^2 + 3 x z^2
+ 3 x^2 z^2 + 3 y z^2 + 3 x y z^2 + z^3
P4=1 + 4 x + 10 x^2 + 16 x^3 + 19 x^4 + 16 x^5 + 10 x^6 + 4 x^7 + x^8 + 4
y + 16 x y
+ 36 x^2 y + 52 x^3 y + 52 x^4 y + 36 x^5 y + 16 x^6 y + 4 x^7 y + 6 y^2 + 24 x y^2
+ 48 x^2 y^2 + 60 x^3 y^2 + 48 x^4 y^2 + 24 x^5 y^2 + 6 x^6 y^2 + 4
y^3 + 16 x y^3
+ 28 x^2 y^3 + 28 x^3 y^3 + 16 x^4 y^3 + 4 x^5 y^3 + y^4 + 4 x y^4 +
6 x^2 y^4
+ 4 x^3 y^4 + x^4 y^4 + 4 z + 12 x z + 24 x^2 z + 28 x^3 z + 24 x^4 z + 12 x^5 z
+ 4 x^6 z + 12 y z + 36 x y z + 60 x^2 y z + 60 x^3 y z + 36 x^4 y z
+ 12 x^5 y z
+ 12 y^2 z + 36 x y^2 z + 48 x^2 y^2 z + 36 x^3 y^2 z + 12 x^4 y^2 z
+ 4 y^3 z
+ 12 x y^3 z + 12 x^2 y^3 z + 4 x^3 y^3 z + 6 z^2 + 12 x z^2 + 18 x^2 z^2 + 12 x^3 z^2
+ 6 x^4 z^2 + 12 y z^2 + 24 x y z^2 + 24 x^2 y z^2 + 12 x^3 y z^2 +
6 y^2 z^2
+ 12 x y^2 z^2 + 6 x^2 y^2 z^2 + 4 z^3 + 4 x z^3 + 4 x^2 z^3 + 4 y z^3
+ 4 x y z^3 + z^4
を利用すれば、例えば、4個のサイコロを投げて、その目の積が立方数をもたらすのは、P4
での候補の項の係数
1→1 、x^3→16 、x^6→10 、y^3→4 、x^3y^3→28 、z^3→4
を合計することで、1+16+10+4+28+4=63(通り)を得て、これから確率P(4)=63/6^4=7/144
とできることになるんですね!私の拙いプログラムであえなくn=7でストップしていたことも、上
記の機械的展開での特定の項の係数を拾い集めればいいわけで、やってみました。
n=8のとき、
1→1 、x^3→112 、x^6→784 、x^9→1016 、x^12→266 、x^15→8 、y^3→56 、x^3y^3→5096
x^6y^3→20328 、x^9y^3→10360 、x^12y^3→448 、y^6→28 、x^3y^6→1960 、x^6y^6→3164
x^9y^6→224 、z^3→56 、x^3z^3→1680 、x^6z^3→2520 、x^9z^3→280 、y^3z^3→560
x^3y^3z^3→10080 、x^6y^3z^3→2800 、z^6→28 、x^3z^6→56
の係数の合計から、61911(通り)を得て、これから確率P(8)=61911/6^8=2293/62208
しかし、これを出すのに目が痛くなった。これ以上やると体によくない。
(これらの作業を自動でやらせるプログラムが作れないのが情けない。)
でも、原理は掴めたと思う。あとは、数式的に表現してやれば一般式ができそうだ。でも私は
できない。どなたかお助けを!
at さんからのコメントです。(平成26年8月27日付け)
なるほど。FNさんのアイデアは強力な方法ですね。このようなアイデアは私には全くありま
せんでした。素晴らしい着想だと思います。
GAIさんの方法を使えば、P(n)は簡単に計算できてしまいますね。
n個のサイコロを振ったとき、出目の積が立方数になるような場合の数は、
(1+x+x^2+y+x*y+z)^n を展開したときの、x^(3a)*y^(3b)*z^(3c) (a,b,cは0以上の整数)
という形にかける項の係数をすべて足し合わせたものになります。
したがって、1 の立方根 ω=(-1+ ・i)/2 とすれば、P(n)は次のように書けます。
・i)/2 とすれば、P(n)は次のように書けます。
P(n)=(1/(27・6n))Σa=0〜2Σb=0〜2Σc=0〜2 (1+ωa+ω2a+ωb+ωa+b+ωc)n
これを計算すると、
P(n)=1/(27・6n)*((-3/2- i/2)n+(-3/2+
i/2)n+(-3/2+ i/2)n+(
i/2)n+( i)n+(3/2+
i)n+(3/2+ i/2)n+(-
i/2)n+(- i)n
i)n
+(3/2- i/2)n+(-
i/2)n+(- i)n+(3/2-
i)n+(3/2- i/2)n+(-3/2-
i/2)n+(-3/2- i/2)n+(-3/2+
i/2)n+(-3/2+ i/2)n+(3/2-
i/2)n+(3/2- i/2)n
i/2)n
+( i)n+2(3/2+
i)n+2(3/2+ i/2)n+(9/2-
i/2)n+(9/2- i/2)n+(3-
i/2)n+(3- i)n+(3/2-3
i)n+(3/2-3 i/2)n+(9/2+
i/2)n+(9/2+ i/2)n
i/2)n
+(3+ i)n+(3/2+3
i)n+(3/2+3 i/2)n+6n)
i/2)n+6n)
私の用意していた解法も母関数を使ったものですが、上記のような明快なものではなく、場
合わけが多く面倒なものでした。
n個のサイコロを振ったとき、出目の積が平方数になるような確率をQ(n)とすると、Q(n)も
P(n)を計算したときと同じ手法で計算できます。
Q(n)=(1/(8・6n))Σa=0〜1Σb=0〜1Σc=0〜1 (1+(-1)a+(-1)2a+(-1)b+(-1)a+b+(-1)c)n
=(1/(8・6n))(6n+4n+3・2n)
=(1+(2/3)n+(1/3)n-1)/8
GAI さんからのコメントです。(平成26年8月28日付け)
これがP(n)の一般式なんですね。(これをあれこれ探していたことがとんでもないことだと
認識しました。)このとんでもない式を利用させてもらい、n=1〜52(個)<トランプにこだ
わっている>での計算をしてみました。
P(1)=1/6、P(2)=0.08333333333333333333333333333、・・(詳細)・・、
P(50)=0.03703693325029630693907580920
P(51)=0.03703696042058939792045299878
P(52)=0.03703698265464195428840635563
サイコロの個数が増えても数値が余り変化せず、むしろ一定値に近づく様子です。でも、こ
れらの数値も、すべて有理数で表せるんですよね。ここは数学ソフトを使い(Mathematica で
のRationalizeコマンド<小数30位まで合わせる設定で>)P(8)以降をズルしてみました。
P(2)= 1/12、P(3)= 1/18、P(4)= 7/144、P(5)= 13/288、・・(詳細)・・、
P(50)= 25072010110766/676946169957671
P(51)= 130479912791332/3522964933126539
P(52)= 5046521554881/136256282050247
いやはや、atさんの出される問題は面白いです。
らすかるさんからのコメントです。(平成26年8月28日付け)
個数が多いとき、2、3、5 のそれぞれの素因数が、0、1、2 個である確率が1/3ずつに近く
なりますので、1/3^3=1/27に近づきます。平方数のときに、1/2^3=1/8に近づくのと同じです
ね。同様に、四乗数なら1/4^3=1/64、五乗数なら1/5^3=1/125に近づくはずです。
GAI さんからのコメントです。(平成26年8月28日付け)
確率P(n)を無理矢理に分数表現に切り替えてみたが、P(n)・6n が整数になる範囲をみて
みましたら、n=25 までが限界のようです。以下、n=2〜25での目の出方の総数に対応か?
3, 12, 63, 351, 1926, 10809, 61911, 362556, 2148363, 12809259,76737942,
461631717,
2785178763, 16827294132, 101680219431, 614036162727, 3704593001670, 22327489473633,
134435477754063, 808746510141036, 4861795845310803, 29209839973829523,
175415198236126038, 1053077368212478701
らすかるさんからのコメントです。(平成26年8月28日付け)
n=1〜50で、分子(立方数の個数)は以下のようになりますね。
1, 3, 12, 63, 351, 1926, 10809, 61911, 362556, 2148363, 12809259, 76737942, 461631717,
2785178763, 16827294132, 101680219431, 614036162727, 3704593001670, 22327489473633,
134435477754063, 808746510141036, 4861795845310803, 29209839973829523,
175415198236126038, 1053077368212478701, 6320464029090163683, 37928479307063294052,
227580132429801824463, 1365444419502637066671, 8192144309770364975046,
49148928249628700733129, 294869092645093345531911, 1769076944125749004450716,
10613737170486756945199323, 63678792533289991988275899, 382055295901106398286387862,
2292250885026034816892779317, 13753143951176715082646845563, 82517310192286599258617930772,
495097468057524608983357225911, 2970559894068548514210522013047,
17823269389655968438194069777990,106939329759883439410998578206833,
641635288811574869099080632755583,3849811543248565861913065815643596,
23098882037604373084181245245854883,138593411211043722459584862789620643,
831561269796849491311462736227739478, 4989372342871482628584989007756679101,
29936259720926695092276782529857658963
以下、工事中
